Abstract
In this work, we focus on collision attacks against instances of SHA-3 hash family in both classical and quantum settings. Since the 5-round collision attacks on SHA3-256 and other variants proposed by Guo et al. at JoC 2020, no other essential progress has been published. With a thorough investigation, we identify that the challenges of extending such collision attacks on SHA-3 to more rounds lie in the inefficiency of differential trail search. To overcome this obstacle, we develop a SAT-based automatic search toolkit. The tool is used in multiple intermediate steps of the collision attacks and exhibits surprisingly high efficiency in differential trail search and other optimization problems encountered in the process. As a result, we present the first 6-round classical collision attack on SHAKE128 with time complexity \(2^{123.5}\), which also forms a quantum collision attack with quantum time  , and the first 6-round quantum collision attack on SHA3-224 and SHA3-256 with quantum time
, and the first 6-round quantum collision attack on SHA3-224 and SHA3-256 with quantum time  and
and  , where S represents the hardware resources of the quantum computer. The fact that classical collision attacks do not apply to 6-round SHA3-224 and SHA3-256 shows the higher coverage of quantum collision attacks, which is consistent with that on SHA-2 observed by Hosoyamada and Sasaki at CRYPTO 2021.
, where S represents the hardware resources of the quantum computer. The fact that classical collision attacks do not apply to 6-round SHA3-224 and SHA3-256 shows the higher coverage of quantum collision attacks, which is consistent with that on SHA-2 observed by Hosoyamada and Sasaki at CRYPTO 2021.
More details are available in the full version of this paper: https://ia.cr/2022/184.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The Keccak hash function [BDPVA13], designed by Bertoni et al. in 2008, was standardized as the Secure Hash Algorithm-3 (SHA-3) [Dwo15] in 2015 by the National Institute of Standards and Technology (NIST) of the U.S. The SHA-3 family has four instances with fixed digest lengths, namely, SHA3-224, SHA3-256, SHA3-384 and SHA3-512, and two eXtendable-Output Functions (XOFs) SHAKE128 and SHAKE256. Being one of the most important cryptographic hash functions, SHA-3 (Keccak) has received intensive security analysis. The most relevant security criteria for cryptographic hash functions include preimage resistance and collision resistance. Preimage attacks of SHA-3 were investigated in [NRM11, MPS13, GLS16, LSLW17, LS19, Raj19, LHY21, HLY21]. The best-known practical attacks reach 3 rounds of SHAKE128 and SHA3-224 [GLS16, LS19]Footnote 1 while the best-known theoretical ones can reach 4 rounds of all its instances [MPS13, Raj19, HLY21]. With marginal time complexity gains over bruteforce, theoretical preimage attacks cover up to 7/8/9 rounds for Keccak-224/256/512, respectively [CKMS14, Ber10, MPS13].
More relevant to this research are the collision attacks on SHA-3 (Keccak) with reduced number of rounds. In [DDS12, DDS14], Dinur et al. presented practical collision attacks on 4 rounds of Keccak-224 and Keccak-256. The actual collisions were found by combining a 3-round differential trail and a 1-round connector (which connects the differential trail to valid initial values). The same authors also presented practical collision attacks on 3-round Keccak-384/Keccak-512, and theoretical collision attacks on 5/4-round Keccak-256/Keccak-384 using internal differentials [DDS13]. Following the framework proposed by Dinur et al. in [DDS12], Qiao et al. introduced 2-round connectors by prepending a fully linearized round to the 1-round connectors and obtained actual collisions for 5-round SHAKE128 [QSLG17]. Further, these connectors were improved in [SLG17, GLL+20] to consume fewer degrees of freedom by using partial linearization. Consequently, 3-round connectors became possible and practical collision attacks on 5-round SHA3-224 and SHA3-256 were obtained.
Collision Attack in Quantum Settings. In the previous works, collision attacks of SHA-3 were studied only in classical settings. Recently, quantum collision attacks are attracting more attention and showing unexpected efficiencies.
The generic security margin of collision attacks in quantum settings has been investigated with the recent progress in post-quantum security of cryptographic schemes and primitives. Several quantum collision algorithms [BHT98, CNPS17] were introduced to provide security bounds for generic hash functions. However, the quantum collision attack against concrete hash functions was not published until 2020 [HS20]. In this work, Hosoyamada and Sasaki demonstrated that differential trails of low probability that couldn’t be utilized in classical collision attacks were exploited to mount quantum collision attacks of more rounds. Later, the authors extended their quantum collision search algorithms to other hash functions and proposed the first quantum collision attacks on SHA-2 at CRYPTO 2021 [HS21]. Additionally, results of quantum rebound attacks on AES hashing modes [DSS+20] and quantum multi-collision distinguishers [BGLP] on dedicated hash functions were also presented.
Challenges. There are two major challenges in mounting quantum collision attacks on SHA-3. The first is to search for differential trails that are more suitable for quantum collision attacks, i.e., trails that cover as many rounds as possible with the bound on the probability relaxed to \(2^{-n}\). As a consequence, the search space expands drastically which calls for more advanced and efficient searching techniques. The second challenge lies in connecting the differential trail with the initial state. When differential trails with lower probability are used, more conditions are imposed on the internal state which should be satisfied by the connector. Thus, to avoid being the bottle neck of the whole attack, connectors must be constructed in more efficient way than before.
SAT-Based Cryptanalysis. Great attention from the cryptography community has been paid on automatic tools for linear and differential trail search. Normally, mathematical problems such as Boolean Satisfiability Problem (SAT), Mixed Integer Linear Programming (MILP), Satisfiability Modulo Theories (SMT), and other related methods are employed to construct such automatic tools. Since the performance of automatic search is determined by the power of the corresponding mathematical solvers, the efficiency is not particularly satisfactory when cryptographic ciphers with large state sizes are analyzed. Practically, most of the previous related works focus on lightweight ciphers where the automatic tools showed incredible strength.
The SAT problem decides whether a set of constraints could be satisfied by giving valid assignments to variables. In the research line of SAT-based cryptanalysis, Mouha and Preneel searched differential trails of ARX ciphers with SAT method in [MP13]. Based on SAT, Sun et al. [SWW18] put forward an automatic search method for ciphers with Sboxes to obtain differential trails of more accurate as well as high probability. In [SWW21], Sun et al. proposed a new encoding method to convert the Matsui’s bounding conditions into Boolean formulas, which could reduce clauses and speed up the SAT solving phase. Besides, Morawiecki and Srebrny presented preimage attack on 3-round Keccak hash functions by developing a SAT toolkit [MS13].
Our Contributions. Inspired by Hosoyamada and Sasaki’s findings from [HS20, HS21] that collision attacks in quantum settings can take advantage of differential trails of low probability, we develop an automatic trail search toolkit based on SAT and propose advanced collision attacks on SHA-3 in both classical and quantum settings. The results of our work and the comparison with previous works are listed in Table 1. Main contributions are summarized in the following.
-
1. The SAT-based automatic trail search toolkit To facilitate differential trail search of the underlying permutation Keccak-\(f\) of SHA-3, an SAT-based automatic search toolkit is developed. The toolkit is not only simple to implement but also provides more flexibility and better efficiency in generating various differential trails compared to dedicated trail search strategies in [DVA12, MDA17, LQT19]. It’s interesting to note that for cryptographic primitives of large state size like Keccak-\(f\), automatic tools such as the MILP-based ones are unlikely to provide advantage in trail search. That’s why specialized search techniques were proposed for SHA-3. Surprisingly, the SAT-based automatic toolkit fills the vacancy and shows excellent performance in trail search of the large-state Keccak-\(f\).
-
2. Advanced collision attack algorithms for SHA-3 Augmented with the SAT-based automatic tool, the collision attack methods used in [DDS12, DDS14, QSLG17, SLG17, GLL+20] are improved in multiple ways. Collision attacks proposed in those works primarily consist of two phases, i.e., a phase of differential trail search that ensures collision on the digest bits, also referred to as the colliding trail search phase in our work, and a second phase of constructing “connectors” that generates message pairs satisfying the constraints imposed by the padding rule and initial value of SHA-3 and the input difference of the colliding trail at the same time. Both phases are considerably improved utilizing our automatic tool.
-
Colliding trail search algorithms that generate colliding trails of any rounds, any digest length, and high probability are presented. In other words, search space of colliding trails is covered efficiently which has been impossible in previous works.
-
Improved connector construction algorithms are proposed. Differential trails of the connectors (which are called connecting differential trails in the rest of the paper) can not only be directly generated but also produce sufficient degrees of freedom which has been the bottleneck in extending the collision attacks to more rounds.
-
-
3. The first 6-round collision attacks on SHA-3 With the novel automatic tool and the improved algorithms, we finally extend the 5-round collision attacks on SHA-3 instances to 6-round. In detail, 6-round classical collision attacks on SHAKE128 with complexity \(2^{123.5}\), 6-round quantum collision attacks on SHA3-224 and SHA3-256 with complexity
 and
and  respectively, are mounted. To the best of our knowledge, this is the first time that quantum collision attacks are mounted on SHA-3 and one more round is covered compared with previous results in classical setting.
respectively, are mounted. To the best of our knowledge, this is the first time that quantum collision attacks are mounted on SHA-3 and one more round is covered compared with previous results in classical setting.
Organization. The rest of the paper is organized as follows. In Sect. 2, an overview of the SAT-aided collision attacks on SHA-3 instances is provided. In Sect. 3, specifications of SHA-3 hash functions and implementations of the SAT-based automatic search toolkit are presented. Section 4 exhibits the first 6-round collision attacks on SHA-3 in both classical and quantum settings. Section 5 concludes the paper. Details of differential trails and message pairs are given in the supplementary material.
2 Overview of SAT-Based Collision Attacks Against SHA-3
In this section, limitations of previous collision attacks are discussed. Subsequently, the SAT-based automatic trail search toolkit that can be conveniently applied to all kinds of cryptanalytic scenarios are introduced. Basic ideas used to extend previous collision attacks by one round in both classical and quantum settings are also presented.
2.1 Limitations of Previous Collision Attacks
As depicted in Fig. 1, the collision attacks on SHA-3 and Keccak instances take a 3-stage analytic framework, i.e.,
-
at stage 1, prepare \(n_{r_2}\)-round colliding trails of high probability that ensure d-bit digest collision. \(\varDelta S_I\) and \(\varDelta S_O\) stand for the input and output difference of colliding trails.
-
at stage 2, construct \(n_{r_1}\)-round connectors that promise a subspace of message pairs which meet both the message difference \(\varDelta \overline{M}\) imposed by the sponge constructionFootnote 2 and the input difference \(\varDelta S_I\) of the colliding trails.
-
at the last stage, exhaustively enumerate the messages pairs generated with the connectors until one message pair that collides in digest bits is found.
A continuous series of investigations [DDS12, DDS14, QSLG17, SLG17, GLL+20] have been conducted on collision attacks against SHA-3. Both the colliding trail search phase and the connector construction phase have been intensively inspected. At first glance, it seems that there is no room for further improvements. Actually, no essential progress has ever been published since the last work [SLG17] presented five years ago. The lack of new results can be explained from two aspects, i.e., the constrained and low-efficiency colliding trail search algorithms, and the quick consumption of degrees of freedom from the connectors by (full) linearization.
2.1.1 Difficulty in Generating Colliding Trails of More Rounds
Due to the huge state size of Keccak-\(f\), trail search of any kind, be it the general truncated differential trail or the colliding trail, is a difficult task. In previous collision attacks, the strategy to search colliding trails is quite simple, i.e.,
-
1.
General 3-round differential trails obtained from dedicated search algorithms, e.g., [DVA12, MDA17, LQT19], are extended forward by one round and exhaustively searched for possible d-bit collision.
-
2.
When sufficient 3-round trails with digest collision are collected, extend them backward by one round to determine satisfactory output differences for connectors, which at the same time are the input differences \(\varDelta S_{I}\) of the \(n_{r_2}\)-round colliding trails.
There are two problems regarding to this colliding trail search strategy. On one hand, the exhaustive colliding trail search, especially the backward extension, drain computing resources significantly. In practice, sophisticated implementation techniques and even GPU resources [SLG17] are introduced to speed up the colliding trail search. However, without dramatical increase in computing power, it’s unlikely that the search efficiency can be improved further. On the other hand, the colliding trails are limited by the results of general truncated differential trail search. For example, the 5-round practical collision attack on SHA3-256 [GLL+20] is not possible until new results on general 3-round trails [LQT19] are published. Particularly, even with ultimate computing power, better colliding trails won’t be possible unless results of general trail search are updated. Then it comes to the common trail search problem again which is a challenging task.
2.1.2 Quick Consumption of Degrees of Freedom in Connector Construction
The connector construction is comprised of two parts. In the first part, as depicted in Fig. 1, connecting trails whose input difference (i.e., \(\varDelta \overline{M}\)) and output difference (i.e., \(\varDelta S_I\)) are partially or fully fixed are constructed. In the second part, data structures that output a subspace of message pairs following the connecting trail are generated. Essentially, as long as the connecting trail is determined, systems of equations (i.e., the data structures) on messages are listed in which the degree of freedom (DF for short) are quickly consumedFootnote 3. As conditions of both \(\varDelta \overline{M}\) and \(\varDelta S_I\) are strict, the sophisticated Target Difference Algorithms (TDA for short) are devised to determine the exact connecting trails. When we try to extend the connector by one more round, \(\varDelta \overline{M}\) and \(\varDelta S_I\) are so heavy that connecting trails are hard to generate. Even if the TDA generates connecting trails, data structures become impossible to construct as almost all DF is consumed to meet conditions of the heavy connecting trail. Therefore, developing new connecting trail search methods to generate lighter connecting trails would be a feasible way to save DF and possibly allow to extend collision attacks for more rounds.
Summary. Limitations of collision attacks lie in inefficiency of differential trail search, more specifically, the lack of effective search techniques for trails of special requirements.
2.2 SAT-based Automatic Trail Search Toolkit
Automatic search has long been introduced to evaluate robustness of symmetric primitives. However, it’s not the case of Keccak-\(f\) permutation. Indeed, the initial attempts with MILP method failed to generate good trails due to the large Keccak-\(f\) state. Researchers have to develop dedicated techniques to investigate the propagation properties of Keccak-\(f\). On the other hand, automatic search based on other mathematical problems, such as SAT and SMT, is not properly studied. In this work, SAT-based automatic search shows productivity in generating trails involved in collision attacks on SHA-3.
2.2.1 SAT-based Colliding Trail Search
With the SAT-based toolkit, differential trails that (1) satisfy the d-bit digest collision, (2) cover more rounds, (3) follow any specific differential pattern, and (4) meet any probability constraint can be effectively generated. The search space is expanded to the extent that efficiency of automatic search tool outperforms dedicated search strategy. Moreover, as the new method does not rely on truncated differential trails, colliding trail search will not be limited by progress of such general trails any more. Cryptanalysts are also free from devising and implementing sophisticated trail search algorithms. We emphasize that colliding trails of low probability, e.g., with complexity near or even beyond the birthday bound, are easily generated. Such trails are utilized to mount collision attacks in quantum settings.
2.2.2 SAT-based Connecting Trail Search
Similar to the case of colliding trail search, the SAT-based connecting trail search is effortlessly implemented. Good connecting trails that (1) follow the fixed input and output differences of the connectors and (2) provide adequate DF for messages are generated. The idea of finding connecting trails with SAT gives insights to the constrained-input constrained-output (CICO) problem [BPVA+11] of sponge constructions. As the input and output differences of connecting trails are partially or fully fixed, this is generally a difficult problem. Except for the sophisticated approach used in [DDS12, DDS14, QSLG17, SLG17, GLL+20], there is no other progress on constructing connecting trails. The SAT-based connecting trail search method presents the first general solution for the problem of bypassing the constraints imposed by the sponge construction in collision attacks on SHA-3.
2.3 Improved (Quantum) Collision Attacks on SHA-3
With the SAT-based automatic tool, collision attacks on SHA-3 instances that cover one more round are mounted in both quantum and classical settings.
2.3.1 6-Round Collision Attacks on SHAKE128
With the SAT-based tool, 4-round colliding trails of 256-bit digest collision are generated. Although one round is extended compared to trails used in previous works, the 4-round colliding trails are of low probability. To mount valid collision attacks, one round of the colliding trails is merged into the connectors, i.e., the 6-round collision attacks consist of a 3-round connecting trail and a 3-round colliding trail. Due to the low probability, the 3-round connectors can only be partially constructed, i.e., only a fraction of the third round conditions are treated while the other constraints are left for the brute force stage. Ultimately, a theoretical 6-round collision attack on SHAKE128 are mounted with complexity \(2^{123.5}\) which is slightly better than the generic attack.
2.3.2 6-Round Quantum Collision Attacks on SHA3-224 and SHA3-256
The identical 4-round colliding trail is used to mount 6-round collision attacks on SHA3-224 and SHA3-256. Constrained by the great amount of DF consumed, it becomes impossible to construct even partial 3-round connectors for these instances. Therefore, for SHA3-224 and SHA3-256, only 2-round connectors are feasible. 6-round collision attacks on SHA3-224 and SHA3-256 cannot be mounted in classical setting as complexity of the 4-round colliding trail exceeds the birthday bound. Fortunately, colliding trails of low complexity can be employed to mount quantum collision attacks. In a nutshell, 6-round quantum collision attacks on SHA3-224 and SHA3-256 with complexity  and
and  are presented.
are presented.
3 SHA-3 and SAT-based Automatic Search Toolkit
In this section, we describe notations used in the collision attacks and specifications of the SHA-3 family hash functions. Afterwards, the SAT-based automatic search toolkit developed for Keccak-\(f\) permutation is presented.
3.1 Notations
Most of the notations to be used in this paper are listed below.
c | Capacity of a sponge function |
r | Rate of a sponge function |
d | Length of the digest in bits |
p | Number of fixed bits in the initial state due to padding |
\(n_r\) | Number of rounds |
Keccak-\(f\) | The underlying permutation of SHA-3 hahs functions |
\(\theta ,\rho ,\pi ,\chi ,\iota \) | The five operations of the round function of Keccak-\(f\). A subscript i denotes the operation at the i-th round, e.g., \(\chi _i\) denotes the \(\chi \) layer at the i-th round where \(i = 0, 1, 2, \cdots \) |
\(\lambda \) | Composition of \(\theta ,\rho ,\pi \) and its inverse denoted by \(\lambda ^{-1}\) |
\(RC_i\) | Round constant of the i-th round, where \(i= 0,1,2,\cdots \) |
\(\texttt{R}^i(\cdot )\) | Keccak-\(f\) permutation reduced to the first i rounds |
\(\texttt{S}(\cdot )\) | 5-bit Sbox operating on each row of Keccak-\(f\) state |
\(\delta _{in},\delta _{out}\) | 5-bit input and output differences of an Sbox |
\(\texttt{DDT} \) | Differential distribution table, and \(\texttt{DDT} (\delta _{in},\delta _{out})=~|\{x:\texttt{S}(x)+\texttt{S}(x+\delta _{in})=\delta _{out}\}|~\), where \(|\cdot |\) denotes the size of a set |
\(\alpha _i\) | Input difference of the i-th round, where \(i= 0,1,2,\cdots \) |
\(\beta _i\) | Input difference of \(\chi \) in the i-th round, where \(i= 0,1,2,\cdots \) |
\(w_i\) | Propagation weight (weight for short) of the i-th round |
\(w(\beta _i)\) | Weight of \(\beta _i\), where \(\beta _i\) is the input difference of \(\chi \) |
\(w^{rev}(\alpha _i)\) | Minimal reverse weight of \(\alpha _i\) |
\({\texttt{DF}} \) | Degree of freedom of the solution space of connectors |
\(\overline{M}\) | Padded message of M. Note that \(\overline{M}\) is of one block in our attacks |
\(M_1||M_2\) | Concatenation of strings \(M_1\) and \(M_2\) |
\(x_i\) | Bit value vector before \(\lambda \) of each round, where \(i= 0,1,2,\cdots \) |
\(y_i\) | Bit value vector before \(\chi \) of each round, where \(i= 0,1,2,\cdots \) |
\(E_{y_i}\) | System of equations on \(y_i\) of each round, where \(i= 0,1,2,\cdots \) |
3.2 Description of SHA-3 Family
The SHA-3 family [Dwo15] consists of a subset of Keccak [BDPVA13] hash functions that are built upon the sponge construction [BDPVA07, GJMG11] with an internal permutation called Keccak-\(f\).
3.2.1 Specification of Keccak-\(f\) Permutation
The underlying permutation Keccak-\(f\) takes a large state size of 1600 bits and there are 24 iterative rounds in total. Each round of Keccak-\(f\) is comprised of five operations, namely, the four linear operations denoted by \(\theta \), \(\rho \), \(\pi \) and \(\iota \), and one solely nonlinear operation denoted by \(\chi \). The 1600-bit state is organized as a 3-dimensional array of bits, i.e., \(5\times 5\times 64\), denoted with A[5][5][64]. Each of the state bits indexed by the coordinate (i, j, k) in the state array is denoted by A[i][j][k] where \(0\le i,j<5\), and \(0\le k<64\). The 5 step mappings of the Keccak-\(f\) round are specified with the following transformations.
- \(\theta \): :
-
\(A[i][j][k]\leftarrow A[i][j][k]\oplus \sum _{j'=0}^4 A[i-1][j'][k]\oplus \sum _{j'=0}^4 A[i+1][j'][k-1]\).
- \(\rho \): :
-
\(A[i][j]\leftarrow A[i][j]\lll T(i,j),\text {where } T(i,j) \text {s are constants}\).
- \(\pi \): :
-
\(A[j][2i+3j]\leftarrow A[i][j]\).
- \(\chi \): :
-
\(A[i][j][k]\leftarrow A[i][j][k]\oplus (A[i+1][j][k]\oplus 1)\cdot A[i+2][j][k]\).
- \(\iota \): :
-
\(A[0][0]\leftarrow A[0][0]\oplus RC_{i_r},\text {where } RC_{i_r} \text { is the } i_r\text {-th round constant}\).
The multiplication used in \(\chi \) operation is in \(\textsf{GF}(2)\). As \(\iota \) won’t affect differences, we ignore it in the rest of the paper unless otherwise stated.
3.2.2 Instances of SHA-3 Family
According to the bit length of digest, SHA-3 contains 6 instances, i.e., the four variants SHA3-224/256/384/512 that have a fixed hash length (where the numbers 224/256/384/512 stand for the hash size) and the two variants SHAKE128 and SHAKE256 of extendable outputs. A multirate padding rule 10\(^*\)1 is defined for all SHA-3 instances. For the four standardized instances SHA3-224/256/384/512, a 2-bit string “01” is concatenated to the message before padded while the capacity is specified as \(c=2\times d\). In regards to the two extendable variants, a 4-bit string “1111” is concatenated to the messages, and the capacity is 256 and 512 bits for SHAKE128 and SHAKE256 respectively. The digest size d of SHAKE128 and SHAKE256 can vary, and therefore the collision resistance level is given by \(\min (d/2, 128)\) and \(\min (d/2,256)\) correspondingly.
3.3 SAT Implementation
In the following, the SAT solver, the descriptions of the Keccak-\(f\) permutation and its differential propagation, and the objective functions are illustrated.
CryptoMiniSAT. We choose CryptoMiniSAT as the underlying solver to implement our automatic toolkit. Since proposed in [SNC09], the conflict-driven clause-learning(CLDL) SAT solver has been improved greatly [SNC10, Soo14, Soo16, SBH+19, SDG+20, SSK+20]. Enhanced with a sequence of advanced search strategies such as Gauss-Jordan elimination and target phases [QUE19], CryptoMiniSAT shows outstanding performances among other SAT solvers. Except for high performance, CryptoMiniSAT also provides a neat interface for XOR expressions. In fact, most well-performed SAT solvers only understand constraints in conjunctive normal form (CNF for short) and users must consider the complicated problem of describing cryptographic primitives with CNFs. By contrast, CryptoMiniSAT allows attackers concentrate on attacks while providing high performance and simple implementation.
To implement SAT-based automatic trail search method, two kinds of constraints are fed into CryptoMiniSAT, namely, conditions imposed by (1) differential propagation over round functions (or in other words the description of round functions), and (2) objective functions such as the number of active Sboxes and the propagation probability.
Round Function. As depicted in the following model,
two state differences, i.e., \(\alpha _r\) (the input difference of the r-th round) and \(\beta _r\) (the input difference of the \(\chi \) operation of the r-th round) are introduced to the SAT implementation for a single r-th round. The 1600-bit difference \(\alpha _r\) is represented by 1600 variables, i.e., variable of each bit (whose coordinate is \(\alpha _r[i][j][k]\) where \(0\le i,j<5\) and \(0\le k<64\)) is indexed with \((320\times j + 64\times i + k)_{\alpha _r}\). This way we establish the mapping relationship between the 1600 variables and the corresponding state difference.
Recall that \(\rho \) and \(\pi \) are simply bit permutations. Differential propagations over the two linear operations are described through mapping the indexes of variables. For example, assuming that an active bit \(c_r[i][j][k]\) is transformed to \(\beta _r[i'][j'][k']\) through \(\pi \circ \rho \), then the index mapping of the two variables is \((320\times j + 64\times i + k)_{c_r} \xrightarrow {\pi \circ \rho } (320\times (2\times i+ 3\times j) + 64\times j + (k -T(i,j))\%64 )_{\beta _r}\). These operations are described with plain index transformation and no additional SAT computation is required.
By definition, \(\theta \) operation updates each bit through XORing itself to two columns. Accordingly, \(\theta \) is described with XOR clauses that could be directly understood by CryptoMiniSAT. That is, the XOR sums of 320 columns (denoted by \(\alpha [i][k]\)) are described with 320 variables each of which is indexed by \(64\times i+ k\). As a result, the mapping of variable indexes induced by \(\theta \) operation is captured with \((320\times j + 64\times i + k)_{c_r} = (320\times j + 64\times i + k)_{\alpha _r} \oplus (64\times (i-1)+ k)_{ColumnSum} \oplus (64\times (i+1) + (k-1))_{ColumnSum}\). Here, the subscript ColumnSum indicates the variables of column sums.
Practically, the three linear operations (i.e., \(\theta \), \(\rho \) and \(\pi \)) are treated as a whole. The total index mapping of variables is described with \((320\times (2\times i+ 3\times j) + 64\times j + (k -T(i,j))\%64 )_{\beta _r} = (320\times j + 64\times i + k)_{\alpha _r} \oplus (64\times (i-1)+ k)_{ColumnSum} \oplus (64\times (i+1) + (k-1))_{ColumnSum}\).
In regard to the only nonlinear operation \(\chi \) which is generally considered as 5-bit Sbox, both the difference distribution table (DDT for short) and the operation itself are interpreted with truth tables. Specifically,
-
The DDT is described with listing a truth table of 11 variables, including 10 variables that represent input and output difference and 1 variable marking compatibility of DDT entries. When fed into Logical Friday (refer to http://sontrack.com), 46 CNFs are generated to describe the DDT. Differential propagation over \(\chi \), i.e., relationship between the input difference \(\beta _r\) and output difference \(\alpha _{r+1}\), is then depicted with simply writing CNFs of each Sbox.
-
Similarly, variables that correspond to the input and output values of \(\chi \) are connected with CNFs generated from \(\chi \) truth table. Empirically, 11 variables are needed to construct truth tables and 29 CNFs are produced.
In summary, \(1600\times 2 +320=3520\) variables are used to describe one round of Keccak-\(f\) permutation in the SAT-based implementation. The relationship among variables are specified with methods illustrated above. Identical round description that is of different variable sets is implemented for each round. Multiple rounds are described by connecting each round, i.e., (1) the input variables of each round are the output variables of its previous round and (2) the output variables of each round are the input variables of its next round.
Objective Function. In the context of 6-round collision attacks on SHA-3, the number of active Sboxes and the propagation weight (weight for short)Footnote 4 are the two mainly considered objectives. To describe the objectives, constraints on integers (i.e., number of active Sboxes and weights) are transformed to CNFs. The sequential encoding method [Sin05] is employed to describe addition over integers, e.g., \(\sum _{i=0}^{n-1}x_i \le w\) where \(w \ge 1\). In this process, \((n\times (w+1)-w)\) auxiliary variables are introduced. More specifically,
-
Constraint on the Number of Active Sbox. To describe the number of active Sboxes of each \(\chi \), 320 variables are introduced to indicate whether an Sbox is active or not. The sum of all the variables needs to satisfy a threshold weight (say w), e.g., \(\sum _{i=0}^{319}x_i \le w\). Accordingly, \((320\times (w+1)-w)\) extra variables are introduced to transform the constraint on the number of active Sboxes to CNFs.
-
Constraint on the Propagation Weight. The DDT entries take 4 possible values (i.e., 2, 4, 8, and 32), and the corresponding propagation weights belong to \(\{0, 2, 3, 4\}\). As shown in Eq. 1, four auxiliary variables denoted by \((p_0, p_1, p_2, p_3)\) are introduced to represent the weight of each Sbox, meaning that \((320\times 4\times (w+1)-w)\) extra variables are added to describe constraints on the weight of a whole state. Likewise, the weight constraint which is obtained through summing up all the variables is then transformed to CNFs.
$$\begin{aligned} (p_0, p_1, p_2, p_3)= {\left\{ \begin{array}{ll} (1, 1, 1, 1), &{} \texttt{DDT} (\delta _{in},\delta _{out})=2;\\ (0, 1, 1, 1), &{} \texttt{DDT} (\delta _{in},\delta _{out})=4;\\ (0, 0, 1, 1), &{} \texttt{DDT} (\delta _{in},\delta _{out})=8;\\ (0, 0, 0, 0), &{}\texttt{DDT} (\delta _{in},\delta _{out})=32. \end{array}\right. } \end{aligned}$$(1)
3.4 SAT-based Automatic Search Toolkit
In this section, we explain how to implement various trail search algorithms based on the SAT implementation. Let’s first review some definitions and concepts introduced in [DVA12, BPVA+11]. The 6-round attack model presented in Sect. 4.1.3 is placed here in advance to better explain definitions.
-
Probabilistic Property of \(\chi \). As the algebraic degree of \(\chi \) is 2, its DDT shows some interesting properties. For a given input difference, all its compatible output differences share equal propagation probability. Correspondingly, for a given \(\beta _i\), all its compatible \(\alpha _{i+1}\) take the same probability or weight. For a given output difference, as the degree of \(\chi ^{-1}\) is 3, there exist one or several compatible input differences that hold a better probability than the other input differences. Likewise, for a given \(\alpha _i\), there exist some compatible \(\beta _{i-1}\) that have the best differential probability, which is also called the minimum reverse weight (and generally denoted by \(w^{rev}(\alpha _i)\)).
-
Trail core. As depicted in Fig. 2, a general 4-round differential trail consists of input and output differences of all four rounds, i.e., \((\alpha _2,\alpha _3 ,\alpha _4,\alpha _5,\alpha _6)\). Recall that as \(\lambda \) is a linear transformation, \(\alpha _i\) propagates to \(\beta _i\) deterministically. The 4-round differential trail is also denoted by \((\beta _2,\beta _3,\beta _4,\beta _5)\). Comparatively, the 4-round trail core is composed of three differences, i.e., \((\beta _3,\beta _4,\beta _5)\), taking advantage of the property that the minimal reverse weight of \(\alpha _3\) can be directly computed to evaluate the family of 4-round trails that have \((\beta _3,\beta _4,\beta _5)\) as their tail.
In the Fig. 2 model, \((\beta _3,\beta _4,\beta _5)\) represents the colliding trail
3.4.1 SAT-based Colliding Trail Search
To set up the colliding trail search model, description of differential trail (\(\alpha _3\),\(\beta _3\),\(\alpha _4\),\(\beta _4\),\(\alpha _5\),\(\beta _5\),\(\alpha _6^d\)) needs to be added into the SAT model. Differential propagation over the round functions is implemented in the way introduced in last section. At this stage, only constraints that are exclusively imposed by the colliding trails are introduced. Aligned with the requirements for constructing colliding trails in [GLL+20], the SAT-based search method is implemented from two aspects, i.e., the digest collision and the connector construction.
From the perspective of collision search, we don’t have to check \(\alpha _6\) for d-bit collision (denoted by \(\alpha _6^d\)). Rather, extra constraints on \(\beta _5\) that ensure \(\alpha _6^d\) collision are considered. Take colliding trail search of SHAKE128 as an example, to guarantee the first 4 lanes of \(\alpha _6\) to be 0, the input difference to the first 64 Sboxes of \(\beta _5\) must belong to the set {00000, 00001, 00101, 10101, 00011, 01011, 00111, 10111, 01111, 11111}. The candidate input differences listed above form a space which is represented by CNFs. Through adding the corresponding CNFs on variables of \(\beta _5\) to the system, constraints on digest collision is implemented.
On the other hand, to maximally facilitate the connector, the minimum reverse weight of \(\alpha _3\) (denoted by \(w^{rev}(\alpha _3)\)) and propagation weight \(w({\beta _3})\) + \(w({\beta _4})\) + \(w({\beta _5^d})\) of the colliding trail are taken into consideration. Altogether, the objective function of \(w^{rev}(\alpha _3)\) + \(w({\beta _3})\) + \(w({\beta _4})\) + \(w({\beta _5^d})\) is described with CNFs and added to the system. In some situations, the constraints on weight are replaced by the constraints on the number of active Sboxes, i.e., \(AS({\alpha _3})\) + \(AS({\alpha _4})\) + \(AS({\beta _4})\) + \(AS({\beta _5^d})\) which results in \((320\times 3 \times (w+1)-w)+(64\times (w+1)-w)\) auxiliary variables included to the SAT system.
With this implementation, 3-round colliding trails are not only generated more efficiently but also of better probability. In contrast, the best 3-round colliding trail used in previous collision attack on SHA3-256 is of probability \(2^{-43}\). It’s worth noticing that 4-round colliding trails which could be utilized to mount collision attacks of 6 rounds is generated for the first time. Table 2 gives comparison of search efficiency. It demonstrates that the new SAT-based trail search is superior to earlier strategies in both efficiency and effectiveness.
3.4.2 SAT-based Connecting Trail Search
In accordance with the considerations for constructing connecting trails that promise valid connectors, the trail search of (\(\alpha _0\),\(\beta _0\),\(\alpha _1\),\(\beta _1\),\(\alpha _2\),\(\beta _2\)) is specified with two phases.
Phase 1. In the first phase, \((\beta _1,\beta _2)\) are to be determined for given \(\alpha _3\). First, description of the differential trail (\(\beta _1\),\(\alpha _2\),\(\beta _2\),\(\alpha _3\)) are added to the SAT system. Afterward, constraints on propagation weight of \(\beta _1\) and \(\beta _2\) are established, i.e., CNFs of a minimal \(w({\beta _1})+w({\beta _2})\) are listed. By now, \(6400 + 320\) variables are used to describe the connecting trail where 6400 variables are introduced for the 2-round propagation and 320 variables correspond to conditions of the summed weight. And we also restrict weight of each round, namely, \(w({\beta _1}) \le w_1\) and \(w({\beta _2}) \le w_2\) which results in an extra \((1280\times (w_1+1)-w_1) + (1280\times (w_2+1)-w_2)\) variables. The objective function of weight is described with the method illustrated in the last section. Overall, this model needs \(6400 + 320 + (1280\times (w_1+1)-w_1) + (1280\times (w_2+1) - w_2)\) variables.
Phase 2. The input difference of \(\chi _0\) of the first round is determined in this phase with the SAT-based implementation. Given the output difference \(\alpha _1\), variables that represent a pair of messages (\(x_0^1\),\(x_0^2\)) and the input difference \(\beta _0\) are introduced to describe the half round propagation. Precisely, constraints on bit positions of capacity and padding are depicted by fixing the corresponding variables to be 0 or some settled value. Constraints on \(w(\beta _0)\), the weight of \(\beta _0\), are also covered to make sure that the degree of freedom will be maximally produced for connectors. Simply put, CNFs for objective function of a minimal \(w(\beta _0)\) are added to the SAT model. With the SAT-based implementation, connecting trails that yield much greater DF are generated.
3.4.3 SAT-based Truncated Trail Search
Except for the special trail search scenarios, SAT-based solution also performs well in general truncated differential trail search. As can be seen from the experimental results, SAT-based implementation handles 3-round Keccak-\(f\) permutation quickly. It turns out that 3-round trail cores generated with the SAT-based automatic trail search method are consistent with results from previous works [DVA12, MDA17, LQT19].
We take 4-round differential trail search as an example to explain the SAT-based trail search implementation. The 4-round trail is modelled with
First, CNF description of the differential trail (\(\alpha _3\),\(\beta _{3}\),\(\alpha _4\),\(\beta _4\),\(\alpha _5\),\(\beta _5\)) is added to the SAT system. As 6 differences are involved, \(10560 = 1600 \times 6 + 3 \times 320\) variables are required to describe the difference propagation. Similar to the colliding trail search implementation, constraint on the sum of weight \(w=w^{rev}(\alpha _3)\) + \(w({\beta _3})\) + \(w({\beta _4})\) + \(w({\beta _5})\) where \(w\le 133\) is also added to the SAT system. Another \(685947 = (1280\times 4 \times (133+1)-133)\) auxiliary variables are included in the process of transforming the objective function to CNFs. In total, there are 696507 variables in this SAT-based 4-round differential trail search implementation.
With respect to search efficiency, although it displays unexpectedly well performance in 3-round trail search, it cannot traverse the search space of 4-round trails efficiently. A tight lower bound on propagation weight for 4-round differential trails is unfortunately not settled in this paper. However, two better 4-round trails of weight 133 which is the lowest known weight so far are generated. Table 8 in supplementary material B shows the two trails (refer to the full version [GLST22]).
The SAT-based differential trail search implementation is further extended to other Keccak permutations [BPVA+11] such as Keccak-\(f\)[800]. Analogous to Keccak-\(f\) (which is also denoted by Keccak-\(f\)[1600]), similar round functions are iterated for multiple rounds in Keccak-\(f\)[800] only that its state size is of 800 bits. Table 9 in supplementary material B shows a good trail that improves the lower bound of 4-round trails for Keccak-\(f\)[800]. Table 2 gives an overview of the advantage of the automatic search compared to previous works.
Summary. By picking up different compositions of constraints on the number of active Sboxes and weight or even considering a single state not in the whole, we obtain variant SAT models with different efficiency. The SAT-based automatic search toolkit helps us understand the differential propagation property of Keccak-\(f\) in a distinct viewpoint. It also demonstrates that automatic solvers perform efficiently on cryptographic primitives with large state size.
4 Collision Attacks Against SHA-3 Instances in Classical and Quantum Settings
In this section, a classical 6-round collision attack on SHAKE128, and two 6-round quantum collision attacks on SHA3-224/SHA3-256 are mounted.
4.1 Basic Attack Strategy
Aided by the SAT-based automatic search toolkit, we propose advanced collision attacks on SHA-3 instances based on the analytic framework described in Sect. 2. The enhanced collision attack is comprised of three phases, i.e.,
-
Phase 1, generate \(n_{r_2}\)-round colliding trails of d-bit digest with the SAT-based tool.
-
Phase 2, generate \(n_{r_1}\)-round connecting trails that link the conditions of sponge construction and the input difference of the colliding trail with the SAT-based tool.
-
Phase 3, construct connectors that generate a subspace of messages which follow the \(n_{r_1}\)-round connecting trails.
The brute force phase where collision messages are generated will not be included as only theoretical collision attacks are presented in this work.
4.1.1 Generating Colliding Trails
Based on the SAT implementation techniques elaborated in Sect. 3, we add the implementation of colliding trail search algorithms to the toolkit. Except that the d-bit collision must be satisfied, the propagation weight of the 4-round colliding trail core must also be small enough to promise a possible 6-round collision attack. Eventually, several 4-round colliding trail cores are generated. We select the best one to mount collision attacks. Without considering the connector, weight of the 4-round colliding trail is 141 (i.e., \(89+24+20+8=141\)). The propagation weight of the 4-round trail core is shown in Fig. 3 while the exact differences are listed in Trail No.1 (shown in Table 5) of supplementary material B.
4.1.2 Generating Connecting Trails
As shown in Fig. 3, even the minimal weight (i.e., \(\ge 141\)) of 4-round colliding trails exceeds the birthday bound (e.g., 128 for SHAKE128 and SHA3-256). It’s impractical to randomly select a 4-round colliding trail and generate the corresponding 2-round connecting trail. We develop a two-step approach to determine the connecting trails. The input difference of the 4-round colliding trail core is generated in combination with the differences of connecting trails. Let’s explain the idea with the 6-round collision attack model shown in Fig. 4.
-
In the first step, the input difference (i.e., \(\beta _2\)) of the 4-round colliding trail core \((\beta _3,\beta _4,\beta _5)\) is determined together with the input difference (i.e., \(\beta _1\)) of the second round of the connecting trails. Practically, the 2-round differential trails \((\beta _1,\beta _2)\) that are not only compatible with \(\alpha _3\), but also of minimal weight are generated with the SAT-based tool.
-
In the second step, the lightest \(\beta _0\) (in terms of weight) that are compatible with \(\alpha _1\) and meet the restrictions on \(\alpha _0\) imposed by the sponge construction are generated with the SAT-based tool.
To demonstrate the strength of the SAT-based method, we compare experimental results on SHA3-256 with previous work. In previous results, when the first round of the connector is processed, the DF remained is estimated to be around 124 (for more illustration refer to Sect. 5.2 of [GLL+20]). In comparison, the new connecting trails provide a DF up to \(330\sim 430\) which is surprisingly superior. This accords with the number of active Sboxes of \(\beta _0\). Almost all of the 320 Sboxes of \(\beta _0\) are active (e.g., the number of nonactive Sboxes is around 10) with the previous target difference algorithm, while with our SAT-based strategy there are around \(40\sim 50\) nonactive Sboxes in \(\beta _0\). Without the extra gain of DF, it’s impossible to extend the attack by one round.
Remark 1
The three undetermined differences \(\beta _0\), \(\beta _1\), and \(\beta _2\) cannot be generated all at once. On one hand, even if \((\beta _0,\beta _1,\beta _2)\) are determined in one step, the distribution of weights (i.e., \(w(\beta _0)\), \(w(\beta _1)\), and \(w(\beta _2)\)) is random. In our experiments, such \((\beta _0,\beta _1,\beta _2)\) cannot sustain a good connector in general. On the other hand, the SAT-based toolkit cannot support searching such trails efficiently.
4.1.3 Constructing Connectors
The connecting trails, combined with the colliding trails, constitute the full 6-round differential trail with which the connectors that generate a subspace of messages that follow the connecting trails can be constructed. Considering that weight of the 4-round colliding trail exceeds the birthday bound, to mount a valid attack, we transfer the first round of the colliding trail to the connector. In detail, the 6-round collision attack on SHAKE128 consists of a 3-round connector and a 3-round colliding trail (refer to Fig. 4). As for SHA3-224 and SHA3-256, 6-round quantum collision attacks that consist of a 2-round connector and a 4-round colliding trail are mounted (refer to Fig. 4). We highlight that the connecting trails cannot provide enough DF to satisfy all the constraints in connectors even for theoretical attacks. Therefore, merely a fraction of constraints of the last round of 2/3-round connectors are picked up to be processed.
2-Round Connectors. We improve the algebraic-aided method adopted by previous works [DDS12, DDS14, QSLG17, SLG17, GLL+20] to construct connectors that generate message pairs following partially the output difference of the connectors.
Principally, the systems of linear equations on messages are listed and solved. The linear equations correspond to the conditions of sponge functions and differences of the connecting trail. The 2-round connector model exhibited in Fig. 5 illustrates how the system of linear equations is established.
-
1.
First, linear equations of the \((c+p)\)-bit conditions imposed by the sponge construction are listed, where c and p correspond to the capacity and padding bits respectively. Take the case of SHA3-256 as an example, the capacity is \(c=256\times 2=512\) bits, and the padding rule is 10\(^*\)1. To provide as many DF as possible, we set the padding as fixed “11” string. Also the 2-bit string “01” is concatenated to the tail of the message block. In total, a 4-bit fixed string (i.e., “0111”) is considered as the p-bit condition. Linear equations on the \((c+p)\)-bit conditions are directly listed on the input messages \(x_0\). As \(y_0\) and \(x_0\) are linked with the linear transformation \(\lambda \), the linear equations on \(x_0\) are easily transferred to equations on \(y_0\). In the case of 2-round connectors, the systems of linear equations on \(y_0\) are listed and denoted by \(E_{y_0}\).
-
2.
Next, linear equations on \(y_0\) that meet conditions imposed by first round differential \((\beta _0,\alpha _1)\) are added to \(E_{y_0}\). Message pairs constructed from the solutions of the current \(E_{y_0}\) system must follow the \((\beta _0,\alpha _1)\) differential. Details on how the equations can be listed are illustrated with Property 1 of the supplementary material A.
-
3.
To list equations of conditions imposed by the second round differential \((\beta _1,\alpha _2)\), the first round must be bypassed. Linearization and partial linearization techniques on \(\chi \) operation proposed in [QSLG17, SLG17] are borrowed directly to ensure that the \(y_1\) bits can be expressed by the linear combinations of involved \(y_0\) bits. Consequently, \(E_{y_1}\), the system of linear equations on \(y_1\) for \((\beta _1,\alpha _2)\), is transferred to a group of linear equations on \(y_0\). To this end, extra equations on \(y_0\) that allows the involved \(y_1\) bits linear with respect to the \(\chi \) operation must be added to \(E_{y_0}\). Practically, as there is a whole round between \(y_1\) and \(y_0\), the \(x_1\) bits that are involved to the corresponding \(y_1\) bits according to \(\lambda \) operation are linearized. The principal property exploited to linearize \(x_1\) bits is briefly summarized in Property 2 of the supplementary material A. The DF left after the last two steps cannot sustain solving all the \(\beta _1\) active Sboxes. A greedy algorithm that sorts the active Sboxes of \(\beta _1\) by the number of unlinearized \(x_1\) bits is utilized to choose the \(\beta _1\) Sboxes to be treatedFootnote 5. To sum up, linear equations on \(y_0\) that linearize the involved \(x_1\) bits of partially chosen \(\beta _1\) Sboxes are added to \(E_{y_0}\) in this step.
-
4.
At last, the system of equations on \(y_1\) (i.e., \(E_{y_1}\)) of the partially treated \(\beta _1\) Sboxes is transferred to linear equations on \(y_0\) with the linearization equations generated in the last step, and added to the system \(E_{y_0}\).
The Algorithm 1 shown in supplementary material A provides a concise description on construction of the 2-round connector. When a consistent system of linear equations on \(y_0\) (i.e., \(E_{y_0}\)) is successfully generated, the alleged 2-round connector is constructed. The solution space of \(E_{y_0}\) is composed of a subspace of messages, i.e., \(y_0\). A pair of messages \((y_0^1,y_0^2)\) generated through XOR-ing \(y_0^1\) with \(\beta _0\), while \(y_0^1\) is a random solution of \(E_{y_0}\), follows (1) the input difference \(\alpha _0\) and (2) a fraction of the output difference \(\alpha _2\) of the 2-round connector.
3-round Connector. In constructing 3-round connector, \(\chi _0\) of the first round is fully linearized, making the first round a linear layer. As a result, the 3-round connector can be viewed as a 2-round connector. We adopt the model shown in Fig. 5 to explain how the system of linear equations of the 3-round connector is constructed.
-
1.
First, list linear equations on \(y_0\) for (1) the \((c+p)\)-bit conditions and (2) the constraints imposed by the first round \((\beta _0,\alpha _1)\) differential. The system of linear equations is denoted by \(E_{y_0}\).
-
2.
Next, fully linearize the \(\chi _0\) layer of the first round and transfer the equations on \(y_0\) to equations on \(y_1\). Namely, additional equations on \(y_0\) that corresponds to linearizing each active and non-active Sbox of \((\beta _0,\alpha _1)\) differential are added to the current \(E_{y_0}\). Expressions of the linearized \(\chi _0\) are utilized to convert the system of linear equations on \(y_0\) (i.e., \(E_{y_0}\)) to the system of linear equations on \(y_1\) (i.e., \(E_{y_1}\)).
-
3.
List linear equations on \(y_1\) for constraints imposed by the second round (\(\beta _1\),\(\alpha _2\)) differential. Add those equations to the present system of equations \(E_{y_1}\).
-
4.
With the same greedy algorithm utilized in 2-round connector construction, select a fraction of conditions of \(\beta _2\) to solve and linearize the related \(x_2\) bits. Add the equations on \(y_1\) that linearize the involved \(x_2\) bits of the partially treated (\(\beta _2\),\(\alpha _3\)) differential to the current \(E_{y_1}\) system.
-
5.
List equations on \(y_2\) for conditions imposed by the partially solved (\(\beta _2\),\(\alpha _3\)) differential of the last round of the 3-round connector. Convert the system of linear equations on \(y_2\) to equations on \(y_1\) based on the linearization of involved \(x_2\) bit in the last step. Add the \(y_1\) equations generated at this step to the whole \(E_{y_1}\) system.
When all equations are listed and organized in the system of equations on \(y_1\) (i.e., \(E_{y_1}\)), the 3-round connector is successfully constructed. A subspace of message pairs generated from the solution space of \(E_{y_1}\) satisfy that (1) the input conditions imposed by sponge constructions are met and (2) the output difference of the 3-round connector is partially met as expected. The Algorithm 2 in supplementary material A illustrates construction of the 3-round connector.
4.2 Collision Attack Against 6-Round SHAKE128
Following the basic attack strategy, a collision attack on 6-round SHAKE128 is mounted. The model in Fig. 6 gives basic details of the attack.
As discussed in Sect. 4.1.2, the minimal weight of the best 4-round colliding trail core exceeds the birthday bound. To make the collision attack feasible, the first round of the 4-round colliding trail is transferred to the connector. Hence, the 6-round collision attack consists of a 3-round connector and a 3-round colliding trail. Propagation weight of each round is identified in Fig. 6. The 4-round colliding trail core is specified in Table 5 of supplementary material B, more specifically, the \((\beta _3,\beta _4,\beta _5)\) differences of Trail No.1. The probability of the 3-round colliding trail is \(2^{-52}\) (where \(2^{-52}=2^{-24}\cdot 2^{-20}\cdot 2^{-8}\)). The two-step SAT-based connecting trail search method described in Sect. 4.1.2 is applied to first determine (\(\beta _1\),\(\beta _2\)) differences and fix \(\beta _0\) difference subsequently. The connecting trail is listed in Table 7, i.e., Trail No.3 in supplementary material B.
Now that the whole 6-round differential trail is determined, the 3-round connector can be constructed with the method illustrated in Sect. 4.1.3. The third round of the 3-round connector is partially solved, e.g., in our experiment, 36 out of the 116 constraints of (\(\beta _2\),\(\alpha _3\)) are solved. The DF of the 3-round connector is 27Footnote 6. Alternatively, the 3-round connector generates a subspace of \(2^{27}\) messages that satisfy the 36 conditions of the input difference \(\alpha _3\) of the colliding trail. A pair of solution messages are given in Table 10 of supplementary material B.
The unsolved conditions of (\(\beta _2\),\(\alpha _3\)) are treated together with the colliding trail through exhaustive search. In the brute force phase, message pairs generated from connectors are verified for whether satisfying \(\alpha _3\) or not. If not, simply abandon the current pair and try another one. Otherwise, further check the 256-bit digests of the pair until a collision is encountered.
Remark 2
Apart from the current work that exemplifies the collision resistance of a typical 128-bit security level, inner collisions [GJMG11] could also be analyzed with the same idea. As indicated in [GLL+20] (an inner collision of a 160-bit Keccak Challenge), the inner collision attack that constructs collision on capacity bits yields collisions of any digest length.
Complexity. The overall complexity includes complexity of both the connector construction phase and the exhaustive search phase.
-
In the exhaustive search phase, the time complexity is \(2^{132}\) 6-round SHAKE128 computations (where \(2^{132} = 2^{116-36}\cdot 2^{52}\)). However, taking advantage of the early-abort technique, the search process is sped up by iteratively filtering out half of the message pairs at each step. The cost of computing each additional bit constraint on \(\beta _{2}\) equals to \(\frac{11}{1600} \cdot \frac{1}{6} = 2^{-9.8}\) 6-round SHAKE128 computation as 11 bits of \(\alpha _{2}\) states are involved. When checking all the \(2^{132}\) message pairs with one bit constraint, only half of the pairs satisfy the restriction while the other half are discarded, i.e., the so-called early-abort. For the remaining message pairs, another bit constraint will be checked and filter out half of those message pairs. This iterative process continues on the surviving message pairs until all the bit constraints on \(\beta _{2}\) are checked.
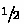 of the messages stop by first bit constraint,
of the messages stop by first bit constraint, 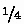 by the second bit constraint,
by the second bit constraint,  by the third bit etc. Hence the time complexity would be
by the third bit etc. Hence the time complexity would be  = \(2^{123.2}\) 6-round SHAKE128 computations.
= \(2^{123.2}\) 6-round SHAKE128 computations. -
In the connector construction phase, the time complexity corresponds to the time used to construct \(2^{105}\) (i.e.,
 ) connectors. Let’s first discuss the equivalent conversion of implementation efficiency between connector construction and 6-round SHAKE128. The computation cost of 6-round SHAKE128 is \(6\cdot (\underbrace{(4\cdot 320 + 2\cdot 1600)}_{\theta }+\underbrace{3\cdot 1600}_{\chi }+\underbrace{64}_{\iota })=56064\) bitwise operations. Further, solving systems of linear equations dominates the time of connector constructionFootnote 7. The time complexity of Gauss-Jordan elimination for system of boolean equations is \(\mathcal {O}{(m^2n)}\) bitwise operations [HJ12], where m is the number of equations and n is the number of variables. In the worst case, there are 1600 non-redundant equations in the final system, i.e., \(m=1600\). The complexity would be no greater than \(1600^3=4.096\times 10^{9}\) bitwise operations. Consequently, time cost of constructing a connector equals to
) connectors. Let’s first discuss the equivalent conversion of implementation efficiency between connector construction and 6-round SHAKE128. The computation cost of 6-round SHAKE128 is \(6\cdot (\underbrace{(4\cdot 320 + 2\cdot 1600)}_{\theta }+\underbrace{3\cdot 1600}_{\chi }+\underbrace{64}_{\iota })=56064\) bitwise operations. Further, solving systems of linear equations dominates the time of connector constructionFootnote 7. The time complexity of Gauss-Jordan elimination for system of boolean equations is \(\mathcal {O}{(m^2n)}\) bitwise operations [HJ12], where m is the number of equations and n is the number of variables. In the worst case, there are 1600 non-redundant equations in the final system, i.e., \(m=1600\). The complexity would be no greater than \(1600^3=4.096\times 10^{9}\) bitwise operations. Consequently, time cost of constructing a connector equals to  6-round SHAKE128. The time complexity in connector construction is equivalent to \(2^{105}\cdot 2^{16.2}=2^{121.2}\) 6-round SHAKE128 computations.
6-round SHAKE128. The time complexity in connector construction is equivalent to \(2^{105}\cdot 2^{16.2}=2^{121.2}\) 6-round SHAKE128 computations.
In total, time complexity of the classical collision attack is \(2^{123.2}+2^{121.2}=\) \(2^{123.5}\) 6-round SHAKE128 computations. Complexity of quantum collision attackFootnote 8 is  .
.
Table 3 gives an overview of the time complexity tradeoff between brute force search phase and connector construction phase according to the number of constraints on \(\beta _{2}\) solved. The more the constraints are solved, the smaller the DF of connectors is, the better the brute force complexity is and the worse the connector complexity is.
Remark 3
Experiments on \(2^{14.3}\) connectors show that solving systems of equations dominates the time of connector construction. In particular,
-
when fully linearizing the first round, due to the large DF, almost all Sboxes are successfully linearized in the first try and very occasionally it needs extra tries;
-
when partially linearizing the second round where no more than 40 constraints are treated, about 1/3 tests succeed with the first or a second try for each Sbox while around 2/3 tests collapse and we should start the partial linearizing process again. But as this process consumes 0.01s on average (compared with 0.8s used to construct the whole connector) it won’t affect the complexity analysis.
Overall, neglected time is consumed in listing equations which is consistent with the observations from [GLL+20].
Remark 4
Experimental results outlined in Table 4 conforms to the theoretical complexity analysis of the connector construction phase. The average execution time of each connector construction (denoted by \(T_c\)) is 0.8 s. In our C++ implementation, around \(2^{20}\) 6-round SHAKE128 are computed in each second. The time of connector construction equals to \(2^{105}\cdot 2^{19.67}=2^{124.67}\) SHAKE128 computations which validates the attack.
4.3 Quantum Collision Attack Against 6-Round SHA3-256
The colliding trail used in 6-round collision attacks on SHAKE128 is also used in attacks on SHA3-256 and SHA3-224. As shown in Fig. 7, the 6-round collision attack on SHA3-256 consists of a 2-round connector and a 4-round colliding trail. Note that, the \((\beta _1,\beta _2)\) used in the attack on SHAKE128 is also applied here. The entire 6-round differential trail is given in Table 5, i.e., Trail No.1 in supplementary material B. The 2-round connector solves 226 out of the total 264 conditions imposed by (\(\beta _1\),\(\alpha _2\)). The solution space of the 2-round connector ensures a subspace of message pairs that follow partial \(\alpha _2\) difference as expected. In our experiment, the 2-round connector is constructed in 3 s on average. The DF of the connector is 5. Or to put it differently, the size of the solution space is \(2^{5}\). Example of a pair of messages that follow the connector is given in Table 11 of supplementary material B.
The unsolved conditions (i.e., 38 left) of (\(\beta _1\),\(\alpha _2\)) are treated together with the colliding trail whose weight is \(116+24+20+8=168\). In classical settings, the time complexity of the brute force phase is \(2^{38}\cdot 2^{168}=2^{206}\) 6-round SHA3-256 computations with which a valid collision attack cannot be conducted. However, such differential trails of low probability can be exploited in quantum settings.
Quantum Collision Attack. As stated in [HS21], no existing quantum collision attack on a random function could outperform classical attack based on parallel rho method [VOW94] in terms of time-space tradeoff. We follow their way and consider a quantum collision attack valid if its time complexity is less than  , where n denotes the digest length, and S is the hardware size required for the attack (or in other words, S is the maximum size of quantum computers and classical computers). Note that instead of designing concrete quantum circuits matching the theoretical bound of time-space tradeoff, the authors of [HS21] assume such quantum circuits exist already and concentrate on complexity evaluation of the quantum attacks. We adopt the same strategy in [HS21] to mount the 6-round quantum collision attack on SHA3-256.
, where n denotes the digest length, and S is the hardware size required for the attack (or in other words, S is the maximum size of quantum computers and classical computers). Note that instead of designing concrete quantum circuits matching the theoretical bound of time-space tradeoff, the authors of [HS21] assume such quantum circuits exist already and concentrate on complexity evaluation of the quantum attacks. We adopt the same strategy in [HS21] to mount the 6-round quantum collision attack on SHA3-256.
Suppose there exists a quantum circuit \(\mathcal {C}_1\) for the connector construction of depth \(T_c\) and width \(S_c\). That is, the quantum circuit constructs a connector in time \(T_c\) with \(S_c\) qubits. Similarly, suppose there exists another quantum circuit \(\mathcal {C}_2\) of depth \(T_s \) and width \(S_s\) for the one-block SHA-3 variants, i.e., the quantum implementation of the 6-round targets (in this case SHA3-256). The idea that converts the classical attacks to the quantum collision attacks is described as follows.
-
1.
Prepare message pairs \((M,M')\) with the quantum circuit \(\mathcal {C}_1\).
-
2.
For each \((M,M')\) pair, compute the digests with quantum circuit \(\mathcal {C}_2\), and check whether they are identical.
-
3.
Repeat the above two steps until a collision is found.
Complexity. Considering the solution space of the 2-round connector (which is \(2^5\)), \(2^{201}\) connectors are needed in theory. There are simply two kinds of operations in the quantum implementation of connectors, namely, listing the system of boolean equations and solving it with Gaussian-Jordan elimination, both of which are linear operations. Compared with \(T_s\) of the nonlinear SHA-3 variants (or more specific the \(\chi \) operation), the depth \(T_c\) of \(\mathcal {C}_1\) where only linear operations are involved is negligible [AMG+16]. Hence, time complexity of quantum collision attack is dominated by the time complexity of the exhaustive search phase.
Suppose we have a quantum computer of size S, taking parallelization into account, the time complexity of Grover search [Gro96] in the exhaustive search phase is

where p is the probability of finding a collision in the classical setting, and \(T_A\) (resp. \(S_A\)) is the depth (resp. width) of the quantum collision attack. The depth (resp. width) of the quantum circuits of the SHA-3 variants (i.e., \(\mathcal {C}_2\)) are defined as the unit depth (resp. width), meaning that \(T_s=1\) and \(S_s=1\). Specifically, as the state size and the digest size are \(2\times 1600+256=3456\) bits, we regard at least 3456 qubits are required in circuit \(\mathcal {C}_2\). The overall depth and width are evaluated with the following analysis.
-
Depth (\(T_A\)). As \(T_c\) is negligible, \(T_A=T_s=1\).
-
Width (\(S_A\)). In the quantum circuits of connectors (i.e., \(\mathcal {C}_1\)), the quantum states include (1) the auxiliary m qubits (as there are 264 conditions, \(m= 264\) ) that mark whether a condition will be treated or not in the partial linearizing step and (2) the \(k\times 1601\) qubits that store the k boolean equations (\(k\le 1600\)) of the system of linear equations. The overall
 Footnote 9.
Footnote 9.
Therefore, the total time complexity of the quantum collision attack on 6-round SHA3-256 is

Comparing to the generic attack cost under the time-space metric which is  , our quantum collision attack is valid as long as \(S\le 2^{47.5}\).
, our quantum collision attack is valid as long as \(S\le 2^{47.5}\).
Remark 5
In the quantum search, we should prepare \(2^{206}\) messages which brings to the concern that whether it’s possible to construct so many connectors. This concern could be answered through introducing multi-blocks. The first block (which is identical for the two messages) provides distinct capacity bits at each time which are used to construct different connectors of the same connecting trails. We can try as many as \(2^{512}\) first blocks which are sufficient for the attack.
4.4 Quantum Collision Attack Against 6-Round SHA3-224
As shown in Fig. 8, the 6-round trail of SHA3-224 (which is listed in Table 6 of supplementary material B) is comprised of the same colliding trail used in attacks on SHAKE128 and SHA3-256 and a 2-round connecting trail searched with the SAT-based tool. In our experiment, the 2-round connectors are averagely constructed in 3 s. The size of the solution space is \(2^{22}\). Example of a pair of messages that follow the connector is given in Table 12 of supplementary material B. The 2-round connector solves 240 out of the 268 conditions imposed by the (\(\beta _1\),\(\alpha _2\)) differential. Therefore, the classical complexity of the brute-force phase is \(2^{28+113+24+20+8} =2^{193}\) 6-round SHA3-224 computations. Similar to the attack on SHA3-256, we mount 6-round quantum collision attack on SHA3-224. Likewise, we adopt the strategy utilized in [HS21]. Suppose we have a quantum computer of size S, the complexity of our attack is

under the time-space metric  , and the quantum collision attack is faster than the generic attack when \(S\le 2^{28.5}\).
, and the quantum collision attack is faster than the generic attack when \(S\le 2^{28.5}\).
5 Conclusion
We investigate the previous collision attacks on SHA-3, identify the limitations of ideas, methods, and techniques employed in those attacks, and summarize directions that can be improved to mount collision attacks on SHA-3 that cover more rounds. Briefly, if the colliding trails that cover more rounds and connecting trails that promise more degree of freedom in constructing connectors are generated, the collision attacks are most likely to be improved. The major challenge lies in the fact that differential trails of Keccak-\(f\) permutation are difficult to search as the large state size results in a search space that is too enormous to be covered effectively. Luckily, we observe that the automatic search tool, i.e., the SAT solver performs extraordinarily well in modeling the differential propagation of Keccak-\(f\). In this work, a powerful SAT-based automatic search toolkit is proposed to overcome the clarified challenges. We demonstrate that the SAT-based trail search methods are applicable to all kind of analytic scenarios where trails are involved. With the SAT-based toolkit, advanced collision attacks on SHA-3 instances are presented. Totally, a 6-round collision attack on SHAKE128 of complexity \(2^{123.5}\), a 6-round quantum collision attack on SHA3-256 of complexity  , and a 6-round quantum collision attack on SHA3-224 of complexity
, and a 6-round quantum collision attack on SHA3-224 of complexity  are proposed. It’s not only that the 6-round classical and quantum collision attacks are introduced for the first time but also shows that quantum collision attack is able to cover more rounds or targets than classical collision attacks.
are proposed. It’s not only that the 6-round classical and quantum collision attacks are introduced for the first time but also shows that quantum collision attack is able to cover more rounds or targets than classical collision attacks.
Notes
- 1.
The preimage attack on 3-round Keccak-256 in [LHY21] has a time complexity \(2^{65}\), but no concrete preimage is given.
- 2.
In this attack model, collision messages of 1-block are generated. The constraints imposed by the sponge construction include (1) the c-bit capacity, i.e., c continuous “0” bits, and (2) 2-bit padding “11” which is concatenated with a “01” or “1111” string at the tail of the message block.
- 3.
The practical algorithms are much more complex. We just describe in this abstract way to express basic ideas.
- 4.
The propagation weight is defined as the opposite of the binary logarithm of the propagation probability. For example, if the propagation probability of a differential trail is \(2^{-32}\), the corresponding weight is 32.
- 5.
The other \(\beta _1\) Sboxes that are not treated are indicated with red block in Fig. 5.
- 6.
Indeed, the size of solution space is not always \(2^{27}\) (or DF=27). This is an average number calculated from our experiments repeated on \(2^{14.3}\) connectors.
- 7.
Refer to Remark 3 for more discussion on the cost of connectors.
- 8.
Complexity analysis of quantum collision attack will be illustrated in Sect. 4.3.
- 9.
More auxiliary qubits may be required for intermediate variables (e.g., in greedy algorithm and Gaussian-Jordan elimination) in \(\mathcal {C}_1\). Those variables are of the state size multiplied by a constant. As the worst case of Gaussian-Jordan elimination is considered and \(\mathcal {C}_2\) also contains intermediate variables, this evaluation is reasonable.
References
Amy, M., Di Matteo, O., Gheorghiu, V., Mosca, M., Parent, A., Schanck, J.: Estimating the cost of generic quantum pre-image attacks on SHA-2 and SHA-3. In: Avanzi, R., Heys, H. (eds.) SAC 2016. LNCS, vol. 10532, pp. 317–337. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69453-5_18
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Sponge functions. In: ECRYPT Hash Workshop, vol. 2007. Citeseer (2007)
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Keccak. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 313–314. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_19
Bernstein, D.J.: Second preimages for 6 (7?(8??)) rounds of keccak. NIST mailing list (2010)
Bao, Z., Guo, J., Li, S., Pham, P.: Quantum multi-collision distinguishers (2020)
Brassard, G., HØyer, P., Tapp, A.: Quantum cryptanalysis of hash and claw-free functions. In: Lucchesi, C.L., Moura, A.V. (eds.) LATIN 1998. LNCS, vol. 1380, pp. 163–169. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054319
Bertoni, G., Peeters, M., Van Assche, G., et al. The keccak reference (2011)
Chang, D., Kumar, A., Morawiecki, P., Sanadhya, S.K.: 1st and 2nd Preimage Attacks on 7, 8 and 9 Rounds of Keccak-224,256,384,512. SHA-3 workshop, August 2014
Chailloux, A., Naya-Plasencia, M., Schrottenloher, A.: An efficient quantum collision search algorithm and implications on symmetric cryptography. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10625, pp. 211–240. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_8
Dinur, I., Dunkelman, O., Shamir, A.: New attacks on keccak-224 and keccak-256. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 442–461. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34047-5_25
Dinur, I., Dunkelman, O., Shamir, A.: Collision attacks on up to 5 rounds of SHA-3 using generalized internal differentials. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 219–240. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43933-3_12
Dinur, I.: Dunkelman, orr, shamir, adi: improved practical attacks on round-reduced keccak. J. Cryptol. 27(2), 183–209 (2014)
Dong, X., Sun, S., Shi, D., Gao, F., Wang, X., Hu, L.: Quantum aHashing with Low Quantum Random Access Memories. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12492, pp. 727–757. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64834-3_25
Daemen, Joan, Van Assche, Gilles: Differential propagation analysis of Keccak. In: Canteaut, Anne (ed.) FSE 2012. LNCS, vol. 7549, pp. 422–441. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34047-5_24
Dworkin, M.J.: SHA-3 standard: Permutation-based hash and extendable-output functions (2015)
Guido, B., Joan, D., Michaël, P., Gilles, V.A.: Cryptographic sponge functions (2011)
Guo, J.: Liao, Guohong, Liu, Guozhen, Liu, Meicheng, Qiao, Kexin, Song, Ling: Practical collision attacks against round-reduced sha-3. J. Cryptol. 33(1), 228–270 (2020)
Guo, J., Liu, M., Song, L.: Linear structures: applications to cryptanalysis of round-reduced Keccak. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 249–274. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_9
Guo, J., Liu, G., Song, L., Tu, Y.: Exploring SAT for cryptanalysis: (Quantum) collision attacks against 6-Round SHA-3 (Full Version) (2022). https://eprint.iacr.org/2022/184
Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, pp. 212–219 (1996)
Han, C.-S., Jiang, J.-H.R.: When Boolean satisfiability meets gaussian elimination in a simplex way. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 410–426. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_31
He, L., Lin, X., Hongbo, Yu.: Improved preimage attacks on 4-round keccak-224/256. IACR Trans. Symmetric Cryptol. 2021(1), 217–238 (2021)
Hosoyamada, A., Sasaki, Y.: Finding hash collisions with quantum computers by using differential trails with smaller probability than birthday bound. In: Advances Cryptology-EUROCRYPT, vol. 249, p. 12106 (2020)
Hosoyamada, A., Sasaki, Y.: Quantum collision attacks on reduced sha-256 and sha-512. IACR Cryptol. ePrint Arch. 292 (2021)
Lin, X., He, L., Hongbo, Y.: Improved preimage attacks on 3-round KECCAK-224/256. IACR Trans. Symmetric Cryptol.2021(3), 84–101 (2021)
Liu, G., Qiu, W., Tu, T.: New techniques for searching differential trails in keccak. IACR Trans. Symmet. Cryptol. 2019, 407–437 (2019)
Ting Li and Yao Sun. Preimage attacks on round-reduced KECCAK-224/256 via an allocating approach. In Yuval Ishai and Vincent Rijmen, editors, Advances in Cryptology - EUROCRYPT 2019–38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, May 19–23, 2019, Proceedings, Part III, volume 11478 of LNCS, pages 556–584. Springer, 2019
Li, T.: Sun, Yao, Liao, Maodong, Wang, Dingkang: Preimage attacks on the round-reduced KECCAK with cross-linear structures. IACR Trans. Symmetric Cryptol. 2017(4), 39–57 (2017)
Mella, S., Daemen, J.J.C., Van Assche, G.: New techniques for trail bounds and application to differential trails in Keccak . IACR Trans. Symmet. Cryptol. 2017(1), 329–357 (2017)
Mouha, N., Preneel, B.: Towards finding optimal differential characteristics for ARX: application to salsa20. Cryptology ePrint Archive, Report 2013/328 (2013). https://eprint.iacr.org/2013/328
Morawiecki, P., Pieprzyk, J., Srebrny, M.: Rotational cryptanalysis of round-reduced Keccak. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 241–262. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43933-3_13
Morawiecki, P.: Srebrny, Marian: a sat-based preimage analysis of reduced Keccak hash functions. Inf. Process. Lett. 113(10–11), 392–397 (2013)
Naya-Plasencia, M., Röck, A., Meier, W.: Practical analysis of reduced-round Keccak. In: Bernstein, D.J., Chatterjee, S. (eds.) INDOCRYPT 2011. LNCS, vol. 7107, pp. 236–254. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25578-6_18
Qiao, K., Song, L., Liu, M., Guo, J.: New collision attacks on round-reduced keccak. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 216–243. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_8
SEPARATE DECISION QUEUE. Cadical at the sat race 2019. SAT RACE 2019, p. 8 (2019)
Rajasree, M.S.: Cryptanalysis of round-reduced KECCAK using non-linear structures. In: Hao, F., Ruj, S., Sen Gupta, S. (eds.) INDOCRYPT 2019. LNCS, vol. 11898, pp. 175–192. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-35423-7_9
Soos, M., Biere, A., Heule, M., Jarvisalo, M., Suda, M.: Cryptominisat 5.6 with yalsat at the sat race 2019. In: Proceedings of SAT Race, pp. 14–15 (2019)
Soos, M., Devriendt, J., Gocht, S.,. Shaw, A., Meel, K.S.: CryptoMiniSat with CCAnr at the sat competition 2020. In: SAT Competition , p. 27 (2020)
Sinz, C.: Towards an optimal CNF encoding of Boolean cardinality constraints. In: van Beek, P. (ed.) CP 2005. LNCS, vol. 3709, pp. 827–831. Springer, Heidelberg (2005). https://doi.org/10.1007/11564751_73
Song, L., Liao, G., Guo, J.: Non-full Sbox linearization: applications to collision attacks on round-reduced Keccak. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 428–451. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_15
Soos, M., Nohl, K., Castelluccia, C.: Extending SAT solvers to cryptographic problems. In: Kullmann, O. (ed.) SAT 2009. LNCS, vol. 5584, pp. 244–257. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02777-2_24
Soos, M., Nohl, K., Castelluccia, K.: Cryptominisat, SAT Race solver descriptions (2010)
Soos, M.: Cryptominisat v4. SAT Competition, p. 23 (2014)
Soos, M.: The CryptoMiniSat 5 set of solvers at sat competition 2016. In: Proceedings of SAT Competition, p. 28 (2016)
Soos, M., Selman, B., Kautz, H., Devriendt, J., Gocht, S.: CryptoMiniSat with Walksat at the SAT competition 2020. In: SAT Competition 2020, pp. 29 (2020)
Sun, L., Wang, W., Wang. M.: More accurate differential properties of led64 and midori64. IACR Trans. Symmet. Cryptol. 2018, 93–123 (2018)
Sun, L., Wang, W., Wang, W.: Accelerating the search of differential and linear characteristics with the sat method. IACR Trans. Symmet. Cryptol. 2021, 269–315 (2021)
Van Oorschot, P.C., Wiener, M.J.: Parallel collision search with application to hash functions and discrete logarithms. In: Proceedings of the 2nd ACM Conference on Computer and Communications Security, pp. 210–218 (1994)
Acknowledgements
This research is partially supported by Nanyang Technological University in Singapore under Start-up Grant 04INS000397C230, and Ministry of Education in Singapore under Grants RG91/20 and MOE2019-T2-1-060. Ling Song is supported by the National Natural Science Foundation of China (Grants 62022036, 62132008).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Guo, J., Liu, G., Song, L., Tu, Y. (2022). Exploring SAT for Cryptanalysis: (Quantum) Collision Attacks Against 6-Round SHA-3. In: Agrawal, S., Lin, D. (eds) Advances in Cryptology – ASIACRYPT 2022. ASIACRYPT 2022. Lecture Notes in Computer Science, vol 13793. Springer, Cham. https://doi.org/10.1007/978-3-031-22969-5_22
Download citation
DOI: https://doi.org/10.1007/978-3-031-22969-5_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-22968-8
Online ISBN: 978-3-031-22969-5
eBook Packages: Computer ScienceComputer Science (R0)





 and
and  respectively, are mounted. To the best of our knowledge, this is the first time that quantum collision attacks are mounted on
respectively, are mounted. To the best of our knowledge, this is the first time that quantum collision attacks are mounted on 





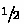 of the messages stop by first bit constraint,
of the messages stop by first bit constraint, 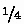 by the second bit constraint,
by the second bit constraint,  by the third bit etc. Hence the time complexity would be
by the third bit etc. Hence the time complexity would be  =
=  ) connectors. Let’s first discuss the equivalent conversion of implementation efficiency between connector construction and 6-round
) connectors. Let’s first discuss the equivalent conversion of implementation efficiency between connector construction and 6-round  6-round
6-round 

