Abstract
OMAC — a single-keyed variant of CBC-MAC by Iwata and Kurosawa — is a widely used and standardized (NIST FIPS 800-38B, ISO/IEC 29167-10:2017) message authentication code (MAC) algorithm. The best security bound for OMAC is due to Nandi who proved that OMAC ’s pseudorandom function (PRF) advantage is upper bounded by \( O(q^2\ell /2^n) \), where n, q, and \( \ell \), denote the block size of the underlying block cipher, the number of queries, and the maximum permissible query length (in terms of n-bit blocks), respectively. In contrast, there is no attack with matching lower bound. Indeed, the best known attack on OMAC is the folklore birthday attack achieving a lower bound of \( \varOmega (q^2/2^n) \). In this work, we close this gap for a large range of message lengths. Specifically, we show that OMAC ’s PRF security is upper bounded by \( O(q^2/2^n + q\ell ^2/2^n)\). In practical terms, this means that for a 128-bit block cipher, and message lengths up to 64 GB, OMAC can process up to \( 2^{64} \) messages before rekeying (same as the birthday bound). In comparison, the previous bound only allows \( 2^{48} \) messages. As a side-effect of our proof technique, we also derive similar tight security bounds for XCBC (by Black and Rogaway) and TMAC (by Kurosawa and Iwata). As a direct consequence of this work, we have established tight security bounds (in a wide range of \(\ell \)) for all the CBC-MAC variants, except for the original CBC-MAC.
A. Jha carried out this work in the framework of the French-German-Center for Cybersecurity, a collaboration of CISPA and LORIA.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Message Authentication Code (or, MAC) algorithms are symmetric-key primitives which are used for data authenticity and integrity. The sender generates a short tag based on message and a secret key which can be recomputed by any authorized receiver. MACs are commonly designed either based on a hash function or a block cipher. CBC-MAC is a block cipher-based MAC (message authentication code) which is based on the CBC mode of operation invented by Ehrsam et al. [11]. Given an n-bit block cipher E instantiated with a key K, the CBC-MAC construction is defined recursively as follows: for any \(x \in \{0,1\}^n\), \(\textsf {CBC} _{E_K}(x):=E_K(x)\). For all \(m=(m[1],\ldots ,m[\ell ]) \in (\{0,1\}^n)^{\ell }\) where \(\ell \ge 2\), we define
It was an international standard, and has been proven secure for fixed-length messages or prefix-free message spaces (i.e., no message is a prefix to another message). Simple length extension attacks prohibit its usage for arbitrary length messages. However, appropriately chosen operations to process the last block can resist these attacks. One such idea was first applied in EMAC [2, 4], where the CBC-MAC output was encrypted using an independently keyed block cipher. It worked for all messages with lengths that are divisible by the block size of the underlying block cipher. Black and Rogaway proposed [5] three-keyed constructions, ECBC, FCBC, and XCBC, which are proven to be secure against adversaries querying arbitrary length messages. Later, in back-to-back works, Iwata and Kurosawa proposed two improved constructions (in terms of the key size), namely, TMAC [17] that uses two keys, and OMACFootnote 1 [12] that requires just a single key. Nandi proposed [20] GCBC1 and GCBC2, a slight improvement over OMAC in terms of the number of block cipher calls for multi-block messages.
1.1 Related Works and Motivation
It is well-established [1] that the security of any deterministic MAC can be quantified via the pseudorandom function (or PRFFootnote 2) security. Consequently, most of the works on CBC-MAC variants analyze their PRF security. For constructions like ECBC, FCBC and EMAC, Pietrzak [25] showed a PRF bound of \(O(q^2/2^n)\) for \(\ell < 2^{n/8}\), where q and \(\ell \) denote the number of messages and the maximum permissible length (no. of n-bit blocks) of the messages. Later, Jha and Nandi [15] discovered a flaw in the proof of the earlier bound and showed a bound of \(O(q/2^{n/2})\) up to \(\ell < 2^{n/4}\). However, in these constructions an extra (independent) block cipher is called at the end. Considering the number of block cipher calls, XCBC, TMAC and OMAC are better choices. XCBC uses two independent masking keys for the last block which are used depending on whether the last block is padded or not. In case of TMAC, the two masking keys are derived from a single n-bit key. OMAC optimized the key derivation further. Here, both the keys are derived using the underlying block cipher itself. Thus, it is much better in this respect. Classical bound for these constructions was \(O(\sigma ^2/2^n)\) [5, 17], \(\sigma \) being the total number blocks among all the messages. Later, in a series of work [13, 19, 21, 22], the improved bounds for XCBC, TMAC, and OMAC were shown to be in the form of \( O(q^2\ell /2^n) \), \( O(\sigma ^2/2^n) \) and \( O(\sigma q/2^n) \). Interestingly, it has also been shown in [14] that if we use a PRF, instead of a block cipher in these constructions, there is an attack with roughly \(\varOmega (q^2\ell /2^n)\) advantage, which is tight. No such attack is known in the presence of a block cipher. This gives an implicit motivation to study the exact security of these constructions in the presence of block ciphers. In this paper, we aim to show birthday-bound security for these block cipher based MACs for a suitable range of message lengths.
In a different paradigm but with similar motivations, recently Chattopadhyay et al. [8] showed birthday-bound security for another standardized MAC called LightMAC [18]. However, similar result for original PMAC [6] is still an open problem (although a result is available for its variant in [7]). In addition to the improved bound for LightMAC, Chattopadhyay et al. proposed a new proof approach called the reset-sampling method. They also hinted (via a very brief discussion) that this method could be useful for proving better security for OMAC. However, the discussion in [8] is overly simplistic and contains no formal analysis of bad events. Indeed, the reset-sampling is more involved than anticipated in [8], giving rise to some crucial and tricky bad events (see Sect. 4). To their credit, they do say that
A more formal and rigorous analysis of OMAC using reset-sampling will most probably require handling of several other bad events, and could be an interesting future research topic.
In this paper, we take up this topic and give a complete and rigorous analysis.
1.2 Our Contributions
In Sect. 3, we show that the PRF advantages for OMAC, XCBC and TMAC are upper bounded by \( O\left( {q^2}/{2^n}\right) + O\left( {q}\ell ^2/{2^n}\right) \), which is almost tight in terms of the number of queries q while \( \ell \ll 2^{n/4} \). This bound is not exactly the birthday bound \(O\left( {q^2}/{2^n}\right) \), but for any fixed target advantage, in terms of the limit on q it behaves almost like the birthday bound for a fairly good range of \(\ell \) (see the following discussion). The proof of our security bound is given in Sect. 4 and follows the recently introduced reset-sampling approach [8]. These improved bounds, in combination with previous results [15, 16] for EMAC, ECBC and FCBC, completely characterize (see Table 1) the security landscape of CBC-MAC variants for message lengths up to \( 2^{n/4} \) blocks.
A Note on the Tightness and Improvement in Bounds: In Fig. 1, we present a graphFootnote 3 comparing the best known bound for OMAC [21], i.e., \(B_1(\ell ,q)=10q^2\ell /2^n\), the ideal birthday bound, i.e., \(B_{\textsf{id}} = q^2/2^n\), and the bound shown in this paper (see Theorem 3.1), i.e., \(B_2(\ell , q) \approx \frac{16q^2}{2^n}+\frac{2q\ell ^2}{2^n}\) (as the remaining terms are dominated by these two terms). In the graph, we show the trade-off curve for the parameters \(X = \log \ell \) and \(Y = \log q\), where \(\log \) denotes “log base 2”, for a fixed choice of advantage value, say \(\epsilon =2^{-a}\) for some \(a \in \mathbb {N}\). Let \( n_a := n-a \). Then, we have
Looking at the equation related to the bound \(B_2\) we can see that it is actually a combination of two linear equations: \(2Y=n_a-4\) and \(2X+Y=n_a-1\), the choice depending on whether \(16q^2/2^n\) or \(2q\ell ^2/2^n\) dominates. Precisely, the curve expressing the relation between \(\log \ell \) and \(\log q\) in \(B_2\) is \(\{(X,Y): X \le n/4, Y=\min \{(n_a-4)/2, n_a-1-2X\}\}\). From the above linear equations two important facts about the curve related to \(B_2\) can be noticed:
-
It remains very close to the straight line corresponding to \(B_{\textsf{id}}\) from \((0,\frac{n_a-4}{2})\) to \((\frac{n_a+2}{4},\frac{n_a-4}{2})\) and then moves downward.
-
At around \((\frac{n_a+1}{3},\frac{n_a-5}{3})\) it starts to degrade below the curve related to \(B_1\) .
For example, if we take \((n,a)=(128,32)\), the bound proved in this paper is very close to the birthday bound for \(\ell \le 2^{25}\) and even after degrading, it remains better than the bound in [21] till \(\ell \le 2^{32}\). Moreover, if we take \((n,a)=(128,64)\), q remains \(2^{30}\) until \(\ell \le 2^{16}\) and degrades below the existing bound only after \(\ell \ge 2^{22}\). Thus, if we consider the advantage in general terms, we can always take the minimum among the advantage proved in this paper and that proved in [21].
\((\log \ell , \log q)\)-Trade-off Graph for the bounds of OMAC. For \( n=128 \), and two different choices of the target advantage, \( \epsilon = 2^{-1} \) (on the left), and \( \epsilon = 2^{-64} \) (on the right), the above graphs show the relation between \(X = \log \ell \) and \(Y = \log q\). The dashed, dotted and continuous curves represent the equations \(B_{\textsf{id}}\), \(B_1\), and \(B_2\), respectively.
2 Preliminaries
For \( n \in \mathbb {N}\), [n] and (n] denote the sets \( \{1,2,\ldots ,n\} \) and \( \{0\} \cup [n] \), respectively. The set of all bit strings (including the empty string \( \bot \)) is denoted \( \{0,1\}^* \). The length of any bit string \( x \in \{0,1\}^* \), denoted |x| , is the number of bits in x. For \( n \in \mathbb {N}\), \( \{0,1\}^n \) denotes the set of all bit strings of length n, and \( \{0,1\}^{\le n} := \bigcup _{i=0}^{n} \{0,1\}^i \). For \( x,y \in \{0,1\}^* \), \( z = x\Vert y \) denotes the concatenation of x and y. Additionally, x (resp. y) is called the prefix (resp. suffix) of z. For \( x,y\in \{0,1\}^* \), let \( \textsf{Prefix}(x,y) \) denote the length of the largest possible common prefix of x and y. For \( 1 \le k \le n \), we define the falling factorial \( (n)_k := n!/(n-k)! = n(n-1)\cdots (n-k+1) \). Any pair of q-tuples \( \widetilde{x} = (x_1,\ldots ,x_q) \) and \( \widetilde{y} = (y_1,\ldots ,y_q) \), are said to be permutation compatible, denoted \( \widetilde{x} \leftrightsquigarrow \widetilde{y} \), if \( (x_i = x_j) \iff (y_i = y_j) \), for all \( i \ne j \). By an abuse of notation, we also use \( \widetilde{x} \) to denote the set \( \{x_i : i \in [q]\} \) for any \( \widetilde{x} \).
2.1 Security Definitions
Distinguishers: A (q, T) -distinguisher \( \mathscr {A}\) is an oracle Turing machine, that makes at most q oracle queries, runs in time at most T, and outputs a single bit. For any oracle \( \mathcal {O}\), we write \( \mathscr {A}^{\mathcal {O}} \) to denote the output of \( \mathscr {A}\) after its interaction with \( \mathcal {O}\). By convention, \( T = \infty \) denotes computationally unbounded (information-theoretic) and deterministic distinguishers. In this paper, we assume that the distinguisher is non-trivial, i.e., it never makes a duplicate query. Let \( \mathbb {A}(q,T) \) be the class of all non-trivial distinguishers limited to q queries and T computations.
Primitives and Their Security: The set of all functions from \( \mathcal {X}\) to \( \mathcal {Y}\) is denoted \( \mathcal {F}(\mathcal {X},\mathcal {Y}) \), and the set of all permutations of \( \mathcal {X}\) is denoted \( \mathcal {P}(\mathcal {X}) \). We simply write \( \mathcal {F}(a,b) \) and \( \mathcal {P}(a) \), whenever \( \mathcal {X}= \{0,1\}^a \) and \( \mathcal {Y}= \{0,1\}^b \). For a finite set \( \mathcal {X}\),  denotes the uniform at random sampling of \( \textsf{X} \) from \( \mathcal {X}\).
denotes the uniform at random sampling of \( \textsf{X} \) from \( \mathcal {X}\).
Pseudorandom Function: A \( (\mathcal {K},\mathcal {X},\mathcal {Y}) \)-keyed function \( {F}\) with key space \( \mathcal {K}\), domain \( \mathcal {X}\), and range \( \mathcal {Y}\) is a function \( {F}: \mathcal {K}\times \mathcal {X}\rightarrow \mathcal {Y}\). We write \( {F}_k(x) \) for \( {F}(k,x) \).
The pseudorandom function or PRF advantage of any distinguisher \( \mathscr {A}\) against a \( (\mathcal {K},\mathcal {X},\mathcal {Y}) \)-keyed function \( {F}\) is defined as

The PRF insecurity of \( {F}\) against \( \mathbb {A}(q,T) \) is defined as
Pseudorandom Permutation: For some \( n \in \mathbb {N}\), a \( (\mathcal {K},\mathcal {B}) \)-block cipher \( {E}\) with key space \( \mathcal {K}\) and block space \(\mathcal {B}:= \{0,1\}^n \) is a \( (\mathcal {K},\mathcal {B},\mathcal {B}) \)-keyed function, such that \( {E}(k,\cdot ) \) is a permutation over \( \mathcal {B}\) for any key \( k \in \mathcal {K}\). We write \( {E}_k(x) \) for \( {E}(k,x) \).
The pseudorandom permutation or PRP advantage of any distinguisher \( \mathscr {A}\) against a \( (\mathcal {K},\mathcal {B}) \)-block cipher \( {E}\) is defined as

The PRP insecurity of \( {E}\) against \( \mathbb {A}(q,T) \) is defined as
2.2 H-coefficient Technique
Let \( \mathscr {A}\) be a computationally unbounded and deterministic distinguisher that’s trying to distinguish the real oracle \( \mathcal {O}_1\) from the ideal oracle \( \mathcal {O}_0\). The collection of all queries and responses that \( \mathscr {A}\) made and received to and from the oracle, is called the transcript of \( \mathscr {A}\), denoted as \( \nu \). Let \( \textsf{V}_1\) and \( \textsf{V}_0\) denote the transcript random variable induced by \( \mathscr {A}\)’s interaction with \( \mathcal {O}_1\) and \( \mathcal {O}_0\), respectively. Let \( \mathcal {V}\) be the set of all transcripts. A transcript \( \nu \in \mathcal {V}\) is said to be attainable if \( {\Pr _{ }\left( \textsf{V}_0= \nu \right) } > 0 \), i.e., it can be realized by \( \mathscr {A}\)’s interaction with \( \mathcal {O}_0\).
Following these notations, we state the main result of the so-called H-coefficient technique [23, 24] in Theorem 2.1. A proof of this result is available in [24].
Theorem 2.1
[H-coefficient]. For \( \epsilon _1,\epsilon _2 \ge 0 \), suppose there is a set  , referred as the set of all bad transcripts, such that the following conditions hold:
, referred as the set of all bad transcripts, such that the following conditions hold:
-
 ; and
; and -
For any
 , \( \nu \) is attainable and \( \displaystyle \frac{{\Pr _{ }\left( \textsf{V}_1=\nu \right) }}{{\Pr _{ }\left( \textsf{V}_0=\nu \right) }} \ge 1-\epsilon _2 \).
, \( \nu \) is attainable and \( \displaystyle \frac{{\Pr _{ }\left( \textsf{V}_1=\nu \right) }}{{\Pr _{ }\left( \textsf{V}_0=\nu \right) }} \ge 1-\epsilon _2 \).
Then, for any computationally unbounded and deterministic distinguisher \( \mathscr {A}\), we have
Reset-Sampling Method: In H-coefficient based proofs, often we release additional information to the adversary in order to make it easy to define the bad transcripts. In such scenarios, one has to define how this additional information is sampled, and naturally the sampling mechanism is construction specific. The reset-sampling method [8] is a sampling philosophy, within this highly mechanized setup of H-coefficient technique, where some of the variables are reset/resampled (hence the name) depending upon the consistency requirement for the overall transcript. We employ this sampling approach in our proof.
3 The CBC-MAC Family
Throughout, n denotes the block size, \( \mathcal {B}:= \{0,1\}^n \), and any \( x \in \mathcal {B}\) is referred as a block. For any non-empty \( m \in \{0,1\}^* \), \( (m[1],\ldots ,m[\ell _m]) \xleftarrow {n} m \) denotes the block parsing of m, where \( \left| m[i]\right| = n \) for all \( 1 \le i \le \ell _m-1 \) and \( 1 \le \left| m[\ell _m]\right| \le n \). In addition, we associate a boolean flag \( \delta _m \) to each \( m \in \{0,1\}^* \), which is defined as
For any \( m \in \{0,1\}^{\le n} \), we define
CBC Function: The CBC function, based on a permutationFootnote 4 \( \pi \in \mathcal {P}(n) \), takes as input a non-empty message \( m \in \mathcal {B}^* \) and computes the output \( \textsf {CBC} _\pi (m) := y^{\pi }_{m}[\ell _m] \) inductively as described below:
\( y^\pi _{m}[0] = 0^n \) and for \( 1 \le i \le \ell _m \), we have
where \((m[1],\ldots ,m[\ell _m]) \xleftarrow {n} m \). For empty message, we define the CBC output as the constant \( 0^n \). Figure 2 illustrates the evaluation of CBC function over a 4-block message m.
Given the definition of \( \textsf {CBC} _\pi \), one can easily define all the variants of CBC-MAC. Here, we define XCBC, TMAC and OMAC— the three constructions that we study in this paper.
XCBC : The XCBC algorithm is a three-key construction, based on a permutation \( \pi \in \mathcal {P}(n) \) and keys \( (L_{-1},L_{0}) \in \mathcal {B}^2 \), that takes as input a non-empty message \( m \in \{0,1\}^* \), and computes the output
where \( (m[1],\ldots ,m[\ell _m]) \xleftarrow {n} m \), and \( m^{*} := m[1]\Vert \cdots \Vert m[\ell _m-1] \).
TMAC : The TMAC algorithm is a two-key construction, based on a permutation \( \pi \in \mathcal {P}(n) \) and key \( L\in \mathcal {B}\), that takes as input a non-empty message \( m \in \{0,1\}^* \), and computes the output
where \( (m[1],\ldots ,m[\ell _m]) \xleftarrow {n} m \), \( m^{*} := m[1]\Vert \cdots \Vert m[\ell _m-1] \), \( \mu _{-1} \) and \( \mu _0 \) are constants chosen from \( \textrm{GF}(2^{n})\) (viewing \( \mathcal {B}\) as \( \textrm{GF}(2^{n})\)), such that \( \mu _{-1},\mu _0,1\oplus \mu _{-1},1\oplus \mu _0 \) are all distinct and not equal to either 0 or 1, and \( \odot \) denotes the field multiplication operation over \( \textrm{GF}(2^{n})\) with respect to a fixed primitive polynomial. For the sake of uniformity, we define \( L_{\delta _m} := \mu _{\delta _m} \odot L\) in context of TMAC.
OMAC : The OMAC algorithm is a single-keyed construction, based on a permutation \( \pi \in \mathcal {P}(n) \), that takes as input a non-empty message \( m \in \{0,1\}^* \), and computes the output
where \( (m[1],\ldots ,m[\ell _m]) \xleftarrow {n} m \), \( m^{*} := m[1]\Vert \cdots \Vert m[\ell _m-1] \), \( \mu _{-1} \) and \( \mu _0 \) are constants chosen analogously as in the case of TMAC. For the sake of uniformity, we define \( L_{\delta _m} := \mu _{\delta _m} \odot \pi (0^n) \) in context of OMAC.
Input and Output Tuples: In the context of CBC evaluation within OMAC, we refer to \( x^\pi _{m} := (x^\pi _{m}[1],\ldots ,x^\pi _{m}[\ell _m-1]) \) and \( y^\pi _{m} := (y^\pi _{m}[0],\ldots ,y^\pi _{m}[\ell _m-1]) \) as the intermediate input and output tuples, respectively, associated to \( \pi \) and m. We define the final input variable as \( x^\pi _{m}[\ell _m] := y^\pi _{m}[\ell _m-1] \oplus \overline{m[\ell _m]} \oplus \mu _{\delta _m} \odot \pi (0^n) \). Clearly, the input and output tuples (including the final input) are well defined for OMAC. Analogous definitions are possible (and useful in proof) for XCBC and TMAC as well. It is worth noting that the intermediate input tuple \( x^\pi _{m} \) is uniquely determined by the intermediate output tuple \( y^\pi _{m} \) and the message m, and it is independent of the permutation \( \pi \). Going forward, we drop \( \pi \) from the notations, whenever it is clear from the context.
3.1 Tight Security Bounds for OMAC, XCBC and TMAC
The main technical result of this paper, given in Theorem 3.1, is a tight security bound for OMAC for a wide range of message lengths. The proof of this theorem is postponed to Sect. 4. In addition, we also provide similar result for XCBC and TMAC in Theorem 3.2. We skip the proof since it is almost identical to the one for Theorem 3.1, and has slightly less relevance given that a more efficient and standardized algorithm OMAC already achieves similar security. In what follows we define
Theorem 3.1
(OMAC bound). Let \( q, \ell , \sigma , T > 0 \). For \( q+\sigma \le 2^{n-1} \), the PRF insecurity of OMAC, based on block cipher \( {E}_{\textsf{K}} \), against \( \mathbb {A}(q,T) \) is given by
where q denotes the number of queries, \( \ell \) denotes an upper bound on the number of blocks per query, \( \sigma \) denotes the total number of blocks present in all q queries, \( T' = T + \sigma O(T_{E}) \) and \( T_{E}\) denotes the runtime of \( {E}\).
Theorem 3.2
(XCBC -TMAC bound). Let \( q, \ell , \sigma , T > 0 \). For \( q+\sigma \le 2^{n-1} \), the PRF insecurity of XCBC and TMAC, based on block cipher \( {E}_{\textsf{K}} \) and respective masking keys \( (\textsf{L},\textsf{L}_{-1},\textsf{L}_{0}) \), against \( \mathbb {A}(q,T) \) is given by
where q denotes the number of queries, \( \ell \) denotes an upper bound on the number of blocks per query, \( \sigma \) denotes the total number of blocks present in all q queries, \( T' = T + \sigma O(T_{E}) \) and \( T_{E}\) denotes the runtime of \( {E}\).
Proof of this theorem is almost same as that of Theorem 3.1. The bad event on a collision on zero block input is redundant and hence dropped here. Rest of the proof remains the same and so we skip the details.
Remark 3.1
Note that the actual advantage cannot exceed 1. Let us denote \(\frac{q^2}{2^n}=\alpha \) and \(\frac{q\ell ^2}{2^n}=\beta \). Looking at \(\epsilon (q,\ell )\) (where \(\epsilon (q,\ell )=\epsilon '(q,\ell )+\frac{4\sigma }{2^n}\) in case of OMAC and \(\epsilon (q,\ell )=\epsilon '(q,\ell )\) in case of XCBC,TMAC), we see that any term in the expression is upper bounded by \(c\cdot \alpha ^s\beta ^t\) for some constant c and \(s, t \ge 0\) such that at least one of s and t is at least 1. As we can assume both \(\alpha , \beta \) to be less than 1, each \(\alpha ^s\beta ^t\) will be less than or equal to \(\alpha \) or \(\beta \). Thus, the above PRF-advantage expressions for \( \textsf {MAC} \in \{\textsf {OMAC}, \textsf {XCBC}, \textsf {TMAC} \} \) can be written as
Indeed, under the assumption that \( \ell \le 2^{n/4-0.5} \) and \( q \le 2^{n/2-1} \), one can simplify the above bounds to \( 20q^2/2^n+ 23q\ell ^2/2^n \).
A Note on The Proof Approach: In the analysis of OMAC, XCBC and TMAC, we have to handle the case that the final input collides with some intermediate input, the so-called full collision event. In earlier works the probability of this event is shown to be \( q^2 \ell /2^n \) (as there are less than \( q\ell \) many intermediate inputs and q final inputs and any such collision happens with roughly \( 1/2^n \) probability). So, in a way they avoid handling this tricky event by disallowing it all together. In this work, we allow full collisions as long as the next intermediate input is not colliding with some other input (intermediate or final). Looking ahead momentarily, this is captured in  . We can do this via the application of reset-sampling, resulting in a more amenable \((q^2/2^n + q\ell ^2/2^n)\) bound.
. We can do this via the application of reset-sampling, resulting in a more amenable \((q^2/2^n + q\ell ^2/2^n)\) bound.
4 Proof of Theorem 3.1
First, using the standard hybrid argument, we get
Now, it is sufficient to bound \( \textbf{Adv}^{\textsf{prf}}_{\textsf {OMAC} _{\mathsf {\Pi }}}(q,\ell ,\sigma ,\infty ) \), where the corresponding distinguisher \( \mathscr {A}\) is computationally unbounded and deterministic. To bound this term, we employ the H-coefficient technique (see Sect. 2.2), and the recently introduced reset-sampling method [8]. The remaining steps of the proof are given in the remainder of this section.
4.1 Oracle Description and Corresponding Transcripts
Real Oracle: The real oracle corresponds to \( \textsf {OMAC} _{\mathsf {\Pi }} \). It responds faithfully to all the queries made by \( \mathscr {A}\). Once the query-response phase is over, it releases all the intermediate inputs and outputs, as well as the masking keys \( \textsf{L}_{-1}\) and \( \textsf{L}_{0}\) to \( \mathscr {A}\). We write \( \textsf{L}= \mathsf {\Pi }(0^n) \).
In addition, the real oracle releases three binary variables, namely, \( \textsf{FlagT}\), \( \textsf{FlagW}\) and \( \textsf{FlagX}\), all of which are degenerately set to 0. These flags are more of a technical requirement, and their utility will become apparent from the description of ideal oracle. For now, it is sufficient to note that these flags are degenerate in the real world.
Formally, we have \( \textsf{V}_1:= (\widetilde{\textsf{M}},\widetilde{\textsf{T}},\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}},\textsf{L}_{-1},\textsf{L}_{0},\textsf{FlagT},\textsf{FlagW},\textsf{FlagX}) \), where
-
\( \widetilde{\textsf{M}}= (\textsf{M}_{1},\ldots ,\textsf{M}_{q}) \), the q-tuple of queries made by \( \mathscr {A}\), where \( \textsf{M}_{i} \in \{0,1\}^* \) for all \( i \in [q] \). In addition, for all \( i \in [q] \), let
 .
. -
\( \widetilde{\textsf{T}}= (\textsf{T}_{1},\ldots ,\textsf{T}_{q}) \), the q-tuple of final outputs received by \( \mathscr {A}\), where \( \textsf{T}_{i} \in \mathcal {B}\).
-
\( \widetilde{\textsf{X}}= (\textsf{X}_{1},\ldots ,\textsf{X}_{q}) \), where \( \textsf{X}_{i} \) denotes the intermediate input tuple for the i-th query.
-
\( \widetilde{\textsf{X}}^*= (\textsf{X}_{1}[\ell _1],\ldots ,\textsf{X}_{q}[\ell _q]) \), where \( \textsf{X}_{i}[\ell _i] \) denotes the final input for the i-th query.
-
\( \widetilde{\textsf{Y}}= (\textsf{Y}_{1},\ldots ,\textsf{Y}_{q}) \), where \( \textsf{Y}_{i} \) denotes the intermediate output tuple for the i-th query.
-
\( \textsf{L}_{-1}\) and \( \textsf{L}_{0}\) denote the two masking keys. Note that \( \textsf{L}_{-1}\) and \( \textsf{L}_{0}\) are easily derivable from \( \textsf{L}\). So we could have simply released \( \textsf{L}\). The added redundancy is to aid the readers in establishing an analogous connection between this proof and the proof for XCBC and TMAC.
-
\( \textsf{FlagT}= \textsf{FlagW}= \textsf{FlagX}= 0 \).
From the definition of OMAC, we know that \( \mathsf {\Pi }(\textsf{X}_{i}[a]) = \textsf{Y}_{i}[a] \) for all \( (i,a) \in [q] \times [\ell _i] \). So, in the real world we always have \( (0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*) \leftrightsquigarrow (\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}}) \), i.e., \( (0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*) \) is permutation compatible with \( (\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}}) \). We keep this observation in our mind when we simulate the ideal oracle.
Ideal Oracle: By reusing notations from the real world, we represent the ideal oracle transcript as \( \textsf{V}_0:= (\widetilde{\textsf{M}},\widetilde{\textsf{T}},\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}},\textsf{L}_{-1},\textsf{L}_{0},\textsf{FlagT},\textsf{FlagW},\textsf{FlagX}) \). This should not cause any confusion, as we never consider the random variables \( \textsf{V}_1\) and \( \textsf{V}_0\) jointly, whence the probability distributions of the constituent variables will always be clear from the context.
The ideal oracle transcript is described in three phases, each contingent on some predicates defined over the previous stages. Specifically, the ideal oracle first initializes \( \textsf{FlagT}= \textsf{FlagW}= \textsf{FlagX}= 0 \), and then follows the sampling mechanism given below:
 In the query-response phase, the ideal oracle faithfully simulates
In the query-response phase, the ideal oracle faithfully simulates  . Formally, for \( i \in [q] \), at the i-th query \( \textsf{M}_{i} \in \{0,1\}^*\), the ideal oracle outputs
. Formally, for \( i \in [q] \), at the i-th query \( \textsf{M}_{i} \in \{0,1\}^*\), the ideal oracle outputs  . The partial transcript generated at the end of the query-response phase is given by \( (\widetilde{\textsf{M}},\widetilde{\textsf{T}}) \), where
. The partial transcript generated at the end of the query-response phase is given by \( (\widetilde{\textsf{M}},\widetilde{\textsf{T}}) \), where
-
\( \widetilde{\textsf{M}}= (\textsf{M}_{1},\ldots ,\textsf{M}_{q}) \) and \( \widetilde{\textsf{T}}= (\textsf{T}_{1},\ldots ,\textsf{T}_{q}) \).
Now, we define a predicate on \( \widetilde{\textsf{T}}\):

If  is true, then \( \textsf{FlagT}\) is set to 1, and \( \widetilde{\textsf{X}}\), \( \widetilde{\textsf{X}}^*\), and \( \widetilde{\textsf{Y}}\) are defined degenerately: \( \textsf{X}_{i}[a] = \textsf{Y}_{i}[b] = 0^n \) for all \( i \in [q] \), \( a \in [\ell _i] \), \( b \in (\ell _{i}-1] \). Otherwise, the ideal oracle proceeds to the next phase.
is true, then \( \textsf{FlagT}\) is set to 1, and \( \widetilde{\textsf{X}}\), \( \widetilde{\textsf{X}}^*\), and \( \widetilde{\textsf{Y}}\) are defined degenerately: \( \textsf{X}_{i}[a] = \textsf{Y}_{i}[b] = 0^n \) for all \( i \in [q] \), \( a \in [\ell _i] \), \( b \in (\ell _{i}-1] \). Otherwise, the ideal oracle proceeds to the next phase.
 Onward, we must have \( \textsf{T}_{i} \ne \textsf{T}_{j} \) whenever \( i \ne j \), and \( \textsf{FlagT}= 0 \), since this phase is only executed when
Onward, we must have \( \textsf{T}_{i} \ne \textsf{T}_{j} \) whenever \( i \ne j \), and \( \textsf{FlagT}= 0 \), since this phase is only executed when  is false. In the offline phase, the ideal oracle’s initial goal is to sample the input and output tuples in such a way that the intermediate input and output tuples are permutation compatible. For now we use notations \( \textsf{W}\) and \( \textsf{Z}\), respectively, instead of \( \textsf{X}\) and \( \textsf{Y}\), to denote the input and output tuples. This is done to avoid any confusions in the next step where we may have to reset some of these variables. To make it explicit, \( \textsf{W}\) and \( \textsf{Z}\) respectively denote the input and output tuples before resetting, and \( \textsf{X}\) and \( \textsf{Y}\) denote the input and output tuples after resetting.
is false. In the offline phase, the ideal oracle’s initial goal is to sample the input and output tuples in such a way that the intermediate input and output tuples are permutation compatible. For now we use notations \( \textsf{W}\) and \( \textsf{Z}\), respectively, instead of \( \textsf{X}\) and \( \textsf{Y}\), to denote the input and output tuples. This is done to avoid any confusions in the next step where we may have to reset some of these variables. To make it explicit, \( \textsf{W}\) and \( \textsf{Z}\) respectively denote the input and output tuples before resetting, and \( \textsf{X}\) and \( \textsf{Y}\) denote the input and output tuples after resetting.
Let \( \textsf{P} \) be a key-value table representing a partial permutation of \( \mathcal {B}\), which is initialized to empty, i.e., the corresponding permutation is undefined on all points. We write \( \textsf{P}.\textsf{domain}\) and \( \textsf{P}.\textsf{range}\) to denote the set of all keys and values utilized till this point, respectively. The ideal oracle uses this partial permutation \( \textsf{P} \) to maintain permutation compatibility between intermediate input and output tuples, in the following manner:

At this stage we have \( \textsf{Z}_{i}[a] = \textsf{Z}_{j}[b] \) if and only if \( \textsf{W}_{i}[a] = \textsf{W}_{j}[b] \) for all \( (i,a) \in [q] \times [\ell _i-1] \) and \( (j,b) \in [q] \times [\ell _j-1] \). In other words, \( (0^n,\widetilde{\textsf{W}}) \leftrightsquigarrow (\textsf{L},\widetilde{\textsf{Z}}) \). But it is obvious to see that the same might not hold between \( (0^n, \widetilde{\textsf{W}}, \widetilde{\textsf{W}}^*) \) and \( (\textsf{L}, \widetilde{\textsf{Z}}, \widetilde{\textsf{T}}) \). In the next stage our goal will be to reset some of the \( \textsf{Z}\) variables in such a way that the resulting input tuple is compatible with the resulting output tuple. However, in order to reset, we have to identify and avoid certain contentious input-output tuples.
Identifying Contentious Input-Outptut Tuples: We define several predicates on \( (\widetilde{\textsf{W}},\widetilde{\textsf{W}}^*) \), each of which represents some undesirable property of the sampled input and output tuples.
First, observe that \( \textsf{L}\) is chosen outside the set \( \widetilde{\textsf{T}}\). This leads to the first predicate:

since, if  is true, then \( (0^n,\widetilde{\textsf{W}}^*) \) is not compatible with \( (\textsf{L},\widetilde{\textsf{T}}) \). In fact,
is true, then \( (0^n,\widetilde{\textsf{W}}^*) \) is not compatible with \( (\textsf{L},\widetilde{\textsf{T}}) \). In fact,  implies that none of the inputs, except the first input which is fully in adversary’s control, can possibly be \( 0^n \). This stronger condition will simplify the analysis greatly. The second predicate simply states that the final input tuple is not permutation compatible with the tag tuple, i.e., we have
implies that none of the inputs, except the first input which is fully in adversary’s control, can possibly be \( 0^n \). This stronger condition will simplify the analysis greatly. The second predicate simply states that the final input tuple is not permutation compatible with the tag tuple, i.e., we have

At this point, assuming  holds true, the only way we can have permutation incompatibility is if \( \textsf{W}_{i}[a] = \textsf{W}_{j}[\ell _j] \), for some \( i, j \in [q] \) and \( a \in [\ell _i-1] \). A simple solution will be to reset \( \textsf{Z}_i[a] \) to \( \textsf{T}_{j} \), for all such (i, a, j) . In order to do this, we need that the following predicates must be false:
holds true, the only way we can have permutation incompatibility is if \( \textsf{W}_{i}[a] = \textsf{W}_{j}[\ell _j] \), for some \( i, j \in [q] \) and \( a \in [\ell _i-1] \). A simple solution will be to reset \( \textsf{Z}_i[a] \) to \( \textsf{T}_{j} \), for all such (i, a, j) . In order to do this, we need that the following predicates must be false:

If  is true, then once \( \textsf{Z}_{i}[a] \) is reset, we lose the permutation compatibility since, the reset next input, i.e., \( \textsf{X}_{i}[a+1] = \textsf{W}_{i}[a+1] \oplus \textsf{Z}_{i}[a] \oplus \textsf{T}_{j} = \textsf{M}_{i}[a+1] \oplus \textsf{T}_{j} \ne \textsf{W}_{k}[b] \) with high probability, whereas \( \textsf{Z}_{i}[a+1] = \textsf{Z}_{k}[b] \) with certainty.
is true, then once \( \textsf{Z}_{i}[a] \) is reset, we lose the permutation compatibility since, the reset next input, i.e., \( \textsf{X}_{i}[a+1] = \textsf{W}_{i}[a+1] \oplus \textsf{Z}_{i}[a] \oplus \textsf{T}_{j} = \textsf{M}_{i}[a+1] \oplus \textsf{T}_{j} \ne \textsf{W}_{k}[b] \) with high probability, whereas \( \textsf{Z}_{i}[a+1] = \textsf{Z}_{k}[b] \) with certainty.  simply represents the scenario where we may have to apply the initial resetting to two indices in a single message. Looking ahead momentarily, this may lead to contradictory induced resettings. Avoiding this predicate makes the resetting operation much more manageable. Similarly, avoiding
simply represents the scenario where we may have to apply the initial resetting to two indices in a single message. Looking ahead momentarily, this may lead to contradictory induced resettings. Avoiding this predicate makes the resetting operation much more manageable. Similarly, avoiding  , is just proactive prevention of contradictory resetting at \( \textsf{Z}_{i}[a] \), since if
, is just proactive prevention of contradictory resetting at \( \textsf{Z}_{i}[a] \), since if  occurs, then we may have a case where \( \textsf{X}_{j}[\ell _j] \) is reset due to induced resetting, leading to the case, \( \textsf{X}_{i}[a] \ne \textsf{X}_{j}[\ell _j] \) and \( \textsf{Y}_{i}[a] = \textsf{T}_{j} \), where recall that \( \textsf{Y}_{i}[a] \) is the resetting value of \( \textsf{Z}_{i}[a] \). We write
occurs, then we may have a case where \( \textsf{X}_{j}[\ell _j] \) is reset due to induced resetting, leading to the case, \( \textsf{X}_{i}[a] \ne \textsf{X}_{j}[\ell _j] \) and \( \textsf{Y}_{i}[a] = \textsf{T}_{j} \), where recall that \( \textsf{Y}_{i}[a] \) is the resetting value of \( \textsf{Z}_{i}[a] \). We write

If  is true, then \( \textsf{FlagW}\) is set to 1, and \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) is again defined degenerately, as in the case of
is true, then \( \textsf{FlagW}\) is set to 1, and \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) is again defined degenerately, as in the case of  . Otherwise, the ideal oracle proceeds to the next and the final phase, i.e., the resetting phase.
. Otherwise, the ideal oracle proceeds to the next and the final phase, i.e., the resetting phase.
 At this stage we must have
At this stage we must have  , i.e.,
, i.e.,  . We describe the resetting phase in two sub-stages. First, we identify the indices affected by the initial resetting operation.
. We describe the resetting phase in two sub-stages. First, we identify the indices affected by the initial resetting operation.
Definition 4.1
[full collision index]. Any \( (i,a,j) \in [q] \times [\ell _i-1] \times [q] \) is called a full collision index (FCI) if \( \textsf{W}_{i}[a] = \textsf{W}_{j}[\ell _j] \). Additionally, let
The first sub-stage, executes a resetting for full collision indices in the following manner:
-
1.
For all \( (i,a,j) \in \textsf{FCI}\), define \( \textsf{Y}_{i}[a] := \textsf{T}_{j} \);
-
2.
For all \( (i,a,j) \in \textsf{FCI}\), define

where \( 1_{a=\ell _i-1} \) is an indicator variable that evaluates to 1 when \( a=\ell _i-1 \), and 0 otherwise.
Once the initial resetting is executed, it may result in new permutation incompatibilities. This necessitates further resettings, referred as induced resettings, which require that the following predicates are false:

Here, the variable highlighted in red denotes the update after initial resetting. Let’s review these predicates in slightly more details. First,  , represents the situation where after resetting the next input (highlighted text) collides with some intermediate input or \( 0^n \). This would necessitate induced resetting at \( \textsf{Z}_{i}[a+1] \). In other words, if
, represents the situation where after resetting the next input (highlighted text) collides with some intermediate input or \( 0^n \). This would necessitate induced resetting at \( \textsf{Z}_{i}[a+1] \). In other words, if  is false then no induced resettings occur, unless the next input collides with some first block input. This case is handled in the next two predicates.
is false then no induced resettings occur, unless the next input collides with some first block input. This case is handled in the next two predicates.  represents the situation when the next input collides with a first block and the subsequent message blocks are all same. This would induce a chain of resetting going all the way to the final input. As
represents the situation when the next input collides with a first block and the subsequent message blocks are all same. This would induce a chain of resetting going all the way to the final input. As  is false, this would immediately result in a permutation incompatibility since tags are distinct. If
is false, this would immediately result in a permutation incompatibility since tags are distinct. If  is false, then the chain of induced resetting must end at some point.
is false, then the chain of induced resetting must end at some point.  is used to avoid circular or contradictory resettings. It is analogous to
is used to avoid circular or contradictory resettings. It is analogous to  defined earlier. If it is false, then we know that the k-th message is free from resetting, so the induced resetting will be manageable. Finally,
defined earlier. If it is false, then we know that the k-th message is free from resetting, so the induced resetting will be manageable. Finally,  represents the situation when two newly reset variables collide. We write
represents the situation when two newly reset variables collide. We write

If  is true, then \( \textsf{FlagX}\) is set to 1, and \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) is again defined degenerately, as in the cases of
is true, then \( \textsf{FlagX}\) is set to 1, and \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) is again defined degenerately, as in the cases of  and
and  . Otherwise, the ideal oracle proceeds to the second and the final sub-stage of resetting.
. Otherwise, the ideal oracle proceeds to the second and the final sub-stage of resetting.
 Here, the goal is to execute the induced resettings necessitated by the initial resetting operation.
Here, the goal is to execute the induced resettings necessitated by the initial resetting operation.
First, we define the index of induced resetting for each \( (i,a) \in \widetilde{\textsf{FCI}}\), as the smallest index j such that \( \textsf{X}_{i}[a+1] = \textsf{M}_{j}[1] \) and
i.e., \( \textsf{Prefix}(\textsf{M}_{i}[a+2,\ldots ,\ell _i],\textsf{M}_{j}[2,\ldots ,\ell _j]) \) maximizes.
Definition 4.2
[induced collision sequence]. A sequence of tuples \( ((i,a+1,j,1),\ldots ,(i,a+p+1,j,p+1)) \) is called an induced collision sequence (ICS), if \( (i,a) \in \widetilde{\textsf{FCI}}\), and j is the index of induced resetting for (i, a) , where \( p := \textsf{Prefix}(\textsf{M}_{i}[a+2,\ldots ,\ell _i],\textsf{M}_{j}[2,\ldots ,\ell _j]) \). The individual elements of an ICS are referred as induced collision index (ICI). Additionally, we let
Now, as anticipated, in the second sub-stage of resetting, we reset the induced collision indices in the following manner:
-
1.
For all \( (i,a,j,b) \in \textsf{ICI}\), define \( \textsf{Y}_{i}[a] := \textsf{Z}_{j}[b] \);
-
2.
For all \( (i,a,j,b) \in \textsf{ICI}\), define

where \( 1_{a=\ell _i-1} \) is an indicator variable that evaluates to 1 when \( a=\ell _i-1 \), and 0 otherwise.
Given  , we know that the induced resetting must stop at some point before the final input. Now, it might happen that once the first chain of induced resetting stops, the next input again collides which may result in nested resetting or permutation incompatibility. The predicates
, we know that the induced resetting must stop at some point before the final input. Now, it might happen that once the first chain of induced resetting stops, the next input again collides which may result in nested resetting or permutation incompatibility. The predicates  ,
,  , and
, and  below represent these scenarios.
below represent these scenarios.
-


where \( p := \textsf{Prefix}(\textsf{M}_{i}[a+2,\ldots ,\ell _i],\textsf{M}_{k}[2,\ldots ,\ell _k]) \).
-
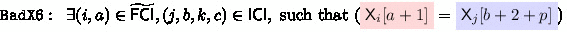 , where \( p := \textsf{Prefix}(\textsf{M}_{j}[b+2,\ldots ,\ell _j],\textsf{M}_{k}[2,\ldots ,\ell _k]) \).
, where \( p := \textsf{Prefix}(\textsf{M}_{j}[b+2,\ldots ,\ell _j],\textsf{M}_{k}[2,\ldots ,\ell _k]) \). -


where \( p := \textsf{Prefix}(\textsf{M}_{i}[a+2,\ldots ,\ell _i],\textsf{M}_{k}[2,\ldots ,\ell _k]) \), and \( p' := \textsf{Prefix}(\textsf{M}_{j}[b+2,\ldots ,\ell _j],\textsf{M}_{l}[2,\ldots ,\ell _l]) \).
Here, the variables highlighted in red and blue denote the update after initial resetting and induced resetting, respectively. These predicates are fairly self-explanatory. First  represents the situation that the immediate input after induced resetting collides with some intermediate input or \( 0^n \). This may cause permutation incompatibility and would lead to nested induced resetting at \( \textsf{Z}_{i}[a+2+p] \).
represents the situation that the immediate input after induced resetting collides with some intermediate input or \( 0^n \). This may cause permutation incompatibility and would lead to nested induced resetting at \( \textsf{Z}_{i}[a+2+p] \).  handles a similar collision with a full collision resetted variable, and
handles a similar collision with a full collision resetted variable, and  handles the only remaining case where the immediate inputs after two different induced resetting collides. Note that,
handles the only remaining case where the immediate inputs after two different induced resetting collides. Note that,  would imply that for each message resetting stops at some point before the final input, and the next input is fresh.Footnote 5 We write
would imply that for each message resetting stops at some point before the final input, and the next input is fresh.Footnote 5 We write

If  is true, then \( \textsf{FlagX}\) is set to 1, and \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) is again defined degenerately, as in the case of
is true, then \( \textsf{FlagX}\) is set to 1, and \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) is again defined degenerately, as in the case of  and
and  . Otherwise, for any remaining index \( (i,a) \in [q] \times (\ell _{i}-1] \setminus (\widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}) \), the ideal oracle resets as follows:
. Otherwise, for any remaining index \( (i,a) \in [q] \times (\ell _{i}-1] \setminus (\widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}) \), the ideal oracle resets as follows:
-
1.
define \( \textsf{Y}_{i}[a] := \textsf{Z}_{i}[a] \);
-
2.
define \( \textsf{X}_{i}[a+1] := \textsf{W}_{i}[a+1] \).
At this point, the ideal oracle transcript is completely defined. Intuitively, if the ideal oracle is not sampling \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) degenerately at any stage, then we must have \( (0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*) \leftrightsquigarrow (\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}}) \). The following proposition justifies this intuition.
Proposition 4.1
For  , we must have \( (0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*) \leftrightsquigarrow (\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}}) \).
, we must have \( (0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*) \leftrightsquigarrow (\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}}) \).
Proof
Let  hold. Recall that \((0^n, \widetilde{\textsf{W}},\widetilde{\textsf{W}}^*)\) may not be permutation compatible with \((\textsf{L}, \widetilde{\textsf{Z}}, \widetilde{\textsf{T}})\). For any \((i,a) \in \widetilde{\textsf{FCI}}\), there exists \(i'\in [q]\) such that \(\textsf{W}_{i}[a]=\textsf{W}_{i'}[\ell _{i'}]\) but \(\textsf{Z}_{i}[a] \ne \textsf{T}_{i'}\). We apply the initial resetting to solve this issue. However, as a result of initial resetting, induced resetting takes place. Our goal is to show that the non-occurrence of the bad events assures that the compatibility is attained in the final reset tuples \((0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*)\) and \((\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}})\). We prove all possible cases as follows:
hold. Recall that \((0^n, \widetilde{\textsf{W}},\widetilde{\textsf{W}}^*)\) may not be permutation compatible with \((\textsf{L}, \widetilde{\textsf{Z}}, \widetilde{\textsf{T}})\). For any \((i,a) \in \widetilde{\textsf{FCI}}\), there exists \(i'\in [q]\) such that \(\textsf{W}_{i}[a]=\textsf{W}_{i'}[\ell _{i'}]\) but \(\textsf{Z}_{i}[a] \ne \textsf{T}_{i'}\). We apply the initial resetting to solve this issue. However, as a result of initial resetting, induced resetting takes place. Our goal is to show that the non-occurrence of the bad events assures that the compatibility is attained in the final reset tuples \((0^n,\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*)\) and \((\textsf{L},\widetilde{\textsf{Y}},\widetilde{\textsf{T}})\). We prove all possible cases as follows:
-
\(\textsf{X}_{i}[a]=0^n \iff \textsf{Y}_{i}[a]=\textsf{L}\): If \(a=1\) and \(\textsf{X}_{i}[a]=0\), then \((i,a) \notin \widetilde{\textsf{FCI}}\) due to
 . Thus, \(\textsf{Y}_{i}[a]=\textsf{Z}_{i}[a]=\textsf{L}\) and the converse also holds. Otherwise, due to
. Thus, \(\textsf{Y}_{i}[a]=\textsf{Z}_{i}[a]=\textsf{L}\) and the converse also holds. Otherwise, due to  , \(\textsf{X}_{i}[a]\) can not be equal to 0. Also, due to
, \(\textsf{X}_{i}[a]\) can not be equal to 0. Also, due to  , \(\textsf{Y}_{i}[a]\) can not be equal to \(\textsf{L}\).
, \(\textsf{Y}_{i}[a]\) can not be equal to \(\textsf{L}\). -
\(\textsf{X}_{i}[a]=\textsf{X}_{i'}[\ell _{i'}] \iff \textsf{Y}_{i}[a]=\textsf{T}_{i'}\): For \((i,a) \in \widetilde{\textsf{FCI}}\), this equivalence holds. Otherwise, \(\textsf{X}_{i}[a]=\textsf{X}_{i'}[\ell _{i'}]\) can not hold due to
 . Also \(\textsf{Y}_{i}[a]=\textsf{T}_{i'}\) can not hold due to definition of \(\widetilde{\textsf{T}}\) and
. Also \(\textsf{Y}_{i}[a]=\textsf{T}_{i'}\) can not hold due to definition of \(\widetilde{\textsf{T}}\) and 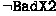 .
. -
\(\textsf{X}_{i}[a]=\textsf{X}_{j}[b] \iff \textsf{Y}_{i}[a]=\textsf{Y}_{j}[b]\): To prove this part we divide it in the following subcases:
-
\(\boxed {(i,a),(i,b) \notin \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}}\):Since in this case the variables are simply renamed due to definitions of resetting and
 , the result follows from \( \widetilde{\textsf{W}} \leftrightsquigarrow \widetilde{\textsf{Z}} \).
, the result follows from \( \widetilde{\textsf{W}} \leftrightsquigarrow \widetilde{\textsf{Z}} \). -
\(\boxed { (i,a),(j,b) \in \widetilde{\textsf{FCI}}}\):Since \( (i,a),(j,b) \in \widetilde{\textsf{FCI}}\), there exists unique \( i',j' \in [q] \), such that \( \textsf{W}_{i}[a] = \textsf{W}_{i'}[\ell _{i'}] \) and \( \textsf{W}_{j}[b] = \textsf{W}_{j'}[\ell _{j'}] \). Now, note that \(\textsf{X}_{i}[a]=\textsf{W}_{i}[a]\) and \(\textsf{X}_{j}[b]=\textsf{W}_{j}[b]\) since \(\widetilde{\textsf{FCI}}\cap \widetilde{\textsf{ICI}}=\emptyset \) due to
 ; \(\textsf{W}_{i'}[\ell _{i'}]=\textsf{X}_{i'}[\ell _{i'}]\) and \(\textsf{W}_{j'}[\ell _{j'}]=\textsf{X}_{j'}[\ell _{j'}]\) due to
; \(\textsf{W}_{i'}[\ell _{i'}]=\textsf{X}_{i'}[\ell _{i'}]\) and \(\textsf{W}_{j'}[\ell _{j'}]=\textsf{X}_{j'}[\ell _{j'}]\) due to  . Therefore, we must have \( \textsf{X}_{j'}[\ell _{j'}] =\textsf{W}_{j'}[\ell _{j'}]=\textsf{W}_{j}[b]= \textsf{X}_{j}[b]= \textsf{X}_{i}[a]=\textsf{W}_{i}[a]=\textsf{W}_{i'}[\ell _{i'}]= \textsf{X}_{i'}[\ell _{i'}] \), which is possible if and only if \( i'=j' \) (since
. Therefore, we must have \( \textsf{X}_{j'}[\ell _{j'}] =\textsf{W}_{j'}[\ell _{j'}]=\textsf{W}_{j}[b]= \textsf{X}_{j}[b]= \textsf{X}_{i}[a]=\textsf{W}_{i}[a]=\textsf{W}_{i'}[\ell _{i'}]= \textsf{X}_{i'}[\ell _{i'}] \), which is possible if and only if \( i'=j' \) (since  holds).
holds). -
\(\boxed {(i,a),(j,b) \in \widetilde{\textsf{ICI}}}\):Since \( (i,a),(j,b) \in \widetilde{\textsf{ICI}}\), there exists \( i', j'\in [q] \) and \(a'\in [\ell _{i'}-1], b'\in [\ell _{j'}-1]\), such that \( \textsf{X}_{i}[a] = \textsf{W}_{i'}[a'] \) and \( \textsf{X}_{j}[b] = \textsf{W}_{j'}[b'] \). Further, \( (i',a'),(j',b') \notin \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}\) (due to
 ). If \(\textsf{X}_{j}[b] = \textsf{X}_{i}[a]\), then we have \(\textsf{W}_{j'}[b'] = \textsf{W}_{i'}[a']\). This gives us \(\textsf{Y}_{j}[b] = \textsf{Z}_{j'}[b'] = \textsf{Z}_{i'}[a'] = \textsf{Y}_{i}[a] \) (due to \( \widetilde{\textsf{W}} \leftrightsquigarrow \widetilde{\textsf{Z}} \)). Similarly, \(\textsf{X}_{i}[a] \ne \textsf{X}_{j}[b]\) implies \(\textsf{Y}_{i}[a] \ne \textsf{Y}_{j}[b]\).
). If \(\textsf{X}_{j}[b] = \textsf{X}_{i}[a]\), then we have \(\textsf{W}_{j'}[b'] = \textsf{W}_{i'}[a']\). This gives us \(\textsf{Y}_{j}[b] = \textsf{Z}_{j'}[b'] = \textsf{Z}_{i'}[a'] = \textsf{Y}_{i}[a] \) (due to \( \widetilde{\textsf{W}} \leftrightsquigarrow \widetilde{\textsf{Z}} \)). Similarly, \(\textsf{X}_{i}[a] \ne \textsf{X}_{j}[b]\) implies \(\textsf{Y}_{i}[a] \ne \textsf{Y}_{j}[b]\). -
\( \boxed {(i,a) \in \widetilde{\textsf{FCI}} and (j,b) \in \widetilde{\textsf{ICI}}}\):Since \( (i,a) \in \widetilde{\textsf{FCI}}\), there exists a unique \( i' \in [q] \), such that \( \textsf{X}_{i}[a] = \textsf{W}_{i}[a] =\textsf{W}_{i'}[\ell _{i'}]=\textsf{X}_{i'}[\ell _{i'}] \) (the first equality is due to
 , the second equality is due to the definition of full collision, the third equality is due to
, the second equality is due to the definition of full collision, the third equality is due to  ). Since \((j,b) \in \widetilde{\textsf{ICI}}\), we also have \(\textsf{X}_{j}[b]=\textsf{W}_{j'}[b']\). If \(\textsf{X}_{i}[a]=\textsf{X}_{j}[b]\), then \( \textsf{W}_{j'}[b'] = \textsf{W}_{i'}[\ell _{i'}] \). Thus, \((j',b')=(i',\ell _{i'})\) due to
). Since \((j,b) \in \widetilde{\textsf{ICI}}\), we also have \(\textsf{X}_{j}[b]=\textsf{W}_{j'}[b']\). If \(\textsf{X}_{i}[a]=\textsf{X}_{j}[b]\), then \( \textsf{W}_{j'}[b'] = \textsf{W}_{i'}[\ell _{i'}] \). Thus, \((j',b')=(i',\ell _{i'})\) due to  . Now, we have \(\textsf{Y}_{i}[a]=\textsf{T}_{i'}\). Also, \(\textsf{Y}_{j}[b]=\textsf{Y}_{j'}[b']=\textsf{Y}_{i'}[\ell _{i'}]=\textsf{T}_{i'}\). Therefore, \(\textsf{Y}_{i}[a]=\textsf{Y}_{j}[b]\). Moreover, \(\textsf{X}_{i}[a] \ne \textsf{X}_{j}[b]\) implies that \(\textsf{Y}_{i}[a] \ne \textsf{Y}_{j}[b]\) due to similar arguments as above and also
. Now, we have \(\textsf{Y}_{i}[a]=\textsf{T}_{i'}\). Also, \(\textsf{Y}_{j}[b]=\textsf{Y}_{j'}[b']=\textsf{Y}_{i'}[\ell _{i'}]=\textsf{T}_{i'}\). Therefore, \(\textsf{Y}_{i}[a]=\textsf{Y}_{j}[b]\). Moreover, \(\textsf{X}_{i}[a] \ne \textsf{X}_{j}[b]\) implies that \(\textsf{Y}_{i}[a] \ne \textsf{Y}_{j}[b]\) due to similar arguments as above and also  .
. -
\(\boxed {(i,a) \in \widetilde{\textsf{ICI}} and (j,b) \in \widetilde{\textsf{FCI}}}\): Similar as the above case.
-
\(\boxed {(i,a) \in \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}} and (j,b) \notin \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}}\): Since \((j,b) \notin \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}\), we have \(\textsf{X}_{j}[b]=\textsf{W}_{j}[b]\) and \(\textsf{Y}_{j}[b]=\textsf{Z}_{j}[b]\). Suppose, \((i,a) \in \widetilde{\textsf{FCI}}\). Then \(\textsf{X}_{i}[a]=\textsf{X}_{j}[b]\) is not possible since it would imply that \((j,b) \in \widetilde{\textsf{FCI}}\). Also, \(\textsf{Y}_{i}[a]=\textsf{Y}_{j}[b]\) is not possible since it would contradict the definition of \(\widetilde{\textsf{T}}\). Now, suppose, \((i,a) \in \widetilde{\textsf{ICI}}\). Therefore, \(\textsf{X}_{i}[a]=\textsf{W}_{i'}[a']\) for some \( i' \in [q] \) and \(a'\in [\ell _{i'}-1]\). If \(\textsf{X}_{i}[a]=\textsf{X}_{j}[b]\), then \(\textsf{W}_{j}[b]=\textsf{X}_{j}[b]=\textsf{X}_{i}[a]=\textsf{W}_{i'}[a']\). So, \(\textsf{Y}_{j}[b]=\textsf{Z}_{j}[b]=\textsf{Z}_{i'}[a']=\textsf{Y}_{i}[a]\). Similarly, \(\textsf{X}_{i}[a] \ne \textsf{X}_{j}[b]\) implies \(\textsf{Y}_{i}[a] \ne \textsf{Y}_{j}[b]\).
-
\(\boxed {(i,a) \notin \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}} and (j,b) \in \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}}\): Similar as the above case.
-
4.2 Transcript Analysis
Set of Transcripts: Given the description of transcript random variable corresponding to the ideal oracle, we can now define the set of transcripts \( \mathcal {V}\) as the set of all tuples \( \nu = (\widetilde{m},\widetilde{t},\widetilde{x},\widetilde{x}^*,\widetilde{y},l_{-1},l_0,\textrm{flagT},\textrm{flagW},\textrm{flagX}) \), where
-
\( \widetilde{m}= (m_1,\ldots ,m_q) \), where \( m_i \in \{0,1\}^* \) for \( i \in [q] \). Let
 for \( i \in [q] \).
for \( i \in [q] \). -
\( \widetilde{t}= (t_1,\ldots ,t_q) \), where \( t_i \in \mathcal {B}\) for \( i \in [q] \).
-
\( \widetilde{x}= (x_1,\ldots ,x_q) \), where \( x_i = (x_i[1],\ldots ,x_i[\ell _i-1]) \) for \( i \in [q] \).
-
\( \widetilde{x}^*= (x_{1}[\ell _1],\ldots ,x_{q}[\ell _q]) \).
-
\( \widetilde{y}= (y_1,\ldots ,y_q) \), where \( y_i = (y_i[0]=0^n,y_i[1],\ldots ,y_i[\ell _i-1]) \) for \( i \in [q] \).
-
\(l_{-1}=\mu _{-1}\odot l, l_0=\mu _{0} \odot l\) where \(l \in \mathcal {B}\) and \(\mu _{-1},\mu _{0}\) are constants chosen from \(\textrm{GF}(2^{n})\) as defined before.
-
\( \textrm{flagT},\textrm{flagW},\textrm{flagX} \in \{0,1\} \).
Furthermore, the following must always hold:
-
1.
if \( \textrm{flagI} = 1 \) for some \( \textrm{I} \in \{\textrm{T,W}\} \), then \( x_i[a]=y_j[b] = 0^n \) for all \( i,j \in [q] \), \( a \in [\ell _i] \), and \( b \in [\ell _j-1] \).
-
2.
if \( \textrm{flagT} = 0 \), then \( t_i \)’s are all distinct.
-
3.
if \( \textrm{flagI} = 0 \) for all \( \textrm{I} \in \{\textrm{T,W,X}\} \), then \( x_{i}[a] = y_{i}[a-1] \oplus \overline{m}_{i}[a] \) and \( (0^n,\widetilde{x},\widetilde{y}^\oplus ) \leftrightsquigarrow (L,\widetilde{y},\widetilde{t}) \).
The first two conditions are obvious from the ideal oracle sampling mechanism. The last condition follows from Proposition 4.1 and the observation that in ideal oracle sampling for any \( \textsf{I} \in \{\textsf{T},\textsf{Z},\textsf{X}\} \), \( \textsf{FlagI} = 1 \) if and only if  is true. Note that, condition 3 is vacuously true for real oracle transcripts.
is true. Note that, condition 3 is vacuously true for real oracle transcripts.
Bad Transcript: A transcript \( \nu \in \mathcal {V}\) is called bad if and only if the following predicate is true:
In other words, we term a transcript bad if the ideal oracle sets \( (\widetilde{\textsf{X}},\widetilde{\textsf{X}}^*,\widetilde{\textsf{Y}}) \) degenerately. Let

All other transcript  are called good. From the preceding characterization of the set of transcripts, we conclude that for any good transcript \( \nu ' \), we must have \( (0^n,\widetilde{x},\widetilde{x}^*) \leftrightsquigarrow (L,\widetilde{y},\widetilde{t}) \). Henceforth, we drop \( \textrm{flagT} \), \( \textrm{flagW} \), and \( \textrm{flagX} \) for any good transcript with an implicit understanding that \( \textrm{flagT} = \textrm{flagW} = \textrm{flagX} = 0 \).
are called good. From the preceding characterization of the set of transcripts, we conclude that for any good transcript \( \nu ' \), we must have \( (0^n,\widetilde{x},\widetilde{x}^*) \leftrightsquigarrow (L,\widetilde{y},\widetilde{t}) \). Henceforth, we drop \( \textrm{flagT} \), \( \textrm{flagW} \), and \( \textrm{flagX} \) for any good transcript with an implicit understanding that \( \textrm{flagT} = \textrm{flagW} = \textrm{flagX} = 0 \).
Following the H-coefficient mechanism, we have to upper bound the probability  and lower bound the ratio \( {\Pr _{ }\left( \textsf{V}_1= \nu \right) }/{\Pr _{ }\left( \textsf{V}_0= \nu \right) } \) for any
and lower bound the ratio \( {\Pr _{ }\left( \textsf{V}_1= \nu \right) }/{\Pr _{ }\left( \textsf{V}_0= \nu \right) } \) for any  .
.
Lemma 4.1
(bad transcript analysis). For \( q+\sigma \le 2^{n-1} \), we have

The proof of this lemma is postponed to Sect. 5.
Good Transcript: Now, fix a good transcript \( \nu = (\widetilde{m},\widetilde{t},\widetilde{x},\widetilde{x}^*,\widetilde{y},l_{-1},l_0) \). Let \( \sigma \) be the total number of blocks (and one additional for \( 0^n \)) and \( \sigma ' := |\widetilde{x}\cup \{0^n\}| \). Since, \( \nu \) is good, we have \( (0^n,\widetilde{x},\widetilde{x}^*) \leftrightsquigarrow (L,\widetilde{y},\widetilde{t}) \). Then, we must have \( |\widetilde{x}^*| = q \). Further, let \( |\widetilde{x}\cap \widetilde{x}^*| = r \). Thus, \( |\{0^n\} \cup \widetilde{x}\cup \widetilde{x}^*| = q+\sigma '-r \).
Real world: In the real world, the random permutation \( \mathsf {\Pi }\) is sampled on exactly \( q+\sigma '-r \) distinct points. Thus, we have
Ideal World: In the ideal world, we employed a two stage sampling. First of all, we have
since each \( \textsf{T}_i \) is sampled uniformly from the set \( \mathcal {B}\) independent of others. Now, observe that all the full collision and induced collision indices are fully determined from the transcript \( \nu \) itself. In other words, we can enumerate the set \( \widetilde{\textsf{CI}}:= \widetilde{\textsf{FCI}}\cup \widetilde{\textsf{ICI}}\). Now, since the transcript is good, we must have \( |\widetilde{\textsf{CI}}| = \sigma -\sigma ' + |\widetilde{x}\cap \widetilde{x}^*| = \sigma -\sigma '+r \), and for all indices \( (i,a) \notin \widetilde{\textsf{CI}}\), we have \( \textsf{Y}_{i}[a] = \textsf{Z}_{i}[a] \). Thus, we have
where the second equality follows from the fact that truncationFootnote 6 of a without replacement sample from a set of size \( (2^n-q) \) is still a without replacement sample from the same set. We have
The above discussion on good transcripts can be summarized in shape of the following lemma.
Lemma 4.2
For any  , we have \( \displaystyle \frac{{\Pr _{ }\left( \textsf{V}_1=\nu \right) }}{{\Pr _{ }\left( \textsf{V}_0= \nu \right) }} \ge 1 \).
, we have \( \displaystyle \frac{{\Pr _{ }\left( \textsf{V}_1=\nu \right) }}{{\Pr _{ }\left( \textsf{V}_0= \nu \right) }} \ge 1 \).
Proof
The proof follows from dividing (12) by (15).
Using Theorem 2.1, and Lemma 4.1 and 4.2, we get
5 Proof of Lemma 4.1
Our proof relies on a graph-based combinatorial tool, called structure graphs [3, 15]. A concise and complete description of this tool and relevant results are available in the full version of this paper [9, Appendix A]. Our aim will be to bound the probability of bad events only when they occur in conjunction with some “manageable” structure graphs. In all other cases, we upper bound the probability by the probability of realizing an unmanageable structure graph. Formally, we say that the structure graph \( \mathcal {G}_{\textsf{P}}({\widetilde{\textsf{M}}}) \) is manageable if and only if:
-
1.
for all \( i \in [q] \), we have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i}})) = 0 \), i.e., each \( \textsf{M}_{i} \)-walk is a path.
-
2.
for all distinct \( i,j \in [q] \), we have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j}})) \le 1 \).
-
3.
for all distinct \( i,j,k \in [q] \), we have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) \le 2 \).
-
4.
for all distinct \( i,j,k,l \in [q] \), we have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k},\textsf{M}_{l}})) \le 3 \).
Let  denote the event that \( \mathcal {G}_{\textsf{P}}({\widetilde{\textsf{M}}}) \) is unmanageable. Then, using [9, Corollary A.1], we have
denote the event that \( \mathcal {G}_{\textsf{P}}({\widetilde{\textsf{M}}}) \) is unmanageable. Then, using [9, Corollary A.1], we have

From now on we only consider manageable graphs. Observe that apart from the fact that a manageable graph is just a union of \( \textsf{M}_{i} \)-paths, there is an added benefit that it has no zero collision. Let  and
and  . Now, we have
. Now, we have

Here, inequalities 1 and 2 follow by definition; 3 follows from the fact that \( \textsf{T}_{i} \) is chosen uniformly at random from \( \mathcal {B}\) for each i; and 4 follows from (17).
 Let
Let  . We have
. We have

We bound the individual terms on the right hand side as follows:
 Fix some \( (i,a) \in [q] \times [\ell _i] \). The only way we can have \( \textsf{W}_{i}[a] = 0^n \), for \( 1< a < \ell _i \), is if \( \textsf{Z}_{i}[a-1] = \textsf{M}_{i}[a] \). This happens with probability at most \( (2^n-q)^{-1} \). For \( a = \ell _i \), the equation
Fix some \( (i,a) \in [q] \times [\ell _i] \). The only way we can have \( \textsf{W}_{i}[a] = 0^n \), for \( 1< a < \ell _i \), is if \( \textsf{Z}_{i}[a-1] = \textsf{M}_{i}[a] \). This happens with probability at most \( (2^n-q)^{-1} \). For \( a = \ell _i \), the equation
must hold non-trivially. The probability that this equation holds is bounded by at most \( (2^n-q-1)^{-1} \). Assuming \( q+1 \le 2^{n-1} \), and using the fact that there can be at most \( \sigma \) choices for (i, a) , we have

 Fix some \( i \ne j \in [q] \). Since
Fix some \( i \ne j \in [q] \). Since  holds, we know that
holds, we know that  . We handle the two resulting cases separately:
. We handle the two resulting cases separately:
-
(A)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j}})) = 1 \):Suppose the collision source of the only accident are (i, a) and (j, b) . Then, we have the following system of two equations
$$\begin{aligned} \textsf{Z}_{i}[a] \oplus \textsf{Z}_{j}[b]&= \textsf{M}_{i}[a+1] \oplus \textsf{M}_{j}[b+1]\\ (\mu _{\delta _{\textsf{M}_{i}}} \oplus \mu _{\delta _{\textsf{M}_{j}}}) \odot \textsf{L}\oplus \textsf{Z}_{i}[\ell _i-1] \oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{i}[\ell _i] \oplus \overline{\textsf{M}}_{j}[\ell _j] \end{aligned}$$Suppose \( \delta _{\textsf{M}_{i}} \ne \delta _{\textsf{M}_{j}} \), i.e. \( \mu _{\delta _{\textsf{M}_{i}}} \oplus \mu _{\delta _{\textsf{M}_{j}}} \ne 0^n \). Using the fact that
 holds, we infer that \( \textsf{L}\notin \{\textsf{Z}_{i}[a],\textsf{Z}_{j}[b],\textsf{Z}_{i}[\ell _i-1],\textsf{Z}_{j}[\ell _j-1]\} \). So, the two equations are linearly independent, whence the rank is 2 in this case. Again, using [9, Lemma A.4], and the fact that there are at most \( q^2/2 \) choices for i and j, and \( \ell ^2 \) choices for a and b, we get
holds, we infer that \( \textsf{L}\notin \{\textsf{Z}_{i}[a],\textsf{Z}_{j}[b],\textsf{Z}_{i}[\ell _i-1],\textsf{Z}_{j}[\ell _j-1]\} \). So, the two equations are linearly independent, whence the rank is 2 in this case. Again, using [9, Lemma A.4], and the fact that there are at most \( q^2/2 \) choices for i and j, and \( \ell ^2 \) choices for a and b, we get 
Now, suppose \( \delta _{\textsf{M}_{i}} = \delta _{\textsf{M}_{j}} \), i.e. \( \mu _{\delta _{\textsf{M}_{i}}} \oplus \mu _{\delta _{\textsf{M}_{j}}} = 0^n \). Then, we can rewrite the system as
$$\begin{aligned} \textsf{Z}_{i}[a] \oplus \textsf{Z}_{j}[b]&= \textsf{M}_{i}[a+1] \oplus \textsf{M}_{j}[b+1]\\ \textsf{Z}_{i}[\ell _i-1] \oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{i}[\ell _i] \oplus \overline{\textsf{M}}_{j}[\ell _j] \end{aligned}$$We can have two types of structure graphs relevant to this case, as illustrated in Fig. 3. For type 1 all variables are distinct. So, the two equations are linearly independent, whence the rank is 2 in this case. Again, using [9, Lemma A.4], we get

For type 2, it is clear that \( \textsf{Z}_{j}[\ell _j-1] = \textsf{Z}_{i}[\ell _i-1] \). So, we can assume that the second equation holds trivially, thereby deriving a system in \( \textsf{Z}_{i}[a] \) and \( \textsf{Z}_{j}[b] \), with rank 1. Further, a and b are uniquely determined as \( \ell _i-p \) and \( \ell _j-p \), where p is the longest common suffix of \( \textsf{M}_{i} \) and \( \textsf{M}_{j} \). So we have

-
(B)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j}})) = 0 \):In this case, we only have one equation of the form
$$\begin{aligned} (\mu _{\delta _{\textsf{M}_{i}}} \oplus \mu _{\delta _{\textsf{M}_{j}}}) \odot \textsf{L}\oplus \textsf{Z}_{i}[\ell _i-1] \oplus \textsf{Z}_{j}[\ell _j-1] = \overline{\textsf{M}}_{i}[\ell _i] \oplus \overline{\textsf{M}}_{j}[\ell _j] \end{aligned}$$If \( \delta _{\textsf{M}_{i}} \ne \delta _{\textsf{M}_{j}} \), we have an equation in three variables, namely \( \textsf{L}\), \( \textsf{Z}_{i}[\ell _i-1] \), and \( \textsf{Z}_{j}[\ell _j-1] \); and if \( \delta _{\textsf{M}_{i}} = \delta _{\textsf{M}_{j}} \), we have an equation in two variables, namely \( \textsf{Z}_{i}[\ell _i-1] \), and \( \textsf{Z}_{j}[\ell _j-1] \). In both the cases, the equation can only hold non-trivially, i.e., rank is 1. Using [9, Lemma A.4], we get

On combining the three cases, we get

 Fix some \( i,j,k \in [q] \). Since
Fix some \( i,j,k \in [q] \). Since  holds, we must have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) \le 2 \). Accordingly, we have the following three cases:
holds, we must have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) \le 2 \). Accordingly, we have the following three cases:
-
(A)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 2 \):Suppose \( (\alpha _1,\beta _1) \) and \( (\alpha _2,\beta _2) \) are collision source leading to one of the accident, and \( (\alpha _3,\beta _3) \) and \( (\alpha _4,\beta _4) \) are collision source leading to the other accident. Then, considering \( \textsf{W}_{i}[a] = \textsf{W}_{j}[\ell _j] \), we have the following system of equations
$$\begin{aligned} \textsf{Z}_{\alpha _1}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{\alpha _1}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{\alpha _3}[\beta _3] \oplus \textsf{Z}_{\alpha _4}[\beta _4]&= \textsf{M}_{\alpha _3}[\beta _3+1] \oplus \textsf{M}_{\alpha _4}[\beta _4+1]\\ \textsf{Z}_{j}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a] \end{aligned}$$The first two equations are independent by definition. Further, using
 , we can infer that the last equation is also independent of the first two equations. Thus the system has rank 3. There are at most \( q^3/6 \) choices for (i, j, k) , and for each such choice we have 3 choices for \( (\alpha _1,\alpha _2,\alpha _3,\alpha _4) \) and at most \( \ell ^5 \) choices for \( (\beta _1,\beta _2,\beta _3,\beta _4,a) \). Using [9, Lemma A.4], we have
, we can infer that the last equation is also independent of the first two equations. Thus the system has rank 3. There are at most \( q^3/6 \) choices for (i, j, k) , and for each such choice we have 3 choices for \( (\alpha _1,\alpha _2,\alpha _3,\alpha _4) \) and at most \( \ell ^5 \) choices for \( (\beta _1,\beta _2,\beta _3,\beta _4,a) \). Using [9, Lemma A.4], we have 
-
(B)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 1 \):Suppose \( (\alpha _1,\beta _1) \) and \( (\alpha _2,\beta _2) \) are collision source leading to the accident. First consider the case \( a < \ell _i-1 \) and \( b < \ell _k \). In this case, we have the following system of equations
$$\begin{aligned} \textsf{Z}_{\alpha _1}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{\alpha _1}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{i}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a]\\ \textsf{Z}_{i}[a] \oplus \textsf{Z}_{k}[b-1]&= \textsf{M}_{i}[a+1] \oplus \textsf{M}_{k}[b]\\ \end{aligned}$$The first two equations are clearly independent. Further, since \( \textsf{M}_{i} \ne \textsf{M}_{k} \), the last equation must correspond to a true collision as a consequence of the accident. So, the rank of the above system is 2. Once we fix (i, j, k) and (a, b) , we have at most 3 choices for \( (\alpha _1,\alpha _2) \), and \( \beta _1 \) and \( \beta _2 \) are uniquely determined as \( a+1-p \) and \( b-p \), where p is the largest common suffix of \( \textsf{M}_{i}[1,\ldots ,a+1] \) and \( \textsf{M}_{k}[1,\ldots ,b] \). So, we have

Now, suppose \( a = \ell _i-1 \). Then we can simply consider the first two equations
$$\begin{aligned} \textsf{Z}_{\alpha _1}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{\alpha _1}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{j}[\ell _i-2] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[\ell _i-1] \end{aligned}$$Clearly, the two equations are independent. We have at most \( q^3 \) choices for (i, j, k) , 3 choices for \( (\alpha _1,\alpha _2) \), and \( \ell ^2 \) choices for \( (\beta _1,\beta _2) \). So we have

The case where \( a < \ell _i-1 \) and \( b = \ell _k \) can be handled similarly by considering the first and the third equations.
-
(C)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 0 \):In this case, we know that the three paths, \( \mathcal {W}_i \), \( \mathcal {W}_j \), and \( \mathcal {W}_k \) do not collide. This implies that we must have \( a = \ell _i-1 \), or \( b = \ell _k \) or both, in order for \( \textsf{W}_{i}[a+1] = \textsf{W}_{k}[b] \) to hold. First, suppose both \( a = \ell _i-1 \) and \( b = \ell _k \). Then, we have the following system of equations:
$$\begin{aligned} \textsf{Z}_{j}[\ell _i-2] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[\ell _i-2]\\ (\mu _{\delta _{\textsf{M}_{i}}} \oplus \mu _{\delta _{\textsf{M}_{k}}}) \odot \textsf{L}\oplus \textsf{Z}_{i}[\ell _i-1] \oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{i}[\ell _i] \oplus \overline{\textsf{M}}_{k}[\ell _k] \end{aligned}$$Using the properties of \( \mu _{-1} \) and \( \mu _0 \), and
 , we can conclude that the above system has rank 2. There are at most \( q^3/6 \) choices for (i, j, k) , and at most \( \ell ^2 \) choices for (a, b) . So, we have
, we can conclude that the above system has rank 2. There are at most \( q^3/6 \) choices for (i, j, k) , and at most \( \ell ^2 \) choices for (a, b) . So, we have 
The remaining two cases are similar. We handle the case \( a = \ell _i-1 \) and \( b < \ell _k \), and the other case can be handled similarly. We have the following system of equations
$$\begin{aligned} \textsf{Z}_{j}[\ell _i-2] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[\ell _i-2]\\ \mu _{\delta _{\textsf{M}_{i}}} \odot \textsf{L}\oplus \textsf{Z}_{i}[\ell _i-1] \oplus \textsf{Z}_{k}[b-1]&= \overline{\textsf{M}}_{i}[\ell _i] \oplus \textsf{M}_{k}[b] \end{aligned}$$If \( \delta _{\textsf{M}_{i}} \ne \delta _{\textsf{M}_{j}} \), then using the same argument as above, we can conclude that the system has rank 2, and we get

So, suppose \( \delta _{\textsf{M}_{i}} = \delta _{\textsf{M}_{j}} \). Now, in order for the second equation to be a consequence of the first equation, we must have \( \textsf{Z}_{i}[\ell _i-2] = \textsf{Z}_{j}[\ell _j-1] \) and \( \textsf{Z}_{i}[\ell _i-1] = \textsf{Z}_{k}[b] \). The only we way this happens trivially is if \( \textsf{M}_{i}[1,\ldots ,\ell _i-1] = \textsf{M}_{j}[1,\ldots ,\ell _j-1] \) and \( \textsf{M}_{i}[1,\ldots ,\ell _i-1] = \textsf{M}_{k}[1,\ldots ,b] \). But, then we have \( b = \ell _i-1 \), and once we fix (i, k) there’s a unique choice for j, since \( \textsf{M}_{j}[1,\ldots ,\ell _j-1] = \textsf{M}_{i}[1,\ldots ,\ell _i-1] \) and \( \overline{\textsf{M}}_{j}[\ell _j] =\overline{\textsf{M}}_{i}[\ell _i] \oplus \textsf{M}_{i}[\ell _i-2] \oplus \textsf{M}_{k}[b] \). So, we get

By combining all three cases, we have

 Fix some \( i,j,k \in [q] \). The analysis in this case is very similar to the one in case of
Fix some \( i,j,k \in [q] \). The analysis in this case is very similar to the one in case of  . So we will skip detailed argumentation whenever possible. Since
. So we will skip detailed argumentation whenever possible. Since  holds, we must have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) \le 2 \). Accordingly, we have the following three cases:
holds, we must have \( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) \le 2 \). Accordingly, we have the following three cases:
-
(A)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 2 \):This can be bounded by using exactly the same argument as used in Case A for
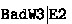 . So, we have
. So, we have 
-
(B)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 1 \):Suppose \( (\alpha _1,\beta _1) \) and \( (\alpha _2,\beta _2) \) are collision source leading to the accident. Without loss of generality we assume \( a < b \). Specifically, \( b \le \ell _i-1 \) and \( a \le b-2 \) due to
 . First consider the case \( b = \ell _i-1 \). In this case, considering \( \textsf{W}_{i}[b] = \textsf{W}_{k}[\ell _k] \), we have the following system of equations $$\begin{aligned} \textsf{Z}_{\alpha _1}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{\alpha _1}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{i}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}} \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{k}[\ell _k] \oplus \textsf{M}_{i}[b] \end{aligned}$$
. First consider the case \( b = \ell _i-1 \). In this case, considering \( \textsf{W}_{i}[b] = \textsf{W}_{k}[\ell _k] \), we have the following system of equations $$\begin{aligned} \textsf{Z}_{\alpha _1}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{\alpha _1}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{i}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}} \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{k}[\ell _k] \oplus \textsf{M}_{i}[b] \end{aligned}$$Using a similar argument as used in previous such cases, we establish that the two equations are independent. Now, once we fix (i, j, k) , we have exactly one choice for b, at most 3 choices for \( (\alpha _1,\alpha _2) \), and \( \ell ^2 \) choices for \( (\beta _1, \beta _2) \). So, we have

Now, suppose \( b < \ell _i-1 \). Here we can have two cases:
-
(B.1)
\( \mathcal {W}_i \) is involved in the accident: Without loss of generality assume that \( \alpha _1 = i \) and \( \beta _1 \in [\ell _i-1] \). Then, we have the following system of equations:
$$\begin{aligned} \textsf{Z}_{i}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{i}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{i}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a]\\ \textsf{Z}_{i}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}} \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{k}[\ell _k] \oplus \textsf{M}_{i}[b] \end{aligned}$$Suppose \( \textsf{Z}_{i}[\beta _1] = \textsf{Z}_{i}[a-1] \). Then, we must have \( \beta _1 = a-1 \) as the graph is manageable.In this case, we consider the first two equations. It is easy to see that the two equations are independent, and once we fix i, j, k, there are at most 2 choices for \( \alpha _2 \) and \( \ell ^2 \) choices for \( (\beta _1,\beta _2) \), which gives a unique choice for a. So, we have

We get identical bound for the case when \( \textsf{Z}_{i}[\beta _1] = \textsf{Z}_{i}[b-1] \). Suppose \( \textsf{Z}_{i}[\beta _1] \notin \{\textsf{Z}_{i}[a-1],\textsf{Z}_{i}[b-1]\} \). Then, using the fact that there is only one accident in the graph and that accident is due to \( (i,\beta _1) \) and \( (\alpha _2,\beta _2) \), we infer that \( \textsf{Z}_{\alpha _2}[\beta _2] \notin \{\textsf{Z}_{i}[a-1],\textsf{Z}_{i}[b-1]\} \). Now, the only way rank of the above system reduces to 2, is if \( \textsf{Z}_{i}[a-1] = \textsf{Z}_{k}[\ell _k-1] \) and \( \textsf{Z}_{i}[b-1] = \textsf{Z}_{j}[\ell _j-1] \) trivially. However, if this happens then a and b are uniquely determined by our choice of \( (i,j,k,\beta _1,\alpha _2,\beta _2) \). See Fig. 4 for the two possible structure graphs depending upon the value of \( \alpha _2 \). Basically, based on the choice of \( \alpha _2 \), \( a \in \{\ell _k,\ell _k-\beta _2+\beta _1\} \). Similarly, \( b \in \{\ell _j,\ell _j-\beta _2+\beta _1\} \). So, using [9, Lemma A.4], we get

-
(B.2)
\( \mathcal {W}_i \) is not involved in the accident: Without loss of generality assume \( \alpha _1 = j \) and \( \alpha _2 = k \). Then, we have the following system of equations:
$$\begin{aligned} \textsf{Z}_{j}[\beta _1] \oplus \textsf{Z}_{k}[\beta _2]&= \textsf{M}_{j}[\beta _1+1] \oplus \textsf{M}_{k}[\beta _2+1]\\ \textsf{Z}_{i}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a]\\ \textsf{Z}_{i}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}} \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{k}[\ell _k] \oplus \textsf{M}_{i}[b] \end{aligned}$$Since the graph is manageable, \( \{\textsf{Z}_{i}[a-1],\textsf{Z}_{i}[b-1]\} \cap \{\textsf{Z}_{j}[\ell _j-1],\textsf{Z}_{k}[\ell _k-1]\} \ne \emptyset \). Suppose \( \{\textsf{Z}_{i}[a-1],\textsf{Z}_{i}[b-1]\} = \{\textsf{Z}_{j}[\ell _j-1],\textsf{Z}_{k}[\ell _k-1]\} \). Without loss of generality, assume \( \textsf{Z}_{i}[a-1] = \textsf{Z}_{k}[\ell _k-1] \) and \( \textsf{Z}_{i}[b-1] = \textsf{Z}_{j}[\ell _j-1] \). This can only happen if the resulting graph is of Type 2 form in Fig. 4, which clearly shows that we have unique choices for a and b when we fix the other indices. Now, suppose \( |\{\textsf{Z}_{i}[a-1],\textsf{Z}_{i}[b-1]\} \cap \{\textsf{Z}_{j}[\ell _j-1],\textsf{Z}_{k}[\ell _k-1]\}| = 1 \). Then, we must have \( \textsf{Z}_{i}[a-1] \in \{\textsf{Z}_{j}[\beta _1],\textsf{Z}_{k}[\beta _2]\} \) since \( a < b \). Without loss of generality we assume that \( \textsf{Z}_{i}[a-1] = \textsf{Z}_{k}[\beta _2] \) and \( \textsf{Z}_{i}[b-1] = \textsf{Z}_{j}[\ell _j-1] \). Using similar argument as before, we conclude that a and b are fixed once we fix all other indices. So using [9, Lemma A.4], we get

-
(B.1)
-
(C)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 0 \):In this case, we know that the three paths, \( \mathcal {W}_i \), \( \mathcal {W}_j \), and \( \mathcal {W}_k \) do not collide. We have the following system of equations:
$$\begin{aligned} \textsf{Z}_{i}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a]\\ \textsf{Z}_{i}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}}) \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{i}[\ell _k] \oplus \textsf{M}_{i}[b] \end{aligned}$$Using a similar analysis as in case C of
 , we get
, we get 
By combining all three cases, we have

 Fix some \( i,j,k \in [q] \). The analysis in this case is again similar to the analysis of
Fix some \( i,j,k \in [q] \). The analysis in this case is again similar to the analysis of  and
and  . We have the following three cases:
. We have the following three cases:
-
(A)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 2 \):This can be bounded by using exactly the same argument as used in Case A for
 . So, we have
. So, we have 
-
(B)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 1 \):Suppose \( (\alpha _1,\beta _1) \) and \( (\alpha _2,\beta _2) \) are collision source leading to the accident. In this case, we have the following system of equations
$$\begin{aligned} \textsf{Z}_{\alpha _1}[\beta _1] \oplus \textsf{Z}_{\alpha _2}[\beta _2]&= \textsf{M}_{\alpha _1}[\beta _1+1] \oplus \textsf{M}_{\alpha _2}[\beta _2+1]\\ \textsf{Z}_{i}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a]\\ \textsf{Z}_{j}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}} \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{k}[\ell _k] \oplus \textsf{M}_{j}[b] \end{aligned}$$We can have two sub-cases:
-
(B.1)
Suppose the third equation is simply a consequence of the second equation. Then, we must have \( \delta _{\textsf{M}_{i}} = \delta _{\textsf{M}_{j}} \) and \( \textsf{Z}_{i}[a-1] = \textsf{Z}_{j}[b-1] \) and \( \textsf{Z}_{j}[\ell _j-1] = \textsf{Z}_{k}[\ell _k-1] \) must hold trivially, since the graph is manageable. We claim that \( a = b = \textsf{Prefix}(\textsf{M}_{i}[1],\textsf{M}_{j}[1])+1 \). If not, then \( \textsf{M}_{i}[\ell _i] = \textsf{M}_{j}[\ell _j] \) which in conjunction with \( \textsf{Z}_{j}[\ell _j-1] = \textsf{Z}_{k}[\ell _k-1] \) implies that \( \textsf{W}_{i}[\ell _i] = \textsf{W}_{j}[\ell _j] \) which contradicts
 . So, using [9, Lemma A.4], we get
. So, using [9, Lemma A.4], we get 
-
(B.2)
The second and third equation are independent. Considering the sub-system consisting of these two equations, and using [9, Lemma A.4], we get

-
(B.1)
-
(C)
\( \textsf{Acc}(\mathcal {G}_{\textsf{P}}({\textsf{M}_{i},\textsf{M}_{j},\textsf{M}_{k}})) = 0 \):We have the following system of equations:
$$\begin{aligned} \textsf{Z}_{i}[a-1] \oplus \mu _{\delta _{\textsf{M}_{j}}} \odot \textsf{L}\oplus \textsf{Z}_{j}[\ell _j-1]&= \overline{\textsf{M}}_{j}[\ell _j] \oplus \textsf{M}_{i}[a]\\ \textsf{Z}_{i}[b-1] \oplus \mu _{\delta _{\textsf{M}_{k}}} \odot \textsf{L}\oplus \textsf{Z}_{k}[\ell _k-1]&= \overline{\textsf{M}}_{i}[\ell _k] \oplus \textsf{M}_{i}[b] \end{aligned}$$Let r denote the rank of the above system. Using a similar analysis as in case B.1 above, we conclude that \( a = b = \textsf{Prefix}(\textsf{M}_{i}[1],\textsf{M}_{j}[1])+1 \) if \( r=1 \). Using [9, Lemma A.4], we get

By combining all three cases, we have

Further, from Eqs. (19)–(24), we have

 In the full version [9, Appendix B] of this paper, we show that
In the full version [9, Appendix B] of this paper, we show that

Combining Eqs. (18), (25), and (26), we have

6 Conclusion
In this paper we proved that \( \textsf {OMAC} \), \( \textsf {XCBC} \) and \( \textsf {TMAC} \) are secure up to \( q \le 2^{n/2} \) queries, while the message length \( \ell \le 2^{n/4} \). As a consequence, we have proved that \( \textsf {OMAC} \) – a single-keyed CBC-MAC variant – achieves the same security level as some of the more elaborate CBC-MAC variants like EMAC and ECBC. This, in combination with the existing results [15, 16], shows that the security is tight up to \( \ell \le 2^{n/4} \) for all CBC-MAC variants except for the original CBC-MAC. It could be an interesting future problem to extend our analysis and derive similar bounds for CBC-MAC over prefix-free message space. In order to prove our claims, we employed reset-sampling method by Chattopadhyay et al. [8], which seems to be a promising tool in reducing the length-dependency in single-keyed iterated constructions. Indeed, we believe that this tool might even be useful in obtaining better security bounds for single-keyed variants of many beyond-the-birthday-bound constructions.
Notes
- 1.
This is same as CMAC [10] — a NIST recommended AES based MAC — for appropriate choice of constants.
- 2.
A keyed construction is called a PRF if it is computationally infeasible to distinguish it from a random function.
- 3.
Using GeoGebra Classic available at https://www.geogebra.org/classic.
- 4.
Instantiated with a block cipher in practical applications.
- 5.
Does not collide with any other input.
- 6.
Removing some elements from the tuple.
References
Bellare, M., Goldreich, O., Mityagin, A.: The power of verification queries in message authentication and authenticated encryption. IACR Cryptol. ePrint Arch. 2004, 309 (2004)
Bellare, M., Kilian, J., Rogaway, P.: The security of cipher block chaining. In: Proceedings of Advances in Cryptology - CRYPTO 1994, pp. 341–358 (1994)
Bellare, M., Pietrzak, K., Rogaway, P.: Improved security analyses for CBC macs. In: Proceedings of Advances in Cryptology - CRYPTO 2005, pp. 527–545 (2005)
Berendschot, A., et al.: Final Report of RACE Integrity Primitives, vol. 1007, LNCS, Springer-Verlag, Berlin (1995). https://doi.org/10.1007/3-540-60640-8
Black, J., Rogaway, P.: CBC macs for arbitrary-length messages: the three-key constructions. In: Proceedings of Advances in Cryptology - CRYPTO 2000, pp. 197–215 (2000)
Black, J., Rogaway, P.: A block-cipher mode of operation for parallelizable message authentication. In: Proceedings of Advances in Cryptology - EUROCRYPT 2002, pp. 384–397 (2002)
Chakraborty, B., Chattopadhyay, S., Jha, A., Nandi, M.: On length independent security bounds for the PMAC family. IACR Trans. Symmet. Cryptol. 2021(2), 423–445 (2021)
Chattopadhyay, S., Jha, A., Nandi, M.: Fine-tuning the ISO/IEC Standard Lightmac. In: Proceedings of Advances in Cryptology - ASIACRYPT 2021, pp. 490–519 (2021)
Chattopadhyay, S., Jha, A., Nandi, M.: Towards tight security bounds for OMAC, XCBC and TMAC. IACR Cryptol. ePrint Arch. 2022, 1234 (2022)
Dworkin, M.: Recommendation for block cipher modes of operation: the CMAC mode for authentication. NIST Special Publication 800–38b, National Institute of Standards and Technology, U. S. Department of Commerce (2005)
Ehrsam, W.F., Meyer, C.H.W., Smith, J.L., Tuchman, W.L.: Message verification and transmission error detection by block chaining. Patent 4,074,066, USPTO (1976)
Iwata, T., Kurosawa, K.: OMAC: One-Key CBC MAC. In: Fast Software Encryption - FSE 2003, Revised Papers, pp. 129–153 (2003)
Iwata, T., Kurosawa, K.: Stronger Security Bounds for OMAC, TMAC, and XCBC. In: Proceedings of Progress in Cryptology - INDOCRYPT 2003, pp. 402–415 (2003)
Jha, A., Mandal, A., Nandi, M.: On the exact security of message authentication using pseudorandom functions. IACR Trans. Symmetric Cryptol. 2017(1), 427–448 (2017)
Jha, A., Nandi, M.: Revisiting structure graphs: applications to CBC-MAC and EMAC. J. Math. Cryptol. 10(3–4), 157–180 (2016)
Jha, A., Nandi, M.: Revisiting structure graphs: applications to CBC-MAC and EMAC. IACR Cryptol. ePrint Arch. 2016, 161 (2016)
Kurosawa, K., Iwata, T.: TMAC: two-key CBC MAC. In: Proceedings of Topics in Cryptology - CT-RSA 2003, pp. 33–49 (2003)
Luykx, A., Preneel, B., Tischhauser, E., Yasuda, K.: A MAC mode for lightweight block ciphers. In: Fast Software Encryption - FSE 2016, Revised Selected Papers, pp. 43–59 (2016)
Minematsu, K., Matsushima, T.: New bounds for PMAC, TMAC, and XCBC. In: Fast Software Encryption - FSE 2007, Revised Selected Papers, pp. 434–451 (2007)
Nandi, M.: Fast and secure CBC-type MAC algorithms. In: Fast Software Encryption - FSE 2009, Revised Selected Papers, pp. 375–393 (2009)
Nandi, M.: Improved security analysis for OMAC as a pseudorandom function. J. Math. Cryptol. 3(2), 133–148 (2009)
Nandi, M., Mandal, A.: Improved security analysis of PMAC. J. Math. Cryptol. 2(2), 149–162 (2008)
Patarin, J.: Etude des Générateurs de Permutations Pseudo-aléatoires Basés sur le Schéma du DES. Ph.D. thesis, Université de Paris (1991)
Patarin, J.: The “coefficients H" technique. In: Selected Areas in Cryptography - SAC 2008. Revised Selected Papers, pp. 328–345 (2008)
Pietrzak, K.: A tight bound for EMAC. In: Proceedings of Automata, Languages and Programming - ICALP 2006, Part II, pp. 168–179 (2006)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 International Association for Cryptologic Research
About this paper
Cite this paper
Chattopadhyay, S., Jha, A., Nandi, M. (2022). Towards Tight Security Bounds for OMAC, XCBC and TMAC. In: Agrawal, S., Lin, D. (eds) Advances in Cryptology – ASIACRYPT 2022. ASIACRYPT 2022. Lecture Notes in Computer Science, vol 13791. Springer, Cham. https://doi.org/10.1007/978-3-031-22963-3_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-22963-3_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-22962-6
Online ISBN: 978-3-031-22963-3
eBook Packages: Computer ScienceComputer Science (R0)






 ; and
; and ,
, 
 .
.



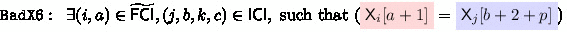 , where
, where 

 . Thus,
. Thus,  ,
,  ,
,  . Also
. Also  .
. , the result follows from
, the result follows from  ;
;  . Therefore, we must have
. Therefore, we must have  holds).
holds). ). If
). If  , the second equality is due to the definition of full collision, the third equality is due to
, the second equality is due to the definition of full collision, the third equality is due to  ). Since
). Since  . Now, we have
. Now, we have  .
. for
for 
 holds, we infer that
holds, we infer that 



 , we can infer that the last equation is also independent of the first two equations. Thus the system has rank 3. There are at most
, we can infer that the last equation is also independent of the first two equations. Thus the system has rank 3. There are at most 


 , we can conclude that the above system has rank 2. There are at most
, we can conclude that the above system has rank 2. There are at most 



 . So, we have
. So, we have 
 . First consider the case
. First consider the case 



 , we get
, we get 
 . So, we have
. So, we have 
 . So, using [
. So, using [

