Abstract
We construct the first four-round non-malleable commitment scheme based solely on the black-box use of one-to-one one-way functions. Prior to our work, all non-malleable commitment schemes based on black-box use of polynomial-time cryptographic primitives require more than 16 rounds of interaction.
A key tool for our construction is a proof system that satisfies a new definition of security that we call non-malleable zero-knowledge with respect to commitments. In a nutshell, such a proof system can be safely run in parallel with any (potentially interactive) commitment scheme. We provide an instantiation of this tool using the MPC-in-the-Head approach in combination with BMR.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Starting from the pioneering work of Dolev et al. [15], a long line of works has focused on constructing new non-malleable commitment schemes with improved characteristics, both in terms of efficiency and assumptions. Given the strong connection of non-malleable commitments with secure multi-party computation [3, 44], improvements in the area of non-malleable commitments have a big impact on the multi-party computation (MPC) landscape. In particular, recent developments on the round complexity of non-malleable commitments led to the first round-optimal MPC protocols in the plain model [1, 7, 10, 26].
The round complexity of commitment schemes based on polynomial-time hardness assumptions in the stand-alone setting is nowadays well understood. Non-interactive commitments can be constructed assuming the existence of 1-to-1 one-way functions (OWFs) [19] and 2-round commitments can be constructed assuming the existence of OWFs only. Moreover, non-interactive commitments do not exist if one relies on the black-box use of OWFs only [34]. Recently many progress have been made also for the case of non-malleable (NM) commitmentsFootnote 1. Indeed, the long sequence of very exciting positive results [2, 8, 9, 20, 22, 24, 31,32,33, 37,38,39,40,41,42,43] led to the work of Khurana [29] in which the authors showed how to obtain a 3-round (which is optimal for the case of polynomial-time assumptions [36]) non-malleable commitment scheme based on specific number-theoretic assumptions, and to [23] where the authors proposed a round optimal scheme based on one-to-one OWFs.
Black-Box (BB) Constructions. While these recent results show round-optimal constructions, they make non-black-box use of cryptography. Constant round BB schemes are known [20, 22, 31, 43], but their round complexity is far to be optimal. More specifically, Goyal et al. [22] give a black-box NM commitment protocol only based on the existence of one-way functions, but this construction requires more than 16 rounds. In another work, Goyal et al. [24] mention that combining their protocol with ideas from [22] would could to a 6-round protocol but no explicit construction was given. Therefore the following question remained open.
Does it exist a non-malleable commitment scheme that makes black-box use of standard polynomial-time cryptographic primitives where the commitment phase consists of less than 16 rounds?
In this work, we provide a positive answer, by proposing a 4-round non-malleable commitment scheme that only makes black-box use of one-to-one one-way functions. Whether it is possible to achieve the same result in three rounds remains a fascinating open question.
1.1 Our Contributions
The state-of-the-art in constructing non-malleable commitments based on minimal assumptions shows a significant gap in the round complexity of black-box and non-black-box protocols. In this work, we almost close this gap by describing the first 4-round non-malleable commitment that makes black-box use of the underlying primitives and is based on the almost minimal assumption of injective one-way functions.Footnote 2 In particular, we prove the following theorem.
Theorem (Informal). Assuming one-to-one OWFs, there exists a 4-round non-malleable commitment scheme that makes black-box use of the OWFs.
Our 4-round non-malleable commitment crucially relies on a novel 3-round public-coin proof system that is zero-knowledge against honest verifiers (HVZK), and such that the statement to be proven can be specified in the last round (delayed-input property). In particular, our protocol enjoys adaptive-soundness and adaptive-HVZK [11, 12, 27]. These properties guarantee that HVZK and soundness hold even against an adversary that decides the statement to be proven (and the witness for the HVZK case) adaptively on the first two rounds of the protocol. A protocol that satisfies such properties and that also makes black-box use of the underlying cryptographic primitives is proposed in [27]. What makes our scheme different is that it also enjoys a special form of non-malleability that we call non-malleable HVZK with respect to commitment (NMZKC).
In a nutshell, this notion allows us to safely compose the proof system in parallel with any type of commitment scheme. In more detail, we consider the following setting. There is a man-in-the-middle (MiM) adversary that interacts (acting as the verifier) with an honest prover of a proof system \(\varPi _\textsf{AI}\) (where AI stands for adaptive-input). In the right session instead, the MiM acts as the sender for a (potentially interactive) commitment scheme \(\varPi _\texttt{com}\), with an honest receiver. The notion of NMZKC guarantees that the distribution of the messages committed by the MiM in the right session is independent of whether the messages of \(\varPi _\textsf{AI}\) are generated honestly (i.e., using the witness for some NP statement x), or are computed using the simulator.
We believe that this tool and notion can be of independent interest. Indeed, NMZKC proof systems might be used in place of rewind secure schemes. A rewind secure proof system guarantees that the zero-knowledge property holds even if an adversarial verifier is allowed to rewind the prover a bounded number of times (this can be seen as a mild form of resettability). The reason why the notion of rewind security has gained a lot of attention recently is exactly that it simplifies the composition of proof systems with other primitives. For example, it simplifies the composition of a proof system with extractable commitments. The high-level idea is that in the security proof it is possible to extract from the commitment without harming the zero-knowledge property of the proof system. Hence, it is possible to check whether the distribution of the committed messages changes depending on whether the messages of the proof system are simulated or are generated honestly. This proof technique has been exploited in many recent works [7, 13, 23]. And, more interestingly, it was used also to construct the first one-one non-malleable commitment [24]Footnote 3. As we will discuss in the technical overview, we will replace the rewind secure proof system proposed in [24] (that inherently makes non-black-box use of the underlying primitives) with our NMZKC proof system.
We believe that NMZKC in some scenarios can replace the use of rewind secure primitives, and this might be particularly helpful given that our protocol is completely black-box in the use of the underlying cryptographic primitives. To the best of our knowledge, no black-box rewind secure three-round HVZK protocol is currently available. In summary, we prove the following theorem.
Theorem (Informal). Assuming one-to-one OWFs, then there exists a 3-round delayed-input public-coin adaptive-input proof system that also is NMZKC and it makes black-box use of the OWFs.
2 Overview of Techniques
We first describe how to construct the main tool required for our construction, which is a commit-and-prove proof system that satisfies the definition of non-malleable HVZK with respect to commitment. Then we show how to use this tool to construct our four-round non-malleable commitment protocol.
2.1 Our NMZKC Protocol and New Commitment Schemes
We start this section by recalling how to turn an MPC protocol into a proof system for any \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}\) following the MPC-in-the-head approach of [28]. Let \(\varPi _\textsf{MPC}\) be an n-party MPC protocol that is secure against up to t semi-honest corruptions. First, the prover secret-shares the witness w using an additive secret-sharing, while f will be a verification function that outputs 1 iff w is a valid witness, i.e., \(f(x,w_1,\dots ,w_n)=1 \Longleftrightarrow (x,w_1\oplus \dots \oplus w_n)\in {\textsf{Rel}}\). Then, it simulates all n parties running the protocol locally and sends the verifier commitments to each parties’ views. Later, the verifier randomly chooses t of the parties’ commitments to be opened, and checks that the committed messages are consistent with an honest execution of the MPC protocol according to the opened views. Since only t parties are opened, the verifier learns nothing about the secret input w, while the random choice of the opened parties ensures that enough views have been computed honestly, ensuring soundness.Footnote 4
Unfortunately, this scheme is inherently non-delayed input since the prover needs both statement and witness to generate the views that must be committed in the first round. To overcome this limitation, we consider a specific class of two-phase MPC protocols. In particular, we require protocols with an input-independent offline phase, where the parties only produce correlated randomness that will be used to speed up the second phase. In the second phase (the online phase) the input is required and used to compute the output of the function. We denote such protocols by \(\varPi _\textsf{MPC}:=(\varPi _\textsf{MPC}^\texttt{off},\varPi _\textsf{MPC}^\texttt{on})\), where the two algorithms \(\varPi _\textsf{MPC}^\texttt{off}\) and \(\varPi _\textsf{MPC}^\texttt{on}\) denote respectively the offline and the online phase of \(\varPi _\textsf{MPC}\).
Equipped with such an MPC protocol, we can modify the approach of [28] as follows. The prover only simulates \(\varPi _\textsf{MPC}^\texttt{off}\), and commits to the individual views. Then the verifier, as described before, selects a random subset of parties to be opened. After receiving the challenge, the prover opens the requested commitments and additionally runs \(\varPi _\textsf{MPC}^\texttt{on}\) to obtain the entire views of the parties requested by the verifier. At the end of this process, the verifier holds complete views for all the parties it requested and can check their consistency as previously described.
Intuitively, (non-adaptive input) HVZK comes again from the hiding of the commitments and the (semi-honest) security of the MPC protocol. However, it is clear that this approach fails completely against malicious provers. Indeed, they might easily generate online messages in a malicious way for all the parties the verifier did not ask to open. Note that in this case, \(\varPi _\textsf{MPC}\) is secure against t corrupted parties, but the adversary might generate ill-formed online messages for the remaining \(n-t\). To work around this problem, we require \(\varPi _\textsf{MPC}\) to enjoy a stronger notion of security that we call robustness. In a nutshell, this notion requires that, when the offline phase of \(\varPi _\textsf{MPC}\) has been honestly computed, then it is always possible to check if a message received during the online phase has been honestly generated or not. In this way, robustness allows to prove soundness also w.r.t. a malicious prover that specifies the inputs in the last round (i.e. adaptive-input soundness).
The above approach guarantees that the protocol enjoys delayed-input completeness and adaptive-input soundness. However, it is not clear how to argue that the protocol is adaptive-input HVZK given that \(\varPi _\textsf{MPC}\) is only semi-honest secure. The reason is that we would like to rely on the security of the underlying MPC protocol thus committing to simulated views in the first round. However, to simulate these views the MPC simulator needs to know the input of the corrupted parties. We recall that such input consists of a share of the witness (which is easy to simulate) and the theorem to be proven. This is problematic since the adaptive-input HVZK simulator needs to generate the first round without knowing the theorem, hence, we cannot run the MPC simulator of the underlying protocol.
To circumvent this issue, we make use of a special type of commitment scheme, that we call ambiguous commitmentFootnote 5. Compared to a standard commitment scheme, they can be opened in two modes: binding and equivocal. If the commitment is computed using the binding mode then the commitment is binding, otherwise, it can be equivocated to any message the sender wants.
Using ambiguous commitments, we modify our protocol as follows. The prover generates the views of \(\varPi _\textsf{MPC}\) as before, but it creates a 2-out-of-2 secret sharing of each of these views and commits to them using the ambiguous commitment scheme in biding mode (i.e., two commitments per view are generated). Then, the verifier challenges the prover asking to open a random subset of views as before. In addition, for each of the opened views, the verifier asks to see the randomness used to generate one of the two commitments and rejects if it notices that a commitment has not been computed using the binding procedure. The rest of the protocol proceeds as before.
The adaptive-input HVZK simulator, which we recall needs to generate the first round without knowing the theorem, works as follows. On input the challenge it can compute one commitment in equivocal mode (the one for which the simulator will not need to disclose its randomness), and one in binding mode. The binding commitments simply contain a random string. The set of commitments computed in the described way constitutes the first round.
Upon receiving the theorem, the adaptive-input HVZK simulator runs the MPC simulator of \(\varPi _\textsf{MPC}\). At this point, the simulator computes the xor of the i-th view with the random string committed in the i-th binding commitment and opens the equivocal commitment to the obtained value.
The soundness still holds because, intuitively, the verifier performs a cut-and-choose to make sure that the commitments are all computed in binding mode. Clearly, an adversary has still a non-negligible probability of cheating, but by repeating the protocol we obtain a sound protocol.
Non-malleable HVZK with Respect to Commitment. So far we have only argued that our protocol, that we denote with \(\varPi _\textsf{AI}\), is adaptive HVZK and adaptive sound. We also want to argue that our protocol is non-malleable HVZK with respect to commitment. We recall that in this security notion, there is a MiM adversary that on the left session acts as the adversary for the adaptive HVZK security game, and in the right session it acts as the sender for a commitment scheme. In more detail, the adversary picks a challenge and sends it to the left session (that acts as a challenger for the experiment). The challenger tosses a coin b, and if \(b=0\) then it computes the first round of \(\varPi _\textsf{AI}\) using the honest prover procedure, otherwise it computes it using the adaptive HVZK simulator. The adversary now picks a statement x and a witness w and sends those to the challenger. If \(b=0\), the challenger runs the honest prover of \(\varPi _\textsf{AI}\) on input (x, w) to compute a third-round message, if \(b=1\) instead the challenger runs the HVZK on input x (and the previous state of the simulator), thus obtaining the third message. The challenger then sends this third message to the MiM in the left session and stops.
While the MiM is acting as described in the left session, it concurrently sends a commitment in the right session. We say that \(\varPi _\textsf{AI}\) is non-malleable HVZK with respect to commitment, if the distribution of the messages committed on the right session by the MiM does not depend on b.
We prove that \(\varPi _\textsf{AI}\) is non-malleable HVZK with respect to any extractable commitment \(\varPi _\texttt{com}\). The idea is to use an adversary to the NMZKC property to construct an adversary for the adaptive-HVZK property. That is, we let the MiM to interact with the adaptive HVZK challenger while at the same time we run the extractor of the commitment scheme to check how the distribution of the committed messages changes. Unfortunately, this simple idea has a major flaw. The rewinds made by the extractor of the commitment might also rewind the challenger of the HVZK security game. Indeed in each rewind made by the extractor, the MiM could send a new theorem-witness pair, and ask for a new third round of \(\varPi _\textsf{AI}\).
To prove that \(\varPi _\textsf{AI}\) can cope with such an adversarial behavior, we exploit how our HVZK simulator works. We note that once the challenge is known, then the simulator knows what commitments will be opened to honestly and what commitments will be equivocated. If an adversary during the rewinds samples new theorem-witness, we simply need to run multiple times the simulator of the underlying MPC protocol and equivocate the commitments accordingly. Hence, we can reduce the adversary that wins in the non-malleable HVZK with respect to commitment experiment to an adversary that either breaks the security of our commitment or the security of the underlying MPC protocol.
\(\varSigma \)-Commitment. In this work, we also consider a class of three-round public commitment schemes that we call \(\varSigma \)-commitment. A \(\varSigma \)-commitment is hiding against honest receiver (HRH), and in addition, it is extractable. To realize a \(\varSigma \)-commitment \(\varSigma =(\mathcal {S}^\varSigma ,\mathcal {R}^\varSigma )\), we use the approach of Goyal et al. [22], which makes use of an information-theoretic verifiable secret sharing protocol \(\varPi ^\textsf{vss}\). The protocol works as follows. To commit to a message w, the sender \(\mathcal {S}^\varSigma \) runs “in its head” the sharing phase of \(\varPi ^\textsf{vss}\), with input a message m. Then the sender commits to the views (obtained by the execution of sharing phase of \(\varPi ^\textsf{vss}\)) of each player separately using a statistical binding commitment scheme \(\varPi ^\texttt{com}\). The receiver, upon receiving these commitments, samples a random set \(I \subset [n]\), with \(|I|\le t\), and sends it to the sender. Finally, the sender replies by decommitting the views corresponding to the challenge I.
The property of HRH comes from the fact that, if the challenge I is known in advance, then we can commit to a random message and simulate the openings of the commitment. We can prove that a simulated transcript is indistinguishable from the transcript generated by an honest committed with input m via a simple reduction to the security of the statistically binding commitments.
Putting Together \(\varSigma \) and \(\varPi _\textsf{AI}\) to Realize a Commit-and-Prove Protocol \(\varPi \). We use \(\varSigma \) and \(\varPi _\textsf{AI}\) to realize a black-box commit-and-prove protocol, which will be the main building block we use to construct our non-malleable commitment scheme. Our commit-and-prove protocol \(\varPi \) works as follows. The prover commits \(\lambda \)-times to the witness w running \(\varSigma \) and proving, using \(\varPi _\textsf{AI}\), that each committed message w satisfies some relation \({\textsf{Rel}}\)Footnote 6. The statement to be proven can be postponed to the last round since \(\varPi _\textsf{AI}\) is delayed-input complete.
To make sure that the same message is committed in all these executions, we use a technique proposed by Khurana et al. in [30]. Namely, in each execution of \(\varSigma \), instead of committing to w, we commit to w||r, for some random value r. Then, we use the protocol \(\varPi _\textsf{AI}\) to prove that \(a=w+r\alpha \), where \(\alpha \) is chosen as part of the challenge, and a is sent in the third round from the prover.
As argued in [30], since r is global across all the executions, if \(w \ne w'\) then \(w+r\alpha \ne w'+r\alpha \) with overwhelming probability due to the Schwartz-Zippel lemma. Therefore, if the committed messages are different across the (multiple) executions, then the statement proven by \(\varPi _\textsf{AI}\) must be false, and the soundness of \(\varPi _\textsf{AI}\) guarantees that the verifier rejects. The adaptive-input SHVZK follows from the adaptive-input SHVZK of \(\varPi _\textsf{AI}\) and the HRH property of \(\varSigma \).
Concrete Instantiation for Robust MPC. As we mentioned, one of the main tool we rely on is a robust MPC protocol. We recall that a robust MPC protocol allows the prover to initially commit only to the offline views, which are input-independent, and only in the last round to “complete the proof” with the online views. The robustness property guarantees that the commitments generated in the first round univocally specify the actual MPC evaluation so that the online steps only consist of an input-distribution phase and deterministic computations. In this way, even if the prover already knows which views are going to be opened, it cannot force the evaluation to output 1 unless \({\textsf{Rel}}(x,w)=1\), except with negligible probability.
Although robustness seems a very strong requirement, we show that a minor modification of the standard BMR protocols leads to an efficient robust MPC scheme. We recall that BMR [3] is a two-phase protocol consisting of an input-independent phase, also called garbling, and an online evaluation. In the garbling step, all parties \(\texttt{P}_1,\dots ,\texttt{P}_n\) involved in the protocol generate a sharing of the garbled circuit according to some fixed secret sharing scheme \({\langle \cdot \rangle }\) with t-privacy. As in any other garbled-circuit based scheme, to garble a Boolean circuit each wire is assigned two random keys \({\boldsymbol{k}}_{w,0},{\boldsymbol{k}}_{w,1}\) encoding, respectively, the 0-value and 1-value. The goal of the process is to generate four ciphertexts for each gate according to the gate function, such that each output-wire key is encrypted according to all combinations of input-wire keys which evaluate that output wire key. During the online evaluation, these encrypted truth tables, are revealed to all parties so to allow local evaluation of the circuit. Intuitively, it is clear that upon collecting all the input keys, parties can start evaluating the circuit. At this point, this evaluation is completely deterministic and does not require any interaction. For this reason, assuming that the garbling phase is correctly generated and the input-keys corresponding to the input-wires of the circuit are correct, namely, they correspond to the keys generated in the offline phase, the online views generated by each party correspond to a correct evaluation of the garbled circuit and cannot lead to an incorrect result. In the full version, we recall the basics of BMR-style protocols and explain the robustness property in more detail.
2.2 4-Round Non-malleable Commitment \(\varPi _\textsf{nmc} \)
We are finally ready to describe how our non-malleable commitment scheme works. Our starting point is the 3-round public-coin commitment scheme of Goyal et al. [24]. This commitment scheme, which we denote with \(\varPi _\textsf{wnmc}\), is non-malleable against adversaries that never commit to \(\bot \) (i.e., the adversary always generates well-formed commitments). To lift the security of such a commitment and build a fully non-malleable commitment scheme, [24] run, in parallel to \(\varPi _\textsf{wnmc}\), a zero-knowledge proof.
As noted in [9, 24], a standard ZK proof does not suffice since the commitment and the zero-knowledge proof might not be composed in parallel. As such, and as we have already anticipated, in [24] the authors rely on a ZK proof that is rewind-secure. We also note that the statement to be proven by the ZK is fully-formed only in the last round (since \(\varPi _\textsf{wnmc}\) consists of 3 rounds.) This inherently requires the ZK protocol to be delayed-input. To the best of our knowledge, the only protocols that satisfy all these properties are that proposed in [23, 24], which, unfortunately, make non-black-box use of the underlying primitives. In [9], the authors propose a ZK proof that can be composed in parallel with the weak-non-malleable commitment of Goyal et al., but this approach requires non-black-box access to the commitment scheme.
The idea is to use our commit-and-prove protocol \(\varPi \), and argue that it can be safely composed in parallel with \(\varPi _\textsf{wnmc}\) due to the property of NMZKC. Unfortunately, \(\varPi \) is only honest-verifier zero-knowledge, and here we need a zero-knowledge proof that is secure against any type of adversaries.
To lift the security of our protocol, we rely on the FLS-trick [16] (with some modifications). More concretely, we construct a 4-round zero-knowledge protocol as follows. The verifier generates two commitments of two random strings, \(\hat{s}_0\) and \(\hat{s}_1\) in the first round and sends two openings in the third round. In parallel, the verifier provides a witness indistinguishable (WI) proof, \(\varPi _\textsf{comWI}\), which guarantees that at least one of the two commitments is binding. In [30], the authors show how to obtain this protocol in a black-box-way. The prover instead uses a 3-round public-coin WI to prove that either the commitment \(\varPi _\textsf{wnmc}\) is well-formed or that it committed to \(\hat{s}_b\), for some \(b\in \{0,1\}\). Since the receiver discloses \(\hat{s}_0, \hat{s}_1\) only in the last round, the sender has no way to commit (already in the second round), to either of these two values. As such, the (potentially corrupted) sender, can complete an accepting WI proof only by proving that the non-malleable commitment is well-formed. For more detail, we refer to the technical part of the paper.
3 Preliminaries
Notation. Here we recall some preliminaries that will be useful in the rest of the paper. Let \(\lambda \) denote the security parameter and \(\textsf{negl}(\lambda )\) any function which tends to zero faster than \(\lambda ^{-c}\), for any constant c. We write [n] to denote the set \(\{1,\dots ,n\}\). We use the abbreviation ppt to denote probabilistic polynomial-time.
Let \(\mathcal {S}\) and \(\mathcal {R}\) two interactive algorithms, we denote by \(\langle \mathcal {S}(x),\mathcal {R}(y) \rangle (z)\) the distribution of \(\mathcal {R}\)’s output after an interaction with \(\mathcal {S}\) on common input z and private inputs x and y. A transcript of \(\langle \mathcal {S}(x),\mathcal {R}(y) \rangle (z)\) consists of all the messages exchanged during an interaction between \(\mathcal {R}\) and \(\mathcal {S}\).
3.1 Commitment Schemes
A commitment scheme \(\varPi _\texttt{com}=(\mathcal {S},\mathcal {R})\) is a two-phase protocol between two ppt interactive algorithms, a sender \(\mathcal {S}\) and a receiver \(\mathcal {R}\). In the first phase, called commit phase, \(\mathcal {S}\) on input a message m interacts with \(\mathcal {R}\). Let \(\texttt{com}\) be the transcript of this interaction. In the second phase, called decommitment phase, the sender \(\mathcal {S}\) reveals \(m'\) and \(\mathcal {R}\) accepts the value committed to be \(m'\) if and only if \(\mathcal {S}\) proves that \(m=m'\). Typically, a commitment scheme satisfies two main properties: informally, the binding property ensures that \(\mathcal {S}\) cannot open the commitment in two different ways; the hiding property guarantees that the commit phase does not reveal any information about the message m. We refer the reader to [18] for more details.
Ambiguous and Extractable Commitments. We formally introduce the notion of ambiguous commitments. Compared to regular commitment schemes, with standard commitment and opening algorithms \((\textsf{Com},\textsf{Dec})\), ambiguous commitments have two additional algorithms \(\textsf{Com}^\textsf{eq}\) and \(\textsf{Eq}\), which allow the committer to equivocate, i.e., \(\textsf{Com}^\textsf{eq}\) produces an “equivocable commitment” that \(\textsf{Eq}\) can open to any message \(m \in \{0,1\}^\ell \). This type of commitment schemes are sometimes called trapdoor or equivocal commitments. We provide a formal definition and construction in the full version. In this work, we also use the notion of extractable commitments (we refer to the full version for the formal definition). Informally, a commitment scheme is said to be extractable if there exists an efficient extractor that, having black-box access to a malicious committer that successfully performs the commitment phase, is able to extract the committed message.
3.2 Non-malleable Commitments
Here we follow the same notation of Goyal et al. [24]. Let \(\mathsf {\varPi }=(\mathcal {S},\mathcal {R})\) be a statistically binding commitment scheme and let \(\lambda \) be the security parameter. Consider a man-in-the-middle (MiM) adversary \({\mathcal {A}}\) that is participating in two interactions called the left and the right interaction. In the left interaction \({\mathcal {A}}\) is the receiver and interacts with an honest committer \(\mathcal {S}\), whereas in the right interaction \({\mathcal {A}}\) is the committer and interacts with an honest receiver \(\mathcal {R}\).
We compare between a MiM execution and a simulated execution. In the MiM execution the adversary \({\mathcal {A}}\), with auxiliary information z, is simultaneously participating in a left and right session. In the left sessions, the MiM adversary \({\mathcal {A}}\) interacts with \(\mathcal {S}\) receiving commitments to values \(m_i, i \in [\textsf{poly}(\lambda )]\), using identities \(\textsf{tg}_i\) of its choice. In the right session, \({\mathcal {A}}\) interacts with \(\mathcal {R}\) attempting to commit to related values \(\tilde{m}_i\) again using identities of its choice \(\mathsf {\widetilde{tg}}_i\). If any of the right commitments is invalid, or undefined, its value is set to \(\bot \). For any i such that \(\mathsf {{tg}}_i = \textsf{tg}_j,\) for some j, set \(\tilde{m}_i=\bot \) (i.e., any commitment where the adversary uses the same identity of the honest sender is considered invalid). Let \(\textsf{mim}^{{\mathcal {A}},{\boldsymbol{m}}}_\mathsf {\varPi }(z)\) denote a random variable that describes the values \(\tilde{m}_i\) and the view of \({\mathcal {A}}\), in the above experiment.
In the simulated execution, an efficient simulator \(\textsf{Sim}\) directly interacts with \(\mathcal {R}\). Let \(\textsf{sim}^\textsf{Sim}_\mathsf {\varPi }(1^\lambda ,z)\) denote the random variable describing the values \(\tilde{m}_i\) committed by \({\mathcal {A}}\), and the output view of \(\textsf{Sim}\); whenever the view contains in the right session the same identity of any of the identities of the left session, then m is set to \(\bot \).
In all the paper we denote by \(\tilde{\delta }\) a value associated with the right session (where the adversary \({\mathcal {A}}\) plays with a receiver) where \(\delta \) is the corresponding value in the left session. For example, the sender commits to v in the left session while \({\mathcal {A}}\) commits to \(\tilde{v}\) in the right session.
Definition 1
(Non-Malleable (NM) commitment scheme[24]). A commitment scheme is NM with respect to commitment if, for every ppt MiM adversary \({\mathcal {A}}\), there exists a ppt simulator \(\textsf{Sim}\) such that for all \({\boldsymbol{m}}\in \{0,1\}^{\textsf{poly}(\lambda )}\) the following ensembles are computationally indistinguishable:
In this work, we also consider a weaker class of MiM adversaries called synchronizing adversaries. A synchronizing adversary is one that sends its message for every round before obtaining the honest party’s message for the next round.
3.3 \(\varSigma \)-Commitments
We introduce the notion of \(\varSigma \)-commitments, which is reminiscent of the notion of \(\varSigma \)-protocols.
Definition 2
A \(\varSigma \)-commitment \(\varPi ^\varSigma =((\mathcal {S}^\varSigma ,\mathcal {R}^\varSigma ), \textsf{Dec}^\varSigma )\) is a commitment scheme where: 1) The commitment phase consists of three rounds and it is public-coin, 2) The decommitment phase is non-interactive, and 3) It satisfies the following properties.
-
Correctness. Let m be the message the sender \(\mathcal {S}^\varSigma \) uses during the commitment phase. If both \(\mathcal {S}^\varSigma \) and \(\mathcal {R}^\varSigma \) follow the protocol, then the receiver always accepts the commitment as valid. Moreover, if the sender follows the protocol during the decommitment procedure \(\textsf{Dec}^\varSigma \) then the receiver accepts m as the committed message.
-
Honest Receiver Hiding (HRH). There exists a polynomial-time simulator \(\textsf{Sim}\) such that for any message \(m \in \{0,1\}^\ell \) and on input a random c (sampled from the space of all the possible \(\mathcal {R}^\varSigma \)’s messages), outputs an accepting commitment transcript of the form (a, c, z) that is computationally indistinguishable from the transcript generated by the honest sender and receiver when the receiver uses m as its input (note that \(\textsf{Sim}\) needs to generate the transcript without knowing m).
-
t -Special Binding. From any set of t accepting transcripts \(\{a,c_i,z_i\}_{i\in [t]}\), with \(c_i\ne c_j\) for all \(i,j\in [t]\), for the commitment phase it is possible to extract the message m in polynomial-time, where m is the only possible message that the (potentially corrupted) sender can decommit to.
3.4 Adaptive-Input SHVZK
Definition 3 (Adaptive-input SHVZK)
A delayed-input 3-round protocol \(\varPi =(\mathcal {P},\mathcal {V})\) for relation \({\textsf{Rel}}\) satisfies adaptive-input special honest-verifier zero-knowledge (AI-SHVZK) if there exists a ppt simulator \(\textsf{Sim}= (\textsf{Sim}_0, \textsf{Sim}_1)\) such that for all ppt adversaries \({\mathcal {A}}\) and for all challenges \(\pi ^2\) there is a negligible function \(\textsf{negl}\) for which \( \big | \Pr [b'=b]-\frac{1}{2} \big | \le \textsf{negl}(\lambda ) \) in the following game.
\(\textsf{ExpAISHVZK}_{{\mathcal {A}},\varPi }(1^\lambda ,b,\pi ^2):\)
-
1.
The challenger sends \(\pi ^1\) to \({\mathcal {A}}\), where:
-
If \(b=0\), \((\pi ^1,\textsf{aux}) \leftarrow \mathcal {P}(1^\lambda ,1^m)\), with \(m=|x|\)
-
Else, if \(b=1\), \((\pi ^1,\textsf{aux}) \leftarrow \textsf{Sim}_0(1^\lambda ,1^m, \pi ^2)\)
-
-
2.
\({\mathcal {A}}\) sends (x, w) to the challenger.
-
If \((x,w) \in {\textsf{Rel}}\), the challenger sends \(\pi ^3\) to \({\mathcal {A}}\), where:
-
If \(b=0\), \(\pi ^3 \leftarrow \mathcal {P}(x,w,\textsf{aux},\textsf{aux},\pi ^2)\)
-
Else, if \(b=1\), \(\pi ^3 \leftarrow \textsf{Sim}_1(x,\textsf{aux})\)
-
-
Else, the challenger sends \(\pi ^3 = \bot \) to \({\mathcal {A}}\)
-
-
3.
The adversary \({\mathcal {A}}\) outputs a bit \(b'\).
3.5 One-of-Two Binding Commitments
We propose a formal definition of the one-of-two binding commitments proposed by Khurana et al. in [30]. A one-of-two binding commitment is a three-round interactive protocol \(\varPi _\textsf{comWI}\) executed between a prover \(\mathcal {P}_\textsf{comWI}\) and a verifier \(\mathcal {V}_\textsf{comWI}\). Informally, in this, the prover generates two commitments in the first round, and sends their opening third round. In parallel, the prover performs a WI proof that guarantees that at least one of the two commitments is binding. Moreover, the prover can equivocate the non-binding commitment to any value he likes. In [30] the authors propose a one-of-two binding commitment scheme that makes black-box use of one-to-one OWFs. We propose a formal definition of the properties held by a one-of-two binding commitment scheme. We assume the prover and verifier algorithms are stateful in the following definitions.
Definition 4 (One-of-Two Binding Commitments)
A commitment is one-of-two binding if the following properties hold.
Correctness:
-
The prover \(\mathcal {P}_\textsf{comWI}\) on input \(1^\lambda \), the message \(m_b\in \{0,1\}^\lambda \), and a bit b returns \(\pi _1^\textsf{comWI}\)
-
The verifier on input \(1^\lambda \) and \(\pi _1^\textsf{comWI}\) samples a random
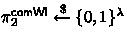 and returns it.
and returns it. -
The prover on input \(\pi _2^\textsf{comWI}\) and a message \(m_{1-b}\in \{0,1\}^\lambda \) computes \(\pi _3^\textsf{comWI}\) and returns \((\pi _3^\textsf{comWI},m_0,m_1)\)
-
The verifier on input \((\pi _1^\textsf{comWI}, \pi _2^\textsf{comWI}, \pi _3^\textsf{comWI},m_0,m_1)\) returns \(d\in \{0,1\}\), where \(d=1\) denotes that the verifier accepts, and 0 that he rejects.
Binding: For any ppt adversary \({\mathcal {A}}\), we have that the following holds. Let \(\tau =(\pi _1^\textsf{comWI},\pi _2^\textsf{comWI})\) be the first two rounds generated during the execution of \(\varPi _\textsf{comWI}\) by an honest receiver \(\mathcal {V}_\textsf{comWI}\) and the stateful adversarial prover \({\mathcal {A}}(1^\lambda )\). We have that
\( \begin{array}{l} \Pr [(\pi _3^\textsf{comWI},m_0,m_1,\overline{\pi }_3^\textsf{comWI},\overline{m}_0,\overline{m}_1) \leftarrow {\mathcal {A}}(1^\lambda ) |\ \mathcal {V}_\textsf{comWI}(\tau ,\pi _3^\textsf{comWI},m_0,m_1)=1\ \wedge \ \\ \mathcal {V}_\textsf{comWI}(\tau ,\overline{\pi }_3^\textsf{comWI},\overline{m}_0,\overline{m}_1)=1\ \wedge \ m_0\ne \overline{m}_0\ \wedge \ m_1 \ne \overline{m}_1]\le \textsf{negl}(\lambda ) \end{array} \)
Equivocability: For any adversary \({\mathcal {A}}\) and any \(m_0,m_1\in \{0,1\}^\lambda \) we have that \( \big | \Pr [b'=b]-\frac{1}{2} \big | \le \textsf{negl}(\lambda )\) in the following game.
\(\textsf{ExpEq}_{{\mathcal {A}},\varPi }(1^\lambda ,b,m_0,m_1):\)
-
1.
The challenger sends \(\pi _1^\textsf{comWI}\leftarrow \mathcal {P}_\textsf{comWI}(1^\lambda ,m_b,b)\) to \({\mathcal {A}}\).
-
2.
\({\mathcal {A}}\) sends \(\pi _2^\textsf{comWI}\) to the challenger
-
3.
The challenger sends \(\pi _3^\textsf{comWI}\leftarrow \mathcal {P}_\textsf{comWI}(\pi _2^\textsf{comWI},m_{1-b})\) to \({\mathcal {A}}\).
-
4.
The adversary \({\mathcal {A}}\) outputs a bit \(b'\).
3.6 MPC Definitions
In this work, we consider MPC protocols \(\varPi =\varPi ^{\texttt{off},\texttt{on}}=(\texttt{P}_1,\dots , \texttt{P}_n)\), among n parties \(\texttt{P}_1,\dots ,\texttt{P}_n\), that are composed of two sub-protocols \(\varPi ^\texttt{off}=(\texttt{P}_1,\dots , \texttt{P}_n)\) and \(\varPi ^\texttt{on}=(\texttt{P}_1,\dots , \texttt{P}_n)\), where the execution \(\varPi ^\texttt{off}\) does not require parties’ private inputs, namely \(\varPi ^\texttt{off}\) is input independent. If each party \(\texttt{P}_i\), for \(i \in [n]\), runs \(\varPi \) honestly, then the execution of \(\varPi \) is called an honest execution. A view \(\textsf{view}_i\) of a party \(\texttt{P}_i\) is composed by its private input \(w_i\), randomness \(r_i\), and transcript \(\tau _i\), where \(\tau _i\) is given by the set of messages received and sent by party \(\texttt{P}_i\) during the execution of the MPC protocol \(\varPi \). We denote the view of the offline and of the online phase for a party \(P_i\) with \(\textsf{view}_i^{\texttt{off}}\) and \(\textsf{view}_i^{\texttt{on}}\) respectively.
In the rest of the paper, we consider MPC protocols where all parties share a public input x, and each party \(\texttt{P}_i\) additionally holds a local private input \(w_i\) and random tape \(r_i\). We consider protocols \(\varPi ^{\texttt{off}, \texttt{on}}\) which securely realize an n-party functionality f. The output \(y=f(x,w_1,\dots ,w_n)\) can be computed from any \(\textsf{view}_i=(\textsf{view}_i^{\texttt{off}},\textsf{view}_i^{\texttt{on}})\), i.e., \(y=\varPi ^{\texttt{off},\texttt{on}}_f(\textsf{view}_i)= \texttt{out}_i\), for each \(i \in [n]\) .
We assume familiarity with the standard definition of MPC (referring the reader to the full version for a formal discussion), and here we formally introduce a new special property for an MPC protocol \(\varPi =\varPi ^{\texttt{off},\texttt{on}}=(\texttt{P}_1,\dots , \texttt{P}_n)\).
Looking ahead, in our delayed-input protocol the prover, while committed to \(\textsf{view}_1^\texttt{off},\dots ,\textsf{view}_n^\texttt{off}\), is allowed to generate the online views \(\textsf{view}_1^\texttt{on},\dots ,\textsf{view}_n^\texttt{on}\) only when it received (x, w), and after it is given any eventual random inputs and the set of k parties/views it will need to open. This means that a malicious prover \(\mathcal {P}\) might arbitrarily create inconsistent views \(\textsf{view}^\texttt{on}_{i_1}, \dots , \textsf{view}^\texttt{on}_{i_{n-k}}\) that will not be opened, easily making all outputs to be incorrect without being caught. For this reason we need an underlying MPC protocol with strong security requirements and introduce the following definition of robustness.
Despite the name, this notion is different from the definition of robustness that was given in [28] to generalize the definition of correctness in case of malicious adversaries.
Roughly, an MPC protocol \(\varPi =\varPi ^{\texttt{off},\texttt{on}}\) is said to be robust if, given two subsets \(A,H \subset [n]\), with \(|H|=n-|A|\), and a correct execution of \(\varPi ^\texttt{off}\), the output \(\texttt{out}_j\) of some \(\texttt{P}_j\), with \(j \in A\), obtained by running the protocol on input \((x,(w_i)_{i \in A}, (w_i)_{i \in H})\) and using some arbitrary randomness \(r'_j\), is not \(\perp \) then \(\texttt{out}_j=y\), where \(y=\varPi ^{\texttt{off},\texttt{on}}_f(\textsf{view}_i)\), \(\forall i \in H\). Note that our definition specifically assumes an MPC protocol \(\varPi ^{\texttt{on},\texttt{off}}\) in the pre-processing model with a correctly executed \(\varPi ^\texttt{off}\) and requires that every unbounded adversary \({\mathcal {A}}\) cannot make the parties in A output a result inconsistent with the views of honest parties. The formal definition of robustness follows.
Definition 5 (Robustness)
Let \(\varPi ^{\texttt{off},\texttt{on}}=(\texttt{P}_1,\dots , \texttt{P}_n)\) be as above. Let \(A\subset [n]\) and \(H=[n]-A\). Let us denote by \(\textsf{view}\) the view \(\{\textsf{view}_{i}=(\textsf{view}^\texttt{off}_{i},\textsf{view}^\texttt{on}_{i})\}_{i \in H}, \{\widetilde{\textsf{view}}_{i}=(\widetilde{\textsf{view}}^\texttt{off}_{i},\widetilde{\textsf{view}}^\texttt{on}_{i})\}_{i \in A}\), such that:
-
\( \widetilde{\textsf{view}}_{i}^\texttt{off}\) and \( \widetilde{\textsf{view}}_{i}^\texttt{on}\) are the views generated by running the code of \(\texttt{P}_i\) for \(\varPi ^\texttt{off}\) and \(\varPi ^\texttt{on}\) on input \((x,w_i)\), respectively, with some arbitrary randomness \(r'_i\in \{0,1\}^\lambda \), for each \(i\in A\);
-
\(\textsf{view}_{i}^\texttt{off}\) is the view generated running the code of party \(\texttt{P}_{i}\) for \(\varPi ^\texttt{off}\) with some arbitrary randomness \(r'_i\in \{0,1\}^\lambda \), for each \(i \in H\);
-
\(\textsf{view}^\texttt{on}_{i} \in \{0,1\}^*\), for each \(i \in H\).
We say that \(\varPi ^{\texttt{off},\texttt{on}}\) realizes a deterministic n-party functionality \(f(x,w_1,\dots ,w_n)\) with robustness if for any A and H, such that \(H=\{i_1,\dots ,i_{n-t}\}\) and \(A=\{j_1,\dots ,j_t\}\), the following holds: if, for each \(j_k \in A\), party \(\texttt{P}_{j_k}\), on input randomness \(r_{j_k}\) and \((x,w_{j_k})\), outputs \(\texttt{out}_{j_k} = F \ne \, \perp \) with respect to the view \(\textsf{view}\), then \(F=f_A(x,w_{i_1},\dots ,w_{i_{n-t}})\), for some \(w_{i_1},\dots ,w_{i_{n-t}}\) with \(\{i_1,\dots ,i_{n-t}\}=H\), where \(f_A\) is the function evaluated on n inputs where the inputs in positions \(A=\{j_1,\dots ,j_{t}\}\) are \(w_{j_1},\dots ,w_{j_{t}}\).
Intuitively, the above definition says that as long as \(\varPi ^\texttt{off}\) is correct (concretely this can be achieved instantiating \(\varPi ^\texttt{off}\) with a malicious secure protocol) and the online phase \(\varPi ^\texttt{on}\) is a deterministic function of the offline phase, then \(\varPi \) is robust. Notice the definition of robustness is independent of the number of corruptions supported by \(\varPi \) and it can be achieved both with an honest and dishonest majority. In the full-version we show a concrete instantiation of a robust MPC protocol.
3.7 Verifiable Secret Sharing (VSS)
A verifiable secret sharing (VSS) scheme [6] is a two-phase protocol carried out among \(n+1\) parties. In the first step, a special party, also referred to as the dealer, shares a secret among all the other n parties, referred to as share-holders, at most t of whom may be corrupt; in the second step, parties reconstruct the secret. While in standard secret-sharing schemes the dealer is assumed to be honest, in VSS schemes also the dealer can be corrupt. Loosely speaking, if the dealer is honest, then no information about the dealer’s secret is revealed to the t corrupt parties by the end of the sharing phase; moreover, by the end of the sharing phase even a dishonest dealer is committed to some value that will be recovered by the honest parties in the reconstruction phase. Furthermore, if the dealer is honest then this committed value must be identical to the dealer’s initial input.
Definition 6
(Verifiable Secret Sharing [5, 6]). An \((n+1, t)\)-perfectly secure Verifiable Secret Sharing (VSS) scheme \(\varPi ^\sigma \) consists of a pair of protocols \((\textsf{Share}, \textsf{Recon})\) that implement respectively the sharing and reconstruction phases as follows.
-
Sharing Phase \((\textsf{Share})\). Party \(\texttt{P}_{n+1}\) (the dealer) runs on input a secret s and randomness \(r_{n+1}\), while any other party \(\texttt{P}_i\), \(i \in [n]\), runs on input a randomness \(r_i\). During this phase parties can send (both private and broadcast) messages in multiple rounds. We will indicate with \(\textsf{view}_i\) the view that \(\texttt{P}_i\) obtains at the end of sharing phase, and with \((\textsf{view}_1, \dots , \textsf{view}_n) =\textsf{Share}(s, r_1, \dots , r_n, r_{n+1})\) the process described above.
-
Reconstruction Phase \((\textsf{Recon})\). Each shareholder sends its view \(\textsf{view}_i\), \(i \in [n]\), of the sharing phase to each other party, and on input the views of all parties (that might include corrupt or empty views) each party outputs a reconstruction of the secret s. All computations performed by honest parties are efficient.
The following security properties hold.
-
Commitment. If the dealer is dishonest then one of the following two cases happen: 1) during the sharing phase honest parties disqualify the dealer, therefore they output a special value \(\bot \) and will refuse to run the reconstruction phase; 2) during the sharing phase honest parties do not disqualify the dealer, therefore such a phase determines a unique value \(s^*\), that belongs to the set of possible legal values that does not include \(\bot \), which will be reconstructed by the honest parties during the reconstruction phase.
-
Secrecy. The computationally unbounded adversary can corrupt up to t parties that can deviate from the above procedures. If the dealer is honest, then the adversary’s view during the sharing phase reveals no information about s. More formally, the adversary’s view is identically distributed under all different values of s.
-
Perfect Correctness. If the dealer is honest throughout the protocols then each honest party will output the shared secret s at the end of protocol \(\textsf{Recon}\) with probability 1.
Assuming a broadcast channel, perfectly-secure \((n+1,\lfloor n/4 \rfloor )\)-VSS scheme are implemented in [17].
4 Non-malleable HVZK with Respect to Commitment
In this section, we introduce the new notion of non-malleable HVZK with respect to commitment (NMZKC). Let \(\varPi =(\mathcal {P},\mathcal {V})\) be a proof system, and \(\varPi _\texttt{com}\) be a (potentially interactive) commitment scheme. We consider a scenario where a man-in-the-middle adversary \({\mathcal {A}}\) interacts in the left session with the prover of \(\varPi \) (hence, \({\mathcal {A}}\) acts as the verifier for \(\varPi \)), and in the right session \({\mathcal {A}}\) acts as the sender for \(\varPi _\texttt{com}\) against an honest receiver. the formal definition of NMZKC follows, and we refer to the introductory section of the paper for an informal discussion about this definition. Let \((\textsf{Sim}_0,\textsf{Sim}_1)\) be the adaptive-input HVZK simulator for \(\varPi \), we define the experiment \(\textsf{ExpZK}_{{\mathcal {A}},\varPi ,{\varPi _\texttt{com}}}(1^\lambda ,b,c)\).
\(\textsf{ExpZK}_{{\mathcal {A}},\varPi ,{\varPi _\texttt{com}}}(1^\lambda ,b,c):\) In the right session, interact with \({\mathcal {A}}\) as the receiver of \(\varPi _\texttt{com}\). In the left session, act as follows.
-
1.
Set \(\pi _2\leftarrow c\) and send \(\pi ^1\) to \({\mathcal {A}}\), where:
-
If \(b=0\),
 , with \(m=|x|\)
, with \(m=|x|\) -
If \(b=1\),

-
-
2.
Upon receiving (x, w) from \({\mathcal {A}}\) in the left session do the following
-
If \((x,w) \in {\textsf{Rel}}\), the experiment sends \(\pi ^3\) to \({\mathcal {A}}\) in the left session where:
-
If \(b=0\), \(\pi ^3 \leftarrow \mathcal {P}(x,w,\textsf{aux},\pi ^2)\)
-
Else, if \(b=1\),

-
-
Else, the experiment sets \(\pi ^3 \leftarrow \bot \)
-
-
3.
Set the output of the experiment as the output of \({\mathcal {A}}\) and its view.
Definition 7 (NMZKC)
Let \(\varPi _\texttt{com}\) be a commitment scheme. We say that an adaptive-input HVZK proof system \(\varPi \), with challenge space \(\mathcal {C}\), is a non-malleable HVZK with respect to commitment for \(\varPi _\texttt{com}\) if there exists a ppt simulator \(\textsf{Sim}=(\textsf{Sim}_0,\textsf{Sim}_1)\) such that, for all ppt adversary \({\mathcal {A}}\), the following two distributions are indistinghuishable:
where \(\textsf{ExpZK}_{{\mathcal {A}},\varPi ,{\varPi _\texttt{com}}}(1^\lambda ,b,c)\) is the experiment described above and \(m_b\), with \(b \leftarrow \{0,1\}\), is the message committed in the right session of \(\textsf{ExpZK}_{{\mathcal {A}},\varPi ,{\varPi _\texttt{com}}}(1^\lambda ,b,c)\) by \({\mathcal {A}}\).
We note that non-malleable HVZK with respect to commitment property is parallel composable w.r.t. multiple left sessions. The proof would follow via standard hybrid arguments.
5 Our Delayed-Input MPC-in-the-Head Protocol \(\varPi _\textsf{AI}\)
Let L be an \(\mathcal {N}\mathcal {P}\)-language and \({\textsf{Rel}}\) be the corresponding \(\mathcal {N}\mathcal {P}\)-relation. Let f be an \((n+1)\)-argument function, with \(n> 2\), corresponding to \({\textsf{Rel}}\), i.e., \(f(x, w_1,\dots ,w_n)= {\textsf{Rel}}(x, w_1\oplus \dots \oplus w_n)\). Our protocol, \(\varPi _\textsf{AI}=(\mathcal {P}_\textsf{AI}, \mathcal {V}_\textsf{AI})\), for the \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}\) makes use of the following tools:
-
A \(t_p\)-private MPC protocol \(\varPi ^{\texttt{off}, \texttt{on}}=(\texttt{P}_1,\dots , \texttt{P}_n)\) that realizes f with robustness (Definition 5).
-
An ambiguous commitment scheme \(\varPi _\texttt{com}=(\textsf{Com},\textsf{Dec},\textsf{Com}^\textsf{eq},\textsf{Eq})\).
A complete description of \(\varPi _\textsf{AI}=(\mathcal {P}_\textsf{AI}, \mathcal {V}_\textsf{AI})\) for the \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}\) can be found in Fig. 1. At a high level, given an MPC protocol \(\varPi ^{\texttt{off},\texttt{on}}\), as specified above, \(\mathcal {P}_\textsf{AI}\) starts by emulating \(\varPi ^\texttt{off}\) in its head. In particular, it generates n views \(\textsf{view}_i^\texttt{off}, i \in [n]\), corresponding to the n virtual parties and separately commits to these views using an ambiguous commitment scheme \(\varPi _\texttt{com}\). This is done by sampling c random values \(\{\textsf{view}^\texttt{off}_{(i,j)}\}_{j \in [c]}\), for each \(i \in [n]\), such that \(\textsf{view}_i^\texttt{off}=\bigoplus _{j \in [c]} \textsf{view}^\texttt{off}_{i,j} \), and computing \(\{(\texttt{com}_{(i,j)}, \texttt{dec}_{(i,j)})\leftarrow \textsf{Com}(\textsf{view}^\texttt{off}_{(i,j)}; R_{(i,j)})\}_{j \in [c]}\). Notice here \(c \ge 2\) is a small integer. This will allow the verifier to check that the commitments are correctly generated and \(\varPi ^\texttt{off}\) is honestly executed; moreover, it will be crucial to prove adaptive-input SHVZK, as we will see later.
The prover sends the first message \(\pi ^1\), given by the concatenation of all the commitments, to \(\mathcal {V}\) which replies with the challenge \(\pi ^2\), i.e., a set of random indices \(I=\{i_1,\dots ,i_k\} \subset [n]\) with \(k \le t_p\), and one index \(q_{i_j} \in [c]\) for each \(i \in I\).
In the last round, both \(\mathcal {P}\) and \(\mathcal {V}\) receive the theorem x, while \(\mathcal {P}\) also receives w. in the last round, \(\mathcal {P}\) first completes the emulation of the MPC protocol, producing all the online views \(\textsf{view}_{i}^\texttt{on}, i \in [n]\); secondly, it sends \(\textsf{view}^\texttt{on}_{i}, i \in I\), and opens the corresponding commitments in \(\pi ^1\) as follows. The commitments corresponding to the indices \(q_{i_j}\) in \(\pi ^2\) are opened in a “binding way”, by sending \(\textsf{view}^\texttt{off}_{i_j,q_{i_j}}\) and \(R_{i_j,q_{i_j}}\), \(i_j \in I\), and the remaining \(c-1\) commitments, for each \(i_j \in I\), are opened by sending the opening information \(\texttt{dec}_{i_j,q}\), along with \(\textsf{view}^\texttt{off}_{i_j,q}\), for each \(q \in \{1,\dots ,c\}\setminus {q_{i_j}}\).
Finally, the verifier checks all the commitments. It verifies that all the parties in I output 1 and that their views are consistent with each other. To simplify the composition of our protocol with other primitives, we design the prover so that it expects to receive a (random) n-out-of-n secret sharing of the witness (instead of the witness itself). This is without loss of generality. We finally note that our protocol can be parameterized to work with any n-out-of-n secret sharing scheme. Moreover, it would remain black-box in the use of the underlying cryptographic primitives as long the reconstruction phase of the secret sharing scheme does make any calls to a cryptographic primitive. We prove the following result.
Theorem 1
If \(\varPi ^{\texttt{off}, \texttt{on}}\) is an MPC protocol that realizes f (which is described above) with \(t_p\)-privacy and robustness, and \(\varPi _\texttt{com}\) is an ambiguous commitment scheme, then \(\varPi _\textsf{AI}=(\mathcal {P}_\textsf{AI}, \mathcal {V}_\textsf{AI})\) (Fig. 1) for the \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}\) is a 3-round public-coin delayed-input protocol satisfying adaptive-input SHVZK adaptive-input soundness with constant soundness error.
We establish adaptive correctness, adaptive-input soundness and adaptive-input SHVZK. Correctness follows by inspection.
Adaptive-input soundness (Intuition). At a high level, we can see that soundness can be proved using the robustness property of the MPC protocol \(\varPi \) and the security properties of \(\varPi _\texttt{com}\). If all the offline views are correctly generated, then robustness ensures that a malicious prover will always get caught. Hence a malicious prover can succeed either if incorrect offline views are generated, or if some of the commitments are not computed in binding mode. We can argue that the probability of the adversary being caught in either of the two cases is noticeable.
Adaptive-input special honest-verifier zero-knowledge (Intuition). At a high level, the simulator \(\textsf{Sim}=(\textsf{Sim}^0_\textsf{AI},\textsf{Sim}^1_\textsf{AI})\) works as follows. Let the challenge be \((I, q_{i_1}, \dots , q_{i_k})\), and let \({C}_{i_j}=\{1, \dots , c\}\setminus \{ q_{i_j}\}\). For each \(i_j\in I\), and each \(l\in {C}_{i_j}\), \(\textsf{Sim}^0_\textsf{AI}\) computes a random value \({\textsf{view}}_{(i_j, l)}\). Then \(\textsf{Sim}^0_\textsf{AI}\) generates the following commitments. For each \(i_j \not \in I\) and \(q \in [c]\) set \(\texttt{com}_{(i_j,q)}\) as a commitment of the the all-zero string; for each \(i_j\in I\) compute the commitment \(\texttt{com}_{(i_j,q_{i_j})}\) in binding mode, and for each \(l\in C_{i_j}\) compute \(\texttt{com}_{(i_j,l)}\) in equivocal mode. These commitments constitute the simulated message \(\pi ^1.\) In the second phase, when x is available, \(\textsf{Sim}^1_\textsf{AI}\) uses the MPC simulator to obtain \((\textsf{view}^\texttt{off}_{i},\textsf{view}_{i}^\texttt{on}), i\in [n]\). For each \(i_j\in I\) and for each \(l\in C_{i_j}\) compute \({\textsf{view}}^\texttt{off}_{i_j, l}\), such that \(\textsf{view}^\texttt{off}_{i_j,q_{i_j}}=\textsf{view}^{\texttt{off}}_{i_j} \bigoplus _{l \in C_{i_j}} {\textsf{view}}^\texttt{off}_{i_j, l}\). Finally, for each \(i_j\in I\), \(l\in C_{i_j}\) equivocate the commitment \(\texttt{com}_{i_j,l}\) to \({\textsf{view}}^\texttt{off}_{i_j, l}\), and sends the openings of all the commitments to complete the third round.
Lemma 1
Let \(\varPi _{\textsf{Com}\textsf{Ext}}\) be a 3-round extractable commitment scheme with a polynomial time extractor \(\textsf{Ext}\), that extracts with non-negligible probability, then \(\varPi _\textsf{AI}\) is non-malleable HVZK with respect to commitment \(\varPi _{\textsf{Com}\textsf{Ext}}\) against synchronizing adversaries.
The proof of the lemma can be found in the full version.
We recall that the commitment scheme \(\varPi _\texttt{com}\) used in \(\varPi _{\textsf{AI}}\) can be instantiated with any NI statistically binding scheme, which can be constructed from any one-to-one OWF. In addition, following [28], when we say that our protocols make black-box use of \(\varPi ^{\texttt{off},\texttt{on}}\), it simply means that they are invoking the “next-message function” of each party. Therefore, when \(\varPi _\texttt{com}\) is implemented using a black-box reduction to one-way functions, the protocol \(\varPi _\textsf{AI}\) only makes black-box use of one-way functions. More formally,
Corollary 1
Assuming the existence of one-to-one one-way functions, there exists a 3-round public-coin delayed-input protocol satisfying adaptive-input soundness (with constant soundness error), and adaptive-input SHVZK, which makes black-box use of 1-1 OWFs. Moreover, let \(\varPi _{\textsf{Com}\textsf{Ext}}\) be a 3-round extractable commitment scheme with a polynomial time extractor, that extracts with non-negligible probability, then there exists a 3-round public-coin delayed-input protocol that is non-malleable HVZK with respect to commitment for \(\varPi _{\textsf{Com}\textsf{Ext}}\) against synchronizing adversaries that makes black-box use of the 1-1 OWFs.
6 The Building Blocks of the 4-Round Black-Box Non-malleable Commitment Scheme
In this section, we define the main building blocks necessary to define our 4-round non-malleable commitment scheme.
6.1 Commitment from Verifiable Secret Sharing
We start by recalling some of the techniques introduced by Goyal et al. [22]. We show that these techniques can be used to build a \(\varSigma \)-commitment (Definition 2) that we denote by \(\varPi =(( \mathcal {S}^\varSigma , \mathcal {R}^\varSigma ), \textsf{Dec}^\varSigma )\) and formally describe it in Fig. 2. The protocol makes use of the following primitives:
-
An \((n+ 1, t)\)-VSS protocol \(\varPi ^\textsf{vss}=(\varPi _\textsf{Share},\varPi _\textsf{Recon})\) as defined in Definition 6. Concretely, the protocol uses a VSS scheme with a deterministic reconstruction procedure, like the \((n+1,\lfloor n/4 \rfloor )\)-VSS scheme described by Gennaro et al. [17]
-
A statistically binding commitment scheme \(\varPi ^\texttt{com}=(\textsf{Com},\textsf{Dec})\).
The protocol works as follows. To commit to a message w, the sender \(\mathcal {S}^\varSigma \) runs “in its head” the protocol \(\varPi _\textsf{Share}\), which implements the sharing phase of \(\varPi ^\textsf{vss}\), with input w. Then the sender commits to the views \(\textsf{view}_j\) (obtained by the execution of \(\varPi _\textsf{Share}\)) of each \(\texttt{P}_j\) separately using a statistical binding commitment scheme \(\varPi ^\texttt{com}\). The receiver, upon receiving these commitments, samples a random set \(I \subset [n]\), with \(|I|\le t\), and sends it to the sender. Finally, the sender replies by decommitting the views corresponding to the challenge I. This concludes the commit phase.
In the full version, we prove the following theorem that we shall use in the next sections.
Theorem 2
Let \(\varPi ^\textsf{vss}\) be a \((n+ 1, t)\)-VSS protocol satisfying Definition 6, with \(t=k\), \(t< \frac{1}{4}n\), and let \(\varPi ^\texttt{com}\) be a statistically binding commitment scheme, then \(\varPi =(( \mathcal {S}^\varSigma , \mathcal {R}^\varSigma ), \textsf{Dec}^\varSigma )\) (see Fig. 2) is a \(\varSigma \)-commitment.
6.2 Commit-and-Prove
In this section we construct a 3-round public-coin commit-and-prove protocol \(\varPi _\textsf{CP}=(\mathcal {P}_\textsf{CP}, \mathcal {V}_\textsf{CP})\) that allows proving the knowledge of a committed value w such that \({\textsf{Rel}}(x,w)=1\), for some statement x. Our protocol makes black-box use of the underlying primitives.
The protocol \(\varPi _\textsf{CP}=(\mathcal {P}_\textsf{CP}, \mathcal {V}_\textsf{CP})\) is fully described in Fig. 3. It makes use of the following tools:
-
The \(\varSigma \)-commitment \(\varSigma =((\mathcal {S}^\varSigma , \mathcal {R}^\varSigma ), \textsf{Dec}^\varSigma )\) defined in Fig. 2, Sect. 6.1.
-
The adaptive-input SHVZK \(\varPi _\textsf{AI}=(\mathcal {P}_\textsf{AI}, \mathcal {V}_\textsf{AI})\) with adaptive-input soundness for the \(\mathcal {N}\mathcal {P}\)-relation
\( \begin{array}{l} {\textsf{Rel}}_\textsf{AI}=\{(x,a,\alpha ,\{\textsf{view}_{i_j}\}_{j\in [k]}),(r, \{\textsf{view}_{i}\}_{j\in [n]}): 1\le i_1<\dots< i_k <n\ \wedge \ \\ w=\textsf{Recon}(\{\textsf{view}_{i}\}_{j\in [n]})\ \wedge \ {\textsf{Rel}}(x,w)=1\ \wedge \ a=w+r\alpha \}. \end{array} \)
where \(\textsf{Recon}\) is the reconstruction phase of an information-theoretic \((n+1,t)\)-VSS protocol \(\varPi ^\textsf{vss}\), with \(k\le t\). We recall that to run \(\varPi _\textsf{AI}\) the prover needs the statement and the witness only in the third round. Moreover, the prover expects to receive the witness in a secret shared form. We recall that \(\varPi _\textsf{AI}\) works for any type of secret sharing scheme, and in our case \(\varPi _\textsf{AI}\) is parametrized by the reconstruction algorithm of the verifiable secret sharing \(\varPi ^\textsf{vss}\) (i.e., the prover expects to receive n views generated using the sharing algorithm of \(\varPi ^\textsf{vss}\)). We note that given that \(\varPi ^\textsf{vss}\) is information-theoretic, then \(\varPi _\textsf{AI}\) still makes black-box use of the underlying cryptographic primitives. We also need \(\varPi _\textsf{AI}\) with the same parameters n, k, t as \(\varSigma \).
At a high-level \(\mathcal {P}_\textsf{CP}\) commits \(\lambda ^2\)-times to the witness w running \(\varSigma \) (as described in Fig. 2) and proving, using \(\mathcal {P}_\textsf{AI}\), that each committed message w satisfies the relation \({\textsf{Rel}}\), and moreover that the views opened in the third round of \(\varSigma \) contain shares of the witness w. To make sure that the same message is committed in all the executions of \(\varSigma \), we use a technique proposed by Khurana et al. in [30]. Namely, in each execution of \(\varSigma \), instead of committing to w, we commit to w||r, for some random value r, and use the protocol \(\varPi _\textsf{AI}\) to additionally prove that \(a=w+r\alpha \), where \(\alpha \) is chosen as part of the second round, and a is sent in the third round from the prover. As argued in [30], since r is global across all the executions, if \(w \ne w'\) then \(w+r\alpha \ne w'+r\alpha \) with overwhelming probability due to the Schwartz-Zippel lemma. Therefore, if the committed messages are different across the (multiple) executions, then the statement proven by \(\varPi _\textsf{AI}\) must be false, and the soundness of \(\varPi _\textsf{AI}\) guarantees that the verifier rejects.
More formally, we prove the following result.
Theorem 3
Let \(\varPi _\textsf{AI}=(\mathcal {P}_\textsf{AI}, \mathcal {V}_\textsf{AI})\) be a 3-round public-coin, delayed-input complete, adaptive-input SHVZK with adaptive-input soundness for the \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}_\textsf{AI}\), and \(\varSigma =(( \mathcal {S}^\varSigma , \mathcal {R}^\varSigma ), \textsf{Dec}^\varSigma )\) (as defined in Fig. 2) be a \(\varSigma \)-commitment, then \(\varPi _\textsf{CP}= (\mathcal {P}_{\textsf{CP}}, \mathcal {V}_{\textsf{CP}})\) is a 3-round public-coin adaptive-input SHVZK commit-and-prove protocol for the \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}\).
We first give an intuition for the adaptive-SHVZK proof by describing how the simulator \((\textsf{Sim}^0_\textsf{CP}, \textsf{Sim}^1_\textsf{CP})\) works. For ease of exposition let us focus on the i-th transcript (out of \(\lambda ^2\)) w.r.t. challenge \((\alpha ,\pi _{2,i})\), where \(\pi _{2,i}\) is composed by two sets of indices I, C. The simulator \(\textsf{Sim}^0_\textsf{CP}\) on input challenge \(\pi _{2,i}\) runs the HRH simulator of \(\varSigma \) on input I obtaining \(\pi ^\sigma _1, \pi ^\sigma _3\) and, consequently, the shares \(\{\textsf{view}^\sigma _{i_j}\}_{i_j \in I}\) which will be opened in the third round (denoted by \(\pi ^\sigma _3\)). \(\textsf{Sim}^0_\textsf{CP}\) then runs \(\textsf{Sim}^0_\textsf{AI}\) on input \(\pi _{2,i}\) thus obtaining \((\pi _{1,i}, \textsf{aux})\). The simulator \(\textsf{Sim}^1_\textsf{CP}\) on input theorem x samples a at random, sets \(X=\{(x,a,\alpha ,\{\textsf{view}^\sigma _{i_j}\}_{i_j\in I})\) and runs \(\textsf{Sim}^1_\textsf{AI}\) on input theorem \((X,\textsf{aux})\) thus obtaining \(\pi _{3,i}\).
The full proof of Theorem 3 can be found in the full version. Similarly to previous protocols, we have the following result.
Corollary 2
Assuming the existence of one-to-one one-way functions, there exists a 3-round public-coin adaptive-input SHVZK commit-and-prove \(\varPi _\textsf{CP}\) for the \(\mathcal {N}\mathcal {P}\)-relation \({\textsf{Rel}}\) that makes black-box use of the 1-1 OWFs.
Remark 1
To simplify the exposition of our non-malleable commitment scheme that internally uses the commit-and-prove protocol we have just described, we will consider the messages of \(\varPi _\textsf{CP}\) as divided into two parts: the messages related to the proof phase, and the messages related to the commitment phase. Hence, each round of \(\varPi _\textsf{CP}\) consists of two distinct components (e.g., the i-th round of \(\varPi _\textsf{CP}\) will be denoted by \(\{\pi _i,\pi ^\sigma _i\}\)).
6.3 The 4-Round Non-malleable Commitment Scheme of [24]
The 4-round non-malleable commitment of Goyal et al. [24] is composed of two parts: the first one is a special public-coin \(\varPi _{\textsf{wnmc}}\) commitment scheme, that enjoys a weak form of non-malleability. Loosely speaking, \(\varPi _{\textsf{wnmc}}\) is non-malleable as long as the MiM, acting as a sender, is committing to a well-formed commitment. The second part is a zero-knowledge PoK that ensures that \(\varPi _{\textsf{wnmc}}\) is computed correctly. In Fig. 4, we recall the protocol \(\varPi _{\textsf{wnmc}}\). This uses as an underlying building block a non-interactive commitment that is statistically binding. We replace this commitment with our interactive \(\varSigma \)-commitment \(\varSigma \) where the challenge is a default value (i.e., this trivially makes the \(\varSigma \)-commitment non-interactive). Finally, we prove that, after this modification, \(\varPi _{\textsf{wnmc}}\) remains hiding.
Lemma 2
Let \(\varSigma \) be the \(\varSigma \)-commitment described in Fig. 2, then \(\varPi _\textsf{wnmc}= (\mathcal {S}_{\textsf{wnmc}}, \mathcal {R}_{\textsf{wnmc}})\) described in Fig. 4 enjoys the hiding property.
This follows from Theorem 2 and from the fact that \(r_1, \dots , r_{\ell _\textsf{4nmc} }\) and \(a_1, \dots , a_{\ell _\textsf{4nmc} }\) information theoretically hide the committed message.
7 Our 4-Round Black-Box Non-malleable Commitment Scheme
An informal overview of our 4-round NM commitment is given in the Introduction. Here we provide a formal description of the protocol \(\varPi _\textsf{nmc} \) presented in Fig. 5. We conclude this section with a sketch of the proof.
7.1 Formal Description of \(\varPi _\textsf{nmc} = ((\mathcal {S}_{\textsf{nmc} }, \mathcal {R}_{\textsf{nmc} }), \textsf{Dec}_\textsf{nmc} )\)
Our 4-round non-malleable commitment \(\varPi _\textsf{nmc} = ((\mathcal {S}_{\textsf{nmc} }, \mathcal {R}_{\textsf{nmc} }), \textsf{Dec}_\textsf{nmc} )\) makes use of the following tools.
-
A 3-round public-coin delayed-input adaptive-input SHVZK commit-and-prove protocol \(\varPi _\textsf{tr}=(\mathcal {P}_\textsf{tr}, \mathcal {V}_\textsf{tr})\) (as defined in Fig. 3) for the relation \( {\textsf{Rel}}_\textsf{tr}=\{((m_0,m_1), w): m_0=w \vee m_1=w\} \). We denote the adaptive-input SHVZK simulator with \(\textsf{Sim}_\textsf{tr}\).
-
A 3-round public-coin SHVZK, delayed-input complete commit-and-prove protocol \(\varPi _\textsf{CP}=(\mathcal {P}_\textsf{CP}, \mathcal {V}_\textsf{CP})\) (as defined in Fig. 3, but using \(\lambda ^3\) parallel repetitions) for the relation \({\textsf{Rel}}_\textsf{CP}\) defined as follows:
$$ { {\textsf{Rel}}_\textsf{CP}= \left\{ \begin{array}{l} \texttt{st}=\big (\{a_i, \alpha _i\}_{i \in [\ell _\textsf{nmc} ]}) \\ w = \big (m, \{r_i\}_{i \in [\ell _\textsf{nmc} ]} \big )\\ \end{array} \begin{array}{|l} \ \forall \ i\ \in [\ell _\textsf{nmc} ]\ a_i=m+r_i\alpha _i \end{array} \right\} }. $$ -
A one-of-two binding commitment scheme \(\varPi _\textsf{comWI}=(\mathcal {P}_\textsf{comWI}, \mathcal {V}_\textsf{comWI})\) (Definition 4).
The reason why we explicitly require \(\varPi _\textsf{tr}\) and \(\varPi _\textsf{CP}\) to be protocols constructed following the approach described in Sect. 6.2 is that in the security proof we will exploit the fact that \(\varPi _\textsf{tr}\) and \(\varPi _\textsf{CP}\) are based on non-malleable HVZK with respect to commitment protocols. We refer the reader to the full version for a thorough discussion on this and for the full proof.
Theorem 4
Let \(\varPi _\textsf{tr}=(\mathcal {P}_\textsf{tr}, \mathcal {V}_\textsf{tr})\) be the 3-round public-coin adaptive-input SHVZK commit-and-prove for the relation \({\textsf{Rel}}_\textsf{tr}\), defined in Fig. 3, let \(\varPi _\textsf{CP}=(\mathcal {P}_\textsf{CP}, \mathcal {V}_\textsf{CP})\) be the 3-round public-coin SHVZK commit-and-prove for the relation \({\textsf{Rel}}_\textsf{CP}\), defined in Fig. 3, let \(\varPi _\textsf{comWI}=(\mathcal {P}_\textsf{comWI}, \mathcal {V}_\textsf{comWI})\) be the one-of-two binding commitment scheme, then \(\varPi _\textsf{nmc} = ((\mathcal {S}_{\textsf{nmc} }, \mathcal {R}_{\textsf{nmc} }), \textsf{Dec}_{\textsf{nmc} })\), described in Fig. 5 is a 4-round non-malleable commitment.
The corollary given below immediately follows from the results shown in the previous sections and from the fact that \(\varPi _\textsf{comWI}\) can be instantiated in a black-box way from one-to-one one-way functions.
Corollary 3
Assuming the existence of one-to-one one-way functions, there exists a 4-round non-malleable commitment that makes black-box use of the OWFs.
8 Comparison with Previous Non-black-box Approaches to Four-Round Non-malleable Commitments
As we argued, our main strategy to construct a non-malleable commitment scheme is to lift the security of the weak non-malleable commitment scheme of [25, Fig. 2] (that we also recall in Fig. 4), relying on a special notion of zero-knowledge that we call non-malleable HVZK with respect to commitment. This notion guarantees that a sender of a commitment scheme does not change the distribution of the committed messages depending on whether they receive an honestly generated zero-knowledge proof or a simulated one. We construct a NMZKC for a specific class of commitments, which includes the weak-non-malleable commitment scheme of [25, Fig. 2] that we mention above.
Although our approach is inspired by [25], where the authors also lift the security of a weak-non-malleable commitment scheme relying on zero-knowledge, concretely, our techniques significantly depart from those of [25]. In the next paragraphs, we highlight the main difference between the two approaches and explain why we could use as one of the main building block the simple weak-non-malleable commitment of [25, Fig. 2], instead of a modified version, as the authors of [25] do.
The main technical challenge in designing non-malleable commitments with low round complexity is due to arguing in the proof that the security of the primitives involved in the protocol is maintained despite performing rewinds to extract the message committed by the MiM (on the right session). One of the primitives involved in the scheme of Goyal et al. is a non-rewind secure witness-indistinguishable proof denoted by \(\varPi \), and to cope with the rewinds performed by the extractor in the proof (while still relying on the WI property of \(\varPi \)), the prover prepares n first rounds for the non-rewind secure WI protocol (denoted with \(\varPi \)). Upon receiving one valid second round from the verifier, the prover picks one instance of \(\varPi \) at random (let us say the i-th) and completes the proof providing an accepting third round only with respect to the i-th instance. Let us denote the above protocol by \(\varPi _\textsf{rew}\).
Despite this protocol being rewind secure, Goyal et al. cannot use just one execution of \(\varPi _\textsf{rew}\), which proves that either the committer has behaved honestly in the algebraic part of the commitment or that the committer knows a trapdoor. The reason is that there is a simple adversarial strategy for which such a proof would not work in this case. Intuitively, consider a MiM that completes an execution on the right session only if it receives a proof for the j-th instance of \(\varPi \), and aborts in any other case (note that this MiM is non-aborting with non-negligible probability). This MiM would make the reduction to the WI of \(\varPi \) fail. In particular, any rewind performed by the extractor on the right session would make the MiM ask different second rounds for the same execution of \(\varPi \) (or abort if on the left session a different instance of \(\varPi \) is completed). To solve this problem the authors of [25] compute a secret sharing of the message and perform one execution of \(\varPi _\textsf{rew}\) for each of the shares. Now, even if the MiM applies the same strategy to one run of \(\varPi _\textsf{rew}\), it is safe to allow the MiM to perform this rewind since the only thing that will be leaked is a share of the message m (note that two accepting transcripts for the same execution of \(\varPi \) for two different second rounds might completely leak the witness). In the formal proof, Goyal et al. need to rely on the fact that the number of executions of \(\varPi \) that are not rewound (and consequently the number of shares not leaked) is sufficient to protect the secrecy of the message m. This modification also requires changing how the extractor works (e.g., by relying on the quadratic polynomials). Hence, to obtain their non-malleable commitment scheme, Goyal et al. rely on a more sophisticated version of the weak-non-malleable commitment described in their work. In our paper, we do not rely on any rewind secure primitive (which we replace with a proof system non-malleable with respect to commitments), so we do not need to split the message into shares and follow the strategy described above. We note that similarly to us, also [9] relies on the simpler sub-scheme of [25, Fig. 2] to obtain a 4-round concurrent non-malleable commitment scheme. To summarize, the main difference between ours and the approach of [25] (that relies on rewind secure primitive) is that our work is based on the observation that the rewinds are performed in the reductions or during the simulation, and as such, the adversary does not have clue that the rewinds are happening. Hence, relying on primitives that are rewind-secure (i.e., the adversary can consciously make rewinds and collect the transcripts generated during the rewinds) can be avoided for the application we consider in the paper.
Notes
- 1.
- 2.
Our BB 4-round non-malleable commitment scheme satisfies the notion of standalone (or one-one) non-malleability. Obtaining a concurrent (or many-many) BB non-malleable commitment scheme in just 4 rounds, or less, still remains an open question.
- 3.
- 4.
This sketch protocol gives a noticeable probability of cheating to the prover, typically the soundness of the protocol can be easily amplified via parallel repetition.
- 5.
Such commitments are sometimes called equivocal or trapdoor commitments.
- 6.
\(\varPi _\textsf{AI}\) works for any type of secret sharing scheme, and in our case \(\varPi _\textsf{AI}\) is parametrized by the reconstruction algorithm of the verifiable secret sharing \(\varPi ^\textsf{vss}\) (i.e., the prover of \(\varPi _\textsf{AI}\) expects to receive n views generated using the sharing algorithm of \(\varPi ^\textsf{vss}\)). We note that given that \(\varPi ^\textsf{vss}\) is information-theoretic, then \(\varPi _\textsf{AI}\) still makes black-box use of the underlying cryptographic primitives.
References
Badrinarayanan, S., Goyal, V., Jain, A., Kalai, Y.T., Khurana, D., Sahai, A.: Promise zero knowledge and its applications to round optimal MPC. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 459–487. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_16
Barak, B.: Constant-round coin-tossing with a man in the middle or realizing the shared random string model. In: FOCS (2002)
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols. In: 22nd Annual ACM Symposium on Theory of Computing, pp. 503–513. ACM Press, Baltimore, MD, USA (1990). https://doi.org/10.1145/100216.100287
Cao, Z., Visconti, I., Zhang, Z.: Constant-round concurrent non-malleable statistically binding commitments and decommitments. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 193–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_12
Chatterjee, R., Liang, X., Pandey, O.: Improved black-box constructions of composable secure computation. In: Czumaj, A., Dawar, A., Merelli, E. (eds.) ICALP 2020: 47th International Colloquium on Automata, Languages and Programming. LIPIcs, vol. 168, pp. 28:1–28:20. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Saarbrücken, Germany (2020). https://doi.org/10.4230/LIPIcs.ICALP.2020.28
Chor, B., Goldwasser, S., Micali, S., Awerbuch, B.: Verifiable secret sharing and achieving simultaneity in the presence of faults. In: 26th Annual Symposium on Foundations of Computer Science, pp. 383–395. IEEE Computer Society Press, Portland, Oregon (1985). https://doi.org/10.1109/SFCS.1985.64
Rai Choudhuri, A., Ciampi, M., Goyal, V., Jain, A., Ostrovsky, R.: Round optimal secure multiparty computation from minimal assumptions. In: Pass, R., Pietrzak, K. (eds.) TCC 2020. LNCS, vol. 12551, pp. 291–319. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64378-2_11
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Concurrent non-malleable commitments (and more) in 3 rounds. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 270–299. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_10
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Four-round concurrent non-malleable commitments from one-way functions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 127–157. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_5
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Round-optimal secure two-party computation from trapdoor permutations. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 678–710. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_23
Ciampi, M., Parisella, R., Venturi, D.: On adaptive security of delayed-input sigma protocols and fiat-shamir nizks. In: Galdi, C., Kolesnikov, V. (eds.) SCN 2020. LNCS, vol. 12238, pp. 670–690. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-57990-6_33
Ciampi, M., Persiano, G., Scafuro, A., Siniscalchi, L., Visconti, I.: Improved or-composition of sigma-protocols. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 112–141. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_5
Ciampi, M., Ravi, D., Siniscalchi, L., Waldner, H.: Round-optimal multi-party computation with identifiable abort. In: Dunkelman, O., Dziembowski, S. (eds.) EUROCRYPT 2022. LNCS, vol. 13275, pp. 335–364. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-06944-4_12
Dachman-Soled, D., Malkin, T., Raykova, M., Venkitasubramaniam, M.: Adaptive and concurrent secure computation from new adaptive, non-malleable commitments. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 316–336. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_17
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography. In: 23rd Annual ACM Symposium on Theory of Computing, pp. 542–552. ACM Press, New Orleans, LA, USA (1991). https://doi.org/10.1145/103418.103474
Feige, U., Lapidot, D., Shamir, A.: Multiple non-interactive zero knowledge proofs based on a single random string. In: 31st Annual Symposium on Foundations of Computer Science, pp. 308–317. IEEE Computer Society Press, St. Louis, MO, USA (1990). https://doi.org/10.1109/FSCS.1990.89549
Gennaro, R., Ishai, Y., Kushilevitz, E., Rabin, T.: The round complexity of verifiable secret sharing and secure multicast. In: 33rd Annual ACM Symposium on Theory of Computing, pp. 580–589. ACM Press, Crete, Greece (2001). https://doi.org/10.1145/380752.380853
Goldreich, O.: Foundations of Cryptography, vol. 1. Cambridge University Press, New York (2006)
Goldreich, O., Levin, L.A.: A hard-core predicate for all one-way functions. In: Proceedings of the 21st Annual ACM Symposium on Theory of Computing, 14–17 May 1989, Seattle, Washigton, USA, pp. 25–32 (1989)
Goyal, V.: Constant round non-malleable protocols using one way functions. In: STOC (2011)
Goyal, V., Khurana, D., Sahai, A.: Breaking the three round barrier for non-malleable commitments. In: 57th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2016. IEEE (2016)
Goyal, V., Lee, C.K., Ostrovsky, R., Visconti, I.: Constructing non-malleable commitments: a black-box approach. In: 53rd Annual Symposium on Foundations of Computer Science, pp. 51–60. IEEE Computer Society Press, New Brunswick, NJ, USA (2012). https://doi.org/10.1109/FOCS.2012.47
Goyal, V., Richelson, S.: Non-malleable commitments using Goldreich-Levin list decoding. In: Zuckerman, D. (ed.) 60th Annual Symposium on Foundations of Computer Science, pp. 686–699. IEEE Computer Society Press, Baltimore, MD, USA (2019). https://doi.org/10.1109/FOCS.2019.00047
Goyal, V., Richelson, S., Rosen, A., Vald, M.: An algebraic approach to non-malleability. In: 55th Annual Symposium on Foundations of Computer Science, pp. 41–50. IEEE Computer Society Press, Philadelphia, PA, USA (2014). https://doi.org/10.1109/FOCS.2014.13
Goyal, V., Richelson, S., Rosen, A., Vald, M.: An algebraic approach to non-malleability. Cryptology ePrint Archive, Paper 2014/586 (2014). https://eprint.iacr.org/2014/586
Halevi, S., Hazay, C., Polychroniadou, A., Venkitasubramaniam, M.: Round-optimal secure multi-party computation. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 488–520. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_17
Hazay, C., Venkitasubramaniam, M.: On the power of secure two-party computation. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 397–429. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_14
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Zero-knowledge from secure multiparty computation. In: Johnson, D.S., Feige, U. (eds.) 39th Annual ACM Symposium on Theory of Computing, pp. 21–30. ACM Press, San Diego, CA, USA (2007). https://doi.org/10.1145/1250790.1250794
Khurana, D.: Round optimal concurrent non-malleability from polynomial hardness. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 139–171. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_5
Khurana, D., Ostrovsky, R., Srinivasan, A.: Round optimal black-box Commit-and-Prove. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 286–313. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_11
Lin, H., Pass, R.: Constant-round non-malleable commitments from any one-way function. In: Fortnow, L., Vadhan, S.P. (eds.) Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC 2011, 6–8 June 2011, San Jose, CA, USA, pp. 705–714. ACM (2011)
Lin, H., Pass, R.: Constant-round nonmalleable commitments from any one-way function. J. ACM 62(1), 5:1-5:30 (2015)
Lin, H., Pass, R., Venkitasubramaniam, M.: Concurrent non-malleable commitments from any one-way function. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 571–588. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_31
Mahmoody, M., Pass, R.: The curious case of non-interactive commitments – on the power of black-box vs. non-black-box use of primitives. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 701–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_41
Ostrovsky, R., Persiano, G., Visconti, I.: Simulation-based concurrent non-malleable commitments and decommitments. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 91–108. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_7
Pass, R.: Unprovable security of perfect nizk and non-interactive non-malleable commitments. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 334–354. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_19
Pass, R., Rosen, A.: Bounded-concurrent secure two-party computation in a constant number of rounds. In: 44th Symposium on Foundations of Computer Science (FOCS 2003), 11–14 October 2003, Cambridge, MA, USA, Proceedings, pp. 404–413. IEEE Computer Society (2003)
Pass, R., Rosen, A.: Concurrent non-malleable commitments. In: Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science (FOCS 2005), 23–25 October 2005, Pittsburgh, PA, USA, pp. 563–572 (2005)
Pass, R., Rosen, A.: New and improved constructions of non-malleable cryptographic protocols. In: STOC (2005)
Pass, R., Rosen, A.: Concurrent nonmalleable commitments. SIAM J. Comput. 37(6), 1891–1925 (2008)
Pass, R., Rosen, A.: New and improved constructions of nonmalleable cryptographic protocols. SIAM J. Comput. 38(2), 702–752 (2008)
Pass, R., Wee, H.: Constant-round non-malleable commitments from sub-exponential one-way functions. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 638–655. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_32
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: 51th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2010, 23–26 October 2010, Las Vegas, Nevada, USA, pp. 531–540. IEEE Computer Society (2010)
Yao, A.C.C.: Space-time tradeoff for answering range queries. In: 14th Annual ACM Symposium on Theory of Computing, pp. 128–136. ACM Press, San Francisco, CA, USA (1982). https://doi.org/10.1145/800070.802185
Acknowledgements
We thank Carmit Hazay and Muthuramakrishnan Venkitasubramaniam for insightful discussions on the MPC-in-the-head approach. Emmanuela Orsini was supported by the Defense Advanced Research Projects Agency (DARPA) under contract No. HR001120C0085, and by CyberSecurity Research Flanders with reference number VR20192203. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the DARPA, the US Government or Cyber Security Research Flanders. The U.S. Government is authorized to reproduce and distribute reprints for governmental purposes notwithstanding any copyright annotation therein.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Ciampi, M., Orsini, E., Siniscalchi, L. (2022). Four-Round Black-Box Non-malleable Schemes from One-Way Permutations. In: Kiltz, E., Vaikuntanathan, V. (eds) Theory of Cryptography. TCC 2022. Lecture Notes in Computer Science, vol 13748. Springer, Cham. https://doi.org/10.1007/978-3-031-22365-5_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-22365-5_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-22364-8
Online ISBN: 978-3-031-22365-5
eBook Packages: Computer ScienceComputer Science (R0)





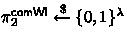 and returns it.
and returns it. , with
, with 





