Using the Strongest Adversarial Example to Alleviate Robust Overfitting

Abstract

Overfitting is considered to be one of the dominant phenomena in machine learning. A recent study suggests that, just like standard training, adversarial training(AT) also suffers from the phenomenon of overfitting, which is named robust overfitting. It also points out that, among all the remedies for overfitting, early stopping seems to be the most effective way to alleviate it. In this paper, we explore the role of data augmentation in reducing robust overfitting. Inspired by MaxUp, we apply data augmentation to AT in a new way. The idea is to generate a set of augmented data and create adversarial examples(AEs) based on them. Then the strongest AE is applied to perform adversarial training. Combined with modern data augmentation techniques, we can simultaneously address the robust overfitting problem and improve the robust accuracy. Compared with previous research, our experiments show promising results on CIFAR-10 and CIFAR-100 datasets with PreactResnet18 model. Under the same condition, for $\boldsymbol{l_\infty }$ attack we boost the best robust accuracy by $\boldsymbol{1.57\%}$–$\boldsymbol{2.89\%}$ and the final robust accuracy by $\boldsymbol{7.51\%}$–$\boldsymbol{9.42\%}$, for $\boldsymbol{l_2}$ attack we improve the best robust accuracy by $\boldsymbol{1.64\%}$–$\boldsymbol{1.74\%}$ and the final robust accuracy by $\boldsymbol{3.80\%}$–$\boldsymbol{5.99\%}$, respectively. Compared to other state-of-the-art models, our model also shows better results under the same experimental conditions. All codes for reproducing the experiments are available at https://github.com/xcfxr/adversarial_training.

1 Introduction

Despite deep neural models have made an unprecedented progress on a wide range of computer vision tasks, they can be easily fooled by adversarial examples(AEs) [1] , which can be crafted by adding small and invisible perturbation to original images. With such intentional changes called adversarial attack to inputs, many models fail to provide a satisfied performance. To prevent these attacks, a whole lot of defense methods are being proposed. Adversarial training(AT) [2], which creates AEs and then treats them as training sets, is considered as the most efficient approach against adversarial attack.

Fig. 1.

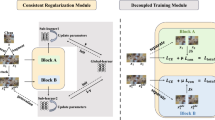
This is the robust test on accuracy between baseline [2] and our method under the P$GD^{10}$ attack. The baseline method suffers serious robust overfitting, but our method doesn’t. Further more, our final model surpasses the best checkpoint of the baseline, which can be achieved by early-stopping [3].

However, recently a study [3] finds something intriguing in AT. It observes that just like standard training, AT also suffers from the phenomenon of overfitting (see left picture of Fig. 1). Namely, after several epochs of training, especially after the adjustment of learning rate, the robust test accuracy begins to decrease while robust train accuracy still increases. Various technologies are proposed to address the problem, among which early stopping seems to be the most effective way to alleviate the problem, while other tricks, such as regularization effect of data augmentation, including mixup [4] and cutout [5], seem to be ineffective.

Fig. 2.

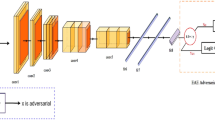
We show the gap between the early stopping method [3] and our method. Left column: the original images. Middle column: the $l_{\infty }$ adversarial noises by applying P$GD^{10}$ for 10 iterations. We normalize the noise into $\left[ 0, 255\right] .$ Right column: the generated adversarial images. We also show the predicted labels and probabilities of these images.

In this paper, we use data augmentation to counter this robust overfitting phenomenon and to achieve better robust accuracy. As shown in the right picture of Fig. 1, throughout the whole training process, the robust test accuracy and the robust train accuracy rises continuously.

Inspired by MaxUp [6], we apply data augmentation to adversarial training process. In our approach, we first generate a set of augmented data and then create adversarial examples(AEs) based on them. The AE which causes the maximal loss is used to perform AT. While MaxUp [6] minimizes the average risk of the worst augmented data, we use the attack method to create AEs and then minimize the average risk of the worst AEs. Our experiments demonstrate that combined with our approach, augmentations including mixup and cutmix can neutralize robust overfitting partially and meanwhile achieve a better prediction result than early stopping scheme. As shown in Fig. 2, compared with the early stopping approach [3], our approach still produces a correct label for perturbed image, while the baseline approach returns a false one.

Our experiments achieve promising results on the CIFAR-10 and CIFAR-100 datasets with the PreactResnet18 model. Under the same condition, for $l_\infty$ attack we boost the best robust accuracy by $1.57\%-2.89\%$ and the final robust accuracy by $7.51\%-9.42\%$, for $l_2$ attack we improve the best robust accuracy by $1.64\%-1.74\%$ and the final robust accuracy by $3.80\%-5.99\%$, respectively. All codes for reproducing the experiments are available at https://github.com/xcfxr/adversarial_training.

2 Related Work

Szegedy et al. [1] observe that deep neural models are vulnerable to imperceptible perturbations. With such perturbations, vanilla images become adversarial examples(AEs) which can successfully fool the models. The approaches of generating AE are known as an adversarial attack. Some early approaches adopt the fast gradient sign method(FGSM) [7], which crafts AE with a single gradient step. BIM [8] on the other hand, extends FGSM to iterative small gradient steps. DeepFool [9] declare that changing one pixel is enough to fool the classifier [10]. Among all approaches, projected gradient decent(PGD) [2] is considered as one of the strongest first-order attack. As a result, a lot of PGD-based work was studied, e.g. PGD combined with momentum [11] and logit pairing [12].

To address the problem of adversarial attack, many defense-related work have been proposed. Some defense approaches are not always effective, such as distillation [13] and generator [14, 15]. Normally, adversarial training(AT) [2] is considered as the most successful defensive approach. AT has attracted a series of research efforts [10, 16, 17], among which Trades [17] is a notable work, achieving a trade-off between the efficiency and robust accuracy.

Recently, Rice et al. [3] demonstrate that there is a serious overfitting phenomenon called robust overfitting during AT and there is no effective way as good as early-stopping to tackle it. Another research [18] also points out that despite of their excellent performances on improving robustness in standard training, data-driven augmentations do not improve robustness to $l_p$ norm bounded perturbations. Contrary to their finding, Rebuffi et al. [19] show that data augmentation has the potential to alleviate robust overfitting. In their experiment, although data augmentation alone cannot improve robustness, with smoothing the weights by model weight averaging(WA) [20], augmentation techniques can alleviate overfitting and achieve a significant performance improvement. In another research, Chen et al. [21] show that schemes of learned smoothening is supposed to be a possible way to resist robust overfitting. They smooth the weights by WA and the logits via self-training. In the latest research, Rebuffi et al. [19] incorporate a large number of tricks to achieve the state-of-the-art robust accuracy.

3 Preliminaries

3.1 Notations

In this section, we use $x\in \mathbb {R}^{W\times H\times C}$ and y to denote a training image and its label, respectively. $\left( x^{\prime }, y^{\prime }\right)$ is obtained from $\left( x,y\right)$ by data transformation.Let $\mathcal {D}_n$ and $\mathcal {L}$ denote the training dataset with N input-label pairs and the loss function, respectively. The neural network parameterized by $\theta$ is represented as $f_{\theta }$. So the empirical risk minimization(ERM) can be denoted as $\min \limits _{\theta }\mathbb {E}_{\left( x,y\right) \sim \mathcal {D}_n}\left[ \mathcal {L}\left( f_\theta \left( x\right) , y\right) \right]$. And we use $\delta$ to represent the perturbation created by adversarial attack and $\delta$ are limited to the range of S, where S is chosen to be a $l_p$-norm ball and represents a closed interval $\left[ -\epsilon , \epsilon \right]$($\epsilon$ defines the maximum perturbation allowed).The letter m is the hyper-parameter of our algorithm, which represents the number of AEs generated for each sample. We denote the accuracy rate on the adversary as “robust accuracy", so the accuracy rate on the training adversary and test adversary are called “robust train accuracy" and “robust test accuracy", respectively.

3.2 MaxUp

The key idea of MaxUp is that for each $\left( x, y\right)$, Gong et al. [6] generates m samples by applying data transformations, which can be Gaussian Sampling $\mathcal {N}\left( x, \sigma ^2\boldsymbol{I}\right)$ or data augmentations. In the next step, among the m data points, they choose the one that maximizes the loss function as a new training sample. The method can be summarized as:

$$\begin{aligned} MaxUp \quad \arg \min \limits _{\theta } \mathbb {E}_{(x, y)\sim \mathcal {D}_n} \left[ \max \limits _{i \in \left[ m\right] } \mathcal {L}\left( f_{\theta }\left( x^{\prime }_{i}\right) , y^{\prime }_{i}\right) \right] \end{aligned}$$

(1)

Gong et al. consider MaxUp as a smoothness Regularization. They define

$$\begin{aligned} \begin{aligned} \mathcal {L}_{m}^{max}\left( f_\theta \left( x\right) , y\right) = \mathbb {E}\left[ \max \limits _{i\in [m]}\mathcal {L}\left( f_{\theta }\left( x_i\right) \right) \right] \\ \mathcal {L}_{m}^{avg}\left( f_\theta \left( x\right) , y\right) = \mathbb {E}\left[ \frac{1}{m}{\sum _{i=1}^{m}}\mathcal {L}\left( f_{\theta }\left( x_i\right) \right) \right] \end{aligned} \end{aligned}$$

(2)

and prove the following equal equation:

$$\begin{aligned} \begin{aligned} \mathcal {L}_{m}^{max}\left( f_\theta \left( x\right) , y\right) = {L}_{m}^{avg}\left( f_\theta \left( x\right) , y\right) + \Phi \left( x, \theta \right) + \textbf{O}\left( \sigma ^2\right) \\ c_{m}^{-}\Vert \nabla _x\mathcal {L}\left( f_{\theta }\left( x\right) , y\right) \Vert \le \Phi \left( x, \theta \right) \le c_{m}^{+}\Vert \nabla _x\mathcal {L}\left( f_{\theta }\left( x\right) , y\right) \Vert , \end{aligned} \end{aligned}$$

(3)

where $c_{m}^{+} \ge c_{m}^{-} \ge 0$ and $\sigma ^2$ bounds the range of changes in x caused by transformation or data augmentation.

3.3 Projected Gradient Descent

Projected Gradient Descent(PGD) [2] is a method for generating reliable first-order adversaries. An $l_p$ PGD adversarial example would start at some random initial perturbation $\delta ^{\left( 0\right) }$, where $\delta ^{\left( 0 \right) } \sim \mathcal {U}\left( -\epsilon ,\epsilon \right)$ . Then the perturbation will be iteratively adjusted with the following gradient steps while projecting back onto $l_p$ ball with radius $\epsilon$. The whole process can be described as:

$$\begin{aligned} \begin{aligned}&\tilde{\delta } = \delta ^{\left( t\right) } + \alpha \cdot \textrm{sign} \left( \nabla _x\mathcal {L}\left( f_{\theta }\left( x+\delta \right) , y\right) \right) \\&\delta ^{\left( t+1\right) }=\max \left( \min \left( \tilde{\delta },\epsilon \right) , -\epsilon \right) . \end{aligned} \end{aligned}$$

(4)

Madry et al. [2] treat these newly generated adversaries as datasets and train the robust model to defense adversarial attack, which is known as Adversarial training(AT).

4 Methods

4.1 Algorithm

Our approach extends MaxUp and AT as follows. For each training example $\left( x, y\right)$, we first use augmentation techniques to generate m augmented data $X\in \mathbb {R}^{m\times W\times H\times C}$¹. Then we apply PGD-attack to those generated data points. By adding restricted perturbation, we can create m adversarial examples(AEs).

Among the m adversarial examples, we choose the one that generates the maximal loss in our new training dataset. In this way, we can gain new and more complex adversarial examples as our samples. The final step is utilizing the new generated AEs to perform adversarial training. Overall, we propose a new way of applying data augmentations to adversarial training(AT), which can be summed up as:

$$\begin{aligned} \arg \min \limits _{\theta } \mathbb {E}_{(x,y)\sim \mathcal {D}_n} \left[ \max \limits _{i \in [m]} \mathcal {L}\left( f_{\theta }\left( x_i+\delta _i\right) , y_i\right) \right] . \end{aligned}$$

(5)

The complete process of our method is described in Algorithm 1. The first six lines are about the input and output. Lines 10 to 15 specifically describe how we create AEs and apply data augmentation into AT at the formula level.

4.2 Analysis

When m is equal to 1, our algorithm degenerates into ordinary adversarial training. When m become larger, more powerful and more sophisticated adversarial examples(AEs) can be crafted, so that both in quantity and intensity our AEs is more dominant. A trade-off of the approach is that, although parallel computing is possible, from the perspective of computing resources, resources consumed and memory occupied per epoch will increase linearly as m increases. A larger m, on the other hand, can result in a faster convergence.

Here is a plausible explanation of why our approach works. With the conclusion of MaxUp(3.2) and our methods, the empirical risk in the AT turns into

$$\begin{aligned} \begin{aligned} \mathbb {E}_{\left( x,y\right) \sim \mathcal {D}_n}&\Bigg [\frac{1}{m}\sum \limits _{i=1}^{m}\mathcal {L}_m^{avg}\left( f_\theta \left( x_i+\delta _i\right) , y_i\right) \\&c_m\Vert \nabla _{x_i}\mathcal {L}\left( f_{\theta }\left( x_i + \delta _i\right) , y_i\right) \Vert +\textbf{O}\left( \sigma ^2\right) \Bigg ], \end{aligned} \end{aligned}$$

(6)

where $c_{m}^{+} \ge c_{m} \ge c_{m}^{-} \ge 0$. So when we perform AT with the worst AE that costs the maximal loss, the loss function has become a combination of a loss term which measures how well the model fits the AE, a regularization term related to the norm of $\nabla _x$ and a high-order infinitesimal term which can be ignored. The expectation of the loss term equals the expectation with normal AT, so our algorithm essentially adds a penalty which restricts the magnitude of $\nabla _x$ in the process of AT. Because of the regularization term, the first step of generating AEs(3.3) has also changed. It turns into

$$\begin{aligned} \tilde{\delta } = \delta ^{\left( t\right) } + \alpha \cdot \textrm{sign}\left( \nabla _{x_i}\left[ \mathcal {L}\left( f_{\theta }\left( x_i+\delta _i\right) , y_i\right) + \Phi (x_i, \theta )\right] \right) , \end{aligned}$$

(7)

where $\Phi (x_i, \theta )$ equals $c_m\Vert \nabla _{x_i}\mathcal {L}\Vert$. It is clear that the sign of the gradient may change due to the extra term $\Phi \left( x, \theta \right)$, so our methods can affect the process of making the AEs to some extent.

In summary, our approach is a crafty combination of adversarial training and data augmentation, by making sophisticated AEs in parallel to train a more robust model.

5 Experiments

5.1 Experimental Settings

For a complete experimental comparison, most of our experimental setups follow the original study [3], including the weight decay, the learning schedule and epochs of training, etc.

5.1.1 Datasets and Architecture

Our experiments are conducted across two datasets: CIFAR-10, CIFAR-100 [23]. The CIFAR-10 dataset consists of 60000 32$\,\times \,$32 colour images in 10 classes, with 6000 images per class. There are 50000 training images and 10000 test images. The CIFAR-100 dataset is just like the CIFAR-10, except it has 100 classes containing 600 images each. There are 500 training images and 100 testing images per class. And most of the experiments are implemented on CIFAR-10. In order to observe the whole process of the robust accuracy change and pick the checkpoint of the best performance, after each training epoch, we output the robust loss and robust accuracy on the test set. Because of hardware and time costs during training, all of our experiments are based on ResNet-18 [24].

5.1.2 Attack Methods

During the adversarial training, we use P$GD^{10}$ with random initialization and the step size of attack is 2/255. We consider two mainstream types of adversarial perturbation $l_\infty$ and $l_2$, and the norm of them are 8/255 and 128/255 respectively. For evaluation, we keep the same settings as training.

5.1.3 Other Setup

We use a fairly common learning schedule: for 200 epochs, the learning rate begins with the rate of 0.1 and decays by a factor of 10 at the 100th and 150th. We also adopt the SGD optimizer in a common way, with a momentum of 0.9 and weight decay of $5 \times 10^{-4}$. For all datasets, we set batch size as 128 for PreActResNet-18. When applying augmentation methods like cutmix [22] and mixup [4] in our method, we default the $\alpha$ to 1.

5.2 Experimental Results

5.2.1 Across Datasets and Perturbations

Table 1 shows the improvement brought by our methods across different datasets and perturbations. We report robust test accuracy(RA) at two periods to numerically demonstrate the phenomenon. The final-RA indicates the average robust accuracy of last five epochs, the best-RA indicates the best robust accuracy in the whole process of training and the diff-RA equals the best-RA minus final-RA, which can measure the degree of robust overfitting. We consider adversarial training(AT) [2] as baseline. The overfitting shows up across all datasets and perturbations in baseline cases, with the gap between final and best reaching as large as $7.05\%$(CIFAR-10). Compared with $l_\infty$ perturbation, the overfitting of $l_2$ are much less serious, espeicially in the CIFAR-10, the diff-RA is only $2.72\%$. We use the code provided by Rice et al. [3] to reproduce the baseline results².

Table 1. Robust test accuracy under attack with P$GD^{10}$ against $l_\infty$ with radius $\epsilon =8/255$ across CIFAR-10 and CIFAR-100. Both experiments are based on ResNet-18. The Final equals the average robust test accuracy of last five epochs and the Best is the checkpoint with best robustness during the whole training process. The best results and the smallest difference between best and final are marked in bold.

With our method, both the final-RA and the best-RA are boosted a lot. For $l_{\infty }$ attack, we observe the best RA is pushed higher by 1.57%–2.89%. For example, the best robust accuracy on CIFAR-10 rises from $53.28\%$ to $56.17\%$. Further, the difference between best-RA and final-RA is reduced to only $0.52\%$(CIFAR-10) and $0.78\%$(CIFAR-100) respectively, where the overfitting problem is almost solved. Unlike baseline cases whose best robust accuracy is nearly the first decay of learning rate, the checkpoint which has the best-RA in ours is close to the end, which also means robust overfitting phenomenon is mitigated. And for $l_2$ attack, the final-RA was boosted from 68.90% to 72.70% on CIFAR-10 and from 37.50% to 43.49% on CIFAR-100 respectively.

Fig. 3.

Results of robust test accuracy under attack of $l_2$ and $l\infty$ over epochs for ResNet-18 trained on CIFAR-10, CIFAR-100. Blue/Yellow lines show the our best model and baseline. (Color figure online)

Figure 3 further plots the robust test accuracy curves during training, from which we can clearly observe the diminishing of robust overfitting. The training curve is robustly improved until the end without compromising training accuracy.

5.2.2 With Different Augmentation Techniques

Table 2 demonstrates the effectiveness of our methods among various regularization. The baseline is still adversarial training. In Rice et al.’s [3] experiments, data augmentation mitigates overfitting to some degree at the expense of losing accuracy, and early-stopping seems to be the best way to fight against robust overfitting. As Rebuffi et al. [19] point out, cutmix have powerful ability to increase the robustness of model. And in our experiment, mixup [4] mitigates the overfitting but loses a lot of accuracy. Cutmix [22] achieves better result than early stopping under the same conditions and helps to alleviate overfitting well. Combined with our method, both cutmix and mixup acquire significant power. When m is set to 4, cutmix push the final accuracy of normal AT from $46.23\%$ to $55.65\%$ and best accuracy from $53.28\%$ to $56.17\%$, which also surpass early stopping and normal cutmix a lot. And with m setting to 3, mixup can also be better than normal cutmix, let alone early stopping.

Table 2. Robust test accuracy with different regularization methods on CIFAR-10 based on PreActResNet18 under the attack of P$GD^{10}$. The perturbation type is $l_\infty$ and the radius of it is 8/255. The Final equals the average robust test accuracy of last five epoch and the Best is the checkpoint during the whole training period. The best results and the smallest difference between best and final are marked in bold.

Fig. 4.

Robust test accuracy against $\epsilon _{\infty } = 8/255$ on CIFAR-10 with different data augmentation schemes($\textrm{method}^1$ and $\textrm{method}^2$ correspond to Table 3). The model is a ResNet-18 and the panel show the evolution of robust accuracy as training progresses(against P$GD^{10}$). The jump in robust accuracy half and two-thirds through training is due to a drop in learning rate.

Figure 4 shows the whole training process of robust accuracy with different regularizations. Though mixup doesn’t achieve as good results as other methods, all data augmentations seem to help to resist the phenomenon of robust overfitting because the robust accuracy doesn’t decrease significantly except for baseline. And we can also observe, without our methods, the fluctuation of robust accuracy curve is large, which indicates that our schemes can make the training process more smooth and stable. Near the end of training, the vibration of our accuracy curves(green and red curves) is much smaller than others.

5.2.3 Ablation Study of m

We test our methods with different sizes of m and observe their performance against $l_\infty$ attack. The experiments are based on ResNet-18 [24] and incorporate data augmentation including mixup [4] and cutmix [22]. We vary the size in 1, 2, 3, 4. Note that when $m=1$, our methods degenerate into normal adversarial training with cutmix or mixup. Against adversarial attack, naive cutmix get stronger performance than mixup, this rule stays the same when m increase. As shown in Table 3, in our experiments, cutmix gets best result when m equals 4, achieving the 56.17% best-RA and 55.65% final-RA respectively. When using mixup, we get similar excellent results when $m\in \left[ 2,4\right]$. The difference is the smallest when m is equal to 2 for both cutmix and mixup. But when m continues to be larger, the performance begins to degrade, especially the model trained with mixup. Combined with the conclusions in MaxUp [6], we consider the reason is that ResNet-18 is not complex enough.

Table 3. Ablation studies on CIFAR-10 with ResNet-18 when m varies. The attack type is $l_\infty$ with radius 8/255. Experiments are performed with cutmix and mixup respectively and they yield the best robust test accuracy observed during training, the final robust test error averaged over the last five epochs, and the differences between them.

Figure 5 demonstrates the whole training process when m varies. With our schemes, we can see both cutmix and mixup achieved great improvement. Especially when the learning rate drops for the second time, our accuracy curves continue to rise while normal methods have not changed.

Fig. 5.

Results of robust test accuracy over epochs with the changing of m. All experiments are training on CIFAR-10 with PreActResNet18 against $\epsilon _{\infty }=8/255$. The left and right pictures represent the performance of our methods, combined with mixup and cutmix respectively.

5.3 Other Attempts

Drawing on the method of Rebuffi et al. we used the synthetic dataset [18] provided by them and the model weighted average method [20], which improved the robust accuracy by 4.66% to 61.18%. We control the ratio of synthetic data to original data to be 7:3, which is the same as Rebuffi et al. [19]. Here we compare our model with other state-of-the-art methods under the same experimental conditions. We directly used the pretrained model³ provided by the authors. As shown in Table 4, under the same conditions of Res-18 and PGD-10, our model outperforms the second model on attacked data and get a similar result on clean data. The third method gets the best results because they use all the 100M synthetic data.

Table 4. Robust test accuracy on CIFAR-10 based on PreActResNet18 under the attack of P$GD^{10}$. The perturbation type is $l_\infty$ and the radius of it is 8 /255.We use augmentation to denote the Rebuffi et al.’s model [19] and generation to denote Gowal’s model [18].

We have also tried other methods to prevent robust-overfitting in our experiments. Like MaxUp [6] we replace the augmentation step with $\mathcal {N}\left( X, \sigma ^2 I\right)$, our attempt in this experiment doesn’t get desired result, it does prevent the overfitting but loses a lot of accuracy. And inspired by the procedure of SoftPatchup [25], we change the mix step of cutmix [22]. In original cutmix, $\tilde{x} = M \odot x_A + (1-M) \odot x_B, \quad \tilde{y} = \lambda y_A + (1 - \lambda )y_B$, we try the transformation of $\tilde{x} = M \odot x_A+ (1-M) \odot x_A * \lambda _2 + (1 - \lambda _2)*(1-M)\odot X_B, \quad \tilde{y} = \lambda _1 y_A + (1-\lambda _1)(\lambda _2 y_A + (1-\lambda _2) y_B)$, where $1 - \lambda _1$ denotes the portion of the cut area and $\lambda _2$ is sampled from the uniform distribution$\left( 0, 1\right)$. This attempt prevents the overfitting and is better than baseline but the gap with the best result of ours is not small. Because data augmentations help to create complex adversaries, we try to use P$GD^{20}$ to make adversarial examples during training and P$GD^{10}$ to test robustness during testing, but it doesn’t work and still suffers overfitting.

6 Conclusion

This paper proves that, combining with modern data augmentation techniques, we can improve the robustness of models and alleviate robust overfitting. Compared with Rebuffi et al. we propose a stronger augmentation technique and explore the ability of it. By making more sophisticated and more strong adversarial examples, our methods seem to overcome the classifier’s weakness of robust overfitting and get a more promising result. Although it seems to work well, the reason of robust overfitting is still hard to explain. Our future work will delve into the causes of robust overfitting and try to give some reasonable explanation. We will also explore other useful tricks that can improve the robustness of deep neural models to get a more powerful and strong robust model.