Keywords

14.1 Introduction

The problem of reducing the level of vibrations affects many areas of engineering, instrumentation and construction. Often the solution is to increase the strength and stability of protected objects, but apart from the widely known methods of vibration (vibration, balancing, balancing machines, changing the materials of the protected object) [1] there is a less known method of applying a mass damper (MD). The use of MD takes a special place because their use can be implemented not only at the design and construction stage, but also in the case when unsatisfactory dynamic characteristics of the structure are identified already during operation. In addition, the advantage of dampers is that at a relatively low cost of additional material, they make it relatively easy to get the effect of reducing the level of vibrations.

To create forces that dampen harmful vibrations of the protected object, it is important to choose the optimal actuator that will meet various requirements to the desired extent, for example, such as compactness or scale of force generation. Known components of actuators (electromagnetic devices, pneumatic drives, rotors and linear motors [2], etc.) can be used effectively in vibration damping tasks. In contrast to the mentioned devices, modern technical materials, which are often referred to as smart materials, have a number of advantages, since they can be lightweight and, more importantly, can be seamlessly integrated structurally into an already designed system without changing the inertial characteristics of the system. Smart materials are materials that have one or more properties that can be changed significantly in a controlled way by external perturbations such as voltage, temperature, humidity, pH, electric or magnetic fields. There are many types of smart materials, some of which are already common. Due to the possibility of generating forces, piezoelectric materials are preferable for solving this problem. Among the many types of piezoelectric devices, bending piezoactuators are of particular interest, the use of which is considered in this article for damping vibrations.

A striking example of such integration is the composite aeroelastic wing, equipped with thin piezoelectric plates in the wing structure, which allow to suppress unwanted vibrations, without adding significant mass and without changing the shape of the wing. A similar quenching method is used in the wing of an FA-18 deck aircraft equipped with piezoelectric plates for vertical stabilization [3] (Fig. 14.1).

Fig. 14.1
figure 1

Wing carrier-based aircraft FA-18

Full size image

14.2 Statement of the Problem

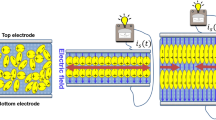
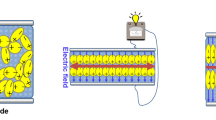
To dampen vibrations of the structure (Fig. 14.2a), which is under the influence of external perturbations, we consider piezoelectric layers that partially cover the surface of the beam and have different forms of electrode plates (Fig. 14.2b, c). In other words, we consider a piezoelectric layer consisting of a piezoceramic plate, which is covered with electrode plates along the length. A mathematical model of vibration damping of an elastic beam with piezoelectric layer actuators is derived. A comparative analysis of the action of piezoelectric layers with identical piezoceramic plates, but with electrode plates of different shapes, is performed. The location of the piezoelectric layer is selected from the conditions for the most effective control of vibrations. The effectiveness of quenching is considered relative to two criteria: the control voltage applied to the piezoelectric layer and the deflection of the beam at the end. In other words, it is necessary to find a Pareto set of solutions with respect to two criteria, while the maximum value of the control voltage does not exceed the maximum allowable value of the voltage for piezoelectric layers.

Fig. 14.2
figure 2

Protected object with piezoelectric layers: a general view, with b rectangular and c triangular plates attached to the beam

Full size image

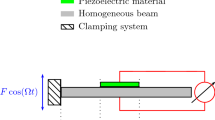
The main object of research is a cantilever metal beam (Fig. 14.2a), the size and weight of which are so small in comparison with the size and weight of the base that the influence of the beam on the base can be ignored. Piezoelectric layers are represented with triangular and rectangular electrode forms of plates, the length of the layers is 5 times less than the length of the beam, and the thickness is less by an order of magnitude. The behavior of the beam is considered in the framework of the Bernoulli–Euler hypothesis, the influence of the thickness of the piezoelectric layer at the moment of inertia of the beam is ignored, since it does not significantly change the stiffness and inertia characteristics of the system, the hysteresis of the piezoelectric layer is not taken into account.

14.3 Mathematical Model of Active Damping of Transverse Beam Vibrations

A linear viscoelastic model is used to describe the transverse vibrations [4] of a beam in the framework of the Bernoulli–Euler hypotheses in dimensionless variables:

$$\frac{{\partial }^{2}\omega }{\partial {t}^{2}}+{a}^{2}\left(\frac{{\partial }^{4}\omega }{\partial {x}^{4}}+{\vartheta }_{0}\frac{{\partial }^{5}\omega }{\partial {x}^{4}\partial \mathrm{t}}\right) =-\frac{{u}_{0}}{\rho A}+{v}_{0} \left(t\right)$$
(14.1)

where \(\omega =\omega (x,t)\) is dimensionless deflection of the beam, \(K=\frac{{\partial }^{4}}{\partial {x}^{4}}\) is the differential operator of the fourth degree, \(\beta =\frac{a}{{l}^{2}}\vartheta\) is dimensionless damping coefficient of the system \(\vartheta\) is the coefficient of internal viscosity, \({a}^{2}=EJ/\rho A,\) \(E\) is elastic modulus, \(J\) is moment of inertia of the section, \(\rho\) is density, \(A\) is cross-sectional area of the beam, \(l\) is beam length, \(v\left(t\right)\) is acceleration acting on the base, \(t\) is time, \(f\left(u,{x}_{1},..,{x}_{n}\right)\) is control function applied at certain points of the beam \({x}_{1},..,{x}_{n}\) or at intervals between points, \(u\) is the control, which will be mainly discussed later.

Equation (14.1) in partial derivatives is reduced to the equation in principal coordinates (relative to the time function). For this purpose, the methods of separated variables and normal forms are used, described in more detail in [5].

$$\omega \left(x,t\right)=\sum_{i=1}^{\infty }{X}_{i}\left(x\right){T}_{i}\left(t\right), {\int }_{0}^{1}{X}_{i}{X}_{j}dx=1, {\int }_{0}^{1}K{X}_{i}{X}_{j}dx= \left\{\begin{array}{c}{\lambda }_{i}^{4}, i=j\\ 0, i\ne j\end{array}\right.$$
(14.2)

\({\lambda }_{i}\) is eigenvalues of a beam, analogous to the eigenfrequency of a beam in dimensionless variables. \({X}_{i}\) are parameters that are functions of the beam shape. The values of eigenvalues and form functions are derived from the boundary conditions of the cantilever beam described by the Krylov function [6]. The transformation (14.1) to the main coordinates is represented in the equation:

$${\ddot{T}}_{i}+\beta {\lambda }_{i}^{4}{\dot{T}}_{i}+{\lambda }_{i}^{4}{T}_{i}=-{\int }_{0}^{1}{X}_{i}f(u,{x}_{1},..,{x}_{n})dx+{\int }_{0}^{1}{X}_{i}dxv\left(t\right)$$
(14.3)

Equation (14.3) is a mathematical model for controlling transverse vibrations of a beam under external perturbation. However, when considering a practical problem, the control is implemented using actuators, which makes very impressive changes to the mathematical model for controlling transverse vibrations, which is described in more detail later.

14.4 Active Damping of the Cantilever Beam with a Piezoelectric Layer

The piezoelectric layer is a piezoceramic plate with electrode plates attached to it on both sides (Fig. 14.3), through which control is performed by changing the potential difference between them. Piezoceramic material that is not covered with an electrode lining on both sides is useless to use as an active material.

Fig. 14.3
figure 3

Cantilever beam with a piezoelectric layer along its entire length

Full size image

Linear equations of electrostatics and deformation for piezoceramics can be written as:

$$\begin{array}{c}\left[S\right]=\left[s\right]\left\{T\right\}+\left[d\right]\left\{E\right\}\\ \left[D\right]={\left[d\right]}^{T}\left\{T\right\}+\left[\varepsilon \right]\left\{E\right\}\end{array}$$
(14.4)

where \(\left\{S\right\}, \{T\}\) is strain and stress vectors, \([s]\) is the matrix of elastic compliance, \(\left[d\right]\) is tensor of piezoelectric constants, \(\left[\varepsilon \right]\) is the tensor of the dielectric constants, \(\{E\}\) is vector of electric field strength, \(\left[D\right]\) is vector of electrical induction. In Eq. (14.4), the first equation describes the reverse effect, and the second one describes the direct effect. Since the variables are interconnected in pairs, any pair of mechanical and electrical variables can be selected as independent [7].

The electrical energy of a piezoelectric element is found from the expression:

$${W}_{e}=\frac{1}{2}\underset{\Omega }{\overset{ }{\int }}({\left\{E\right\}}^{T}\left[\varepsilon \right]\left\{E\right\}+2\left\{S\right\}\left[e\right]\left\{E\right\}-{\left\{S\right\}}^{2}\left[c\right]\left\{S\right\})d\Omega$$

For the case of a piezoelectric plate polarized along the \(z\) axis operating on a pure bend \(\left({S}_{1}=-z\omega{^{\prime}}{^{\prime}}\right)\) applied to the beam at the interval \({[x}_{1},{x}_{2}]\) written as:

$${W}_{e}^{*}=\frac{1}{2}{\int }_{0}^{l}{\int }_{A}{({\varepsilon }_{33}E}_{3}^{2}-2\omega {^{\prime}}{^{\prime}}zH\left({x}_{1}^{0},{x}_{2}^{0}\right){e}_{31}{E}_{3}-{c}_{11}{\left(\omega {^{\prime}}{^{\prime}}\right)}^{2})dAdx$$
(14.5)

гдe \({c}_{11}\) is the modulus of elasticity of the piezoelectric ceramics, \({e}_{31}={d}_{31}{c}_{11}\), \(H\left({x}_{1}^{0},{x}_{2}^{0}\right)\) is Heaviside function describing the location of the piezoelectric layer. Applying the Hamilton least action principle for the considered beam the following equation is derived:

$${\int }_{{t}_{0}}^{{t}_{1}}{\int }_{0}^{l}\frac{1}{2}(\rho A\delta {\dot{\omega }}^{2}-{ 2e}_{31}{z}_{m}{b}_{p}(x)H\left({x}_{1}^{0},{x}_{2}^{0}\right)V\delta \omega {^{\prime}}{^{\prime}}+EI\delta {\omega }^{{{\prime}}{^{\prime}}2})dxdt=0$$
(14.6)

where \(V={E}_{3}{h}_{p}\) is the voltage applied to the piezoelectric layer, \({h}_{p}\) is the piezolayer height, \({b}_{p}(x)\) is the width of the electrode plate, in the future we will consider cases of changing the width, so it is accepted \({b}_{p}^{0}=\mathrm{max}({b}_{p}(x))\), also \({b}_{p}\left(x\right)={b}_{p}^{0}\overline{{b }_{p}\left(x\right)},\) \(\overline{{b }_{p}\left(x\right)}\) is a dimensionless function of changing the width of the electrode lining along the length. Thus, a dimensionless model of transverse vibrations of a beam with consideration for friction and an applied piezoelectric layer with an arbitrary shape electrode plate at the interval will take the following form:

$$\ddot{\omega }+\beta K\dot{\omega }+K\omega =\gamma (\overline{{b }_{p}\left(x\right)}H\left({x}_{1},{x}_{2}\right)){^{\prime}}{^{\prime}}U$$
(14.7)

where \(\gamma =l{b}_{p}^{0}{z}_{m}{{e}_{31}V}_{0}/EI\) is a dimensionless coefficient of influence of the piezoelectric layer, \(\left({x}_{1},{x}_{2}\right)=\frac{\left({x}_{1}^{0},{x}_{2}^{0}\right)}{l}\) is the dimensionless interval of the application, \(U\) is the dimensionless voltage applied to the piezoelectric layer that is the control.

$$U=\sum_{i=1}^{m}{\theta }_{i}^{\left(1\right)}{T}_{i}+{\theta }_{i}^{\left(2\right)}{\dot{T}}_{i}$$
(14.8)

where \({\theta }_{i}^{(1)}, {\theta }_{i}^{(2)}\) are the feedback coefficients for movement and speed, respectively, m is the number of the first modes considered.

Quantification of damping design is usually based on the results of solving two problems. The first one is connected with consideration of free oscillations, where the dissipation of the system is manifested in the damping of the oscillations and the decay rate quantifies the dissipative properties of the system. The second task is focused on dealing with forced steady-state oscillation [8]. In addition, the damping of the system’s vibrations is manifested in the restriction of resonant amplitudes. Figure 14.4 shows amplitude history for a piezoelectric layer with an electrode lining distributed along the entire length of the beam (Fig. 14.3).

Fig. 14.4
figure 4

Amplitude history: a free and b forced oscillations of the system

Full size image

From the above amplitude histories of natural and forced vibrations of the beam, with a piezoelectric layer distributed along the entire length, the effect of control is obvious. However, choosing such a feedback with minimal control costs that has the maximum possible amplitude reduction is not a trivial task, and it is obvious that it is more difficult than the task of single-criteria optimization.

14.5 Statement of the Two-Criteria Problem of Control Theory

The need to transfer the problem in point 1 to the problem of control theory is due to the fact that for this problem, the search for an optimal set of solutions with respect to the quenching efficiency criteria (moving the end of the beam and controlled stress), at least for three modes, is extremely cumbersome. Moreover, it is difficult to implement, and the solution by iteration cannot always give optimal solutions. Hence, the system of Eqs. (14.3) reduces to the canonical form of a controlled linear system with two outputs:

$$\begin{array}{c}\dot{T}=AT+{B}_{u}V+{B}_{v}v\\ {z}_{1}=CT\\ {z}_{2}=Du\end{array}$$
(14.9)

where \(T={\left({T}_{1}\dots {T}_{m}, {\dot{T}}_{1}\dots {\dot{T}}_{m}\right)}^{T}\) is the state vector, \(A\) is the control matrix, \({B}_{u}, {B}_{v}\) are the control and perturbation vectors, \(v\) is the external impact on the system, \({z}_{1}, {z}_{2}\) are the output values of the system and indicate the movement of the free end of the beam and the voltage generated by the feedback (quenching efficiency criteria). The theory of linear matrix inequalities and effective algorithms for solving them, implemented in the MATLAB package, is used to find optimal feedback about the two criteria.

Despite the fact that over the past two decades, progress has been made in solving optimal control problems with criteria such as \({H}_{\infty }\)- and \({H}_{2}\)-norms that have correct physical interpretations in the form of levels of damping of deterministic or stochastic perturbations from various classes, the consideration of multi-criteria problems with these criteria causes significant difficulties. These difficulties are mainly related to the complexity of characterization of the Pareto set and finding the corresponding scalar multi-purpose function that would define this set. In addition, the task is complicated by the fact that each of the criteria is characterized by its quadratic Lyapunov function with a matrix which is the solution of Riccati equations or linear matrix inequalities and scalar optimization multi-purpose function in the form of a particular convolution leads in general to a bilinear system of inequalities matrices of these functions that are Lyapunov matrices and controller feedback. To solve such a system, an additional condition was often introduced about the equality of all Lyapunov functions, which introduced conservatism to the problem under consideration [7, 9,10,11,12,13]. At the same time, the main question remained unanswered, as to what extent the obtained control laws differ from the Pareto optimal ones.

In recent works [14,15,16,17,18] on multi-criteria optimization with criteria in the form of \({H}_{\infty }\)-and \({\gamma }_{0}\)-norms in deterministic and stochastic settings, we have found Pareto suboptimal control laws whose relative losses in comparison with Pareto optimal ones do not exceed \(1-\frac{\sqrt{N}}{N}\), where \(N\) is the number of criteria. Therefore, we will use the generalized \({H}_{2}\) norm. [19, 20] Using two competing outputs is associated with bringing the task to practical implementation, since the limited control resource imposes certain restrictions on the feedback values.

For solving two-criterion problem of minimization, it is necessary to use functionality that combines both criteria, generally used for this convolution. In this problem, the Germeyer convolution is implemented, since the solution within the Germeyer convolution for the generalized \({H}_{2}\) -norm gives optimal solutions:

$${J}_{\alpha }\left(\theta \right)=\mathrm{max}\left\{\frac{{J}_{1}\left(\theta \right)}{\alpha };\frac{{J}_{2}\left(\theta \right)}{1-\alpha }\right\}, \alpha \in (\mathrm{0,1})$$
(14.10)

The search for an optimal set of solutions with respect to two criteria is implemented by linear matrix inequalities describing the finding of a generalized \({H}_{2}\)-norm:

$$\left(\begin{array}{cc}AY+Y{A}^{T}+{B}_{u}Z+{Z}^{T}{B}_{u}^{T}& {B}_{v}\\ {B}_{v}^{T}& -I\end{array}\right)<0 \left(\begin{array}{cc}Y& {C}_{\alpha }^{T}\\ {C}_{\alpha }& { {\alpha }^{2} \gamma }^{2}\end{array}\right)\ge 0 \left(\begin{array}{cc}Y& {Z}^{T}{D}_{\alpha }^{T}\\ {D}_{\alpha }Z& {\left(1-\alpha \right)}^{2}{\gamma }^{2}\end{array}\right)\ge 0$$

where \(Z=\theta Y\), \(Y={X}^{-1}\) is the inverse Lyapunov matrix. The result of the solution will be a Pareto set of optimal solutions with respect to the two outputs of the deflection of the end of the beam and the control value, which are found from the expressions:

$$\begin{array}{c}{J}_{1}{=\Vert {H}_{{z}_{1}v}\Vert }_{{g}_{2}}=\underset{v\in {L}_{2}}{\mathrm{sup}}\frac{{\Vert {z}_{1}\left(t\right)\Vert }_{{g}_{\infty }}}{{\Vert v\Vert }_{2}}=\underset{v\in {L}_{2}}{\mathrm{sup}}\frac{{sup}_{t\ge 0}{\left|{z}_{1}\left(t\right)\right|}_{{g}_{\infty }} }{{\Vert v\Vert }_{2}}={\lambda }_{max}^\frac{1}{2}\left(CY{C}^{T}\right)\\ {J}_{2}{=\Vert {H}_{{z}_{2}v}\Vert }_{{g}_{2}}=\underset{v\in {L}_{2}}{\mathrm{sup}}\frac{{\Vert {z}_{2}\left(t\right)\Vert }_{{g}_{\infty }}}{{\Vert v\Vert }_{2}}={\lambda }_{max}^\frac{1}{2}\left(D\theta Y{\theta }^{T}{D}^{T}\right)\end{array}$$
(14.11)

This describes the mathematical apparatus for searching for optimal quenching values, and it is necessary to find a mathematical model of active quenching of a beam by piezoelectric layers with different forms of electrode plates.

14.6 Mathematical Model of Active Damping of a Beam by Piezolelectric Layers of Various Shapes

Let’s consider special cases of application of piezoelectric layers, using the model of active vibration damping of the piezoelectric layer with an arbitrary shape of the electrode lining (14.7) (Figs. 14.5 and 14.6).

Fig. 14.5
figure 5

Application of piezoelectric layers with different shapes of electrode plates: a rectangular, b triangular

Full size image
Fig. 14.6
figure 6

Piezoelectric layer with a triangular electrode plate

Full size image

For a piezoelectric layer with an electrode lining, based on the results obtained using (14.7), we can derive the equation in the main coordinates:

$$\ddot{\omega }+\beta K\dot{\omega }+K\omega =\gamma (-{\delta }^{{\prime}}\left(x-{x}_{1}\right)+{\delta }^{{\prime}}\left(x-{x}_{2}\right))U$$
(14.12)

After the discovery of the piezoelectric effect in the study of the electrical properties of solid dielectrics of the crystal structure, Pierre Curie formulated a general principle, which is now called the Curie principle. Its meaning is that the phenomenon has all the attributes of symmetry that the cause that gave them birth has; the asymmetry of the phenomenon is predetermined by the asymmetry of the cause. If we consider that the piezoelectric material is self-balancing, then the question arises about the behavior of the piezoelectric element for the case of transverse asymmetry. For example, what will be the behavior and influence of the piezoelectric layer when changing the shape of the electrode plates and, consequently, the generated mechanical loads. The shape of the surface electrode plates determines the nature of the mechanical load represented by the piezoelectric layer. Therefore, consider a piezoelectric layer covered with a triangular electrode plate on both sides.

The equations of transverse vibrations of a beam with a triangular overlay are written as follows:

$$\ddot{\omega }+\beta K\dot{\omega }+K\omega =\gamma (-{\delta }^{{\prime}}\left(x-{x}_{1}\right)-\frac{l}{{l}_{p}}\delta \left(x-{x}_{1}\right)+\frac{l}{{l}_{p}}\delta \left(x-{x}_{2}\right))U$$
(14.13)

Thus, piezoelectric layers, depending on the shape of the plates when applying voltage, can be described as mechanical loads that are controlled by an external energy source with a limited resource:

$$\begin{array}{c}{\ddot{T}}_{i}+\beta {\lambda }_{i}^{4}{\dot{T}}_{i}+{\lambda }_{i}^{4}{T}_{i}=-{M}_{p}{X}_{i}^{{\prime}}\left(1\right)U+v\left(t\right)\\ {\ddot{T}}_{i}+\beta {\lambda }_{i}^{4}{\dot{T}}_{i}+{\lambda }_{i}^{4}{T}_{i}=-{M}_{p}\left({X}_{i}^{^{\prime}}\left({x}_{2}\right)-{X}_{i}^{^{\prime}}\left({x}_{1}\right)\right)U+v\left(t\right)\\ {\ddot{T}}_{i}+\beta {\lambda }_{i}^{4}{\dot{T}}_{i}+{\lambda }_{i}^{4}{T}_{i}=-{(F}_{p}\left({X}_{i}\left({x}_{2}\right)-{X}_{i}\left({x}_{1}\right)\right)-{M}_{p}{X}_{i}^{^{\prime}}\left({x}_{1}\right))U+v(t)\end{array}$$
(14.14)

where the first equation describes the behavior of a piezoelectric layer evenly distributed along the entire length of the beam (Fig. 14.7a), a kind of the most efficient and limiting case, the second and third equations describe the behavior of a piezoelectric layer with rectangular and triangular facings, respectively (Fig. 14.7b, c).

Fig. 14.7
figure 7

Mechanical loads of piezolayers with different plates: a distributed along the entire length; b rectangular and c triangular forms of electrode plates

Full size image

14.7 Results

All calculations were given for the coefficient γ = 0.0516, (see (14.7)). In Fig. 14.8 optimal sets of solutions for the criteria are given.

Fig. 14.8
figure 8

Optimal Pareto sets of solutions

Full size image

Judging by the optimal Pareto sets, the efficiency of a piezo layer with a rectangular lining is higher than that of a triangular one in both operating modes. It would seem that it is possible to talk about the inefficient use of a piezo layer with a triangular lining for the tasks of active damping of the cantilever beam, but the following is an amplitude history for both cases of operation with respect to forced vibrations of the system (Fig. 14.9).

Fig. 14.9
figure 9

Amplitude history: a at the limit and b at the operating voltage

Full size image

From amplitude history obviously, when an operating voltage (Fig. 14.9a) the difference between amplitude history for different plates is minimal, but extreme voltage differences amplitude history (Fig. 14.9b) has more noticeable, but still not much. It is worth noting that the length of the piezoelectric layers was 5 times less than the length of the beam, and the thickness of the layers is less by an order of magnitude. That is, when using thin piezoelectric layers, it is possible to reduce significantly the amplitude of vibrations in the case of external influence on the cantilever metal beam, both for the case of the limit voltage of the piezoelectric layer and for the operating voltage.

14.8 Conclusions

The use of piezoelectric layers in the system of active vibration damping of a cantilever beam is considered. To solve the problem of the efficiency of using piezoelectric layers as an active damping device, two related criteria are introduced: the level of voltage applied to the piezoelectric layer and the level of deflection of the beam end. A comparison was made with respect to the selected criteria for rectangular and triangular forms of plates, which were compared with a variant of a piezo layer evenly distributed over the entire length.

Based on the Hamilton Principle, the influence of the electrode shape on the generation of various mechanical loads by the piezoelectric layer was derived (14.7). It was found that with respect to two Pareto criteria, the efficiency of a piezoelectric plate of standard sizes with a rectangular shape of the electrode plate shows a better result compared to a triangular plate.