Semantic Characterizations of AGM Revision for Tarskian Logics

Abstract

Given the increasingly dynamic nature of knowledge in the era of Web-based information exchange, techniques to revise recorded knowledge – such as knowledge graphs or ontologies – with respect to new findings are more important than ever. For knowledge representation approaches based on formal logics, the AGM belief revision postulates by Alchourrón, Gärdenfors, and Makinson continue to represent a cornerstone in research related to belief change. Katsuno and Mendelzon (K &M) adopted the AGM postulates for changing belief bases and characterized AGM belief base revision in propositional logic over finite signatures. We generalize K &M’s approach to (multiple) base revision in arbitrary Tarskian logics, covering all logics with a classical model-theoretic semantics and hence a wide variety of logics used in knowledge representation and beyond. Our generic formulation applies to various notions of “base”; such as belief sets, arbitrary or finite sets of sentences, or single sentences. The core result is a representation theorem showing a two-way correspondence between AGM base revision operators and certain “assignments”: functions mapping belief bases to total — yet not transitive — “preference” relations between interpretations. We also provide a characterization of all Tarskian logics for which our result can be strengthened to assignments producing transitive preference relations as in K &M’s original work.

1 Introduction

The question of how a rational agent should change her beliefs in the light of new information is crucial to AI systems. It gave rise to the area of belief change, which has been massively influenced by the AGM paradigm of Alchourrón, Gärdenfors, and Makinson [2]. The AGM theory assumes that an agent’s beliefs are represented by a deductively closed set of sentences (commonly referred to as a belief set). A change operator for belief sets is required to satisfy appropriate postulates in order to qualify as a rational change operator. While the contribution of AGM is widely accepted as solid and inspiring foundation, it lacks support for certain relevant aspects: it provides no immediate solution on how to deal with multiple inputs (i.e., several sentences instead of just one), with bases (i.e., arbitrary collections of sentences, not necessarily deductively closed), or with the problem of iterated belief changes.

Katsuno and Mendelzon [14] – henceforth abbreviated K &M – deal with the issues of belief bases and multiple inputs in an elegant way: as in propositional logic, every set of sentences (including an infinite one) is equivalent to one single sentence, belief states and multiple inputs are considered as such single sentences. In this setting, K &M provide the following set of postulates, derived from the AGM revision postulates, where $\varphi ,\varphi _1,\varphi _2,\alpha$, and $\beta$ are propositional sentences, and $\circ$ is a base change operator:

• (KM1) $\varphi \circ \alpha \models \alpha$.

• (KM2) If $\varphi \wedge \alpha$ is consistent, then $\varphi \circ \alpha \equiv \varphi \wedge \alpha$.

• (KM3) If $\alpha$ is consistent, then $\varphi \circ \alpha$ is consistent.

• (KM4) If $\varphi _1 \equiv \varphi _2$ and $\alpha \equiv \beta$, then $\varphi _1 \circ \alpha \equiv \varphi _2 \circ \beta$.

• (KM5) $(\varphi \circ \alpha ) \wedge \beta \models \varphi \circ (\alpha \wedge \beta )$.

• (KM6) If $(\varphi \circ \alpha ) \wedge \beta$ is consistent, then $\varphi \circ (\alpha \wedge \beta ) \models (\varphi \circ \alpha ) \wedge \beta$.

The postulates (KM1)–(KM6) together are equivalent to the AGM revision postulates, thus they also yield minimal change with respect to the initial beliefs. Note that, in this setting, the semantic content of the revision result is fully determined by the semantic contents of the prior base and the new incoming information; syntactic variations are irrelevant. This sets K &M’s approach apart from other prominent lines of work, where revision is performed on a syntactic level and thus the syntactic form of the input may have a semantic effect on the result. A prominent example for such syntactic approaches is base change according to Hansson [13].

While the AGM paradigm is axiomatic, much of its success originated from operationalizations via representation theorems. Yet, most existing characterizations of AGM revision impose additional assumptions on the underlying logic such as compactness, closure under standard connectives, deduction, or supra-classicality [22]. Leaving the safe grounds of these assumptions complicates matters; representation theorems do not easily generalize to arbitrary logics. This has sparked investigations into tailored characterizations of AGM belief change for specific logics, such as Horn logic [6], temporal logics [3], action logics [25], first-order logic [28], and description logics [8, 12, 19]. More general approaches to revision in non-classical logics were given by Ribeiro, Wassermann, and colleagues [20,21,22], Delgrande, Peppas, and Woltran [7], Pardo, Dellunde, and Godo [17], or Aiguier et al. [1].

In this article, we consider (multiple) base revision in arbitrary Tarskian logics, i.e., logics exhibiting a classically defined model theory. We thereby refine and generalize the popular approach by Katsuno and Mendelzon [14] which was tailored to belief base revision in propositional logic with a finite signature. K &M start out from belief bases, assigning to each a total preorder on the interpretations, which expresses – intuitively speaking – which interpretation is “closer to being a model”. The models of the result of any AGM revision then coincide with the preferred (i.e., preorder-minimal) models of the injected information.

We consider base revision in base logics, which provides an abstraction that elegantly captures different notions of bases. Our approach extends the idea of preferences over interpretations from the propositional to the general setting of Tarskian logics. This requires to adjust the nature of the assignments indicating the degree of model-alikeness: We have to explicitly require that minimal models always exist (min-completeness) and that they can be described in the logic (min-expressibility). Moreover, we show that demanding preference relations to be preorders is infeasible in the general setting; we have to waive transitivity and retain only a weaker property (min-retractivity).

The main contributions of this article are the following:

• We introduce the notion of base logics to uniformly capture various popular ways of defining belief states by certain sets of sentences over Tarskian logics. Among others, this includes the cases where belief states are arbitrary sets of sentences and where belief states are belief sets.

• We extend K &M’s semantic approach from the setting of singular base revision in propositional logic to multiple base revision in arbitrary base logics.

• For this setting, we provide a representation theorem characterizing AGM belief change operators via appropriate assignments.

• We characterize all those logics for which every AGM operator can even be captured by preorder assignments (i.e., in the classical K &M way). In particular, this condition applies to all logics supporting disjunction and hence all classical logics. For those logics, we provide one representation theorem for the syntax-independent and one for the syntax-dependent setting.

Detailed proofs, illustrative examples and comprehensive discussions on related aspects can be found in the extended online version of the paper [9].

2 Preliminaries

In this section, we introduce the logical and algebraic notions used in the paper.

2.1 Logics with Classical Model-Theoretic Semantics

We consider logics endowed with a classical model-theoretic semantics. The syntax of such a logic $\mathbb {L}$ is given syntactically by a (possibly infinite) set $\mathcal {L}$ of sentences, while its model theory is provided by specifying a (potentially infinite) class ${\Omega }$ of interpretations (also called worlds) and a binary relation $\models$ between ${\Omega }$ and $\mathcal {L}$ where $\omega \models \varphi$ indicates that $\omega$ is a model of $\varphi$. Hence, a logic $\mathbb {L}$ is identified by the triple $(\mathcal {L},\Omega ,\models )$. We let $\llbracket \varphi \rrbracket = \{\omega \in {\Omega } \mid \omega \models \varphi \}$ denote the set of all models of $\varphi \in \mathcal {L}$. Logical entailment is defined as usual (overloading “$\models$") via models: for two sentences $\varphi$ and $\psi$ we say $\varphi$ entails $\psi$ (written $\varphi \models \psi$) if $\llbracket \varphi \rrbracket \subseteq \llbracket \psi \rrbracket$.

Notions of modelhood and entailment are easily lifted from single sentences to sets. We obtain the models of a set $\mathcal {K}\subseteq \mathcal {L}$ of sentences via $\llbracket \mathcal {K}\rrbracket = \bigcap _{\varphi \in \mathcal {K}} \llbracket \varphi \rrbracket$. For $\mathcal {K}\subseteq \mathcal {L}$ and $\mathcal {K}' \subseteq \mathcal {L}$ we say $\mathcal {K}$ entails $\mathcal {K}'$ (written $\mathcal {K}\models \mathcal {K}'$) if $\llbracket \mathcal {K}\rrbracket \subseteq \llbracket \mathcal {K}'\rrbracket$. We write $\mathcal {K}\equiv \mathcal {K}'$ to express $\llbracket \mathcal {K}\rrbracket =\llbracket \mathcal {K}'\rrbracket$. A (set of) sentence(s) is called consistent with another (set of) sentence(s) if the two have models in common. Unlike many other belief revision frameworks, we impose no further requirements on $\mathcal {L}$ (like closure under certain operators or compactness).

The existence of such a classical model-theoretic semantics ensures that the logic is Tarskian, meaning that taking all consequences is a closure operator [24, 26], which also implies the monotonicity condition: $\text {if } \mathcal {K}_1 \models \varphi \text { and } \mathcal {K}_1 \subseteq \mathcal {K}_2 \text {, then } \mathcal {K}_2 \models \varphi$. Besides many well-known classical logics, the model-theoretic framework assumed by us captures many more (and more expressive) logics, e.g. first-order and second-order predicate logic, modal logics, and description logics. Our considerations do, however, not apply to non-monotonic formalisms, such as default logic, circumscription, or logic programming using negation as failure.

2.2 Relations over Interpretations

For describing belief revision on the semantic level, it is purposeful to endow the interpretation space ${\Omega }$ with some structure. In particular, we will employ binary relations $\preceq$ over ${\Omega }$ (formally: ${\preceq } \subseteq \Omega \times \Omega$), where the intuitive meaning of $\omega _1\preceq \omega _2$ is that $\omega _1$ is “equally good or better” than $\omega _2$ when it comes to serving as a model. We call $\preceq$ total if $\omega _1\preceq \omega _2$ or $\omega _2\preceq \omega _1$ for any $\omega _1,\omega _2 \in {\Omega }$ holds. We write $\omega _1\prec \omega _2$ as a shorthand, whenever $\omega _1 \preceq \omega _2$ and $\omega _2 \not \preceq \omega _1$ (the intuition being that $\omega _1$ is “strictly better” than $\omega _2$). For a selection $\Omega ' \subseteq {\Omega }$ of interpretations, an $\omega \in \Omega '$ is called $\preceq$-minimal in $\Omega '$ if $\omega \preceq \omega '$ for all $\omega '\in \Omega '$.¹ We let $\min (\Omega ',\preceq )$ denote the set of $\preceq$-minimal interpretations in $\Omega '$. We call $\preceq$ a preorder if it is transitive and reflexive.

2.3 Bases

This article addresses the AGM revision of and by bases. In the belief revision community, the term of base commonly denotes an arbitrary (possibly infinite) set of sentences [10]. However, in certain scenarios, other assumptions might be more appropriate. Hence, for the sake of generality, we decided to define the notion of a base on an abstract level with minimal requirements (just as we introduced our notion of logic), allowing for its instantiation in many ways.

Definition 1

A base logic is a quintuple $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup ),$ where

• $(\mathcal {L},\Omega ,\models )$ is a logic,

• $\mathfrak {B}\subseteq \mathcal {P}(\mathcal {L})$ is a family of sets of sentences, called bases, and

• $\Cup : \mathfrak {B}\times \mathfrak {B}\rightarrow \mathfrak {B}$ is a binary operator over bases, called the abstract union, satisfying $\llbracket \mathcal {B}_1 \Cup \mathcal {B}_2\rrbracket = \llbracket \mathcal {B}_1\rrbracket \cap \llbracket \mathcal {B}_2\rrbracket$.

Next, we will demonstrate how, for some logic $\mathbb {L}=(\mathcal {L},\Omega ,\models )$, a corresponding base logic can be chosen depending on one’s preferred notion of base.

Arbitrary Sets. If all (finite and infinite) sets of sentences should qualify as bases, one can simply set $\mathfrak {B}= \mathcal {P}(\mathcal {L})$. In that case, $\Cup$ can be instantiated by set union $\cup$, then the claimed behavior follows by definition.

Finite Sets. In some settings, it is more convenient to assume bases to be finite (e.g. when computational properties or implementations are to be investigated). In such cases, one can set $\mathfrak {B}= \mathcal {P}_\textrm{fin}(\mathcal {L})$, i.e., all (and only) the finite sets of sentences are bases. Again, $\Cup$ can be instantiated by set union $\cup$ (as a union of two finite sets will still be finite).

Belief Sets. This setting is closer to the original framework, where the “knowledge states” to be modified were assumed to be deductively closed sets of sentences. We can capture such situations by accordingly letting $\mathfrak {B}= \{ \mathcal {B}\subseteq \mathcal {L} \mid \forall \varphi \in \mathcal {L}: \mathcal {B}\models \varphi \Rightarrow \varphi \in \mathcal {B}\}$. In this case, the abstract union operator needs to be defined via $\mathcal {B}_1 \Cup \mathcal {B}_2 = \{\varphi \in \mathcal {L} \mid \mathcal {B}_1 \cup \mathcal {B}_2 \models \varphi \}$.

Single Sentences. In this popular setting, one prefers to operate on single sentences only (rather than on proper collections of those). For this to work properly, an additional assumption needs to be made about the underlying logic $\mathbb {L}=(\mathcal {L},\Omega ,\models )$: it must be possible to express conjunction on a sentence level, either through the explicit presence of the Boolean operator $\wedge$ or by some other means. Formally, we say that $\mathbb {L}=(\mathcal {L},\Omega ,\models )$ supports conjunction, if for any two sentences $\varphi , \psi \in \mathcal {L}$ there exists some sentence satisfying (if $\wedge$ is available within the logic, we would simply have ). For such a logic, we can “implement” the single-sentence setting by letting $\mathfrak {B}= \{ \{\varphi \} \mid \varphi \in \mathcal {L} \}$ and defining .

For any of the four different notions of bases, one can additionally choose to disallow or allow the empty set as a base, while maintaining the required closure under abstract union. In the following, we will always operate on the abstract level of “base logics”; our notions, results and proofs will only make use of the few general properties specified for these. This guarantees that our results are generically applicable to any of the four described (and any other) instantiations, and hence, are independent of the question what the right notion of bases ought to be. The cognitive overload caused by this abstraction should be minimal; e.g., readers only interested in the case of arbitrary sets can safely assume $\mathfrak {B}= \mathcal {P}(\mathcal {L})$ and mentally replace any $\Cup$ by $\cup$.

2.4 Base Change Operators

In this paper, we use base change operators to model multiple revision, which is the process of incorporating multiple new beliefs into the present beliefs held by an agent, in a consistent way (whenever that is possible). We define change operators over a base logic as follows.

Definition 2

Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic. A function $\circ : \mathfrak {B}\times \mathfrak {B}\rightarrow \mathfrak {B}$ is called a multiple base change operator over $\mathbb {B}$.

We will use multiple base change operators in the “standard” way of the belief change community: the first parameter represents the actual beliefs of an agent, the second parameter contains the new beliefs. The operator then yields the agent’s revised beliefs. The term “multiple” references the fact that the second input to $\circ$ is not just a single sentence, but a belief base that may consist of several sentences. For convenience, we will henceforth drop the term “multiple” and simply speak of base change operators instead.

So far, the pure notion of base change operator is unconstrained and can be instantiated by an arbitrary binary function over bases. Obviously, this does not reflect the requirements or expectations one might have when speaking of a revision operator. Hence, in line with the traditional approach, we will consider additional constraints (called “postulates”) for base change operators, in order to capture the gist of revisions.

2.5 Postulates for Revision

We consider multiple revision, focusing on package semantics for revision, which is that all given sentences have to be incorporated, i.e. given a base $\mathcal {K}$ and new information $\Gamma$ (also a base here), we demand success of revision, i.e. $\mathcal {K}\circ \Gamma \models \Gamma$.

Besides the success condition, the belief change community has brought up and discussed several further requirements for belief change operators to make them rational [10, 13]. This has led to the now famous AGM approach of revision [2], originally proposed through a set of rationality postulates, which correspond to the postulates (KM1)–(KM6) by K &M presented in the introduction. In our article, we will make use of the K &M version of the AGM postulates adjusted to our generic notion of a base logic $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$:

• (G1) $\mathcal {K}\circ \Gamma \models \Gamma$.

• (G2) If $\llbracket \mathcal {K}\Cup \Gamma \rrbracket \ne \emptyset$ then $\mathcal {K}\circ \Gamma \equiv \mathcal {K}\Cup \Gamma$.

• (G3) If $\llbracket \Gamma \rrbracket \ne \emptyset$ then $\llbracket \mathcal {K}\circ \Gamma \rrbracket \ne \emptyset$.

• (G4) If $\mathcal {K}_1 \equiv \mathcal {K}_2$ and $\Gamma _1 \equiv \Gamma _2$ then $\mathcal {K}_1 \circ \Gamma _1 \equiv \mathcal {K}_2 \circ \Gamma _2$.

• (G5) $(\mathcal {K}\circ \Gamma _1)\Cup \Gamma _2 \models \mathcal {K}\circ (\Gamma _1\Cup \Gamma _2)$.

• (G6) If $\llbracket (\mathcal {K}\circ \Gamma _1)\Cup \Gamma _2\rrbracket \ne \emptyset$ then $\mathcal {K}\circ (\Gamma _1\Cup \Gamma _2) \models (\mathcal {K}\circ \Gamma _1)\Cup \Gamma _2$.

Together, the postulates implement the paradigm of minimal change, stating that a rational agent should change her beliefs as little as possible in the process of belief revision. We consider the postulates in more detail: (G1) guarantees that the newly added belief must be a logical consequence of the result of the revision. (G2) says that if the expansion of $\mathcal {K}$ by $\Gamma$ is consistent, then the result of the revision is equivalent to the expansion of $\mathcal {K}$ by $\Gamma$. (G3) guarantees the consistency of the revision result if the newly added belief is consistent. (G4) is the principle of the irrelevance of the syntax, stating that the revision operation is independent of the syntactic form of the bases. (G5) and (G6) ensure more careful handling of (abstract) unions of belief bases. In particular, together, they enforce that $\mathcal {K}\circ (\Gamma _1\Cup \Gamma _2) \equiv (\mathcal {K}\circ \Gamma _1)\Cup \Gamma _2$, unless $\Gamma _2$ contradicts $\mathcal {K}\circ \Gamma _1$.

We can see that, item by item, (G1)–(G6) tightly correspond to (KM1)–(KM6) presented in the introduction. Note also that further formulations similar to (G1)–(G6) are given in multiple particular contexts, e.g. in the context of belief base revision specifically for Description Logics [19], for parallel revision [5] and investigations on multiple revision [15, 18, 27]. An advantage of the specific form of the postulates (G1)–(G6) chosen for our presentation is that it does not require $\mathcal {L}$ to support conjunction (while, of course, conjunction on the sentence level is still implicitly supported via (abstract) union of bases).

3 Base Revision in Propositional Logic

A well-known and by now popular characterization of base revision has been described by Katsuno and Mendelzon [14] for the special case of propositional logic. To be more specific and apply our terminology, K &M’s approach applies to the base logic

$$\begin{aligned} \mathbb{P}\mathbb{L}_n = (\mathcal {L}_{\mathbb{P}\mathbb{L}_n},\Omega _{\mathbb{P}\mathbb{L}_n},\models _{\mathbb{P}\mathbb{L}_n},\mathcal {P}_{\textrm{fin}}(\mathcal {L}_{\mathbb{P}\mathbb{L}_n}),\cup ) \end{aligned}$$

for arbitrary, but fixed n, where $\mathcal {L}_{\mathbb{P}\mathbb{L}_n}$ contains all propositional formulae over the atom set $\{p_1,\ldots ,p_n\}$ and $\Omega _{\mathbb{P}\mathbb{L}_n}$ consists of all functions mapping $\{p_1,\ldots ,p_n\}$ to $\{\textbf{true},\textbf{false}\}$ and $\models _{\mathbb{P}\mathbb{L}_n}$ is the usual satisfaction relation of propositional logic. The requirement that the number of propositional atoms must be finite is not overtly explicit in K &M’s paper, but it becomes apparent upon investigating their arguments and proofs, and their characterization fails as soon as this assumption is dropped. K &M’s approach also hinges on other particularities of this setting: As discussed earlier, any propositional belief base $\mathcal {K}$ can be equivalently written as a single propositional sentence. Consequently, in their approach, belief bases are actually represented by single sentences, without loss of expressivity.

One key contribution of K &M is to provide an alternative characterization of the propositional base revision operators satisfying (KM1)–(KM6) by model-theoretic means, i.e. through comparisons between propositional interpretations. We next present their results in a formulation that facilitates later generalization. One central notion for the characterization is the notion of faithful assignment.

Definition 3 (assignment, faithful)

Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic. An assignment for $\mathbb {B}$ is a function that assigns to each belief base $\mathcal {K}\in \mathfrak {B}$ a total binary relation $\preceq _{\mathcal {K}}$ over ${\Omega }$. An assignment for $\mathbb {B}$ is called faithful if it satisfies the following conditions for all $\omega ,\omega '\in \Omega$ and all $\mathcal {K},\mathcal {K}'\in \mathfrak {B}$:

• (F1) If $\omega ,\omega ' \models \mathcal {K}$, then $\omega \prec _{\mathcal {K}}\omega '$ does not hold.

• (F2) If $\omega \models \mathcal {K}$ and $\omega '\not \models \mathcal {K}$, then $\omega \prec _{\mathcal {K}}\omega '$.

• (F3) If $\mathcal {K}\equiv \mathcal {K}'$, then ${\preceq _{\mathcal {K}}} = \preceq _{\mathcal {K'}}$.

An assignment is called a preorder assignment if $\preceq _{\mathcal {K}}$ is a preorder for every $\mathcal {K}\in \mathfrak {B}$.

Intuitively, faithful assignments provide information about which of the two interpretations is “closer to $\mathcal {K}$-modelhood”. Consequently, the actual $\mathcal {K}$-models are $\preceq _{\mathcal {K}}$-minimal. The next definition captures the idea of an assignment adequately representing the behaviour of a revision operator.

Definition 4 (compatible)

Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ a base logic. A base change operator $\circ$ for $\mathbb {B}$ is called compatible with some assignment for $\mathbb {B}$ if it satisfies $\llbracket \mathcal {K}\circ {\Gamma }\rrbracket = \min (\llbracket \Gamma \rrbracket ,\preceq _{\mathcal {K}})$ for all bases $\mathcal {K}$ and ${\Gamma }$ from $\mathfrak {B}$.

With these notions in place, K &M’s representation result can be smoothly expressed as follows:

Theorem 1

(Katsuno and Mendelzon [14]). A base change operator $\circ$ for $\mathbb{P}\mathbb{L}_n$ satisfies (G1)–(G6) if and only if it is compatible with some faithful preorder assignment for $\mathbb{P}\mathbb{L}_n$.

In the next section, we discuss and provide a generalization of this characterization to the setting of arbitrary base logics.

4 Approach for Arbitrary Base Logics

In this section, we prepare our main result by revisiting K &M’s concepts for propositional logic and investigating their suitability for our general setting of base logics. The result by Katsuno and Mendelzon established an elegant combination of the notions of preorder assignments, faithfulness, and compatibility in order to semantically characterize AGM base change operators. However, as we mentioned before, K &M’s characterization hinges on features of signature-finite propositional logic that do not generally hold for Tarskian logics. Here we go further, by extending the K &M approach by novel notions to the very general setting of base logics.

4.1 First Problem: Non-existence of Minima

The first issue with K &M’s original characterization when generalizing to arbitrary base logics is the possible absence of $\preceq _\mathcal {K}$-minimal elements in $\llbracket \Gamma \rrbracket$: for arbitrary base logics, the minimum from Definition 4, required in Theorem 1, might be empty. To remedy this problem, one needs to impose the requirement that minima exist whenever needed, as specified in the notion of min-completeness, defined next.

Definition 5

(min-complete). Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic. A binary relation $\preceq$ over ${\Omega }$ is called min-complete (for $\mathbb {B}$) if $\min (\llbracket \Gamma \rrbracket ,\preceq ) \not = \emptyset$ holds for every $\Gamma \in \mathfrak {B}$ with $\llbracket \Gamma \rrbracket \not = \emptyset$.

In the special case of $\preceq$ being transitive and total, min-completeness trivially holds whenever ${\Omega }$ is finite (as, e.g., in the case of propositional logic over n propositional atoms). In the infinite case, however, it might need to be explicitly imposed, as already noted in earlier works [7] (cf. also the notion of limit assumption by Lewis [16]). Note that min-completeness does not entirely disallow infinite descending chains (as well-foundedness would), it only ensures that minima exist inside all model sets of consistent belief bases.

4.2 Second Problem: Transitivity of Preorder

When generalizing from the setting of propositional to arbitrary base logics, the requirement that assignments must produce preorders (and hence transitive relations) turns out to be too restrictive.

In fact, it has been observed before that the incompatibility between transitivity and K &M’s approach already arises for propositional Horn logic [6]. As a consequence, we cannot help but waive transitivity (and hence the property of the assignment providing a preorder) if we want our characterization result to hold for all Tarskian logics. However, for our result, we need to retain a new, weaker property (which is implied by transitivity) defined next.

Definition 6

(min-retractive). Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic. A binary relation $\preceq$ over ${\Omega }$ is called min-retractive (for $\mathbb {B}$) if, for every $\Gamma \in \mathfrak {B}$ and $\omega ',\omega \in \llbracket \Gamma \rrbracket$ with $\omega '\preceq \omega$, $\omega \in \min (\llbracket \Gamma \rrbracket ,\preceq )$ implies $\omega '\in \min (\llbracket \Gamma \rrbracket ,\preceq )$.

We conveniently unite the two identified properties into one notion.

Definition 7

(min-friendly). Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic. A binary relation $\preceq$ over ${\Omega }$ is called min-friendly (for $\mathbb {B}$) if it is both min-retractive and min-complete. An assignment is called min-friendly if $\preceq _{\mathcal {K}}$ is min-friendly for all $\mathcal {K}\in \mathfrak {B}$.

5 One-way Representation Theorem

We are now ready to generalize K &M’s representation theorem from propositional to arbitrary Tarskian logics, by employing the notion of compatible min-friendly faithful assignments.

Theorem 2

Let $\circ$ be a base change operator for some base logic $\mathbb {B}$. Then, $\circ$ satisfies (G1)–(G6) if and only if it is compatible with some min-friendly faithful assignment for $\mathbb {B}$.

For the “if” direction, we show that the notion of min-friendly compatible assignment is sufficient to enforce that any compatible base revision operator satisfies (G1)–(G6).

For the more involved “only if” direction, we provide a canonical way of obtaining an assignment for a given revision operator and show that our construction indeed yields a compatible min-friendly faithful assignment. To this end, we suggest the following construction, which we consider one of this paper’s core contributions. It realizes the idea that one should (strictly) prefer $\omega _1$ over $\omega _2$ only if there is a witness belief base $\Gamma$ that certifies that $\circ$ prefers $\omega _1$ over $\omega _2$. Should no such witness exist, $\omega _1$ and $\omega _2$ will be deemed equally preferable.

Definition 8

Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic, let $\circ$ be a base change operator for $\mathbb {B}$ and let $\mathcal {K}\in \mathfrak {B}$ be a belief base. The relation $\sqsubseteq ^\circ _{\mathcal {K}}$ over ${\Omega }$ is defined by $\omega _1 \sqsubseteq ^\circ _{\mathcal {K}}\omega _2 \ \ \text { if }\ \omega _2 \models \mathcal {K}\circ \Gamma \text { implies } \omega _1 \models \mathcal {K}\circ \Gamma \text { for all } \Gamma \in \mathfrak {B}\text { with } \omega _1,\omega _2\in \llbracket \Gamma \rrbracket$.

Definition 8 already yields an adequate encoding strategy for many base logics. However, to also properly cope with certain “degenerate” base logics, we have to hard-code that the prior beliefs of an agent are prioritized in all cases, that is, only models of the prior beliefs are minimal. The following relation builds upon the relation $\sqsubseteq ^\circ _{\mathcal {K}}$ and takes explicit care of handling prior beliefs, which is strong enough for always obtaining a relation that is total and reflexive.

Definition 9

Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic, let $\circ$ be a base change operator for $\mathbb {B}$ and let $\mathcal {K}\in \mathfrak {B}$ be a belief base. The relation $\preceq ^\circ _{\mathcal {K}}$ over ${\Omega }$ is then defined by $\omega _1 \preceq ^\circ _{\mathcal {K}}\omega _2 \ \ \text { if } \ \omega _1 \models \mathcal {K}\text { or } \left( \ \omega _1,\omega _2 \not \models \mathcal {K}\text { and } \omega _1 \sqsubseteq ^\circ _{\mathcal {K}}\omega _2 \ \right)$. Let denote the mapping $\mathcal {K}\mapsto {\preceq ^\circ _{\mathcal {K}}}$.

6 Two-way Representation Theorem

Theorem 2 establishes the correspondence between operators and assignments under the assumption that $\circ$ is given and therefore known to exist. What remains unsettled is the question if generally every min-friendly faithful assignment is compatible with some base change operator that satisfies (G1)–(G6). As this is not the case, a full, two-way correspondence, requires an additional condition on assignments, capturing operator existence. More specifically, it is essential that any minimal model set of a belief base obtained from an assignment corresponds to some belief base, a property which is formalized by the following notion.

Definition 10

(min-expressible). Let $\mathbb {B} = (\mathcal {L},\Omega ,\models ,\mathfrak {B},\Cup )$ be a base logic. A binary relation $\preceq$ over ${\Omega }$ is called min-expressible if for each $\Gamma \in \mathfrak {B}$ there exists a belief base $\mathcal {B}_{\Gamma ,\preceq } \in \mathfrak {B}$ such that $\llbracket \mathcal {B}_{\Gamma ,\preceq }\rrbracket \,{=}\, \min (\llbracket \Gamma \rrbracket ,\preceq )$. An assignment will be called min-expressible, if for each $\mathcal {K}\in \mathfrak {B}$, the relation $\preceq _{\mathcal {K}}$ is min-expressible. Given a min-expressible assignment , let denote the base change operator defined by .

It should be noted that min-expressibility is a straightforward generalization of the notion of regularity by Delgrande and colleagues [7] to base logics. By virtue of this extra notion, we now find the following bidirectional relationship between assignments and operators, amounting to a full characterization.

Theorem 3

Let $\mathbb {B}$ be a base logic. Then the following hold:

• Every base change operator for $\mathbb {B}$ satisfying (G1)–(G6) is compatible with some min-expressible min-friendly faithful assignment.

• Every min-expressible min-friendly faithful assignment for $\mathbb {B}$ is compatible with some base change operator satisfying (G1)–(G6).

As an aside, note that the above theorem also implies that every min-expressible min-friendly faithful assignment is compatible only with AGM base change operators. This is because, one the one hand, any such assignment fully determines the corresponding compatible base change operator model-theoretically and, on the other hand, (G1)–(G6) are purely model-theoretic conditions.

7 Total-Preorder-Representability

As we have shown, regrettably, not every AGM belief revision operator in every Tarskian logic can be described by a total preorder assignment. Yet, we also saw that, for some logics (like $\mathbb{P}\mathbb{L}_n)$, this correspondence does indeed hold. Consequently, this section is dedicated to finding a characterization of precisely those logics wherein every AGM base change operator is representable by a compatible min-complete faithful preorder assignment. The following definition captures the notion of operators that are well-behaved in that sense.

Definition 11

(total-preorder-representable). A base change operator $\circ$ for some base logic is called total-preorder-representable if there is a min-complete faithful preorder assignment compatible with $\circ$.

Recall that transitivity implies min-retractivity, and thus, every min-complete preorder is automatically min-friendly. The following definition describes the occurrence of a certain relationship between several bases. Such an occurrence will turn out to be the one and only reason to prevent total-preorder-representability.

Definition 12

(critical loop). Let $\mathbb {B}=(\mathcal {L},{\Omega },\models ,\mathfrak {B},\Cup )$ be a base logic. Three or more bases $\Gamma _{0,1},\Gamma _{1,2},\ldots ,\Gamma _{n,0} \in \mathfrak {B}$ are said to form a critical loop of length $(n+1)$ if there are a base $\mathcal {K}\in \mathfrak {B}$ and consistent bases $\Gamma _0,\ldots ,\Gamma _n \in \mathfrak {B}$ such that

• (1) $\llbracket \mathcal {K}\Cup \Gamma _{i,i \oplus 1}\rrbracket = \emptyset$ for every $i\in \{0,\ldots ,n\}$, where $\oplus$ is addition ${\textrm{mod}\, (n+1)}$,

• (2) $\llbracket \Gamma _{i}\rrbracket \cup \llbracket \Gamma _{i \oplus 1}\rrbracket \subseteq \llbracket \Gamma _{i,i\oplus 1}\rrbracket$ and $\llbracket \Gamma _{j}\Cup \Gamma _{i}\rrbracket = \emptyset$ for each $i,j\in \{0,\ldots ,n\}$ with $i \ne j$, and

• (3) for each $\Gamma _{\!\!\triangledown }\in \mathfrak {B}$ that is consistent with at least three bases from $\Gamma _{0}, \ldots , \Gamma _{n}$, there is a $\Gamma _{\!\!\triangledown }' \in \mathfrak {B}$ such that $\llbracket \Gamma _{\!\!\triangledown }'\rrbracket \ne \emptyset$ and $\llbracket \Gamma _{\!\!\triangledown }'\rrbracket \subseteq \llbracket \Gamma _{\!\!\triangledown }\rrbracket \setminus \left( \llbracket \Gamma _{0,1}\rrbracket \cup \ldots \cup \llbracket \Gamma _{n,0}\rrbracket \right)$.

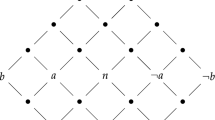
The three conditions in Definition 12, illustrated in Fig. 1, describe the canonic situation brought about by some bases $\Gamma _{0,1},\ldots ,\Gamma _{n,0}$ allowing for the construction of a revision operator that unavoidably gives rise to a circular compatible relation. Note that due to Condition (3), every three of $\Gamma _{0,1},\Gamma _{1,2},\ldots ,\Gamma _{n,0}$ together are inconsistent, but each two of them which have an index in common are consistent, i.e. $\Gamma _{i,i\oplus {1}}\Cup \Gamma _{i\oplus {1},i\oplus {2}}$ is consistent for each $i\in \{0,\ldots ,n\}$.

Fig. 1.

Illustrations of Conditions (1)–(3) of a critical loop from Definition 12.

The next theorem is the central result of this section, confirming that the notion of critical loop captures exactly those base logics for which some operator exists that is not total-preorder-representable.

Theorem 4

Let $\mathbb {B}$ be a base logic which does not admit a critical loop. Then the following hold:

• Every base change operator for $\mathbb {B}$ satisfying (G1)–(G6) is compatible with some min-expressible min-complete faithful preorder assignment.

• Every min-expressible min-complete faithful preorder assignment for $\mathbb {B}$ is compatible with some base change operator satisfying (G1)–(G6).

We close this section with an important implication of Theorem 4. A base logic $\mathbb {B} \,{=}\, (\mathcal {L},{\Omega },\models$, $\mathfrak {B}, \Cup )$ is called disjunctive, if for every two bases $\Gamma _1,\Gamma _2 \in \mathfrak {B}$ there is a base such that . This includes the case of any (base) logic allowing disjunction to be expressed on the sentence level, i.e., when for every $\gamma ,\delta \in \mathcal {L}$ there exists some with , such that can be obtained as .

Corollary 1

In a disjunctive base logic, every belief change operator satisfying (G1)–(G6) is total-preorder-representable.

As a consequence, for a vast amount of well-known logics, including all classical logics such as first-order and second order predicate logic, one directly obtains total-preorder-representablility of every AGM base change operator by Corollary 1.

8 Related Work

In settings beyond propositional logic, we are aware of three closely related approaches that propose model-based frameworks for revision of belief bases (or sets) without fixing a particular logic or the internal structure of interpretations, and characterize revision operators via minimal models à la K &M with some additional assumptions.

One semantic-based approach related to the one of K &M was proposed by Grove [11] in the setting of Boolean-closed logics. He originally characterized AGM revision operators via systems of spheres, collections S of sets of interpretations satisfying certain conditions. Delgrande and colleagues [7] then reformulated Grove’s representation theorem stating that (expressed in our terminology) any AGM revision operator can be obtained from a compatible min-complete faithful preorder assignment, provided the set of interpretations is $\Omega$-expressible, i.e. for any subset $\Omega '\subseteq \Omega$ there exists a base $\Gamma$ such that $\llbracket \Gamma \rrbracket = \Omega '$. In this formulation, Groves result also holds for logics with infinite $\Omega$. Grove’s result constitutes a special case of our representation theorem: from the assumption of Boolean-closedness, it follows that the considered logics are disjunctive and therefore free of critical loops (cf. Theorem 4 and Corollary 1). The assumption of $\Omega$-expressibility immediately implies min-expressibility for all relations.

The representation result of Delgrande et al. [7] confines the considered logics to those where the set $\Omega$ of interpretations (or possible worlds) is finite² and where any two different interpretations $\omega ,\omega ' \in \Omega$ can be distinguished by some sentence $\varphi \in \mathcal {L}$, i.e., $\omega \in \llbracket \varphi \rrbracket$ and $\omega ' \not \in \llbracket \varphi \rrbracket$. Moreover, they extend the AGM postulates by the following extra one, denoted (Acyc). With these ingredients in place, they [7] establish that, for the logics they consider, there is a two-way correspondence between those AGM revision operators satisfying (Acyc) and min-expressible faithful preorder assignments. Instead of the term “min-expressible”, they use the term regular. The approach of Delgrande et al. [7] can be seen as complementary to ours. While our proposal is to relinquish the requirement of using preorders, their (Acyc) postulate allows for a preorder characterization even in logics with critical loops by disallowing some “unnatural” AGM revision operators.

The approach of Aiguier et al. [1] considers AGM belief base revision in logics with a possibly infinite set $\Omega$ of interpretations. Notably, they propose to consider certain bases, that actually do have models, as inconsistent (and thus in need of revision). While, in our view, this is at odds with the foundational assumptions of belief revision (revision should be union/conjunction unless facing unsatisfiability), this appears to be a design choice immaterial to the established results. As far as the postulates are concerned, Aiguier et al. [1] decide to rule out (KM4)/(G4), arguing in favor of syntax-dependence. Like us, they [1] propose to drop the requirement that assignments have to yield preorders. In addition to the standard notion of compatibiliy, their result hinges on an additional correspondence between the assignment and the preorder (third bullet point).

9 Conclusion

The central objective of our treatise was to provide an exact model-theoretic characterization of AGM belief revision in the most general reasonable sense, i.e., one that uniformly applies to every logic with a classical model theory (i.e., every Tarskian logic), to any notion of bases that allows for taking some kind of “unions” (including the cases of belief sets, sets of sentences, finite sets of sentences, and single sentences), and to all base change operators adhering to the unaltered AGM postulates (without imposing further restrictions through additional postulates).

We found that in the general case considered by us, the original result of K &M for signature-finite propositional logic fails in many ways and needs substantial adaptations. In particular, aside from delivering total relations and being faithful, the assignment now needs to satisfy (i) min-expressibility, guaranteeing existence of a describing base for any model set obtained by taking minimal interpretations among some base’s models, (ii) min-completeness, ensuring that minimal interpretations exist in every base’s model set, and (iii) min-retractivity instead of transitivity, making sure that minimality is inherited to more preferable elements.

While the first two adjustments have been recognized and described in prior work, the notion of min-retractivity (and the decision to replace transitivity by this weaker notion and thus give up on the requirement that preferences be preorders) seems to be novel. Yet, it turns out to be the missing piece for establishing the desired two-way compatibility-correspondency between AGM revision operators and preference assignments of the described kind (cf. Theorem 3).

Conceding that transitivity is a rather natural choice for preferences and preorder assignments might be held dear by members of the belief revision community, we went on to investigate for which logics our general result holds even if assignments are required to yield preorders. We managed to pinpoint a specific logical phenomenon (called critical loop), the absence of which in a logic is necessary and sufficient for total-preorder-representability. While the criterion by itself maybe somewhat technical and unwieldy, it can be shown to subsume all logics featuring disjunction and therefore all classical logics.

Next to advancing the general model-theoretic understanding of AGM belief revision for the vast class of Tarskian logics, our research also opens up more concrete opportunities: Among others, it allows for the definition of novel AGM belief revision operators from a model-theoretic perspective, through the design of an appropriate assignment. Another interesting direction may be to study the potential relationship between our notion of min-retractivity and notions of quasi-transitivity and Suzumura-consistency in social choice theory [4] or interval orders in belief set contraction [23].