Discrete Neural Networks with Maximum and Non-instantaneous Impulses with Computer Simulation

Abstract

A nonlinear non-instantaneous impulsive difference equations with maximum of the state variable over a past time interval is investigated. The exponential stability concept is studied and some criteria are derived. These results are also applied for a neural networks with switching topology at certain moments and long time lasting impulses. It is considered the general case of time varying connection weights. The equilibrium is defined and exponential stability is studied. The obtained results are illustrated on examples.

1 Introduction

One of the most important problems in the theory and application of difference equations is stability (see, for example, [3, 6, 7, 9, 11, 12]). At the same time impulses are a very useful mathematical apparatus to model some instantaneous perturbations in the process. In the case when the acting time of the impulses is not possible to be neglected, these impulses are called non-instantaneous impulses (for continuous case, see, [4]).

In this paper we study nonlinear difference equations with a special type of delay in the case there are some impulses starting at initially given points and acting on finite time intervals. The delay is presented as the maximum value of the unknown function over a past time discrete interval. By utilizing the Lyapunov stability theory and discrete-time Gronwall inequality, we establish some sufficient conditions for exponential stability of the zero solution.

Neural networks have received extensive interests in recent years in connection with their potential applications in signal processing, content addressable memory, pattern recognition, combinatorial optimization. It is well known that the existence of delays in neural networks causes undesirable complex dynamical behaviors such as instability, oscillation and chaotic phenomena. In practice, for computation convenience, continuous-time neural networks are often discretized to generate discrete-time neural networks. Thus, the study of discrete-time neural networks attracts more and more interests.

In this paper, we deal with a class of discrete-time neural networks with a special type of delay subject to long time lasting impulsive perturbations. The delay is presented by the maximum value of the state variables ove a past time interval with fixed interval. The basic characteristic of these perturbations is that the time of their action is not negligible small, so we consider the so called non-instantaneous impulses. We consider the general case when the connection weights between neurons are changeable in time. We apply the obtained theoretical results to obtain exponential stability criteria and new exponential convergence rate for non-instantaneous impulsive discrete-time neural networks with delays and variable connection weights.

Some discrete neural networks are considered and the theoretical results are applied. The example is computer realized by the help of Wolfram Mathematica. Following the theoretical schemes for solving the problems, the corresponding algorithms are coded to calculate the values of the solution for each step. The graphs are generated by CAS Wolfram Mathematica.

2 Statement of the Problem and Definition of Solution

We will introduce basic notations used in this paper. Most of them are well known and used in the literature. Let $\mathbb {Z}_+$ be the set of all nonegative integers; the increasing sequence $\{n_i\}_{i=0}^{\infty }:\ n_0=0,\ n_i\in \mathbb {Z}_+,\ n_i\ge n_{i-1}+3$, $i=1,\,2,\,\dots$ and the sequence $\{d_i\}_{i=1}^{\infty }:\ d_i\in \mathbb {Z}_+,\ 1 \le d_i\le n_{i+1}-n_i-2$, $i=1,\,2,\,\dots$ be given; $\mathbb {Z}[a,b]= \{ z \in \mathbb {Z}_+ : a \le z \le b \}$, $a,\ b \in \mathbb {Z}_+,\ a<b$, $\mathbb {Z}_a=\{ z \in \mathbb {Z}_+ : z \ge a \}$ and $I_{k}=\mathbb {Z}[n_k+d_k,n_{k+1}-1]$, $k \in \mathbb {Z}_+,$ and $J_k=\mathbb {Z}[n_k+1,n_k+d_k]$, $k \in \mathbb {Z}_1,$ where $d_0=0$.

Let $\phi \in \mathbb {Z}(-h,0)\rightarrow \mathbb {R}^N$ with $\Vert \phi \Vert _0=\max \limits _{\sigma \in [-h,0]}||\phi (\sigma )||$, where ||.|| is a norm in $\mathbb {R}^N$.

Consider the initial value problem (IVP) for the system of nonlinear difference equation with non-instantaneous impulses

$$\begin{aligned} \begin{aligned}&x(n+1) =Ax(n)+F\left( n,\max _{\xi \in \mathbb {Z}[n-h,n]}x(\xi )\right) \ \ \ \text{ for }\ \ n \in \bigcup _{k=0}^{\infty }I_{k}, \\&x(n) =P_k(n, x(n_k)),\ \ \ \text{ for } \ \ n \in J_k, \ k \in \mathbb {Z}_1, \\&x(n)=\phi (n),\ \ \ \ n \in \mathbb {Z}[-h,0], \end{aligned} \end{aligned}$$

(1)

where $x\in \mathbb {R}^n$, $x=(x_1,\,x_2,\,\dots ,\,x_N)\in \mathbb {R}^N$, A is $N\times N$ square matrix, $F=(F_1,\,F_2,\,\dots ,\,F_N)$, $F_i:\bigcup _{k=0}^{\infty }I_{k}\times \mathbb {R}^N\rightarrow \mathbb {R}$, $P_k=(P_{k,1},\,P_{k,2},\,\dots ,\,P_{k,N})$, $P_{k,i}:J_k\times \mathbb {R}^N\rightarrow \mathbb {R}$, $i=1,\,2,\,\dots ,\,N$, $k=1,\,2,\,\dots$, and h is a natural number.

Denote by $\mathbb {M}_N$ the set of all quadratic $N\times N$ dimensional matrices with the spectral norm $|A|=\sqrt{\lambda _{max}(A^TA)}$, and for any vector $x\in \mathbb {R}^N$ we will use the norm $|x|=\sqrt{\sum \limits _{i=1}^Nx_i^2}$. Moreover, denote by $\lambda _{min}(A)$ and $\lambda _{max}(A)$ the minimum and the maximum eigenvalue of a positive definite symmetric matrix A and $\Phi (A)=\frac{\lambda _{max}(A)}{\lambda _{min}(A)}$.

Usually, the difference equation describes the development of a certain phenomenon by recursively defining a sequence, each of whose terms is defined as a function of the preceding terms, once one or more initial terms are known (see, for example, [10]). Differently than that, we consider a difference equation in which the present state is also involved nonlinearly in the right side part. It makes the answer of the question about the existence of the solution more complicated.

Definition 1

The trivial solution of the system (1) is called globally exponentially stable, if there exist constants $L>0$ and $\alpha \in (0,1)$ such that for any initial function $\phi$ the inequality $|x(n)|\le L\alpha ^n ||\phi ||_0,\ \ n=1,2,\dots$ holds.

The constant $\alpha$ is called the exponential convergence rate.

Consider the Lyapunov equation

$$\begin{aligned} A^THA-H=-C, \end{aligned}$$

(2)

where $A,\ H,\ C\in \mathcal {M}_N$.

3 Exponential Stability of Linear Delay Discrete Equations

We will study the exponential stability of the linear system (1).

Theorem 1

(Exponential stability results). Let

• 1. The matrix $A\in \mathbb {M}_N$ and $C\in \mathbb {M}_N$ be a positive definite matrix.

• 2. The function $F\in C(\mathbb {Z}_+\times \mathbb {R}^N, \mathbb {R}^N)$, $F(n,0)=0$ for any $n\in \mathbb {Z}_+$ and there exists a constant $K>0$ such that $|F(n,u)|\le \sqrt{K}|u|$ for $u\in \mathbb {R}^N, n\in \mathbb {Z}_+$.

• 4. The functions $P_k\in C(\mathbb {Z}_+\times \mathbb {R}^N, \mathbb {R}^N)$, $P_k(n,0)=0, \ k=1,\,2,\,\dots$ and there exist constants $M_k>0$ such that $|P_k(n,u)|\le \sqrt{M_k}|u|$ for any $u\in \mathbb {R}^N$, $n\in J_k$ and $k=1,\,2,\,\dots$.

• 5. There exists a solution $H\in \mathbb {M}_n$ of (2) such that $|H|\ M_k<1, \ k=1,\,2,\,\dots ,$ $L_1(H)-L_2(H)< \lambda _{max}(H)-\lambda _{min}(H),$ and

  $$\begin{aligned}&\Phi (H)\Big (|A^TH|+ |HA|+K\lambda _{max}(H)\Big )\\&{min}(C)<\lambda _{max}(H)+0.5\Phi (H)(|A^TH|+ |HA|) \end{aligned}$$

  where $L_1(H)=\lambda _{max}(H)- \lambda _{min}(C)+ 0.5\Phi (H)(|A^TH|+ |HA|),$ and $L_2(H)=\lambda _{min}(H)-\Phi (H)K\Big (\lambda _{max}(H)+0.5|HA|+0.5 |A^TH|\Big ).$

Then the zero solution of (1) is exponentially stable.

Proof

Denote $\Theta =\max \Big \{\Lambda , \frac{L_1(H)}{\lambda _{max}(H)}-L_2+\lambda _{min}(H)\Big \}<1,$ where $\Lambda =\sup \limits _{k\ge 1}|M_k^THM_k|.$

Consider the function $V(x)=x^THx$ for $x\in \mathbb {R}^N.$ Then $\lambda _{min}(H)|x|^2\le V(x)\le \lambda _{max}(H)|x|^2.$

Let $x(n),\ n\in \mathbb {Z}[-h+1,\infty ),$ be a solution of the IVP (1) with the initial function $\phi$.

Let $n\in \bigcup _{k=0}^{p}I_{k}$. Then we have

$$\begin{aligned} \begin{aligned}&V(x(n+1))-V(x(n))\\ {}&\le \left( -\lambda _{min}(C)+0.5 |A^TH|+0.5 |HA|\right) |x(n)|^2 \\&\ \ \ \ + \left( \lambda _{max}(H)+0.5|HA|+0.5 |A^TH|\right) K| \max _{\xi \in \mathbb {Z}[n-h,n]}x(\xi )|^2\\&\le -\lambda _{min}(C)|x(n)|^2+ |A^THB|\ |x(n)|^2 \\&\ \ \ + \Big (|A^THB|+|B^THB|\Big ) |\max _{\xi \in \mathbb {Z}[n-h,n]}x(\xi )|^2. \end{aligned} \end{aligned}$$

(3)

Apply the inequalities $-|x(n)|^2\le -\frac{V(x(n)}{\lambda _{max}(H)},$ and

$$\left| \max _{\xi \in \mathbb {Z}[n-h,n]}x(\xi )\right| ^2=\left| x(\eta )\right| ^2\le \frac{V(x(\eta ))}{\lambda _{min}(H)}\le \frac{\lambda _{max}(H)}{\lambda _{min}(H)} \Vert \phi \Vert _0^2$$

to (3) and obtain

$$\begin{aligned} \begin{aligned}&V(x(n+1))\le \Big (1- \frac{\lambda _{min}(C)}{\lambda _{max}(H)}+ \frac{|A^THB|}{\lambda _{min}(H)}\Big )V(x(n)) \\&\ \ \ + \Big (|A^THB|+|B^THB|\Big ) \frac{\lambda _{max}(H)}{\lambda _{min}(H)} \Vert \phi \Vert _0^2. \end{aligned} \end{aligned}$$

(4)

From equalities

$$\begin{aligned}\begin{aligned}&1- \frac{\lambda _{min}(C)}{\lambda _{max}(H)}+ 0.5\frac{ |A^TH|+ |HA|}{\lambda _{min}(H)}\\&=\frac{1}{\lambda _{max}(H)}\left( \lambda _{max}(H)- \lambda _{min}(C)+ 0.5\Phi (H)(|A^TH|+ |HA|)\right) \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\Big (\lambda _{max}(H)+0.5|HA|+0.5 |A^TH|\Big ) \frac{K}{\lambda _{min}(H)}\\&= \Phi (H)\Big (\lambda _{max}(H)+0.5|HA|+0.5 |A^TH|\Big ) \frac{K}{\lambda _{max}(H)} \end{aligned} \end{aligned}$$

and inequality (4) we get

$$\begin{aligned} \begin{aligned} V(x(n+1))&\le \frac{L_1(H)}{\lambda _{max}(H)}V(x(n-1)) +\Big (\lambda _{min}(H)-L_2(H)\Big ) \Vert \phi \Vert _0^2.\end{aligned} \end{aligned}$$

(5)

Let $n=0$. Then from inequality (5) we obtain

$$\begin{aligned} \begin{aligned} V(x(1))&\le \Big (L_1(H)-L_2(H)+\lambda _{min}(H)\Big )\Vert \phi \Vert _0^2< \root 1+h \of {\Theta (H)} \Vert \phi \Vert _0^2. \end{aligned} \end{aligned}$$

(6)

Let $n=1$. Then from inequalities (5) and (6) we get

$$\begin{aligned} \begin{aligned} V(x(2))&\le \frac{L_1(H)}{\lambda _{max}(H)}V(x(1)) +\Big (\lambda _{min}(H)-L_2(H)\Big ) \Vert \phi \Vert _0^2\\&\le \Theta (H) \Vert \phi \Vert _0^2< \root 1+h \of {\Theta ^2(H)} \Vert \phi \Vert _0^2. \end{aligned} \end{aligned}$$

(7)

Consider the following two possible cases:

Case 1. Let $m\ge n_1-1$. Then using induction, the inequalities $\Theta < \root p \of {\Theta }$ for $p>1$, $n\le n_1-1<m+1$, i.e. $\frac{m+1}{n}>1$ for $n\in I_0$ and inequality (5), we prove that

$$V(x(n+1))\le \root 1+h \of {\Theta ^n(H)}\Vert \phi \Vert _0^2,\ \ \ \text{ for }\ \ n\in \mathbb {Z}[0,n_{1}-1].$$

Case 2. Let $h< n_1-1$. Then using induction and inequality (5) we prove that

$$ V(x(n+1))\le \root 1+h \of {\Theta ^n(H)} \Vert \phi \Vert _0^2, \ \text{ for }\ n=1,2,\dots ,h.$$

Then for $k=1,\,2,\,\dots ,\,n_1-h$ we get

$$\begin{aligned} \begin{aligned} V(x(h+k))&\le \frac{L_1(H)}{\lambda _{max}(H)}V(x(h))+\Big (\lambda _{min}(H)-L_2(H)\Big ) \Vert \phi \Vert _0^2\\&\le \Theta (H)\root 1+h \of {\Theta ^k(H)} \Vert \phi \Vert _0^2< \root 1+h \of {\Theta ^{h+k}(H)} \Vert \phi \Vert _0^2. \end{aligned} \end{aligned}$$

(8)

By induction we prove that

$$V(x(n_1+k))<\root 1+h \of {\Theta ^{n_1+k-1}}v_0,\ \ \ k=0,1,\dots ,d_1.$$

Let $n=n_1+d_1$. Then using the inequalities $n_1+d_1+1-h>0$ and (5) we get

$$\begin{aligned} \begin{aligned}&V(x(n_1+d_1+1))\le \frac{1}{\lambda _{max}(H)}L_1(H)\root 1+h \of {\Theta ^{n_1+d_1}} \Vert \phi \Vert _0^2\\&\ \ \ \ \ \ +\Big (-L_2(H)+\lambda _{min}(H)\Big )\root 1+h \of {\Theta ^{n_1+d_1+1-h}} \Vert \phi \Vert _0^2\\&<\Theta ^{\frac{n_1+d_1+1}{h+1}} \Vert \phi \Vert _0^2. \end{aligned} \end{aligned}$$

(9)

Similarly, $V(x(n_1+d_1+2))<\Theta ^{\frac{n_1+d_1+2}{h+1}}\Vert \phi \Vert _0^2.$

By induction process we prove the validity of the inequality

$$\begin{aligned} V(x(n))<\Theta ^{\frac{n}{h+1}} \Vert \phi \Vert _0^2\ \ \ \ \ \text{ for } \text{ all }\ n\in \mathbb {Z}_1.\end{aligned}$$

(10)

Therefore, we get $|x(n)|< L\Vert \phi \Vert _0\alpha ^n$, for all $n\in \mathbb {Z}_1$ with $\alpha =\root 2(h+1) \of {\Theta }<1$, and $L=\sqrt{\Phi (H)}= \sqrt{\frac{\lambda _{max}(H)}{\lambda _{min}(H)}}$.

   $\square$

4 Exponential Stability of Discrete Neural Networks with Maximum, Non-instantaneous Impulses and Time Variable Connection Weights

Consider the following neural network modeled by discrete system with maximum, non-instantaneous impulses and time variable connection weights

$$\begin{aligned} \begin{aligned}&u_i(n+1) =a_iu_i(n) +\sum _{j=1}^n\Psi _{ij}(n)f_j \left( \max _{\xi \in \mathbb {Z}[n-h,n]}u_j(\xi )\right) +G_i \\&\ \ \ \ \ \ \ \text{ for } \ \ n\in \bigcup _{k=0}^{\infty }I_{k},\ \ i\in \mathbb {Z}[1,N],\\&u_i(n) =M_{ik}u_i(n_k)+\sum _{j=1}^n\Phi _{ij}^k(n)S_j(u_j(n_k))+Q_{ik},\\&\ \ \ \ \ \ \ \ \text{ for }\ \ n\in J_k, \ k\in \mathbb {Z}_1,\ \ i\in \mathbb {Z}[1,N],\\&u_i(n)=\phi _i(n),\ \ n\in \mathbb {Z}[-h,0], \ \ i\in \mathbb {Z}[1,N], \end{aligned} \end{aligned}$$

(11)

where $u_i(n)$, $i\in \mathbb {Z}[1,N],$ denotes the state of the i-th neuron at discrete time n, $a_i, \ i\in \mathbb {Z}[1,N],$ represents the passive decay rate, $f_j$ is the neuron activation function with $f_j(0)=0$, $G_i$ is the exogenous input, $P_j$ is the neuron output signal function which is a continuous function, $\Psi _{ij}(n)$ and $\Phi _{ij}^k(n)$ denote the connection weight from the neuron j to the neuron i at time n, $m\in \mathbb {Z}(1)$ is the transmission delay, $\phi _i(n)$, $n\in \mathbb {Z}[-h,0]$ is the initial function for the i-th neuron.

For any $u=(u_1,\,u_2,\,\dots ,\,u_N)$ we denote $f(u)=\big (f_1(u_1),\,f_2(u_2),\,\dots \,,\,f_N(u_N)\big )$ and $S(u)=\big (S_1(u_1),\,S_2(u_2),\,\dots \,,\,S_N(u_N)\big )$.

We will introduce the following assumptions:

A1. The functions $f_i\in C(\mathbb {R},\mathbb {R}),\ \ i\in \mathbb {Z}[1,N],$ and there exist positive constants $L_i$, $i\in \mathbb {Z}[1,N]$, such that $|f_i(u)-f_i(v)|\le L_i|u-v|$, $u,\ v\in \mathbb {R}$.

A2. The functions $S_i\in C(\mathbb {R}, \mathbb {R}),\ \ i\in \mathbb {Z}[1,N],$ and there exist positive constants $K_i$, $i\in \mathbb {Z}[1,N]$, such that $|S_i(u)-S_i(v)|\le K_i|u-v|$, $u,v\in \mathbb {R}$.

A3. The functions $\Psi _{ij}: \bigcup \limits _{k=0}^{\infty }I_{k}\rightarrow \mathbb {R}$, $i,\ j\in \mathbb {Z}[1,N],$ and $\Phi _{ij}^k:J_k\rightarrow \mathbb {R}$, $i,\ j\in \mathbb {Z}[1,N]$, $k\in \mathbb {Z}_+,$ are bounded, i.e. there exists constants $\beta _{ij}^k>0$, $\gamma _{ij}>0$ such that $|\Psi _{ij}(n) | \le \beta _{ij}$ for $n\in \bigcup \limits _{k=0}^{\infty }I_{k}$ and $| \Phi _{ij}^k(n) | \le \gamma _{ij}^k$ for $n\in J_k$, $k\in \mathbb {Z}_+$, $i,\ j\in \mathbb {Z}[1,N]$.

In the non-homogeneous case we will define an equilibrium of the model (11):

Definition 2

([2]) A vector $u^{*}\in \mathbb {R}^N:\ u^{*}=(u^{*}_1,\,u^{*}_2,\,\dots ,\, u^{*}_N)$ is said to be an equilibrium point of the impulsive discrete-time neural network (11) if it satisfies the equalities

$$\begin{aligned} \begin{aligned}&u^*_i =a_iu^*_i +\sum _{j=1}^N\Psi _{ij}(n)f_j(u^*_j)+G_i \ \ \ \text{ for } \ \ n\in \bigcup _{k=0}^{\infty }I_{k}, \ i\in \mathbb {Z}[1,N],\\&u^*_i=M_{ik}u^*_i+\sum _{j=1}^N\Phi _{ij}^k(n)S_j(u^*_j )+Q_{ik} \ \ \ \text{ for } \ \ n\in J_k, \ k\in \mathbb {Z}_1. \end{aligned} \end{aligned}$$

(12)

Let (11) has an equilibrium $u^*\in \mathbb {R}^N$. Substitute $x=u-u^*\in \mathbb {R}^N$ in (11) and obtain

$$\begin{aligned} \begin{aligned}&x_i(n+1) =a_ix_i(n) +\sum _{j=1}^N\Psi _{ij}(n)\mathcal {F}_j\left( \max _{\xi \in \mathbb {Z}[n-h,n]}x_j(\xi )\right) , \ n\in \bigcup _{k=0}^{\infty }I_{k}, \\&x_i(n) =M_{ik}x_i(n_k))+\sum _{j=1}^N\Phi _{ij}^k(n)r_j(x_j(n_k)), \ n\in J_k, \ k\in \mathbb {Z}_1, \end{aligned} \end{aligned}$$

(13)

where $\mathcal {F}_i(y)=f_i(y-u_i^*)-f_i(u_i^*)$ and $r_i(y)=S_i(y-u_i^*)-S_i(u_i^*)$, $i=1,\,2,\,\dots ,\, N,$ for $y\in \mathbb {R}$.

The stability behavior of the equilibrium of (11) is equivalent to the stability behavior of zero solution of (13).

The system (13) could be written in the matrix form (1) where

$$ A= \begin{bmatrix} a_1 &{} 0 &{} 0 &{} \dots \dots &{} 0 \\ 0 &{} a_2 &{} 0 &{} \dots \dots &{} 0\\ \dots &{} \dots &{} \dots &{}\dots &{} \dots \\ 0 &{} 0 &{} 0 &{} \dots \dots &{}a_N \end{bmatrix}, \mathcal {B}(n)= \begin{bmatrix} \Psi _{11}(n) &{} \Psi _{12} (n)&{} \Psi _{13}(n) &{} \dots \dots &{} \Psi _{1N} (n)\\ \Psi _{21}(n) &{} \Psi _{22}(n) &{} \Psi _{23}(n) &{} \dots \dots &{}\Psi _{2N}(n)\\ \dots &{} \dots &{} \dots &{}\dots &{}\dots \\ \Psi _{N1} (n)&{} \Psi _{N2}(n) &{}\Psi _{N3}(n) &{} \dots \dots &{}\Psi _{NN}(n) \end{bmatrix},$$

$$ \mathcal {F}(u)= \begin{bmatrix} \mathcal {F}_1(u_1)\\ \mathcal {F}_2(u_2)\\ \dots \\ \mathcal {F}_N(u_N) \end{bmatrix}, r(u)= \begin{bmatrix} r_1(u_1)\\ r_2(u_2)\\ \dots \\ r_N(u_N) \end{bmatrix}, \mathcal {M}_k= \begin{bmatrix} M_{1k} &{} 0 &{} 0 &{} \dots \dots &{} 0 \\ 0 &{} M_{2k} &{} 0 &{} \dots \dots &{} 0\\ \dots &{} \dots &{} \dots &{}\dots &{} \dots \\ 0 &{} 0 &{} 0 &{} \dots \dots &{}M_{Nk} \end{bmatrix}, $$

$$ \mathcal {G}_k(n)= \begin{bmatrix} \Phi _{11}^k (n)&{} \Phi _{12}^k (n)&{} \gamma _{13}^k (n)&{} \dots \dots &{} \Phi _{1N}^k (n)\\ \Phi _{21}^k(n) &{} \Phi _{22}^k(n) &{} \Phi _{23}^k (n)&{} \dots \dots &{}\Phi _{2N}^k(n)\\ \dots &{} \dots &{} \dots &{}\dots &{}\dots \\ \Phi _{N1}^k (n)&{} \Phi _{N2}^k (n)&{}\Phi _{N3}^k (n)&{} \dots \dots &{}\Phi _{NN}^k(n) \end{bmatrix}, $$

$u=(u_1,\,u_2,\dots ,\,u_N)$, $F=(F_1,\,F_2,\dots ,\,F_N)$, $F(n,u)=\mathcal {B}(n) \mathcal {F}(u)$, $P_k=(P_{k,1},\,P_{k,2},\dots ,\,P_{k,N})$, $P_k(n,u)=\mathcal {G}_k(n) r(u)+\mathcal {M}_ku^T$.

From assumption (A1) and the inequality $\left( \sum \limits _{j=1}^N\gamma _ju_j\right) ^2\le N\sum \limits _{j=1}^N\left( \gamma _ju_j\right) ^2$ we have $|F(n,u)|\le \sqrt{N\sum _{i=1}^N \max _j(L_j\beta _{ij})^2}\sqrt{\sum _{j=1}^N u_j^2},$ i.e. the condition 3 of Theorem 1 is satisfied with $K=N\sum \limits _{i=1}^N \max _j(L_j\beta _{ij})^2.$

From assumption (A2) and the inequality $\Big (\sum \limits _{j=1}^N\gamma _ju_j\Big )^2\le N\sum \limits _{j=1}^N\left( \gamma _ju_j\right) ^2$ we have $|P_k(n,u)|\le \sqrt{2\Big (\max _i M_{ik}^2+\sum _{i=1}^N N \max _j\Big (\gamma _{ij}^kK_j\Big )^2\Big )\sum _{i=1}^Nu_i^2}$, i.e. the condition 4 of Theorem 1 is satisfied with $M_k=2\Big (\max _i M_{ik}^2+\sum _{i=1}^N N \max _j\big (\gamma _{ij}^kK_j\big )^2\Big ).$

Theorem 2

Let the conditions (A1)–(A3) be satisfied and:

• 1. The discrete model (11) has an equilibrium $u^*$.

• 2. The constants $a_i$, $M_{ik}\in \mathbb {R}$, $\beta _{ij}$, $\gamma _{ij}^k>0$, $G_i$, $Q_{ik}\in \mathbb {R}$, $i,\ j\in \mathbb {Z}[1,N\,\ k\in \mathbb {Z}_1$.

• 3. The inequalities $\max _i M_{ik}^2+N\sum _{i=1}^N \max _j\big (\gamma _{ij}^kK_j\big )^2<1$ for $k\in \mathbb {Z}_1$, $\max _i a_i^2+\max _i|a_i|+N(1-\max _i|a_i|)\sum _{i=1}^N \max _j(L_j\beta _{ij})^2) <1,$ and $\max _i a_i^2+ \max _i |a_i|+K\Big (1+\max _i |a_i|\Big )<1$ hold.

Then the equilibrium point of the difference neural network with non-instantaneous impulses (11) is exponentially stable with a rate $\alpha =\root 2(h+1) \of {\Theta }<1.$ where $\Theta =\max \Big \{\Lambda ,\max _i a_i^2+ \max _i |a_i|+K\Big (1+\max _i |a_i|\Big )\Big \}<1$ with $\Lambda =\sup \limits _{k\ge 1}\Big (\max \limits _i M_{ik}^2+\sum \limits _{i=1}^N N \max \limits _j\big (\gamma _{ij}^kK_j\big )^2\Big ).$

Proof

Let $H=E$, where $E\in \mathbb {M}_n$ is the unit matrix. Then (2) is satisfied with $C\in \mathbb {M}_n:\ c_{ii}=1-a_i^2$ and $c_{ij}=0$ for $i\not =j$. Then $\lambda _{max}(H)=\lambda _{min}(H)=\phi (H)=1$ and $\lambda _{min}(C)=1-\max _i a_i^2$, $|A|=\max _i|a_i|$. According to Theorem 1 the zero solution of (13) is exponentially stable.

5 Application

Consider a system with three agent with constant connection weights modeled by the following discrete model of neural network

$$\begin{aligned} \begin{aligned} u_1(n+1)&=\frac{1}{2}u_1(n) +\frac{1}{8}\sin \Big (\max _{\xi \in \mathbb {Z}(n-3,n)}u_1(\xi )\Big )-\frac{1}{4}\sin \Big (\max _{\xi \in \mathbb {Z}(n-3,n)}u_2(\xi )\Big )\\&\ \ \ \ \ \ \ \ \ \ \ \ \ +\frac{1}{16}\max _{\xi \in \mathbb {Z}(n-3,n)}u_3(\xi )+1\\ u_2(n+1)&=\frac{1}{3}u_2(n) +\frac{1}{4}\sin \Big (\max _{\xi \in \mathbb {Z}(n-3,n)}u_1(\xi )\Big ) +\frac{1}{8}\sin \Big (\max _{\xi \in \mathbb {Z}(n-3,n)}u_2(\xi )\Big )+2\\ u_3(n+1)&=\frac{1}{4}u_3(n) +\frac{1}{16}\sin \Big (\max _{\xi \in \mathbb {Z}(n-3,n)}u_1(\xi )\Big )-\frac{1}{8}\sin \Big (\max _{\xi \in \mathbb {Z}(n-3,n)}u_2(\xi )\Big ) \\&+\frac{1}{16}\max _{\xi \in \mathbb {Z}(n-3,n)}u_3(\xi ))+1\ \ \ \ \text{ for } \ \ n\in \bigcup _{k=0}^{\infty }I_{k}, \end{aligned} \end{aligned}$$

(14)

with non-instantaneous impulses for $n\in J_k, \ k\in \mathbb {Z}_1$

$$\begin{aligned} \begin{aligned} u_1(n)&=\frac{1}{2}u_1(n_k) +\frac{1}{8}\sin (u_1(n_k))-\frac{1}{4}\sin (u_2(n_k)) +\frac{1}{16}u_3(n_k)+1\\ u_2(n)&=\frac{1}{3}u_2(n_k) +\frac{1}{4}\sin (u_1(n_k)) +\frac{1}{8}\sin (u_2(n_k))+2\\ u_3(n)&=\frac{1}{4}u_3(n_k) +\frac{1}{16}\sin (u_1(n_k)) -\frac{1}{8}\sin (u_2(n_k)) +\frac{1}{16}u_3(n_k)+1, \end{aligned} \end{aligned}$$

(15)

and initial conditions

$$\begin{aligned} u_i(n)=\phi _i(n),\ \ \ n=-3,\,-2,\,-1,\,0, \end{aligned}$$

(16)

where $n_0=0$, $d_0=0$, $n_1=4, d_1=6$, $n_{2}=18, d_2=5$, $n_3=33$, $d_3=7$, $n_4=45$. In this particular case $I_0=\mathbb {Z}[0,3]$, $I_1=\mathbb {Z}[10,17]$, $I_2=\mathbb {Z}[23,32]$, $I_3=\mathbb {Z}[40,44]$ $J_1=\mathbb {Z}[5,10]$, $J_2=\mathbb {Z}[19,23]$, $J_3=\mathbb {Z}[34,40]$. (The whole interval is $\mathbb {Z}$[$-3$,45]).

The point $u^*=(2.40568,\, 3.23436,\,1.53241)$ is the equilibrium point of (14), (15). The conditions of Theorem 2 are reduced to $0.25+3(\frac{1}{16}+\frac{1}{16}+\frac{1}{64})=0.680556<1,$ and $0.25+0.5+3(1-0.5)(\frac{1}{16}+\frac{1}{16}+\frac{1}{64})=0.965278<1.$ Therefore, the equilibrium $u^*$ is exponentially stable with a rate $\alpha =\root 8 \of {0.965278}\approx 0.995592$ and $L=\sqrt{\Phi (H)}$, $\Phi (H)=\frac{\lambda _{max}(H)}{\lambda _{min}(H)}$, $H=E$, where $E\in \mathbb {M}_n$ is the unit matrix.

Fig. 1

Graphs of the bound $\alpha ^n\Vert \phi -u^*\Vert _0= 2.87314*0.995592^n$ and the differences $|u_1(n)-2.40568|,\ |u_2(n)-3.23436|,\ |u_3(n)-1.53241|$ for $n\in [1,45]$

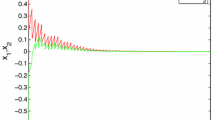
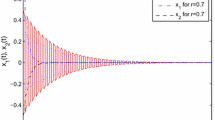
Consider the solution $\tilde{u}(n)$ of the discrete model (14), (15), (16) with initial functions $\phi _1(n)=3n+2$, $\phi _2(n)=2n+2$, $\phi _3(n)=n+4$, $n=-3,\,-2,\,-1,\,0$. In this case $\Vert \phi -u^*\Vert _0=\max \limits _{\sigma \in [-h,0]}||\phi (\sigma )-u^*||=2.87314$. The graphs of the differences $|u_1(n)-2.40568|$, $|u_2(n)-3.23436|$, $|u_3(n)-1.53241|$ and the bound $\alpha ^n\Vert \phi -u^*\Vert _0= 2.87314*0.995592^n$ are given on Fig. 1 and Table 1. From both it could be seen the equilibrium point $u^*$ is exponentially stable.

Table 1 Values of the bound $\alpha ^n\Vert \phi -u^*\Vert _0= 2.87314*0.995592^n$ and the differences $|u_1(n)-2.40568|,\ |u_2(n)-3.23436|,\ |u_3(n)-1.53241|$ for $n=1,\, \dots , \, 45$