Keywords

1 Introduction

Over the past few years, derivative securities (options, futures and forward contracts, swaps, warrants) have become essential instruments for both speculators and investors, regardless of their corporate profile. Derivatives facilitate the transfer of financial risks. As such, they can be used to hedge risky positions or to take risks in anticipation of gains [1].

Options are essentially contracts between two parties which give their holders the right, but not the obligation to buy or sell a prescribed amount of an underlying asset at a specified price within a specified time period. The value of the option is tied to the value of the underlying asset, which can be stocks, bonds, currencies, interest rates, market indices, exchange traded funds, futures contracts, other derivatives, and so on. Options themselves are securities, like stocks or bonds, and it is because they derive their value from something else, they are called derivatives [2].

The price of an option is constituted by two components: The first one is the internal value, which is defined as the difference between the market price of the underlying asset and the strike price of an option. The second one is the time value, which through a varying, nonlinear relationship reflects the expected value at the maturity date discounted to the present [3].

The pricing of options and other financial instruments is one of the most important problems in finance, since its purpose is to determine the fair price of a security with respect to more liquid securities whose price is determined by the law of supply and demand (most commonly priced are “vanilla” and “exotic” options, convertible bonds, etc.) [4]. To determine the option price, one must first choose a model of the price dynamics of the underlying asset, usually in the form of ordinary differential equations [5, 6] or stochastic differential equation depending on market parameters such as interest rate, volatility of the asset, etc., then find a solution to the chosen model in some form, and finally obtain the required option price. The volatility of the asset can be constant (Black–Scholes model) [7], may depend on the value of the underlying asset (volatility smile), the time (volatility term structure) [8], on both (local volatility model) or may satisfy some other stochastic differential equation (stochastic volatility model) [9]. An exact analytical formula for the European vanilla option price has been derived from the Black–Scholes model and several other local and stochastic volatility models, but in general, approximations or numerical methods must be used to estimate options (when it is difficult or impossible to use other approaches) [10]. To solve the problem, we use the Monte Carlo method to construct the empirical density of the underlying asset distribution and then determine the option value [11,12,13]. Possible applications of local volatility models with parallel computation include modeling and managing large equity portfolios [14, 15], assessing and managing market and credit risks [16, 17].

Option pricing via Monte Carlo simulation is among the most popular ways to value certain types of financial options (e.g., exotic path-dependent derivatives, such as Asian options) by directly simulating several thousand possible (but random) price paths of the underlying asset with the corresponding option strike price for each path and then calculating the average outcome of the process discounted to the present day and that is the option value today [18]. This is the first from the two main Monte Carlo approaches [19], while the other is based on Monte Carlo approximation of multidimensional integrals. Monte Carlo simulation is essentially useful in evaluating derivative contracts [20].

The method can guarantee that with a certain probability the Monte Carlo approximation error is less than a given value (probabilistic error). Monte Carlo methods approach the solution faster than numerical integration methods, require less memory, have fewer data dependencies, and are easier to program [21].

In this paper, various simulations of Geometric Brownian Motion paths are considered, the approximation error of the Euler–Maruyama and Milstein methods is evaluated, and the convergence rate of the two methods is empirically determined. Employing these simulations, the value of European and Asian options is obtained.

2 Simulations by the Euler–Maruyama and Milstein Methods

In order to simulate the price of a European call option, one must first determine the process that the price of the underlying asset follows over the life of the option \(\mathrm{t}\in \left[0,\mathrm{ T}\right].\) The underlying asset is known to follow the Geometric Brownian Motion (GBM) given by the stochastic differential Eq. (1), widely used in the study and modeling of dynamical systems that are subject to various random disturbances. The price of the underlying asset \({S}_{t}\) is assumed to have an expected return μ and a constant volatility σ:

$$\mathrm{d}{S}_{t}=\mu {S}_{t}\mathrm{d}t+\sigma {S}_{t}\mathrm{d}{W}_{t}.$$
(1)

The Euler–Maruyama (2) and Milstein (3) techniques are commonly used to approximate the solution of stochastic differential equations, where μ represents the mean return, σ is the volatility, h is the size of the discretization time step, and ∆\({W}_{i}\) is the increment of the Brownian motion at each time step. The latter is simulated by generating random numbers with a standard normal distribution (4):

$${S}_{i+1}={S}_{i}+\mu {S}_{i}h+\sigma {S}_{i}\Delta {W}_{i},$$
(2)
$${S}_{i+1}={S}_{i}+\mu {S}_{i}h+\sigma {S}_{i}\Delta {W}_{i}+\frac{{\sigma }^{2}{S}_{i}}{2}\left({\Delta {W}_{i}}^{2}-h\right),$$
(3)
$$\Delta {W}_{j}={W}_{{t}_{j+1}}-{W}_{{t}_{j}}=Z\sqrt{\Delta t } \mathrm{with} Z\sim \mathrm{N}(\mathrm{0,1}).$$
(4)

As can be seen from the formulas above (Formulas (2) and (3)), the Milstein method is almost the same as the Euler–Maruyama method, but here in order to obtain a higher accuracy of approximation, an additional term is added by including one of the double integrals from the Itô–Taylor expansion for Itô processes.

$$\begin{gathered} {\text{X}}_{\text{t}} = {\text{X}}_{t_{\text{0}} } + \int_{t_{\text{0}} }^t {\{ a({\text{X}}_{t_{\text{0}} } ) + \int_{t_{\text{0}} }^s {[a{\text{'}}(X_z )a(X_z ) + \frac{1}{2}a{\text{''}}(X_z )b^2 (X_z )]dz} } \hfill \\ + \int_{t_{\text{0}} }^s {a{\text{'}}(X_z )b(X_z ){\text{dW}}_{\text{z}} \} {\text{ds + }}\int_{t_{\text{0}} }^t {\{ b({\text{X}}_{t_{\text{0}} } )} } \hfill \\ + \int_{t_{\text{o}} }^s {[b{\text{'}}(X_z )a(X_z ) + \frac{1}{2}b{\text{''}}(X_z )b^2 (X_z )]dz} \hfill \\ + \int_{t_{\text{0}} }^s {{\text{b'}}({\text{X}}_z )b(X_z )dW_z \} dW_s } \hfill \\ \end{gathered}$$
$$= > {\text{X}}_{{t}} - {\text{X}}_{t_0 } = a({\text{X}}_{t_0 } )(t - t_0 ) + b({\text{X}}_{t_0 } )\int_{t_0 }^t {dW_s } + R.$$

If R is neglected, the Euler–Maruyama method is obtained (2).

It can be found that the dominant term in the residual R is

$$\underset{{t}_{0}}{\overset{{t}_{0}+h}{\int }}\underset{{t}_{0}}{\overset{s}{\int }}d{W}_{z}d{W}_{s}\approx \mathcal{O}(h)$$

Then:

$$\int_{t_0 }^t {\int_{t_0 }^s {b{\text{'}}({\text{X}}_z )b({\text{X}}_z )dW_z dW_z \approx b{\text{'}}({\text{X}}_z )b({\text{X}}_z )} \int_{t_0 }^t {\int_{t_0 }^s {dW_z dW_s = \frac{{b{\text{'}}b}}{2}((\Delta W)^2 - h)} } }$$
$$=>{\mathrm{X}}_{\mathrm{t}}-{\mathrm{X}}_{{t}_{0}}=a\left({\mathrm{X}}_{{t}_{0}}\right)\left(t-{t}_{0}\right)+b\left({\mathrm{X}}_{{t}_{0}}\right)\underset{{t}_{0}}{\overset{t}{\int }}d{W}_{s}+\frac{{b}^{^{\prime}}b}{2}\underset{{t}_{0}}{\overset{t}{\int }}\underset{{t}_{0}}{\overset{s}{\int }}d{W}_{z}d{W}_{s}+\stackrel{\sim }{R.}$$

If \(\tilde{R }\) is neglected, the Milstein method (3) is obtained.

Geometric Brownian Motion.

Let the following parameter values be given as input to the simulations:

$$\upmu = 0.06;\upsigma = 0.3;{ S}_{0} = 50; h={10}^{-2};\mathrm{ t }\in \left[\mathrm{0,1}\right],$$

where \({S}_{0}\) is the price of the underlying asset today; and the output is \(S(t)\), which represents the dynamics of the underlying asset price for the given realization of the Brownian motion in the interval \([0, T]\), where \(T\) is the maturity date of the option.

Fifty paths are plotted using the Milstein (Fig. 1) method. On the graphs, the abscissa represents the time points \([t]\) and the ordinate \([S]\) is the realization of the price of the underlying asset.

Fig. 1
figure 1

Stock price dynamics for \(h=0.01\) using Milstein method

Full size image

Let us calculate the exact analytical solution of the Geometric Brownian Motion by considering the step size ℎ = \({10}^{- i}\) for i = 1, 2, 3, 4, 5 using formula (5), where \(t\) is a specified time moment in the future and W is the Wiener process itself, which is the accumulated sum of the increments \(\mathrm{d}W\) up to the time instant \(t\).

$$S\left(t\right)={S}_{0}{e}^{\left(\mu - \frac{{\sigma }^{2}}{2}\right)t+\sigma W}.$$
(5)

For each step size h, this exact solution (\({S}_{T,k}\)) is compared with the approximations \(({\widehat{S}}_{T,k})\) from the Euler–Maruyama and Milstein methods, and the error \(\widehat{\epsilon }(h)\) is computed using the following formula:

$$\hat{\epsilon }(h): = \frac{1}{M}\sum_{k = 1}^M {\left| {S_{T,k} - \hat{S}_{T,k} } \right|}.$$

Here, we only need the price of the underlying asset at the maturity date T, which is why only the last calculated value from the exact solution and the approximation is taken into account to estimate the error. So, to get the average error, we first take the sum of the absolute errors for each path and then divide this sum by M, the number of paths we have simulated.

Table 1 shows the approximation errors for the price of the underlying asset at maturity date T using the Euler–Maruyama (Err_EM) and Milstein (Err_M) methods, where h is the time step size.

Table 1 Approximation error by the Euler–Maruyama and Milstein methods
Full size table

As can be seen from the table, when the step size h decreases, the errors of both methods also decrease. At the largest step size ℎ = \({10}^{- 1}\), the errors are also the largest, and vice versa. It can be noted that the Milstein method is more accurate and the errors are smaller than those of the Euler–Maruyama method, just because it has a higher order of convergence.

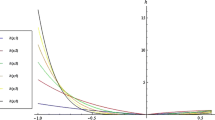
The quality of any algorithm that approximates the true value of the solution depends heavily on the convergence rate. It is necessary to evaluate how fast the approximation converges to the true solution. To evaluate the strong convergence rate of each method, we take the decimal logarithm of the step sizes ℎ = \({10}^{-i}\) for i = 1,2,3,4,5 and the logarithm of the errors computed for the two methods, Euler–Maruyama and Milstein.

As can be seen from Fig. 2, the estimated error for the Milstein method is not only smaller than the error for the Euler–Maruyama method, but also decreases much faster (the slope is steeper). Therefore, at ℎ = \({10}^{- 1}\), it can be seen that the difference between the two methods is smaller than the difference for ℎ = \({10}^{- 5}\), because the convergence order of the Milstein method is higher than that of the Euler–Maruyama method. Applying linear regression, we find the strong convergence rate for both methods. It can be seen that the results converge to the theoretical values of the convergence orders: ½ for the Euler–Maruyama method and 1 for the Milstein method.

Fig. 2
figure 2

Empirical estimation of the strong convergence rate of the Euler–Maruyama and Milstein methods

Full size image

3 Valuation of European and Asian Options

In order to find the fair value of the European call option, in addition to the above values of the Geometric Brownian Motion parameters, we set the strike price of the option \(K=50\) and the interest rate \(r=0.05\). We apply the Black–Scholes formula:

$${\mathrm{V}}^{\mathrm{EC}}={S}_{t}\mathrm{N}\left({d}_{1}\right)-K{e}^{-r\left(T-t\right)}\mathrm{N}\left({d}_{2}\right),$$

where

$$\mathrm{N}\left(x\right)=\frac{1}{\sqrt{2\pi }}\underset{-\infty }{\overset{x}{\int }}{e}^{-\frac{{s}^{2}}{2}}\mathrm{d}s,$$
$${d}_{1}=\frac{\mathrm{ln}\left(\frac{{S}_{t}}{K}\right)+\left(r+\frac{{\sigma }^{2}}{2}\right)(T-t)}{\sigma \sqrt{T-t}},$$
$${d}_{2}=\frac{\mathrm{ln}\left(\frac{{S}_{t}}{K}\right)+\left(r-\frac{{\sigma }^{2}}{2}\right)(T-t)}{\sigma \sqrt{T-t}}.$$

To approximate the price of the European call option, the Euler–Maruyama and Milstein methods are applied, and for this purpose, firstly μ must be replaced by r, i.e., the price of the underlying asset S must have an expected return μ equal to the risk-free rate r. So, it is obtained the risk-neutral stochastic differential equation:

$$\mathrm{d}{S}_{t}=r{S}_{t}\mathrm{d}t+\sigma {S}_{t}\mathrm{d}{W}_{t}.$$

To estimate today's option price \({\mathrm{V}}_{0}\), we take the expected value of the payoff function under a risk-neutral measure \({\mathbb{Q}}\) discounted to today's point in time:

$${\mathrm{V}}_{0}^{\mathrm{EC}}={e}^{-rT}*{\mathbb{E}}^{\mathbb{Q}}{\left[{S}_{T}-K\right]}^{+}.$$

To approximate the expected value of the payoff function under the risk-neutral measure, the Monte Carlo simulation method is used, where M paths are simulated and, using the index i, a certain path from 1 to M is fixed. The payoff function \({\left[{S}_{T}^{i}-K\right]}^{+}\) is calculated for each simulation by taking the last estimated price of the underlying asset for each path, i.e., at the maturity date T. Then, the sum of the payoff functions for all paths is divided by the number of simulations M to obtain the average value of the payoff function, which is multiplied by \({e}^{-rT}\) to discount to today's point in time.

Thus, the fair value of the option today is found:

$$ {\tilde{\text{V}}}^{{\text{EC}}}_0 = e^{ - rT} \ast \frac{1}{M} \ast \sum_{i = 1}^M {[S_T^i - K]^+ } $$
(6)

Finally, the results obtained by Euler–Maruyama and Milstein methods are compared with the Black–Scholes solution for different number of simulated paths M = {10,100,1000,10,000} and fixed time step size \(h={10}^{-4}\). For this purpose, the absolute error of the estimated option price (6) and the exact Black–Scholes solution is computed for both methods:

$$\left|{\stackrel{\sim }{{\mathrm{V}}_{0}}}^{\mathrm{EC}}-{V}_{0}^{\mathrm{EC}}\right|.$$
(7)

Similarly, the values of the Asian call option are calculated. It is known that the Asian arithmetic option does not possess an exact solution. It differs from its European counterpart in the way its payoff is calculated. The Asian option belongs to the class of the path-dependent options since its payoff depends on the realization of the underlying price \({S}_{t}\) for the whole life of the option \(t\in [0,T]\):

$${\mathrm{V}}_{0}^{\mathrm{AC}}={e}^{-rT}*{\mathbb{E}}^{\mathbb{Q}}{\left[\frac{1}{J}\sum_{j=1}^{J}{S}_{{t}_{j}}-K\right]}^{+},$$
(8)

where \({\{{t}_{j}\}}_{j=1}^{J}\) is a discrete set with observation times (for a discretely monitored Asian option).

By the same argument, the Monte Carlo approximation to the Asian call premium is given by averaging the simulations, M in number:

$${\stackrel{\sim }{{\mathrm{V}}_{0}}}^{\mathrm{AC}}={e}^{-rT}*\frac{1}{M}*\sum_{i=1}^{M}{\left[\frac{1}{J}\sum_{j=1}^{J}{S}_{{t}_{j}}^{i}-K\right]}^{+}.$$
(9)

Table 2 provides an estimate of the fair price of a European call option using the Black–Scholes method, an approximation of the option price using the Euler–Maruyama and Milstein methods, and an estimate of the approximation error. The Euler–Maruyama and Milstein approximations (9) of the fair value of an Asian call option are given as well, but since there is no exact formula for (8), the approximation error cannot be obtained.

Table 2 Estimation of the fair value of the European and Asian call option
Full size table

The first column of Table 2 is the number of simulated paths M, but as can be seen, the exact option price (in the C_BS column) does not depend on the number of simulations M, so here in the table it is the same for each M = [10,100,1000,10000].

C_EM is the approximated European call option price calculated using the Euler–Maruyama method, and Err_EM is the error of this approximation. C_M is the approximated price of the European call option calculated using the Milstein method and Err_M is the error of this approximation. A_C_EM and A_C_M are the approximated prices of the Asian option by the both methods, respectively.

As can be seen from Table 2, when only 10 paths are simulated, the approximated price is far from the theoretical price, but as M increases, the approximation results get closer and closer to the exact European call option price. The error decreases as M increases, and, for example, by the Euler–Maruyama method from 5.87 it drops to 0.13. The error from the Milstein method is plotted on Fig. 3a. Also, here it can be seen that there is no significant difference between the results obtained by the Euler–Maruyama and the Milstein methods since the number of simulated paths M is too small. Therefore, to obtain better results when using the Monte Carlo method, possibly many more paths should be simulated.

Fig. 3
figure 3

Absolute error in the option valuation, associated with the Milstein method. Call option error (a) and put option error (b)

Full size image

The same results apply for the put option valuation (Table 3). We apply the Black–Scholes formula to find the exact European put option value:

Table 3 Estimation of the fair value of the European and Asian put option
Full size table
$${\mathrm{V}}^{\mathrm{EP}}={K{e}^{-r\left(T-t\right)}\mathrm{N}\left(-{d}_{2}\right)-S}_{t}\mathrm{N}\left(-{d}_{1}\right),$$

where \(\mathrm{N}\left(x\right)\), \({d}_{1}\) and \({d}_{2}\) are the same as in \({\mathrm{V}}^{\mathrm{EC}}\). Its exact value is \({\mathrm{V}}^{\mathrm{EP}}=4.677099\).

The put premium approximations and the difference between them are calculated analogously to (6) and (7), but only the call payoff is replaced by the put payoff \({\left[K-{S}_{T}\right]}^{+}\):

$${\stackrel{\sim }{{\mathrm{V}}_{0}}}^{\mathrm{EP}}={e}^{-rT}*\frac{1}{M}*\sum_{i=1}^{M}{\left[K-{S}_{T}^{i}\right]}^{+}.$$

In similar manner, for the valuation of the Asian put option, the payoff is replaced by \({\left[K-\frac{1}{J}\sum_{j=1}^{J}{S}_{{t}_{j}}\right]}^{+}\):

$${\stackrel{\sim }{{\mathrm{V}}_{0}}}^{\mathrm{AP}}={e}^{-rT}*\frac{1}{M}*\sum_{i=1}^{M}{\left[K-\frac{1}{J}\sum_{j=1}^{J}{S}_{{t}_{j}}^{i}\right]}^{+}.$$

The same implications could be drawn for the pricing of the put options. In that case, the results seem to be more precise, but this phenomenon is due to the randomness of the simulations. It is also visible that the more simulations are performed, the more accurate the results are (Fig. 3b).

4 Conclusion

In this study, we have shown the advantages of applying the Monte Carlo simulation approach for valuation of European and Asian options. Firstly, the Euler–Maruyama and Milstein discretization methods are introduced, and they are employed in simulating trajectories of the Geometric Brownian Motion. Then, we proposed a simple way to empirically estimate the strong convergence rates for the both methods, which fully coincide with the theoretical ones. This is done by calculating the approximation error of the simulation of the underlying asset price development. Furthermore, the Black–Scholes formula is given in brief and it is explained how to estimate the approximation error of the option valuation through Monte Carlo simulations. Next, the fair values of European and Asian options are calculated and the accuracy dependence on the number of simulations is commented. For the European options, the error could be computed, but unfortunately this is not the case with the Asian options, since they do not experience an exact formula. The aforementioned calculations are done for call and put options. Finally, some implications are outlined which are of help when estimating vanilla and exotic options via Monte Carlo simulations for a wide variety of purposes from hedging to portfolio management.