A Non-Negative Matrix Tri-Factorization Based Method for Predicting Antitumor Drug Sensitivity

Abstract

Large annotated cell line collections have been proven to enable the prediction of drug response in the pre-clinical setting. We present an enhancement of Non-Negative Matrix Tri-Factorization method, which allows the integration of different data types for the prediction of missing associations. To test our method we retrieved a dataset from the Cancer Cell Line Encyclopedia (CCLE), containing the connections among cell lines and drugs by means of their IC50 values, and we integrated it by linking cell lines to their respective tissue of origin and genomic profile. We performed two different kind of experiments: a) prediction of missing values in the matrix, b) prediction of the complete drug profile of a new cell line, demonstrating the validity of the method in both scenarios.

1 Background

Cancer is a highly complex disease due to the enormous level of both intra- and inter-tumor heterogeneity that often displays. Indeed, several tumors of the same organ may vary significantly in important tumor-associated attributes. This is the reason why patients with the same diagnosis can respond in different ways to the same therapy, and this represents the main obstacle to effective treatments [1]. For this reason, it becomes essential to be able to predict if a patient is sensitive or resistant to a specific drug before the administration. Being sensitive to a drug means that the drug manages to have the desired effect on the person, with tolerable side effects; on the contrary, drug resistance represents the inability of the active principle to perform its function. The parameter most extensively used to characterize the response and sensitivity to a drug is the half-maximal inhibitory concentration (IC50), that is the concentration needed to inhibit the 50% of the targeted biological process or component [2]. In particular, in the field of anticancer therapies, the IC50 represents the concentration of drugs needed to kill half of the cells in vitro. Since experimental approaches for the estimation of IC50 values are costly and time-consuming, researchers are increasingly putting efforts into developing computer-based methods for predicting the responsiveness of a patient to a drug. This was made possible thanks to the huge amount of biological, medical and chemical data that have started to be grouped and made publicly available through several tools and databases. In particular, in the context of drug sensitivity, we can certainly cite the Cancer Cell Line Encyclopedia (CCLE) [3] and the Genomics of Drug Sensitivity in Cancer (GDSC) [4] projects, which succeeded in collecting the genetic and pharmacological profile of hundreds of cancer cell lines.

The work of Berrettina et al. [3] can be also considered one of the pioneering machine learning methods proposed for the prediction of sensitive or resistant drug response of a cell line. It exploited CCLE data for a predictive model based on the naïve Bayes classifier. Subsequently, Dong et al. [5] used gene expression features and drug sensitivity data to build SVM-RFE, a wrapper method that firstly performs a feature selection operation and successively uses top features to fit the Support Vector Machine, a supervised learning algorithm for classification. HNMDRP, a network-based method which takes into consideration cell lines, drugs and targets relationships, was then proposed by Zhang et al. [6]. Xu et al. [7] developed the AutoBorutaRF model, which performs a two step feature selection by means of a combination of an autoencoder artificial neural network and the Boruta algorithm, and then uses random forest for classification. More recently, Choi et al. [8] presented a deep neural network model, RefDNN, which pairs molecular structure similarity profiles of drugs and gene expression data of cell lines. In the meanwhile, we can also find DSPLMF, a prediction approach presented by Emdadi et al. [9] based on logistic matrix factorization which allows to compute the probability of cell lines to be sensitive to a drug and thus to classify drug response. To improve the accuracy of the method, gene expression profiles, copy number alterations and single-nucleotide mutation for cell line similarity and chemical structures for drug similarity have been incorporated.

In this scenario fits our work, which has the purpose to address the issue of predicting the sensitivity of a cell line to a drug with a network-based approach based on Non-negative Matrix Tri-Factorization (NMTF), an algorithm designed to factorize an input positive-defined matrix (such as an association matrix of a bipartite graph) in three matrices of non-negative elements. The decomposition has proven to be useful also to predict missing associations. One of the main advantages of NMTF is the possibility to expand the bipartite network integrating several information and thus forming a multi-partite graph; the NMTF algorithm is then used to decompose each of the association matrices, in such a way that the decomposition of each matrix is influenced by the decomposition of the others [10]. The NMTF approach has been used in several domains and in particular it demonstrated to have elevated performances in both finding new indications for approved drugs and new synergistic drug pairs, in particular when including several heterogeneous data types [10, 11]. The main focus of this work is to adapt the model to predict the sensitivity of a cancer cell line to a set of anti-tumor drugs integrating the associations between cell lines and drugs with tissue and gene expression-related data. In the context of precision medicine, the prediction of drug response and sensitivity based on genetic features is becoming of fundamental relevance to speed the emergence of ‘personalized’ therapeutic regimens. Being able to determine a priori to which drugs a patient, with its genomic features, is sensitive or resistant would save a lot of precious time and improve the efficiency of the therapy.

2 Material and Methods

2.1 Datasets

For our experiments, we used the dataset retrieved from the Cancer Cell Line Encyclopedia (CCLE) [3] which comprised the association among 1065 cell lines and 266 antitumor drugs, measured in terms of IC50. In light of the presence of a large amount of missing values in the dataset, we firstly performed a filtering operation that allowed us to reduce them from 20% to 2%, by eliminating both cell lines and drugs with more than the 50% of missing data. Subsequently, we binarized the matrix: since the IC50 is representative of the response of a cell line to a drug, we considered a cell line to be sensitive to a drug if the corresponding IC50 value was lower than a threshold and, on the contrary, a cell line was considered resistant if that value was higher. As threshold for classification we selected the median of IC50 values of each drug, considering all the cell lines. From CCLE we have been able to retrieve also further datasets containing additional information; in particular, we took into consideration tissues of origin of the tumors and the gene expression profiles quantified by RNA-seq experiments. After processing and integrating all these data, as described in detail in Sect. 2.2, we obtained a final dataset containing 379 cell lines and 202 drugs.

2.2 Model

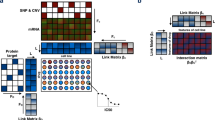
In order to integrate all the available information, we modeled the set of cell lines C, the set of drugs D, the set of tissues T and the set of genes G as the multipartite network in Fig. 1, where each cell line is connected to the drugs to which it is sensitive, the tissue of origin and a set of genes, with the weight of the edge representing the expression of the gene in the cell line.

Fig. 1.

Multipartite graph connecting Tissues, Gene expression, Cell lines and Drugs. The three association matrices of the graph are also indicated.

Such network is equivalent to the set of its association matrices: a binary matrix $X_{CD}$ connecting cell lines to drugs, a binary matrix $X_{TC}$ connecting cell lines to tissues, and a real matrix $X_{GC}$ connecting cell lines to genes. We built the three matrices as follows:

• we represented the IC50 data as a matrix $X\in \overline{\mathbb {R}}^{|C|\times |D|}_{\ge 0}$, being $\overline{\mathbb {R}}_{\ge 0} = \mathbb {R}_{\ge 0} \cup \{+\infty \}$, such that X[i, j] indicates the IC50 value of the j-th drug on the i-th cell line if a measure is available, or $+\infty$ otherwise. We transform X into the binary matrix $X_{CD} \in \{0,1\}^{|C|\times |D|}$, such that:

  $$ X_{CD}[i,j] = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if } X[i,j]< M_{j}\\ 0 &{} \quad \text {otherwise} \end{array}\right. } $$

  where $M_j$ is the median of the IC50 values for the j-th drug that are different from $+\infty$. This step is necessary as different drugs work on different scale of dosage. In other words, we define the i-th cell line to be sensitive to the j-th drug if the IC50 value X[i, j] is lower than the median for that particular drug;

• we built the matrix $X_{TC} \in \{0,1\}^{|T|\times |C|}$ that connects cell lines to tissues as:

  $$ X_{TC}[c,t] = {\left\{ \begin{array}{ll} 1 &{} \quad \text {if }{c}\text { belongs to the tissue }{t}\\ 0 &{} \quad \text {otherwise} \end{array}\right. } $$

• we considered the matrix $X'_{GC} \in \mathbb {R}^{|G|\times |C|}$, where G is a set of genes and $X'_{GC}[g,c]$ represents the RPKM, that means reads per kilobase of transcript, per million mapped reads, measured for the given gene g in the specific cell line c, by a RNA-seq experiment. To select a valuable subset of genes, we retrieved the 1,000 genes with the highest standard deviation of the expression across the cell lines. Then, for each drug (that is each column in the matrix $X_{CD}$) we performed a LASSO [12] feature selection. Finally, we kept into consideration only the 532 genes that are selected as predictive features for at least two drugs and build the matrix $X''_{GC} \in \mathbb {R}^{532\times |C|}$. Finally we performed a minmax scaling on the columns of the matrix and considered the $X_{GC} \in [0,1]^{532\times |C|}$ matrix.

2.3 Method

Let’s consider a multipartite graph $\mathcal {G}$; for the purpose of this work, we can represent the graph as a set of association matrices, that is $\mathcal {G} = \{X_{IJ}\}$, such that each association matrix $X_{IJ} \in \mathbb {R}^{|I|\times |J|}_{\ge 0}$ connects nodes of a set I to nodes of a set J.

We can apply the NMTF method to factorize each association matrix $X_{IJ}$ into three matrices:

$$\begin{aligned} X_{IJ} \cong U_I S_{IJ} V_J^\top \end{aligned}$$

(1)

where $U_I\in \mathbb {R}^{|I|\times k_i}_{\ge 0}$,$S_{IJ}\in \mathbb {R}^{k_i \times k_j}_{\ge 0}$, and $V_J\in \mathbb {R}^{|J|\times k_j }_{\ge 0}$ with $k_i,k_j\in \mathbb {N}$ and $k_i<|I|, k_j<|J|$. The Parameters $k_i$ and $k_j$ are the factorization ranks of NMTF and describe the number of hidden vectors into which we want to represent the $X_{IJ}$ association matrix.

Furthermore, the following constraint has to hold:

$$\begin{aligned} \forall X_{IJ}, X_{JL}\in \mathcal {G},\quad X_{IJ}\cong U_I S_{IJ} V_J^\top , X_{JL}\cong U_J S_{JL} V_L^\top \implies V_J\equiv U_J \end{aligned}$$

(2)

The factorization matrices are computed so as to minimize the objective function based on the Frobenius norm:

$$\begin{aligned} \mathcal {L}(\mathcal {G}|\varTheta ) = \sum _{X_{ij} \in \mathcal {G}} {X_{ij} - U_i S_{ij} V_j^\top }_{Fro}^2 \end{aligned}$$

(3)

where $\varTheta$ represents the set of all the factorization matrices.

A minimum of the objective function can be computed algorithmically by (a) initializing the factorization matrices and (b) applying the following multiplicative update rules:

$$\begin{aligned} U_I \leftarrow U_I \odot \frac{\displaystyle \sum _Q{X_{IQ} V_Q S_{IQ}^\top }+\displaystyle \sum _Q{X_{QI}^\top U_Q S_{QI}}}{\displaystyle \sum _Q{U_I S_{IQ} V_Q^\top V_Q S_{IQ}^\top } +\displaystyle \sum _Q{U_I S_{QI}^\top U_Q^\top U_Q S_{QI}}} \end{aligned}$$

(4)

$$\begin{aligned} V_J \leftarrow V_J \odot \frac{\displaystyle \sum _Q{X_{QJ}^\top U_Q S_{QJ}}+\displaystyle \sum _Q{X_{JQ} V_Q S_{JQ}^\top }}{\displaystyle \sum _Q{V_J S_{QJ}^\top U_Q^\top U_Q S_{QJ}} +\displaystyle \sum _Q{V_J S_{JQ} V_Q^\top V_Q S_{JQ}^\top }} \end{aligned}$$

(5)

$$\begin{aligned} S_{IJ} \leftarrow S_{IJ} \odot \frac{U_I^\top X_{IJ} V_J}{U_I^\top U_I S_{IJ} V_J^\top V_J} \end{aligned}$$

(6)

where $\odot$ and $\frac{~\bullet ~}{~\bullet ~}$ stand for Hadamard element-wise multiplication and division, respectively. Updating rules must be iteratively calculated. We perform 100 warm-up iteration and then we iterate until a stop criterion is met; in our experiments we used $\frac{\mathcal {L}^{i-1} - \mathcal {L}^i}{\mathcal {L}^{i-1}} < 10^{-6}$, where $\mathcal {L}^{i-1}$ and $\mathcal {L}^{i}$ are respectively the values of the loss function after the last and the previous iterations [13].

For matrices initialization, which is a critical aspect of the method, we adopted a k-means approach [14,15,16].

2.4 Prediction of Novel Associations

The prediction of novel associations between two sets of nodes can be interpreted as a matrix completion task. The NMTF method is applied in order to predict novel links between two classes of nodes. In particular, we focused on the associations between cell lines and drugs. After that

$$\tilde{X}_{CD} = U_C S_{CD} V_D^\top $$

has been computed with the following updating rules

$$\begin{aligned} U_C \leftarrow U_C \odot \frac{{X_{CD} V_D S_{CD}^\top }}{{U_C S_{CD} V_D^\top V_D S_{CD}^\top }} \end{aligned}$$

(7)

$$\begin{aligned} V_D \leftarrow V_D \odot \frac{{X_{CD}^\top U_C S_{CD}}}{{V_D S_{CD}^\top U_C^\top U_C S_{CD}}} \end{aligned}$$

(8)

$$\begin{aligned} S_{CD} \leftarrow S_{CD} \odot \frac{U_C^\top X_{CD} V_D}{U_C^\top U_C S_{CD} V_D^\top V_D} \end{aligned}$$

(9)

we applied a threshold $\tau$, typically $0<\tau <1$, and we considered that the i-th cell line is associated with the j-th drug if the predicted value $\tilde{X}_{CD}[i,j]>\tau$.

2.5 Prediction of the Whole Drug Profile for a New Cell Line

Another scenario is when a novel cell line is included in the network. In this situation, while we know the genetic feature of the cell line and its tissue of origin, we do not have information about the drugs to which it is sensitive.

We here propose a slight modification of the NMTF multiplicative update rules, in order to being able to predict the complete drug profile for the novel cell line. Since we have no correct information in the matrix we aim to reconstruct for the novel cell line, we do not consider the influence of $X_{CD}$ during the update of $U_C$ matrix. Thus, the new rules to update U (for our network) were:

$$\begin{aligned} U_C \leftarrow U \odot \frac{X_{TC}^\top U_T S_{TC}}{U_C S_{TC}^\top U_T^\top U_T S_{TC}} \end{aligned}$$

(10)

$$\begin{aligned} U_C \leftarrow U \odot \frac{X_{GC}^\top U_G S_{GC}}{U_C S_{GC}^\top U_G^\top U_G S_{GC}} \end{aligned}$$

(11)

when only $X_{TC}$ or $X_{GC}$ are taken into account, while

$$\begin{aligned} U_C \leftarrow U \odot \frac{X_{TC}^\top U_T S_{TC} + X_{GC}^\top U_G S_{GC}}{U_C S_{TC}^\top U_T^\top U_T S_{TC} + U_C S_{GC}^\top U_G^\top U_G S_{GC}} \end{aligned}$$

(12)

when both $X_{TC}$ and $X_{GC}$ are added to the network. Updating rules for V and S remained unvaried with respect to 8 and 9.

3 Results

Here, we report the results of different trials that we performed on the dataset illustrated in Sect. 2.1. In particular, we apply NMTF method, illustrated in Sect. 2.3, for two different tasks: the prediction of novel cell line-drug associations and the prediction of the drug profile for a new cell line. We evaluate our results using the AUROC (that means area under the receiver operating characteristic curve) and the comparison between the actual IC50 values of pairs predicted sensitive ($\tilde{X}_{CD}>0.6$) and predicted resistant ($\tilde{X}_{CD}<0.4$).

3.1 Prediction of Novel Associations

In order to validate the model, we apply a mask that covers randomly the 5% of the association matrix $X_{CD}$. We run the method on the single matrix $X_{CD}$ without passing other information and we compute the evaluation metrics, testing various combination of the parameter k1 and k2. The best configuration corresponds to $k1=25$ and $k2=15$. With these parameters the model performs well and leads to a AUROC equal to 0.84417 as shown in Fig. 2a. On the best configuration we run also the Welch test, a two-sample location test which is used to test the hypothesis that two populations have equal means and is more reliable when the two samples have unequal variances and possibly unequal sample sizes. Comparing the two box plots, the predicted sensitive and resistant associations appear to be significantly different (p-val $\approx$ 0.0). Results are shown in Fig. 2b.

Fig. 2.

Performances using a random mask on $X_{CD}$; (a) reports the ROC curve with several values of k1 and k2, where k1 and k2 are the factorization ranks of the NMTF. The best configuration corresponds to k1 = 25 and k2 = 15; (b) Boxplots of the IC50 values, divided by the means, of the predicted sensitive and resistant pairs using a random mask on $X_{CD}$, with the best configuration.

3.2 Prediction of the Whole Drug Profile for a New Cell Line

In this case, we apply a mask on a single row of the matrix $X_{CD}$ in order to simulate the addition of a novel cell line.

Considering only $X_{CD}$ matrix does not provide meaningful results, as shown in Fig. 3a, 3b. As expected, without any additional information, the AUROC is 0.50506, and the two classes are not different. This result proves that it is impossible to predict a complete drug profile for a novel cell line without considering other data.

Fig. 3.

Performances using a mask on a single row of $X_{CD}$ with k1 = 25 and k2 = 15, where k1 and k2 are the factorization ranks of NMTF. (a) ROC curve using a mask on a single row on $X_{CD}$. (b) Boxplots of the IC50 of the predicted sensitive and resistant pairs using a mask on a single row of $X_{CD}$.

Thus, we tested the method by also adding the $X_{TC}$ matrix alone, $X_{GC}$ matrix alone as well as the two together.

The AUROCs in Fig. 4a proves that adding information increases the performances of the predictor. Including the tissue of origin, the method is able to reach an AUROC = 0.60244. If also gene expressions are added to the model, we observe a significant improvement (AUROC = 0.71063). Finally, when both gene expressions and tissues of origin are considered, and the AUROC increases to 0.71163. In Fig. 4b the comparison between predicted resistant and sensitive drugs, when all the information is used, is shown; the Welch test confirms the difference in the distribution of the two classes (p-val = ${9.302 32\times 10^{-18}}$), with the IC50 of the predicted sensitive drugs clearly below the median.

Fig. 4.

Performances using a mask on a single row of $X_{CD}$ considering also $X_{TC}$ and $X_{GC}$ with k1 = 25, k2 = 15, k3 = 5, k4 = 30, where k1, k2, k3, k4 are the factorization ranks of NMTF. (a) ROC curves using a mask on a single row of $X_{CD}$ considering also $X_{TC}$ and $X_{GC}$. (b) Boxplots of the IC50 of the predicted sensitive and resistant pairs using a mask on a single row of $X_{CD}$ considering also $X_{TC}$ and $X_{GC}$.

4 Discussion and Concluding Remarks

One of the main obstacles in the treatment of cancer is its heterogeneity, which leads to a difference in the response of patients with the same cancer to the same drug [17, 18]. In this context, computer-based approaches can be very powerful tools in order to identify in advance which drugs a patient is sensitive to and to which drugs does not respond instead [19]. To reach this goal, we proposed a network-based method which exploits Non-Negative Matrix Tri-Factorization algorithm for the prediction of the sensitiveness of a patient, which is represented by the cell line extracted from his tumor mass, to a drug. We performed the experiments on a dataset retrieved from CCLE, which contains cell lines and antitumor drugs linked by means of their IC50 values. In our work, we demonstrated that predicting the sensitivity of a specific drug for a given cell line for which many IC50 experiments are available is a rather easy task. In our experiments, using plain NMTF method without additional information for this task allows to reach high performances (AUROC = 0.84417). On the contrary, predicting drug sensitivity profile for a novel cell line is more complex: indeed, NMTF method without other data scores as bad as a random predictor.

To overcome this limitation, we proposed a two-fold solution: (a) we developed an improved version of NMTF algorithm, which generates predictions taking into account only meaningful information, and (b) we integrated other information, namely the tissues of origin and the gene expressions of the corpus of cell lines. When all the available data are provided, the proposed method shows much better performances: the resulted AUROC is equal to 0.71163.

Our results suggest that NMTF is a valid method for the prediction of sensitiveness and resistance of a patient to a drug. In particular, the method gives very high results for the matrix completion task, meaning that with this approach is easy to predict novel sensitivity or resistance associations to missing drugs, even without adding further information to the primary association matrix. Instead, for new cell lines with no previous connections to drugs the prediction is a little more complicated and the link with more data matrices is needed. Indeed, the initial value of prediction is quite low, but it increases adding patient related data. In particular, it has only a 5% increase adding just the tissues matrix, while the addition of gene expression data leads to a higher 10% increase of the AUROC value. However, the employment of both matrices causes a slight increase of the AUROC value with respect to the use of gene expression data alone. This confirms the hypothesis that, since each cell line is linked only to one tissue, information about tissues are poorly informative and supply a minor contribution to the prediction compared to gene expression data.

Finally, to test the effect and the need of NMTF with respect to a baseline method, we computed a leave-one-out validation for 202 binary logistic regressors (one for each drug). Each predictor uses as feature the gene expression of a cell and the one-hot-encoding of the tissues, and as label the response of the cell for the drug associated to the regressor. The average AUROC of this experiment is 0.69128, thus performing almost the 3% worse than NMTF.

As future development we would like to enlarge the network to further improve the performance. Moreover, we want to implement a regression method in order to being able to predict also the weight of the connection, that means the IC50 value.

To conclude, we believe that our method could certainly help to find more rapidly the right therapy for the patient, saving time and providing the best treatment from the start, which is one of the most critical part in the discovery of the correct therapeutic plan of a person. Indeed, for a patient with cancer, time is the most important resource and a “trial-and-error” approach is not the most advantageous way to proceed in finding the right cure. A priori knowledge of which drug will work and which will not on each specific patient should become one of the fundamental strongholds in the context of precision medicine based treatments.