On the Transversal Number of Rank k Hypergraphs

Abstract

For $k\ge 2$, let H be a hypergraph with rank k on n vertices and m edges. The transversal number $\tau (H)$ is the minimum number of vertices that intersect every edge. In this paper, the following conjecture is proposed: Is $\tau (H)\le \frac{(k-1)m+1}{k}$? We prove the inequality in some special hypergraphs: (i) the inequality holds for $k=2$ and $k=3$. (ii) the inequality holds for the hypergraphs with the König Property. (iii) the inequality holds for the hypergraphs with maximum degree 2 and the extremal hypergraphs with equality holds are characterized.

Supported by National Natural Science Foundation of China under Grant No.11901605, No.12101069, the disciplinary funding of Central University of Finance and Economics, the Emerging Interdisciplinary Project of CUFE, the Fundamental Research Funds for the Central Universities and Innovation Foundation of BUPT for Youth (500422309).

1 Introduction

A hypergraph is a generalization of a graph in which an edge can join any number of vertices. A simple hypergraph is a hypergraph without multiple edges. Let $H=(V,E)$ be a simple hypergraph with vertex set V and edge set E. As for a graph, the order of H, denoted by n, is the number of vertices. The number of edges will be denoted by m. The rank is $r(H)=max_{e\in E}|e|$.

For each vertex $v\in V$, the degree d(v) is the number of edges in E that contains v. We say v is an isolated vertex of H if $d(v)=0$. Hypergraph H is k-regular if each vertex’s degree is k ($d(v)=k, \forall v\in V$). The maximum degree of H is $\varDelta (H) = \max _{v\in V}d(v)$. Hypergraph H is k-uniform if each edge contains exactly k vertices ($|e|=k, \forall e\in E$). Hypergraph H is called linear if any two distinct edges have at most one common vertex. ($| e_{1}\cap e_{2}|\le 1,\forall e_{1},e_{2}\in E$).

Let $k\ge 2$ be an integer. A cycle of length k, denoted as k-cycle, is a vertex-edge sequence $C= v_{1}e_{1}v_{2}e_{2}\cdots v_{k}e_{k}v_{1}$ with: $(1) \{e_{1}, e_{2},\ldots ,e_{k}\}$ are distinct edges of H. $(2) \{v_{1}, v_{2},\ldots , v_{k}\}$ are distinct vertices of H. $(3) \{v_{i},v_{i+1}\}\subseteq e_{i}$ for each $i\in [k]$, here $v_{k+1}=v_{1}$. We consider the cycle C as a sub-hypergraph of H with vertex set $\{v_{i}, i\in [k]\}$ and edge set $\{e_{j}, j\in [k]\}$. For any vertex set $S\subseteq V$, we write $H\setminus S$ for the sub-hypergraph of H obtained from H by deleting all vertices in S and all edges incident with some vertices in S. For any edge set $A\subseteq E$, we write $H\setminus A$ for the sub-hypergraph of H obtained from H by deleting all edges in A and keeping vertices. If S is a singleton set $\{s\}$, we write $H\setminus s$ instead of $H\setminus \{s\}$.

Given a hypergraph H(V, E), a set of vertices $S\subseteq V$ is a vertex transversal if every edge has at least a vertex in S which means that $H\setminus S$ has no edges. The vertex transversal number is the minimum cardinality of a vertex transversal, denoted by $\tau (H)$. A set of edges $A\subseteq E$ is an edge cover if every vertex is adjacent to at least an edge in A. The edge covering number is the minimum cardinality of an edge cover, denoted by $\tau '(H)$. A set of edges $A\subseteq E$ is a matching if every two distinct edges have no common vertex. The matching number is the maximum cardinality of a matching, denoted by $\nu (H)$. In this paper, we consider the vertex transversal set in simple hypergraphs with rank k.

1.1 Known Results

Hypergraphs are systems of sets which are conceived as natural extensions of graphs. A subset S of vertices in a hypergraph H is a transversal (also called vertex cover or hitting set in many papers) if S has a nonempty intersection with every edge of H. The transversal number $\tau (H)$ of H is the minimum size of a transversal in H. Transversals in hypergraphs are well studied in the literature (see [5, 10, 11, 13,14,15, 17, 18]).

Chvátal and McDiarmid [5] established the following upper bound on the transversal number of a uniform hypergraph in terms of its order and size.

Theorem 1

[5] For $k\ge 2$, if H is a k-uniform hypergraph on n vertices with m edges, then $\tau (H)\le \frac{n+\lfloor \frac{k}{2}\rfloor m}{\lfloor \frac{3k}{2}\rfloor }$.

Henning and Yeo [8] proposed the following question:

Conjecture 1

[8] For $k\ge 2$, let H be a k-uniform hypergraph on n vertices with m edges. If H is linear, then $(k+1)\tau (H)\le n+m$ holds for all $k\ge 2$?

The Chvátal and McDiarmid theorem implies that $(k+1)\tau (H)\le n+m$ holds for $k\in \{2,3\}$ even without the linearity constraint imposed on H. Henning and Yeo [8] remarked that if H is not linear, then conjecture 1 is not always true, showing an example by taking $k=4$ and letting $\overline{F_{7}}$ be the complement of the Fano plane $F_{7}$. Henning and Yeo [8] proved the following theorem which verified conjecture 1 for linear hypergraphs with maximum degree two:

Theorem 2

[8] For $k\ge 2$, let H be a k-uniform linear hypergraph satisfying $\varDelta (H)\le 2$. Then, $(k+1)\tau (H)\le n+m$ with equality if and only if each component of H consists of a single edge or is the dual of a complete graph of order $k+1$ and k is even.

Henning and Yeo [12] proposed the following conjecture in another paper:

Conjecture 2

[12] $\tau (H)\le \frac{n}{k}+\frac{m}{6}$ holds for all uniform hypergraphs with maximum degree at most 3.

Henning and Yeo [12] showed that $\tau (H)\le \frac{n}{k}+\frac{m}{6}$ holds when $k=2$ and characterized the hypergraphs for which equality holds. Chvátal and McDiarmid [5] showed that $\tau (H)\le \frac{n}{k}+\frac{m}{6}$ holds when $k=3$. Henning and Yeo characterized the extremal hypergraphs. Henning and Yeo [12] showed that $\tau (H)\le \frac{n}{k}+\frac{m}{6}$ holds when $\varDelta (H)\le 2$ and characterized the hypergraphs for which it holds with equality in that case.

1.2 Our Results

In this paper, for $k\ge 2$, we propose a conjecture as follows:

Conjecture 3

For every connected rank k hypergraph H(V, E) with m edges, $\tau (H)\le \frac{(k-1)m+1}{k}$.

By a simple operation of adding vertices, it is easy to show if the conjecture holds in k-uniform hypergraphs, then it holds in hypergraphs with rank k. To prove the conjecture, it only needs to consider k-uniform hypergraphs.

For k-uniform hypergraphs, Conjecture 3 and Conjecture 1 are related. If Conjecture 1 holds, combined with the relationship between vertex number and edge number of connected rank k hypergraphs: $n\le (k-1)m+1$, we have

$$\begin{aligned} (k+1)\tau (H)\le n+m, n\le (k-1)m+1\Rightarrow \tau (H)\le \frac{n+m}{k+1}\le \frac{km+1}{k+1}, \end{aligned}$$

which is a weaker result of Conjecture 3. The main content of the article is organized as follows:

• In Sect. 2, we transform the conjecture on hypergraphs with rank k to the conjecture on k-uniform hypergraphs. For the consequent sections, we prove Conjecture 3 holds in some special hypergraphs.

• In Sect. 3, we prove Conjecture 3 holds for $k=2$.

• In Sect. 4, we prove Conjecture 3 holds for $k=3$.

• In Sect. 5, we prove Conjecture 3 holds for the hypergraphs satisfying the König Property with $\tau (H)=\nu (H)$.

• In Sect. 6, we prove Conjecture 3 holds for the hypergraphs with maximum degree 2 and characterize the extremal hypergraphs with equality holds.

2 The Conjecture

Conjecture 3 is our central problem and restated as follows:

For every connected rank k hypergraph H(V, E) with m edges, $\tau (H)\le \frac{(k-1)m+1}{k}$.

The next lemma tells us to prove Conjecture 3, it just needs to focus on uniform hypergraphs. The basic method in the proof of Lemma 1 is frequently used later.

Lemma 1

If the conjecture holds in connected k-uniform hypergraphs, then it holds in connected hypergraphs with rank k.

Proof

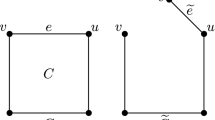
Let H be a connected hypergraph with rank k. If H is not k-uniform, we can construct a connected k-uniform hypergraph $H'$ by adding new vertices to each edge. As shown in Fig. 1, for each edge e in H, if $|e|< k$, add $k-|e|$ new vertices to form an edge $e'$ in $H'$. We derive that edge number does not change and $\tau (H)=\tau (H')$, which completes the proof.

Fig. 1.

Adding new vertices to form k-uniform hypergraphs

The following sections will consider Conjecture 3 in some special cases.

3 The Rank 2 Hypergraphs

In this section, we prove Conjecture 3 holds for the rank 2 hypergraphs. Such hypergraphs are actually general graphs.

Theorem 3

For any connected graph G(V, E) with m edges, $\tau (G)\le \frac{m+1}{2}$.

Proof

Suppose the theorem fails. Let us take out a counterexample $G=(V,E)$ with minimum number of edges, thus $\tau (G)>\frac{m+1}{2}$. For any vertex $v\in V$, let $C_1,C_2,\ldots ,C_p$ be p components of $G\setminus v$ and $C_i$ contains $m_i$ edges for $i\in [p]$. Thus, $d(v)\ge p$. We have

$$\frac{m+1}{2}<\tau (G)\le \tau (G\setminus v) + 1\le \sum _{i=1}^p\frac{m_i+1}{2}+1=\frac{m-d(v)+p}{2}+1\le \frac{m+2}{2}.$$

Then, we derive that $\tau (G) = \frac{m+2}{2}$, $p = d(v)$ and $\tau (C_i)=\frac{m_i+1}{2}$ for $i\in [p]$. Due to the arbitrariness of vertex v and the fact that $p = d(v)$, G contains no cycles. Thus, G is tree with $m+1$ vertices and satisfies the König property [7] $\tau (G)=\nu (G)$. We have $\tau (G)=\nu (G)\le \frac{m+1}{2}$, which is a contradiction.

Remark 1

For any connected graph, Theorem 3 implies a polynomial-time algorithm for computing a vertex transversal with cardinality no more than $\frac{m+1}{2}$.

Next, we establish a necessary condition of the extremal graphs G with m edges satisfying $\tau (G)=\frac{m+1}{2}$.

Theorem 4

If a connected graph G(V, E) with m edges satisfies that $\tau (G)=\frac{m+1}{2}$, then every block of G is an edge or a cycle, where a block is a maximal biconnected subgraph.

Proof

For any block B of G, take arbitrarily a vertex v in B. Suppose that $C_1,C_2,\ldots ,C_p$ are all components of $G\setminus v$ and $C_i$ contains $m_i$ edges. According to Theorem 3, we have

$$\frac{m+1}{2}=\tau (G)\le \tau (G\setminus v) + 1\le \sum _{i=1}^p\frac{m_i+1}{2}+1=\frac{m-d(v)+p+2}{2}.$$

Thus, $m+1\le m-d(v)+p+2$, which means $d(v)\le p+1$. Since $d(v)\ge p$, we know that v has at most two adjacent vertices in B. If v has only one adjacent vertex in B, then B is an edge. If v has exactly two adjacent vertices in B, by the arbitrariness of v in B, then B is a cycle.

Remark 2

According to the result of Theorem 4, the extremal graphs belong to the partial 2-tree graph classes [3]. For the graphs with bounded tree width, the optimal vertex transversal can be computed in linear time in [2]. Then we derive a linear time algorithm to decide whether a m-edge graph G possesses the property $\tau (G)=\frac{m+1}{2}$.

4 The Rank 3 Hypergraphs

In this section, we prove Conjecture 3 holds for the rank 3 hypergraphs. This is an immediate corollary of the results by Chen [4]. Furthermore, Diao [6] characterize the extremal 3-uniform hypergraphs with equality holds. This demonstrates a polynomial-time algorithm to decide whether a rank 3 hypergraph is extremal.

Theorem 5

[4] For every 3-uniform connected hypergraph H(V, E) with m edges, $\tau (H)\le \frac{2m+1}{3}$.

Theorem 6

[6] For every 3-uniform connected hypergraph H(V, E) with m edges, $\tau (H)= \frac{2m+1}{3}$ if and only if H(V, E) is a hypertree with perfect matching.

Combined with Lemma 1, the next two corollaries are derived immediately.

Corollary 1

For every connected rank 3 hypergraph H(V, E) with m edges, $\tau (H)\le \frac{2m+1}{3}$.

Corollary 2

For every connected rank 3 hypergraph H(V, E) with m edges, $\tau (H)= \frac{2m+1}{3}$, then H(V, E) is a hypertree with perfect matching.

Remark 3

For a hypertree, there is a polynomial-time algorithm to compute the vertex transversal number. Thus for every connected hypergraph H(V, E) with rank 3, it is decidable whether $\tau (H)= \frac{2m+1}{3}$ holds in polynomial time.

5 The Hypergraphs with König Property

In this section, we prove Conjecture 3 holds for the hypergraphs with the König Property. A hypergraph H has the König Property [1] if the transversal number is equal to the matching number: $\tau (H)=\nu (H)$.

Lemma 2

For every connected rank k hypergraph H(V, E) with n vertices and m edges, $n\le (k-1)m+1$.

Proof

We prove this lemma by induction on m. When $m=0$, H(V, E) is an isolate vertex, $n\le (k-1)m+1$ holds on. Assume this lemma holds on for $m\le k$. When $m=k+1$, take arbitrarily one edge e and consider the subgraph $H\setminus e$. Obviously, $H\setminus e$ has at most k components. Assume $H\setminus e$ has p components $H_{i}(V_{i},E_{i})$ with $n_{i}=|V_{i}|$ and $m_{i}=|E_{i}|$ for each $i\in [p]$. Then by induction, $n_{i}\le (k-1)m_{i}+1$ holds on. So we have

$$\begin{aligned} n=n_{1}+\cdots +n_{p}\le (k-1)m_{1}+\cdots +(k-1)m_{p}+p=(k-1)(m-1)+p\le (k-1)m+1, \end{aligned}$$

which completes the proof.

Lemma 3

Let H(V, E) be a k-uniform connected hypergraph with m edges. If H has the König Property, then $\tau (H)\le \frac{(k-1)m+1}{k}$.

Proof

According to the König Property and Lemma 2, we have the following inequalities:

$$\begin{aligned} \tau (H)=\nu (H)\le \frac{n}{k}\le \frac{(k-1)m+1}{k}. \end{aligned}$$

According to Lemma 1 and Lemma 3, the next theorem is derived directly.

Theorem 7

Let H(V, E) be a connected rank k hypergraph with m edges. If H has the König Property, then $\tau (H)\le \frac{(k-1)m+1}{k}$.

Proof

Let H be a connected hypergraph with rank k. H has the König Property with $\tau (H)=\nu (H)$. If H is not k-uniform, we can construct a connected k-uniform hypergraph $H'$ by adding new vertices to each edge. As shown in Fig. 1, for each edge e in H, if $|e|< k$, add $k-|e|$ new vertices to form an edge $e'$ in $H'$. During this process, the edge number does not change and $\tau (H)=\tau (H'), \nu (H)=\nu (H')$. Thus, the new hypergraph $H'$ maintains the König property with $\tau (H')=\nu (H')$. According to Lemma 3, we have

$$\begin{aligned} \tau (H')\le \frac{(k-1)m+1}{k}, \tau (H)=\tau (H')\Rightarrow \tau (H)\le \frac{(k-1)m+1}{k}. \end{aligned}$$

6 The Hypergraphs with Maximum Degree 2

In this section, we prove Conjecture 3 holds for the hypergraphs with maximum degree 2 and characterize the extremal hypergraphs with equality holds. These results are proved by the dual hypergraphs. For a hypergraph H(V, E), the dual hypergraph [1] $H^{*}(V^{*},E^{*})$ is a hypergraph whose vertices $V^{*}$ correspond to the edges E of H and edges $E^{*}$ correspond to the vertices V of H. Denote that $n = |V|$, $m = |E|$, $n^*= |V^*|$ and $m^*= |E^*|$. We have the following relationships of parameters between a hypergraph and its dual hypergraph: (i) $n^*= m$; (ii) $m^*= n$; (iii) $\tau (H) = \tau ^\prime (H^*)$.

6.1 The Bound of Hypergraphs with Maximum Degree 2

In this subsection, we prove Conjecture 3 holds for the hypergraphs with maximum degree 2. For a hypergraph H(V, E) with maximum degree 2, its dual hypergraph is a multi-graph $G^{*}(V^{*},E^{*})$. The transversal number $\tau (H)$ corresponds to the edge covering number $\tau '(G^{*})$. The edge covering number is related to the matching number by the theorem of Gallai [9]. The content of proof is organized as follows:

• An lower bound of matching number is proven by Lemmas 4, 5 and 6.

• An upper bound of edge covering number is proven by Lemma 7.

• Conjecture 3 for the hypergraphs with maximum degree 2 is proven by Theorem 9.

Theorem 8

[9] [Gallai’s Theorem]For every connected graph G(V, E) with n vertices and the minimum degree $\delta (G)>0$, $\nu (G)+\tau '(G)=n$.

Lemma 4

For every tree T(V, E) with m edges and $\varDelta (T)\le k$, $\nu (T)\ge \frac{m}{k}$.

Proof

We prove this lemma by contradiction. Let us take out the counterexample T(V, E) with minimum edges. Thus $d(v)\le k$ for each $v\in V$ and $\nu (T)< \frac{m}{k}$. Obviously T(V, E) has at least three vertices. The longest path in T is p, which connects one leaf $v_{1}$ to another leaf $v_{2}$, as shown in Fig. 2. v is the only adjacent vertex of $v_{1}$. The degree of v is d(v) and $T\setminus v$ has d(v) components, denoted as $\{T_{i},1\le i\le d(v)\}$.

Fig. 2.

The longest path p between leaves $v_1$ and $v_2$

Claim 1: $\nu (T\setminus v)\ge \frac{m-k}{k}$.

T is the counterexample with minimum edges, thus $\nu (T_{i})\ge \frac{m_{i}}{k}$. Combined with $d(v)\le k$, we have the following inequality:

$$\begin{aligned} \nu (T\setminus v)= \sum _{1\le i\le d(v)}\nu (T_{i})\ge \sum _{1\le i\le d(v)}\frac{m_{i}}{k}=\frac{m-d(v)}{k}\ge \frac{m-k}{k}. \end{aligned}$$

Claim 2: $\nu (T)\ge \nu (T\setminus v)+1$.

$v_{1}$ is a leaf in T. For every matching M in $T\setminus v$, $M\cup e(v_{1},v)$ is a matching in T.

According to these claims, we have the following inequality:

$$\begin{aligned} \nu (T)\ge \nu (T\setminus v)+1\ge \frac{m-k}{k}+1=\frac{m}{k}, \end{aligned}$$

which is a contradiction with $\nu (T)< \frac{m}{k}$.

Lemma 5

For every tree T(V, E) with n vertices and $\varDelta (T)\le k$, $\nu (T)\ge \frac{n-1}{k}$.

Proof

Every tree T(V, E) has $m=n-1$. According to Lemma 4, $\nu (T)\ge \frac{n-1}{k}$ holds.

Lemma 6

For every connected graph G(V, E) with n vertices and $\varDelta (G)\le k$, $\nu (G)\ge \frac{n-1}{k}$.

Proof

Take out a spanning tree T of G. According to Lemma 5, $\nu (G)\ge \nu (T)\ge \frac{n-1}{k}$.

Lemma 7

For every connected graph G(V, E) with n vertices and $\varDelta (G)\le k$, $\tau '(G)\le \frac{(k-1)n+1}{k}$.

Proof

According to Theorem 8 and Lemma 6, $\tau '(G)=n-\nu (G)\le n-\frac{n-1}{k}=\frac{(k-1)n+1}{k}$ holds.

Theorem 9

Let H(V, E) be a connected hypergraph with m edges and rank k. If maximum degree of H is no more than 2, then $\tau (H)\le \frac{(k-1)m+1}{k}$.

Proof

Consider the dual hypergraph $H^{*}(V^{*},E^{*})$ of H whose vertices correspond to the edges of H and edges correspond to the vertices of H. A vertex transversal in H correspond to an edge cover in $H^{*}$. Thus we have

$$\begin{aligned} n^{*}=m,m^{*}=n,\tau (H)=\tau '(H^{*}),\tau (H)\le \frac{(k-1)m+1}{k}\Leftrightarrow \tau '(H^{*})\le \frac{(k-1)n^{*}+1}{k}. \end{aligned}$$

The rank of H is k, which means every edge of H contains at most k vertices. Thus every vertex’s degree is at most k in $H^{*}$. The maximum degree of H is no more than 2, thus every edge of $H^{*}$ contains at most 2 vertices. This means the hypergraph $H^{*}$ is a multigraph, denoted by $G^{*}$. Delete the loops and multiedges to a simple graph. The deleting operations do not change the edge covering number. According to Lemma 7, $\tau '(G^{*})\le \frac{(k-1)n^{*}+1}{k}$, which means $\tau (H)\le \frac{(k-1)m+1}{k}$.

6.2 The Extremal Hypergraphs with Maximum Degree 2

In this subsection, we characterize the extremal hypergraphs with maximum degree 2, meaning the equality $\tau (H)= \frac{(k-1)m+1}{k}$ holds. As shown before, the maximum degree restricts its dual hypergraph is a multi-graph. The transversal number of a hypergraph corresponds to the edge covering number of its dual multi-graph. For a graph, the edge covering number is related to the matching number by the theorem of Gallai [9]. The content of proof is organized as follows:

• An family of graphs called k -star tree is introduced by Definitions 1, 2, 3 and Lemma 8.

• The extremal graphs with matching number are characterized by Lemmas 9, 10 and 11.

• The extremal graphs with edge covering number are characterized by Lemma 12.

• The extremal maximum degree 2 hypergraphs with transversal number are characterized by Theorem 10.

Recall that k-star is a $(k+1)$-vertex tree with k leaves and the central vertex of a k-star is the k-degree vertex. Then we introduce the definition of k-star tree.

Definition 1

For $k \ge 3$, a tree T(V, E) is called a k -star tree if it satisfies

• Each vertex’s degree is no more than k.

• The edges of T can be decomposed into several k-stars.

Definition 2

For a k-star tree T(V, E), the central vertices of k-stars are called central vertices and other vertices are called noncentral vertices. The vertices connecting different k-stars are called adjacent vertices. Noncentral vertices are formed by adjacent vertices and leaves.

Definition 3

For a k-star tree T(V, E), the structure tree describes the structure of T as formed by its k-stars. Let A denote the set of adjacent vertices of T, and B the set of its k-stars. Then, we have a natural tree $T'(A\cup B,E')$ on vertex set $A\cup B$ formed by the edges $e'(a,b)\in E'$ with $a\in A$, $b\in B$ and $a\in b$, which means the adjacent vertex a belongs to the k-star b in T. An example is shown in Fig. 3.

Fig. 3.

A k-star tree, where the squares, the hollow dots and the solid dots are central vertices, adjacent vertices and leaves, respectively.

Lemma 8

For a k-star tree T(V, E), there is a unique k-star decomposition of T.

Proof

Let p be the number of k-stars in T. This proof can be finished by induction on p.

• When $p=0$, T is an isolated vertex and there is a unique k-star decomposition.

• When $p=1$, T is a k-star and there is a unique k-star decomposition.

• Assume the lemma holds for $p\le t$. When $p=t+1$, let us consider the structure tree $T'$ of the k-star tree T. $v'$ is a leaf in $T'$ and $S_{v'}$ is the corresponding k-star in T. v is the central vertex of $S_{v'}$, as shown in Fig. 4. $T\setminus v$ is also a k-star tree and the number of k-stars in $T\setminus v$ is exactly t. By induction, there is a unique k-star decomposition D in $T\setminus v$. Thus $D\cup S_{v'}$ is the unique k-star decomposition in T. The lemma holds for $p= t+1$. Therefore, the lemma holds for every k-star tree.

Fig. 4.

The central vertex v in k-star tree T

Lemma 9

For every tree T(V, E) with $m\ge 2$ edges and $\varDelta (T)\le k$, $\nu (T)= \frac{m}{k}$ if and only if T is a k-star tree.

Proof

Necessity: T(V, E) is a tree with $\varDelta (T)\le k$ and $\nu (T)= \frac{m}{k}$ holds. It needs to show T is a k-star tree. Since $m\ge 2$, T(V, E) has at least three vertices. Take out a leaf u in T arbitrarily and v is the only adjacent vertex of u. The degree of v is d(v) and $T\setminus v$ has d(v) components, denoted as $\{T_{i},1\le i\le d(v)\}$.

Claim 1: $\nu (T\setminus v)\ge \frac{m-k}{k}$.

According to Lemma 4, $\nu (T_{i})\ge \frac{m_{i}}{k}$. Combined with $d(v)\le k$, we have the following inequality:

$$\begin{aligned} \nu (T\setminus v)= \sum _{1\le i\le d(v)}\nu (T_{i})\ge \sum _{1\le i\le d(v)}\frac{m_{i}}{k}=\frac{m-d(v)}{k}\ge \frac{m-k}{k}. \end{aligned}$$

Claim 2: $\nu (T)\ge \nu (T\setminus v)+1$.

u is a leaf in T. For every matching M in $T\setminus v$, $M\cup e(u,v)$ is a matching in T.

According to these claims, we have the following inequality:

$$\begin{aligned} \nu (T)\ge \nu (T\setminus v)+1\ge \frac{m-k}{k}+1=\frac{m}{k}. \end{aligned}$$

Combined with $\nu (T)= \frac{m}{k}$, we have $\nu (T\setminus v)=\frac{m-k}{k}$. This means the degree of v is exactly k and in $T\setminus v$, each component $\{T_{i},1\le i\le d(v)\}$ satisfies $\nu (T_{i})= \frac{m_{i}}{k}$ holds.

Take out $\{T_{i},1\le i\le d(v)\}$ as T and repeat the above analysis process. Finally, there are some isolated vertices. Denote the deleted vertices as $\{v_{j},1\le j\le t\}$. A k-star $S_{j}$ is deleted when $v_{j}$ is deleted. Thus the edges of T can be decomposed into several k-stars. According to Definition 1, T is a k-star tree.

Sufficiency: T is a k-star tree. It needs to show $\nu (T)= \frac{m}{k}$. Let p be the number of k-stars in T. We do induction on p.

• When $p=0$, T is an isolated vertex and $\nu (T)= \frac{m}{k}$ holds.

• When $p=1$, T is a k-star and $\nu (T)= \frac{m}{k}$ holds.

• Assume the sufficiency holds for $p\le t$. When $p=t+1$, let us consider the structure tree $T'$ of the k-star tree T. $v'$ is a leaf in $T'$ and $S_{v'}$ is the corresponding k-star in T. v is the central vertex of $S_{v'}$, as shown in Fig. 4. $T\setminus v$ is also a k-star tree and the number of k-stars in $T\setminus v$ is exactly t. By induction, $\nu (T\setminus v)= \frac{m-k}{k}$ holds. Thus we have

  $$\begin{aligned} \nu (T)= \nu (T\setminus v)+1= \frac{m-k}{k}+1= \frac{m}{k}. \end{aligned}$$

  The sufficiency holds for $p= t+1$. Therefore, the sufficiency holds for every k-star tree.

Remark 4

The above proof also demonstrates a polynomial-time algorithm to decide whether a tree T is a k-star tree. In addition, If T is a k-star tree, the algorithm gives the unique k-star decomposition.

Lemma 10

For every tree T(V, E) with n vertices and $\varDelta (T)\le k$, $\nu (T)= \frac{n-1}{k}$ if and only if T is a k-star tree.

Proof

Every tree T(V, E) has $m=n-1$ edges. According to Lemma 9, $\nu (T)= \frac{n-1}{k}$ if and only if T is a k-star tree.

Lemma 11

For every connected graph G(V, E) with n vertices and $\varDelta (G)\le k$, $\nu (G)= \frac{n-1}{k}$ if and only if G is a k-star tree.

Proof

Sufficiency: G is a k-star tree. According to Lemma 10, $\nu (G)= \frac{n-1}{k}$ holds.

Necessity: G(V, E) is a connected graph with $\varDelta (G)\le k$, $\nu (G)= \frac{n-1}{k}$. It needs to show G is a k-star tree. Take out arbitrarily a spanning tree T of G. According to Lemma 5, we have

$$\begin{aligned} \nu (G)\ge \nu (T)\ge \frac{n-1}{k},\nu (G)= \frac{n-1}{k}\Rightarrow \nu (T)= \frac{n-1}{k}. \end{aligned}$$

According to Lemma 10, T is a k-star tree. By arbitrariness, the next claim holds.

Claim 1: Each spanning tree in G is a k-star tree.

T is a k-star tree. The vertices are divided into central vertices and noncentral vertices. Central vertices are only connected with noncentral vertices and vice versa. Thus the next claim holds.

Claim 2: For each path p in T, central vertices and noncentral vertices are adjacent in p.

We will show G is T. This is proved by contradiction. Suppose there is an edge $e(u,v)\in G\setminus T$. T is a k-star tree. According to Definition 2, the vertices are divided into central vertices and noncentral vertices. Noncentral vertices are divided into adjacent vertices and leaves. Two cases are discussed as follows:

• u or v is a central vertex. Without loss of generality, suppose u is a central vertex. The degree of u is k in T. In $T\cup e(u,v)$, the degree of u is $k+1$, which is a contradiction with any degree no more than k in G. This case is impossible.

• u and v are noncentral vertices. The unique $u-v$ path in T is denoted as p. w is the adjacent vertex of v in p. By Claim 2, w is a central vertex. Take out the longest path with start vertex w from $T\setminus e(v,w)$, denoted as $\tilde{p}(w,v_1)$. Thus, $v_1$ is a leaf in T. Consider the spanning tree $\tilde{T}=T\cup e(u,v)\setminus e(v,w)$, as shown in Fig. 5. By Claim 1, $\tilde{T}$ is also a k-star tree. $\tilde{p}(w,v_1)$ is a path in both T and $\tilde{T}$. By Claim 2, w is also a central vertex in $\tilde{T}$. This is a contradiction with $d(w)=k-1<k$ in $\tilde{T}$. This case is impossible.

Fig. 5.

The case when u and v are noncentral vertices

Above all, there is a contradiction for each cases. Thus our hypothesis does not hold and there is no edge $e(u,v)\in G\setminus T$. Thus G is T, which is a k-star tree.

Lemma 12

For every connected graph G(V, E) with n vertices and $\varDelta (G)\le k$, $\tau '(G)= \frac{(k-1)n+1}{k}$ holds if and only if G is a k-star tree.

Proof

According to Theorem 8 and Lemma 11, $\tau '(G)=n-\nu (G)= n-\frac{n-1}{k}=\frac{(k-1)n+1}{k}$ holds if and only if G is a k-star tree.

Theorem 10

Let H(V, E) be a connected rank k hypergraph with m edges. If maximum degree of H is no more than 2, then $\tau (H)= \frac{(k-1)m+1}{k}$ if and only if the simple dual graph $G^{*}$ is a k-star tree.

Proof

Consider the dual hypergraph $H^{*}(V^{*},E^{*})$ of H whose vertices correspond to the edges of H and edges correspond to the vertices of H. A vertex transversal in H correspond to an edge cover in $H^{*}$. Thus we have

$$\begin{aligned} n^{*}=m,m^{*}=n,\tau (H)=\tau '(H^{*}),\tau (H)= \frac{(k-1)m+1}{k}\Leftrightarrow \tau '(H^{*})= \frac{(k-1)n^{*}+1}{k}. \end{aligned}$$

The rank of H is k, which means every edge of H contains at most k vertices. Thus every vertex’s degree is at most k in $H^{*}$. The maximum degree of H is no more than 2, thus every edge of $H^{*}$ contains at most 2 vertices. This means the hypergraph $H^{*}$ is a multigraph, denoted by $G^{*}$. Delete the loops and multiedges to a simple graph. The deleting operations do not change the edge covering number. According to Lemma 12, $\tau '(G^{*})= \frac{(k-1)n^{*}+1}{k}$ if and only if $G^{*}$ is a k-star tree. This means $\tau (H)= \frac{(k-1)m+1}{k}$ if and only if the simple dual graph $G^{*}$ is a k-star tree.

Remark 5

For a simple graph, there is a polynomial-time algorithm to compute the edge covering number [16]. Thus for every connected hypergraph H(V, E) with maximum degree 2, it is decidable whether $\tau (H)= \frac{(k-1)m+1}{k}$ holds in polynomial time.

Remark 6

For a k-star tree as a dual graph, the primal hypergraph is a k-flower. The extremal hypergraphs are exactly k-flowers connected by common edges as shown in Fig. 6. Some 1-degree vertices are added in the edges which correspond to the deleted loops in a k-star tree.

Fig. 6.

A k-star tree and its primal hypergraph