A Comparison of Ring and Disk Resonator Gyroscopes Based on Their Degenerate Eigenmode Shapes

Abstract

Micromachined gyroscopes are beginning to compete with their macro-scale counterparts in terms of performance. This has been made possible because of a remarkable design change that has come to be known as a Disk Resonator Gyroscope (DRG). The design of a DRG can be thought of as an extension of the Ring Resonator Gyroscope (RRG) or vibratory ring gyroscope (VRG). After experimenting with various ring configurations and their suspensions attached to the ring, research has now moved to multiple configurations of DRGs. Central to all these designs are the degenerate eigenmode shapes: a pair of mode shapes for the same frequency. As one mode shape is used for resonant electrostatic actuation and another for sensing the energy transferred to it due to Coriolis acceleration, mode shapes decide the change in capacitance per unit angular rate. The objective of maximizing the capacitance change is to be balanced with the performance constraints on keeping the eigenfrequency low (but not too low) and quality factor high. In this paper, we compare different designs of ring and disk resonators from the literature in terms of eigenfrequency and mode shapes. We conclude that it is beneficial to have the mode shape of a gyroscope design close to the elliptical mode shape of a free ring.

1 Introduction

Micromachined gyroscopes are preferred in aerospace, automotive, and consumer products due to their low weight, small size, and low cost [1]. Beginning with the tuning fork and dual-mass designs, several configurations were explored. All of them work on the principle of Coriolis acceleration and depend on two degenerate mode shapes belonging to the same eigenfrequency. One mode is used to set the device into resonant vibration. This is often done using the electrostatic force. The other mode is used to sense the motion that results due to the transfer of energy from the first mode when the base, on which the gyroscope is mounted, begins to rotate. Apart from these, ring vibratory gyroscopes have also received special attention from researchers because of their symmetry and because they have improved resistance to external vibrations and shocks [2].

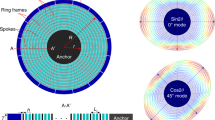
Just like the Foucault’s pendulum (Fig. 1a), and a hemispherical bowl (a wineglass, Fig. 1b) [3], a ring or a disk also have two degenerate mode shapes (Fig. 1c) [4]. A free ring needs to be suspended by attaching it to a central post where it is anchored to the substrate (Fig. 1d). The same is true with a disk (Fig. 1e). Different configurations of ring resonators (Fig. 1f) and disk resonators (Fig. 1g) are shown. In ring resonator gyroscopes, the central post needs to be connected with the ring. In disk resonators, holes are made in the disk to make it flexible by introducing concentric rings attached to one another in various ways using short connecting beams. This structure helps increase the number of sense electrodes and thereby the change in capacitance ($\Delta C$). The quality factor (Q-factor) of a DRG is further improved by adding several lumped masses to it (stiffness-mass decoupling technique), but it reduces the available capacitance area [5, 6]. A DRG also has structural imperfections that create high relative frequency errors after fabrication. This led to the development of a new gyroscope that is based on a honeycomb structure. The honeycomb-like disk resonator gyroscope (HDRG) has high immunity to fabrication errors [7], but the Q-factor is much lower than the DRG [8]. Furthermore, researchers developed a cobweb-like disk resonator gyroscope (CDRG) with linear beams instead of circular beams to reduce fabrication errors [9]. A high Q-factor for CDRG is obtained with the stiffness-mass decoupling technique. Apart from the above, researchers developed a gear-like disk resonator gyroscope (GDRG) and stated that it has high immunity to fabrication errors through computational results [10], but the fabrication trials were not yet done on GDRG. There are also other studies reporting new geometries for gyroscope applications to improve the Q-factor, mechanical sensitivity, and high immunity to the fabrication errors individually. There is scope for a new design that can improve all three of the above-mentioned performance measures. A comparison study among the existing designs provides some insights to lead further development. We limit the comparison criteria to frequency and mode shapes.

Fig. 1.

The working principle and design configurations of resonator gyroscopes (a) Focoult pendulum; (b) a wineglass with hemispherical shell; (c) degenerate mode shapes of a ring; (d) a ring gyroscope; (e) a disk gyroscope; (f) ring resonators; and (g) disk resonators.

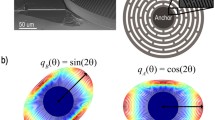
Unlike previous works, we analyzed the gyroscope designs by calculating the eigenfrequency that contains stiffness information; and the change in sense capacitance based on the eigenmodes. Relative sense capacitance (${{\Delta C} \mathord{\left/ {\vphantom {{\Delta C} {C_{0} }}} \right. \kern-\nulldelimiterspace} {C_{0} }}$) is defined as the ratio between the change in sense capacitance ($\Delta C$) and the base capacitance ($C_{0}$) before the excitation. These two are tunable by geometric design. Furthermore, we feel that the total displacement of a point on a ring is a good measure of the change in capacitance. As shown in Fig. 2, the total displacement, $u_{t} = \sqrt {u_{r}^{2} + u_{\theta }^{2} }$, can be plotted for all points, where $u_{r}$ is the radial displacement and $u_{\theta }$ is the tangential displacement. The total displacement is plotted for the two degenerate mode shapes of a free ring in Fig. 2. They are perfect ellipses for a free ring. For all other designs, ring or disk resonators, they will be distorted ellipses. The distortion plays a role in change in capacitance. Hence, the total displacement plotted against $\theta$ is a good measure for comparison. It helps to see the change in gap between corresponding points on the ring and the mode shape. We assumed a certain modal amplitude, which will be proportional to the angular rate in reality and use that to compute the change in capacitance. As shown in Fig. 2, we consider the displaced point on the mode shape and use a parallel-plate approximation for computing the capacitance in the changed configuration.

Fig. 2.

Total displacement of a point on the mode shape of a free ring for the two degenerate mode shapes. This is compared with considered designs to quantify the deviation from a perfect ellipse for all other designs. The method of computing the changed capacitance is also illustrated pictorially.

2 Methodology

Five different designs shown in Fig. 3 as RRG, DRG, HDRG, CDRG, and GDRG are selected to compare their performance. Further details of these are given in Table 1. All five gyroscopes are surrounded by 16 external stator electrodes, out of which four are used for driving, four are used for sensing, and the remaining eight are for tuning. Additionally, DRG, HDRG, CDRG, and GDRG have inner electrodes in between the concentric rings. For fair comparison, the five gyroscopes have the same structural parameters as follows: outer diameter = 8 mm, in-plane ring width = 10 µm, spoke width = 10 µm, number of concentric rings = 9, spoke length = 200 µm, out-of-plane thickness = 150 µm, and initial gap between the static electrode and the moving gyroscope structure = 10 µm.

The eigenfrequency and relative sense capacitance are computed by COMSOL Multiphysics 6.0 and MATLAB. The following procedure is used for computing the relative sense capacitance in a MATLAB script, using parallel-plate capacitance assumption:

• (a) The eigenmode is normalized to a maximum displacement of 1 µm to obtain the normalized eigenmode.

• (b) The sense capacitance is calculated from the normalized eigenmode with the reference capacitive gap of 10 microns (see also Fig. 2)

Fig. 3.

Five selected gyroscopes for the comparative study of eigenfrequency and relative sense capacitance; from left to right: ring resonator gyroscope (RRG) with semi-circular spokes, disk resonator gyroscope (DRG), honey-comb disk resonator gyroscope (HDRG), cob-web disk resonator gyroscope (CDRG), and gear-like disk resonator gyroscope (GDRG).

Fig. 4.

$u_{t}$ versus θ plot for the outer ring of the selected five gyroscopes.

Table 1 shows the stator electrodes for all five designs in the second column. In the third and fourth columns, the two degenerate mode shapes are shown. As stated earlier, except in RRG, the others have stator electrodes inside the concentric rings. For the sake of clarity of illustration, the static electrodes are shown only for one sector. We draw attention to the distortion of the mode shapes to notice how much they deviate from an ellipse. We presume that the closer the mode shape is to the ellipse the better the performance. It need not be true. Ideally, the capacitance change needs to be computed. Doing it using parallel-plate assumption is not accurate, but it does give an indication. Computing it using a finite element analysis software is accurate as it accounts for fringing fields and the actual 3D geometry. In lieu of this, to understand.

Table 1. Five different gyroscopes along with static electrodes are presented in the first two columns respectively. The static electrodes which are in green colour are used for actuating, red colour is used for sensing and blue colour are for tuning. Third and fourth columns contain the two degenerated modes.

The change in capacitance computed in this manner, we wanted to see how the mode shapes compare to the ellipse. This is shown in Fig. 4. It can be seen that mode shapes of RRG and HDRG are closer to the ellipse than that of the others. A similar trend was seen when this was plotted for inner rings too. In this case, RRG needs to be excluded because it lacks inner electrodes.

3 Results and Discussions

Table 2 contains a comparison of different designs. Also included is the free ring, which forms the basis of comparison in terms of mode shape. It would have a perfect ellipse as its mode shape. A free ring has the lowest eigenfrequency. One implication of this is that it has the least stiffness. But it is impractical to use a free ring.

In terms of eigenfrequency, the best design is RRG to limit it under 2k Hz for the practical consideration of tracking the displacement of the electronically. But RRG has lower change in capacitance and lower relative sense capacitance than HDRG. DRG, which is the trend-setting design that triggered the competitive performance of micromachined gyroscopes, is surprisingly not better than HRDG or RRG, but it is close. The recently reported CDRG and GDRG fare poorly because their unique features are not in terms of relative sense capacitance. Since RRG and free ring are included here, the capacitance is calculated based only on the outer stator electrodes. Table 3 illustrates how the numbers in Table 2 can be interpreted by considering the mode shapes plotted in terms of total displacement versus $\theta$.

Table 2. Comparison of eigenfrequency, base capacitance, relative sense capacitance for all five selected gyroscopes with proper elliptical eigenmode when only external electrodes are present.

In Table 3, one degenerate mode shape, the plot of the total displacement, and two performance measures are indicated. The first is ratio of the eigenfrequency of a gyroscope design to that of the free ring. It needs to be low, preferably below 2000 Hz. Since the free ring has a frequency of 641, the frequency ratio should be below 3.1. Only RRG satisfies this requirement. It is easy to see why this is so. All designs in the DRG-category have much more stiffness than RRG. When it comes to relative capacitance, RRG fares well but when only the outer electrodes are used to compute the capacitance. DRG class of gyroscopes have inner electrodes too. So, RRG does not fare well when we consider inner electrodes that fill the “disk” in DRGs.

Table 3. Comparison of eigenmode, total displacement versus angle plot, ratio of resonant frequency of gyroscope with respect to that of the free ring, and relative sense capacitance of all five gyroscopes when only outer electrodes are considered.

In Table 4, we compare the DRG class of gyroscopes by considering all stator electrodes, outer and inner. HDRG is a clear winner here in terms of the frequency ratio as well as the relative sense capacitance. The former has to do with the stiffness and the latter has to do with how close the mode shape is to the ellipse. It can be seen in Table 3 that, the mode shape of HDRG’s outer ring has the least deviation from the ellipse. This feature holds for the inner rings also (a figure of this not included here). Thus, future designs should pay attention the mode shape as well as the frequency.

Table 4. Comparison of eigenmode, ratio of resonant frequency of gyroscope with respect to free ring, relative sense capacitance all four disk resonators when both inner and outer electrodes are considered.

Any of the microfabricated DRG designs have degenerate eigenmodes only in principle. There is often a frequency mismatch in the two mode shapes due to uncertainties in microfabrication. This mismatch can be modelled under a spring-mass-damper framework as damping mismatch and stiffness mismatch assuming material uniformity. Both the mismatches are modelled as absolute difference in values and axis difference from the preferred axis of excitation and sensing. Static stiffness matching can be done by electrostatic tuning, but the mismatches vary with respect to temperature and aging. This renders tuning difficult. Damping mismatches are not tuned generally but compensated after extensive calibration and testing. Since the performance will be deteriorated due to the presence of these asymmetries, it is always preferred to tackle the problem at the source itself by envisaging novel geometries which reduces dependencies on fabrication precision. The current fabrication technologies (photolithography and etching) are developed based on linear structures, which may create issues while fabricating other geometries. To increase the “fabrication immunity”, one can modify the arc structures which are presented in the geometry to linear structures. The focus of the possible design is to minimize the fabrication errors, thus helping us to reduce the effort for frequency mismatch.

4 Conclusions

In this work, we compared the performance of the five different resonator gyroscopes based on the eigenfrequency and eigenmodes. This study was undertaken because the reports of various designs directly went to consider quality factor and overall sensitivity rather than studying the intrinsic geometric feature. It is true that the quality factor also is influenced by the geometric design, but it is a derived quantity. Here, we considered only the mode shape to highlight the fact that a mode shape that stays close to the ellipse (which is the mode shape of a free ring) helps in increasing the relative sense capacitance. The honeycomb disk resonator gyroscope (HDRG) emerged as the best among the DRG class of designs. However, DRG class of designs have much larger eigenfrequency values as compared to the free ring and ring resonator gyroscope (RRG). This comparative analysis thus points to the need for a different design that keeps the eigenfrequency low and yet has a mode shape that remains close to an ellipse.

Future work points to fabrication and mechanical characterization of these designs to benchmark the simulation results. Comparison of other performance measures such as scale factor, frequency mismatch, quality factor, and angle random walk may provide insights for a better of design gyroscope. Our ongoing work is focused on a possible candidate design, which needs to be evaluated for these performance measures along with detailed finite element analysis.