Analyzing the 3-path Vertex Cover Problem in Planar Bipartite Graphs

Abstract

Let $G=(V,E)$ be a simple graph. A set $C \subseteq V$ is called a k-path vertex cover of G, if each k-path in G contains at least one vertex from C. In the k-path vertex cover problem, we are given a graph G and asked to find a k-path vertex cover of minimum cardinality. For $k=3$, the problem becomes the well-known 3-path vertex cover (3PVC) problem, which has been widely studied, as per the literature. In this paper, we focus on the 3PVC problem in planar bipartite (pipartite) graphs for the most part. We first show that the 3PVC problem is NP-hard, even in pipartite graphs in which the degree of all vertices is bounded by 4. We then show that the 3PVC problem on this class of graphs admits a linear time 1.5-approximation algorithm. Finally, we show that the 3PVC problem is APX-complete in bipartite graphs. The last result is particularly interesting, since the vertex cover problem in bipartite graphs is solvable in polynomial time.

This research was supported in part by the Air-Force Office of Scientific Research through Grant FA9550-19–1-0177 and in part by the Air-Force Research Laboratory, Rome through Contract FA8750-17-S-7007.

1 Introduction

Given a simple undirected graph $G=(V,E)$, the open neighborhood (resp. closed neighborhood) of a vertex $v_i\in V$ is defined by $N(v_i)=\{v_j\in V\mid v_iv_j\in E\}$ (resp. $N[v_i]=N(v_i)\cup \{v_i\}$). The degree of a vertex v in the graph G is defined as $d_G(v)=|N(v)|$, whereas the maximum degree of a graph is $\varDelta (G)=\max \limits _{v\in V}\{d_G(v)\}$. A vertex cover C of G is a subset of V such that for each edge $uv\in E$, either $u \in C$ or $v \in C$. The (minimum) vertex cover problem asks to find a vertex cover of minimum size in a given graph. One generalization of the vertex cover problem is the k-path vertex cover problem. A k-path vertex cover $C_k$ of G is a subset of V such that each path in G having k vertices (path of order k) contains at least one vertex from $C_k$. In other words, $C_k$ is called a k-path vertex cover (kPVC) of G, if there does not exist a path of order k in the induced subgraph $G'=(V\setminus C_k,E')$, where an edge $e \in E$ belongs to $E'$, if both its endpoints are in $V \setminus C_k$. The (minimum) k-path vertex cover problem asks to find a vertex subset of minimum size satisfying the k-path vertex cover property in a given graph G. For $k=3$, the k-path vertex cover problem is called the 3-path vertex cover (3PVC) problem.

In the 3PVC problem, we are given an undirected, unweighted graph $G=(V,E)$ and the goal is to find a minimum cardinality set $V' \subseteq V$, such that at least one vertex from every two-edge path is in $V'$. It is clear that the 3PVC problem is a variant of the well-known vertex cover (VC) problem and a specialization of the k-path vertex cover problem, discussed in [1]. The 3PVC problem finds applications in several practical domains, including wireless networks and data integrity [1, 6]. Prior work has established the computational difficulty of this problem in general graphs. Indeed, the 3PVC problem is known to be NP-hard for planar graphs and bipartite graphs. This paper studies the 3PVC problem in planar bipartite (pipartite) graphs, i.e., the intersection of the above-mentioned graph classes.

The principal contributions of the paper are as follows:

• 1. A proof that the 3PVC problem is NP-complete in pipartite graphs, even with $\varDelta (G) \le 4$ (Sect. 3).

• 2. The design and analysis of a linear time 1.5-approximation algorithm for the 3PVC problem in pipartite graphs, with $\varDelta (G) \le 4$ (Sect. 4).

• 3. A proof of APX-completeness for the 3PVC problem in bipartite graphs (Sect. 5).

The rest of this paper is organized as follows: In Sect. 2, we discuss related work in the literature. The computational complexity of the 3PVC problem in pipartite graphs is detailed in Sect. 3. An approximation algorithm for this problem on a selected class of pipartite graphs is discussed in Sect. 4. In Sect. 5, we show that the 3PVC problem is APX-complete in bipartite graphs. Finally, we conclude in Sect. 6 by summarizing our contributions and identifying avenues for future research.

2 Related Work

In this section, we discuss the state-of-the-art results of the 3-path vertex cover problem. The generalized version of the 3-path vertex cover (3PVC) problem is the k-path vertex cover (kPVC) problem. Motivated by two problems, viz., (i) secure communication in wireless sensor networks [1, 11] and (ii) controlling traffic at street crossings [15], Brešar et al. [1] introduced the kPVC problem in 2011. For $k\ge 2$, Brešar et al. [1] proved that determining $\psi _k(G)$ (minimum cardinality of a kPVC) in a graph G is NP-hard. They proved that the problem can be solved in linear time in trees. For $k=2$, the problem is known as the vertex cover (VC) problem in the literature. The VC problem is known to be NP-hard, in general [8]. Brešar et al. [1] proved the existence of an r-approximation algorithm for the VC problem from an r-approximation algorithm of the kPVC problem. Note that a k-approximation algorithm for the kPVC problem is trivial [1]. The authors also presented several estimations and exact values to provide the upper bound for $\psi _k(G)$. They proved $\psi _3(G)\le (2\cdot n+m)/6$ for any graph G with n vertices and m edges. For outerplanar graphs of order n, they proved $\psi _3(G)\le \frac{n}{2}$. In [13], Tu and Yang proved that the 3PVC problem is NP-hard in cubic planar graphs with girth 3. They also proposed a linear time 1.57-approximation algorithm for the 3PVC problem in cubic graphs. Whether a polynomial-time c-approximation algorithm exists for the kPVC problem for $k\ge 2$ [1, 7] is an open problem.

For the 3PVC problem, many constant factor approximation results are known. Kardoš et al. [7] proposed a polynomial-time randomized approximation algorithm with an expected approximation ratio of $\frac{23}{11}$. In [14, 15], Tu and Zhou proposed several approximation algorithms for the weighted kPVC problem (each vertex has a weight). The two techniques they used were the primal-dual method and graph layering. Zhang et al. [16] considered the kPVC problem in d-regular graphs and proposed several approximation results. The 3PVC problem in planar graphs admits an EPTAS [12], which means that the problem is not APX-hard in pipartite graphs unless $\mathbf{P=NP}$.

3 Computational Complexity

In this section, we reduce the vertex cover (VC) problem in planar graphs to the 3-path vertex cover (3PVC) problem in pipartite graphs via a linear time algorithm. Note that the VC problem in planar graphs with maximum degree three is known to be NP-hard [10].

The decision versions of both the problems are defined below.

• The vertex cover problem in planar graphs (Vc-Pla)

  Given a planar graph G having maximum degree three and a positive integer k, does G has a VC of size at most k?

• The 3PVC problem in pipartite graphs (3Pvc-Pb)

  Given a pipartite graph G and a positive integer k, does there exist a 3PVC of size at most k?

Construction: The construction from a given instance of a planar graph G to an instance of a pipartite graph $G'$ takes place in three steps.

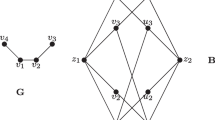
Step 1: For each vertex $v_i$ in G, create a corresponding vertex $u_i$ in $G'$.

Step 2: For each vertex $u_i$ in $G'$, create a support vertex $u_i'$ and put an edge between $u_i$ and $u_i'$.

Step 3: For each edge $v_iv_j\in E$ in the graph G, take the corresponding vertices $u_i$ and $u_j$ in $G'$ and put three vertices $u_{ij}$, $u_{ij}'$, and $u_{ij}''$ between them. Now, add four edges in the order $u_iu_{ij}$, $u_{ij}u_{ij}'$, $u_{ij}'u_{ij}''$, and $u_{ij}''u_j$ (see the three vertices and four edges added between $u_1$ and $u_2$ in Fig. 1 (b), corresponding to the edge $v_1v_2$ of Fig. 1 (a)).

Lemma 1

For a given instance of a planar graph $G=(V,E)$ ($\varDelta (G) \le 3$), an instance of a pipartite graph $G'=(V_1,V_2,E')$ ($\varDelta (G') \le 4$) can be constructed in linear time using the above construction.

Proof

Observe that, for each vertex $v_i$ in G, there is a corresponding vertex $u_i$ and a support vertex $u_i'$ in $G'$ (for example, see the vertices $u_1$ and $u_1'$ in Fig. 1 (b) corresponding to the vertex $v_1$ in Fig. 1 (a)).

Again for each edge $v_iv_j\in E$ in G, there are three vertices added in the corresponding edge $u_iu_j$ in $G'$, i.e., $u_{ij},u_{ij}'$, and $u_{ij}''$ (for example, see the three vertices added between $u_1$ and $u_2$ in Fig. 1 (b)). Observe that the extra vertices added in the graph $G'$ do not affect the graph’s planarity, and the odd cycles of the graph (if any) become even. Moreover, the degree of each vertex in the graph $G'$ is at most four. Thus, $G'$ is a planar bipartite graph with $\varDelta (G') \le 4$. If the total number of vertices and edges in graph G is n and m, respectively, then the number of vertices and edges in graph $G'$ is $|V'|=2\cdot n+3\cdot m$ and $|E'|=n+4\cdot m$. In a planar graph $G=(V,E)$, $|E|\le 3\cdot |V|-6$. So, $|V'|<11\cdot n$ and $|E'|<13\cdot n$. Hence $G'$ can be constructed in linear time. $\square$

Fig. 1.

Construction of a planar bipartite graph $G'$ from a planar graph G.

Now, we prove that 3Pvc-Pb is NP-hard. For the hardness proof, we show a linear time reduction from Vc-Pla to 3Pvc-Pb. Let $G=(V,E)$ be an instance of Vc-Pla. Construct an instance $G'=(V_1,V_2,E')$ of 3Pvc-Pb as discussed in Lemma 1. We prove the following claims to establish the NP-hardness result for the 3Pvc-Pb.

Claim 1

For each edge $v_iv_j\in E$ in graph G, there exist three vertices $u_{ij},u_{ij}'$, and $u_{ij}''$ in graph $G'$. Out of these three vertices, one must be present in any 3-path vertex cover of graph $G'$.

Proof

The proof of the claim follows directly from the definition of the 3-path vertex cover. As the three vertices $u_{ij},u_{ij}'$, and $u_{ij}''$ form a path of order three, any 3-path vertex cover of the graph $G'$ must contain at least one vertex out of these three vertices. $\square$

Claim 2

For an edge $v_iv_j\in E$ in G, if the corresponding vertices $u_i$ and $u_j$ of the edge in $G'$ are not in a 3-path vertex cover set D, then either at least two vertices from the set $\{u_{ij},u_{ij}', u_{ij}''\}$ or both the support vertices $u_i'$ and $u_j'$ are in D.

Proof

Assume that none of the vertices from the set $\{u_i',u_i,u_j,u_j'\}$ are in D. Moreover, there exists exactly one vertex from the set $\{u_{ij},u_{ij}', u_{ij}''\}$ in D and D is a 3-path vertex cover in the graph $G'$. If $u_{ij}\in D$, then there are two paths of order three containing no vertices from D. The two paths are $u_{j}'-u_{j}-u_{ij}''$ and $u_{j}-u_{ij}''-u_{ij}'$. It contradicts the fact that D is a 3-path vertex cover. If $u_{ij}'\in D$, then $u_{i}'-u_{i}-u_{ij}$ and $u_{j}'-u_{j}-u_{ij}''$ create two paths of order three, containing no vertices from D. It also contradicts the fact that D is a 3-path vertex cover. In the case that only $u_{ij}''\in D$, similar combinatorial arguments can be given to obtain a contradiction. Consider the case when neither of $u_i$ and $u_j$ belongs to D. Furthermore, we assume that D contains exactly one vertex from the set $\{u_{ij},u_{ij}', u_{ij}''\}$. In this case, D must contain both the support vertices $u_i'$ and $u_j'$ along with $u_{ij}'$ in D to satisfy the condition of the 3-path vertex cover.

Therefore, it is proved that if both $u_i$ and $u_j$ are not in D, then either (i) at least two vertices from the set $\{u_{ij},u_{ij}', u_{ij}''\}$ are in D or (ii) both the support vertices $u_i'$ and $u_j'$ must be in D. This proves the claim. $\square$

Fig. 2.

A 3PVC solution for $G'$ constructed from a VC solution in G.

Now, we prove that 3Pvc-Pb is NP-hard by proving the following lemma.

Lemma 2

G has a vertex cover C with $|C| \le k$, if and only if $G'$ has a 3-path vertex cover D with $|D| \le k +m$.

Proof

Let $C\subseteq V$ be a vertex cover in the graph $G=(V,E)$ having cardinality at most k. For each $v_i\in C$, take the corresponding vertices of $v_i$ as $u_i$ in the graph $G'=(V',E')$. Update $D=D\cup \{u_i\}$. After adding all the corresponding vertices of C in D, $|D| \le k$. As C is a vertex cover in G, for each edge $v_iv_j \in E$, either $v_i$ or $v_j$ must be in C (the tie can be broken by arbitrarily choosing one vertex if both the vertices are in C). Without loss of generality, assume that $v_i \in C$. Take the corresponding vertex $u_i$ in the graph $G'$. Now, add the $4^{th}$ vertex encountered in the path $u_i \rightsquigarrow u_j$ in D (for example, see the path $u_1 \rightsquigarrow u_2$ in Fig. 2 (b) corresponding to the edge $v_1v_2$ in Fig. 2 (a). As $v_1\in C$, the $4^{th}$ vertex $u_{12}''$ in the path $u_1 \rightsquigarrow u_2$ is chosen in D). Repeat the process for each edge in G and add one vertex to D. So, after completion of this step, the number of vertices added in D is m (number of edges present in G). Now, observe that D is a 3-path vertex cover in $G'$ as each path of order three contains at least one vertex from D and $|D|\le k+m$.

Conversely, let $D\subseteq V'$ be a 3-path vertex cover of size at most $k+m$. We argue that G has a vertex cover C of size at most k. Consider each vertex $u_i \in D$ in $G'$. Take its corresponding vertex $v_i$ in C. Clearly $|C|\le k$ (follows from Claim 1). If C is a vertex cover in G, then the proof completes. If C is not a vertex cover in G, then there must exist an edge $v_iv_j\in E$ in G, such that $v_i,v_j \not \in C$. Take the corresponding vertices of $v_i$ and $v_j$ as $u_i$ and $u_j$, respectively, in $G'$. As $v_i,v_j\not \in C$, the corresponding vertices $u_i,u_j \not \in D$. That means D contains either at least two vertices from the set $\{u_{ij},u_{ij}',u_{ij}''\}$ or both the support vertices $u_i'$ and $u_j'$ (follows from Claim 2). If both the support vertices $u_i'$ and $u_j'$ belong to D, then update $D=D\cup \{u_i,u_j\}\setminus \{u_i',u_j'\}$. If the above condition fails, then there must exist two vertices from the set {$u_{ij},u_{ij}'$, $u_{ij}''\}$ in D. Now, update $D=D\cup \{u_i\}\setminus \{u_{ij}\}$, if $u_{ij}\in D$, else update $D=D\cup \{u_j\}\setminus \{u_{ij}''\}$.

Update C and repeat the process till every edge in G has one of its end vertex in C. Due to Claim 1, C is a vertex cover having $|C|\le k$. Therefore, 3Pvc-Pb is NP-hard. $\square$

Theorem 1

3Pvc-Pb is NP-complete

Proof

For a given set $D\subseteq V$ in a pipartite graph $G=(V,E)$ and a positive integer k, one can verify whether D is a 3PVC of size at most k. This can be done in linear time by checking whether there exists a path of order 3 in the subgraph induced by $V\setminus D$. Hence, the problem 3Pvc-Pb is in NP. As per Lemma 2, 3Pvc-Pb is NP-hard. Therefore, 3Pvc-Pb is NP-complete.

4 Approximation Algorithm

In this section, we design a 1.5-approximation algorithm for the 3PVC problem in pipartite graphs having maximum degree four. The proposed algorithm is a greedy algorithm, which runs in linear time. Note that, for the 3PVC problem, there exists a 1.57-approximation algorithm in cubic graphs [13] and a 2-approximation algorithm in general graphs [14, 15]. Let $\psi _3(G)$ denote the cardinality of a minimum 3-path vertex cover set in G. Observe that if a graph G is a path or a cycle, then the following lemma for $\psi _3(G)$ is valid.

Lemma 3

Let $P_n$ denote a simple path on n vertices and $C_n$ denote a cycle on n vertices, then $\psi _3(P_n)=\lfloor \frac{n}{3}\rfloor \le \frac{n}{3}$ and $\psi _3(C_n)=\lceil \frac{n}{3}\rceil \le \frac{n+2}{3}$.

Proof

Consider a simple path $P_n$ on n vertices. For $i=1,2,\cdots , \frac{n}{3}$, select every $3\cdot i^{th}$ vertex from the path $P_n$ in a set D. Observe that D is a 3PVC for the path $P_n$ and $|D|\le \frac{n}{3}$. In the case of a cycle $C_n$, a similar combinatorial argument can be given to prove that $\psi _3(C_n)\le \frac{n+2}{3}$. $\square$

Now, we discuss the algorithm to get a 3PVC set D in a pipartite graph $G=(V,E)$, where $V=V_1\cup V_2$. The algorithm sequentially checks for all the vertices of G. When it encounters a vertex $v\in V$ having degree three, it checks for the neighbors of v. Let $\lambda$ denote the number of vertices in N(v) having degree at least three. If $\lambda <2$, then the algorithm adds v in D and updates G by removing v from G. If $\lambda \ge 2$, then the algorithm computes the optimal solution (say $D'$) in the subgraph induced by N[v], and the neighbors of N(v). Let $V'$ be the set containing the vertices in N[v] and the neighbors of N(v). As the input graph G is a pipartite graph with $\varDelta (G)\le 4$, there does not exist an edge between any pair of vertices in N(v) and $|V'|\le 13$. Now, the algorithm updates $D=D\cup D'$ and removes the vertices selected in $D'$ from G.

When the algorithm encounters a vertex $v\in V$ having degree four, it calculates the value of $\lambda$ in N(v). If $\lambda <3$, then the algorithm adds v in D and updates G by removing v from G. If $\lambda \ge 3$, then the algorithm computes the optimal solution (say $D'$) in the subgraph induced by N[v], and the neighbors of N(v). Let $V'$ be the set containing the vertices in N[v] and the neighbors of N(v). Observe that, $|V'|\le 17$. Now, the algorithm updates $D=D\cup D'$ and removes the vertices selected in $D'$ from G.

The algorithm continues the above procedure for each vertex in G. At last, when the graph contains only paths and cycles, it optimally computes the solution and adds it to D.

The above steps are summarized in Algorithm 1.

Lemma 4

The set D, returned by Algorithm 1, is a 3PVC for the given pipartite graph G.

Proof

The algorithm sequentially checks for all the vertices of G. For each vertex $v\in V$ encountered with a degree three, the algorithm checks for its neighbors. If less than two neighbors have degree at least three, the algorithm adds the vertex v in D and removes v from G. If there are at least two neighbors of v having degree at least three, then the algorithm finds the optimal solution for the subgraph induced by N[v] and neighbors of N(v). Then, it adds the optimal solution obtained from this induced subgraph in D and removes the vertices of the optimal solution from G. When the algorithm encounters a vertex $v\in V$ of degree four, it checks for its neighbors. If less than three vertices in N(v) have degree at least three, it adds the vertex v in D and removes v from G. Otherwise, it finds the optimal solution in the subgraph induced by N[v] and neighbors of N(v). Then, it adds the optimal solution obtained from this induced subgraph in D and removes the vertices of the optimal solution from G. The algorithm repeats the process in the updated graph $G'$ until only paths and/or cycles remain in $G'$. Note that the set $D'$ is the minimum 3-path vertex cover of $G'$ (follows from Lemma 3). Thus, $D=D\cup D'$ returned by Algorithm 1 is a 3-path vertex cover for the given pipartite graph G. $\square$

Lemma 5

Algorithm 1 runs in time linear in the number of vertices of the input graph, in the worst case.

Proof

Observe that Algorithm 1 checks all the vertices sequentially in step 2. If the number of vertices in the input graph G is n, then this step will take O(n) time. For each vertex $v\in V$ with $d_G(v)\ge 3$, the algorithm computes $\lambda$, the number of vertices in N(v) having degree at least three. Based on $\lambda$, the algorithm computes the solution for the subgraph induced by N[v] and neighbors of N(v). These steps of the algorithm take constant time. Again, Algorithm 1 finds a 3-path vertex cover in the updated graph $G'$ in step 24. This step can be computed in O(n) time as $G'$ consists of only paths and cycles. All the other steps of the algorithm take constant time. Hence, the worst-case time taken by Algorithm 1 is O(n). $\square$

Lemma 6

Let D be a 3PVC set returned by Algorithm 1 and OPT be a 3PVC set of minimum size for the given pipartite graph G, then $|D|\le \frac{3}{2}\cdot |OPT|$.

Proof

Observe that Algorithm 1 evaluates a 3-path vertex cover of minimum size for the cycles and paths (see step 24 of the algorithm). So, for proving the approximation factor, we consider the vertices with degree at least three taken in D and prove that $\frac{|D|}{|OPT|}\le \frac{3}{2}$.

Consider each vertex $v\in D$ of degree at least three. If $v\in OPT$, then the algorithm achieves the best-case scenario by including v in D. Without loss of generality, assume that $v\not \in OPT$. If $d_G(v)=3$, the algorithm considers two cases to add v in D.

Fig. 3.

Instance of a degree 3 vertex having exactly one neighbor with degree at least 3.

The first case, considered by the algorithm, is when there exists at most one vertex $u\in N(v)$ such that $d_G(u)\ge 3$ (see steps 5–7 in Algorithm 1). As $v\not \in OPT$, at least two vertices from N(v) must be in OPT to make the OPT a 3PVC in G (for example, see Fig. 3 (a)). If the algorithm chooses two vertices from N(v) along with v in D, then the approximation factor is $\frac{3}{2}$. If the algorithm chooses all the three vertices of N(v), then either OPT contains N(v) or $u \not \in OPT$. In the former case, the approximation factor is $\frac{4}{3}< \frac{3}{2}$. Note that the two vertices (say x and y) in $N(v)\setminus \{u\}$ has degree at most two. The algorithm selects v in D and removes v from G. Now, the degree of the two vertices x and y is one, and still, the algorithm includes them in D, which means both the vertices x and y are in OPT.

In the latter case, as both $u,v \not \in OPT$, N(u) must be in OPT (for example, see Fig. 3 (b)). For the worst-case scenario, assume that $N(u)\subseteq D$. In that case, $d_G(u)=4$. If $d_G(u)=3$, then after removing the vertex v from G, makes the degree of u as two. The algorithm computes the optimal solution for all the degree one and two vertices at last. There is no way the algorithm selects N[u] optimally. If the degree of the vertices of N(u) is at least three and selected by the algorithm earlier, then after removing N(u), the degree of u becomes 0 (cannot be in D). So, the only way the algorithm includes N[u] in D, if $d_G(u)=4$.

Now, we argue the approximation factor of the algorithm by considering both the vertices u ($d_G(u)=4$) and v ($d_G(v)=3$). Observe that OPT contains at least five vertices from N(u) and N(v) (see Fig. 3 (b)), whereas D contains at most seven vertices, including both u and v. So, the approximation factor is $\frac{7}{5}< \frac{3}{2}$.

For $d_G(v)=3$, the second case considered by the algorithm is when there exist at least two vertices $w,u\in N(v)$ such that $d_G(w)\ge 3$ and $d_G(u)\ge 3$ (see steps 9–12 in Algorithm 1). In the second case, the algorithm finds an optimal solution for the subgraph induced by N[v] and neighbors of N(v). As $v\not \in OPT$, at least two vertices from N(v) must be in OPT. If the algorithm computes three vertices in D from the induced subgraph, then the approximation factor is $\frac{3}{2}$.

Consider the case that the algorithm chooses all the four vertices of N[v] in D, i.e., $N[v]\subseteq D$. Assume that OPT consists of two vertices from N(v), i.e., there exists a vertex $w\in N(v)$, such that $w\not \in OPT$ (for example, see Fig. 4 (a)). As both v and w are not in OPT, there must be the case that $N(w)\subseteq OPT$ (for example, see Fig. 4 (b)). As the algorithm chooses w in D, $d_G(w)\ge 3$. Otherwise, the algorithm would not choose w in D as already $v\in D$, and the algorithm computes the optimal solution in the subgraph induced by N[v] and neighbors of N(v). Now, we argue the approximation factor of the algorithm by considering both the vertices v ($d_G(v)=3$) and w. Observe that OPT contains at least two vertices from N(v) and N(w), whereas D contains N[v] and N(w). If $d_G(w)=3$, the approximation factor is $\frac{6}{4}$. If $d_G(w)=4$, the approximation factor is $\frac{7}{5}$ (for example, see Fig. 4 (c)). So, for $d_G(v)=3$, the approximation factor is at most $\frac{3}{2}$. Observe that, for each vertex $v\in D$ with $d_G(v)=4$, the algorithm considers two cases to include v in D. Out of these two cases, the first case deals with the scenario when at most two vertices in N(v) have a degree of at least three. The second case deals with the scenario when at least three vertices in N(v) have a degree of at least three. The rest of the proof follows the similar combinatorial arguments given for the degree three vertices above. Thus, for each possible case, the approximation factor is at most $\frac{3}{2}$. Therefore, the solution D, returned by the algorithm, is $\frac{3}{2}\cdot |OPT|$, i.e., $|D|\le \frac{3}{2}\cdot |OPT|$. $\square$

Fig. 4.

Instance of a degree 3 vertex with at least two neighbors of degree at least 3.

Theorem 2

Algorithm 1 is a $\frac{3}{2}$-approximation algorithm for the 3-path vertex cover problem in pipartite graph G with maximum degree four. The algorithm runs in O(n) time.

Proof

Follows from Lemma 4, Lemma 5, and Lemma 6. $\square$

5 Approximation Complexity

In this section, we show that the 3-path vertex cover (3PVC) problem is APX-complete in bipartite graphs by exhibiting an L-reduction [4] from the vertex cover problem in cubic graphs (Vc-Cg) to the 3PVC problem in bipartite graphs (3Pvc-Bp). Note that Vc-Cg is known to be APX-complete [4].

Lemma 7

[3]. If $G=(V,E)$ is a cubic graph and $C_{opt}$ is a minimum vertex cover in G, then $|C_{opt}|\ge \frac{|V|}{2}$.

Construction: Let cubic graph $G=(V,E)$ denote an instance of Vc-Cg. We construct an instance of 3Pvc-Bp (bipartite graph $G'=(V_1,V_2,E')$) as follows:

Replace each edge $uv\in E$ of G by a path $u \rightsquigarrow v$ of five vertices in $G'$, where the end vertices of the path are u and v (see Fig. 5). We call these three vertices added in the path $u \rightsquigarrow v$ other than u and v as added vertices. We also call the end vertices u and v as node vertices. For each vertex $v_i\in V$ in the graph G, add a support vertex, say $v_i''$ and an edge $vv_i''$ in the graph $G'$ (for example, see the edges $uu''$ and $vv''$ in Fig. 5). Note that the construction is similar to the NP-hardness proof construction of Sect. 3 (see Fig. 1). From this construction, it follows that $|V'|=2\cdot |V|+3\cdot |E|=2\cdot |V|+\frac{3\cdot |V|}{2}\cdot 3<7\cdot |V|$ and $|E'|=4\cdot |E|+|V|=4\cdot \frac{3\cdot |V|}{2}+|V|=7\cdot |V|$.

Fig. 5.

Gadget for an edge of the graph G.

To prove that 3Pvc-Bp is APX-complete, we first prove that 3Pvc-Bp is APX-hard. The APX-hardness is proved by reducing the Vc-Cg to the 3Pvc-Bp via an L-reduction. Let $G=(V,E)$ be an instance of Vc-Cg. Construct the instance $G'=(V',E')$ of 3Pvc-Bp as discussed above.

Lemma 8

3Pvc-Bp is APX-hard.

Proof

Let $C\subseteq V$ be a vertex cover (VC) in the graph $G=(V,E)$. We construct a 3-path vertex cover D for the graph $G'=(V',E')$ from C as follows:

For each vertex $v_i\in C$ in G, take the corresponding vertex $v_i$ in D from $G'$. As C is a VC in G, for each edge $uv\in E$ in G, at least one of the end vertices of the edge uv must be in C. If $u\in C$, then include the added vertex $v'$ from $G'$ in D; otherwise, include the added vertex $u'$ in D.

Now, we prove that D is a 3PVC in $G'$. Observe that, for each edge-gadget corresponding to each edge uv in G, D contains either the vertices u and $v'$, if $u\in C$ or v and $u'$. So, from every edge-gadget, the vertices selected in D forbid a 3-path with no vertices in D. Further, if one of the vertices among u and v is not in D, then its two adjacent vertices from the other two edge-gadgets must be in D. Therefore, the subgraph induced by the vertices $V'\setminus D$ does not have a path of order three. Thus, D is a 3PVC for the graph $G'$.

Let the number of vertices in the graph G be n, i.e., $|V|=n$. As G is a cubic graph, $|E|=\frac{3\cdot n}{2}$. There is precisely one added vertex taken in D from each edge-gadget along with the vertices in C. Therefore, $|D|=|C|+|E|=|C|+\frac{3\cdot n}{2}$. Let $C_{opt}$ be a minimum vertex cover for G, then by Lemma 7, $|C_{opt}|\ge \frac{n}{2}$. Let $D_{opt}$ be a minimum 3PVC for $G'$, then $|D_{opt}|\le |C_{opt}|+3\cdot \frac{n}{2}\le |C_{opt}|+3\cdot |C_{opt}|\le 4\cdot |C_{opt}|$.

Conversely, let D be a 3-path vertex cover in $G'$. If D contains any of the support vertices, we delete the support vertex and add its neighbor (node vertex) in D if the neighbor is not in D. We construct a vertex cover C from the 3-path vertex cover D as follows:

For each node vertices $v_i\in D$ in $G'$, take its corresponding vertex from G in C. If C is a VC in G, then the proof is complete. If C is not a VC in G, then there exists an edge $uv\in E$ in G, for which neither of the end vertices is in C. Observe that, in the corresponding edge-gadget of the edge uv, D does not contain the node vertices and the support vertices (otherwise, one of the vertices u or v must be in C). That means D contains the added vertices $u'$ (otherwise, $u''-u-u'$ form a 3-path) and $v'$ (otherwise, $v''-v-v'$ form a 3-path) to satisfy the 3PVC condition. We remove the vertex $u'$ from D and add u in D. Repeat the process until getting a VC in the graph G.

Observe that $|C|\le |D|-|E| \le |D|-3\cdot \frac{n}{2}$ (as from each edge-gadget, at least one vertex out of three added vertices must be in D). Let D be any 3PVC of $G'$ and C be a corresponding VC for G, and $D_{opt}$, $C_{opt}$ be the minimum 3PVC for $G'$ and corresponding minimum VC for G, respectively.

Then $|D|-|D_{opt}|\ge |C|+3\cdot \frac{n}{2}-|C_{opt}|-3\cdot \frac{n}{2}$.

$|D|-|D_{opt}|\ge |C|-|C_{opt}|$.

This gives an L-reduction from Vc-Cg to 3Pvc-Bp with $\alpha =4$ and $\beta =1$. $\square$

Note that 3Pvc-Bp is in APX [9]. As per Lemma 8, 3Pvc-Bp is APX-hard. Therefore, 3Pvc-Bp is APX-complete.

6 Conclusion

In this paper, we studied the 3-path vertex cover problem in different graph classes. We provided a linear time NP-completeness proof for the problem in planar bipartite graphs. With respect to approximation algorithms, we proposed a 1.5-approximation algorithm for the 3PVC problem in linear time. We proved that the 3PVC problem is APX-complete in bipartite graphs.

From our perspective, the following open problems are worth pursuing:

• 1. An exact exponential algorithm [5] for the 3PVC problem in pipartite graphs - Note that such algorithms exist for general graphs, but we hope to exploit the pipartite structure to obtain more efficient algorithms.

• 2. Unit disk graphs [2] - It is well-known that the 3PVC problem is NP-hard in unit disk graphs. We plan to investigate non-trivial approximation algorithms for the same.