Deductive Verification Based Abstraction for Software Model Checking

Abstract

The research community working on formal software verification has historically evolved into two main camps, grouped around two verification methods that are typically referred to as Deductive Verification and Model Checking. In this paper, we present an approach that applies deductive verification to formally justify abstract models for model checking in the TLA framework. We present a proof-of-concept tool chain for C programs, based on Frama-C for deductive verification and $\text{ TLA}^+$ for model checking. As a theoretical foundation, we summarise a previously developed abstract contract theory as a framework for combining these two methods. Since the contract theory adheres to the principles of contract based design, this justifies the use of the approach in a real-world system design setting. We evaluate our approach on two case studies: a simple C program simulating opening and closing of files, as well as a C program based on real software from the automotive industry.

This work has been funded by the FFI Programme of the Swedish Governmental Agency for Innovation Systems (VINNOVA) as the AVerT2 project 2021-02519.

1 Introduction

The literature on formal software verification can roughly be grouped into two branches, typically referred to as Deductive Verification and Model Checking. Deductive verification historically stems from Floyd-Hoare style logics. Hoare logic contracts in term of pre- and post-conditions (see, e.g., [10]) are meaningful in the context of programs that are understood as state transformers, i.e., programs the purpose of which is to transform certain initial values to certain final values, where the intermediate values are just implementation details irrelevant to the computed function. Deductive verification thus focuses on the transformational behaviour of programs. Technically, it is typically based on symbolic approaches, such as computing Weakest Preconditions or Symbolic Execution, to convert programs annotated with specifications to formulas in First-Order Logic, and then on (back-end) algorithmic SAT/SMT solving.

On the other hand, model checking historically stems from algorithmic approaches to evaluating whether a formula of (some) Temporal Logic holds in a given state of a Kripke structure (see, e.g., [6]). It focuses on the non-terminating, temporal behaviour of programs. Technically, it is typically based on property-preserving abstractions of programs (or system descriptions) to finite-state representations, and then on algorithmic state-space exploration.

While this dichotomy of transformational versus temporal behaviour of programs is useful, the two aspects are not mutually exclusive and can be relevant for one and the same software system. For instance, the software embedded in modern vehicles is typically structured in two layers. The lower, infrastructure layer contains a scheduler, which essentially executes an infinite loop that periodically calls, in a predefined order, a fixed set of modules (called applications) in the upper, application layer. The individual applications are of a purely transformational nature: they read certain input values coming from the sensors and set by the infrastructure, and compute, in a finite number of steps, certain output values which are then propagated by the infrastructure software to the actuators. If we have to formally verify the safety of such embedded software, both transformational and temporal properties need to be taken into account. In this particular domain, one can even observe a hierarchy between the two, as a consequence of the hierarchy between the two software layers: one can view the temporal behaviour on top of the transformational one.

In this paper, we propose an approach that can be described as Deductive Verification Based Abstraction for Software Model Checking. The essence of our approach is to relativise the verification of the temporal properties of a program on the transformational properties of certain selected program components. The transformational properties are phrased as Hoare logic style contracts, and deductive verification is performed to verify that the components indeed fulfil their contracts. Then, for the purpose of model checking of the temporal properties of the program, the selected components are replaced by their contracts. Since this results in modular verification, it has good chances of scaling better than model checking on its own, which is a monolithic technique.

Our approach allows the results of deductive verification to be lifted to (and utilised in) the temporal domain. In the context of our embedded software example mentioned above, one would apply deductive verification to verify the transformational properties of the modules in the application layer, and then combine their contracts with the infrastructure software into a model that is model checked against the temporal properties. To combine such heterogeneous approaches to formal verification in a sound and consistent manner, a unifying semantic foundation is needed. In this paper, we summarise a previously developed abstract contract theory [14] as a theoretical framework for combining deductive verification with model checking, and show how our approach can be formalised in this abstract contract theory.

To test our idea, we are currently experimenting with a tool chain for C programs, based on Frama-C for deductive verification and $\text{ TLA}^+$ for model checking. As preliminary evaluation, we have applied our approach on two example C-programs, with one being based on a real software module taken from the automotive industry.

Related Work. The idea of combining code with contracts when performing model checking is explored in several previous works.

Sun et al. [20] show how contracts can be used when creating models to be verified with the PAT model checker, by means of a case study where PAT is used to model check itself. The target language is C#, and the approach is to include code and contracts into the models by allowing PAT models to dynamically load C# code (possibly annotated with contracts). This differs from our approach where code and contracts are translated statically into the modelling language. The main focus of their work is, however, the verification of PAT, and they do not evaluate how the use of contracts affects scalability. Their approach also differs from ours in that they perform runtime verification of the contracts.

Beckert et al. [4] use contracts to introduce modularity into the bounded model checker JBMC for Java programs. Their approach differs from ours in that they integrate the program and the contracts by performing transformations on the original Java program, whereas we translate the program and the contracts separately into the modelling language before we integrate them. Similarly, Champion et al. [7] use contracts to achieve modularization for the SMT-based model checker Kind2. They show on an example that their approach improves the scalability of the tool. Contracts are part of the modelling language and specify the behaviour of nodes in the model, as there is no underlying programming language, and thus no translation of programs into models, unlike in our approach.

Closest to our philosophy of using deductive verification for the purposes of formally justifying abstract models of program behaviour, to be then used for model checking, is perhaps the work by Ortwijn et al. [18]. It can be seen as a generalisation of our approach to concurrent programs, where Separation Logic with Fractional Permissions is used for deductive verification, and where the abstraction is into process algebraic muCRL terms. Finally, it should be pointed out that the model of programs proposed here, where certain parts have been abstracted into TLA actions, is very close in spirit to the notion of flow graph studied in [19]. The authors consider there the problem of how to compositionally model check flow graphs against temporal properties, but do not address the problem of extracting flow graphs from source code in a provably correct manner, as we do here.

Structure. The paper is organised as follows. In Sect. 2 we present an overview of our approach and the envisaged tool chain. Deductive verification and Frama-C are described in Sect. 3, while model checking and TLA in Sect. 4. Then, Sect. 5 gives a summary of our abstract contract theory from [14], and explains how it serves as a theoretical foundation for our approach. We present a preliminary practical evaluation of our approach in Sect. 6, and conclude with Sect. 7.

Fig. 1.

Flowchart illustrating our verification approach and tool chain

2 Overview of the Verification Approach

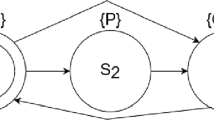
The starting point of our approach is a C program and some temporal property, which we want the program to satisfy. Our proposed verification approach and tool chain are illustrated in Fig. 1. As shown, we rely on Frama-C for (abstraction using) deductive verification, and on $\text{ TLA}^+$ for modelling and model checking.

Fig. 2.

A simplified temperature converter program

Illustrating Example. Consider the simple program shown in Fig. 2. The main function of the program repeatedly reads a temperature value, converts it from Kelvin to Celsius, and finally outputs the converted value (the value of the variable in_kelvin is expected to be updated between each iteration in the loop). Assume that we want to use the TLC model checker to verify the program against some chosen temporal property (TLA and TLC is described in more detail in Sect. 4.1). Then, the first step of our approach would be to identify sequential blocks in the code that can be recognised as atomic with respect to the chosen temporal property, and then to provide these blocks with contracts. For specifying block contracts, we use the (Hoare logic style) ACSL specification language, which is the annotation language supported by Frama-C (described in Sect. 3). For our example program, we have chosen to consider the convert_temp function as an atomic block, which we have annotated with an ACSL function contract (see the text in green preceding the function). Next, we use WP, the Frama-C plugin for deductive verification, to verify that convert_temp satisfies its contract. Then comes the key point of our approach: when creating the $\text{ TLA}^+$ model of the program, we rely on the (deductively verified) ACSL contract of convert_temp, instead of on its code, to abstract the block into a TLA action. The remaining parts of the main function (i.e., the while loop and the reading/writing) are modelled directly from their code. By using the contract of convert_temp instead of its code, the created model abstracts from the irrelevant implementation details of convert_temp, such as the use of the intermediate variable res, thus decreasing the complexity of the model.

Tool Chain. Figure 1 also shows the envisaged tool chain supporting our approach. On the contract side, we are working with Frama-C, by specifying contracts in ACSL and verifying them using the WP plugin. On the modelling side, we work with the TLA framework by using the TLA toolbox, which allows both for specifying models in $\text{ TLA}^+$ and performing model checking with TLC over the models. To translate contracts code into $\text{ TLA}^+$, we use the Frama-C plugin C2TLA+ [15] (see Sect. 4.2).

The steps in Fig. 1 where no specific tool or plugin is specified have, in this work, been carried out manually. There is potential to automate more of the steps. In particular, automating the translation of contracts into $\text{ TLA}^+$, and interleaving contract and code translations in $\text{ TLA}^+$, should be straightforward. However, automating some of the steps may be challenging. For instance, automating the (first) step of identifying which code blocks to identify as atomic is problematic. The difficulty stems from the conflicting goals of producing an abstract model of the program that, on one hand, has as a reduced state space as possible, and on the other hand, is faithful with respect to the temporal properties we want to verify. The approach we take in our case study (Sect. 6) is to use functions as atomic blocks. However, this may not always be adequate; in particular, larger functions with side-effects may not be atomic with respect to certain temporal properties.

A further challenge is to automate the (second) step of providing the selected code blocks with contracts. Automated inference of specifications (contracts) is an area of active research showing promising results; see, e.g., [1]. However, automatically generated contracts tend to document the code rather than the intention behind it, and tend thus to be more verbose than contracts provided by humans. Future work is needed to address these challenges. Another possibility is that the code has already been verified against contracts using deductive verification in some other verification context, in which case one can get the contracts for free by reusing the already existing ones.

Abstract Contract Theory. The approach outlined above is compatible with the contract based design methodology. This typically entails designing a system in a top-down manner, through refinement and decomposition of contracts, so that low-level components can be independently implemented against their contracts, while ensuring that top-level properties still hold. In Sect. 5 we show that the proposed method of procedure-modular verification can be cast in a previously developed contract theory [14]. This provides a strong theoretical foundation for our verification approach, and, since the contract theory supports a contract based design workflow, this translates to the approach presented here.

3 Deductive Verification and Frama-C

Frama-C is a software verification and analysis platform [8] for the C language (specifically, the C99 ISO standard [11]). It follows a modular design, and numerous plugins provide various types of analyses. One of these plugins is $\textsf{WP}$ [3], with which deductive verification (based on Weakest Preconditions) can be performed. Frama-C has its own specification language, called ANSI/ISO C Specification Language (ACSL) [2]. ACSL specifications are written as annotations directly in the source code, as C comments starting with an @ character. A commonly used construct is the function contract, which specifies the behaviour of a function and is annotated in the source code. In Fig. 2, an example of an ACSL function contract for is shown. The requires clause specifies the pre-condition, which is an assertion that must be fulfilled by callers before calling the function. In this case, the original temperature must be at least 0, which is the lowest possible temperature in Kelvin. The ensures clause specifies the post-condition, an assertion that should hold after executing the function. Here it specifies that the return value will be the converted temperature. The assigns clause specifies the frame condition, i.e., what memory locations may have their values changed during execution. In this case only local variables are updated, so the special keyword is used to let callers know that no global memory is changed. ACSL also support so-called ghost variables and code. Ghost variables are similar to regular variables, except they are only visible in specifications, much like logical variables in standard Hoare logic [10]. Ghost statements, such as ghost variable declarations, are preceded by the ghost keyword.

If we take the view of an ACSL contract as separated from the function it specifies, and denote it by $C = (P, Q, L)$, where P is the pre-condition, Q the post-condition, and L all the mutable memory locations per the frame condition, one can give it a denotational semantics as follows:

$$\begin{aligned} \left[ \!\left[ C\right] \!\right] \>{\mathop {=}\limits ^{\textsf{def}}}\>\{ (s, s')\ |\ \forall \mathcal {I}.\, (s \models _{\mathcal {I}} P \Rightarrow s' \models _{\mathcal {I}} Q) \wedge \forall l \not \in L.\, s'(l) = s(l) \} \end{aligned}$$

(1)

where $\mathcal {I}$ ranges over the possible interpretations of logical variables. This is in line with the standard definition of a function satisfying an ACSL contract [2].

4 Model Checking and TLA

This section describes the TLA framework, and how to abstract (deductively verified) contracts into TLA actions, for model checking of programs against temporal properties.

4.1 The TLA Framework

The Temporal Logic of Actions (TLA) is a temporal logic for specifying and reasoning about concurrent systems. TLA defines systems and system behaviours using the temporal operators $\square$ (always) and $\lozenge$ (future) over actions as elementary formulas. Below, we summarise the concepts of TLA required for understanding this paper. The formalisation is based on Lamport [12], but adjusted for better integration with our abstract contract theory presented in Sect. 5.1.

Actions. In TLA, an action is a predicate representing transitions between two sets of states. Following the terminology of [12], we say that an action is a predicate over primed and non-primed flexible variables and rigid variables. From a programming perspective, rigid variables act as constants and flexible variables as program variables. Furthermore, a non-primed flexible variable x represents the value of x in the state we are transitioning from, while a primed variable $x'$ represents the value in the state we are transitioning to. Here, we consider states to be mappings from flexible variables to values, and use $\textbf{State}$ to denote the set of all states. For example, the action $x' > x$ specifies a transition between any two states s and t such that $t(x) > s(x)$. Semantically, actions are defined, for a given interpretation over rigid variables, as a binary relation on $\textbf{State}$. In Fig. 3, we illustrate, using some example operators, how actions are defined formally, where $\mathcal {I}$ now ranges over all interpretations of rigid variables.

Fig. 3.

The semantics of actions in TLA

Temporal Formulas. TLA can be lifted to a temporal logic by including the LTL operators $\square$ and $\lozenge$. Formally, we first lift the domain of actions from $\textbf{State}\times \textbf{State}$ to $\textbf{State}^{\omega }$ (the set of infinite traces), denoted $\left[ \!\left[ A\right] \!\right] ^{\omega }_{\mathcal {I}}$, as follows:

$$\begin{aligned} \left[ \!\left[ A\right] \!\right] ^{\omega }_{\mathcal {I}} \>{\mathop {=}\limits ^{\textsf{def}}}\>\{\langle \sigma _1\sigma _2\ldots \rangle \mid (\sigma _1, \sigma _2) \in \left[ \!\left[ A\right] \!\right] _\mathcal {I}\} \end{aligned}$$

That is, an action is defined to hold over an infinite trace if it holds when evaluated over the first two states of the trace. With this, we can now treat actions as temporal formulas, and can define the semantics of the temporal operators $\square$ and $\lozenge$ as usual. Let T be a temporal formula, then:

$$\begin{aligned} \left[ \!\left[ \square T\right] \!\right] _\mathcal {I}^\omega \>{\mathop {=}\limits ^{\textsf{def}}}\>\{\sigma ^\omega = \langle \sigma _1,\sigma _2,\ldots \rangle \mid \forall n \in \mathbb {N}. \ \langle \sigma _n, \sigma _{n+1}, \ldots \rangle \in \left[ \!\left[ T\right] \!\right] _{\mathcal {I}}^{\omega } \} \\ \left[ \!\left[ \lozenge T\right] \!\right] _\mathcal {I}^\omega \>{\mathop {=}\limits ^{\textsf{def}}}\>\{\sigma ^\omega = \langle \sigma _1,\sigma _2,\ldots \rangle \mid \exists n \in \mathbb {N}. \ \langle \sigma _n, \sigma _{n+1}, \ldots \rangle \in \left[ \!\left[ T\right] \!\right] _{\mathcal {I}}^{\omega } \} \end{aligned}$$

Modelling Programs in TLA. A program is modelled from a triple $( Init , \mathcal {M}, F)$, where $Init$ specifies the constraints on the initial state, $\mathcal {M}$ the next-state relation describing possible state-transitions in the program, and F defines some fairness constraints. From such a triple, a program is defined by a formula:

$$\begin{aligned} \varPhi \>{\mathop {=}\limits ^{\textsf{def}}}\> Init \wedge \square [\mathcal {M}]_{ vars } \wedge F, \end{aligned}$$

where $vars$ are the program variables in $\mathcal {M}$ and $[\mathcal {M}]_{ vars }$ is syntactic sugar for $\mathcal {M} \vee vars ' = vars$. This allows “stuttering” steps between (identical) states, which can be useful (in particular) when specifying concurrent systems.

As a simple example, let $\mathcal {M} = (x < 100 \rightarrow x' = x+1) \wedge (x \ge 100 \rightarrow x' = 0)$ and consider the following TLA formula specifying a program that increments the variable x from 0 to 100, and then wraps around to start from 0 again:

$$\begin{aligned} x = 0 \wedge \square [\mathcal {M}]_{\langle x \rangle } \wedge \square \lozenge \langle \mathcal {M} \rangle _{\langle x \rangle } \end{aligned}$$

(2)

The expression $\langle \mathcal {M} \rangle _x$ is syntactic sugar for $\mathcal {M} \wedge x' \ne x$; thus, the fairness condition simply states that x must always eventually be incremented.

Verifying Temporal Properties (Model Checking). TLA also allows for specifying temporal properties, against which programs can be verified. Since both programs and properties are defined in TLA, verification amounts to showing that the denotation of the temporal property subsumes the denotation of the program: given a temporal property T and an interpretation $\mathcal {I}$, we say that a TLA program $\varPhi$ satisfies T over $\mathcal {I}$ iff $\left[ \!\left[ \varPhi \right] \!\right] _{\mathcal {I}}^{\omega } \subseteq \left[ \!\left[ T\right] \!\right] _{\mathcal {I}}^{\omega }$. For example, let $\varPhi$ be the example program in (2) and T be the formula $\square (x \ge 0)$. Then, $\varPhi$ satisfies T since $\sigma ^\omega \in \left[ \!\left[ \varPhi \right] \!\right] \Rightarrow \sigma ^\omega \in \left[ \!\left[ T\right] \!\right]$, thus $\left[ \!\left[ \varPhi \right] \!\right] _{\mathcal {I}}^{\omega } \subseteq \left[ \!\left[ T\right] \!\right] _{\mathcal {I}}^{\omega }$. In practice, one applies the model checker TLC (see below) to verify that the subset relation between a program $\varPhi$ and a temporal property T holds.

$\text{ TLA}^+$ and TLC. $\text{ TLA}^+$ [13] is a concrete language that implements the TLA framework and allows for specifying models of computer programs. The syntax of $\text{ TLA}^+$ is intended to resemble mathematical notation: for example, “/$\backslash$” and “$\backslash$/” denote $\wedge$ and $\vee$, respectively. TLC [21] is an explicit-state model checker, which can be used to model check $\text{ TLA}^+$ specifications for both safety and liveness properties (which are also specified in $\text{ TLA}^+$). An example of a $\text{ TLA}^+$ is shown in Fig. 4. The specification is a translation of the temperature conversion program in Fig. 2 (see Sect. 4.2 for a further description of the translation of the program into the $\text{ TLA}^+$ specification).

4.2 Translating Code and Contracts into TLA

For contracts, the translation is performed by converting the contract into an action equivalent to the denotation of the contract. Since both contracts and actions are evaluated over $\textbf{State}\times \textbf{State}$, we can convert the contract into a TLA action by taking its denotation. That is, let $A^c$ denote the action obtained from translating a contract $C = (P,Q, L)$. We then define:

$$\begin{aligned} A^C \>{\mathop {=}\limits ^{\textsf{def}}}\>\forall \mathcal {I}.\ (P \Rightarrow Q) \wedge \forall l \not \in L.\, l' = l \end{aligned}$$

The so-defined translation is semantics-preserving, since the definition of the action $A^C$ is equivalent to the definition of the denotation of C.

For the translation of C code into TLA, we do not define a concrete translation function here. Instead, we rely on the C2TLA+ [15] plugin for Frama-C, which automatically translates a program into a $\text{ TLA}^+$ specification. C2TLA+ translates a given C program into TLA+ by defining, for each statement in the code, an action corresponding to that statement. The control flow of the program is translated by defining a variable in the TLA+ model representing the call stack, program counter, frame pointers, and (global and local) memory. The control flow is then simulated in the model using the program counter and call stack to ensure that, in every reachable state, only one action (statement) is feasible (can be executed).

Fig. 4.

Translation of the temperature conversion program into $\text{ TLA}^+$

Example. Consider again the temperature conversion program in Fig. 2. In Fig. 4, we show a $\text{ TLA}^+$ specification created by translating the code in the main function and the contract in the program into $\text{ TLA}^+$ (following the approach described in Sect. 2). In the model, the control flow of the original C program is simulated using the pc (program counter) variable. Note also that, for each action, we are required to specify variables that are not updated using the built-in UNCHANGED predicate. Here, both the program code and the contract have been translated manually into $\text{ TLA}^+$. In Sect. 6, we provide more details regarding how to apply the approach and how the C2TLA+ tool can be used to automate the translation of program code into $\text{ TLA}^+$. Using the model checker TLC, it is possible to verify temporal properties for the specification in Fig. 4. For example, TLC verifies that the specification satisfies the following temporal property stating that if the temperature is always above 273 K, then it will also always be above $0^\circ$ C:

$$\begin{aligned} \square (\texttt {in\_kelvin} \ge 273) \Rightarrow \square (\texttt {out\_celsius} \ge 0) \end{aligned}$$

(3)

5 Contracts as a Unifying Theory

In this section, we introduce our abstract contract theory and present our work in the setting of this theory. In doing so, we provide a strong theoretical foundation for our work and show that the methodology follows established principles in contract-based design.

5.1 An Abstract Contract Theory

In previous work, we proposed an abstract contract theory [14], which supports the Design-by-Contract methodology developed and advocated by Meyer in [16]. Our theory instantiates the contract meta-theory of Benveniste et al. [5], and thus satisfies several properties considered crucial in system design methodologies, such as independent implementation, and reuse, of components. The contract theory is developed at the semantic level, and can be implemented by means of concrete languages for writing program components and contracts.

Fig. 5.

Our abstract contract theory

As the basic unit of behaviour, we take the abstract notion of a run, representing a single execution of a system (or part thereof), and let $\textbf{Run}$ denote the set of all runs. In a concrete setting, an example of a run could be an element of $\textbf{State}\times \textbf{State}$, i.e., a pair of states constituting a possible pre-state and post-state of a procedure call. We focus on procedural, sequential programming languages, and assume some finite universe of procedure names $\mathcal {P}$. For a given set of procedure names $P \subseteq \mathcal {P}$, a procedure environment $\textbf{Env}_{P} = P \rightarrow 2^{\textbf{Run}}$ is a mapping from procedure names to their possible runs. Let $\textbf{Env}\>{\mathop {=}\limits ^{\textsf{def}}}\>\bigcup _{P \subseteq \mathcal {P}} \textbf{Env}_{P}$. We define a partial order on procedure environments as follows. For any two procedure environments $\rho \in \textbf{Env}_{P}$ and $\rho ' \in \textbf{Env}_{P'}$, we have $\rho \sqsubseteq \rho '$ iff $P \subseteq P'$ and $\forall p \in P. \rho (p) \subseteq \rho '(p)$. The partial order $(\textbf{Env}, \sqsubseteq )$ forms a complete lattice, since both a greatest lower bound (glb), and a least upper bound (lub), exists for every subset of $\textbf{Env}$. The glb operation on environments is denoted as usual by $\sqcap$, and the lub operation by $\sqcup$.

To formally define components and contracts, we first equip both notions with an interface $I_{} = (P^-_{}, P^+_{})$, where $P^-_{}$ and $P^+_{}$ are disjoint subsets of $\mathcal {P}$. $P^+_{}$ is the set of procedures (to be) implemented in a component, and $P^-_{}$ are the procedures called by it, but not implemented within it. Our contract theory is summarised in Fig. 5. We use $\mu x.\, f(x)$ to denote the least fixed-point of the function f (when it exists), $\rho ^\top _P$ to denote the (top) environment mapping every procedure in P to $\textbf{Run}$, and for any mapping $h : A \rightarrow B$ and set $A' \subseteq A$, we use $h_{|A'}$ to denote the restriction of h on the sub-domain $A'$.

Instantiation of the Theory. In our contract theory, we have deliberately left the domain of $\textbf{Run}$ unspecified. This allows the domain to be instantiated as needed by the concrete application domain, and even to combine multiple domains. Certain constraints do need to be fulfilled, though. For the theory to be well-defined (e.g., that the involved fixed-points exist), all base components used to build larger components must be monotonic mappings (monotonicity of composed components is then ensured by the composition operator).

In our previous work [14], we argued for the importance of separating contracts from their implementation, and gave contracts a denotational semantics, defining the denotation of a contract C in a way that guarantees that the equation:

$$\begin{aligned} \left[ \!\left[ C\right] \!\right] = \bigcup _{S\,\models \,C} \left[ \!\left[ S\right] \!\right] \end{aligned}$$

(4)

is fulfilled, i.e., that the denotation of a contract is the union of the denotations of all programs that satisfies it. The rationale for this is that we desire programs to satisfy their contracts exactly when $\left[ \!\left[ S\right] \!\right] \subseteq \left[ \!\left[ C\right] \!\right]$. Procedure-modular verification is then facilitated by considering a special contract environment $\rho _c$ induced by the above equality: let every procedure p be equipped with a contract $C_p$, we then define $\rho _c(p) \>{\mathop {=}\limits ^{\textsf{def}}}\>\left[ \!\left[ C_p\right] \!\right]$. Now, programs are given a contract-relative semantics $\left[ \!\left[ S\right] \!\right] ^ cr$, where the denotations of procedure calls is defined by the denotations of their contracts instead of their bodies. This gives rise to a separate satisfaction relation $S_p \models ^{ cr } C_p$, based on the contract-relative semantics.

For each domain used to instantiate the contract theory, concrete syntax for implementing and specifying programs is needed. Then, each instantiation requires abstraction functions, which take the concrete syntax and produce components and contracts in the abstract contract theory, as well as a contract-relative satisfaction relation $\models ^{ cr }$. The abstraction to components and contracts must be such that the following properties hold:

• 1. For any two disjoint sets of functions $P^+_{1}$ and $P^+_{2}$, abstracted individually into components $m_{1}$ and $m_{2}$, respectively, and $P^+_{1} \cup P^+_{2}$ abstracted into component m, we have $m_{1} \times m_{2} = m$.

• 2. For any procedure p with procedure contract $C_p$, abstracted into component $m_p$ with contract $c_p$, we have $S_p \models ^{ cr } C_p$ whenever $m_p \models c_p$.

Contracts in Our Approach. In our concrete setting, when working with components in the domain $\textbf{State}\times \textbf{State}$, contracts and the contract-relative semantics of statements will also be over this domain (by design of the approach, not because of theoretical restrictions). However, when in the domain $\textbf{State}^{\omega }$, we allow certain procedures (which we assume are marked in some way) to have contracts in the domain $\textbf{State}\times \textbf{State}$, by defining the contract-relative semantics for contracts in both domains. This allows us to verify some components in the setting of pre- and post-states, and then reuse their contracts to verify temporal properties in the domain of infinite traces. Since we are adhering to the contract theory, which follows the axioms of the meta-theory [5], we ensure that the desired properties for proper design-chain management hold. As an example, recall the temperature conversion program in Fig. 2. For this program, we consider the main function to be defined in the domain $\textbf{State}^\omega$, while the contract for the conversion function is in $\textbf{State}\times \textbf{State}$.

5.2 Deductive Verification in the Abstract Contract Theory

In the following paragraph, we provide some intuition for the instantiation of the contract theory with a concrete semantics. We assume that every procedure p is associated with a body $S_p$. The semantics of statements is defined relative an interface $(P^-_{}, P^+_{})$ and environments $\rho ^- \in \textbf{Env}_{P^-_{}}$ and $\rho ^+ \in \textbf{Env}_{P^+_{}}$, denoted $\left[ \!\left[ S\right] \!\right] ^{\rho ^+}_{\rho ^-}$. Specifically, the semantics of a function call is then defined as $\rho ^+(p)$ when $p \in P^+_{}$, and as $\rho ^-(p)$ when $p \in P^-_{}$. Given $\rho ^- \in \textbf{Env}_{P^-_{}}$, we define the function $\xi : \textbf{Env}_{P^+_{}} \rightarrow \textbf{Env}_{P^+_{}}$ by $\xi (\rho ^+) (p) \>{\mathop {=}\limits ^{\textsf{def}}}\>\left[ \!\left[ S_p\right] \!\right] _{\rho ^-}^{\rho ^+}$ and consider its least fixed point $\rho ^+_0$. This is used as the basis of a standard denotation $\left[ \!\left[ S\right] \!\right] _{\rho ^-} \>{\mathop {=}\limits ^{\textsf{def}}}\>\left[ \!\left[ S\right] \!\right] _{\rho ^-}^{\rho ^+_0}$. Using this, we can define the contract-relative semantics of statements as $\left[ \!\left[ S\right] \!\right] ^{ cr } \>{\mathop {=}\limits ^{\textsf{def}}}\>\left[ \!\left[ S\right] \!\right] _{\rho _c}$. Details of this formalisation for a simple procedural language can be found in [9].

In this setting, we can now define how to abstract programs and contracts into components and denotational contracts, respectively. For any set of procedures $P^+_{}$, calling procedures $P'$, we define the component $m : \textbf{Env}_{P^-_{m}} \rightarrow \textbf{Env}_{P^+_{m}}$, where $P^-_{m} \>{\mathop {=}\limits ^{\textsf{def}}}\>P' \setminus P^+_{m}$ and $P^+_{m} \>{\mathop {=}\limits ^{\textsf{def}}}\>P^+_{}$, so that $\forall \rho ^-_m \in \textbf{Env}_{P^-_{m}}.\ \forall p \in P^+_{m}.\ m(\rho ^-_m)(p) \>{\mathop {=}\limits ^{\textsf{def}}}\>\left[ \!\left[ S_p\right] \!\right] _{\rho ^-_m}$. For a procedure p with an ACSL contract $C_p$, calling other procedures $P^-$, we define the denotational contract $c_p = (\rho ^-_{c_p}, \rho ^+_{c_p})$ with interface $P^+_{c_p} \>{\mathop {=}\limits ^{\textsf{def}}}\>\{ p \}$ and $P^-_{c_p} \>{\mathop {=}\limits ^{\textsf{def}}}\>P^-$, so that $\rho ^+_{c_p}(p) \>{\mathop {=}\limits ^{\textsf{def}}}\>\rho _c(p)$, and $\forall p' \in P^-.\ \rho ^-_{c_p}(p') = \rho _c(p')$.

The full semantics of the concrete languages, C and ACSL, is implicitly defined by Frama-C and will not be expanded upon here. Note that, per the semantics of an ACSL function contract as given in (1), which is the only ACSL construct of concern in the present paper, a function can be verified against its contract, and relative to the contracts of other functions, only if its denotation is subsumed by that of its contract. This is in accordance with condition (4). Thus, the contract-relative satisfaction relation $\models ^ cr$ is such that the two properties of abstraction discussed in Sect. 5.1 hold.

5.3 Procedure-Modular Verification with TLA

Verification in the two domains can now be combined, by abstracting the contracts of the already-verified contracts into actions. This can also be viewed as a form of procedure-modular verification, where temporal properties are checked for a larger program, relative the ACSL contracts of some of the called procedures. To this end, we take the view that a procedure environment $\rho \in \textbf{Env}_{P}$ in the domain $\textbf{State}\times \textbf{State}$ as discussed in Sect. 3, maps procedure names to actions. We let $\textbf{Run}= (\textbf{State}\times \textbf{State}) \cup \textbf{State}^{\omega }$, and as previously explained, assume that certain procedures have been selected to be considered actions. For a TLA program S with interface $(P^-_{}, P^+_{})$, we can define the denotation $\left[ \!\left[ S\right] \!\right] _{\rho _c}$ where, for some $p \in P^-_{}$, $\rho _c(p) \in \textbf{Env}_{P^-_{}}$ are actions, or denotations of type $\textbf{State}\times \textbf{State}$ of the called procedure. In this way we get a contract-relative semantics where programs produce infinite state sequences, but depend partially on procedures producing actions, or state pairs. We can then abstract the concrete languages in the same way as in Sect. 5.2.

Note that, while the concrete contract languages are different in the domains (in one case it is ACSL, and in the other $\text{ TLA}^+$), the concrete language for defining components is the same, namely C, meaning that the abstraction from procedures to components is in reality performed in two steps, first from C code and ACSL contracts to $\text{ TLA}^+$ specifications and actions, and from there to components. We use TLC to verify programs. From a denotational viewpoint, successful verification in TLC means that there is a subset relation between the denotation of the program and the specification. Hence, the two required properties listed in Sect. 5.1 are fulfilled.

Considering again the example from Fig. 2, the component $m_ main$ resulting from abstracting the main function would map denotations for the called function convert_temp in the domain $\textbf{State}\times \textbf{State}$ to denotations of main in the domain $\textbf{State}^{\omega }$. The exact behaviour is obtained from the body of main translated to TLA, and parameterised on the behaviour of convert_temp. Verification is performed by substituting the contract of convert_temp for its behaviour, on the concrete level, which is shown in Fig. 4.

5.4 Contract Based System Design

As we have previously shown [14], our contract theory is an instance of the meta-theory of Benveniste et al. [5], thus establishing a number of properties desired of system design methodologies, such as independent implementation and verification of components. In contract-based design, a system is typically designed in a top-down manner, starting from the desired high-level properties that the system must satisfy, which are then decomposed into contracts for the (sub-)components. The components are then implemented independently, relying only on the contracts of other components.

By casting the approach proposed in the present paper, we have established that it is compatible with the principles of contract-based design. In particular, ensuring correctness of a system as a whole reduces to showing, one the one hand, that the composition of the contracts of the sub-components of the system refines the top-level contracts, and, on the other hand, that the concrete procedures satisfy their concrete specifications, according to the contract-relative semantics.

In the example from Fig. 2, we would typically have a top-level contract c specifying the temporal behaviour of the system, without any required procedures. This contract would then be decomposed into contracts $c_ conv$ and $c_ main$ for the two procedures, respectively. The former would be defined concretely in ACSL, expressing the possible state pairs resulting from conversion, without needing any assumptions on other procedures. The latter would be defined by a concrete TLA formula, with assumptions on the actions produced by the conversion function. By showing that $c_ conv \otimes c_ main \preceq c$, and that the two concrete implementations satisfy their contracts according to the methodology outlined in the preceding sections, it is, by the properties of the contract theory, then established that $m_ conv \otimes m_ main \models c$.

6 Preliminary Evaluation

To evaluate our approach, we conducted two experiments, one using a simple toy program simulating some file operation, and the second one using a simplified software module taken from the automotive industry. Both experiments were carried out on a Dell Latitude 7420 using Ubuntu 20.04 running in VirtualBox with 8 GB RAM and on Intel i5 CPU (2 cores).

Fig. 6.

Program imitating behaviours including reading and writing to a file

6.1 Simple File Open-Close Example

The first test case consists of a simple example that simulates a program performing file operations. The program, which is shown in Fig. 6, repeatedly reads from the file, performs some operation and writes to the file. For this program, the temporal property we are interested in verifying (using model checking) is that, whenever the file is open, it will eventually be closed. This property is captured by the following TLA formula:

$$\begin{aligned} \square \, ( file\_status = OPEN \Rightarrow \lozenge \, ( file\_status = CLOSED )) \end{aligned}$$

(5)

To evaluate our method, we created two $\text{ TLA}^+$ models: one modelled directly from the program code, and a second abstract model that was created following the approach outlined in Sect. 2. After creating the two models, we compared the size of the state space of the models, and the time required for verifying property (5).

Creating the Models. The first model was translated directly from the C program code using the C2TLA+ tool. Due to limitations in C2TLA+, some manual overhead was required to achieve a correct specification. We also added a fairness constraint to the model (since this is not performed automatically by C2TLA+), stating that the program should never get stuck (i.e., “stutter”) indefinitely. Furthermore, we made some abstractions regarding the domain of the variables: input is given the domain $[-2*N,N]$ and file_status the domain [0,1]. Moreover, in the main function, a call is made to a havoc_input function in each iteration of the loop, which represents non-deterministic assignment of the input variable. In a real setting, input is expected to be assigned by some external component between each iteration of the loop. In the $\text{ TLA}^+$ model, the havoc effect is achieved by manually inserting an action that simply assigns input non-deterministically within its domain.

The second model is a more abstract version of the first model, achieved by modelling the file_operation function from a contract instead of the program code. The contract used to model file_operation was written in ACSL and is shown as an annotation above the function in Fig. 6. Note that, since the temporal property we are interested in verifying concerns only the open/close property of the file, i.e., the value of the file_status variable, the contract only specifies the behaviour of this variable. Using the WP plugin of Frama-C, we verified that file_operation satisfies its contract. Thereafter, we translated the contract into a TLA action, following the method in Sect. 4.2; that is, it was translated into the action:

$$ (0<= n \wedge n < N \wedge file\_status = OPEN ) \Rightarrow ( file\_status = CLOSED ) $$

Lastly, we completed the creation of the second abstract model by replacing the parts of the $\text{ TLA}^+$ model corresponding to file_operation with the translation of the contract. To properly integrate the contract action into the model, we also added a conjunct to handle appropriately the program counters and stack registers of the model.

Table 1. Results of model checking two models for property (5)

Model Checking. Model checking was performed using TLC on both the full model, created directly from the program code and on the second abstract model including the contract action for file_operation. The results of the model checking are shown in Table 1 and, as expected, the state space of the second abstract model was significantly smaller than the state space of the full model. Moreover, verification time decreased from 51 s to 5 s, showing that the smaller state space, for this example, factored into the time required for verification by TLC. For a fair comparison of the verification time between the two models, one should also add the time required by WP for verifying the contract to the total verification time of the abstract model. However, for this example, the time required by WP was negligible (0.15 s).

Fig. 7.

The steering function from the steering module together with the main function which simulates a scheduler

6.2 Simplified Industrial Example

As a second example, we use a C program based on a real software module taken from the automotive industry. The structure of, and C constructs used in, the case study program follows that of the real module, but the code have been rewritten and to some extent simplified, for proprietary reasons and due to limitations in the current tool-chain. The evaluation method for this example follows exactly that of the previous example. That is, we first created a full model, directly from the program code and then created a second model by abstracting one function using a contract for the function. Then, we model checked both models for a given property and compared the state spaces and verification times.

Description the Software Module. The software module used in this example performs a diagnosis of the status of the primary power steering of a vehicle and, in case of malfunction, activates the secondary (backup) power steering. A power steering is a device that reduces the manual effort required by the driver to rotate the steering wheel of the vehicle. The entry-point function of the module (the steering function) and the scheduler (the main function) of the simplified version are shown in Fig. 7. The full case study module is roughly 120 lines of code. In a real setting, the scheduler would be some external software that repeatedly calls several modules in a given order; here, we encoded the scheduler with the infinite while loop in the main function.

Upon invocation, the steering function first reads the current state of the vehicle, then calculates if secondary power steering should be activated and, lastly, writes the result. In a real setting, the reading and writing consist of communicating with a real-time database but, in our simplified version, this is simulated by reading and writing to the global array state, which represents the state of the vehicle. Note that, from the perspective of the steering module, the state of the vehicle consists of both inputs and outputs. Similar to our previous example, all (input) variables of the modules are assumed to be assigned by some external component at any time during program execution, which is represented with the call to havoc_inputs. The module also contains a counter as the global variable primaryCircuitNoFlowTime, the purpose of which is to remember if some property holds over several sequential executions. Specifically, the counter keeps track of the number of sequential iterations (if any) the electric motor of the vehicle has suffered from hydraulic malfunction.

Creating the Models. As for our first example, the first model is created by using the C2TLA+ tool, adding a fairness constraint, and abstracting the domains of certain variables (e.g., variables that are treated as Boolean values in the C programs are assigned the domain [0, 1]). The havoc statement in the main function was also treated similarly as in the first example, i.e., by inserting a TLA action in the model that assigns all input variables non-deterministically within their respective domains.

The second model was created by first identifying the steering function as a block of code that we consider as atomic and thus should be specified with an ACSL contract. It might appear surprising that we consider almost the entire example program as atomic, but recall that, in a real setting, the steering module will be only one of several modules called by the scheduler. As a contract for the steering function, we used an ACSL contract already written in a previous case study [17]. It should be pointed out that since we re-used a contract originally written for deductive verification of the module, no additional manual labour was required for this step in this particular example (and as pointed out above, we indeed advocate such a way of combing deductive verification with model checking). Using WP, we verified that steering satisfies the contract. Lastly, we translated the contract into $\text{ TLA}^+$ and integrated it into the first model to create the second abstract model.

Model Checking. We model checked the two models, using TLC, against the following liveness property:

If the electric motor of the engine suffers from hydraulic malfunction,

then the secondary steering should eventually be activated.

In TLA, this property is captured with the formula:

$$\begin{aligned} \square \, ( hydraulic\_malfunction \Rightarrow \lozenge \, secondary\_steering ) \end{aligned}$$

(6)

where $hydraulic\_malfunction$ represents the condition that the electric motor has suffered from hydraulic malfunction, and $secondary\_steering$ the condition that the secondary steering is activated.

Table 2. Results of model checking two models for property (6)

The results of model checking the two different models are shown in Table 2. As seen, verification was successful for both models. Furthermore, we again see that the state space (number of unique states) was significantly smaller for the abstract model. However, for this example, we did not observe any significant difference in the time required for verification (12 s vs 10 s). Moreover, as with the previous example, one should also consider the time required by WP for verifying the contract (2.150 s) to the total verification time of the abstract model.

7 Conclusion

In this paper, we proposed an approach of how to combine deductive verification with model checking in a natural manner, subordinating the former to the latter. First, deductive verification is used to abstract blocks of code, which can be considered atomic, into Hoare logic style contracts, in a provably correct manner. Then, the program model resulting (conceptually) from replacing the code blocks with their contracts, is model-checked against the temporal properties of interest. The Temporal Logic of Actions was proposed as a framework for representing the resulting program models, since both programs and Hoare logic contracts can be naturally expressed in TLA. We gave a semantic foundation of our modular approach, in terms of an abstract contract theory we developed earlier. Finally, we illustrated our approach on two example programs, using Frama-C for the deductive verification of the selected code blocks, and the $\text{ TLA}^+$ Toolbox (with TLC) for representing the abstract program models and for their model checking.

Our preliminary experiments are far too few as yet to allow any definitive conclusions to be drawn. Both examples in Sect. 6 showed that our approach led to a significant reduction in the size of the state space of the $\text{ TLA}^+$ model. Furthermore, the first example indicates that the reduction of the state space may significantly reduce verification time. However, in the second example, no speedup in verification time was observed. A key difference in the two examples is that the contract used in the first example was an incomplete specification (in the sense that it does not describe fully the indented behaviour of the program), while the contract used in the second example was a complete one (it models fully the intended behaviour of the function). We are as of yet not sure as to why, for the second example, the difference in verification time was not proportionate to the difference in the size of the state space, and it remains to be shown that our approach can improve scalability also when relying on complete specifications for the abstraction.

Another aspect is that the performance of our approach may have been influenced by the particular choice of tools. In particular, the choice of the C2TLA+ plugin and the TLC model checker may not have been optimal as tool support for our approach. One hypothesis is that a symbolic model checker may be a better choice.

Future work includes performing a proper evaluation of our proposed approach, both for complete and incomplete specifications, and to complete and improve the tool chain. Another question that needs investigation is how to adequately choose the granularity of the code blocks to be considered as atomic actions. Lastly, better support for showing decomposition and refinement of contracts is desired, for instance by further developing the contract theory in that direction.