Abstract
Most structured data today is still stored in relational databases, which makes it important to provide a translation between relational and semantic data. A relational to RDF mapping, such as R2RML [13], provides a way to view existing relational data in the RDF data model through declarative mappings. While relational to RDF mapping translates relational instance data to RDF, it does not specify any translation of existing relational constraints such as primary and foreign key constraints. Since the introduction of R2RML, interest in RDF constraint languages has increased and SHACL [15] has been standardised. This raises the question of which SHACL constraints are guaranteed to be valid on a dataset produced by a relational to RDF mapping. For arbitrary SQL constraints and relational to RDF mappings, this is a hard problem, but we introduce a number of restrictions on the mappings that allow us to introduce a constraint rewriting for relational to RDF mappings that faithfully transfers SQL integrity constraints to SHACL constraints. We define and prove two fundamental properties, namely maximal semantics preservation and monotonicity.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
In relational database theory, one can restrict data to a set of relations that are considered to be useful to applications at hand by imposing relevant integrity constraints upon them, i.e., the semantics properties, also known as data dependencies, that the data in the database must obey. However, such integrity constraints of relational data are not explicit when mapped into RDF. A relational to RDF (R2R) mapping outputs an RDF graph that no longer contains the integrity constraints information. To overcome the problem, one can restore the semantic properties of R2R transformed data by using a semantics preserving constraint rewriting [7, 23, 26] that maps the integrity constraints of relational data into a well-behaved constraint formalism, which provides a closed-world description for the mapped RDF graph. The integrity constraints of the dataset that is being stored or represented in the RDF graph are a critical piece of information in practice, both to detect problems in the RDF dataset and provide data quality guarantees for RDF data exchange and interoperability.
In this paper, we study constraint rewriting for R2R mapping to make it more faithful by transforming the integrity constraints, such as primary and foreign keys, unique and not null integrity constraints as well as data types, from SQL database to RDF graph. In an attempt to transfer such integrity constraints of relational data, such as key constraints and functional dependency in direct mapping [2] to a larger perspective of relational constraints [1, Sect. 10] in more expressive ontology-based mapping [18] of relational data, into OWL DL axioms [20] as well as Epistemic DL axioms [14], the problem has recently been studied in [7, 23] and [10, 11, 21] respectively. However, for our work, we follow the constraint rewriting technique proposed in [26] that explicitly transforms integrity constraints of SQL database into integrity constraints on the RDF graph, expressed in SHACL [15] as opposed to OWL/Epistemic DL axioms. Contrary to OWL, SHACL, the Shapes Constraint Language recommended by W3C since 2017, has a closed world semantics and uses the unique name assumption, which makes it a more suitable candidate than OWL for expressing as well as detecting the violations of integrity constraints on an RDF graph.
For arbitrary SQL constraints and relational to RDF mappings, constraint rewriting is a hard problem. For simplicity, we restrict ourselves to (a) the most common SQL constraints, namely keys, uniqueness and not null constraints, and (2) simple R2R mappings (Definition 4), which are restricted in such a way that the resulting RDF is structurally close enough to the source that it remains possible to analyse the propagation of source constraints to the target. Thus, once the SHACL descriptions of the mapped RDF graph are available, they can be used to validate that the facts in the graph are compatible with the constraints of the relational source and the mapping, using the SHACL validation engine. However, R2R mappings are also known for their mapping inconsistency and redundancy anomalies [9, 16], thus one-to-one semantics correspondence such as semantics preservation proposed in [26, Defn. 6] and [23, Defn. 12] between the relational and the mapped RDF data can not be established in general [23, 26, Prop. 1]. One of the prominent reasons behind such flaws is that R2R mappings often imply SHACL constraints that satisfy the mapped RDF graph with respect to database constraints even if the key constraints are violated in the source database, which can not be easily fixed as the mappings rely on the values of database keys to produce RDF terms [26, Exam. 4 and 5]. We can thus not hope for semantic equivalence between the SQL and SHACL constraints. In this work we instead define a notion of maximal semantics preservation to express that any additional SHACL constraints are either implied by the generated ones, or not implied by the SQL constraints.
Example 1
Consider the following database instance \(\mathcal {D}\) with schemas that describes students and their enrollment in courses being offered by a university:

In general, an R2R mapping is an assertion of the form \(Q \longrightarrow \psi \) that transforms a set of tuples projected by SQL query \(Q \), called source query, over a relational source \(\mathcal {D}\) into a set of RDF triples defined by graph triple patterns \(\psi \). Assume an R2R mapping M to retrieve students and their enrollment in the university’s courses,
where \(\texttt {iri}_1\) and \(\texttt {iri}_2\) are injective functions that construct iris for students and courses from their respective id’s. The mapping \( M \) yields the following RDF graph \( G \) (on the left) from the database instance \(\mathcal {D}\):

Next, consider a SHACL document \( S \) (on the right), which consists of node shapes :Student and :Course with implicit target classFootnote 1 that define the constraints, intuitively, all students must be enrolled for exactly one course, and all courses must be enrolled by zero or more students. Now observe that the document \( S \) not only validates the graph \( G \) but also guarantee the validation of every RDF graphs that can be generated via mappings \( M \) from any valid instance \(\mathcal {D}\) of the schemas in Example 1, i.e., semantics preservation. Moreover, any further restrictions on the property paths of \( S \), such as all courses must be enrolled by at least one students, would easily be violated, meaning that a valid database instance \(\mathcal {D}\) can be found such that mapped RDF graphs would not validate the document \( S \). Thus, we say that \( S \) is a maximally implied set of SHACL shapes for the given relational source and the mappings \( M \). For proof details, we refer the readers to the extended version [28].
Example 1 illustrates that an assessment of R2R mapping is necessary to guarantee whether the integrity constraints of relational data are maximally propagated via mappings to the RDF. We thus take the process of R2R transformation into account and define constraint rewriting as a function from constraints in SQL database to the sets of SHACL shapes over RDF graph. We first introduce two fundamental properties of constraint rewriting, namely maximal semantics preservation and monotonicity. Finally, we show that our proposed constraint rewriting is both maximal semantics preserving and monotone, even in the most general and practical scenario where relational databases contain null values. A constraint rewriting for R2R mappings is monotonic if it assures that the result of constraint rewriting that is already computed no longer requires alteration after the addition of new mappings.
2 Preliminaries
In this section, we fix notions and notations fundamental to the definition of R2R mapping, and SHACL constraints [15].
Databases. Let \(\varDelta \) be a countably infinite set of constants, including the reserved symbol \(\texttt {null} \). A relational schema \(\mathcal {R}\) is a finite set of relation names, known as relation schemas. We associate with each relation schema \(R\in \mathcal {R}\) a finite, non-empty set of named attributes, denoted by \(\textsf{att}(R)\). An instance \(\mathcal {D}\) of \(\mathcal {R}\) assigns each relation schema \( R \in \mathcal {R}\) a finite set of tuples \(R^{\mathcal {D}}\), where each tuple \(t\in {R}^{\mathcal {D}}\) is a function that assigns to each attribute in \(\textsf{att}(R)\) a value from domain \(\varDelta \).
We write X as shorthand for a non-empty set \(\{x_1,\dots , x_n\}\) of attributes for \(n\ge 1\), and \(x\in X\) to say that x is one of the elements of the set. \(|X|=n\) denotes the cardinality of the set. We further write \( X\triangleleft R\) to denote that X is a non-empty subset of \(\textsf{att}(R)\). We write \( t(x) \) to denote the restriction of a tuple \(t\in {R}^{\mathcal {D}}\) to an attribute \(x\in \textsf{att}(R)\), which can be extended to a set \( X\triangleleft R\), i.e., \( t( X) \). Finally, we define a relational database as a pair of \(\mathcal {R}\) and \(\mathcal {D}\), where \(\mathcal {R}\) is a relational schema and \(\mathcal {D}\) is a database instance of \(\mathcal {R}\). The active domain \(\varGamma _{\mathcal {D}}\) of a database is the set of constants appearing in \(\mathcal {D}\), i.e., \(\varGamma _{\mathcal {D}}\subseteq \varDelta \setminus \{\texttt {null} \}\).
SQL Constraints. We consider declarations of the SQL: (a) primary (\(\texttt {PK}\)) and foreign (\(\texttt {FK}\)) keys, (b) not null (\(\texttt {NN}\)) and unique (\(\texttt {UNQ}\)) integrity, and (c) data types, constraints on the relational schema \(\mathcal {R}\). We write \(\varSigma \) for the set of SQL constraints. \(\texttt {NN}\), \(\texttt {UNQ}\) and \(\texttt {PK}\) constraints on a relational schema \(\mathcal {R}\) are expressions of the form \(\texttt {NN}(X,R)\), \(\texttt {UNQ}(X,R)\) and \(\texttt {PK}(X,R)\), resp., for any \( X\triangleleft R\) such that \(R\in \mathcal {R}\). An instance \(\mathcal {D}\) of \(\mathcal {R}\) satisfies:
- \(\square \):
-
\(\texttt {NN}(X,R)\) if for every \(t\in {R}^{\mathcal {D}}\) and \(x\in X\), \(t(x)\ne \texttt {null} \).
- \(\square \):
-
\(\texttt {UNQ}(X,R)\) if for every \(t,t'\in {R}^{\mathcal {D}}\), if \(t(x)=t'(x)\ne \texttt {null} \) for every \(x\in X\) then \(t=t'\).
- \(\square \):
-
\(\texttt {PK}(X,R)\) if: (a) for every \(t\in {R}^{\mathcal {D}}\) and \(x\in X\), \(t(x)\ne \texttt {null} \), and (b) for every \(t,t'\in {R}^{\mathcal {D}}\), if \(t(X)=t'(X)\) then \(t=t'\).
An \(\texttt {FK}\) constraint on \(\mathcal {R}\) is an expression of the form \(\texttt {FK}( X,R,Y,S)\) for any \( X\triangleleft R\) and \( Y\triangleleft S\) with \(|X|=|Y|\) and \(R,S\in \mathcal {R}\). An instance \(\mathcal {D}\) of \(\mathcal {R}\) satisfies \(\texttt {FK}( X,R, Y,S)\) if for every \(t\in {R}^{\mathcal {D}}\): either (a) \(t(x)=\texttt {null} \) for some \(x\in X\), or (b) there exists a tuple \(t'\in {S}^{\mathcal {D}}\) such that \(t( X)=t'(Y)\). Next, to handle SQL data types, let the domain of an SQL data type \(\nu \) be a subset \(\varDelta _\nu \subseteq \varDelta \). An SQL data type declaration on \(\mathcal {R}\) is an expression of the form \(\texttt {Type}(x,\nu ,R)\) for every \(x\in \textsf{att}(R)\) such that \(R\in \mathcal {R}\), where \(\nu \) is an SQL data type. An instance \(\mathcal {D}\) of \(\mathcal {R}\) satisfies \(\texttt {Type}(x,\nu ,R)\) for an attribute \(x\in \textsf{att}(R)\), if \(t(x)\in \varDelta _{\nu }\) for every \(t\in {R}^{\mathcal {D}}\).
A relational schema \(\mathcal {R}\) with source constraints \(\varSigma \) consists of the relational schema \(\mathcal {R}\) and a set \(\varSigma \) of SQL constraints on \(\mathcal {R}\), such that \(\texttt {UNQ}(Y,R)\in \varSigma \) for all \(\texttt {FK}( X,R, Y,S)\in \varSigma \), as usual in all SQL implementations. W.l.o.g., we also assume that for every \(X\triangleleft R\): (a) if \(\texttt {PK}(X,R)\in \varSigma \), then \(\texttt {UNQ}(X,R)\in \varSigma \) and \(\texttt {NN}(X,R)\in \varSigma \), (b) if \(\texttt {NN}(X,R)\in \varSigma \), then \(\texttt {NN}(x,R)\in \varSigma \) for every \(x\in X\) and (c) if \(\texttt {NN}(x,R)\in \varSigma \) for every \(x\in X\), then \(\texttt {NN}(X,R)\in \varSigma \). Finally, given a relational schema \(\mathcal {R}\) with constraints \(\varSigma \), and an instance \(\mathcal {D}\) of \(\mathcal {R}\), we call \(\mathcal {D}\) a legal instance of \(\mathcal {R}\) with \(\varSigma \), denoted by \(\mathcal {D}\models \varSigma \), if \(\mathcal {D}\) satisfies all constraints in \(\varSigma \).
Queries. Assume relational algebra with Selection \(\sigma _{\lnot \textsf{isNull}}\), Projection \(\pi \), Equi Join \(\bowtie _{\texttt {equality}}\), Right Outer Join
 , Left Outer Join
, Left Outer Join
 and Full Outer Join
and Full Outer Join
 operations as query language that corresponds to a sub-class of basic fragment of SQL standard. We use notation \(\sigma _{\lnot \texttt {isNull}}\) for the select condition ‘\(\texttt {IS\ NOT\ NULL}\)’ over an attribute as in SQL, which can be extended to a set of attributes. Assume that \(\mathcal {R}\) is a relational schema, \(\mathcal {D}\) is an instance of \(\mathcal {R}\) and \(Q\) is a relational algebra expression over \(\mathcal {R}\). Then \(\textsf{att}(Q)\), the set of attributes of \(Q\), is recursively defined as follows, where we write \(X\triangleleft Q \) to denote that X is a non-empty subset of \(\textsf{att}(Q)\):
operations as query language that corresponds to a sub-class of basic fragment of SQL standard. We use notation \(\sigma _{\lnot \texttt {isNull}}\) for the select condition ‘\(\texttt {IS\ NOT\ NULL}\)’ over an attribute as in SQL, which can be extended to a set of attributes. Assume that \(\mathcal {R}\) is a relational schema, \(\mathcal {D}\) is an instance of \(\mathcal {R}\) and \(Q\) is a relational algebra expression over \(\mathcal {R}\). Then \(\textsf{att}(Q)\), the set of attributes of \(Q\), is recursively defined as follows, where we write \(X\triangleleft Q \) to denote that X is a non-empty subset of \(\textsf{att}(Q)\):
-
1.
If \(Q = R\) such that \(R\in \mathcal {R}\), then \(\textsf{att}(Q)=\textsf{att}(R)\).
-
2.
If \(Q '\) is a relational algebra expression over \(\mathcal {R}\), \(X\triangleleft Q '\) and \(Q =\sigma _{\lnot \texttt {isNull}(X)}(Q ')\), i.e., \(\sigma _{\lnot \texttt {isNull}(x_1)\wedge \,\dots \,\wedge \lnot \texttt {isNull}(x_n)}(Q ')\), then \(\textsf{att}(Q)=\textsf{att}(Q ')\).
-
3.
If \(Q '\) is a relational algebra expression over \(\mathcal {R}\), \(X\triangleleft Q '\) and \(Q = \pi _{ X}(Q ')\), then \(\textsf{att}(Q)= X\).
-
4.
Let \(Q _1,Q _2\) be relational algebra expressions over \(\mathcal {R}\) such that \(X\triangleleft Q _1\) and \(Y\triangleleft Q _2\) have compatible data types. If \(Q = Q _1\,\texttt {OP}_{X=Y}\,Q _2\) s.t.
 , then \(\textsf{att}(Q)=\textsf{att}(Q _1)\cup \textsf{att}(Q _2)\).
, then \(\textsf{att}(Q)=\textsf{att}(Q _1)\cup \textsf{att}(Q _2)\).
The evaluation of \(Q\) over \(\mathcal {D}\), a set of tuples denoted by \(Q ^{\mathcal {D}}\), is recursively defined as follows,
-
1.
If \(Q = R\) such that \(R\in \mathcal {R}\), then \(Q ^{\mathcal {D}}=R^{\mathcal {D}}\).
-
2.
If \(Q '\) is a relational algebra expression over \(\mathcal {R}\), \(X\triangleleft Q '\) and \(Q =\sigma _{\lnot \texttt {isNull}(X)}(Q ')\), then \(Q ^{\mathcal {D}}=\{t\in {Q '}^{\mathcal {D}}\ \mid \ t( x)\ne \texttt {null} \text { for every }x\in X\}\).
-
3.
If \(Q '\) is a relational algebra expression over \(\mathcal {R}\), \(X\triangleleft Q '\) and \(Q = \pi _{ X}(Q ')\) then, for every \(t\in Q ^{\mathcal {D}}\) there exists \(t'\in {Q '}^{\mathcal {D}} \) such that \(t( X)=t'( X)\).
-
4.
Let \(Q _1,Q _2\) be relational algebra expressions over \(\mathcal {R}\) such that \(X\triangleleft Q _1\) and \(Y\triangleleft Q _2\) have compatible data types.
-
a.
If \(Q = Q _1\bowtie _{X=Y}Q _2\) then for every \(t\in Q ^{\mathcal {D}}\): (i) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) and \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t(x)=t_1( x)=t_2( y)\ne \texttt {null} \) for every \(x\in X\) and \(y\in Y\), (ii) \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\), and (iii) \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\).
-
b.
If
 then for every \(t\in Q ^{\mathcal {D}}\): either (i) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) and \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t(x)=t_1( x)=t_2( y)\ne \texttt {null} \) for every \(x\in X\) and \(y\in Y\), \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\) and \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\), or (ii) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) s.t. \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\) and \(t(v)=\texttt {null} \) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\).
then for every \(t\in Q ^{\mathcal {D}}\): either (i) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) and \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t(x)=t_1( x)=t_2( y)\ne \texttt {null} \) for every \(x\in X\) and \(y\in Y\), \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\) and \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\), or (ii) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) s.t. \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\) and \(t(v)=\texttt {null} \) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\). -
c.
If
 then for every \(t\in Q ^{\mathcal {D}}\): either (i) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) and \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t( x)=t_1( x)=t_2(y)\ne \texttt {null} \) for every \(x\in X\) and \(y\in Y\), \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\) and \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\), or (ii) there exist \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\) and \(t(u)=\texttt {null} \) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\).
then for every \(t\in Q ^{\mathcal {D}}\): either (i) there exist \(t_1\in {Q _1}^{\mathcal {D}}\) and \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t( x)=t_1( x)=t_2(y)\ne \texttt {null} \) for every \(x\in X\) and \(y\in Y\), \(t(u)=t_1(u)\) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\) and \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\), or (ii) there exist \(t_2\in {Q _2}^{\mathcal {D}}\) s.t. \(t(v)=t_2(v)\) for every \(v\in (\textsf{att}(Q _2)\setminus \textsf{att}(Q _1))\) and \(t(u)=\texttt {null} \) for every \(u\in (\textsf{att}(Q _1)\setminus \textsf{att}(Q _2))\). -
d.
If
 then \(Q ^{\mathcal {D}}={Q _a}^{\mathcal {D}}\cup {Q _b}^{\mathcal {D}}\) s.t.
then \(Q ^{\mathcal {D}}={Q _a}^{\mathcal {D}}\cup {Q _b}^{\mathcal {D}}\) s.t.
 and
and
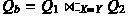 .
.
-
a.
Henceforth, we denote by \(\texttt {SP}\) the relational expression containing only select-project relational operations, and \(\texttt {SPJ}\) the relational expression containing select-project-(outer)join relational operations, respectively.
Definition 1
Let \(Q \) be a relational expression over a relational schema \(\mathcal {R}\). Then, we say that the \(Q \) is a \(\texttt {valid~query}\) if and only if there exist foreign key references between every two sets of attributes participating in an equality join condition in the \(Q\).
RDF Graphs. Assume that \(\mathcal {I}, \mathcal {B}\) and \(\mathcal {L}\) are countably infinite disjoint sets of Internationalized Resource Identifiers (IRIs), Blank nodes and Literals, respectively. The set of RDF terms \(\mathcal {T}\) is \(\mathcal {I}\cup \mathcal {L}\cup \mathcal {B}\). A well-defined RDF triple is defined as a triple \(\langle s,p,o\rangle \) where \(s\in \mathcal {I}\cup \mathcal {B}\) is called the subject, \(p\in \mathcal {I}\) is called the predicate and \(o\in \mathcal {T}\) is called the object. An RDF graph \(G\subseteq (\mathcal {I}\cup \mathcal {B})\times \mathcal {I}\times \mathcal {T}\) is a finite subset of RDF triples.
Definition 2
The set of nodes of an RDF graph G is the set of subjects and objects of triples in the graph, i.e., \(\{s,o\mid \langle s,p,o\rangle \in G\}\).
Assume a countably infinite set \(\mathcal {V}\) of variables disjoint from \(\mathcal {T}\). A triple pattern is defined as a triple in \((\mathcal {I}\cup \mathcal {B}\cup \mathcal {V})\times (\mathcal {I}\cup \mathcal {V})\times (\mathcal {T}\cup \mathcal {V})\). A basic graph pattern (BGP) is a finite set of triple patterns. The schema \(\textit{sch}(\psi )\) of a triple pattern \(\psi \) is the RDF property and class predicates [17] from the \(\psi \).
Mappings. Formally, we adopt R2R mapping [6, 22] that generate RDF triples from the active domain of a database \(\varGamma _{\mathcal {D}}\). Assume countably infinite and disjoint sets \(\mathbb {F}\) and \(\mathbb {T}\) of iri-template and typing functions respectively, with each function \(\alpha \in \mathbb {F}\cup \mathbb {T}\) has an associated arity \(n>0\). W.l.o.g., we assume that functions \(\mathbb {F}\cup \mathbb {T}\) are injective, and map only \(\texttt {null} \) to \(\texttt {null} \).
Definition 3
We specify R2R-mapping \(\mathcal {M}\), from relational database-to-RDF, partitioned into three disjoint sets: \(\mathcal {M}_{\mathcal {C}}\), \(\mathcal {M}_{\mathcal {P}}\) and \(\mathcal {M}_{\mathcal {U}}\) such that
-
i.
\(\mathcal {M}_{\mathcal {C}}\) is a set of data-to-RDF concept mappings, each one of the form
$$\begin{aligned} Q _X\longrightarrow \langle \textbf{f}(X),\texttt {rdf:type},C\rangle , \end{aligned}$$where
-
a.
\(Q _X\) is a source query \(Q\) over \(\mathcal {R}\) with \(X\triangleleft Q \),
-
b.
\(\textbf{f}\in \mathbb {F}\) and C is an RDF concept.
-
a.
-
ii.
\(\mathcal {M}_{\mathcal {P}}\) is a set of data-to-RDF object property mappings, each one of the form
$$\begin{aligned} Q _{X,Y}\longrightarrow \langle \textbf{f}(X),P,\textbf{f}'(Y)\rangle , \end{aligned}$$where
-
a.
\(Q _{X,Y}\) is a source query \(Q\) over \(\mathcal {R}\) with \(X,Y\triangleleft Q \),
-
b.
\(\textbf{f},\textbf{f}'\in \mathbb {F}\) and P is an RDF object property.
-
a.
-
iii.
\(\mathcal {M}_{\mathcal {U}}\) is a set of data-to-RDF datatype property mappings, each one of the form
$$\begin{aligned} Q _{X,Y}\longrightarrow \langle \textbf{f}(X),U,\textbf{t}(Y)\rangle , \end{aligned}$$where
-
a.
\(Q _{X,Y}\) is a source query \(Q\) over \(\mathcal {R}\) with \(X,Y\triangleleft Q \),
-
b.
\(\textbf{f}\in \mathbb {F}\), \(\textbf{t}\in \mathbb {T}\) and U is an RDF datatype property.
-
a.
Let m be a mapping \(Q \longrightarrow \psi \) of a triple pattern \(\psi \), as in Definition 3. The source query \(Q \) is the \(\textit{body}(m)\) of m, whereas the triple pattern \(\psi \) is the \(\textit{head}(m)\). The schema \(\textit{sch}(\mathcal {M})\) of a mapping set \(\mathcal {M}\) is the union of \(\textit{sch}(\textit{head}(m))\) of each \(m\in \mathcal {M}\). For any two mapping sets \(\mathcal {M}\) and \(\mathcal {M'}\) defined over a relational schema \(\mathcal {R}\) with source constraint \(\varSigma \), we write \(\mathcal {M'}\subseteq \mathcal {M}\), if for every mapping definition m, if \(m\in \mathcal {M}'\) then \(m\in \mathcal {M}\).
Definition 4
Let \(Q _C\), \(Q _P\) and \(Q _{U}\) be the source queries of mappings of an RDF concept C, object property P and datatype property U, respectively. Then, we say that a mapping set \(\mathcal {M}\) (according to Definition 3) is a simple mapping if: (a) \(\mathcal {M}\) contains exactly one mapping definition per concept C, object property P and datatype property U predicates in \(\textit{sch}(\mathcal {M})\); (b) each \(Q _P\) is a valid \(\texttt {SPJ} \) query with one join operation, (c) each \(Q _U\) is an \(\texttt {SP} \) query, d) if C and \(C'\) are the concepts whose instances are subject and object of an object property P, then the \(Q _C\) and \(Q _{C'}\) are either equal to \(Q _P\) or \(\texttt {SP} \) queries with a projected set of attributes whose (tuple) values are mapped to instances of C and \(C'\), and (e) if C is the concept whose instances are the subject of a datatype property U, then \(Q _C\) is either equal to \(Q _U\) or an \(\texttt {SP} \) query with a projected set of attributes whose (tuple) values are mapped into the instances of C.
Example 2
Consider the mapping of object property ‘\(\texttt {EnrolledFor}\)’ in Example 1. Instances of concepts ‘\(\texttt {Student}\)’ and ‘\(\texttt {Course}\)’ are mapped to subject and object of the property ‘\(\texttt {EnrolledFor}\)’, respectively. Then, according to simple mapping in Definition 4, the source queries used in the mappings of those ‘\(\texttt {Student}\)’ and ‘\(\texttt {Course}\)’ concepts must be either the exact same source query used in the mapping of the property ‘\(\texttt {EnrolledFor}\)’ or the \(\texttt {SP}\) source queries as in Example 1. Thus, a distinct simple mapping could be defined for the same purpose that maps RDF concepts ‘\(\texttt {Student}\)’ and ‘\(\texttt {Course}\)’ using the same \(\texttt {SPJ}\) source query \(Q _P\),
as used in the mapping of object property ‘\(\texttt {EnrolledFor}\)’ as follows:
Let \( t \in Q ^{\mathcal {D}}\) be a tuple of constants, and let \(\textbf{f}\)(X) be a term such that \(\textbf{f}\in \mathbb {F}\) and \(X\triangleleft Q \). Then, \(\textbf{f}(t(X))\) is a ground term of \(\textbf{f}\)(X) obtained by substituting occurrence of every \(x\in X\) with t(x).
Definition 5
Let \(\mathcal {M}_{\mathcal {C}}\cup \mathcal {M}_{\mathcal {P}}\cup \mathcal {M}_{\mathcal {U}}\) be an R2R mapping set \(\mathcal {M}\) defined over a relational schema \(\mathcal {R}\), and \(\mathcal {D}\) an instance of \(\mathcal {R}\). Then, we call the set of well-defined RDF triple assertions \(\mathcal {M}(\mathcal {D})\), i.e.,
the RDF graph projected by the mapping set \(\mathcal {M}\) and the instance \(\mathcal {D}\).
We recall that R2R mappings in Definition 3 generate RDF triples from the active domain of a database \(\varGamma _{\mathcal {D}}\), i.e., \(\texttt {null} \) cannot appear in the output RDF triples. Therefore, in this paper, we explicitly consider that (a) mappings \(\mathcal {M}\) is simple, and (b) w.l.o.g., source query \(Q\) of each mapping in \(\mathcal {M}\) contains \(\sigma _{\lnot \texttt {isNull}(X)}\) and \(\sigma _{\lnot \texttt {isNull}(Y)}\) filters over every projected set of \(X,Y\triangleleft \textsf{att}(Q)\).
SHACL. Our formal treatment of the core constraints of SHACL [15] is based on the approach of Corman et al. [12]. Each SHACL constraint is a set of conditions, usually referred to as shape, defined as a triple \(\langle {s}, \tau _{s}, \phi _{s} \rangle \) consisting of a shape IRI \( s \), a target definition \(\tau _s\), and a constraint definition \(\phi _s\). The \(\tau _s\) and \(\phi _s\) are expressions that determine for every RDF graph G and node n of G, whether n is a target of the shape, \(G\models \tau _s(n)\), respectively, whether n satisfies the constraint, \(G\models \phi _s(n)\). All shapes generated by our transformation have an ‘implicit target class,’ which means that s is also the IRI of a class and \(G\models \tau (n)\) iff n is a SHACL instance of class s.Footnote 2 For the purpose of our work, the constraint \(\phi _{s}\) is an expression defined according to the following grammar:
where \(\top \) stands for truth, \(\ell \) is an XML schema datatype, C and P are an RDF concept and property names respectively, the superscript ± stands for a property or its inverse, \(n\in \mathbb {N}\), \(\lnot \) for negation, \((\ge _n P^{\pm }.\alpha )\) means ‘must have at least n \(P^{\pm }\)-successor verifying \(\alpha \)’ for any \(n\in \mathbb {N}\) and \((\vartriangleright _{C} P^{\pm })\) means ‘all values of \(P^{\pm }\)-successor must be uniqueFootnote 3 among instances of concept C’. As syntactic sugar, we use \((=_n P^{\pm }. \alpha )\) for \((\ge _n P^{\pm }.\alpha )\wedge (\le _n P^{\pm }.\alpha )\), \((\vartriangleright _{C} P^{\pm }. \alpha )\) for \((\le _1 P^{\pm }.\alpha )\wedge (\vartriangleright _{C} P^{\pm })\) and \((\trianglerighteq _{C} P^{\pm }. \alpha )\) for \((=_1 P^{\pm }.\alpha )\wedge (\vartriangleright _{C} P^{\pm })\).
A SHACL document is a set of SHACL shapes. An RDF graph G validates against a shape \(\langle {s}, \tau _{s}, \phi _{s} \rangle \) if for every nodes n of G, if \(G\models \tau _s(n)\) then \(G\models \phi _s(n)\). An RDF graph \( G \) validates against a SHACL document \( S \), written \(G\models S\), iff \( G \) validates against all shapes in \( S \). The schema \(\textit{sch}(s)\) of a SHACL shape \( s \) is the set of RDF concept and property predicates [17] used in the target \(\tau _s\) and constraint \(\phi _s\) definition. The schema \(\textit{sch}(S)\) of a SHACL document \( S \) is the union of \(\textit{sch}(s)\) of every shape \(s\in S\).
3 Constraint Rewriting: Definition and Properties
Our goal is to generate a set of SHACL constraints that is as strong as possible while being guaranteed to hold for all RDF graphs resulting from valid database instances. Let \(\mathcal {M}\) be a mapping set defined over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \).
Definition 6
A SHACL document \( S \) is an \(\varSigma \)-implied set of shapes with respect to \(\mathcal {M}\), written as \(\varSigma \models _{\mathcal {M}} S\), if for every instance \(\mathcal {D}\) of \(\mathcal {R}\):
Definition 7
Let \(\varSigma \models _{\mathcal {M}} S\). Then, we say that \( S \) is a maximally \(\varSigma \)-implied set of shapes with respect to \(\mathcal {M}\), written as \(\varSigma \models ^{*}_{\mathcal {M}} S\), if for every \(\varSigma \models _{\mathcal {M}} S'\) s.t. \(\textit{sch}(S')\subseteq \textit{sch}(\mathcal {M})\) and every RDF graph \(\mathcal {G} :\)
We now formalise a constraint rewriting and some desirable properties. Let \(\mathbb {S}\) be the set of all SHACL shapes and \(\mathbb {Q}\) be the set of all pairs \((\mathcal {M},\varSigma )\) such that \(\mathcal {M}\) is a mapping set defined over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \).
Definition 8
(Constraint rewriting). A constraint rewriting is a function \( \mathcal {T}\!:\mathbb {Q}\rightarrow \mathcal {P}(\mathbb {S})\).
We next introduce central properties of a constraint rewriting \(\mathcal {T}\).
Definition 9
(Semantics preservation). A constraint rewriting \(\mathcal {T}\) is semantics preserving if for every mapping set \(\mathcal {M}\) and every source constraints \(\varSigma \):
Definition 10
(Maximal semantics preservation). A constraint rewriting \(\mathcal {T}\) is maximal semantics preserving if for every mapping set \(\mathcal {M}\) and every source constraints \(\varSigma \):
Definition 11
(Monotonicity). A constraint rewriting \(\mathcal {T}\) is monotone if for any mapping sets \(\mathcal {M'}\subseteq \mathcal {M}\) defined over a relational schema \(\mathcal {R}\) with source constraint \(\varSigma \) and every RDF graph \(\mathcal {G}\):
4 View Constraint: Definitions
As introduced in Sect. 2, R2R mapping relies on database views based on a source query to compute RDF terms from the database values. As a first step of our constraint transformation, we have to analyse the propagation of database constraints to these views.
Let \(\mathcal {R}\) be a relational schema with source constraints \(\varSigma \), and \(R\in \mathcal {R}\). The constraint \(\varSigma \) restricted to the set of \(\textsf{att}(R)\), denoted by \({\varSigma |_{R}}\), is the set of constraints such that for every constraint \(\sigma \in \varSigma \) on any \(X\triangleleft R\), there is \(\sigma \in {\varSigma |_{R}}\). For example, if \(\texttt {FK}(X,R, Y,S)\in \varSigma \) (resp., \(\texttt {FK}(Y,S, X,R)\in \varSigma \)) on any \(X\triangleleft R\), then there is \(\texttt {FK}(X,R,Y,S)\in {\varSigma |_{R}}\) (resp., \(\texttt {FK}(Y,S,X,R)\in {\varSigma |_{R}}\)).
Definition 12
Let \(Q\) be a relational expression over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \). Then, the set \(\varSigma \) propagated to the set of \(\textsf{att}(Q)\), denoted by \({\varSigma |_{Q}}\), is recursively defined as follows,
-
a.
If \(Q = R\) such that \(R\in \mathcal {R}\), then \({\varSigma |_{Q}}={\varSigma |_{R}}\).
-
b.
\(Q =\sigma _{\lnot \texttt {isNull}(X)}(Q ')\) where \(X\triangleleft Q '\), then \({\varSigma |_{Q}}={\varSigma |_{Q '}}\).
-
c.
If \(Q = \pi _{ X}(Q ')\) where \(X\triangleleft Q '\) then \({\varSigma |_{Q}}=\{\texttt {PK}(Y,R),\texttt {UNQ}(Y,R), \texttt {NN}(Y,R), \texttt {FK}(Y,R,Z,S), \texttt {FK}(Z,S,Y,R)\in {\varSigma |_{Q '}}\mid Y\subseteq X\text { and } R,S\in \mathcal {R}\}\).
-
d.
If \(Q =Q _1\,\texttt {OP}_{X=Y}\,Q _2\) where \(X\triangleleft Q _1\) and \(Y\triangleleft Q _2\) have compatible data types, and
 , then \({\varSigma |_{Q}}={\varSigma |_{Q _1}}\cup {\varSigma |_{Q _2}}\).
, then \({\varSigma |_{Q}}={\varSigma |_{Q _1}}\cup {\varSigma |_{Q _2}}\).
SQL constraints are not well suited to direct translation to SHACL, so we introduce an intermediate representation similar to functional dependencies. Let R be a relation name with \(X,Y\triangleleft R\). Then, we write a functional dependency as an expression of the form \(\texttt {FD}_{ X\rightarrow Y}\), i.e., meaning \(X\triangleleft R\) functionally determines \(Y\triangleleft R\). Relational data dependencies, such as functional, multi-value and others, are originally defined on databases without \(\texttt {null} \) [3, 5]. However, we need notions of data dependencies that also apply to databases with \(\texttt {null} \), such as in [4], which we define as follows:
Definition 13
Let \(Q \) be a source query over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \), \(R\in \mathcal {R}\) a relation name and \(\mathcal {D}\) an arbitrary instance of \(\mathcal {R}\). Let V be the pair \(({Q}^{\mathcal {D}},{\varSigma |_{Q}})\) of projected view \({Q}^{\mathcal {D}}\) and propagated constraints \({\varSigma |_{Q}}\). Then, for any \(X,Y\triangleleft Q \),
-
a.
\(V\models \texttt {FP}_{X\rightarrow Y}\) if for every \(t,t'\in {Q}^{\mathcal {D}}\), if \(t(X)=t'(X)\) then \(t( Y)=t'( Y)\).
-
b.
\(V\models \texttt {UF}_{X\rightarrow Y}\) if \({Q}^{\mathcal {D}}\models \texttt {FP}_{X\rightarrow Y}\) and \({Q}^{\mathcal {D}}\models \texttt {FP}_{Y\rightarrow X}\).
-
c.
\(V\models \texttt {FD}_{X\rightarrow Y}\) if \({Q}^{\mathcal {D}}\models \texttt {FP}_{X\rightarrow Y}\) and \(\texttt {NN}(X,R),\texttt {NN}(Y,R)\in {\varSigma |_{Q}}\).
-
d.
\(V\models \texttt {UFD}_{X\rightarrow Y}\) if \({Q}^{\mathcal {D}}\models \texttt {FD}_{X\rightarrow Y}\) and \({Q}^{\mathcal {D}}\models \texttt {FD}_{Y\rightarrow X}\).
Henceforth, we will keep the SQL notations intuitively simple in examples, i.e., we write \(\texttt {NN}(X)\in {\varSigma |_{X\triangleleft R}}\) instead of \( \texttt {NN}(X,R)\in {\varSigma |_{X\triangleleft R}}\) for the propagated \(\texttt {NN}(X,R)\in \varSigma \) to \({\varSigma |_{X\triangleleft R}}\).
Example 3
Following Example 1, assume a mapping set \(\mathcal {M}\) with \(\textbf{f}_{S}\) and \(\textbf{f}_{C}\) iri-templates and a typing function \(\textbf{t}_{\nu }\)Footnote 4 as follows:
-
a.
\(\pi _{\texttt {S\_id,Name}}\sigma _{\lnot \texttt {isNull}(\texttt {S\_id})\wedge \lnot \texttt {isNull}(\texttt {Name})}(\texttt {student})\longrightarrow \langle \textbf{f}_{\texttt {S}}({\texttt {S\_id}}),\texttt {hasName},\textbf{t}_{\nu }(\texttt {Name})\rangle \).
-
b.
\(\pi _{\texttt {C\_id,Title}}\sigma _{\lnot \texttt {isNull}(\texttt {C\_id})\wedge \lnot \texttt {isNull}(\texttt {Title})}(\texttt {course})\longrightarrow \langle \textbf{f}_{\texttt {C}}({\texttt {C\_id}}),\texttt {hasTitle},\textbf{t}_{\nu }(\texttt {Title})\rangle \).
Let \(Q _1=\pi _{\texttt {S\_id,Name}}\sigma _{\lnot \texttt {isNull}(\texttt {S\_id})\wedge \lnot \texttt {isNull}(\texttt {Name})}(\texttt {student})\), and \(V_1=({Q _1}^{\mathcal {D}},{\varSigma |_{Q _1}})\). Then,
-
\(\textsf{att}(Q _1)=\{\texttt {S\_id,Name}\}\) and \({\varSigma |_{\textsf{att}(Q _1)}}=\{\texttt {PK}(\texttt {S\_id}), \texttt {UNQ}(\texttt {S\_id}), \texttt {NN}(\texttt {S\_id}), \texttt {Type}(\texttt {S\_id},\nu ), \texttt {Type}(\texttt {Name},\nu )\}\), i.e., from assumption in Sect. 2, if \(\texttt {PK}(\texttt {S\_id})\) then \(\texttt {UNQ}(\texttt {S\_id})\) and \( \texttt {NN}(\texttt {S\_id})\).
-
\(V_1\models \texttt {FP}_{\texttt {S\_id}\rightarrow Name}\) since for every \(t,t'\in {Q _1}^{\mathcal {D}}\), if \(t(\texttt {S\_id})=t'(\texttt {S\_id})\) then \(t(\texttt {Name})=t'(\texttt {Name})\).
Filter \(\sigma _{\lnot \texttt {isNull}(\texttt {Name})}\) excludes tuples from \({Q _1}^{\mathcal {D}}\) that contains null for the \(\texttt {Name}\in \textsf{att}(Q _1)\).
Similarly, let \(Q _2=\pi _{\texttt {C\_id, Title}}\sigma _{\lnot \texttt {isNull}(\texttt {C\_id})\wedge \lnot \texttt {isNull}(\texttt {Title})}(\texttt {course})\), and \(V_2=({Q _2}^{\mathcal {D}},{\varSigma |_{Q _2}})\). Then,
-
\(\textsf{att}(Q _2)=\{\texttt {C\_id, Title}\}\) and \({\varSigma |_{\textsf{att}(Q _2)}}=\{\texttt {PK}(\texttt {C\_id)},\texttt {UNQ}(\texttt {C\_id)}, \texttt {NN}(\texttt {C\_id}), \texttt {Type}(\texttt {C\_id},\nu ), \texttt {UNQ}(\texttt {Title}), \texttt {Type}(\texttt {Title},\nu ),\texttt {FK}(\texttt {Code},\texttt {student},\texttt {C\_id},\texttt {course})\}\)
-
\(V_2\models \texttt {FP}_{\texttt {C\_id}\rightarrow \texttt {Title}}\) since for any \(t,t'\in {Q _2}^{\mathcal {D}}\), if \(t(\texttt {C\_id})=t'(\texttt {C\_id})\) then \(t(\texttt {Title})=t'(\texttt {Title})\).
-
\(V_2\models \texttt {FP}_{\texttt {Title}\rightarrow \texttt {C\_id}}\) since for any \(t,t'\in {Q _2}^{\mathcal {D}}\), if \(t(\texttt {Title})=t'(\texttt {Title})\) then \(t(\texttt {C\_id})=t'(\texttt {C\_id})\).
-
\(V_2\models \texttt {UF}_{\texttt {C\_id}\rightarrow \texttt {Title}}\) since \({Q _2}^{\mathcal {D}}\models \texttt {FP}_{\texttt {C\_id}\rightarrow \texttt {Title}}\) and \({Q _2}^{\mathcal {D}}\models \texttt {FP}_{\texttt {Title}\rightarrow \texttt {C\_id}}\).
5 Source to View Constraint Implication
The next step is to determine which of the data dependencies from Definition 13 hold for the view defined by the source queries, i.e., they are implied by the propagated SQL constraints.
Let \(Q\) be a source query over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \). Then, we say that \(\varSigma \) implies a data dependency \(\sigma _{ X\rightarrow Y}\) s.t. \(\sigma \in \{\texttt {UFD,FD,UFP,FP}\}\) on \(X,Y\triangleleft Q \), denoted by \(\varSigma _Q \Vdash \sigma _{ X\rightarrow Y}\), if \(V\models \sigma _{ X\rightarrow Y}\) for every legal instance \(\mathcal {D}\) of \(\mathcal {R}\), where \(V=({Q}^{\mathcal {D}},{\varSigma |_{Q}})\) is the pair of projected view \({Q}^{\mathcal {D}}\) and propagated constraints \({\varSigma |_{Q}}\). We now concentrate on \(\texttt {SP} \) source queries.
Lemma 1
Let \(Q \) be a source query \(\pi _{X,Y}\sigma _{\lnot \texttt {isNull}(X)\wedge \lnot \texttt {isNull}(Y)}(R)\) over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \), \(R\in \mathcal {R}\) a relation name and \({\varSigma |_{Q}}\) the set \(\varSigma \) propagated to set of \(\textsf{att}(Q)\). Then, for any \(X,Y\triangleleft Q \),
-
a.
\(\varSigma _Q \Vdash \texttt {FP}_{X\rightarrow Y}\) if \(\texttt {UNQ}(X,R)\in {\varSigma |_{Q}}\).
-
b.
\(\varSigma _Q \Vdash \texttt {UF}_{X\rightarrow Y}\) if \(\texttt {UNQ}(X,R),\texttt {UNQ}(Y,R)\in {\varSigma |_{Q}}\).
-
c.
\(\varSigma _Q \Vdash \texttt {FD}_{X\rightarrow Y}\) if \(\texttt {UNQ}(X,R)\in {\varSigma |_{Q}}\) and \(\texttt {NN}(X,R),\texttt {NN}(Y,R)\in {\varSigma |_{Q}}\).
-
d.
\(\varSigma _Q \Vdash \texttt {UFD}_{X\rightarrow Y}\) if \(\texttt {UNQ}(X,R),\texttt {UNQ}(Y,R)\in {\varSigma |_{Q}}\) and \(\texttt {NN}(X,R),\texttt {NN}(Y,R)\in {\varSigma |_{Q}}\).
Corollary 1
Let \(Q \) be a source query \(\pi _{X,Y}\sigma _{\lnot \texttt {isNull}(X)\wedge \lnot \texttt {isNull}(Y)}(R)\) over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \), \(R\in \mathcal {R}\) a relation name and \({\varSigma |_{Q}}\) the set \(\varSigma \) propagated to set of \(\textsf{att}(Q)\). Then, for any \(X,Y\triangleleft Q \),
-
a.
\(\varSigma _Q \Vdash \texttt {UFD}_{X\rightarrow Y}\rightarrow \varSigma _Q \Vdash \texttt {FD}_{X\rightarrow Y}\) and \(\varSigma _Q \Vdash \texttt {FD}_{X\rightarrow Y}\rightarrow \varSigma _Q \Vdash \texttt {FP}_{X\rightarrow Y}\)
-
b.
\(\varSigma _Q \Vdash \texttt {UFD}_{X\rightarrow Y}\rightarrow \varSigma _Q \Vdash \texttt {UF}_{X\rightarrow Y}\) and \(\varSigma _Q \Vdash \texttt {UF}_{X\rightarrow Y}\rightarrow \varSigma _Q \Vdash \texttt {FP}_{X\rightarrow Y}\)
We next concentrate on \(\texttt {SPJ} \) source queries. An \(\texttt {SPJ} \) source query \(Q \) over a relational schema \(\mathcal {R}\) with source constraints \(\varSigma \) is a relational algebra expression of the form,
where \(R_1,R_2\in \mathcal {R}\) are relation names with \(X,U\triangleleft R_1\) and \(Y,V\triangleleft R_2\), \(|U|=|V|\) and
 . Since mapping in Definition 3 generates RDF triples from the active domain \(\varGamma _{\mathcal {D}}\subseteq \varDelta \setminus \{\texttt {null} \}\) of the database, w.l.o.g., we equivalently express the stated \(\texttt {SPJ}\) source query \(Q\), that yields the same set of RDF triples as the original \(Q\), as follows,
. Since mapping in Definition 3 generates RDF triples from the active domain \(\varGamma _{\mathcal {D}}\subseteq \varDelta \setminus \{\texttt {null} \}\) of the database, w.l.o.g., we equivalently express the stated \(\texttt {SPJ}\) source query \(Q\), that yields the same set of RDF triples as the original \(Q\), as follows,
Note that the \(\texttt {SPJ} \) query \(Q \) is valid if and only if \(\texttt {FK}( U,R_1,V,R_2)\in {\varSigma |_{Q}}\) or \(\texttt {FK}( V,R_2,U,R_1)\in {\varSigma |_{Q}}\), see Definition 1. Henceforth, we use symbol \(\rightarrow ^{*}\) to express dependency in the opposite direction of foreign key reference, i.e., we write \(\textsc {FD}_{X\rightarrow ^{*} Y} \) to state functional dependency from \(X\triangleleft Q\) to \(Y\triangleleft Q\) if \(\texttt {FK}( Y,R_2,X,R_1)\in {\varSigma |_{Q}}\) or \(\texttt {FK}( V,R_2,U,R_1)\in {\varSigma |_{Q}}\) s.t. \(X,U\triangleleft R_1\) and \(Y,V\triangleleft R_2\).
Lemma 2
Let \(\mathcal {R}\) be a relational schema with source constraints \(\varSigma \), and let \(Q \) be an \(\texttt {SPJ} \) source query over \(\mathcal {R}\),
s.t. \(Q _1\) and \(Q _2\) are \(\texttt {SP}\) expressions over \(R_1\in \mathcal {\mathcal {R}}\) and \(R_2\in \mathcal {R}\) with \(X,U\triangleleft Q _1\) and \(Y,V\triangleleft Q _2\) respectively,
 and \(\texttt {FK}(U,R_1,V,R_2)\in {\varSigma |_{Q}}\). Then, for any \(X,Y\triangleleft Q:\)
and \(\texttt {FK}(U,R_1,V,R_2)\in {\varSigma |_{Q}}\). Then, for any \(X,Y\triangleleft Q:\)
-
a.
\(\varSigma _Q \Vdash \sigma _{ X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \sigma _{ X\rightarrow U}\) and \(\varSigma _{Q _2}\Vdash \sigma _{V\rightarrow Y}\) s.t. \(\sigma \in \{\texttt {UFD,FD,UF}\}\).
-
b.
\(\varSigma _{Q}\Vdash \sigma _{X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \texttt {UFD}_{ X\rightarrow U}\) and \(\varSigma _{Q _2}\Vdash \sigma _{V\rightarrow Y}\) s.t. \(\sigma \in \{\texttt {FD,UF}\}\).
-
c.
\(\varSigma _{Q}\Vdash \sigma _{X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \sigma _{ X\rightarrow U}\) s.t. \(\sigma \in \{\texttt {FD,UF}\}\) and \(\varSigma _{Q _2}\Vdash \texttt {UFD}_{V\rightarrow Y}\).
-
d.
\(\varSigma _{Q}\Vdash \texttt {FP}_{X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \texttt {FD}_{X\rightarrow U}\) and \(\varSigma _{Q _2}\Vdash \texttt {UF}_{V\rightarrow Y}\).
-
e.
\(\varSigma _{Q}\Vdash \texttt {FP}_{X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \texttt {UF}_{X\rightarrow U}\) and \(\varSigma _{Q _2}\Vdash \texttt {FD}_{V\rightarrow Y}\).
-
f.
\(\varSigma _{Q}\Vdash \texttt {FP}_{ X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \texttt {FP}_{ X\rightarrow U}\).
-
g.
\(\varSigma _{Q}\Vdash \texttt {FP}_{X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \sigma _{ X\rightarrow U}\) and \(\varSigma _{Q _2}\Vdash \texttt {FP}_{V\rightarrow Y}\) s.t. \(\sigma \in \{\texttt {UFD,FD,UF}\}\).
-
h.
\(\varSigma _{Q}\Vdash \sigma _{Y\rightarrow ^* X}\) if \(\varSigma _{Q _1}\Vdash \sigma _{{ U}\rightarrow { X}}\) and \(\varSigma _{Q _2}\Vdash {\sigma }_{{Y}\rightarrow { V}}\) s.t. \(\sigma \in \{\texttt {UFD,UF}\}\).
-
i.
\(\varSigma _{Q}\Vdash \texttt {FP}_{Y\rightarrow ^* X}\) if \(\varSigma _{Q _1}\Vdash \sigma _{ U\rightarrow X}\) s.t. \(\sigma \in \{\texttt {UFD,FD,FP}\}\) and \(\varSigma _{Q _2}\Vdash \texttt {UF}_{Y\rightarrow V}\).
-
j.
\(\varSigma _{Q}\Vdash \sigma _{Y\rightarrow * X}\) if \(\varSigma _{Q _1}\Vdash \sigma _{ U\rightarrow X}\) s.t. \(\sigma \in \{\texttt {FD,UF,FP}\}\) and \(\varSigma _{Q _2}\Vdash \texttt {UFD}_{Y\rightarrow V}\).
On the correctness of Lemma 2, e.g., assume the case (f). Then, \(\texttt {UNQ}(V,R_2)\in {\varSigma |_{Q _2}}\) since \(\texttt {FK}( U,R_1, V,R_2)\in {\varSigma |_{Q}}\). Thus, \(\varSigma _{Q _2}\Vdash {\sigma }_{{ V}\rightarrow {Y}}\) s.t. \(\sigma \in \{\texttt {UFD,FD,UF,FP}\}\) is the set of all possible constraints implication. Hence, the case (f) of Lemma 2 covers the following possible cases of constraints implication:
-
\(\varSigma _{Q}\Vdash \texttt {FP}_{ X\rightarrow Y}\) if \(\varSigma _{Q _1}\Vdash \texttt {FP}_{ X\rightarrow U}\) and \(\varSigma _{Q _2}\Vdash {\sigma }_{{ V}\rightarrow {Y}}\) s.t. \(\sigma \in \{\texttt {UFD,FD,UF,FP}\}\).
Further, by applying similar arguments and the implication rules stated in Corollary 1 to the rest of cases in Lemma 2, the correctness proof of the Lemma can be enumerated.
Example 4
Following Examples 1 and 4, assume an R2R mapping:
where \(Q \) is a source query \(\pi _{\texttt {S\_id,C\_id}}\sigma _{\lnot \texttt {isNull}(\texttt {S\_id})\wedge \lnot \texttt {isNull}(\texttt {C\_id})}(Q _1\bowtie _{\texttt {Code}=\texttt {C\_id}}Q _2)\) such that \(Q _1=\sigma _{\lnot \texttt {isNull}(\texttt {S\_id})\wedge \lnot \texttt {isNull}(\texttt {Code})}(\texttt {student})\) and \(Q _2=\sigma _{\lnot \texttt {isNull}(\texttt {C\_id})}(\texttt {course})\). Then,
-
a.
for \(\texttt {SP}\) expression \(Q _1 :\)
-
\(\textsf{att}(Q _1)=\{\texttt {S\_id,Code}\}\) and \(\{\texttt {UNQ}(\texttt {S\_id}), \texttt {NN}(\texttt {S\_id}), \texttt {NN}(\texttt {Code})\}\subseteq {\varSigma |_{Q _1}}\) from Definition 12.
-
\(\varSigma _{Q _1}\Vdash \texttt {FD}_{ \texttt {S\_id}\rightarrow \texttt {Code}}\) from the case (c) of Lemma 1
-
-
b.
for \(\texttt {SP}\) expression \(Q _2\, :\)
-
c.
finally, for \(\texttt {SPJ}\) expression \(Q\):
-
\(\textsf{att}(Q)=\{\texttt {S\_id},\texttt {C\_id}\}\)
-
\(\texttt {FK}(\texttt {Code},\texttt {student},\texttt {C\_id},\texttt {course})\in {\varSigma |_{Q _1}}\cap {\varSigma |_{Q _2}}\), i.e., \(Q\) is a valid \(\texttt {SPJ}\) query.
-
\(\varSigma _{Q}\Vdash \texttt {FD}_{\texttt {S\_id}\rightarrow \texttt {C\_id}}\) from case (c) of Lemma 2, since
-
i.
\(\varSigma _{Q _1}\Vdash \texttt {FD}_{\texttt {S\_id}\rightarrow \texttt {Code}}\), and
-
ii.
\(\varSigma _{Q _2}\Vdash \texttt {FD}_{\texttt {C\_id}\rightarrow \texttt {C\_id}}\) from \(\varSigma \Vdash \texttt {UFD}_{\texttt {C\_id}\rightarrow \texttt {C\_id}}\rightarrow \varSigma \Vdash \texttt {FD}_{\texttt {C\_id}\rightarrow \texttt {C\_id}}\) following the case (a) of Corollary 1
-
i.
-
6 The Constraint Rewriting
We now introduce a constraint rewriting \(\varGamma \) for a simple mapping \(\mathcal {M}\) (Definition 4), and prove the properties defined in Sect. 3. The constraint rewriting \(\varGamma \) in Definition 15 transforms the view constraints implied by the relational source \(\varSigma \) (as introduced in Sects. 4 and 5) into sets of SHACL shapes. Since the semantic equivalence of generated SHACL constraints to the source constraints \(\varSigma \) also depends on the combination of source queries used in mappings of RDF triples, we first introduce the classification functions \(\iota \) and \(\kappa \) to distinguish between the various cases that can occur.
Let \(\textbf{f}_C\) and \(\textbf{f}_{C'}\) be \(\texttt {iri}\) mapping templates for the respective RDF concepts \( C \) and \( C' \), and let \(\textbf{t}\) be an \(\texttt {iri}\) typing template. Let \(Q _C\), \(Q _P\) and \(Q _{U}\) be the source queries of mapping Definition 3 of an RDF concept C, object property P and datatype property U, respectively.
Definition 14
Let \(\mathcal {M}\) be a simple mapping with RDF predicates \(C,C',P,U\in \textit{sch}(\mathcal {M})\). Let \(\iota \) and \(\kappa \) be classification functions that take a triple pattern of the form \(\langle \textbf{f}_{C}( X),P,\textbf{f}_{C'}(Y)\rangle \) and \(\langle \textbf{f}_{C}( X),U,\textbf{t}(Y)\rangle \) respectively, and the mapping set \(\mathcal {M}\) as input, and classifies the groups of the respective source queries \((Q _C,Q _P,Q _{C'})\) and \((Q _{C},Q _{U})\) as follows,
Let \(Q\) be a source query over a relational schema \(\mathcal {R}\) with source constraint \(\varSigma \). Then, we write \(\varSigma _{Q}\Vdash \sigma _{X\twoheadrightarrow Y}\) s.t. \(\sigma \in \{\texttt {UFD,FD,UF,FP}\}\) to express the dependency that is either \(\varSigma _{Q}\Vdash \sigma _{X\rightarrow Y}\) or \(\varSigma _{Q}\Vdash \sigma _{X\rightarrow ^* Y}\) on \(X,Y\triangleleft Q \).
Definition 15
(Constraint rewriting \(\varGamma \)). Let \(\mathcal {M}\) be a simple mapping defined over a relational schema \(\mathcal {R}\) with source constraint \(\varSigma \), and let \(\iota \) and \(\kappa \) be the classification functions. Then, the constraint rewriting \(\varGamma (\mathcal {M},\varSigma )\) of \(\varSigma \) w.r.t. \(\mathcal {M}\) is a set of SHACL shapes that for each RDF concept C with mapping \( Q _X\longrightarrow \langle \textbf{f}_C( X),\texttt {rdf:type},C\rangle \), contains \(\langle C,\tau _C,\phi _C\rangle \) with an implicit targetClass \(\tau _C\) and conjunctive set of constraints \(\phi _C=\bigwedge _{1\le i\le 3}\varPhi _i\), where
-
1.
for mapping m of each object property \( P \) such as \( Q _{X,Y}\longrightarrow \langle {\textbf{f}_C}(X),P,{\textbf{f}_{C'}}( Y)\rangle \),
$$\varPhi _1=\left\{ \begin{array}{rl} (\le _0\, P.\,\lnot C') \wedge (\ge _0 P.\, C' )\wedge (\mathop {\bigwedge }\nolimits _{ \varSigma _Q \Vdash \sigma }\lambda _1(\sigma )) &{} \text { if }\iota (\textit{head}(m),\mathcal {M})=A \\ (\le _0\, P.\,\lnot C') \wedge (\ge _1 P.\, C' )\wedge (\mathop {\bigwedge }\nolimits _{ \varSigma _Q \Vdash \sigma }\lambda _2(\sigma )) &{} \text { if }\iota (\textit{head}(m),\mathcal {M})=B \end{array}\right. $$where
$$\lambda _1(\sigma )=\left\{ \begin{array}{rl} (\trianglerighteq _{C} P.\, C' ) &{} \text {if }\sigma =\texttt {UFD}_{X\rightarrow Y} \\ (=_1 P.\, C' ) &{} \text {if }\sigma =\texttt {FD}_{X\rightarrow Y} \\ (\vartriangleright _{C} P.\, C' ) &{}\text {if }\sigma =\texttt {UF}_{X\twoheadrightarrow Y} \\ (\le _1 P.\, C' ) &{}\text {if }\sigma =\texttt {FP}_{X\twoheadrightarrow Y} \end{array}\right. \text { and } \lambda _2(\sigma )=\left\{ \begin{array}{rl} (\trianglerighteq _{C} P.\, C' ) &{} \text {if }\sigma =\texttt {UF}_{X\twoheadrightarrow Y} \\ (=_1 P.\, C' ) &{} \text {if }\sigma =\texttt {FP}_{X\twoheadrightarrow Y} \end{array}\right. $$ -
2.
for mapping m of each object property \( P \) such as \( Q _{X,Y}\longrightarrow \langle {\textbf{f}_{C'}}(X),P,{\textbf{f}_C}( Y)\rangle \),
$$\varPhi _2=\left\{ \begin{array}{rl} (\le _0\, P^{-}.\,\lnot C') \wedge (\ge _0 P^{-}.\, C' )\wedge (\mathop {\bigwedge }\nolimits _{ \varSigma _Q \Vdash \sigma }\delta _1(\sigma )) &{} \text { if }\iota (\textit{head}(m),\mathcal {M})=A \\ (\le _0\, P^{-}.\,\lnot C') \wedge (\ge _1 P^{-}.\, C' )\wedge (\mathop {\bigwedge }\nolimits _{ \varSigma _Q \Vdash \sigma }\delta _2(\sigma )) &{} \text { if }\iota (\textit{head}(m),\mathcal {M})=B \end{array}\right. $$where
$$\delta _1(\sigma )=\left\{ \begin{array}{rl} (\trianglerighteq _{C} P^{-}.\, C' ) &{} \text {if }\sigma =\texttt {UFD}_{X\rightarrow Y} \\ (=_1 P^{-}.\, C' ) &{} \text {if }\sigma =\texttt {FD}_{X\rightarrow Y} \\ (\vartriangleright _{C} P^{-}.\, C' ) &{}\text {if }\sigma =\texttt {UF}_{X\twoheadrightarrow Y} \\ (\le _1 P^{-}.\, C' ) &{}\text {if }\sigma =\texttt {FP}_{X\twoheadrightarrow Y} \end{array}\right. \text { and } \delta _2(\sigma )=\left\{ \begin{array}{rl} (\trianglerighteq _{C} P^{-}.\, C' ) &{} \text {if }\sigma =\texttt {UF}_{X\twoheadrightarrow Y} \\ (=_1 P^{-}.\, C' ) &{} \text {if }\sigma =\texttt {FP}_{X\twoheadrightarrow Y} \end{array}\right. $$ -
3.
for mapping m of each datatype property \( U \) such as \( Q _{X,Y}\longrightarrow \langle {\textbf{f}_{C}}(X),U,\textbf{t}( Y)\rangle \),
$$\varPhi _3=\left\{ \begin{array}{rl} (\le _0\, U.\,\lnot \textbf{t}) \wedge (\ge _0 U.\, \textbf{t} )\wedge (\mathop {\bigwedge }\nolimits _{ \varSigma _Q \Vdash \sigma }\mu _1(\sigma )) &{} \text { if }\iota (\textit{head}(m),\mathcal {M})=A \\ (\le _0\, U.\,\lnot \textbf{t}) \wedge (\ge _1 U.\, \textbf{t} )\wedge (\mathop {\bigwedge }\nolimits _{ \varSigma _Q \Vdash \sigma }\mu _2(\sigma )) &{} \text { if }\iota (\textit{head}(m),\mathcal {M})=B \end{array}\right. $$where
$$\mu _1(\sigma )=\left\{ \begin{array}{rl} (\trianglerighteq _{C} U.\,\textbf{t} ) &{} \text {if }\sigma =\texttt {UFD}_{X\rightarrow Y} \\ (=_1 U.\,\textbf{t} ) &{} \text {if }\sigma =\texttt {FD}_{X\rightarrow Y} \\ (\vartriangleright _{C} U.\,\textbf{t} ) &{}\text {if }\sigma =\texttt {UF}_{X\twoheadrightarrow Y} \\ (\le _1 U.\,\textbf{t}) &{}\text {if }\sigma =\texttt {FP}_{X\twoheadrightarrow Y} \end{array}\right. \text { and } \mu _2(\sigma )=\left\{ \begin{array}{rl} (\trianglerighteq _{C} U.\,\textbf{t}) &{} \text {if }\sigma =\texttt {UF}_{X\twoheadrightarrow Y} \\ (=_1 U.\,\textbf{t}) &{} \text {if }\sigma =\texttt {FP}_{X\twoheadrightarrow Y} \end{array}\right. $$
Observe that in Definition 15, the first constraint components, such as \( (\le _0\, P^{\pm }.\,\lnot C')\) and \( (\le _0\, U.\,\lnot \textbf{t})\) in the definitions of \(\varPhi _i\), are implied by the restriction on the mapping set \(\mathcal {M}\), i.e., by the fact that \(\mathcal {M}\) contains exactly one mapping defining per object and datatype property predicates. The second constraint components, such as \( (\ge _0\, P^{\pm }.\,\lnot C')\) or \( (\ge _1\, P^{\pm }.\,\lnot C')\) and \( (\ge _0\, U.\,\lnot \textbf{t})\) or \( (\ge _1\, U.\,\lnot \textbf{t})\), in the \(\varPhi _i\) are implied by the combination of \(\iota \)- and \(\kappa \)-classifications. Finally, the third constraints components \(\bigwedge _{ \varSigma _Q \Vdash \sigma } f(\sigma )\) s.t. \(f\in \lambda _i\cup \delta _i\cup \mu _i\) for \(1\le i\le 2\) are implied by the source constraint \(\varSigma \) w.r.t. \(\mathcal {M}\).
The constraint definition \(\phi _C{:}{=}(\le _0\, P^{\pm }.\,\lnot C')\) requires all nodes \(n'\) in the graph that are reachable from a node n s.t. \(\langle n,\texttt {rdf:type},C\rangle \) via property path \(P^{\pm }\) to have a typing triple s.t. \(\langle n',\texttt {rdf:type},C'\rangle \), which is exactly what we needed for the mapped object property paths \(P^{\pm }\) in the RDF graph given the restriction that set \(\mathcal {M}\) contains exactly one mapping definitions per object property predicates. Thus, to extend the constraint rewriting \(\varGamma \) Definition in 15 beyond the simple mapping \(\mathcal {M}\), the rewriting \(\varGamma \) must: (i) not generate constraint components such as \((\le _0\, P^{\pm }.\,\lnot C')\) and \((\le _0\, U.\,\lnot \textbf{t})\) when there exist more than one mapping definition per object P and datatype U properties, respectively, in the set \(\mathcal {M}\), (ii) accommodate classification of all possible combinations of sources queries in the definitions of \(\iota \) and \(\kappa \), and (iii) revise the definitions of \(\lambda _i\), \(\delta _i\) and \(\mu _i\) for additional consequences of \(\varSigma \)-implications w.r.t. the extended \(\mathcal {M}\).
We now state the properties of the constraint \(\varGamma \) rewriting. Theorem 1 is a soundness statement that guarantees that all constraints produced by \(\varGamma \) will be validated by the RDF graph mapped from any valid database instance.
Theorem 1
The constraint rewriting \(\varGamma \) is semantics preserving.
Theorem 2 expresses the completeness of \(\varGamma \), i.e., every SHACL constraint expressible with the schema \(\textit{sch}(\mathcal {M})\) of the mappings, and that is implied by \(\varSigma \) is implied by the generated shapes \(\varGamma (\mathcal {M}, \varSigma )\). This does not hold in general for SHACL constraints on predicates not in \(\textit{sch}(\mathcal {M})\). Finally, Theorem 3 expresses that adding mappings will never invalidate generated constraints.
Theorem 2
The constraint rewriting \(\varGamma \) is maximal semantics preserving.
Theorem 3
The constraint rewriting \(\varGamma \) is monotone.
7 Discussion
We have presented a constraint rewriting \(\varGamma \) for simple R2R mapping that is useful in the context of relational to RDF data transformation [13, 19, 23] and data integration [22, 31]. Observe that simple R2R mappings can express a comprehensive catalog of useful mapping patterns studied in [8, 24, 25]. Simplifying simple R2R mapping further yields direct mapping [2] since that requires additional restrictions on Definition 4; therefore, the results for our constraint rewriting for simple mappings also seamlessly holds for direct mapping [2, 23, 27]. In future work, we believe that it would interesting to extend our constraint rewriting \(\varGamma \) in two different directions: (a) for arbitrary R2R mappings, e.g., admitting the full relational algebra or arbitrary \(\texttt {SPJ}\) expressions as the source query in mapping Definition 3, and (b) for a broader class of relational constraints such as (disjunctive) tuple and equality generating dependencies [1].
There are several approaches that map relational schemas and constraints to RDFS and OWL/Epistemic DL axioms since, with an appropriate closed world semantics, OWL can express integrity constraints. In particular, we first refer the reader to the implications of constraints in ontology-based data access platform under different names, such as protection and faithfulness in [10, 11], which is equivalent to relational constraints-to-OWL, i.e., to check whether the mapped RDF of every source dataset satisfying the source constraints can be extended to a model of the mapped \(\texttt {DL\text {-}Lite}_\texttt {A}\) axioms, and OWL-to-relational constraints, i.e., opposite of former, constraints implication in [21]. Even though these proposals for combining OWL/Epistemic DL axioms with integrity constraints have some promising results for target constraints specification in the OBDA setting, there has been no unanimity on the correct semantics.
The problem of direct mapping of source schemas and constraints into RDFS/OWL axioms has been studied in [7, 23]. Sequeda et al. [23] attempted to capture the database constraints on the RDF graph resulting from direct mapping using OWL. However, the bootstrapped OWL axioms did not trigger the unsatisfiability of the directly mapped graph whenever keys are violated in the source database unless the database instance is explicitly encoded in the constraint rewriting. Further, Sequeda et al. [23, Theorem 3] established that the desirable monotonicity property of direct mapping is an obstacle to obtain a semantics preserving OWL axioms even if the database instance is explicitly encoded in the constraint rewriting. To accomplish the desired one-to-one semantics correspondence between legal relational data and RDF graph satisfying OWL axioms, Calvanese et al. [7] further extended the direct mapping of relational schemas into \(\texttt {DL\text {-}Lite}_\texttt {RDFS}\) with disjointness - as constraints over mapped RDF graphs.
Finally, Thapa et al. [26] have studied the problem of translating database constraints into SHACL, instead of OWL/Epistemic DL, giving a direct transformation from SQL constraints to SHACL, preserving their semantics when source key constraints are satisfied [26, Theorem 2]. The present work improves on this by a) not being restricted to direct mappings, and b) lifting the requirement on satisfied key constraints.
8 Conclusion
In this paper, we study the problem of constraint rewriting for relational to RDF data transformation based on the central property of maximal semantics preservation. We translate standard SQL database constraints to shapes in the SHACL constraint language for RDF graphs. We show that our proposed rewriting \(\varGamma \) for the simple relational to RDF mappings satisfies the central properties of a constraint rewriting.
We believe that the propose constraint rewriting constitutes a core component of R2R mapping tools for the crucial task of constructing and maintaining a quality-assured RDF graph with SHACL constraints. The SHACL description of the generated RDF graph provides a data quality guarantee for data exchange, interoperability and query optimization. Hence, an important direction for future work will be the implementation and practical evaluation of our rewriting for relational to RDF data transformation and query optimization [30] in an ontology-based data access platform [29, 31].
Notes
- 1.
- 2.
- 3.
dash:uniqueValueForClassConstraintComponent from http://datashapes.org.
- 4.
\(\textbf{t}_{\nu }\) specify XML Schema datatype of RDF literal \(\textbf{t}_{\nu }(d)\) corresponding to the SQL data type \(\nu \) of the database constant \(d\in \varDelta _{\nu }\), e.g., \(\textbf{t}_{\nu }\) is an \(\text {xsd:string}\) IRI term if \(\nu \) is \(\text {varchar}\) SQL data type.
References
Abiteboul, S., Hull, R., Vianu, V.: Foundations of Databases, vol. 8. Addison-Wesley, Reading (1995)
Arenas, M., Bertails, A., Prud’hommeaux, E., Sequeda, J.: A direct mapping of relational data to RDF. W3C Recommendation 27, 1–11 (2012)
Armstrong, W.W.: Dependency structures of data base relationships. In: IFIP Congress, vol. 74, pp. 580–583. Geneva, Switzerland (1974)
Badia, A., Lemire, D.: Functional dependencies with null markers. Comput. J. 58(5), 1160–1168 (2015)
Beeri, C., Fagin, R., Howard, J.H.: A complete axiomatization for functional and multivalued dependencies in database relations. In: Proceedings of the 1977 ACM SIGMOD International Conference on Management of Data, pp. 47–61 (1977)
Calvanese, D.: Ontologies and databases: the DL-Lite approach. In: Tessaris, S., et al. (eds.) Reasoning Web 2009. LNCS, vol. 5689, pp. 255–356. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03754-2_7
Calvanese, D., Fischl, W., Pichler, R., Sallinger, E., Simkus, M.: Capturing relational schemas and functional dependencies in RDFS. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 28 (2014)
Calvanese, D., Gal, A., Lanti, D., Montali, M., Mosca, A., Shraga, R.: Mapping patterns for virtual knowledge graphs. arXiv preprint arXiv:2012.01917 (2020)
Civili, C., Mora, J., Rosati, R., Ruzzi, M., Santarelli, V.: Semantic analysis of R2RML mappings for ontology-based data access. In: Ortiz, M., Schlobach, S. (eds.) RR 2016. LNCS, vol. 9898, pp. 25–38. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45276-0_3
Console, M., Lenzerini, M.: Data quality in ontology-based data access: the case of consistency. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 28 (2014)
Console, M., Lenzerini, M.: Epistemic integrity constraints for ontology-based data management. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, pp. 2790–2797 (2020)
Corman, J., Reutter, J.L., Savković, O.: Semantics and validation of recursive SHACL. In: Vrandečić, D., Bontcheva, K., Suárez-Figueroa, M.C., Presutti, V., Celino, I., Sabou, M., Kaffee, L.-A., Simperl, E. (eds.) ISWC 2018. LNCS, vol. 11136, pp. 318–336. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00671-6_19
Das, S., Sundara, S., Cyganiak, R.: R2RML: RDB to RDF mapping language, September 2012. http://www.w3.org/TR/2012/REC-r2rml-20120927/
Donini, F.M., Nardi, D., Rosati, R.: Description logics of minimal knowledge and negation as failure. ACM Trans. Comput. Logic (ToCL) 3(2), 177–225 (2002)
Knublauch, H., Kontokostas, D.: Shapes constraint language (SHACL). W3C recommendation, W3C, July 2017. http://www.w3.org/TR/2017/REC-shacl-20170720/
Lembo, D., Mora, J., Rosati, R., Savo, D.F., Thorstensen, E.: Mapping analysis in ontology-based data access: algorithms and complexity. In: Arenas, M., Corcho, O., Simperl, E., Strohmaier, M., d’Aquin, M., Srinivas, K., Groth, P., Dumontier, M., Heflin, J., Thirunarayan, K., Staab, S. (eds.) ISWC 2015. LNCS, vol. 9366, pp. 217–234. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25007-6_13
Manola, F., Miller, E., McBride, B., et al.: RDF primer. W3C Recommendation 10(1–107), 6 (2004)
Mecca, G., Rull, G., Santoro, D., Teniente, E.: Ontology-based mappings. Data Knowl. Eng. 98, 8–29 (2015)
De Medeiros, L.F., Priyatna, F., Corcho, O.: MIRROR: automatic R2RML mapping generation from relational databases. In: Cimiano, P., Frasincar, F., Houben, G.-J., Schwabe, D. (eds.) ICWE 2015. LNCS, vol. 9114, pp. 326–343. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19890-3_21
Motik, B., Horrocks, I., Sattler, U.: Bridging the gap between OWL and relational databases. J. Web Semant. 7(2), 74–89 (2009)
Nikolaou, C., Grau, B.C., Kostylev, E.V., Kaminski, M., Horrocks, I.: Satisfaction and Implication of Integrity Constraints in Ontology-based Data Access. In: IJCAI, pp. 1829–1835 (2019)
Poggi, A., Lembo, D., Calvanese, D., De Giacomo, G., Lenzerini, M., Rosati, R.: Linking data to ontologies. In: Spaccapietra, S. (ed.) Journal on Data Semantics X. LNCS, vol. 4900, pp. 133–173. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-77688-8_5
Sequeda, J.F., Arenas, M., Miranker, D.P.: On directly mapping relational databases to RDF and OWL. In: Proceedings of the 21st International Conference on World Wide Web, pp. 649–658 (2012)
Sequeda, J.F., Miranker, D.P.: Ultrawrap mapper: a semi-automatic relational database to RDF (RDB2RDF) mapping tool. In: International semantic web conference (posters & demos) (2015)
Juan, F., Sequeda, F.P., Villazón-Terrazas, B.: Relational database to RDF mapping patterns. In: WOP (2012)
Thapa, R.B., Giese, M.: A source-to-target constraint rewriting for direct mapping. In: Hotho, A., Blomqvist, E., Dietze, S., Fokoue, A., Ding, Y., Barnaghi, P., Haller, A., Dragoni, M., Alani, H. (eds.) ISWC 2021. LNCS, vol. 12922, pp. 21–38. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-88361-4_2
Thapa, R.B., Giese, M.: A source-to-target constraint rewriting for direct mapping (extended version). Research Report 498, Dept. of Informatics, University of Oslo, September 2021. http://www.urn.nb.no/URN:NBN:no-90764
Thapa, R.B., Giese, M.: Mapping relational database constraints to SHACL (extended version). Research Report 503, Dept. of Informatics, University of Oslo, July 2022. http://www.urn.nb.no/URN:NBN:no-35645
Xiao, G., et al.: A survey. IJCAI Organization, Ontology-based data access (2018)
Xiao, G., Kontchakov, R., Cogrel, B., Calvanese, D., Botoeva, E.: Efficient handling of SPARQL OPTIONAL for OBDA. In: Vrandečić, D., Bontcheva, K., Suárez-Figueroa, M.C., Presutti, V., Celino, I., Sabou, M., Kaffee, L.-A., Simperl, E. (eds.) ISWC 2018. LNCS, vol. 11136, pp. 354–373. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00671-6_21
Xiao, G., Lanti, D., Kontchakov, R., Komla-Ebri, S., Güzel-Kalaycı, E., Ding, L., Corman, J., Cogrel, B., Calvanese, D., Botoeva, E.: The virtual knowledge graph system ontop. In: Pan, J.Z., Tamma, V., d’Amato, C., Janowicz, K., Fu, B., Polleres, A., Seneviratne, O., Kagal, L. (eds.) ISWC 2020. LNCS, vol. 12507, pp. 259–277. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-62466-8_17
Acknowledgements
This work is supported by the Norwegian Research Council via the SIRIUS SFI (237898). We thank Egor Kostylev for many constructive suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Thapa, R.B., Giese, M. (2022). Mapping Relational Database Constraints to SHACL. In: Sattler, U., et al. The Semantic Web – ISWC 2022. ISWC 2022. Lecture Notes in Computer Science, vol 13489. Springer, Cham. https://doi.org/10.1007/978-3-031-19433-7_13
Download citation
DOI: https://doi.org/10.1007/978-3-031-19433-7_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-19432-0
Online ISBN: 978-3-031-19433-7
eBook Packages: Computer ScienceComputer Science (R0)





 , then
, then  then for every
then for every  then for every
then for every  then
then  and
and
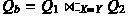 .
. , then
, then