Keywords

1 Introduction

With the rapid development of Internet of Things (IoT), various transport system applications win growing popularity in recent years. Intelligent vehicle services generate high performance demands, such as low-latency commuication and intensive computation. Vehicle edge computing (VEC) thus emerges for supporting computing, storage and network bandwidth [1]. Many studies introduce a variety of VEC technology, including vehicle fog computing [2], hybrid combination of fog computing architecture and vehicle cloud computing [3] and so on. VEC servers execute computation tasks, generated by the vehicles at the end, while reducing the delay. To improve the QoS of vehicle applications, studies have investigated if peripheral vehicles with free resources cooperate with VEC server to complete computing tasks. Authors in [4] studied task scheduling scheme for enhancing computing resource utilization with system stability and low latency. Some other studies on vehicle edge computing are also discussed in [5, 6].

In this paper, we are motivated to achieve mutual cooperation for vehicle task offloading. Vehicles, constrained by limited resources, require VEC serves for task execution. A large number of computation tasks burden VEC servers. To improve VEC efficiency, we consider numerous vehicles with free resources to assist the computing work of VEC servers. However, due to energy usage, most vehicles unenthusiastically participate in task calculation. In doing so, a framework of resource allocation and pricing is designed to economically compensate their costs and stimulate their cooperation.

2 System Module and Game Formulation

2.1 System Model

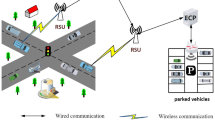
Our model focuses on task offloading between one VEC server and a group of vehicles. The proposed model is illustrated. Assume that a VEC server connects m CRVs and n CAVs within its coverage, denoted by \(\mathcal {M} = \{1,2,\dots ,m \} \) and \(\mathcal {N} = \{1,2,\dots ,n \} \). We also assume CRV i’s total computation tasks as \(w_{i}^{r}\), \(i\in \mathcal {M}\). Let \({\boldsymbol{p}^{r}}\) denote CRVs’ transmit powers over the VEC server’s sub-channels with \({\boldsymbol{p}^{r}}=\left\{ p_{1}^{r},p_{2}^{r},\ldots ,p_{m}^{r} \right\} \) while offloading tasks to VEC server. Specially, \(p_{i}^{r}\) is the transmit power from CRV i to VEC server, \(i\in \mathcal {M}\). Similarly, the allocated powers for transmitting tasks to CAVs are denoted as \({\boldsymbol{p}^{a}}=\left\{ p_{1}^{a},p_{2}^{a},\ldots ,p_{n}^{a} \right\} \), where \(p_{j}^{a}\) corresponds to the transmit power from VEC server to CAV j, \(j\in \mathcal {N}\).

According to the communication model in [7], the channel rate from CRV \(i, i\in \mathcal {M}\) to VEC server is defined,

$$\begin{aligned} R_{i}^{r}=B_{i}^{r}lo{{g}_{2}}\left( 1+\frac{p_{i}^{r}h_{i}^{r}}{\sigma _{i}^{2}} \right) , \end{aligned}$$
(1)

The channel rate from VEC server to CAV j is also defined,

$$\begin{aligned} R_{j}^{a}=B_{j}^{a}lo{{g}_{2}}\left( 1+\frac{p_{j}^{a}h_{j}^{a}}{\sigma _{j}^{2}} \right) , \end{aligned}$$
(2)

where \(B_{i}^{r}\) and \(B_{j}^{a}\) represent the transmission bandwidth of the subchannel, \({{\sigma }_{i}}\) and \({{\sigma }_{j}}\) represent noise power, and \(h_{i}^{r}\) and \(h_{j}^{a}\) represent the subchannel power gain.

We here define the utility function of a CRV as the difference between its gains and its costs. Service satisfaction contributes to its gain. Local computation cost, incentive payment and task transmission cost incur its total costs. Let \(T_{i}^{r}\) represent the uplink transmission time of delivering CRV i’s tasks to VEC server, which indicates its task size of \(R_{i}^{r}T_{i}^{r}\). Given the unit pricing \({{u}_{0}}\) that VEC server charges CRVs, we define the utility of CRV \(i, i\in \mathcal {M}\),

$$\begin{aligned} U_{i}^{r}\left( {{u}_{0}},p_{i}^{r} \right) =s_{i}^{r}R_{i}^{r}T_{i}^{r}-\varepsilon _{i}^{r}\left( w_{i}^{r}-R_{i}^{r}T_{i}^{r} \right) -{{u}_{0}}p_{i}^{r}-\xi _{i}^{r}p_{i}^{r}, \end{aligned}$$
(3)

where \(s_{i}^{r}\) is CRV i’s internal demand rate, \(\varepsilon _{i}^{r}\) is the unitary local computation cost and \(\xi _{i}^{r}\) is the unitary transmission cost. Accordingly, the utility of CAV \(j, j\in \mathcal {N} \) is outlined as,

$$\begin{aligned} U_{j}^{a}\left( u_{j}^{a},p_{j}^{a} \right) =u_{j}^{a}p_{j}^{a}-\varepsilon _{j}^{a}R_{j}^{a}T_{j}^{a}, \end{aligned}$$
(4)

where \(u_{j}^{a}\) is the incentive gain per unitary transmit power, \(\varepsilon _{j}^{a}\) is the unitary computation consumption. The parameter \(T_{j}^{a}\) represents computation tasks’ uplink transmission time while delivering from VEC server to CAV j. It indicates the task size of \(R_{j}^{a}T_{j}^{a}\), offloaded by CAV j. For the VEC server, its gain is the payment offered by CRVs. The total costs include local computation cost, incentive payment for CAVs, and power cost of transmitting task to the CAVs. So, the utility function \({{U}^{vec}}\) of VEC server can be defined as:

$$\begin{aligned} \begin{aligned} {{U}^{vec}}\left( {{u}_{0}},{\boldsymbol{u}^{a}},{\boldsymbol{p}^{r}},{\boldsymbol{p}^{a}} \right) =\underset{i=1}{\mathop {\overset{\mathcal {M}}{\mathop {\sum }}\,}}\,{{u}_{0}}p_{i}^{r}-\underset{j=1}{\mathop {\overset{\mathcal {N}}{\mathop {\sum ~}}\,}}\,u_{j}^{a}p_{j}^{a}\\ -\tau \underset{j=1}{\mathop {\overset{\mathcal {N}}{\mathop {\sum ~}}\,}}\,p_{j}^{a}-{{\varepsilon }_{0}}\left( \underset{i=1}{\mathop {\overset{\mathcal {M}}{\mathop {\sum }}\,}}\,R_{i}^{r}T_{i}^{r}-\underset{j=1}{\mathop {\overset{\mathcal {N}}{\mathop {\sum }}\,}}\,R_{j}^{a}T_{j}^{a} \right) , \end{aligned} \end{aligned}$$
(5)

where \({{\varepsilon }_{0}}\) is the unitary computation cost of VEC server and \(\tau \) is the unit transmission cost. Denote \({\boldsymbol{u}^{a}}\) as \({\boldsymbol{u}^{a}}=\left\{ u_{1}^{a},u_{2}^{a},\ldots ,u_{n}^{a} \right\} \). For ease of illustration, we decompse the utility function in (5) into \({{U}^{vec}}=U_{1}^{vec}+U_{2}^{vec}\), in which,

$$\begin{aligned} U_{1}^{vec}\left( {{u}_{0}},{\boldsymbol{p}^{r}} \right) =\underset{i=1}{\mathop {\overset{\mathcal {M}}{\mathop {\sum }}\,}}\,{{u}_{0}}p_{i}^{r}-{{\varepsilon }_{0}}\underset{i=1}{\mathop {\overset{\mathcal {M}}{\mathop {\sum }}\,}}\,R_{i}^{r}T_{i}^{r}, \end{aligned}$$
(6)
$$\begin{aligned} U_{2}^{vec}\left( {\boldsymbol{u}^{a}},{\boldsymbol{p}^{a}} \right) =\underset{j=1}{\mathop {\overset{\mathcal {N}}{\mathop {\sum }}\,}}\,{{\varepsilon }_{0}}R_{j}^{a}T_{j}^{a}-\underset{j=1}{\mathop {\overset{\mathcal {N}}{\mathop {\sum }}\,}}\,\left( u_{j}^{a}+\tau \right) p_{j}^{a}. \end{aligned}$$
(7)

2.2 Problem Formulation

In the three-tiered model, each participant has its own strategy and goal. Their different goals formulate different computation task management and pricing problems.

For player CRV i, \({\forall }i\in \mathcal {M}\), its strategy is to determine the transmit power \(p_{i}^{r}\) from it to VEC server in order to maxmize the utility in (3). So, the CRV i’s optimization problem is stated as,

$$\begin{aligned}&p{{_{i}^{r}}^{*}}=\textrm{arg}~ma{{x}_{p_{i}^{r}>0}}U_{i}^{r}\left( {{u}_{0}},p_{i}^{r} \right) \end{aligned}$$
(8a)
$$\begin{aligned}&\text { subject to } \quad {{\underline{p}}^{r}}\le p_{i}^{r}\le {{\bar{p}}^{r}}, \end{aligned}$$
(8b)

where \({{\underline{p}}^{r}}\) and \({{\bar{p}}^{r}}\) correspond to minimal and maximum transmit powers of CRVs.

For the player of VEC server, its strategy is to decide the pricing \({{u}_{0}}\) of CRVs’s computation tasks and transmit power \({\boldsymbol{p}^{a}}\) from it to CAVs in order to maximize the utility in  (5). So, the VEC server’s optimization problem is stated as,

$$\begin{aligned} \left( {\boldsymbol{p}^{{{a}^{\text {*}}}}},{{u}_{0}} \right) =\textrm{arg}~ma{{x}_{\left( p_{j}^{a*},{{u}_{0}} \right) }}&{{U}^{vec}}\left( {{u}_{0}},{\boldsymbol{u}^{a}},{\boldsymbol{p}^{r}},{\boldsymbol{p}^{a}} \right) \end{aligned}$$
(9a)
$$\begin{aligned} \text { subject to } \quad&{{\underline{p}}^{r}}\le p_{i}^{r}\le {{\bar{p}}^{r}},\end{aligned}$$
(9b)
$$\begin{aligned}&{{\underline{p}}^{a}}\le p_{j}^{a}\le {{\bar{p}}^{a}}, \end{aligned}$$
(9c)

where \({{\underline{p}}^{a}}\) and \({{\bar{p}}^{a}}\) correspond to minimal and maximum transmit powers of CAVs.

Since the utility function in (5) can be seperately divided into \({{U}^{vec}}=U_{1}^{vec}+U_{2}^{vec}\), problem (9) is thus decomposed into two subproblems as follows,

$$\begin{aligned}&u_{0}^{*}=\textrm{arg}~ma{{x}_{{{u}_{0}}}}U_{1}^{vec}\left( {{u}_{0}},{\boldsymbol{p}^{r}} \right) \end{aligned}$$
(10a)
$$\begin{aligned}&\text { subject to } \quad {{\underline{p}}^{r}}\le p_{i}^{r}\le {{\bar{p}}^{r}}, \end{aligned}$$
(10b)

and,

$$\begin{aligned}&p_{j}^{a}=\textrm{arg}~ma{{x}_{p_{j}^{a}}}U_{2}^{vec}\left( u_{j}^{a},p_{j}^{a} \right) \end{aligned}$$
(11a)
$$\begin{aligned}&\text { subject to } \quad {{\underline{p}}^{a}}\le p_{j}^{a}\le {{\bar{p}}^{a}}. \end{aligned}$$
(11b)

For player CAV \(j, {\forall }j\in \mathcal {N}\), its strategy is to determine the pricing \(u_{j}^{a}\) of VEC server’s overloaded tasks for maximizing the utility in (4). So, the CAV j’s optimization problem is described as,

$$\begin{aligned}&u_{j}^{a*}=\textrm{arg}~ma{{x}_{u_{j}^{a}>0}}U_{j}^{a}\left( u_{j}^{a},p_{j}^{a} \right) \end{aligned}$$
(12a)
$$\begin{aligned}&\text { subject to } \quad {{\underline{p}}^{a}}\le p_{j}^{a}\le {{\bar{p}}^{a}}. \end{aligned}$$
(12b)

2.3 Stackelberg Game Building

We here build two consecutive Stackelberg games for describing the interactions among CRVs, CAVs and VEC server, shown in Fig. 2. The VEC server acts as the leader of CRVs to determine the power pricing \({{u}_{0}}\) for CRVs’ task. CRVs, as the followers of VEC server, then decide their transmit power strategy \({\boldsymbol{p}^{r}}\). The interactions between CRVs and VEC server formulates the first two-stage Stackelberg game. Problem (8) and Problem (10) jointly formulates such noncooperative game \({{\mathcal {G}}^{CRV}}=\left\{ \mathcal {M},{{\left\{ p_{i}^{r} \right\} }_{i\in \mathcal {M}}},{{\left\{ U_{i}^{r} \right\} }_{i\in \mathcal {M}}} \right\} \), where \(\mathcal {M}\) is the set of CRVs, \({{\left\{ p_{i}^{r} \right\} }_{i\in \mathcal {M}}}\) is the strategy set and \({{\left\{ U_{i}^{r} \right\} }_{i\in \mathcal {M}}}\) is the cost function set.

CAVs, as the leaders, determine power pricing \({\boldsymbol{u}^{a}}\) for VEC server’s overloaded tasks. Accordingly, VEC server acts as the follower of CAVs in the second stage to determine its transmit power strategy \({\boldsymbol{p}^{a}}\). The interaction between CAVs and VEC server formulates the second two-stage Stackelberg game. In detail, Problem (11) and Problem (12) composes CAVs’ game \({{\mathcal {G}}^{CAV}}=\left\{ \mathcal {N},{{\left\{ u_{j}^{a} \right\} }_{j\in \mathcal {N}}},{{\left\{ U_{j}^{a} \right\} }_{j\in \mathcal {N}}} \right\} \), where \(\mathcal {N}\) is the set of CAVs, \({{\left\{ u_{j}^{a} \right\} }_{j\in \mathcal {N}}}\) is the strategy set and \({{\left\{ U_{j}^{a} \right\} }_{j\in \mathcal {N}}}\) is the set of profit functions.

Fig. 1.
figure 1

Interactions in Stackelberg game

Full size image

Definition 1

Subgame Perfect Equilibrium (SPE) in \({{\mathcal {G}}^{CRV}}\): If the stratification strategy \(\left\{ u_{0}^{*},{\boldsymbol{p}^{{{r}^{\text {*}}}}} \right\} \) represents SPE, it can reach NE in each stage of subgame, i.e.:

$$\begin{aligned} \left\{ \begin{array}{c} \text {Stage I}:u_{0}^{*}=\textrm{arg}~ma{{x}_{{u}_{0}}}U_{1}^{vec}\left( {{u}_{0}},{\boldsymbol{p}^{r}} \right) \\ \text {Stage II}:p{{_{i}^{r}}^{*}}=\textrm{arg}~ma{{x}_{p_{i}^{r}}}U_{i}^{r}\left( {{u}_{0}},p_{i}^{r} \right) \forall i\in \mathcal {M} \\ \end{array} \right. \end{aligned}$$
(13)

Definition 2

Subgame Perfect Equilibrium (SPE) in \({{\mathcal {G}}^{CAV}}\): If the stratification strategy \(\left\{ {\boldsymbol{u}^{{{a}^{\text {*}}}}},{\boldsymbol{p}^{{{a}^{\text {*}}}}} \right\} \) represents SPE, it can reach the NE in each stage of subgame, i.e.:

$$\begin{aligned} \left\{ \begin{array}{c} \text {Stage I}:u_{j}^{a*}=\textrm{arg}~ma{{x}_{u_{j}^{a}}}U_{j}^{a}\left( u_{j}^{a},p_{j}^{a} \right) ,\forall \text {j}\in \mathcal {N} \\ \text {Stage II}:{\boldsymbol{p}^{{{a}^{\text {*}}}}}=\textrm{arg}~ma{{x}_{\boldsymbol{p}^{{{a}^{\text {*}}}}}}U_{2}^{vec}\left( u_{j}^{a},{\boldsymbol{p}^{{{a}^{\text {*}}}}} \right) \\ \end{array} \right. \end{aligned}$$
(14)

Each game reaches SPE, which corresponds to a stable solution point of these problems. Under NE, no player has incentive to deviate. In detail, we use backward induction to analyze Stackelberg game. CRVs initiate the transmission strategy \({\boldsymbol{p}^{r}}\) based on VEC server’s pricing \({{u}_{0}}\). To finish CRVs’ computation tasks, the VEC server also recruits computation-assisted vehicles. CAVs determine a power pricing for VEC server’s overloaded tasks, on which VEC server allocates the transmit power \({\boldsymbol{p}^{a}}\) for CAVs. The process continues until Nash equilibrium reaches. The best strategy \(\left\{ u_{0}^{*},{\boldsymbol{u}^{{{a}^{\text {*}}}}},{\boldsymbol{p}^{{{r}^{\text {*}}}}},{\boldsymbol{p}^{{{a}^{\text {*}}}}} \right\} \) corresponds to the Nash equilibrium point, which is solved in the following theorems.

Theorem 1

Given the unit price \({{u}_{0}}\), the optimal strategy \({\boldsymbol{p}^{r}}\) of CRVs is calculated in (15).

$$\begin{aligned} p{{_{i}^{r}}^{*}}=\text { }\!\!\gamma \!\!\text { }_{i}^{r}\left( {{\boldsymbol{p}}^{r}} \right) =\left\{ \begin{matrix} {{{\underline{p}}}^{r}} &{} \begin{matrix} if &{} \frac{\left( s_{i}^{r}+\varepsilon _{i}^{r} \right) B_{i}^{r}T_{i}^{r}}{ln2\left( {{u}_{0}}+\xi _{i}^{r} \right) }-\frac{{{\sigma }^{2}}}{h_{i}^{r}}<{{{\underline{p}}}^{r}}, \\ \end{matrix} \\ \frac{\left( s_{i}^{r}+\varepsilon _{i}^{r} \right) B_{i}^{r}T_{i}^{r}}{ln2\left( {{u}_{0}}+\xi _{i}^{r} \right) }-\frac{{{\sigma }^{2}}}{h_{i}^{r}} &{} otherwise , \\ {{{\bar{p}}}^{r}} &{} \begin{matrix} if &{} \frac{\left( s_{i}^{r}+\varepsilon _{i}^{r} \right) B_{i}^{r}T_{i}^{r}}{ln2\left( {{u}_{0}}+\xi _{i}^{r} \right) }-\frac{{{\sigma }^{2}}}{h_{i}^{r}}>{{{\bar{p}}}^{r}}. \\ \end{matrix}~ \\ \end{matrix} \right. \end{aligned}$$
(15)

Theorem 2

VEC server achieves the unique optimal pricing strategy \(u_{0}^{*}\) by solving subproblem (10) while \(p_{i}^{r}\in \left[ {{{\underline{p}}}^{r}},{{{\bar{p}}}^{r}} \right] ,i\in \mathcal {M}\).

Proof

Substituting (15) into (6), we calculate the first derivative and second derivative of \(U_{1}^{vec}\) with respect to \({{u}_{0}}\),

$$\begin{aligned} \begin{aligned}&\frac{\partial U_{1}^{vec}}{\partial {{u}_{0}}}=\underset{i=1}{\mathop {\overset{\mathcal {M}}{\mathop {\sum }}\,}}\,\frac{\left( s_{i}^{r}+\varepsilon _{i}^{r}+{{\varepsilon }_{0}} \right) B_{i}^{r}T_{i}^{r}}{ln2\left( {{u}_{0}}+\xi _{i}^{r} \right) } -\frac{\sigma _{i}^{2}}{h_{i}^{r}}-\frac{{{u}_{0}}\left( s_{i}^{r}+\varepsilon _{i}^{r} \right) B_{i}^{r}T_{i}^{r}}{ln2{{\left( {{u}_{0}}+\xi _{i}^{r} \right) }^{2}}}, \end{aligned} \end{aligned}$$
(16)
$$\begin{aligned} \frac{{{\partial }^{2}}U_{1}^{vec}}{\partial {{u}_{0}}^{2}}=-\underset{i=1}{\mathop {\overset{\mathcal {M}}{\mathop {\sum }}\,}}\,B_{i}^{r}T_{i}^{r}\left[ \frac{2\left( s_{i}^{r}+\varepsilon _{i}^{r} \right) \xi _{i}^{r}+{{\varepsilon }_{0}}\left( {{u}_{0}}+\xi _{i}^{r} \right) }{ln2{{\left( {{u}_{0}}+\xi _{i}^{r} \right) }^{3}}} \right] . \end{aligned}$$
(17)

Obviously, the second derivative of \(U_{1}^{vec}\) on \({{u}_{0}}\) is always negative. So, \(U_{1}^{vec}\) is a strict concave function with respect to \({{u}_{0}}\), which indicates the uniqueness of optimal solution \(u_{0}^{*}\). Because of non-linear complexity of \(\frac{\partial U_{1}^{vec}}{\partial {{u}_{0}}}\) in (16), we approximate \(u_{0}^{*}\) by gradient ascent method.

Theorem 3

VEC server achieves the unique optimal transmit power strategy \({\boldsymbol{p}^{{{a}^{\text {*}}}}} \) in (18) by solving subproblem (11) while \(p_{j}^{a}\in \left[ {{{\underline{p}}}^{a}},{{{\bar{p}}}^{a}} \right] ,j\in \mathcal {N}\).

$$\begin{aligned} p{{_{j}^{a}}^{*}}=\text { }\!\!\delta \!\!\text { }_{j}^{a}\left( {\boldsymbol{p}^{a}} \right) =\left\{ \begin{matrix} {{{\underline{p}}}^{a}} &{} \begin{matrix} if &{} \frac{{{\varepsilon }_{0}}T_{j}^{a}B_{j}^{a}}{ln2\left( u_{j}^{a}+\tau \right) }-\frac{\sigma _{j}^{2}}{h_{j}^{a}}<{{{\underline{p}}}^{a}}, \\ \end{matrix} \\ \frac{{{\varepsilon }_{0}}T_{j}^{a}B_{j}^{a}}{ln2\left( u_{j}^{a}+\tau \right) }-\frac{\sigma _{j}^{2}}{h_{j}^{a}} &{} otherwise, \\ {{{\bar{p}}}^{a}} &{} \begin{matrix} if &{} \frac{{{\varepsilon }_{0}}T_{j}^{a}B_{j}^{a}}{ln2\left( u_{j}^{a}+\tau \right) }-\frac{\sigma _{j}^{2}}{h_{j}^{a}}>{{{\bar{p}}}^{a}}. \\ \end{matrix}~ \\ \end{matrix} \right. \end{aligned}$$
(18)

Theorem 4

CAV \(j, j\in \mathcal {N}\) reaches the optimal pricing \(u_{j}^{{{a}^{*}}}\) in (19) by solving problem (12),

$$\begin{aligned} {u{_{j}^{a}}^{*}=\text {R}_{j}^{a}\left( {{\textbf{u}}^{a}} \right) =\frac{\sqrt{{{\left( {{ \triangle }_{j}^{1}}-{{ \triangle }_{j}^{2}}-2{{ \triangle }_{j}^{3}}\tau \right) }^{2}}+4\tau {{ \triangle }_{j}^{3}}\left( {{ \triangle }_{j}^{1}}-{{ \triangle }_{j}^{3}}\tau \right) }-\left( 2{{ \triangle }_{j}^{3}}+{{ \triangle }_{j}^{2}}-{{ \triangle }_{j}^{1}} \right) }{2{{ \triangle }_{j}^{3}}},j\in \mathcal {N},} \end{aligned}$$
(19)

with \(~{{\triangle }_{j}^{1}}=\left( {{\varepsilon }_{0}}+\varepsilon _{j}^{a} \right) T_{j}^{a}B_{j}^{a}, {{\triangle }_{j}^{2}}=T_{j}^{s}B_{j}^{a}{{\varepsilon }_{0}}\) and \({{\triangle }_{j}^{3}}=~ln2~\frac{\sigma _{j}^{2}}{h_{j}^{a}}\).

3 Performance Evaluation

3.1 Simulation Setup

We consider a simulation scenario in which a VEC server provides services for m CRVs with assistance of n CAVs for task offloading. Each VEC server is able to cover about 10–30 CRVs. Referring to [8,9,10], the default model parameters are stated as follows. It is assumed that the bandwidth of each subchannel is 20 MHz and its channel gain is 53 dbm. The noise power of the channel of the relevant vehicles is 10 db. The task transmission time \(T_{i}^{r}\) and \(T_{j}^{a}\) is set from 0.5 ms to 1.5 ms. CRVs’ satisfaction on offloaded tasks follows a normal distribution \(N\left( {{e }_{0}},{{\sigma }_{0}} \right) \). The number of CRVs and CAVs are 10 and 10 by default.

3.2 Simulation Results

We first investigate the effect of VEC server’s computation cost on its utility under different number of participants. We see from Fig. 2(a) and (b) that the increasing number of CRVs and CAVs is indeed helpful for enhancing VEC utility. While fixing the CRV number and CAV number, we start with observing a descending trend of VEC utility on computation cost. However, VEC server’s utility finally improves with incremental computation cost. Such situation is illustrated in Fig. 2(c) and (d). The growing computation cost incurs CRV’s decreasing contribution on VEC utility and CAV’s increasing contribution on VEC utility. While VEC server’ payoff increased by CRV completely cover that decreased by CAV, VEC utility turns into improvement.

Fig. 2.
figure 2

Effect of computation cost on utility of VEC server

Full size image

We next observe the comparison by altering the transmit power cost of VEC server. Figure 3(a) and (b) shows an ascending trend of VEC utility while more CRVs and CAVs participate in computation offloading. We also observe that the utility of VEC server tends to decline with the increasing VEC power cost in Fig. 3(a) and (b). Such result is explained in Fig. 3(c) and (d). VEC power cost has a negative effect on CAV’ contribution for VEC server’s payoff. However, CRV’s contribution on VEC server’s payoff don’t follow a significant change. Accordingly the utility of VEC server decreases.

Fig. 3.
figure 3

Effect of VEC power cost on profit of VEC server

Full size image

The CRV computation cost is also explored if it determines the performance of the proposed model. It can be observed in Fig. 4(a) that local computation cost of CRV has no obvious effect on pricing, determined VEC server. With the increase of local computation cost, the steady pricing motivates the CRV to improve the transmit power for reducing local computation consumption in Fig. 4(a). We see from Fig. 4(b) that CRV utility depends on its computation cost, as well as task transmission time. Given a computation task, shorter task transmission time incurs higher local computation consumption. So, CRV utility tends to dwindle with the increasing local computation cost.

We finally evaluate CAV computation cost on the model performance. Figure 4(c) shows the transmit power, allocated by VEC server, and power pricing, determined by CAV. The large CAV computation cost incurs CAV’s high pricing. Accordingly, VEC server reduces the transmit power for utility maximization. Therefore, Fig. 4(c) shows an increasing pricing for VEC power, as well as a decreasing VEC transmit power. Under such scenario, CAV utility gradually degrades with the increasing CAV computation cost in Fig. 4(d). While the power pricing is large enough, the VEC power decreases to zero. CAV utility accords with being zero. Given the computation cost, long task transmission time for CAV promotes the improvement of power pricing and transmit power, on which CAV utility increases.

Fig. 4.
figure 4

Effect of CRV and CAV computation cost on utility of VEC server

Full size image

4 Conclusion

In this paper, we study the incentive mechanism of task offloading based on vehicle edge computing. Vehicles, constrained by limited computation resources, request VEC server for executing computation tasks. To avoid more burdens on VEC server, vehicles with free resources are recruited to assist VEC server’s computation work. We are motivated to quantify their gains and costs by defining utility function. Specially, the establishment of utility function considers the modes of task transmission and task computation among them, which is aimed to accurately describe their profits. Moreover, we build resource management and pricing framework by tools of Stackelberg game to ensure that each participant has appropriate incentives to participate in task offloading. Simulation results show that our incentive framework is stable and effective. In the future work, we will concentrate on computation resource management in extensive edge computing networks.