Keywords

1 Introduction

An outlier is a data point that is significantly different from the rest of the data. They are also called abnormalities, discordants, deviants, or anomalies [1]. Eventually, these outliers have useful information about abnormal characteristics of the systems that impact the data generation process. The detection of such unusual characteristics provides useful insights in many application domains [2, 24, 26]. Since outlier detection is relevant in any data science task, many techniques have been proposed in the literature [5, 25, 29]. Among them, the support vector data description (SVDD) [27, 28] has been widely used given its flexibility and applicability to real-world problems [3, 6, 11, 30]. However, SVDD does not consider the data distribution, and consequently, all observations contribute equally to the hypersphere and thus to the decision boundary [12].

As stated by Tax and Duin [27, 28] and Ben Hur et al. [4], the support vectors define the contour of dense data regions. Therefore they should contribute more to the decision boundary than other data points. In consequence, many research works have been proposed in the literature to deal with the equally-treated data when building the SVDD classifier [7, 9, 10, 12, 13, 15, 36, 37]. All these works introduced a weight, usually called membership degreeFootnote 1, into the mathematical formulation of the SVDD model. In this way, each data point receives a different membership degree reflecting its importance to the decision boundary. On the other hand, they differ in the mechanisms used to compute the membership degrees for each observation. These mechanisms usually rely on external methods like k-nearest neighbor approaches, clustering algorithms, and density-based methods, among others.

In this paper, we present the Induced Ordered Weighted Average Rough-Fuzzy Support Vector Data Description (IOWA-RFSVDD). This novel approach combines the concepts defined in fuzzy logic and rough set theory to compute the observations’ degrees of membership of being outliers. At the same time, it assigns a weight to these data points, reducing their influence on the decision boundary. The main contributions of our work are:

  • The IOWA-RFSVDD uses two values to assess the importance of a data point to construct the classifier: (1) a membership degree that measures its belongingness to the target class, and (2) a weight that controls its contribution to the decision boundary. As we show in Sect. 2.3, state-of-the-art approaches only use the weights to reduce the effect of noise data on the decision boundary.

  • The weight generation mechanism of the IOWA-RFSVDD relies on linguistic quantifier functions which are not data-dependent. In this way, our approach avoids using local and global data centers, which are usually computationally expensive to calculate.

  • The target class is a rough-fuzzy set instead of a fuzzy set like in state-of-the-art approaches. This way, data points are classified either in the lower approximation or the fuzzy boundary. We compute the membership degrees for these elements using the information available in the kernel matrix. This property is inherited from the base method, the rough-fuzzy support vector data description (RFSVDD) introduced in [21].

  • The IOWA-RFSVDD does not rely on any external algorithm to obtain the data points located in sparse regions, which are possible outliers.

The rest of the paper is arranged as follows: Sect. 2 provides the basics of the RFSVDD algorithm, the OWA and IOWA operators, and an overview of the relevant literature. In Sect. 3 the proposed methodology for IOWA-RFSVDD is presented. Its potential is shown in Sect. 4 in several computational experiments. Section 5 concludes our work and hint at possible future developments.

2 Literature Review

2.1 Rough-Fuzzy Support Vector Data Description

In 2015, Saltos and Weber [21] presented a soft-computing version of the classical Support Vector Data Description (SVDD) Algorithm [27, 28] called Rough-Fuzzy Support Vector Data Description (RFSVDD), which is the basic method of the approach introduced in this paper. The contribution made by RFSVDD is constructing a rough-fuzzy description of the dataset where outliers can be clearly identified and separated from the main classes.

The RFSVDD algorithm has two phases that will be explained below in more detail. First, there is a training phase, in which the classic SVDD is used to obtain a hypersphere (in a higher-dimensional, projected feature space) that encloses most of the data points. All observations that fall outside this sphere are usually considered outliers. Then, a fuzzification phase is performed over those objects that were classified as outliers in the first stage. The novelty of RFSVDD lies in this step, in which each outlier gets a membership degree of being or not an outlier. A formal description of the phases follows.

Training Phase. Let \(X = \{\textbf{x}_i \in \mathcal {R}^d / i = 1,\ldots ,N\}\) be the set of N data points of dimension d. The first step projects the data to a reproducing kernel Hilbert space (RKHS), in which we construct a hypersphere with minimal radius that encloses most of the training samples. The following quadratic optimization problem is solved:

$$\begin{aligned}&\min _{R,\boldsymbol{a},\boldsymbol{\xi }} \ z = R^2 + C \sum _{i=1} ^N \xi _i \end{aligned}$$
(1)
$$\begin{aligned}&\textit{s.t.} \nonumber \\&\parallel \phi (\textbf{x}_i) - \boldsymbol{a} \parallel ^2 \le R^2 + \xi _i&\qquad \quad \forall i=1,\ldots ,N \end{aligned}$$
(2)
$$\begin{aligned}&\xi _i \ge 0&\qquad \quad \forall i=1,\ldots ,N, \end{aligned}$$
(3)

where R is the radius of the sphere and \(\boldsymbol{a}\) its center; \(\phi \) is a non-linear mapping; \(\boldsymbol{\xi }\) is a vector of slack variables used to allow some observations falling outside the hypersphere; \(\parallel \cdot \parallel \) is the Euclidean norm; and \(C \in [0,1]\) is a constant regularization parameter that controls the trade-off between the volume of the sphere and the number of data points it includes. The dual formulation of the model (1)–(3) is as follows:

$$\begin{aligned}&\max _{\boldsymbol{\beta }} \ z_D = \sum _{i=1} ^N \beta _i K(\textbf{x}_i,\textbf{x}_i) - \sum _{i=1} ^N \sum _{j=1} ^N \beta _i \beta _j K(\textbf{x}_i,\textbf{x}_j) \end{aligned}$$
(4)
$$\begin{aligned}&\textit{s.t.} \nonumber \\&\sum _{i=1} ^N \beta _i = 1 \end{aligned}$$
(5)
$$\begin{aligned}&0 \le \beta _i \le C \qquad \quad \forall i=1,\ldots ,N, \end{aligned}$$
(6)

where \(\boldsymbol{\beta }\) are Lagrange multipliers and \(K(\textbf{x}_i,\textbf{x}_j)=\phi (\textbf{x}_i) \cdot \phi (\textbf{x}_j)\) is the kernel function. A widely used kernel is the Gaussian kernel, which is given by:

$$\begin{aligned} K(\textbf{x}_i,\textbf{x}_j)= e ^{-q \parallel \textbf{x}_i - \textbf{x}_j \parallel ^2} \end{aligned}$$
(7)

where \(q > 0\) is a parameter that controls the kernel’s width [23]. From the optimal solution of the model (4)–(6) we get:

  • Data points with \(\beta _i = 0\) are called inside data points (ID) since they lie inside the hypersphere.

  • Data points with \(0< \beta _i < C\) are called support vectors (SV) and define the decision boundary.

  • Data points with \(\beta _i = C\) are called bounded support vectors (BSV) since they lie outside the hypersphere. For this reason they are also called outliers.

Data points are assigned in any of two classes: the target class and the rejection class. The target contains the data points whose images lie inside the enclosing hypersphere, while the rejection class/outlier class contains the bounded support vectors. These classes together with the decision boundary define the description of the data set [27, 28].

Fuzzification Phase. Saltos and Weber [21] proposed a fuzzification phase to calculate the membership degrees of bounded support vectors to the target class. The procedure is:

  1. 1.

    Cast the hard data description structure of the training phase into a rough-fuzzy one with two components: a lower approximation and a fuzzy boundary.

  2. 2.

    Assign the support vectors and inside data points to the lower approximation of the target class.

  3. 3.

    Assign the bounded support vectors to the fuzzy boundary.

  4. 4.

    Calculate the membership degree \(\mu _{i}\) of bounded support vector i to the target class with the following equation:

    $$\begin{aligned} \mu _{i}&=\mu (BSV_i,SV_{i}) = K(BSV_i,SV_{i}) \nonumber \\&={e}^{-q \parallel BSV_i - SV_{i} \parallel ^2} \end{aligned}$$
    (8)

    where \(SV_i\) is the closest support vector to the bounded support vector i.

A simple example of the RFSVDD method using a two-dimensional toy data set is available in [22].

2.2 Ordered Weighted Average

Yager [32] presented the ordered weighted average (OWA) operator to aggregate numbers coming from different information sources. Formally, an OWA operator of dimension n is a mapping from \(\mathcal {R}^n\) to \(\mathcal {R}\) that has associated a weighting vector \(\textbf{w} \in \mathcal {R}^n\) such that \(\sum _{j = 1}^n w_j = 1\) and \(w_j \in [0,1]\). The OWA function is given by:

$$\begin{aligned} \text {OWA}\left(a_1,\ldots ,a_n, {\textbf {w}}\right) = \sum _{j = 1}^n w_j b_j \end{aligned}$$
(9)

where \(b_j\) is the j-th largest \(a_j\). A wide range of possible aggregation operators can be obtained when varying the weighting vector. The next ones are worth noting among others [8, 19]:

  • If \(w_1 = 1\) and \(w_j = 0\) for all \(j \ne 1\), the OWA operator becomes the maximum.

  • If \(w_n = 1\) and \(w_j = 0\) for all \(j \ne n\), the OWA operator becomes the minimum.

  • If \(w_j = \frac{1}{n}\) for all \(j = 1,2,\ldots ,n\), we get the arithmetic mean.

A critical step when using the OWA operator is how to set the weight vector \(\textbf{w}\). Fortunately, there are many approaches in the literature for setting these weights [8, 14, 19]. A common approach relies on using linguistic quantifiers [16]. The weights are generated by a regular increasing monotone (RIM) function \(Q:\mathcal {R}\rightarrow \mathcal {R}\) as follows:

$$\begin{aligned} w_j = Q\left(\frac{j}{n}\right) - Q\left(\frac{j-1}{n}\right) \qquad \forall j = 1,2,\ldots ,n \end{aligned}$$
(10)

Some common RIM quantifiers available in the literature are [16, 17]:

  • The basic linguistic quantifier:

    $$\begin{aligned} Q(r) = r^{\alpha } \end{aligned}$$
    (11)

  • The quadractic linguistic quantifier:

    $$\begin{aligned} Q(r) = \frac{1}{1 - \alpha \cdot r^{0.5}} \end{aligned}$$
    (12)

  • The exponential linguistic quantifier:

    $$\begin{aligned} Q(r) = e^{-\alpha \cdot r} \end{aligned}$$
    (13)

  • The trigonometric linguistic quantifier:

    $$\begin{aligned} Q(r) = \arcsin (\alpha \cdot r) \end{aligned}$$
    (14)

where \(\alpha > 0\). The OWA operator is monotonic, commutative, bounded, and idempotent [32].

Another relevant aggregation operator is the Induced Ordered Weighted Average (IOWA) introduced by Yager and Filev in 1999 [34]. It is an extension of the OWA function. The main difference is in the ordering step. The IOWA operator uses a second variable to induce the order of the argument variables. The IOWA operator fits well in applications where the argument variables are not comparable. For example, in this paper, the argument variables are \(d-\)dimensional data vectors which are clearly not comparable. Formally, the IOWA operator is a function given by:

$$\begin{aligned} \text {IOWA}\left(\langle a_1, u_1\rangle , \ldots ,\langle a_n, u_n\rangle , {\textbf {w}}\right) = \sum _{j = 1}^n w_j b_j \end{aligned}$$
(15)

where the vector \(\textbf{b}\) is the vector \(\textbf{a}\) sorted in decreasing order based on the values of the variable \(\textbf{u}\). The variable \(\textbf{u}\) is the order-inducing variable, and \(\textbf{a}\) is the argument variable. The IOWA operator is also monotonic, bounded, idempotent, and commutative [34]. Other properties and special cases of the IOWA operator are discussed in [33, 34]. The OWA and the IOWA operator have been applied successfully in many areas such as engineering, medicine, and finance, among others [8, 18, 31, 35].

2.3 Recent Advances on SVDD

The RFSVDD without the fuzzification phase leads to the classical SVDD algorithm proposed by Tax and Duin [27, 28] in 1999. From the derivation of the dual form of the model (1)–(3) we get that:

$$\begin{aligned} \boldsymbol{a} = \sum _{i = 1}^n \beta _i \phi (\textbf{x}_i) \end{aligned}$$
(16)

where \(\boldsymbol{a}\) is the center of the hypersphere in the projected feature space. From the Eq. (16) we note that only support vectors (\(\beta _i \in (0,C)\)) and bounded support vectors (\(\beta _i = C\)) affect this center, and therefore, the decision boundary. Since \(\beta _{SV} < \beta _{BSV}\) and the number of SVs is usually lower than the number of BSVs, it is clear that the BSV data influences more on the sphere’s center than non-BSV data. This issue originates from the fact that all data points have the same importance when building the classifier. Several works have been proposed in the literature to reduce or solve this issue. In what follows, we explain some of the most relevant and recent approaches.

The first approaches looking at reducing the importance of the training samples when constructing a support vector classifier were proposed by Liu and Huang [15] and Lin and Wang [13] in the context of binary classification using support vector machines (SVM). In their works, the authors cast the crisp nature of the training set to a fuzzy one in which every data point receives a membership degree to the new fuzzy training set. Their approaches differ in how they compute the membership degrees for the data points. Liu and Huang [15] used an outlier detection combination of techniques for separating the extreme data points from the main target class. Then, the membership degrees are computed based on the distance of the data points to the center of the main body (target class). On the other hand, Lin and Wang [13] proposed a function of the time of arrival of the data point to the training set to get the membership degrees. In this way, recent observations are more important than older ones.

The first approach that explicitly incorporates the notion of the relative importance of the training samples into the SVDD model is due to Zheng et al. [37] within the context of Support Vector Clustering (SVC) [4]. Given that the SVC algorithm uses the SVDD model in the training phase, the authors proposed the approach for both the SVDD and the SVC algorithms simultaneously by introducing the following optimization problem:

$$\begin{aligned}&\min _{R,\boldsymbol{a},\boldsymbol{\xi }} \ z = R^2 + C \sum _{i=1} ^N w_i \xi _i \end{aligned}$$
(17)
$$\begin{aligned}&\textit{s.t.} \nonumber \\&\parallel \phi (\textbf{x}_i) - \boldsymbol{a} \parallel ^2 \le R^2 + \xi _i&\qquad \quad \forall i=1,\ldots ,N \end{aligned}$$
(18)
$$\begin{aligned}&\xi _i \ge 0&\qquad \quad \forall i=1,\ldots ,N, \end{aligned}$$
(19)

where \(w_i \in [0,1]\) is the membership degree assigned to data point \(\textbf{x}_i\) and represents the relative importance it has in the training set. The Wolfe dual of the model (17)–(19) is:

$$\begin{aligned}&\max _{\boldsymbol{\beta }} \ z_D = \sum _{i=1} ^N \beta _i K(\textbf{x}_i,\textbf{x}_i) - \sum _{i=1} ^N \sum _{j=1} ^N \beta _i \beta _j K(\textbf{x}_i,\textbf{x}_j) \end{aligned}$$
(20)
$$\begin{aligned}&\textit{s.t.} \nonumber \\&\sum _{i=1} ^N \beta _i = 1 \end{aligned}$$
(21)
$$\begin{aligned}&0 \le \beta _i \le w_i C \qquad \quad \forall i=1,\ldots ,N, \end{aligned}$$
(22)

The only difference between the model (4)–(6) and the model (20)–(22) is the upper bound of the Lagrange multipliers. Zheng et al. used a k-nearest neighbor (K-NN) approach to set up the membership degrees for each data point. Since Zheng’s work, other approaches have been proposed in the literature [7, 9, 10, 12, 36]. All use the same mathematical formulation but differ on how they set the membership degrees.

Fan et al. [9] proposed the Grid-based Fuzzy Support Vector Data Description (G-FSVDD). The membership degrees are computed based on grids. The key idea relies on grouping the data points based on the dense regions surrounded by sparse regions. The authors divided the data space into grids at different scales several times. After obtaining enough grids, the apriori algorithm finds the grids with high density. After that, the membership values are set for each observation. On the other hand, Zhang et al. [36] used the improved possibilistic c-means to compute the membership degree of each data point to the cluster found in the kernel reproducing Hilbert space. Then, these membership degrees are used as weights in the model (20)–(22).

Hu et al. [10] used a completely different approach for setting up the membership degrees for the fuzzy support vector data description (F-SVDD). Based on the Rough Set theory [20], they divide the training set into three regions. Then, a neighborhood model of the samples is used to discriminate the data points in each region. Finally, the weight value is computed based on the region of the data point. Consequently, different weight values are assigned based on the locations of the observations.

Similarly to Zheng’s work, Cha et al. [7] introduced a density approach for the SVDD. In this case, the weights reflect the density distribution of a dataset in real space using the k-nearest neighbor algorithm. Then, each data point receives its weight according to the data density distribution. By applying this idea in the training process, the data description prioritizes observations in high-density regions. Eventually the optimal description shifts toward these dense regions. Finally, Li et al. [12] presented a method called Boundary-based Fuzzy-SVDD (BF-SVDD). BF-SVDD uses a local-global center distance to search for the data points near the decision boundary. Then, it enhances the membership degrees of that data using a k nearest neighbor approach and the global center of the data.

Based on the literature reviewed, we can conclude that almost all of the related work focuses on how to compute the weights for each training sample to give them different importance when building the classifier. Most rely on external techniques like k-nearest neighbor, clustering algorithms, or outlier detection methods in a pre-processing step of the SVDD task. To the best of our knowledge, aggregation operators were not used to compute weights to affect the contribution of the training samples when constructing the SVDD classifier. In this paper, we propose a methodology using the IOWA operator and the rough-fuzzy version of SVDD that naturally obtain the membership degrees with the information of the kernel matrix.

3 Proposed Methodology for IOWA-RFSVDD

As stated in Sect. 2, the RFSVDD algorithm builds a rough-fuzzy description of the data set by computing the membership degrees of data samples depending on whether they belong to the lower approximation or the fuzzy boundary. In this section, we use the classical RFSVDD together with the IOWA aggregation function to weigh the contribution of each data point to the decision boundary. Instead of assigning a weight to each data point for constructing the classifier, we propose using two values: (1) a membership degree that measures the belongingness of a data point to the target class, and (2) a weight that controls the contribution of the data point to the decision boundary.

In the training phase of the RFSVDD, we replace the model (1)–(3) by the model (17)–(19). Next, by setting up \(w_i = 1\) for all \(i = 1,2,\ldots ,N\), we solve the optimization model to get the support vectors, bounded support vectors, and inside data points. Then, we run the fuzzification phase to obtain membership degrees \(\mu _i\) of each data sample. After that, using a linguistic quantifier, we recalculate the weights \(w_i\) only for those data points that are bounded support vectors and assign the weights based on the order-induced variable \(\mu _i\). In this way, BSVs closer to the decision boundary will have higher weights than BSVs that are far away (outliers). Finally, we update the constant penalty parameter C and repeat the above steps until convergence or the maximum number of BSV data is achieved. We call this novel approach Induced Ordered Weighted Average Rough-Fuzzy Support Vector Data Description (IOWA-RFSVDD). Algorithm 1 presents its details.

figure a

In the first iteration of Algorithm 1, the steps 5–13 are the traditional RFSVDD method since the weights \(w_i\) are the same for all data points. The steps 14–16 which correspond to weight generation, BSV data ordering, and weight assignment, are the IOWA phase of the proposed approach. Finally, step 17 updates the value of the constant penalty parameter C to control the number of BSV data in each iteration and to guarantee convergence. We present the following example to illustrate the proposed method.

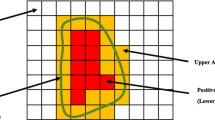
The Motivation Data Set [22] is an artificially generated data set with 316 instances, 16 of which are outside the main classes (Fig. 1(a)). The parameters of the SVDD algorithm \(q = 12\) and \(\upsilon = 0.074\) were fixed based on the values reported in [22]. After the training phase, support vectors, bounded support vectors, and inside data points are identified as is shown in Fig. 1(b), where red points are SV, orange points are BSV, and the remaining ones are inside data.

Fig. 1.
figure 1

Motivation Data Set

Full size image
Table 1. Results for bounded support vectors
Full size table
Table 2. Results support vectors
Full size table

Table 1 presents the results for bounded support vectors after running both RFSVDD and IOWA-RFSVDD algorithms. The columns \(\beta _i\) and \(\beta ^*_i\) show the optimal values of the Lagrange multipliers when all data points are weighted equally and differently, respectively. Due to the newly proposed weighting mechanism, the contribution of BSV data has been reduced by an average of 80% approximately. At the same time, the membership degrees of these data points are close to zero, indicating them as outliers.

Similarly, Table 2 presents the results for support vectors. As can be seen, the contribution of the support vectors to the decision boundary has been increased by more than 100%. At the same time, the membership degrees prevent SV data from being treated incorrectly as BSV data which is a common issue in state-of-the-art approaches cited in Sect. 2. For example, Li et al. [12] argue most weighting mechanisms are based on the k-nearest neighbor method, and some support vectors will be located in sparse areas with relatively fewer neighbors than others, producing their misclassification as BSVs.

As can be seen, the IOWA-RFSVDD reduces the influence of possible outliers in the construction of the SVDD classifier. The proposed approach uses the RIM quantifier function to generate the weights and the membership degrees as an order-induced variable for the assignation. In this way, our method does not require external procedures like the k-nearest neighbors or clustering algorithms, among others. Finally, using the membership degrees, as proposed in this paper, avoids the misclassification of SV data as BSVs due to their location in sparse areas.

4 Computational Experiments

To assess the effectiveness of the proposed approach, we performed computational experiments on nine data sets where eight are from the UCI Machine Learning Repository. Additionally, we introduced outliers randomly to the data sets to show how IOWA-RFSVDD reduces their effect on the decision boundary (sphere radius). We set the parameters for RFSVDD and IOWA-RFSVDD according to [22]. Table 3 shows the parameters fixed for each data set tested. Note since both methods use the same parameters, we report them once.

Table 3. Algorithms’ Parameters
Full size table

Based on the optimal solution of model (17)–(19), the distance of any data point \(\textbf{x}\) to the center of the hypersphere is given by:

$$\begin{aligned} d(\textbf{x},\boldsymbol{a}) = \sqrt{K(\textbf{x},\textbf{x}) - 2 \sum _{i=1}^N \beta _i K(\textbf{x},\textbf{x}_i) + \sum _{i=1}^N \sum _{j=1}^N \beta _i \beta _j K(\textbf{x}_i,\textbf{x}_j)} \end{aligned}$$
(23)

Then, the radius of the hypersphere is \(R = d(\textbf{x},\boldsymbol{a})\) where \(\textbf{x}\) is a support vector. Using (23), we computed the radius of the sphere for both RFSVDD and IOWA-RFSVDD. Table 4 shows these results for all data sets tested.

Table 4. Sphere Radius
Full size table

From Table 4, we can see that IOWA-RFSVDD reduces the sphere radius in almost all data sets tested. Hence, the decision boundary is tighter than in the RFSVDD approach since BSV data does not significantly influence the sphere center. Therefore, the proposed method is less prone to misclassifying outliers in an unsupervised setting. These results show the potential that IOWA-RFSVDD has to outperform the SVDD and RFSVDD algorithms for outlier detection tasks.

5 Conclusions and Future Work

In this paper, we proposed the IOWA Rough Fuzzy Support Vector Data Description. IOWA-RFSVDD is a novel approach to treat available data points differently for SVDD classifier construction according to their position in the feature space. The main advantages of the method are:

  1. 1.

    It uses two values to assess the importance of a data point for the construction of the classifier: (1) a membership degree that measures the belongingness of a data point to the target class, and (2) a weight that controls the contribution of the data point to the decision boundary.

  2. 2.

    The weight generation mechanism of the IOWA-RFSVDD relies on linguistic quantifier functions which are not data-dependent. These functions only need the number of BSVs.

  3. 3.

    It does not rely on external algorithms to obtain the data points of sparse regions.

We performed several computational experiments on diverse data sets to evaluate the effectiveness of our approach. The results showed that IOWA-RFSVDD tightens the decision boundary reducing the possibility of misclassifying outlier data. Finally, the proposed method can be extended to other support vector-based algorithms like support vector machines for classification, regression, or clustering.