Blow-ups of Three-dimensional Toric Singularities

Abstract

The purely log terminal blow-ups of three-dimensional terminal toric singularities are described. The three-dimensional divisorial contractions $f:(Y,E)\rightarrow (X\ni P)$ are described provided that ${\text {Exc}}f=E$ is an irreducible divisor, $(X\ni P)$ is a toric terminal singularity, f(E) is a toric subvariety and Y has canonical singularities.

In memory of Vasily Alexeevich Iskovskikh.

Introduction Let $(X \ni P)$ be a log canonical singularity and let $f:Y \rightarrow X$ be its blow-up. Suppose that the exceptional locus of f consists of only one irreducible divisor: ${\text {Exc}}f=E$. Then $f:(Y,E) \rightarrow (X \ni P)$ is called a purely log terminal blow-up, canonical blow-up or terminal blow-up, if (1), (2) or (3) are satisfied respectively: (1) $K_Y+E$ is plt and $-E$ is f-ample; (2) $-K_Y$ is f-ample and Y has canonical singularities; (3) $-K_Y$ is f-ample and Y has terminal singularities.

The definition of plt blow-up implicitly requires that the divisor E be ${\mathbb Q}$-Cartier. Hence Y is a ${\mathbb Q}$-gorenstein variety. By the inversion of adjunction (see [11, Theorem 17.6]) $K_E+{\text {Diff}}_E(0)=(K_Y+E)|_E$ is klt.

The importance of study of purely log terminal blow-ups is that: some very important questions of birational geometry for n-dimensional varieties, contractions can be reduced to the smaller dimension $n-1$, using purely log terminal blow-ups (for instance, see the papers [20,21,22, 26]). In dimension two, purely log terminal blow-ups are completely classified and the classification of two-dimensional non-divisorial log terminal extremal contractions of local type is obtained using them [22]. For three-dimensional varieties the first similar problem is to get the same explicit geometric classification of three-dimensional Mori contraction of local type as in two-dimensional case. The next problem is the first difficulty to realize this approach.

FormalPara Problem

Describe the class of all log del Pezzo surfaces, generic ${\mathbb P}^1$-fibrations which can be the exceptional divisors of some purely log terminal blow-ups of three-dimensional terminal singularities.

Suppose that $f(E)=P$ is a point. Then we solve this problem in the case of terminal toric singularities (Theorem 6.2). Moreover we obtain the description of plt blow-ups of ${\mathbb Q}$-factorial three-dimensional toric singularities (Theorem 6.4). Purely log terminal and canonical blow-ups are divided into toric and non-toric blow-ups up to analytic isomorphism. The study of non-toric plt blow-ups is reduced to the description of plt triples $(S,D,\Gamma )$ in dimension two (Definition 4.9).

Also we obtain the description of canonical blow-ups of three-dimensional terminal toric singularities (Theorem 6.5). The study of non-toric canonical blow-ups is reduced to the description of the following two interrelated objects: (a) toric canonical blow-ups of $(X\ni P)$ and (b) some triples $(S,D,\Gamma )$ in dimension two.

Immediate corollary of Theorem 6.5 is that the terminal blow-ups of three-dimensional terminal toric singularities are toric up to analytic isomorphism. This corollary was proved in the papers [2, 6, 8] by another methods.

Suppose that f(E) is a one-dimensional toric subvariety (curve) of the toric singularity $(X\ni P)$. Then the description of plt and canonical blow-ups is given in Theorems 3.7, 3.8, 3.9 and in Corollary 3.10.

I am grateful to Professors Yu.G. Prokhorov and I.A. Cheltsov for valuable advices.

1 Preliminary Results and Facts

All varieties are algebraic and are assumed to be defined over ${\mathbb C}$, the complex number field. The main definitions, notations and notions used in the paper are given in [9, 11, 22]. See [1, Sect. 3.10] on minimal model program with scaling. The definition of ${\text {Diff}}$ and its main properties are given in the papers [25, Sect. 3], [11, Chap. 16]. By $(X\ni P)$ denote the algebraic germ of the variety X at the point P.

A smooth point is a special case of singularity by our definition. For example, Du Val singularity of type ${\mathbb A}_0$ is a smooth point.

Let $f:Y\dashrightarrow X$ be a birational map and let D be a divisor on the variety X. By $D_Y$ denote the proper transform of D on the variety Y. If $Y=\widetilde{X}$, $Y=X'$ or $Y=\overline{X}$, then for notational convenience we use the notation $\widetilde{D}=D_{\widetilde{X}}$, $D'=D_{X'}$ or $\overline{D}=D_{\overline{X}}$ respectively. The similar notation is used for subvarieties of X.

The contraction $f:Y\rightarrow X$ is a projective morphism of the normal variety such that $f_*{\mathcal O}_Y={\mathcal O}_X$. A blow-up is a birational divisorial contraction. A ${\mathbb Q}$-factoriality means analytical ${\mathbb Q}$-factoriality in this paper.

The proper irreducible subvariety $\Gamma$ of X is said to be a center of canonical singularities of (X, D), if there exist the birational morphism $f:Y\rightarrow X$ and the exceptional divisor $E\subset Y$ such that $\Gamma =f(E)$ and $a(E,D)\le 0$. The set of canonical singularity centers of (X, D) and X is denoted by ${\text {CS}}(X,D)$ and ${\text {CS}}(X)$ respectively.

By our definition the toric varieties, toric morphisms are considered up to analytic isomorphism (analytical identification), if they are not explicitly defined by fans. Shokurov’s (hypothetical) criterion on the characterization of toric varieties is formulated in [26, Chap. 6]. By definition of weighted blow-up, its center is a point always, that is, its every weight is positive.

We write all singularities of surface in brackets. For example, the notation $S({\mathbb A}_1+\frac{1}{5}(1,2))$ means that the surface S has two singular points of types ${\mathbb A}_1$ and $\frac{1}{5}(1,2)$ exactly.

We actively use a structure of the local toric conic bundle $f:S\rightarrow (C\ni P)$, where $\dim S=2$ and $\rho (S/C)=1$. By [22, Lemma 7.1.11] the surface S has two singularities of types $\frac{1}{r}(1,q)$ and $\frac{1}{r}(1,-q)$ over the point P only, where $r\ge 1$.

Proposition 1.1

([11, Lemma 6.2]) Let $f_i:Y_i\rightarrow X$ be two divisorial contractions of normal varieties, where ${\text {Exc}}f_i=E_i$ are irreducible divisors and $-E_i$ are $f_i$-ample divisors. If $E_1$ and $E_2$ define the same discrete valuation of the function field $\mathcal K(X)$, then the contractions $f_1$ and $f_2$ are isomorphic.

Proposition 1.2

Let $f_i:Y_i\rightarrow (X\ni P)$ be two divisorial contractions to a point P, where ${\text {Exc}}f_i=E_i$ are irreducible divisors. Suppose that the varieties $Y_i$, X have log terminal singularities, $E_1$ and $E_2$ define the same discrete valuation of the function field $\mathcal K(X)$, the divisor $-E_1$ is $f_1$-ample, the divisor $-E_2$ is not $f_2$-ample. Then there exists the small flopping contraction (with respect to $K_{Y_2})$ $g:Y_2\rightarrow Y_1$ such that $f_2$ and $f_1\circ g$ are isomorphic.

Proof

Let $K_{Y_2}=f_2^*K_X+aE_2$. If $a>0$, then we put $L=-K_{Y_2}$. If $a\le 0$, then we put $L=-(K_{Y_2}+(-a+\varepsilon )E_2)$, where $\varepsilon$ is a sufficiently small positive rational number. Since $-E_2$ is a $f_2$-nef divisor, then the linear system |nL| is free over X for $n\gg 0$ and gives a contraction $g:Y_2\rightarrow Y'_2$ over X by the base point free theorem [9, Remark 3.1.2]. A curve C is exceptional for g if and only if $L\cdot C=E_2\cdot C=K_{Y_2}\cdot C=0$. Therefore g is a flopping contraction and $Y'_2\cong Y_1$ by Proposition 1.1.   $\square$

The next example shows the idea of Proposition 1.2.

Example 1.3

Let $(X\ni P)\cong (\{x_1x_2+x_3^2+x_4^4{=}0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. Consider the divisorial contraction $f_1:Y_1\rightarrow (X\ni P)$ induced by the blow-up of the maximal ideal of the point $({\mathbb C}^4 \ni 0)$. Then ${\text {Exc}}f_1\cong {\mathbb P}(1,1,2)$, the variety $Y_1$ has only one singular point denoted by Q, and $(Y_1\ni Q)\cong (\{y_1y_2+y_3^2+y_4^2=0\}\subset ({\mathbb C}^4_{y_1y_2y_3y_4},0))$. This singularity is not ${\mathbb Q}$-factorial and let $g:Y_2\rightarrow (Y_1\ni P)$ be its ${\mathbb Q}$-factorialization. We obtain the divisorial contraction $f_2:Y_2\rightarrow (X\ni P)$, where $Y_2$ is a smooth 3-fold, ${\text {Exc}}f_2\cong {\mathbb F}_2$, and $-K_{Y_2}$ is not a $f_2$-ample divisor.

Definition 1.4

Let $(X \ni P)$ be a log canonical singularity and let $f:Y \rightarrow X$ be its blow-up. Suppose that the exceptional locus of f consists of only one irreducible divisor: ${\text {Exc}}f=E$. Then $f:(Y,E) \rightarrow (X \ni P)$ is called a canonical blow-up if $-K_Y$ is f-ample and Y has canonical singularities. Note that the definition of canonical blow-up implies that $(X\ni P)$ is a canonical singularity. The canonical blow-up is said to be a terminal blow-up if Y has terminal singularities.

Remark 1.5

Using the notation of Definition 1.4, we have the following properties of canonical blow-ups.

• (1) The definition of canonical (resp. terminal) blow-up implies easily that $(X\ni P)$ is a canonical (resp. terminal) singularity.

• (2) The divisor $-E$ is f-ample and $a(E,0)>0$.

• (3) Let $f_i:(Y_i,E_i)\rightarrow (X \ni P)$ be two canonical blow-ups. If $E_1$ and $E_2$ define the same discrete valuation of the function field $\mathcal K(X)$ then the blow-ups $f_1$ and $f_2$ are isomorphic by Proposition 1.1.

• (4) Let $(X \ni P)$ be a ${\mathbb Q}$-factorial singularity. Then Y is a ${\mathbb Q}$-factorial variety also, $\rho (Y/X)=1$ and $\rho (E)=1$ [4, Sect. 5].

Theorem 1.6

Let $(X\ni P)$ be a canonical singularity and $(X\ni P,D)$ be a pair with canonical singularities, where D is a boundary. Assume that $a(E,D)=0$ and $a(E,0)>0$ for some irreducible exceptional divisor E. Then there exists a canonical blow-up such that its exceptional divisor and E define the same discrete valuation of the function field $\mathcal K(X)$. Moreover, if E is a unique exceptional divisor with $a(E,D)=0$ then its canonical blow-up is a terminal blow-up.

Proof

By Proposition 21.6.1 of the paper [11] we consider the birational contraction $\widetilde{f}:(\widetilde{Y},\widetilde{E})\rightarrow (X\ni P)$ with the following three properties:

(1) $\widetilde{E}$ is a unique irreducible exceptional divisor of ${\text {Exc}}\widetilde{f}$;

(2) $\widetilde{E}$ and E define the same discrete valuation of the function field $\mathcal K(X)$;

(3) if $(X\ni P)$ is ${\mathbb Q}$-factorial then $\rho (\widetilde{Y}/X)=1$ and ${\text {Exc}}\widetilde{f}=\widetilde{E}$.

The proof of Proposition 21.6.1 of [11] holds in any dimension since we can apply MMP with scaling to prove it. Let $\widetilde{f}$ be not the required canonical blow-up. If ${\text {Exc}}\widetilde{f}=\widetilde{E}$ then by Proposition 1.2 we have $\widetilde{f}\cong f\circ g$, where f is the required blow-up. Consider the remaining case when ${\text {Exc}}\widetilde{f}=\widetilde{E} \cup \Delta$, where $\Delta \ne \emptyset$ and ${\text {codim}}_{\widetilde{Y}}\Delta \ge 2$. Let H be a general Cartier divisor containing the set $\widetilde{f}({\text {Exc}}\widetilde{f})$. Then $K_{\widetilde{Y}}+D_{\widetilde{Y}}+\varepsilon H_{\widetilde{Y}}\equiv -\varepsilon a \widetilde{E}$ over X, where $a>0$. For $0<\varepsilon \ll 1$ we apply $K_{\widetilde{Y}}+D_{\widetilde{Y}}$—MMP with scaling of $H_{\widetilde{Y}}$. We obtain a birational map $\varphi :\widetilde{Y}\dashrightarrow Y'$, which is a composition of log flips, and we also obtain a divisorial contraction $f':Y' \rightarrow X$ such that ${\text {Exc}}f'=E'$, where $E'$ is an irreducible divisor. Therefore, by Proposition 1.2 we have the required canonical blow-up.   $\square$

Definition 1.7

Let $(X \ni P)$ be a log canonical singularity and let $f:Y \rightarrow X$ be its blow-up. Suppose that the exceptional locus of f consists of only one irreducible divisor: ${\text {Exc}}f=E$. Then $f:(Y,E) \rightarrow (X \ni P)$ is called a purely log terminal blow-up if the divisor $K_Y+E$ is purely log terminal and $-E$ is f-ample.

Remark 1.8

Definition 1.7 implicitly requires that the divisor E be ${\mathbb Q}$-Cartier. Hence Y is a ${\mathbb Q}$-gorenstein variety. By the inversion of adjunction $K_E+{\text {Diff}}_E(0)=(K_Y+E)|_E$ is klt.

Remark 1.9

Using the notation of Definition 1.7 we have the following properties of purely log terminal blow-ups.

• (1) The variety f(E) is normal [19, Corollary 2.11].

• (2) If $(X \ni P)$ is a log terminal singularity then $-(K_Y+E)$ is a f-ample divisor. A purely log terminal blow-up of log terminal singularity always exists by Theorem 1.5 of [13] since we can apply MMP with scaling to prove it (see also Theorem 1.10).

• (3) If $(X \ni P)$ is a strictly log canonical singularity then $a(E,0)=-1$. A purely log terminal blow-up of strictly log canonical singularity exists if and only if there is only one exceptional divisor with discrepancy $-1$ [13, Theorem 1.9], since we can apply MMP with scaling to prove Theorem 1.9 of [13].

• (4) If $(X \ni P)$ is a ${\mathbb Q}$-factorial singularity then Y is a ${\mathbb Q}$-factorial variety also, $\rho (Y/X)=1$ and $\rho (E)=1$ [19, Remark 2.2], [4, Sect. 5]. Hence, for ${\mathbb Q}$-factorial singularity we can omit the requirement that $-E$ be f-ample in Definition 1.7 because it holds automatically.

• (5) Let $f_i:(Y_i,E_i)\rightarrow (X \ni P)$ be two purely log terminal blow-ups. If $E_1$ and $E_2$ define the same discrete valuation of the function field $\mathcal K(X)$ then the blow-ups $f_1$ and $f_2$ are isomorphic by Proposition 1.1.

• (6) Let $-E$ be not a f-ample divisor in Definition 1.7. Then such blow-up can differ from some plt blow-up by a small flopping contraction only (with respect to the canonical divisor $K_Y$) [13, Corollary 1.13]. This statement is similar to Proposition 1.2.

• (7) Let $f:(Y,E) \rightarrow (X \ni P)$ be a toric blow-up of a toric ${\mathbb Q}$-gorenstein singularity. Assume that Y is a ${\mathbb Q}$-gorenstein variety and ${\text {Exc}}f=E$ is an irreducible divisor. It is obvious that $K_Y+E$ is a plt divisor. Therefore, if $(X\ni P)$ is ${\mathbb Q}$-factorial singularity then f is a plt blow-up.

Theorem 1.10

([13, Theorem 1.5], [19, Proposition 2.9]) Let X be a kawamata log terminal variety and let $D\ne 0$ be a boundary on X such that (X, D) is log canonical, but not purely log terminal. Then there exists an inductive blow-up $f:Y\rightarrow X$ such that:

• (1) the exceptional locus of f contains only one irreducible divisor $E\ ({\text {Exc}}(f)=E)$;

• (2) $K_Y+E+D_Y=f^*(K_X+D)$ is log canonical;

• (3) $K_Y+E+(1-\varepsilon )D_Y$ is purely log terminal and anti-ample over X for any $\varepsilon >0$;

• (4) if X is ${\mathbb Q}$-factorial then Y is also ${\mathbb Q}$-factorial and $\rho (Y/X)=1$.

Proof

The proofs of [13, Theorem 1.5], [19, Proposition 2.9] hold in any dimension since we can apply MMP with scaling to prove them.   $\square$

Remark 1.11

Inductive blow-up is a plt blow-up. Conversely, for any plt blow-up $f:(Y,E) \rightarrow (X \ni P)$ there exists a pair (X, D) such that f is its inductive blow-up. Indeed, put $D=f(\frac{1}{n}D_Y)$, where $D_Y\in |-n(K_Y+E)|$ is a general element for $n\gg 0$.

Definition 1.12

Let (X/Z, D) be a contraction of varieties, where D is a subboundary. Then a ${\mathbb Q}$-complement of $K_X+D$ is an effective ${\mathbb Q}$-divisor $D'$ such that $D'\ge D$, $K_X+D'$ is log canonical and $K_X+D'\sim _{{\mathbb Q}} 0/Z$ for some $n\in {\mathbb N}$.

Definition 1.13

Let (X/Z, D) be a contraction of varieties. Let $D=S+B$ be a subboundary on X such that B and S have no common components, S is an effective integral divisor and $\llcorner B \lrcorner \le 0$. Then we say that $K_X+D$ is n-complementary if there is a ${\mathbb Q}$-divisor $D^+$ (called an n-complement) such that

• (1) $n(K_X+D^+)\sim 0/Z$ (in particular, $nD^+$ is an integral divisor);

• (2) the divisor $K_X+D^+$ is log canonical;

• (3) $nD^+\ge nS+\llcorner (n+1)B \lrcorner$.

The divisor $K_X+D^+$ is also called an n-complement.

Definition 1.14

For $n\in {\mathbb N}$ put

$$ {\mathcal {P}}_n=\{ a \mid 0\le a \le 1,\ \llcorner (n+1)a \lrcorner \ge n a \}. $$

Proposition 1.15

([25, Lemma 5.4]) Let $f:X\rightarrow Y$ be a birational contraction and let D be a subboundary on X. Assume that $K_X+D$ is n-complementary for some $n\in {\mathbb N}$. Then $K_Y+f(D)$ is also n-complementary.

Proposition 1.16

([26, Lemma 4.4]) Let $f:X\rightarrow Z$ be a birational contraction of varieties and let D be a subboundary on X. Assume that

• (1) the divisor $K_X+D$ is f-nef;

• (2) the coefficient of every non-exceptional component of D meeting ${\text {Exc}}f$ belongs to ${\mathcal {P}}_n$;

• (3) the divisor $K_Z+f(D)$ is n-complementary.

Then the divisor $K_X+D$ is also n-complementary.

Proposition 1.17

([22, Proposition 4.4.1]) Let $f:X\rightarrow (Z\ni P)$ be a contraction and D be a boundary on X. Put $S=\llcorner D \lrcorner$ and $B=\{ D\}$. Assume that

• (1) the divisor $K_X+D$ is purely log terminal;

• (2) the divisor $-(K_X+D)$ is f-nef and f-big;

• (3) $S\ne 0$ near $f^{-1}(P)$;

• (4) every coefficient of D belongs to ${\mathcal {P}}_n$.

Further, assume that near $f^{-1}(P)\cap S$ there exists an n-complement $K_S+{\text {Diff}}_S(B)^+$ of $K_S+{\text {Diff}}_S(B)$. Then near $f^{-1}(P)$ there exists an n-complement $K_X+S+B^+$ of $K_X+S+B$ such that ${\text {Diff}}_S(B)^+={\text {Diff}}_S(B^+)$.

2 Toric Blow-ups

We refer the reader to [18] for the basics of toric geometry.

Definition 2.1

Let N be the lattice ${\mathbb Z}^n$ in the vector linear space $N_{{\mathbb R}}=N\otimes _{{\mathbb Z}}{\mathbb R}$ and M be its dual lattice ${\text {Hom}}_{{\mathbb Z}}(N, {\mathbb Z})$ in the vector linear space $M_{{\mathbb R}}=M\otimes _{{\mathbb Z}}{\mathbb R}$. We have a canonical pairing $\langle \ ,\ \rangle :N_{{\mathbb R}}\times M_{{\mathbb R}}\rightarrow {\mathbb R}$.

For a fan $\Delta$ in N the corresponding toric variety is denoted by $T_{N}({\Delta })$. For a k-dimensional cone $\sigma \in {\Delta }$ the closure of corresponding orbit is denoted by $V(\sigma )$. This is a closed subvariety of codimension k in $T_N({\Delta })$.

Example 2.2

(1) Let the vectors $e_1,\ldots ,e_n$ be a ${\mathbb Z}$-basis of N, where $n\ge 2$. Consider the cone

$$ \sigma ={\mathbb R}_{\ge 0}e_1+\ldots +{\mathbb R}_{\ge 0}e_{n-1}+{\mathbb R}_{\ge 0}(a_1e_1+\ldots +a_{n-1}e_{n-1}+re_n). $$

Let the fan ${\Delta }$ consists of the cone $\sigma$ and its faces. Then the affine toric variety $T_{N}({\Delta })$ is the quotient space $({\mathbb C}^n\ni 0)/{\mathbb Z}_r$ with the action $\frac{1}{r}(-a_1,\ldots ,-a_{n-1},1)$.

(2) Let

$$ \sigma =\langle e_1,e_2,e_3,e_4 \rangle = \langle (1,0,0),(0,1,0),(0,0,1),(1,1,-1) \rangle $$

for the lattice $N\cong {\mathbb Z}^3$. Let the fan ${\Delta }$ consists of the cone $\sigma$ and its faces. The affine toric variety $(X\ni P)=T_{N}({\Delta })$ is a three-dimensional non-degenerate quadratic cone in ${\mathbb C}^4$. Let

$$ {\Delta }^1=\{\langle e_1,e_2,e_3\rangle , \langle e_1,e_2,e_4\rangle , \text {their faces}\} $$

and

$$ {\Delta }^2=\{\langle e_1,e_3,e_4\rangle , \langle e_2,e_3,e_4\rangle , \text {their faces}\}. $$

Then the birational contractions $\psi _i:T_N({\Delta }^i)\rightarrow T_N({\Delta })$ are small resolutions for $i=1$, 2, and ${\text {Exc}}\psi _1=V(\langle e_1,e_2\rangle )$, ${\text {Exc}}\psi _2=V(\langle e_3,e_4\rangle )$. The birational map $T_N({\Delta }^1)\dashrightarrow T_N({\Delta }^2)$ is a flop.

Let $f:(Y,E) \rightarrow (X \ni P)$ be a toric blow-up, where Y is ${\mathbb Q}$-gorenstein, ${\text {Exc}}f=E$ is an irreducible divisor. Then f is a plt blow-up. Let us prove it. The divisor $K_Y+E$ is plt. Let $a=(a_1,a_2,a_3)$ be a primitive vector defining f. Consider any three-dimensional cone $\sigma '$ giving non-${\mathbb Q}$-factorial singularity of subdivision of the cone $\sigma$ by a. Then the cone $\sigma '$ gives non-${\mathbb Q}$-gorenstein singularity by Proposition 4.3 (i) [24], since there is no any vector $m\in M_{{\mathbb Q}}$ such that $\langle m, e_i \rangle =1$ for every i and $\langle m, a \rangle =1$. Hence $-E$ is a f-ample divisor. This completes the proof.

Let $f(E)=P$. Then $Y=T_N(\widetilde{\Delta })$ and

$$ \widetilde{\Delta }=\{\langle e_1,e_3,a\rangle , \langle e_1,e_4,a\rangle , \langle e_2,e_3,a\rangle , \langle e_2,e_4,a\rangle , \text {their faces}\}, $$

where $a=(a_1,a_2,a_3)$, $\gcd (a_1,a_2,a_3)=1$, $a_1>0$, $a_2>0$, $a_1+a_3>0$ and $a_2+a_3>0$.

Obviously, the converse is also true. Any such vector a defines a plt blow-up.

Let $f(E)=C$ and $\dim C=1$. Then, up to a permutation of the faces of the cone $\sigma$ we have $C=\langle e_2,e_3 \rangle$, $Y=T_N(\widehat{\Delta })$ and

$$ \widehat{\Delta }=\{\langle e_2,e_4,a\rangle , \langle e_1,e_3,a\rangle , \langle e_1,e_4,a\rangle , \text {their faces}\}, $$

where $a=(0,a_2,a_3)$, $\gcd (a_2,a_3)=1$, $a_2>0$, $a_3>0$.

Obviously, the converse is also true. Any such vector a defines a plt blow-up.

The variety Y has the singularities $\frac{1}{a_3}(0,-a_2,1)$, $\frac{1}{a_2}(0,1,-a_3)$, $\frac{1}{a_2+a_3}(-a_3,-a_2,1)$. The surface E is a toric conic bundle, $\rho (E/C)=2$, the single singular point of E (with a center of the third singularity of Y) has type ${\mathbb A}_{a_2+a_3-1}$ and ${\text {Diff}}_E(0)=\frac{a_2-1}{a_2}E_1+\frac{a_3-1}{a_3}E_2$, where $E_1$, $E_2$ are corresponding sections.

We will calculate a structure of f by the following way (for convenience). Let us consider $(X\ni P)\subset ({\mathbb C}^4,0)$ as the embedding $\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}_{x_1x_2x_3x_4}^4,0)$. The weighted blow-up of $({\mathbb C}^4,0)$ with weights $w=(w_1,w_2,w_3,w_4)$ provided that $w_1+w_2=w_3+w_4$ induces a toric blow-up $f':(Y',E') \rightarrow (X \ni P)$, where

$$ {\text {Exc}}f'=E'\cong \{x_1x_2+x_3x_4\subset {\mathbb P}_{x_1x_2x_3x_4}(w_1,w_2,w_3,w_4)\} - $$

is an irreducible divisor. If put $w_1=a_1+a_3$, $w_2=a_2$, $w_3=a_2+a_3$ and $w_4=a_1$, then we can easily compare the natural affine covers of Y and $Y'$ and prove that f and $f'$ are isomorphic blow-ups. Note that $C=\{x_1=x_2=x_3=0\}$ in the case $C=f'(E')$.

Proposition 2.3

([18, pages 36–37]) The following statements are satisfied:

• (1) $(X\ni P)$ is a three-dimensional ${\mathbb Q}$–factorial toric terminal singularity if and only if $(X\ni P)\cong ({\mathbb C}^3\ni 0)/{\mathbb Z}_r(q,-1,1)$, where $\gcd (r,q)=1;$

• (2) $(X\ni P)$ is a three-dimensional non-${\mathbb Q}$–factorial toric terminal singularity if and only if $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$.

Theorem 2.4

([17]) Let $(X\ni P)$ be a three-dimensional cyclic singularity of type $\frac{1}{r}(a_1,a_2,a_3)$. Then $(X\ni P)$ is a canonical singularity if and only if one of the following holds:

$(1) \ a_1+a_2+a_3\equiv 0({\text {mod}} r);$

$(2)\ a_i+a_j\equiv 0({\text {mod}} r)$ for some $i\ne j;$

(3) $(X\ni P)$ has type $\frac{1}{9}(1,4,7)$ or type $\frac{1}{14}(1,9,11)$.

Proposition 2.5

Let $f:(Y,E)\rightarrow (X\ni P)$ be a toric canonical blow-up of three-dimensional toric terminal singularity, $f(E)=C$ and $\dim C=1$. Then we have the following statements.

(1) Let $(X\ni P)$ be a ${\mathbb Q}$-factorial singularity, that is, it is $({\mathbb C}^3_{x_1x_2x_3}\ni 0)/{\mathbb Z}_r(-1,-q,1)$, where $\gcd (r,q)=1$, $0<q\le r-1$ and $r\ge 1$. Determine the numbers u, v by the equality $uq+vr=1$, where $0\le u\le r-1$ and $u,v\in {\mathbb Z}$. Consider the cone $\sigma$ defining $(X\ni P)$ (see example 2.2 (1)). Let $(w_1,w_2,w_3)$ be a primitive vector defining f.

Then we have one of the two following cases up to permutation of coordinates: either 2A) $C=\{x_1=x_2=0\}/{\mathbb Z}_r$, $(w_1,w_2,w_3)=(1,w_2,0)$, or 2B) $C=\{x_2=x_3=0\}/{\mathbb Z}_r$, $(w_1,w_2,w_3)=(0,w_2,1)$. The variety Y has the singularities $\frac{1}{r}(-1,w_2-q,1)$, $\frac{1}{rw_2}(-1+uw_2,-uw_2,1)$ in Case 2A) and $\frac{1}{r}(-1,-w_2-q,1)$, $\frac{1}{rw_2}(uw_2,-uw_2-1,1)$ in Case 2B).

Converse is also true: every such numbers $(w_1,w_2,w_3)$ define a canonical blow-up.

A general element of the linear system $|-K_Y|$ has Du Val singularities.

Let Q be a central point of second singularity in each of the two cases. Then $Q\in {\text {CS}}(Y)$ if and only if $r\ge 2$. Therefore f is a terminal blow-up if and only if it is the blow-up of the ideal of the curve C [8].

(2) Let $(X\ni P)$ be a non-${\mathbb Q}$-factorial singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. Then $C=\{x_1=x_2=x_3=0\}$ up to permutation of coordinates, f is induced by the blow-up of $({\mathbb C}^4,0)$ with weights $(w_1,w_2,w_1+w_2,0)$, where $w_1=1$, $w_2>0$ or $w_1>0, w_2=1$. Converse is also true: every such numbers induce a canonical blow-up. A general element of the linear system $|-K_Y|$ has Du Val singularities.

The morphism f is a terminal blow-up if and only if $(w_1,w_2,w_3,w_4){=}(1,1,2,0)$.

Proof

Let us prove (1). Put $e'_1=e_1$, $e'_2=e_2$ and $e'_3=e_1+qe_2+re_3$ (see Example 2.2 (1)). Then $w=w_ie'_i+w_je'_j$ for some $i<j$ and $w_i$, $w_j\in {\mathbb Z}_{\ge 1}$. We have $Y=T_N({\Delta })$ and

$$ {\Delta }=\{\langle e'_k,e'_i,w\rangle , \langle e'_k,e'_j,w\rangle , \text {their faces}\}, $$

where k is a third index other than the indices i and j. Consider an induced blow-up of general hyperplane section passing through the general point of C. Then $w_1=1$ or $w_2=1$. Now the statement is proved by a simple enumeration of the indices i and j. As an example, consider $i=1$, $j=2$. There are the two possibilities of weights: $(w_1,1,0)$ and $(1,w_2,0)$. Let $(w_1,1,0)$. The variety Y is covered by two affine charts with singularities of types $\frac{1}{r}(-q,qw_1-1,1)$ and $\frac{1}{rw_1}(-w_1,qw_1-1,1)$. By Theorem 2.4 applied to the second singularity it follows that either $q=1$, or $w_1=1$, or $r=1$. All these variants are realized, it is Case (2A). The possibility $(1,w_2,0)$ is considered similarly.

The proper transform of $\{x_2=0\}/{\mathbb Z}_r(-1,-q,1)$ is Du Val element of $|-K_Y|$.

The statement $Q\in {\text {CS}}(Y)$ is obvious if we consider a blow-up with the weights $(-1+uw_2, (r-u)w_2, 1)$ in Case (2A) and $(uw_2,(r-u)w_2-1,1)$ in Case (2B) provided that $r\ge 2$.

Statement (2) obviously follows from Example 2.2 (2). The proper transform of $\{x_1^{w_2}+x_2=0\}|_X$ ($\{x_1+x_2^{w_1}=0\}|_X$) is Du Val element of $|-K_Y|$ for the first (second) possibility.   $\square$

Proposition 2.6

Let $f:(Y,E)\rightarrow (X\ni P)$ be a toric canonical blow-up of three-dimensional toric terminal point, where $f(E)=P$. Then we have the following statements.

(1) Let $(X\ni P)$ be a smooth point. Then f is a weighted blow-up with weights $(w_1,w_2,1)$, $(l,l-1,2)$, (15, 10, 6), (12, 8, 5), (10, 7, 4), (9, 6, 4), (8, 5, 3), (7, 5, 3), (6, 4, 3), (5, 3, 2) or (9, 5, 2) in some coordinate system, where $l \ge 3$. Converse is also true: every such weights define a canonical blow-up. In all cases, except case (9, 5, 2), a general element of the linear system $|-K_Y|$ has Du Val singularities. In case (9, 5, 2) we have

$$\begin{aligned} \min \{m|\exists D\in |-mK_Y|\ \text {such that} \ (Y,(1/m)D) \text {has canonical singularities}\}=3. \end{aligned}$$

The morphism f is a terminal blow-up if and only if it is a weighted blow-up with weights $(w_1,w_2,1)$ in some coordinate system, where $\gcd (w_1,w_2)=1$.

(2) Let $(X\ni P)$ be a ${\mathbb Q}$-factorial singularity of an index $\ge 2$, that is, it is of type $\frac{1}{r}(-1,-q,1)$, where $\gcd (r,q)=1$, $0<q\le r-1$ and $r\ge 2$. Let us consider the cone $\sigma$ defining the singularity $(X\ni P)$ (see Example 2.2 (1)). Determine the numbers u, v by the equality $uq+vr=1$, where $0\le u\le r-1$ and $u,v\in {\mathbb Z}$. Let $(w_1,w_2,w_3)$ be a primitive vector defining f.

Then we have one of the two following cases: either 2A) $(w_1,w_2,w_3)=(1,w_2,w_3)$, $w_3\le \min (r-1,\frac{rw_2-1}{q})$ up to permutation of the numbers $w_1$ and $w_2$ provided that $q=1$, or 2B) $(w_1,w_2,w_3)=(w_1,w_2,w_1+w_2-1)$, $w_1\ge 2$, $w_2\ge 2$, $0\le w_1(r-1)-w_2\le r-2$, $q=r-1$. Converse is also true: every such numbers $(w_1,w_2,w_3)$ define a canonical blow-up. A general element of the linear system $|-K_Y|$ has Du Val singularities.

The morphism f is a terminal blow-up if and only if it is a weighted blow-up with weights $(u,1,r-u)$ [8].

(3) Let $(X\ni P)$ be a non-${\mathbb Q}$-factorial singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. Then f is induced by the weighted blow-up of $({\mathbb C}^4,0)$ with weights $(w_1,w_2,w_3,w_4)$ up to analytical isomorphism of $({\mathbb C}^4,0)$, where $1+w_2=w_3+w_4$, $w_1=1$. Converse is also true: every such weights induce a canonical blow-up. A general element of the linear system $|-K_Y|$ has Du Val singularities.

The morphism f is a terminal blow-up if and only if $(w_1,w_2,w_3,w_4)=(1,1,1,1)$ [2].

Proof

Let us prove (1). Now we classify canonical blow-ups. To be definite, assume that $w_1\ge w_2\ge w_3$, where $(w_1,w_2,w_3)$ are primitive weights of f. By $P_1$, $P_2$ and $P_3$ denote the zero-dimensional orbits (points) of Y. These points have types $\frac{1}{w_1}(w_2,w_3,w_1-1)$, $\frac{1}{w_2}(w_1,w_3,w_2-1)$ and $\frac{1}{w_3}(w_1,w_2,w_3-1)$ respectively.

Assume that Cases (1) and (1) of Theorem 2.4 are satisfied at the points $P_1$ and $P_2$ respectively. Then $w_1=w_2+w_3-1$ and $w_2|(2w_3-2)$. Thus we obtain the weights (l, l, 1), where $l\ge 1$ and $(3w_3-3,2w_3-2,w_3)$, where $w_3\ge 2$. For the second possibility, the singularity is of type $\frac{1}{w_3}(3,2,1)$ at the point $P_3$, therefore $w_3\le 6$, and it is easy to prove that every value $w_3=2,\ldots ,6$ is realized.

Assume that Cases (1) and (2) of Theorem 2.4 are satisfied at the points $P_1$ and $P_2$ respectively. As above we obtain $w_1=w_2+w_3-1$ and have one of the following possibilities: (i1) $w_3=1$, $w_3=2$ or (i2) $2w_3-1=w_2$, $w_2=1,\ldots ,4$. These possibilities are realized.

Assume that Cases (1) and (3) of Theorem 2.4 are satisfied at the points $P_1$ and $P_2$ respectively. Then $w_1=w_2+w_3-1$. Let the singularity be of type $\frac{1}{9}(1,4,7)=\frac{1}{9}(5,2,8)$ at the point $P_2$, in particular, $w_2=9$. Hence $w_3=2$ or $w_3=5$. It follows easily that these possibilities are not realized. Let the singularity be of type $\frac{1}{14}(1,9,11)=\frac{1}{14}(5,3,13)$ at the point $P_2$, in particular, $w_2=14$. Hence $w_3=3$ or $w_3=5$. It follows easily that these possibilities are not realized.

Assume that Cases (2) and (1) of Theorem 2.4 are satisfied at the points $P_1$ and $P_2$ respectively. Then we obtain the two possibilities: (i) $w_1=w_2+w_3$, $w_2=2w_3-1$, $w_3=2,3$ or (ii) $w_3=1$. These possibilities are realized.

Assume that Cases (2) and (2) of Theorem 2.4 are satisfied at the points $P_1$ and $P_2$ respectively. As above it is easy to prove that new weights do not appear.

Assume that Cases (2) and (3) of Theorem 2.4 are satisfied at the points $P_1$ and $P_2$ respectively. As above it is easy to prove that this case is not realized.

Assume that Cases (3) of Theorem 2.4 are satisfied at the point $P_1$. Then $(w_1,w_2,w_3)=(9,5,2)$ or (14, 5, 3). It is obvious that only the first possibility is realized.

For any weights obtained, except case (9, 5, 2), we can easily find a surface $S\subset X$ with Du Val singularity at the point P such that $a(S,E)=0$. For example, the surface S is given (locally at the point P) by the equations $x_1x_2+x_3^{w_1+w_2}=0$ and $x_1^2+x_2^3+x_2x_3^3=0$ for cases $(w_1,w_2,1)$ and (5, 3, 2) respectively. Therefore $S_Y\in |-K_Y|$ has Du Val singularities.

In case (9, 5, 2) the variety Y has the two non-terminal isolated singularities at the points $P_1$ and $P_2$ (${\text {CS}}(Y)=\{P_1, P_2\}$). Let $C\subset E={\mathbb P}(9,5,2)$ be a curve not passing through the points $P_1$ and $P_2$. Then a (quasihomogeneous) degree of C is at least 45 since it must be divided by 9 and 5. Hence $m\ge 3$, and the required element D is the proper transform of $x_1^5+x_2^9+x_3^{23}=0$. The other statements of (1) are obvious.

Let us prove (2). Now we classify canonical blow-ups. The variety Y is covered by three affine charts with singularities of types $\frac{1}{w_3}(-w_1,-w_2,1)$, $\frac{1}{rw_2-qw_3}(-w_1+uw_2+vw_3,-uw_2-vw_3,1)$ and $\frac{1}{rw_1-w_3}(-w_1,qw_1-w_2,1)$ respectively. The corresponding zero-dimensional orbits of Y are denoted by $P_1$, $P_2$ and $P_3$. Note that $rw_1-w_3, rw_2-qw_3\in {\mathbb Z}_{\ge 1}$. Obviously, $a(S,0)=\frac{1}{r}(w_3+rw_2-qw_3+rw_1-w_3)-1$. The minimal discrepancy of $(X\ni P)$ is equal to $\frac{1}{r}$. If $a(S,0)=\frac{1}{r}$, that it is easy to calculate that f is a terminal blow-up, that is, a weighted blow-up with weights $(u,1,r-u)$ [8]. Therefore we suppose that $a(S,0)>\frac{1}{r}$.

Since Y has canonical singularities, then for some $j\in \{1,2,3\}$ we have the inequality $\frac{1}{r}\ge a(S,0)/N_j$ and one of the two following requirements: either $P_j\in {\text {CS}}(Z)$, or the singularity at the point $P_j$ is of type $\frac{1}{N_j}(1,-1,0)$, where $N_j\ge 2$, $N_1=w_3$, $N_2=rw_1-w_3$, $N_3=rw_2-qw_3$. This is called Property $R_j$. Note if $j=3$ then $w_1=1$. Therefore we suppose that $j\le 2$.

Let $w_1=\max \{w_1,w_2,w_3\}$. Assume that Case (1) of Theorem 2.4 is satisfied at the point $P_2$. Then $q=1$ and $w_2=1$. Assume that Case (2) of Theorem 2.4 is satisfied at the point $P_2$. Then, either $w_1=w_2=w_3=1$, or $q=2$, $w_1=w_2$, $w_1\ge 2$, $r\ge 3$. Since the inequality of Property $R_2$ holds then the second possibility is not realized. It is not hard to prove that Case (3) of Theorem 2.4 is not realized at the point $P_2$.

Let $w_2=\max \{w_1,w_2,w_3\}$. Property $R_1$ is not realized. Therefore Property $R_2$ holds. Then $w_2=w_3$, and we have $w_1=1$ by Theorem 2.4 for the point $P_1$.

Let us consider the last case $w_3>\max \{w_1,w_2\}$. The possibility $w_1=1$ holds. Therefore we suppose that $w_1\ge 2$. If $w_2=1$ then Theorem 2.4 for the point $P_2$ implies $q=1$. Therefore we suppose that $w_2\ge 2$.

Assume that Case (1) of Theorem 2.4 is satisfied at the point $P_1$. Then $w_1+w_2-1=w_3$. If the inequality of Property $R_1$ holds then $q=r-1$. Therefore we suppose that Property $R_2$ holds and $N_2>w_3$. It is not hard to prove that Case (3) of Theorem 2.4 is not realized at the point $P_2$. If Case (1) of Theorem 2.4 is satisfied at the point $P_2$ then the inequality of Property $R_2$ implies that $(q-1)w_1-w_2+1=0$, but this equality contradicts the same inequality. Therefore the singularity is of type $\frac{1}{N_2}(1,-1,0)$ at the point $P_2$. Therefore $w_1=1$. We obtain the contradiction.

Assume that Case (2) of Theorem 2.4 is satisfied at the point $P_1$. Then $w_1+w_2=w_3$ and Property $R_2$ holds. Let Case (3) of Theorem 2.4 be satisfied at the point $P_2$. Then it is not hard to prove that $(w_1,w_2,w_3,r)=(2,2q+5,2q+7,q+8)$. We obtain a contradiction with Theorem 2.4 for the point $P_3$ since $0<uw_2+vw_3\le N_3$. Let Case (1) of Theorem 2.4 be satisfied at the point $P_2$. The inequality of Property $R_2$ implies that $(q-1)w_1-w_2+1=0$, but this equality contradicts the same inequality. Therefore the singularity is of type $\frac{1}{N_2}(1,-1,0)$ at the point $P_2$. Considering two possibilities: $N_2\le w_1$ and $N_2>w_1$, it is easy to obtain a contradiction.

Now, applying the blow-up classification obtained, we can prove that the proper transform of the divisor

$$S_k=\{x_k=0\}/{\mathbb Z}_r \subset ({\mathbb C}^3_{x_1x_2x_3},0)/{\mathbb Z}_r(-1,-q,1)$$

is Du Val element of $|-K_Y|$ for some k. The other statements of 2) are obvious.

Let us prove (3). Consider Example 2.2 (2). Now we classify canonical blow-ups. Obviously, $a(S,0)=w_1+w_2-1=w_3+w_4-1$. The variety Y is covered by three affine charts with singularities of types $\frac{1}{w_1}(w_3,w_4,-1)$, $\frac{1}{w_2}(w_3,w_4,-1)$, $\frac{1}{w_3}(w_1,w_2,-1)$ and $\frac{1}{w_4}(w_1,w_2,-1)$ respectively. The minimal discrepancy of $(X\ni P)$ is equal to 1. If $a(S,0)=1$ then it is easy to calculate that f is a terminal blow-up induced by the weighted blow-up with weights (1, 1, 1, 1) [2]. Therefore we suppose that $a(S,0)>1$. Since Y has canonical singularities then $1\ge a(S,0)/w_j$ for some j. Hence $w_i=1$ for some $i\ne j$ such that $w_i+w_j-1=a(S,0)$. The proper transform of $\{x_i^{w_j}+x_j=0\}|_X$ is Du Val element of $|-K_Y|$. The other statements of (3) are obvious.   $\square$

Definition 2.7

Let $(X\ni P)$ be an n-dimensional ${\mathbb Q}$-factorial toric singularity. Then $(X\ni P)\cong ({\mathbb C}^n\ni 0)/G$, where G is an abelian group acting freely in codimension 1. The singularity $({\mathbb C}^n\ni 0)/G$ is given by the simplicial cone $\sigma _G$ in the lattice $N={\mathbb Z}^n$.

Let a power series (polynomial) $\varphi =\sum _{m}a_{m}x^m \in {\mathbb C}[[x_{1},x_{2},\ldots ,x_{n}]]$ be G-semiinvariant.

The Newton polyhedron $\Gamma _{+}(\varphi )$ in ${\mathbb R}^n$ is the convex hull of the set

$$ \bigcup _{x^m\in \varphi } (m+\sigma _G^{\vee }),\ \text {where}\ \sigma _G^{\vee }\ \text {is a dual cone in}\ M_{{\mathbb R}}. $$

For any face $\gamma$ of $\Gamma _{+}(\varphi )$ we define

$$\begin{aligned} \varphi _{\gamma }=\sum _{m\in \gamma }a_{m}x^m. \end{aligned}$$

The function $\varphi$ is said to be non-degenerate if, for any compact face $\gamma$ of the Newton polyhedron, the polynomial equation $\varphi _{\gamma }=0$ defines a smooth hypersurface in the complement of the set $x_1x_2\ldots x_{n}=0$. The effective Weil divisor D on X is said to be non-degenerate if the G-semiinvariant polynomial $\varphi$ defining D in ${\mathbb C}^n$ is non-degenerate.

For any effective Weil divisor D there exists the fan $\Delta$ depending on Newton polyhedron $\Gamma _{+}(\varphi )$ such that $T_N(\Delta )$ is a smooth variety and a toric birational morphism $\psi :T_N(\Delta ) \rightarrow {\mathbb C}^n$ is a resolution of non-degenerate singularities of D. So, $\psi$ is said a partial resolution of (X, D). In particular, if D is a non-degenerate boundary then $\psi$ is a toric log resolution of the pair (X, D). If $(X\ni P)$ is a smooth variety then this statement was proved in the paper [27]. Note that the proof from the paper [27] is rewritten immediately in our case if we will use our Newton polyhedron instead of standard Newton polyhedron.

The next Theorems 2.8 and 2.9 are criteria of the characterization of toric plt and canonical blow-up respectively. They explicitly show a nature of non-toric contractions.

Theorem 2.8

Let $f:(Y,E) \rightarrow (X \ni P)$ be a plt blow-up of ${\mathbb Q}$-factorial toric singularity, and let f(E) be a toric subvariety. Then f is a toric morphism (under a suitable identification) if and only if there exists an effective non-degenerate Weil divisor D on $(X\ni P)$ and a number $d>0$ with the following properties:

• (1) $a(E,dD)=-1;$

• (2) E is a unique exceptional divisor of (X, dD) with discrepancy $\le -1$ and $\llcorner dD \lrcorner =0$.

Proof

First let us prove the necessary condition. Let $D_Y\in |-n(K_Y+E)|$ be a general element for $n\gg 0$. Put $D=f(D_Y)$ and $d=\frac{1}{n}$. Then $K_Y+E+dD_Y=f^*(K_X+dD)$ is a plt divisor. Since $D_Y$ is a general divisor by construction, then D is an irreducible reduced non-degenerate divisor.

Finally let us prove the sufficient condition. Consider the toric log resolution $\psi :Z\rightarrow X$ of (X, dD). Write

$$ K_Z+dD_Z+\sum a_iE_i=\psi ^*\Big (K_X+dD\Big ). $$

By theorem assertion $(Z,dD_Z+\sum a_iE_i)$ is a plt pair. Therefore $E\subset {\text {Exc}}\psi$.

Considering corresponding fans (see [24]) we have the composition of toric log flips $Z\dashrightarrow Z'$ over $(X\ni P)$ such that the (induced) toric divisorial contraction $\psi ':Z'\rightarrow (X\ni P)$ is isomorphic to $\psi '_1\circ \psi '_2$, where $\psi '_1$, $\psi '_2$ are toric divisorial contractions and $E={\text {Exc}}\psi '_1$. Therefore f and $\psi '_1$ are isomorphic by Remark 1.9 (5).   $\square$

Theorem 2.9

Let $f:(Y,E)\rightarrow (X\ni P)$ be a canonical blow-up of ${\mathbb Q}$-factorial toric singularity, and let f(E) be a toric subvariety. Then f is a toric morphism (under a suitable identification) if and only if there exists an effective non-degenerate Weil divisor D on $(X\ni P)$ and a number $d>0$ with the following properties:

• (1) $a(E,dD)=0;$

• (2) (X, dD) has canonical singularities and $\llcorner 2dD \lrcorner =0$.

Proof

First let us prove the necessary condition. Let $D_Y\in |-nK_Y|$ be a general element for $n\gg 0$. Put $D=f(D_Y)$ and $d=\frac{1}{n}$. Then the divisor $K_Y+dD_Y=f^*(K_X+dD)$ has canonical singularities. Since $D_Y$ is a general divisor by construction, then D is an irreducible reduced non-degenerate divisor.

Finally let us prove the sufficient condition. Consider the toric log resolution $\psi :Z\rightarrow X$ of (X, dD). Write

$$ K_Z+dD_Z+\sum a_iE_i=\psi ^*\Big (K_X+dD\Big ). $$

By theorem assertion $(Z,dD_Z+\sum a_iE_i)$ is a terminal pair. Therefore $E\subset {\text {Exc}}\psi$. Considering corresponding fans (see [24]) we have the composition of toric log flips $Z\dashrightarrow Z'$ over $(X\ni P)$ such that the (induced) toric divisorial contraction $\psi ':Z'\rightarrow (X\ni P)$ is isomorphic to $\psi '_1\circ \psi '_2$, where $\psi '_1$, $\psi '_2$ are toric divisorial contractions and $E={\text {Exc}}\psi '_1$. Therefore f and $\psi '_1$ are isomorphic by Proposition 1.1.   $\square$

Definition 2.10

The subvariety Y is said to be a non-toric subvariety of the toric pair (X, D), if there is not any toric structure of X such that (X, D) is a toric pair and Y is a toric subvariety.

Example 2.11

Consider the toric variety $X={\mathbb P}_{x_1x_2x_3}(1,2,3)$.

(1) Let $D=0$. The point P is a non-toric subvariety of (X, D) if and only if $P=(0:1:a)$, where $a\ne 0$. The irreducible curve C is a non-toric subvariety of (X, D) if and only if $C\ne \{x_1=0\}$, $C\ne \{x_2+ax_1^2=0\}$ and $C\ne \{x_3+ax_2x_1+bx_1^3=0\}$.

(2) Let $D=\{x_1=0\}+\{x_2=0\}$. The point P is a non-toric subvariety of (X, D) if and only if $P=(0:1:a)$, where $a\ne 0$. The irreducible curve C is a non-toric subvariety of (X, D) if and only if $C\ne \{x_1=0\}$, $C\ne \{x_2=0\}$ and $C\ne \{x_3+ax_2x_1+bx_1^3=0\}$.

(3) Let $D=\{x_1=0\}+\{x_2=0\}+\{x_3=0\}$. The point P is a non-toric subvariety of (X, D) if and only if $P\ne (1:0:0)$, $P\ne (0:1:0)$ and $P\ne (0:0:1)$. The irreducible curve C is a non-toric subvariety of (X, D) if and only if $C\ne \{x_1=0\}$, $C\ne \{x_2=0\}$ and $C\ne \{x_3=0\}$.

Next Theorems 2.12 and 2.13 are two-dimensional analogs of main theorems. Their proofs clearly describe the main method used in this paper.

Theorem 2.12

([22]) Let $f:(Y,E) \rightarrow (X \ni P)$ be a plt blow-up of two-dimensional toric singularity. Then f is a toric morphism (under a suitable identification).

Proof

A two-dimensional toric singularity is always ${\mathbb Q}$-factorial. Let f be a non-toric morphism (up to identification). Let $D_Y\in |-n(K_Y+E)|$ is a general element of $n\gg 0$. Put $D_X=f(D_Y)$ and $d=\frac{1}{n}$. Then $(X,dD_X)$ is a log canonical pair, $a(E,dD_X)=-1$ and E is a unique exceptional divisor with discrepancy $-1$.

By Criterion 2.8 there exists a toric divisorial contraction $g:Z\rightarrow X$ with the following properties.

• (A) The exceptional set ${\text {Exc}}g=S$ is an irreducible divisor ($S\cong {\mathbb P}^1$), the divisors S and E define the different discrete valuations of the function field $\mathcal K(X)$.

• (B) By $\Gamma$ denote the center of E on S. Then the point $\Gamma$ is a non-toric subvariety of Z for any toric structure of $(X \ni P)$. In the other words, $\Gamma$ is a non-toric subvariety of the toric pair $(S,{\text {Diff}}_S(0))$.

Condition (B) implies that the surface Z has the two singular points $P_1$ and $P_2$, which lie on the curve S. Also $\Gamma$ is a non-toric point of $(S,{\text {Diff}}_S(0))\cong ({\mathbb P}^1, \frac{n_1-1}{n_1}P_1+\frac{n_2-1}{n_2}P_2)$, where $n_1\ge 2, n_2 \ge 2$. Write

$$ K_Z+dD_Z+aS=g^*\big (K_X+dD_X\big ), $$

where $a<1$. Hence

$$ a\big (E,S+dD_Z\big )< a\big (E,aS+dD_Z\big )=-1. $$

Therefore $K_Z+S+dD_Z$ is not a log canonical divisor at the point $\Gamma$ and is an anti-ample over X divisor. Hence, by the inversion of adjunction, $K_S+{\text {Diff}}_S(dD_Z)$ is not a log canonical divisor at the point $\Gamma$ and is an anti-ample divisor. We obtain the contradiction

$$\begin{aligned} 0>\deg \big (K_S+{\text {Diff}}_S(dD_Z)\big )>-2+\frac{n_1-1}{n_1}+\frac{n_2-1}{n_2}+1\ge 0. \end{aligned}$$

   $\square$

Theorem 2.13

[16] Let $f:(Y,E)\rightarrow (X\ni P)$ be a canonical blow-up of two-dimensional toric singularity. Then $(X\ni P)$ is a smooth point, and f is a weighted blow-up with weights $(1,\alpha )$ (under a suitable identification).

Proof

Theorem assertion implies that $(X\ni P)$ is a terminal point, therefore it is smooth.

Assume that f is a toric morphism then f is a weighted blow-up of the smooth point with weights $(\beta ,\alpha )$. Since Y is Du Val surface then $\alpha =1$ or $\beta =1$.

Let f be a non-toric morphism (up to identification). Let $D_Y\in |-nK_Y|$ be a general element for $n\gg 0$. Put $D_X=f(D_Y)$ and $d=\frac{1}{n}$. The pair $(X,dD_X)$ has canonical singularities and $a(E,dD_X)=0$.

By Criterion 2.9 there exists a toric divisorial contraction $g:Z\rightarrow X$ with the following properties.

• (A) The exceptional set ${\text {Exc}}g=S$ is an irreducible divisor ($S\cong {\mathbb P}^1$), the divisors S and E define the different discrete valuations of the function field $\mathcal K(X)$.

• (B) By $\Gamma$ denote the center of E on S. Then the point $\Gamma$ is a non-toric subvariety of Z for any toric structure of $(X \ni P)$. In the other words, $\Gamma$ is a non-toric subvariety of the toric pair $(S,{\text {Diff}}_S(0))$.

Condition (B) implies that the surface Z has the two singular points $P_1$ and $P_2$, which lie on the curve S. Also $\Gamma$ is a non-toric point of $(S,{\text {Diff}}_S(0))\cong ({\mathbb P}^1, \frac{n_1-1}{n_1}P_1+\frac{n_2-1}{n_2}P_2)$, where $n_1\ge 2, n_2 \ge 2$. Write

$$ K_Z+dD_Z+S=g^*\big (K_X+dD_X\big )+(a(S,dD_X)+1)S, $$

where $a(S,dD_X)\ge 0$. Since S is (locally) Cartier divisor at the point $\Gamma$, then

$$ a\big (E,S+dD_Z\big )\le a\big (E,dD_X\big )-1=-1. $$

Therefore $K_Z+S+dD_Z$ is not a plt divisor at the point $\Gamma$ and is an anti-ample divisor over X. Hence, by the inversion of adjunction $K_S+{\text {Diff}}_S(dD_Z)$ is not a klt divisor at the point $\Gamma$ and is an anti-ample divisor. We obtain the contradiction

$$\begin{aligned} 0>\deg \big (K_S+{\text {Diff}}_S(dD_Z)\big )\ge -2+\frac{n_1-1}{n_1}+\frac{n_2-1}{n_2}+1\ge 0. \end{aligned}$$

   $\square$

Example 2.14

Theorems 2.12 and 2.13 cannot be generalized in dimension at least three for divisorial contraction to a point. Consider the blow-up $g:Z\rightarrow (X\ni P)$ with the weights $(1,\ldots ,1)$, where $(X\ni P)\cong ({\mathbb C}^n_{x_1\ldots x_n}\ni 0)$ and consider the divisors $D=\{x_1^2+\cdots +x_n^2=0\}$, $T^i=\{x_i=0\}$, where $i=1,\ldots ,n$ and $n\ge 3$. The exceptional set ${\text {Exc}}g=S$ is isomorphic to ${\mathbb P}^{n-1}$, $Q=S\cap D_Z$ is a smooth quadric. Let $\widetilde{g}:\widetilde{Z}\rightarrow Z$ be the standard blow-up of the ideal $I_Q$. By the base point free theorem [9] the linear system $|mD_{\widetilde{Z}}|$ gives a divisorial contraction $\varphi :\widetilde{Z}\rightarrow Y$, which contracts the divisor $S_{\widetilde{Z}}\cong {\mathbb P}^{n-1}$ for $m\gg 0$. Since the divisor $K_{\widetilde{Z}}+S_{\widetilde{Z}}+\sum _{i=1}^nT^i_{\widetilde{Z}}\sim 0/Y$ has log canonical singularities, then by Shokurov’s criterion on the characterization of toric varieties for divisorial contractions to a ${\mathbb Q}$-factorial singularity [11, Theorem 18.22], the morphism $\varphi$ is toric. Hence Y has only one singularity and its type is $\frac{1}{r}(1,\ldots ,1)$. Let l be a straight line in a general position in $S_{\widetilde{Z}}$. Considering $\varphi$ we have $S_{\widetilde{Z}}\cdot l=-r$, and considering $g\circ \widetilde{g}$ we have $S_{\widetilde{Z}}\cdot l=-3$, hence $r=3$.

We obtain a non-toric divisorial contraction $f:Y\rightarrow (X\ni P)$. The variety Y has only one singularity and its type is $\frac{1}{3}(1,\ldots ,1)$. Thus, if $n\ge 4$, then Y is a terminal variety, and if $n=3$, then Y is a canonical non-terminal variety (cf. [6]). The blow-up f is plt since the exceptional set ${\text {Exc}}f$ is a cone over a smooth $(n-2)$-dimensional quadric.

We will apply the following special case of Shokurov’s criterion on the characterization of toric varieties.

Proposition 2.15

Let $f:(X,D)\rightarrow (Z\ni P)$ be a small contraction of the ${\mathbb Q}$-factorial threefold X. Assume that $D=\sum _{i=1}^rD_i$, where $D_i$ is a prime divisor for each i. Assume that $K_X+D$ is a log canonical divisor, $-(K_X+D)$ is a f-nef divisor and ${\text {Exc}}f=C$ is an irreducible curve $(\rho (X/Z)=1)$. Then $r\le 4$. Moreover, the equality holds if and only if the pair $(X/Z\ni P,D)$ is analytically isomorphic to a toric pair, in particular, $K_X+D\sim 0/Z$.

Proof

If the pair $(X/Z\ni P,D)$ is analytically isomorphic to a toric pair then all statements immediately follow from the description of toric log flips [24]. Let $r\ge 4$. Let the divisor $K_X+D'$ be a ${\mathbb Q}$-complement of $K_X+D$. It exists, since we can add to the divisor D the necessary number of general hyperplane sections of X. So, by abundance theorem [11, Theorem 8.4] the ${\mathbb Q}$-complement $D'$ required is constructed for our contraction $(X/Z\ni P,D)$.

Put $D'=\sum d_iD_i'$. We will prove that $D'=D$. For any ${\mathbb Q}$-Weil divisor $B=\sum b_iB_i$ we define $||B||=\sum b_i$. Put

$$ D^{{\text {hor}}}=\sum _{i:D'_i\cdot C>0} d_iD'_i \ \ \ \text {and}\ \ \ D^{{\text {vert}}}=\sum _{i:D'_i\cdot C\le 0} d_iD'_i. $$

Let $f^+:X^+\rightarrow Z$ be a log flip of f and ${\text {Exc}}f^+=C^+$.   $\square$

Lemma 2.16

([23, Lemma 2.10]) We have $||D^{{\text {hor}}}||=||D^{{\text {vert}}}||=2$. Hence, $D=D'$. Moreover, $C\not \subset {\text {Supp}}D^{{\text {hor}}}$, $C^+\not \subset {\text {Supp}}(D^{{\text {vert}}})^+$ and $D'_i\cdot C\ne 0$ for all i.

Proof

Since $K_X+D$ is a log canonical divisor then $||D^{{\text {vert}}}||\le 2$. Since $K_{X^+}+D^+$ is a log canonical divisor then $||D^{{\text {hor}}}||\le 2$. The statements remained are obvious.   $\square$

Let S be an irreducible component of the divisor $D^{{\text {vert}}}$ and let $F=D-S$. The divisorial log contraction $(S,{\text {Diff}}_S(F))\rightarrow (f(S)\ni P)$ is toric by the two-dimensional Shokurov’s criterion on the characterization of toric varieties [26, Theorem 6.4]. In particular, it is a toric blow-up of cyclic singularity. Thus, the singularities of X are toric by three-dimensional Shokurov’s criterion on the characterization of toric varieties for ${\mathbb Q}$-factorial singularities [11, Theorem 18.22]. Replacing X by $X^+$ it can be assumed that $-(K_X+S)$ is a f-ample divisor and $S\cdot C<0$.

In order to prove the proposition we will apply some modification, which is a toric one by its nature. After it we will get some small contraction, which is analytically isomorphic to a small toric contraction of Example 2.2 (2). Therefore the initial contraction is a toric up to analytical isomorphism.

Now, taking toric blow-ups of X (every time we take an one blow-up with a unique exceptional divisor that has a minimal discrepancy of a singularity considered and consider two extremal rays on a variety obtained), it can be assumed that S is a smooth surface, and X is a smooth variety outside the curves C. The condition that $-(K_X+S)$ is f-ample holds is preserved, since the discrepancies of exceptional divisors of (X, S) are less than and equal to 0. In some analytical neighborhood of every point of C the variety X is analytically isomorphic to $\frac{1}{k}(q,1)\times {\mathbb C}^1$, where $(k,q)=1$.

Assume that $k\ge 2$. Consider a natural cyclic cover $\psi :\overline{X}\rightarrow X$ of degree k. Put $\overline{C}=\psi ^{-1}(C)$ and let $\overline{Z}$ be the normalization of Z in the function field of $\overline{X}$. Let $\overline{f}:\overline{X}\rightarrow (\overline{Z}\ni \overline{P})$ be the induced small contraction of the curve $\overline{C}$. Thus we can assume that $k=1$, that is, X is a smooth variety.

Since $-K_S$ is a f-ample divisor then $f:S\rightarrow f(S)$ is the contraction of the (−1) curve C and $(K_X+S)\cdot C=-1$. We have $S\cdot C=-m$, $K_X\cdot C=m-1$ for some $m\in {\mathbb Z}_{\ge 1}$.

Let $m\ge 2$. Using the natural section of ${\mathcal O}_X(S)$ we can construct a degree m-cyclic cover $\varphi :\widetilde{X}\rightarrow X$ ramified along S (cf. [11, Theorem 5.4]). Let $\widetilde{C}=\varphi ^{-1}(C)$ and let $\widetilde{Z}$ be the normalization of Z in the function field of $\widetilde{X}$. Let $\widetilde{f}:\widetilde{X}\rightarrow (\widetilde{Z}\ni \widetilde{P})$ be the induced small contraction of the curve $\widetilde{C}$. By the ramification formula

$$ K_{\widetilde{X}}\cdot \widetilde{C}=\varphi ^*\Big (K_X+\frac{m-1}{m} S\Big ) \cdot \widetilde{C}= K_X\cdot C+\frac{m-1}{m}S\cdot C=0. $$

Thus we can assume that f is a small flopping contraction with respect to $K_X$ ($K_X\cdot C=0$), that is, we can assume that $m=1$.

Since the minimal discrepancy of three-dimensional terminal non-cDV singularity is strict less than 1 then $(Z\ni P)\cong (g=0\subset ({\mathbb C}^4,0))$ is an isolated cDV (terminal) singularity. Note that $(D_1+D_2)\cdot C=(D_3+D_4)\cdot C=0$ up to permutation of components of D. Hence $L_1$ and $L_2$ are Cartier divisors, where $L_1=f(D_1)+f(D_2)$ and $L_2=f(D_3)+f(D_4)$. By Bertini theorem [12, Theorem 4.8] the pair $(Z\ni P,H+L_i)$ is log canonical for any $i=1,2$, where H is a general hyperplane section passing through the point P. By the inversion of adjunction $(H\ni P,L_i|_H)$ is a log canonical pair. Thus, the classification of two-dimensional log canonical pairs [11] implies that $(H\ni P)$ is a cyclic singularity at the point P, that is, it has type ${\mathbb A}_k$. By the paper [5] or the paper [7] the singularity $(H\ni P)$ is of type ${\mathbb A}_1$. Thus

$$ (Z\ni P)\cong (xy+z^2+t^{2l}=0\subset ({\mathbb C}^4,0)) $$

and $f(D)=\{x=0\}|_Z+\{y=0\}|_Z$. Since $(Z\ni P, f(D))$ is a log canonical pair then we can take the weighted blow-up of $({\mathbb C}^4,0)$ with the weights (l, l, l, 1) and obtain $l=1$. This completes the proof.

Remark 2.17

Let $\rho (P)$ be a rank of local analytic group of Weil divisors at the point P. Then the Proposition 2.15 implies easily Shokurov’s criterion on the characterization of toric varieties for three-dimensional singularities $(Z\ni P)$ if $\rho (P)=1$, and hence the same criterion for three-dimensional divisorial contractions $f:X\rightarrow (Z\ni P)$ if $\rho (P)=1$.

Fig. 1

Case of Curve. Construction in ${\mathbb Q}$-factorial case

3 Three-dimensional Blow-ups. Case of Curve

Example 3.1

Now we construct the examples of three-dimensional non-toric plt blow-ups $f:(Y,E)\rightarrow (X\supset C\ni P)$ provided that $(X\ni P)$ is a ${\mathbb Q}$-gorenstein toric singularity, $\dim f(E)=1$ and the curve $C=f(E)$ is a toric (smooth) subvariety. Depending on a type of $(X\ni P)$ we consider two Cases A1) and A2).

(A1) Let $(X\ni P)$ be a ${\mathbb Q}$-factorial toric singularity, that is, $(X\ni P)\cong ({\mathbb C}^3\ni 0)/G$, where G is an abelian group acting freely in codimension 1.

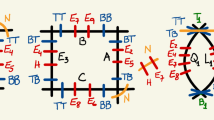
All plt blow-ups are constructed by the procedure illustrated on the next diagram (Fig. 1) and defined below.

First step. Let $g_0:(Z_0,S_0)\rightarrow (X\supset C\ni P)$ be a toric blow-up, where ${\text {Exc}}g_0=S_0$ is an irreducible divisor and $g_0(S_0)=C$. Recall that $g_0$ is a plt blow-up, the surface $S_0$ is a toric conic bundle, $\rho (S_0/C)=1$ and ${\text {Diff}}_{S_0}(0)=\frac{w^1_0-1}{w^1_0}E^1_0+\frac{w^2_0-1}{w^2_0}E^2_0+\frac{d_0-1}{d_0}F_0$, where $E^1_0$, $E^2_0$ are some sections of conic bundle, $F_0$ is a fiber over P and $w^1_0, w^2_0, d_0\in {\mathbb Z}_{\ge 1}$. Let us remark that the numbers $w^1_0, w^2_0$ determine $g_0$. Moreover, $d_0=1$ if $(X\ni P)$ is a smooth point.

Assume that there exists a curve $\Gamma _0\subset S_0$ with the following two properties: (1) $K_{S_0}+{\text {Diff}}_{S_0}(0)+\Gamma _0$ is a plt and $g_0$-anti-ample divisor; (2) $\Gamma _0$ is a non-toric subvariety in any analytical neighborhood of the fiber $F_0$ on the toric variety $Z_0$ for any toric structure of $(X\ni P)$, that is, the curve $\Gamma _0$ is a non-toric subvariety of $(S_0,{\text {Diff}}_{S_0}(0))$ in any analytical neighborhood of $F_0$ on $S_0$.

By considering the general fiber over a general point of C we obtain $w^i_0=1$ for some $i=1,2$. To be definite, put $w^1_0=1$ and let $Q_0=E^2_0\cap F_0$. Applying the adjunction formula it is easy to prove that $\Gamma _0\cap F_0=Q_0$, $w^2_0\ge 2$, $d_0=1$, $(S_0\ni Q_0)$ is of type $\frac{1}{r_0}(1,1)$ ($r_0\ge 1$) and $\Gamma _0\cdot F_0=\Gamma \cdot E_0^2=\frac{1}{r_0}$.

Remark 3.2

Let $(X\ni P)$ be a terminal singularity, that is, $(X\ni P)\cong ({\mathbb C}^3_{x_1, x_2, x_3}\ni 0)/{\mathbb Z}_r(-1, -q, 1)$. Then $r=r_0$ and one of the following cases holds by simple calculation.

(1) $C=\{x_1=x_2{=}0\}$, $g_0$ is a blow-up with weights $(w_0^2, 1, 0)$, $r_0|w_0^2$ or $(1, w_0^2, 0)$, $r_0|(w_0^2-q+1)$.

(2) $C=\{x_1=x_3=0\}$, $g_0$ is a blow-up with weights $(w_0^2, 0, 1)$, $r_0|(w_0^2+1+q)$ or $(1, 0, w_0^2)$, $r_0|(w_0^2-q+1)$.

(3) $C=\{x_2=x_3=0\}$, $g_0$ is a blow-up with weights $(0, w_0^2, 1)$, $r_0|(w_0^2+1+q)$ or $(0, 1, w_0^2)$, $r_0|w_0^2$.

Consider an arbitrary toric structure of $Z_0$ in any neighborhood of the point $Q_0$ such that $\Gamma _0$ is also a toric subvariety of $Z_0$. Let $h_0:(Y_0,(S_1)_{Y_0})\rightarrow (Z_0\supset \Gamma _0\ni Q_0)$ be an arbitrary toric blow-up of the curve $\Gamma _0$ with an unique exceptional divisor (${\text {Exc}}h_0=(S_1)_{Y_0}$). The structures of $h_0$ and $g_0$ are similar, in particular, $h_0$ is determined by some numbers $w^1_1$ and $w^2_1$, $(S_0)_{Y_0}\cong S_0$.

The set of all possible blow-ups $h_0$ for any toric structure of $(Z_0\ni Q_0, \Gamma _0)$ is denoted by $\mathcal H_0$.

Let $(D_0)_{Z_0}$ be a toric Weil divisor of $(Z_0\ni Q_0)$ such that $(D_0)_{Z_0}|_{S_0}=\Gamma _0$ and $a((S_1)_{Y_0},(D_0)_{Z_0}+S_0)=-1$. Let T be a toric Weil divisor of $(X\ni P)$ such that $T_{Z_0}\cap S_0=E^2_0$. Then $K_{Y_0}+(S_1)_{Y_0}+(S_0)_{Y_0}+(D_0)_{Y_0}+T_{Y_0}\sim 0$ is lc by Inversion of Adjunction. The ray ${\mathbb R}_+[(F_0)_{Y_0}]$ gives the divisorial contraction of $(S_0)_{Y_0}$ onto a curve, denoted by $h'_0$ in our diagram. We obtain a non-toric blow-up $g_1:(Z_1,S_1)\rightarrow (X\supset C\ni P)$, where $S_1={\text {Exc}}g_1$, $g_1(S_1)=C$ and $(S_1)_{Y_0}\cong S_1$. Since $g_1$ be a toric blow-up (under identification) in some neighborhood of any point other than P, then ${\text {Diff}}_{S_1}(0)=\frac{w^3_1-1}{w^3_1}E^2_1+\frac{w^j_1-1}{w^j_1}E^1_1+\frac{d_1-1}{d_1}(F_1)_{Z_0}$, $j\in \{1,2\}$, $E^2_1=h'_0((S_0)_{Y_0})$ and $E^1_1$ are some sections, $F_1$ is a fiber over P, $w^3_1\in {\mathbb Z}_{\ge 3}$ and $d_1\in {\mathbb Z}_{\ge 1}$. Hence $g_1$ is a plt blow-up.

Second step. Assume that there exists a curve $\Gamma _1\subset (S_1)_{Y_0}$ with the following two properties: (1) $K_{(S_1)_{Y_0}}+{\text {Diff}}_{(S_1)_{Y_0}}(0)+\Gamma _1$ is a plt and $h_0$-anti-ample divisor, $h_0:\Gamma _1\rightarrow \Gamma _0$ is a surjective morphism and (2) $\Gamma _1$ is not a center of any blow-up of ${\mathcal H_0}$, that is, $\Gamma _1$ is a non-toric subvariety of $((S_1)_{Y_0},{\text {Diff}}_{(S_1)_{Y_0}}(0))$ in any analytical neighborhood of the fiber $(F_1)_{Y_0}$ over P.

The triples $((S_1)_{Y_0},{\text {Diff}}_{(S_1)_{Y_0}}(0), \Gamma _1)$ and $(S_0,{\text {Diff}}_{S_0}(0), \Gamma _0)$ have the same structures and (with similar notation) $w^1_1=1$, $Q_1=(E^2_1)_{Y_0}\cap (F_1)_{Y_0}$, $\Gamma _1\cap (F_1)_{Y_0}=Q_1$, $w^2_1\ge 1$, $d_1=1$, $((S_1)_{Y_0}\ni Q_1)$ is of type $\frac{1}{r_1}(1,1)$ ($r_1\ge 1$) and $\Gamma _1\cdot (F_1)_{Y_0}=\Gamma _1\cdot (E_1^2)_{Y_0}=\frac{1}{r_1}$.

Consider an arbitrary toric structure of $Y_0$ in any neighborhood of the point $Q_1$ such that $\Gamma _1$ is also a toric subvariety of $Y_0$. Let $h_1:(Y_1,(S_2)_{Y_1})\rightarrow (Y_0\supset \Gamma _1\ni Q_1)$ be an arbitrary toric blow-up of the curve $\Gamma _1$ with an unique exceptional divisor (${\text {Exc}}h_1=(S_2)_{Y_1}$), $(S_1)_{Y_1}\cong (S_1)_{Y_0}$.

The set of all possible blow-ups $h_1$ for any toric structure of $(Y_0\ni Q_1, \Gamma _1)$ is denoted by $\mathcal H_1$.

Let $(D_1)_{Y_0}$ be a toric Weil divisor of $(Y_0\ni Q_1)$ such that $(D_1)_{Y_0}|_{S_1}=\Gamma _1$ and $a((S_2)_{Y_1},(D_1)_{Y_0}+(S_0)_{Y_0}+(S_1)_{Y_0})=-1$. We have 1-complement $K_{Y_1}+(S_2)_{Y_1}+(S_1)_{Y_1}+(S_0)_{Y_1}+(D_1)_{Y_1}\sim 0/X$ by Inversion of Adjunction applied to the surfaces $(S_i)_{Y_1}$. By the cone theorem we have:

(1) there exists a divisorial contraction $h'_{1,1}:Y_1\rightarrow Y_{1,1}$ of $(S_1)_{Y_1}$ onto a curve, $(S_2)_{Y_1}\cong (S_2)_{Y_{1,1}}$;

(2) there exists a small contraction $\varphi _{1,1}$ of an extremal ray generated by $(F_0)_{Y_{1,1}}$. Let $\varphi ^+_{1,1}$ be a log flip of $\varphi _{1,1}$, ${\text {Exc}}\varphi ^+_{1,1}=(F^+_0)_{Y_{1,2}}$, $h'_{1,2}:Y_{1,1}\dashrightarrow Y_{1,2}$ be a corresponding birational map;

(3) there exists a divisorial contraction $h'_{1,3}:Y_{1,2}\rightarrow Z_2$ of $(S_0)_{Y_{1,2}}$ onto a curve.

Thus we obtain a birational map $h'_1=h'_{1,3}\circ h'_{1,2}\circ h'_{1,1}:Y_1\dashrightarrow Z_2$. Put $S_2=(S_2)_{Z_2}$. Since $(E^2_0)_{Y_{1,1}}\cap (F_0)_{Y_{1,1}}=(Q_0)_{Y_{1,1}}$ then $(D_1)_{Y_{1,1}}\cdot (F_0)_{Y_{1,1}}>0$ and the divisor $(D_1)_{Z_2}$ contains the fiber $(F^+_0)_{Z_2}$ and two sections of the local conic bundle $S_2\rightarrow C$, $\rho (S_2/C)=1$, $K_{Z_2}+S_2+(D_1)_{Z_2}\sim 0/X$ is lc. By Shokurov’s criterion on the characterization of toric varieties $(S_2, {\text {Diff}}_{S_2}(0))\rightarrow C$ is a toric conic bundle [26]. We obtain a non-toric plt blow-up $g_2:(Z_2,S_2)\rightarrow (X\supset C\ni P)$.

We prove the following proposition.

Proposition 3.3

The pair $(S_i,{\text {Diff}}_{S_i}(0))$ is klt and local toric conic bundle (1-complementary), $\rho (S_i/C)=1$, $g_i$ is a non-toric plt blow-up for $i=1, 2$.

Third step. Assume that there exists a curve $\Gamma _2\subset (S_2)_{Y_1}$ with the following two properties: (1) $K_{(S_2)_{Y_1}}+{\text {Diff}}_{(S_2)_{Y_1}}(0)+\Gamma _2$ is a plt and $h_1$-anti-ample divisor, $h_1:\Gamma _2\rightarrow \Gamma _1$ is a surjective morphism and (2) $\Gamma _2$ is not a center of any blow-up of ${\mathcal H_1}$, that is, $\Gamma _2$ is a non-toric subvariety of $((S_2)_{Y_1},{\text {Diff}}_{(S_2)_{Y_1}}(0))$ in any analytical neighborhood of the central fiber $F_2$ of $(S_2)_{Y_1}$ over P.

The triple $((S_2)_{Y_1},{\text {Diff}}_{(S_2)_{Y_1}}(0), \Gamma _2)$ has the same structures as the previous ones. In particular (with similar notation), $w^1_2=1$ and $w^2_2\ge 1$.

Proposition 3.4

There is no any blow-up $h_2:(Y_2, (S_3)_{Y_2})\rightarrow (Y_1\supset \Gamma _2)$ of the curve $\Gamma _2$ with unique exceptional divisor such that $(S_3)_{Y_2}$ is realized by some plt blow-up $g_3:(Z_3, (S_3)_{Z_3})\rightarrow (X\supset C\ni P)$.

Proof

Assume the converse. Consider a general point of C. Let $F_3$ be a fiber of $(S_3)_{Y_2}$ over P. Put $\Theta ={\text {Diff}}_{(S_3)_{Z_3}}(0)$ for simplicity. Since $w^2_0+w^2_1+w^2_2+1\ge 5$ then $\Theta$ has some component (a section of conic bundle) with a coefficient $\ge 4/5$.

We claim that $K_{(S_3)_{Z_3}}+\Theta$ is 1 or 2-complementary. Assume that $K_{(S_3)_{Z_3}}+\Theta$ is not 1-complementary. Then the divisor $K_{(S_3)_{Z_3}}+\alpha F_3+\Theta$ is lc, but not plt for some $\alpha \le 1$, and consider its inductive blow-up $\sigma :\widetilde{X}\rightarrow (S_3)_{Z_3}$ with exceptional divisor $\widetilde{E}$. The curve $(F_3)_{\widetilde{X}}$ can be contracted in the appropriate MMP over C. Denote this contraction by $\widetilde{X}\rightarrow \overline{X}$. The divisor $K_{\overline{X}}+\overline{E}+\Theta _{\overline{X}}$ is plt.

Let $K_{\widetilde{X}}+\widetilde{E}+\Theta _{\widetilde{X}}$ be nonnegative on $(F_3)_{\widetilde{X}}$. We can extend complement of $K_{\overline{E}}+{\text {Diff}}_{\overline{E}}(\Theta _{\overline{X}})$ on $\overline{X}$, pull back on $\widetilde{X}$ and push-down them on $(S_3)_{Z_3}$. There are only two cases: (1) ${\text {Diff}}_{\overline{E}}(\Theta _{\overline{X}})=1/2P_1+1/2P_2+(1-1/m)P_3$ and 2) ${\text {Diff}}_{\overline{E}}(\Theta _{\overline{X}})=1/2P_1+2/3P_2+4/5P_3$, where $\{P_i\}$ are some points, $m\ge 5$. We obtain 2- or 6-complement.

Let $K_{\widetilde{X}}+\widetilde{E}+\Theta _{\widetilde{X}}$ be negative on $(F_3)_{\widetilde{X}}$. The divisor $-(K_{\widetilde{X}}+\widetilde{E}+\Theta _{\widetilde{X}})$ is ample over C. Similarly 2- or 6-complement of $K_{\widetilde{E}}+{\text {Diff}}_{\widetilde{E}}(\Theta _{\widetilde{X}})$ can be extended on $\widetilde{X}$ and we have 2- or 6-complement $D^+$ of $K_X$ with $a((S_3)_{Y_2}, D^+)=-1$.

Consider the case of 6-complement. Since $a((S_3)_{Y_2}, D^+)=-1$ then there is one possibility $a((S_0)_{Y_2}, D^+)=-1/2$, $D^+|_{S_0}=(7/6)\Gamma _0+\ldots$ and $a((S_1)_{Y_2}, D^+)\le -2/3$. Since $F_3\subset (S_i)_{Y_2}$ for $i=0, 1$ then $K_{Y_2}+a((S_0)_{Y_2}, D^+)(S_0)_{Y_2}+a((S_1)_{Y_2}, D^+)(S_1)_{Y_2}+(S_3)_{Y_2}$ is not lc, the contradiction.

Thus we have 1- or 2-complement. Therefore the coefficients of $D^+$ are equal 1 or 1/2 and $a((S_0)_{Y_2}, D^+)\le -1/2$. We have the same contradiction as above.   $\square$

(A2) Let $(X\ni P)$ be a non-${\mathbb Q}$-factorial terminal toric three-dimensional singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$ by Proposition 2.3.

Let $f:(Y, E)\rightarrow (X\supset C\ni P)$ be some plt blow-up. Let $\varphi _i:X_i\rightarrow (X\ni P)$ be any of two ${\mathbb Q}$-factorializations, ${\text {Exc}}\varphi _i=C_i$ ($i=1, 2$). Let $\psi _i:(Y_i, E_i)\rightarrow (X_i\supset C_{X_i}\ni P_{X_i})$ be a plt blow-up of $C_{X_i}$ such that $E_i$ and E define the same discrete valuation of the function field $\mathcal K(X)$, $\rho (E_i/C)=1$. The blow-up $\psi _i$ was constructed in the previous case of ${\mathbb Q}$-factorial singularities. Let $Y_i\dashrightarrow Y$ be a log flip for the curve $(C_i)_{Y_i}$. Thus f has constructed and $\rho (E/C)=2$.

We give another construction and prove that $(E,{\text {Diff}}_E(0))\rightarrow C$ is a toric conic bundle by the procedure illustrated on the next diagram (Fig. 2) and defined below.

Fig. 2

Case of Curve. Construction in non-${\mathbb Q}$-factorial case

First step. Let $g_0:(Z_0,S_0)\rightarrow (X\supset C\ni P)$ be any toric plt blow-up, where $g_0(S_0)=C$. Its description is given in example 2.2 2), whose notation is used. Let $F_0=F^1_0+F^2_0$ be a fiber over the point P. Put $Q_0=F^1_0\cap F^2_0$.

Second step. Assume that there exists a curve $\Gamma _0\subset S_0$ with the following two properties: (1) $K_{S_0}+{\text {Diff}}_{S_0}(0)+\Gamma _0$ is a plt and $g_0$-anti-ample divisor; 2) $\Gamma _0$ is a non-toric subvariety in any analytical neighborhood of the fiber $F_0$ on the toric variety $Z_0$ for any toric structure of $(X\ni P)$, that is, the curve $\Gamma _0$ is a non-toric subvariety of $(S_0,{\text {Diff}}_{S_0}(0))$ in any analytical neighborhood of $F_0$ on $S_0$.

Considering a fiber over a general point of C we have $a_2=1$ or $a_3=1$. To be definite, put $a_2=1$ and $F_0^2\cap E_2\ne \emptyset$. By simple calculations $\Gamma _0\cap (F^1_0\cup F^2_0)=Q_0$, $F_0^1\cdot \Gamma _0=\frac{a_3}{a_3+1}$ and $F^2_0\cdot \Gamma _0=\frac{1}{a_3+1}$.

Consider an arbitrary toric structure of $Z_0$ in any neighborhood of the point $Q_0$ such that $\Gamma _0$ is a toric subvariety of $Z_0$ also. Let $h_0:(Y_0,(S_1)_{Y_0})\rightarrow (Z_0\supset \Gamma _0\ni Q_0)$ be an arbitrary toric blow-up of the curve $\Gamma _0$ with an unique exceptional divisor (${\text {Exc}}h_0=(S_1)_{Y_0}$), $(S_0)_{Y_0}\cong S_0$.

The set of all possible blow-ups $h_0$ for any toric structure of $(Z_0\ni Q_0, \Gamma _0)$ is denoted by $\mathcal H_0$.

Let $(D_0)_{Z_0}$ be a toric Weil divisor of $(Z_0\ni Q_0)$ such that $(D_0)_{Z_0}|_{S_0}=\Gamma _0$ and $a((S_1)_{Y_0}, (D_0)_{Z_0}+S_0)=-1$. Let $T_1$ and $T_2$ be toric Weil divisors of $(X\ni P)$ such that

$$ K_{S_0}+{\text {Diff}}_{S_0}((T_1+T_2)_{Z_0}+(D_0)_{Z_0})=K_{S_0}+F^2_0+E_2+\Gamma _0\sim 0. $$

The pairs $(X\ni P, T_1+T_2+(D_0)_X)$ and $((S_1)_{Y_0},{\text {Diff}}_{(S_1)_{Y_0}}((T_1+T_2)_{Y_0}+(D_0)_{Y_0}+(S_0)_{Y_0}))$ are lc. Since $T_1+T_2$ is Cartier divisor then $(D_0)_X$ is Cartier divisor. The curves $(F^1_0)_{Y_0}$ and $(F^2_0)_{Y_0}$ generate extremal rays of $\overline{{\text {NE}}}(Y_0/X)$ that give small contractions. Let $h'_{0,1}:Y_0\dashrightarrow Y_{0,1}$ be any of two log flips. Since our pairs are lc then $\rho ((S_0)_{Y_{0,1}}/C)=1$. Let $h'_{0,2}:Y_{0,1}\rightarrow Z_1$ be a divisorial contraction of $(S_0)_{Y_{0,1}}$ onto a curve.

Thus we obtain a birational map $h'_0=h'_{0,2}\circ h'_{0,1}:Y_0\dashrightarrow Z_1$ and a non-toric blow-up $g_1:(Z_1, S_1)\rightarrow (X\supset C\ni P)$, $\rho (S_1/C)=2$. It can be proved by direct computation that $-S_1$ is $g_1$-ample divisor, but if we consider the construction of $g_1$ through two ${\mathbb Q}$-factorializations of $(X\ni P)$ as done above, then it is obvious that the divisor $-S_1$ is $g_1$-ample. The divisor ${\text {Diff}}_{S_1}((T_1+T_2)_{Z_1}+(D_0)_{Z_1})$ consists of four curves and gives 1-complement of $K_{S_1}+{\text {Diff}}_{S_1}(0)$. By Shokurov’s criterion on the characterization of toric varieties $(S_1, {\text {Diff}}_{S_1}((T_1+T_2)_{Z_1}+(D_0)_{Z_1})\rightarrow C$ is a toric conic bundle [26]. Thus $g_1$ is a plt blow-up.

Third step. Assume that there exists a curve $\Gamma _1\subset (S_1)_{Y_0}$ with the following two properties: (1) $K_{(S_1)_{Y_0}}+{\text {Diff}}_{(S_1)_{Y_0}}(0)+\Gamma _1$ is plt and $h_0$-anti-ample divisor, $h_0:\Gamma _1\rightarrow (\Gamma _0)_{Z_0}$ is a surjective morphism and (2) $\Gamma _1$ is not a center of any blow-up of ${\mathcal H_0}$, that is, $\Gamma _1$ is a non-toric subvariety of $((S_1)_{Y_0},{\text {Diff}}_{(S_1)_{Y_0}}(0))$ in any analytical neighborhood of the central fiber $F_1$ of $(S_1)_{Y_0}$ over P.

The triple $((S_1)_{Y_0},{\text {Diff}}_{(S_1)_{Y_0}}(0), \Gamma _1)$ has the same structures as in the previous case of ${\mathbb Q}$-factorial singularities, and we use its notation.

Consider an arbitrary toric structure of $Y_0$ in any neighborhood of the point $Q_1$ such that $\Gamma _1$ is also a toric subvariety of $Y_0$. Let $h_1:(Y_1,(S_2)_{Y_1})\rightarrow (Y_0\supset \Gamma _1\ni Q_1)$ be an arbitrary toric blow-up of the curve $\Gamma _1$ with an unique exceptional divisor (${\text {Exc}}h_1=(S_2)_{Y_1}$), $(S_1)_{Y_1}\cong (S_1)_{Y_0}$.

Let $(D_1)_{Y_0}$ be a toric Weil divisor of $(Y_0\ni Q_1)$ such that $(D_1)_{Y_0}|_{S_1}=\Gamma _1$ and $a((S_2)_{Y_1},(D_1)_{Y_0}+(S_0)_{Y_0}+(S_1)_{Y_0})=-1$. Considering the case of ${\mathbb Q}$-factorial singularities and construction of $g_0\circ h_0$ through ${\mathbb Q}$-factorializations of $(X\ni P)$ we have $(E_2)_{Y_0}\subset (D_1)_{Y_0}$ and hence $F^2_0\subset (D_1)_{Y_0}$. Thus we have 1-complement $K_{Y_1}+(S_2)_{Y_1}+(S_1)_{Y_1}+(S_0)_{Y_1}+(D_1)_{Y_1}\sim 0/X$ by Inversion of Adjunction applied to the surfaces $(S_i)_{Y_1}$. By the cone theorem we have:

(1) there exists a divisorial contraction $h'_{1,1}:Y_1\rightarrow Y_{1,1}$ of $(S_1)_{Y_1}$ onto a curve, $(S_2)_{Y_1}\cong (S_2)_{Y_{1,1}}$;

(2) there exists a small contraction of $(F^1_0)_{Y_{1,1}}$, $h'_{1,2}:Y_{1,1}\dashrightarrow Y_{1,2}$ is a corresponding log flip;

(3) there exists a small contraction of $(F^2_0)_{Y_{1,2}}$, $h'_{1,3}:Y_{1,2}\dashrightarrow Y_{1,3}$ is a corresponding log flip;

(4) there exists an divisorial contraction $h'_{1,4}:Y_{1,3}\rightarrow Z_2$ of $(S_0)_{Y_{1,3}}$ onto a curve.

Thus we obtain a birational map $h'_1=h'_{1,4}\circ h'_{1,3}\circ h'_{1,2}\circ h'_{1,1}:Y_1\dashrightarrow Z_2$, the local conic bundle $(S_2)_{Z_2}\rightarrow C$, $\rho ((S_2)_{Z_2}/C)=2$ and $K_{Z_2}+(S_2)_{Z_2}+(D_1)_{Z_2}\sim 0/X$ is lc. Let $F_2=F^1_2+F^2_2$ be a fiber over P and the curves $F^1_2$, $F^2_2$ appear due to log flips $h'_{1,2}$, $h'_{1,3}$ respectively. By the construction the divisor $(D_1)_{Z_2}$ contains two sections of $(S_2)_{Z_2}$ and $F^1_2$.

If we consider this construction through two ${\mathbb Q}$-factorializations of $(X\ni P)$ then $(S_2)_{Z_2}$ is anti-ample over C and $(F^1_0)_{Y_{1,1}}\cap (F^2_0)_{Y_{1,1}}=(Q_0)_{Y_{1,1}}$. Since $(F_0^2)_{Y_{1,2}}\cdot (F_0^2)_{Y_{1,2}}=0$, $K_{Y_{1,2}}+(S_0)_{Y_{1,2}}+(S_2)_{Y_{1,2}}+(D_1)_{Y_{1,2}}\sim 0$ then for some $e>0$ we have $(D_1)_{Y_{1,2}}\cdot (F^2_0)_{Y_{1,2}}=e(E_2)_{Y_{1,2}}\cdot (F_0^2)_{Y_{1,2}}>0$ and $(D_1)_{Z_2}$ contains $F^2_2$.

By Shokurov’s criterion on the characterization of toric varieties $((S_2)_{Z_2}, {\text {Diff}}_{(S_2)_{Z_2}}(0))\rightarrow C$ is a toric conic bundle [26]. We obtain a non-toric plt blow-up $g_2:(Z_2,S_2)\rightarrow (X\supset C\ni P)$, where $S_2=(S_2)_{Z_2}$.

We prove the following proposition.

Proposition 3.5

The pair $(S_i,{\text {Diff}}_{S_i}(0))$ is klt and local toric conic bundle (1-complementary), $\rho (S_i/C)=1$, $g_i$ is a non-toric plt blow-up for $i=1, 2$.

Example 3.6

Let us describe the non-toric canonical blow-ups (they will be non-terminal blow-ups always) $g:(Y,E)\rightarrow (X\supset C\ni P)$ provided that $(X\ni P)$ is a toric terminal singularity, $C=g(E)$ is a toric (smooth) subvariety and $\dim C=1$. Depending on a type of $(X\ni P)$ we consider two Cases (B1) and (B2).

(B1) Let $(X\ni P)$ be a ${\mathbb Q}$-factorial terminal singularity. Let $g:(Z,S)\rightarrow (X\supset C\ni P)$ be any toric canonical blow-up (see Proposition 2.5).

Assume that there exists a curve $\Gamma \subset S$ with the following two properties: (1) $K_S+{\text {Diff}}_S(0)+\Gamma$ is g-anti-ample divisor, and $\Gamma$ does not contain any center of canonical singularities of Z; (2) $\Gamma$ is a non-toric subvariety in any analytical neighborhood of the fiber F (over P) on the toric variety Z for any toric structure of $(X\ni P)$, that is, the curve $\Gamma$ is a non-toric subvariety of $(S,{\text {Diff}}_S(0))$ in any analytical neighborhood of F on S.

Thus $(X\ni P)$ is a smooth point, S is a smooth surface, ${\text {Diff}}_S(0)=\frac{k-1}{k}E$, where $k\ge 2$ and E is some section by Proposition 2.5. By adjunction formula $\Gamma$ is smooth, $Q=\Gamma \cap F\cap E$, $\Gamma \cdot F=1$.

Let $(X\ni P, D)$ be any pair with canonical singularities such that D is a boundary, $\Gamma \in {\text {CS}}(Z,D_Z-a(S,D)S)$. Obviously, $D_Z|_S=\Gamma +aF$ and $a(S, D)=0$, where $a\ge 0$.

Considering the blow-up $({\mathbb C}^3_{x_1x_2x_3}\ni 0)\cong (X\supset C\ni P)$ with weights (k, 1, 0), $C=\{x_1=x_2=0\}$ and the divisor given by the equation $x_1^2+x_1x_2+x_1x_3^m+bx_2^k=0$, then clearly, there is a divisor D for any such curve $\Gamma$.

By Theorem 1.6 there exists a divisorial contraction $h:(\widetilde{Y},\widetilde{E})\rightarrow (Z\supset \Gamma )$ such that $a(\widetilde{E}, D)=0$, ${\text {Exc}}h=\widetilde{E}$ is an irreducible divisor and $h(\widetilde{E})=\Gamma$. Applly $K_{\widetilde{Y}}+D_{\widetilde{Y}}+\varepsilon \widetilde{S}$–MMP. Since $\rho (\widetilde{Y}/X)=2$ and $K_{\widetilde{Y}}+D_{\widetilde{Y}}+\varepsilon \widetilde{S}\equiv \varepsilon \widetilde{S}$ over X, then after log flips $\widetilde{Y}\dashrightarrow \overline{Y}$ (perhaps their lack) we obtain a divisorial contraction $h':\overline{Y}\rightarrow Y$, which contracts $\overline{S}$ onto a curve $C_Y$.

Thus we obtain a non-toric canonical blow-up f. Since $C_Y\in {\text {CS}}(Y)$ by the construction then f is not a terminal blow-up.

(B2) Let $(X\ni P)$ be a non-${\mathbb Q}$-factorial terminal toric three-dimensional singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. Consider a ${\mathbb Q}$-factorialization $g:\widetilde{X}\rightarrow X$, $\widetilde{T}={\text {Exc}}g$ and $\widetilde{P}=\widetilde{T}\cap \widetilde{C}$. We apply the construction from (B1) for the curve $\widetilde{C}\subset (\widetilde{X}\ni \widetilde{P})$ such that the divisor D from the construction has the form $g^*D_X$, where $D_X$ is a ${\mathbb Q}$-Cartier divisor. We obtain a non-toric canonical blow-up $f:Y^+\rightarrow \widetilde{X}$. Let $Y^+\dashrightarrow Y$ be a log flip for the curve $T_{Y^+}$. Thus we obtain a required non-toric canonical blow-up f (anti-amplness of E is proved as in case (A2)).

Let us describe the curves $\Gamma$. Let $g:(Z, S) \rightarrow (\widetilde{X} \ni \widetilde{P})$ be a toric canonical blow-up obtained in the first step of the construction. Let $\psi :Z \dashrightarrow Z^+$ be a toric log flip for the curve $T_Z$. So $g^+ :(Z^+, S^+) \rightarrow (X \ni P)$ is a toric canonical blow-up. The structure of the curve $\Gamma _{S^+}$ is completely identical to the structure of the curve $\Gamma$ considered in case (A2). To prove that any such curve $\Gamma _{S^+}$ is realizable, it suffices to consider a divisor of the form $x_ {i_1}+bx_{i_2}^k=0$ on $(X\ni P)$ for some b, k, $\{i_1, i_2\}=\{1,2\}$ or $\{3,4\}$.

Theorem 3.7

Let $f:(Y,E) \rightarrow (X\supset C\ni P)$ be a plt blow-up of three-dimensional toric terminal singularity, where $\dim f(E)=1$. Assume that the curve $C=f(E)$ is a toric subvariety of $(X\ni P)$. Then, either f is a toric morphism (see Example 2.2), or f is a non-toric morphism described in Example 3.1.

Proof

By Example 3.1 we must only consider the case when $(X\ni P)$ is a ${\mathbb Q}$–factorial singularity. Let f be a non-toric morphism (up to analytic isomorphism). Let $D_Y\in |-n(K_Y+E)|$ be a general element for $n\gg 0$. Put $D_X=f(D_Y)$ and $d=\frac{1}{n}$. The pair $(X,dD_X)$ is log canonical, $a(E,dD_X)=-1$, and E is a unique exceptional divisor with discrepancy $-1$.

By the construction of partial resolution of $(X,dD_X)$ (see Definition 2.7 and the paper [27]) and by Criterion 2.8, there exists a toric divisorial contraction $g:Z\rightarrow X$ dominated by partial resolution of $(X,dD_X)$ (up to toric log flips) and the following properties are fulfilled.

• (A) The exceptional set ${\text {Exc}}g=S$ is an irreducible divisor, the divisors S and E define the different discrete valuations of the function field $\mathcal K(X)$, and $g(S)=C$.

• (B) By $\Gamma$ denote the center of E on the surface S. Then the curve $\Gamma$ is a non-toric subvariety of Z. In the other words, $\Gamma$ is a non-toric subvariety of $(S,{\text {Diff}}_S(0))$.

Obviously, $a(S_0, dD_X)<0$. By Example 3.1 (in its notation) we must prove only that the anti-ample over X divisor $K_{S_0}+{\text {Diff}}_{S_0}(0)+\Gamma _0$ is plt in some analytical neighborhood of the fiber $F_0\subset S_0$. We can choose the divisor $dD_X$ such that ${\text {Supp}}(dD_X|_{S_0})\subset \Gamma _0\cup F\cup \Gamma '_0 \cup E^2_0$, where $\Gamma '_0$ is a general divisor on $S_0$.

Assume that $K_{S_0}+{\text {Diff}}_{S_0}(0)+\Gamma _0$ is not a plt divisor. By the adjunction formula the curve $\Gamma _0$ is smooth. By connectedness lemma $K_{S_0}+{\text {Diff}}_{S_0}(0)+\Gamma _0$ is not a plt divisor at unique point, and denote this point by $G_0$. The point $G_0$ is a non-toric subvariety of $(S_0,{\text {Diff}}_{S_0}(0))$. Moreover, the curve $\Gamma _0$ is locally a non-toric subvariety at the point $G_0$ only. By the construction of partial resolution [27] (in a small analytical neighborhood of the point $G_0$) there exists a divisorial toric contraction $\widehat{g}_0:\widehat{Z}_0\rightarrow Z_0$ such that ${\text {Exc}}\widehat{g}_0=S''_0$ is an irreducible divisor, $\widehat{g}(S''_0)=G_0$ and the two following conditions are satisfied.

(1) Put $S'_0=(S_0)_{\widehat{Z}_0}$ and $C_0=S'_0\cap S''_0$. Let $c(\Gamma _0)$ be the log canonical threshold of $\Gamma _0$ for the pair $(S_0,{\text {Diff}}_{S_0}(0))$. Then ${\widehat{g}_0}|_{S'_0}:S'_0\rightarrow S_0$ is the toric inductive blow-up of $K_{S_0}+{\text {Diff}}_{S_0}(0)+c(\Gamma _0)\Gamma _0$ (see Theorems 1.10 and 2.12), and the point $\widehat{G}_0=C_0\cap (\Gamma _0)_{S'_0}$ is a non-toric subvariety of $(S''_0,{\text {Diff}}_{S''_0}(0))$.

(2) The divisor ${\text {Diff}}_{S''_0}(dD_{\widehat{Z}_0}+a(S_0,dD_X)S'_0)$ is a boundary in some small analytical neighborhood of the point $\widehat{G}_0$.

Let H be a general hyperplane section of sufficiently large degree passing through the point P such that it does not contain the curve C. Then there exists a number $h>0$ such that $a(S''_0,dD_X+hH)>-1$, and the point $\widehat{G}_0$ is a center of $(S''_0,{\text {Diff}}_{S''_0}(dD_{\widehat{Z}_0}+a(S_0,dD_X)S'_0+hH_{\widehat{Z}_0}))$. Therefore we obtain a contradiction for the pair $(S''_0,{\text {Diff}}_{S''_0}(dD_{\widehat{Z}_0}+a(S_0,dD_X)S'_0+hH_{\widehat{Z}_0}))$ and the point $\widehat{G}_0$ by Theorem 4.2.   $\square$

We have proved the next theorem too.

Theorem 3.8

Let $f:(Y,E) \rightarrow (X\supset C \ni P)$ be a plt blow-up of three-dimensional toric ${\mathbb Q}$-factorial singularity, where $\dim f(E)=1$. Assume that the curve $C=f(E)$ is a toric subvariety of $(X\ni P)$. Then, either f is a toric morphism (see Example 2.2), or f is a non-toric morphism described in Example 3.1.

Theorem 3.9

Let $f:(Y,E) \rightarrow (X\supset C \ni P)$ be a canonical blow-up of three-dimensional toric terminal singularity, where $\dim f(E)=1$. Assume that the curve $C=f(E)$ is a toric subvariety of $(X\ni P)$. Then, either f is a toric morphism (see Proposition 2.5), or f is a non-toric morphism and described in Example 3.6.

Proof

Let f be a non-toric morphism (up to analytic isomorphism). Let $D_Y\in |-nK_Y|$ be a general element for $n\gg 0$. Put $D_X=f(D_Y)$ and $d=\frac{1}{n}$. The pair $(X,dD_X)$ has canonical singularities and $a(E,dD_X)=0$. Now the arguments of the proof of Theorem 3.7 can be obviously applied, and we have $a(S,dD_X)=0$, this completes the proof.   $\square$

Corollary 3.10

Under the same assumption as in Theorem 3.9 the two following statements are satisfied:

(1) [8] if f is a terminal blow-up then the (toric) morphism f is isomorphic to the blow-up of the ideal of the curve C and an index of $(X\ni P)$ is equal to 1, that is, either $(X\ni P)$ is a smooth point or $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0));$

(2) if f is a non-toric morphism then an index of $(X\ni P)$ is equal to 1.

4 Toric Log Surfaces

Definition 4.1

Let ${\mathbb P}(\textbf{w})={\mathbb P}_{x_1x_2x_3x_4}(w_1,w_2,w_3,w_4)$, where $w_1+w_2=w_3+w_4$ and $\gcd (w_1,w_2,w_3,w_4){=}1$. Put $(w_1,w_2,w_3,w_4)=(a_1d_{23}d_{24}, a_2d_{13}d_{14}, a_3d_{14}d_{24}, a_4d_{13}d_{23})$, where $d_{ij}=\gcd (w_k,w_l)$ and i, j, k, l are mutually distinct indices from 1 to 4. The toric pair

$$\big (S,D\big )=\big (x_1x_2+x_3x_4\subset {\mathbb P}(\textbf{w}),{\text {Diff}}_{S/{\mathbb P}(\textbf{w})}(0)\big )$$

is called an ODP pair, $\rho (S)=2$. By Proposition 1.6 of [14] we have $D=\sum _{i<j, 1\le i\le 2}\frac{d_{ij}-1}{d_{ij}}C_{ij}$, where $C_{ij}=\{x_i=x_j=0\}\cap S$.

Let $f:(Y,E)\rightarrow (X\ni P)$ be a toric plt blow-up of three-dimensional ordinary double point. Then $(E,{\text {Diff}}_E(0))$ is an ODP pair by Example 2.2. Converse is also true: every ODP pair is realized by some toric plt blow-up of three-dimensional ordinary double point.

To be definite, assume that $w_1\le w_2$, $w_3\le w_4$, $w_2\le w_4$, $P_1=(1:0:0:0)$, $\ldots$, $P_4=(0:0:0:1)$. The surface S has a cyclic singularity at the point $P_i$ for every $i=1,2,3,4$ (see Fig. 3).

Since ${\mathcal O}_{{\mathbb P}(\textbf{w})}(w_i)|_S=\{x_i=0\}|_S=\frac{1}{d_{ik}}C_{ik}+\frac{1}{d_{il}}C_{il}$ for the corresponding different indices k and l, then it is easy to calculate that $C_{13}^2=d_{13}^2(w_3-w_2)/(w_2w_4)\le 0$, $C_{23}^2=d_{23}^2(w_2-w_4)/(w_1w_4)\le 0$, $C_{14}^2=d_{14}^2(w_4-w_2)/(w_2w_3)\ge 0$ and $C_{24}^2=d_{24}^2(w_2-w_3)/(w_1w_3)\ge 0$. In particular, Mori cone $\overline{{\text {NE}}}(S)$ is generated by the two rays ${\mathbb R}_+[C_{13}]$, ${\mathbb R}_+[C_{23}]$.

Fig. 3

ODP surface

Now we prove a two-dimensional non-toric point theorem. An one-dimensional analog ($\dim S=1$) of Theorem 4.2 (1) is obvious (see the proofs of Theorems 2.12 and 2.13 also).

Theorem 4.2

Let (S, D) be a toric pair, where S is a normal projective surface. Assume that $D=\sum _{i=1}^rd_iD_i$, where $D_i$ is a prime divisor and $\frac{1}{2} \le d_i\le 1$ for each i. Assume that there exists the boundary T such that $T\ge D$ and $-(K_S+T)$ is an ample divisor. Assume that some point $\Gamma$ is a center of ${\text {LCS}}(S,T)$, and there exists the analytical neighborhood U of $\Gamma$ such that $K_S+T$ is a log canonical divisor in the punctured neighborhood $U\backslash \Gamma$. Then the point $\Gamma$ is a toric subvariety of (S, D) if one of the two following conditions is satisfied:

(1) $\rho (S)=1$;

(2) $\rho (S)=2$, two different extremal rays of $\overline{{\text {NE}}}(S)$ give two toric conic bundles;

(3) (S, D) is ODP pair.

Proof

Let the point $\Gamma$ be a non-toric subvariety of (S, D). We will obtain a contradiction.

Consider Condition (1). It is clear that this theorem is sufficient to prove in the case $d_i=\frac{1}{2}$ for all i.

Since $-(K_S+T)$ is an ample divisor, then replacing T by some divisor we can assume that ${\text {LCS}}(S,T)\cap U=\Gamma$. Hence, connectedness lemma implies that ${\text {LCS}}(S,T)=\Gamma$.

The toric projective surface S (with Picard number $\rho (S)=1$) is determined by the fan $\Delta$ in the lattice $N\cong {\mathbb Z}^2$, where

$$ \Delta =\big \{\langle n_1, n_2\rangle ,\langle n_2, n_3\rangle , \langle n_1, n_3\rangle , \text {their faces} \big \}. $$

Thus surface S has at most three singular points. If the number of singularities is less than or equal to two, then there exists an isomorphism of the lattice N such that $n_1=(1,0)$, $n_2=(0,1)$, and therefore $S\cong {\mathbb P}_{x_1x_2x_3}(a_1,a_2,1)$.

Suppose that the point $\Gamma$ is a non-toric subvariety of $(S,D')$, where $D'=D-\frac{1}{2}D_j=\sum _{i\ne j}\frac{1}{2}D_i$. Then the divisor D can be replaced by the other divisor $D'<D$. Therefore we have the four possibilities for the pair (S, D) and the point $\Gamma$.

(A) S has three singular points and $D=0$. In this possibility $\Gamma \not \in {\text {Supp}}({\text {Sing}}S)$.

(B) $\Gamma \not \in D_{i_1}\cup D_{i_2}$, where $i_1\ne i_2$. To be definite, let $D_{i_1}-D_{i_2}$ be a nef divisor.

(C) S has two singular points, that is, $S\cong {\mathbb P}(a_1,a_2,1)$, where $a_1\ge 3$, $a_2\ge 2$ and $\Gamma =(b:1:0)$, where $b\ne 0$.

(D) $S\cong {\mathbb P}(a_1,a_2,1)$, $D=\frac{1}{2}\{x_1=0\}+\frac{1}{2}\{x_2=0\}$, $a_1\ge 2$, $a_2\ge 1$ and $\Gamma =(1:0:b)$, where $b\ne 0$.

Possibility (B) is impossible since ${\text {LCS}}(S,T-\frac{1}{2}D_{i_1}+\frac{1}{2}D_{i_2})=\Gamma \cup D_{i_2}$, that is, we have the contradiction with connectedness lemma. Possibility (D) is impossible since ${\text {LCS}}(S,T-\frac{1}{2}\{x_1=0\}+\{x_3=0\})=\Gamma \cup \{x_3=0\}$, that is, we have the contradiction with connectedness lemma. Consider possibility (C). Write $T=a\{x_3=0\}+T'$, where $\{x_3=0\}\not \subset {\text {Supp}}(T')$ and $0\le a<1$. The divisor $K_S+\{x_3=0\}+T'$ is not log canonical at the point $\Gamma$, therefore by the inversion of adjunction we have $\big (\{x_3=0\}\cdot T'\big )_{\Gamma }>1$. We obtain the contradiction

$$ 1<\big (\{x_3=0\}\cdot T'\big )_{\Gamma }<\{x_3=0\}\cdot (-K_S)=\frac{a_1+a_2+1}{a_1a_2}\le 1. $$

Consider possibility (A). Let $f:(Y,E) \rightarrow (S \ni \Gamma )$ be an inductive blow-up of (S, T) (see Theorem 1.10). By Theorem 2.12 the morphism f is a weighted blow-up of smooth point with weights $(\alpha _1,\alpha _2)$. Write $K_Y+E+T_Y=f^*(K_S+T)$.   $\square$

Lemma 4.3

The divisor $K_S$ has a 1-complement $B^{+}$ such that $\Gamma$ is a center of ${\text {LCS}}(S,B^{+})$.

Proof

The divisor $K_Y+E+(1-\delta )T_Y$ is plt and anti-ample for $0<\delta \ll 1$. Since $\rho (Y)=2$ then the cone $\overline{{\text {NE}}}(Y)$ is degenerated by two extremal rays. By $R_1$ and $R_2$ denote these two rays. To be definite, let $R_1$ gives the contraction f. If $-(K_Y+E)$ is a nef divisor then a 1–complement of $K_E+{\text {Diff}}_E(0)=K_E+\frac{\alpha _1-1}{\alpha _1}P_1+\frac{\alpha _2-1}{\alpha _2}P_2$ is extended to a 1–complement of $K_Y+E$ by Proposition 1.17, therefore we obtain the required 1–complement of $K_S$ by Proposition 1.15.

Consider the last possibility: $(K_Y+E)\cdot R_2>0$, $T_Y\cdot R_2<0$. Let $L(\delta )\in |-n(K_Y+E+(1-\delta )T_Y)|$ be a general element for $n\gg 0$ and let $M=(1-\delta )T_Y+\frac{1}{n}L(\delta )$, where $\delta >0$ is a sufficiently small fixed rational number. By construction, $K_Y+E+(1+\varepsilon )M\equiv \varepsilon M$, $K_Y+E+(1+\varepsilon )M$ is a plt divisor. Therefore, applying $(K_Y+E+(1+\varepsilon )M)$–MMP is a contraction of the ray $R_2$ for $0<\varepsilon \ll 1$. The corresponding divisorial contraction is denoted by $h:Y\rightarrow \overline{S}$, and the image of E on the surface $\overline{S}$ is denoted by $\overline{E}$, put ${\text {Exc}}h=C_Y$ and $C_S=f(C_Y)$. The divisor $K_{\overline{S}}+\overline{E}$ is plt and anti-ample. Therefore, if 1–complement of $K_{\overline{E}}+{\text {Diff}}_{\overline{E}}(0)$ exists then we consistently apply Theorems 1.17, 1.16 and 1.15 and obtain the required 1–complement of $K_S$.

Suppose that there does not exist any 1–complement of $K_{\overline{E}}+{\text {Diff}}_{\overline{E}}(0)$. It is possible if and only if there are three singular points of $\overline{S}$ lying on the curve $\overline{E}$. It implies that $\alpha _1\ge 2$, $\alpha _2\ge 2$, the curve $C_Y$ is contracted to a cyclic singularity, and the curve $C_S$ passes through at most one singularity of S (see [11, Chap. 3]). Let us apply Corollary 9.2 of the paper [10] for $K_{\overline{S}}+\overline{E}$. We obtain that S has the two singularities of type ${\mathbb A}_1$, which do not lie on the curve $C_S$. Let $V(\langle n_1\rangle )$ be the closure of one-dimensional orbit passing through the two singular points of type ${\mathbb A}_1$. Then there exists an isomorphism of the lattice N such that $n_1=(1,0)$, $n_2=(1,2)$, and therefore $n_3=(-2n+1,-2)$, where $n\ge 2$. By considering the cone $\langle n_2, n_3 \rangle$ we obtain that the third singularity of S is of type $\frac{1}{4n-4}(2n-1,1)$, its minimal resolution graph consists of three exceptional curve chain with the self-intersection indices $-2$, $-n$ and $-2$ respectively. The following two cases are possible: (i) $\Gamma \in V(\langle n_2\rangle )\cup V(\langle n_3\rangle )$ and (ii) $\Gamma \not \in V(\langle n_2\rangle )\cup V(\langle n_3\rangle )$.

Consider former Case (i). To be definite, let $\Gamma \in V(\langle n_2\rangle )$, then $V(\langle n_2\rangle )\cdot (-K_S)=\frac{n}{2n-2}\le 1$, and therefore we obtain a contradiction for the same reason as in Case (C).

Consider latter Case (ii). Let $g:S^{\min }\rightarrow S$ be a minimal resolution. Let us contract all curves of ${\text {Exc}}g$, except the exceptional curve of the singularity $\frac{1}{4n-4}(2n-1,1)$ with the self-intersection index $-n$. We obtain the divisorial contractions $S^{\min }\rightarrow \widetilde{S}$ and $\widetilde{S}\rightarrow S$. Note that $\rho (\widetilde{S})=2$ and $\widetilde{S}=T_N(\widetilde{\Delta })$, where the fan $\widetilde{\Delta }$ is given by $\Delta$ with the help of subdivision of the cone $\langle n_2, n_3 \rangle$ into the two cones $\langle n_2, n_4 \rangle$, $\langle n_4, n_3 \rangle$, where $n_4=(-1,0)$. The surface $\widetilde{S}$ is a conic bundle with irreducible fibers, and its two fibers are non-reduced. These two fibers are the curves $V(\langle n_2\rangle )$, $V(\langle n_3\rangle )$, and every such curve contains the two singularities of type ${\mathbb A}_1$. By $\widetilde{\Gamma }$ denote the transform of $\Gamma$ on the surface $\widetilde{S}$. We have $K_{\widetilde{S}}+\widetilde{B}^+_1+\widetilde{B}^+_2+V(\langle n_4\rangle )\sim 0$, where $\widetilde{B}^+_1\sim V(\langle n_2\rangle )+V(\langle n_3\rangle )$ is the fiber passing through the point $\widetilde{\Gamma }$, and $\widetilde{B}^+_2\sim V(\langle n_1\rangle )$ is the section passing through the point $\widetilde{\Gamma }$. By Proposition 1.15 we obtain the required 1–complement of $K_S$.   $\square$

Assume that $B^+=B_1^+ + B^{+'}$, where the irreducible curve $B_1^+$ has an ordinary double point singularity at the point $\Gamma$. By the inversion of adjunction we have $B^{+'}=0$, $B_1^+\cap {\text {Supp}}({\text {Sing}}S)=\emptyset$ and $K_S+B_1^+\sim 0$, therefore $K_S$ is Cartier divisor. Classification of Del Pezzo surfaces with Du Val singularities (in our case Du Val singularities are cyclic), with Picard number 1 and with three singular points implies $K^2_S\le 4$ [3]. Write $T=aB_1^++T'$, where $B_1^+\not \subset {\text {Supp}}(T')$ and $0\le a<1$. Since $0\sim K_Y+E+\widetilde{B_1^+}=f^*(K_S+B_1^+)$ then we obtain the contradiction

$$\begin{aligned} 0>&(K_Y+E+T_Y)\cdot \widetilde{B_1^+}\ge (-1+a)\Big (\widetilde{B_1^+}\Big )^2=\\ {}&=(-1+a)\Big (K_S^2-\frac{(\alpha _1+\alpha _2)^2}{\alpha _1\alpha _2}\Big )\ge 0. \end{aligned}$$

Consider the last case $B^+=B_1^+ +B_2^+ +B^{+'}$, where the irreducible curves $B_1^+$ and $B_2^+$ have a simple normal crossing at the point $\Gamma$. We have $(B_1^+\cup B_2^+)\supset {\text {Supp}}({\text {Sing}}S)$ according to Corollary 9.2 of the paper [10] applied for $K_{S}+B_1^+ +B_2^+$. To be definite, let the curve $B_1^+$ contains two singular points of S. By the inversion of adjunction, $\deg {\text {Diff}}_{B_1^+}(0)\le 1$, and therefore the curve $B_1^+$ passes through two singular points only, and they are of type ${\mathbb A}_1$. Such surfaces were classified in the proof of Lemma 4.3, and therefore it can be assumed that the third singularity of S is of type $\frac{1}{4n-4}(2n-1,1)$, $B^{+'}=0$, $B^+_1\cap B^+_2=\Gamma$, $(B_1^+)^2=n-1$ and $(B_2^+)^2=\frac{1}{n-1}$, where $n\ge 2$. To be definite, assume that $f^*(B_1^+)=\widetilde{B_1^+}+\alpha _1E$ and $f^*(B_2^+)=\widetilde{B_2^+}+\alpha _2E$. Thus $(\widetilde{B_1^+})^2=n-1-\alpha _1/\alpha _2$, $(\widetilde{B_2^+})^2=\frac{1}{n-1}-\alpha _2/\alpha _1$, and therefore $(\widetilde{B_k^+})^2\le 0$ for either $k=1$ or $k=2$. Write $T=a_1B_1^++a_2B_2^++T'$, where $B_1^+, B_2^+\not \subset {\text {Supp}}(T')$, $0\le a_1< 1$, $0\le a_2<1$. Since $0\sim K_Y+E+\widetilde{B_1^+}+\widetilde{B_2^+}=f^*(K_S+B_1^++B_2^+)$, then we obtain the contradiction

$$\begin{aligned} 0>&(K_Y+E+T_Y)\cdot \widetilde{B_k^+}= (-1+a_k)\Big (\widetilde{B_k^+}\Big )^2+T'_Y\cdot \widetilde{B_k^+}\ge \\ {}&\qquad \, \ge (-1+a_k)\Big (\widetilde{B_k^+}\Big )^2\ge 0. \end{aligned}$$

Consider Condition (2). Such toric surface is determined by the fan $\Delta$ in the lattice $N\cong {\mathbb Z}^2$, where

$$ \Delta =\big \{\langle m_1, m_2\rangle ,\langle m_2, m_3\rangle , \langle m_3, m_4,\rangle , \langle m_4, m_1\rangle , \text {their faces} \big \}, $$

$m_1=(1,0)$, $m_2=(q,r)$, $m_3=(-1,0)$, $m_4{=}(-q,-r)$, $q\ge 1$, $r\ge 1$ and $\gcd (q,r)=1$. Therefore S has four singularities of types $\frac{1}{r}(1,-q)$, $\frac{1}{r}(1,q)$, $\frac{1}{r}(1,-q)$ and $\frac{1}{r}(1,q)$ respectively.

Two different fibers passing through the point $\Gamma$ are denoted by $F_1$ and $F_2$. Since $T\cdot F_i\ge 1$ by Lemma 4.4 for $i=1,2$, then $T-F_1-F_2$ is nef.

Lemma 4.4

Let O be a smooth point of the surface M. Assume (M, N) is not a log canonical pair at the point O, where $N=dI+\Sigma \ge 0$, $I\not \subset {\text {Supp}}\Sigma$, $d\le 1$, I is an irreducible curve which is a smooth at the point O. Then $(\Sigma \cdot I)_O>1$.

Proof

The proof follows by the inversion of adjunction, see, for example, [12, Theorem 7.5].   $\square$

Consider the index j such that $F_j$ is non-toric subvariety of (S, D). Let $F'$ and $F''$ be the closures of one-dimensional toric orbits provided that $F'\sim _{{\mathbb Q}} F''\sim _{{\mathbb Q}}\frac{1}{r} F_j$. We obtain the contradiction $(K_S+T)\cdot F_i\ge (-F'-F''+D+F_j)\cdot F_i\ge 0$, where the index $i\in \{1,2\}$ satisfies the condition $i\ne j$.

Consider Condition (3). Assume that either $\Gamma \in C_{13}$, or $\Gamma \in C_{23}$. Let us consider the first possibility. The second possibility is considered similarly. If $\Gamma$ is a non-toric point of $(C_{13},{\text {Diff}}_{C_{13}}(D))$ then we have a contradiction with one-dimensional analog of this theorem since $C_{13}^2<0$. Therefore, $a_4=1$ and $d_{23}=1$. The case $C^2_{23}=0$ is impossible also (in this case the surface S is a toric conic bundle, and we use its structure). Thus $C_{23}^2<0$ and consider the contraction $\psi :S\rightarrow S'$ of $C_{23}$. If $\psi (\Gamma )$ is a non-toric point of $(S',\psi (D))$ then we have a contradiction with this theorem under Condition (1). Therefore the curve $C_{23}$ is contracted to a smooth point and $d_{24}=1$. We obtain the contradiction $a_2d_{13}d_{14}=w_2>w_4=d_{13}$.

Assume that $\Gamma \in C_{13}\cup C_{23}$. Let $C_{23}^2=0$. Then $(w_3,w_4)=(w_1,w_2)$, $(S,D)\cong \big ({\mathbb F}_{w_1-w_2},\frac{w_2-1}{w_2}C_{13}+\frac{w_1-1}{w_1}C_{24}\big )$ and $2\le w_1<w_2$. By $F_j$ denote a fiber of S passing through $\Gamma$. Then $T'\cdot F_j\ge 1$ by Lemma 4.4, where $T=T'+\alpha F_j$, $F_j\not \subset {\text {Supp}}(T')$, and we have the contradiction $0>(K_S+T)\cdot F_j\ge (K_S+F_j+T')\cdot F_j\ge 0$.

Therefore $C_{23}^2<0$, $C_{13}^2<0$. Considering case by case the contractions of the curves $C_{13}$ and $C_{23}$, we obtain that these curves are contracted to smooth points and $d_{13}=d_{23}=d_{24}=d_{14}=1$. Since $C_{13}^2=-\frac{1}{a_2a_4}$, $C_{23}^2=-\frac{1}{a_1a_4}$ then $(w_1,w_2,w_3,w_4)=(a_2,a_2,a_2-1,a_2+1)$, $a_2\ge 3$. It is easy to find a birational map

$$ S\dashrightarrow S'\bigg (\frac{1}{a_2-1}(1,-1)+\frac{1}{a_2-1}(1,1)+\frac{1}{a_2-1}(1,-1)+\frac{1}{a_2-1}(1,1)\bigg ), $$

where $\rho (S')=2$, and in result of this map we obtain a contradiction with this theorem under Condition (2). To find this map it is enough to consider two (required) toric blow-ups at the points $P_2$, $P_4$ and a contraction of proper transforms of $C_{13}$ and $C_{23}$.   $\square$

Remark 4.5

Theorem 4.2 (1) can not be generalized to the case $\rho (S)\ge 2$. Consider the toric pair$(S,D)=({\mathbb F}_1,\frac{1}{2}E_0)$ and the divisor $T=\frac{1}{2}E_0+E'_0+F+\delta E_{\infty }$ provided that $F\cap E'_0\not \in E_0\cup E_{\infty }$, where $E_0$, $E'_0$ are two different zero sections, $E_{\infty }$ is the infinity section, F is a fiber and $0<\delta <\frac{1}{2}$. Put $\Gamma =F\cap E'_0$. Then $\Gamma$ is a non-toric point of (S, D), $T\ge D$, $K_S+T$ is anti-ample log canonical divisor and $\Gamma \in {\text {LCS}}(S,T)$.

Nevertheless, it is expected that Theorem 4.2 can be generalized to every dimension and every Picard number $\rho (S)$, if we require the following condition, instead of Conditions (1), (2) and (3): $(S,D)=(E,{\text {Diff}}_E(0))$, where $f:(Y,E)\rightarrow (X\ni P)$ is a toric plt blow-up of some toric singularity.

Definition 4.6

Let $(\Gamma ,D_{\Gamma })\cong ({\mathbb P}^1,\sum _{i=1}^r\frac{m_i-1}{m_i}P_i)$. Assume that $-(K_{\Gamma }+D_{\Gamma })$ is an ample divisor. Then, for set $(m_1,\ldots ,m_r)$ we have one of the following cases up to permutations: $(m_1,m_2)$, it is of type A; (2, 2, m), $m\ge 2$, it is of type $D_{m+2}$; (2, 3, 3), it is of type $E_6$; (2, 3, 4), it is of type $E_7$; (2, 3, 5), it is of type $E_8$. In Propositions 4.7 and 4.8 the classification according to types corresponds to the types of $(\Gamma ,D_{\Gamma })=(\Gamma ,{\text {Diff}}_{\Gamma }(D))$.

Proposition 4.7

Let (S, D) be a toric pair, where S is a normal projective surface with $\rho (S)=1$, and let D be a divisor with standard coefficients. Assume that there exists a curve $\Gamma$ such that $-(K_S+D+\Gamma )$ is an ample divisor and $(S,D+\Gamma )$ is a plt non-toric pair. Let us denote a hypersurface of degree d in a weighted projective space by $X_d$. Then one of the following cases is satisfied.

(1) $(S,D,\Gamma )\cong ({\mathbb P}^2_{x_1x_2x_3},\frac{d_1-1}{d_1}\{x_1=0\},X_2)$ and $d_1\ge 1$. It is of type A.

(2) $(S,D,\Gamma )\cong ({\mathbb P}^2_{x_1x_2x_3},\sum _{i=1}^3\frac{d_i-1}{d_i}\{x_i=0\},X_1)$, the integer number triple $(d_1,d_2,d_3)$ is either (2, 2, k), (2, 3, 3), (2, 3, 4) or (2, 3, 5), where $k\ge 2$. They are of types $D_{k+2}$, $E_6$, $E_7$ and $E_8$ respectively.

(3) $(S,D,\Gamma )\cong ({\mathbb P}_{x_1x_2x_3}(a_1,1,1), \sum _{i=1}^2\frac{d_i-1}{d_i}\{x_i=0\},X_{a_1})$, the integer number triple $(a_1,d_1,d_2)$ is either $(2,2,k_1)$, $(2,3,k_2)$, $(2,k_3,1)$ or (3, 2, 1), where $k_1\ge 1$, $1\le k_2\le 2$, $k_3\ge 4$. In the first possibility, if $k_1\ge 2$ then it is of type $D_{k_1+2}$. In the second possibility, if $k_2=2$ then it is of type $E_6$. The other possibilities are of type A always.

(4) $(S,D,\Gamma )\cong ({\mathbb P}_{x_1x_2x_3}(a_1,1,1), \frac{d_1-1}{d_1}\{x_2=0\},X_{a_1+1})$, $a_1\ge 2$ and $d_1\ge 1$. It is of type A.

(5) $(S,D,\Gamma )\cong ({\mathbb P}_{x_1x_2x_3}(a_2+1,a_2,1), \sum _{i=1}^2\frac{d_i-1}{d_i}\{x_i=0\},X_{a_2+1})$, the integer number triple $(a_2,d_1,d_2)$ is either $(2,2,k_1)$, $(k_2,2,k_3)$ or $(k_4,k_5,1)$, where $k_1\le 3$, $k_2\ge 3$, $k_3\le 2$, $k_4\ge 2$ and $k_5\ge 3$. In the first possibility, if $k_1=2$ then it is of type $D_6$, and, if $k_1=3$ then it is of type $E_7$. In the second possibility, if $k_3=2$ then it is of type $D_{2k_2+2}$. The other possibilities are of type A always.

(6) $(S,D,\Gamma )\cong ({\mathbb P}_{x_1x_2x_3}(2a_2+1,a_2,1), \frac{1}{2}\{x_1=0\},X_{2a_2+1})$, $a_2\ge 2$. It is of type $D_{2a_2+2}$.

(7) $(S,D,\Gamma )\cong ({\mathbb P}_{x_1x_2x_3}(la_2-1,a_2,1), \sum _{i=1}^2\frac{d_i-1}{d_i}\{x_i=0\},X_{la_2})$, $a_2\ge 2$, the integer number triple $(l,d_1,d_2)$ is either (2, 2, 1) or $(k_1,1,k_2)$, where $k_1\ge 2$ and $k_2\ge 1$. They are of types $D_{2a_2+1}$ and A respectively.

(8) $(S,D,\Gamma )\cong ({\mathbb P}_{x_1x_2x_3}(a_1,a_2,1), \frac{d_1-1}{d_1}\{x_3=0\},X_{a_1+a_2})$, $a_1>a_2\ge 2$ and $d_1\ge 1$. It is of type A.

(9) $(S,D)\cong (S(\frac{1}{r_1}(1,1)+\frac{1}{r_2}(1,1)+{\mathbb A}_{r_1+r_2-1}),\frac{d_1-1}{d_1}D_3)$, $\Gamma \sim _{{\mathbb Q}}D_3$ is an irreducible curve being different from $D_3$, where $D_3$ is the closure of one-dimensional orbit passing through the first and second singular points, $d_1\ge 2$ and $r_1$, $r_2\ge 2$. It is of type A.

(10) $(S,D)\cong (S(\frac{1}{r_1}(l,1)+\frac{1}{r_2}(l,1)+{\mathbb A}_{(r_1+r_2)/l-1}),\frac{d_1-1}{d_1}D_3)$, the surface S has three singular points, $\Gamma \sim D_1+D_2$, where $D_i$ is the closure of one-dimensional orbit not passing through the i-th singular point of S, $d_1\ge 1$, $l\ge 2$ and $l|(r_1+r_2)$. It is of type A.

Proof

By the adjunction formula the curve $\Gamma$ is smooth and irreducible. It follows easily that, if $P\in {\text {Supp}}D\cap \Gamma$ then $(S,D+\Gamma )$ is a toric pair in a sufficiently small analytical neighborhood of P. If S is a smooth surface then $S\cong {\mathbb P}^2$ and we have two Cases (1) and (2).

Assume that S is a non-smooth surface having at most two singular points. Then we have $S\cong {\mathbb P}_{x_1x_2x_3}(a_1,a_2,1)$ as before in the proof of Theorem 4.2. At first let us consider the case of one singular point, that is, $a_1\ge 2$ and $a_2=1$. Then either $\Gamma \sim {\mathcal O}_S(1)$, ${\mathcal O}_S(a_1)$ or ${\mathcal O}_S(a_1+1)$. The variant $\Gamma \sim {\mathcal O}_S(1)$ is impossible since $K_S+D+\Gamma$ is not a plt divisor at the point (1 : 0 : 0). The other variants lead us to Cases (3) and (4) respectively. At second let us consider the case of two singular points, that is, $a_1>a_2\ge 2$. Put $\Gamma =\{\psi (x_1,x_2,x_3)=0\}$. Suppose that $\Gamma \not \sim {\mathcal O}_S(a_1+a_2)$, ${\mathcal O}_S(a_1)$, ${\mathcal O}_S(a_2)$, ${\mathcal O}_S(1)$ then $\psi (x_1,x_2,x_3)=bx_1x_3^l+\varphi (x_2,x_3)$, and by considering the point (1 : 0 : 0) we obtain $b\ne 0$, $l=1$, $\Gamma \sim {\mathcal O}_S(a_1+1)$ and $x_2^m\in \varphi (x_2,x_3)$. It leads us to Case (7). If $\Gamma \sim {\mathcal O}_S(a_1)$ then by considering the point (0 : 1 : 0) we obtain $x_1,x_2^lx_3\in \psi (x_1,x_2,x_3)$. It leads us to Cases (5) and 6). It is easy to prove that cases $\Gamma \sim {\mathcal O}_S(a_2)$ and $\Gamma \sim {\mathcal O}_S(1)$ are not realized. If $\Gamma \sim {\mathcal O}_S(a_1+a_2)$ then $x_1x_2,x_3^{a_1+a_2}\in \psi (x_1,x_2,x_3)$, and we have Case (8).

Assume that S is a surface having three singular points (it is the last possibility for S). According to Corollary 9.2 of the paper [10] for the divisor $K_S+\Gamma$, we obtain that the curve $\Gamma$ contains a singular point of S.

Suppose that the curve $\Gamma$ contains only one singular point of S, then arguing as above in the proof of Theorem 4.2, we obtain $S=S(2{\mathbb A}_1+\frac{1}{4n-4}(2n-1,1))$, where $n\ge 2$, and $\Gamma$ is locally a toric subvariety of $(S\ni P)$, where $(S\ni P)$ is of type $\frac{1}{4n-4}(2n-1,1)$. By $T_1$ and $T_2$ denote the closures of one-dimensional orbits passing through the singular point P. Since $T_1\sim T_2$ and $(\Gamma \cdot T_1)_P\ne (\Gamma \cdot T_2)_P$ then $\Gamma \cdot T_i>1$. Therefore $\Gamma -(4n-4)T_1$ is an ample divisor, and we obtain the contradiction with ampleness of $-(K_S+\Gamma )\sim 2nT_1-\Gamma$. Thus this possibility is not realized.

Suppose that the curve $\Gamma$ passes through the two singular points $P_1$ and $P_2$ of S only. There exists a 1-complement of $K_{\Gamma }+{\text {Diff}}_{\Gamma }(0)$, and we obtain the 1-complement $K_S+\Gamma +T\sim 0$ of $K_S+\Gamma$ by Proposition 1.17. There are two Cases (A) and (B).

(A) Let T is a reducible divisor. By the two-dimensional criterion on the characterization of toric varieties [26, Theorem 6.4] we have $T=T_1+T_2$, $\Gamma \sim T_3$, $D=\frac{d_1-1}{d_1}T_3$, the singularities at the points $P_j$ are of type $\frac{1}{r_j}(1,1)$, where $d_1\ge 2$, $r_j\ge 2$ and $T_i$ are the closures of one-dimensional orbits, and $P_1\in T_1$. Let $f:\widetilde{S}\rightarrow S$ be a minimal resolution at the points $P_1$ and $P_2$ only. By $E_1$ denote the curve such that $f(E_1)=P_1$. By the inversion of adjunction $\Gamma \cdot T_3=\frac{1}{r_1}+\frac{1}{r_2}$, hence $(\Gamma _{\widetilde{S}})^2=\Gamma _{\widetilde{S}}\cdot (T_3)_{\widetilde{S}}=0$, and the linear system $|E_1+m\Gamma _{\widetilde{S}}|$ gives the birational morphism $g:\widetilde{S}\rightarrow {\mathbb F}_{r_1}$ for $m\gg 0$ [15, Proposition 1.10] such that the curve $(T_2)_{\widetilde{S}}$ is contracted to a smooth point. The morphism g is toric and the third singularity of S is of type ${\mathbb A}_{r_1+r_2-1}$. We obtain Case (9).

(B) Let T is an irreducible divisor. To be definite, let $D_i$ be the closures of one-dimensional orbits not passing through the i-th singular point of $S=S(\frac{1}{r_1}(a_1,1)+\frac{1}{r_2}(a_2,1)+\frac{1}{r_3}(a_3,1))$. We have $\frac{1}{r_1}D_1\equiv \frac{1}{r_2}D_2\equiv \frac{1}{r_3}D_3$. To be definite, the curve $\Gamma$ passes through the first and second singular point of S. By the definition of 1–complement we obtain $\Gamma \cdot T=\frac{1}{r_1}+\frac{1}{r_2}$, $\Gamma +T\sim \sum _{i=1}^3D_i$. Hence, either $\Gamma \sim D_1+D_2$, $T\sim D_3$ or $\Gamma \sim D_3$, $T\sim D_1+D_2$. Since 1–complement not passing through the third singular point of S then it is of type ${\mathbb A}_{r_3-1}$. The case $\Gamma \sim D_3$ was considered in Case (A). Since the curve $\Gamma$ does not pass through the third singular point then we have to consider the possibility remained: $\Gamma \sim D_1+D_2\sim lD_3$, where $l\ge 2$, $l\in {\mathbb Z}$. We obtain Case (10).

Suppose that the curve $\Gamma$ passes through three singular points of S with the indices $r_1$, $r_2$ and $r_3$ respectively. By the inversion of adjunction the triple $(r_1,r_2,r_3)$ is either (2, 2, k), (2, 3, 3), (2, 3, 4) or (2, 3, 5), where $k\ge 2$. For the second and third variants there does not exist any surface S. For the first and fourth variants we have $S=S(2{\mathbb A}_1+\frac{1}{4n-4}(2n-1,1))$ and $S\cong {\mathbb P}(2,3,5)$ respectively, where $n\ge 2$. These variants are considered as above mentioned case, when the curve $\Gamma$ contains only one singular point of S.   $\square$

Proposition 4.8

Let (S, D) be ODP pair. Assume that there exist a curve $\Gamma$ and an effective ${\mathbb Q}$-divisor $\Gamma '$ such that $K_S+D+\Gamma +\Gamma '$ is an anti-ample and plt divisor, and $(S,D+\Gamma )$ is a non-toric pair. Then $d_{23}=d_{24}=1$, $a_1|a_2$ and $\Gamma \sim {\mathcal O}_{{\mathbb P}(\textbf{w})}(w_2)|_S$ up to permutation of the coordinates. In particular, $-(K_S+D+\Gamma )$ is an ample divisor and $w_1|w_2$. It is of type A.

Proof

The sets $\Gamma \cap C_{13}$, $\Gamma \cap C_{23}$ consist of at most one point by the adjunction formula. Moreover, we may assume that $\Gamma '=\gamma _1C_{13}+\gamma _2C_{23}$, where $\gamma _1<1$ and $\gamma _2<1$. If $C_{i3}^2=0$ then $\gamma _i=0$, where $i=1,2$.

Let us prove that $\Gamma \cdot C_{13}>0$ and $\Gamma \cdot C_{23}>0$. Assuming the converse: $\Gamma \cdot C_{13}=0$, that is, $\Gamma \sim dC_{24}$. The possibility $\Gamma \cdot C_{23}=0$ is considered similarly. Since $C_{23}\cdot C_{24}=\frac{1}{a_1}$, $a_1(C_{23}\cdot \Gamma )\in {\mathbb Z}_{>0}$ then $d\in {\mathbb Z}_{>0}$. The divisor $C_{24}-\gamma C_{13}$ is nef for $0\le \gamma \le \frac{1}{d_{13}}$, hence it is semiample by the base point free theorem [9]. Therefore, if $d\ge 2$ then we have a contradiction with connectedness lemma, since there exists a ${\mathbb Q}$–divisor $\Gamma ''$ such that $\llcorner \Gamma '' \lrcorner =0$ and $D+\Gamma +\Gamma '\sim _{{\mathbb Q}} C_{24}+C_{13}+\Gamma ''$. Thus, $d=1$. Since the curve $\Gamma$ is a non-toric subvariety of (S, D) then $d_{24}\ge 2$, and we have $d_{13}=1$ by connectedness lemma again. We obtain the contradiction

$$\begin{aligned}&\qquad \, \qquad \, 0>(K_S+D+\Gamma +\Gamma ')\cdot C_{23}\ge \\&\ge \Big (\frac{d_{24}-1}{d_{24}}C_{24}-C_{13}-C_{23}-C_{14}+\Gamma '\Big )\cdot C_{23}\ge \\ \ge&\frac{d_{24}-1}{d_{24}}C_{24}\cdot C_{23}-C_{13}\cdot C_{23}=d_{23}\Big (\frac{d_{24}-1}{w_1}-\frac{1}{w_4}\Big )\ge 0. \end{aligned}$$

Thus, we proved that the sets $\Gamma \cap C_{13}$ and $\Gamma \cap C_{23}$ consist of one point only.

Suppose that $P_4\not \in \Gamma$. Then $\Gamma \sim _{{\mathbb Q}} \alpha _1C_{14}+\alpha _2C_{24}$, $\alpha _1=a_2(\Gamma \cdot C_{13})\in {\mathbb Z}_{>0}$ and $\alpha _2=a_1(\Gamma \cdot C_{23})\in {\mathbb Z}_{>0}$. By applying connectedness lemma we have $\alpha _1=\alpha _2=1$. Let us prove that $d_{14}=d_{24}=1$. Assuming the converse: $d_{14}\ge 2$. The possibility $d_{24}\ge 2$ is considered similarly. In order to apply connectedness lemma and obtain a contradiction (for the disjoint curves $C_{14}$, $C_{23}$) we must only prove that $D_1=\frac{d_{14}-1}{d_{14}}C_{14}+C_{24}+\frac{d_{24}-1}{d_{24}}C_{24}-\frac{1}{d_{23}}C_{23}$ is a semiample divisor. Since $D_1\cdot C_{23}>0$ and $D_1\cdot C_{13}=d_{13}(\frac{d_{14}-1}{w_2}-\frac{1}{w_4})\ge 0$ then $D_1$ is a nef divisor and it is semiample by the base point free theorem [9]. Finally, since $K_S+\Gamma +C_{13}+C_{23}\sim 0$ then $K_S$ is Cartier divisor at the point $P_3$, and the singularity at the point $P_3$ is Du Val of type $\frac{1}{w_3}(w_1, w_2)$. Therefore $w_3+w_4=w_1+w_2\equiv 0 ({\text {mod}} w_3)$, $w_3|w_4$ and $a_3|a_4$.

Suppose that $P_4\in \Gamma$. Since the curve $\Gamma$ is a (locally) toric orbit in some analytical neighborhood of $P_4$ then either $\Gamma \cdot C_{13}=\frac{1}{a_4}$ or $\Gamma \cdot C_{23}=\frac{1}{a_4}$. Let us consider the former case. The latter case is considered similarly. Write $\Gamma \sim _{{\mathbb Q}} \alpha _1C_{23}+\alpha _2C_{24}$, $\alpha _1=a_4(\Gamma \cdot C_{13})=1$ and $\alpha _2=a_3(\Gamma \cdot C_{14})\in {\mathbb Z}_{>0}$. Arguing as above, we see that $\alpha _2=1$, $d_{24}=1$. If $d_{23}=1$ then this proposition is proved. Let $d_{23}\ge 2$. By the plt assumption of this proposition $\Gamma \cdot C_{23}=\frac{1}{a_4}$ and $d_{13}=1$. Considering $\Gamma \sim _{{\mathbb Q}} C_{13}+\alpha _2'C_{14}$ we obtain $\alpha _2'=1$, $d_{14}=1$. This completes the proof.   $\square$

Definition 4.9

The triple $(S,D,\Gamma )$ determined by the assertions of Propositions 4.7 or 4.8 is said to be a purely log terminal triple.

The following problem is important for the classification of plt blow-ups of three-dimensional toric non-${\mathbb Q}$-factorial singularity (if we follow the method described in this paper).

Problem

Let $(S,D)=(E,{\text {Diff}}_E(0))$, where $f:(Y,E)\rightarrow (X\ni P)$ is a toric plt blow-up of some toric three-dimensional (non-${\mathbb Q}$-factorial) singularity. Assume that there exist a curve $\Gamma$ and an effective ${\mathbb Q}$-divisor $\Gamma '$ such that $K_S+D+\Gamma +\Gamma '$ is an anti-ample plt divisor, and $\Gamma$ is a non-toric subvariety of (S, D). Classify the triples $(S,D,\Gamma )$.

5 Non-toric Three-dimensional Blow-ups. Case of Point

Example 5.1

Now we construct the examples of three-dimensional non-toric plt blow-ups $f:(Y,E)\rightarrow (X\ni P)$ provided that $(X\ni P)$ is a ${\mathbb Q}$-gorenstein toric singularity and $P=f(E)$. Depending on a type of $(X\ni P)$ we consider two Cases (A1) and (A2).

(A1). Let $(X\ni P)$ be a ${\mathbb Q}$-factorial toric singularity, that is, $(X\ni P)\cong ({\mathbb C}^3\ni 0)/G$, where G is an abelian group acting freely in codimension 1. All plt blow-ups are constructed by the procedure illustrated on the next diagram (Fig. 4) and defined below.

First step. Let $g_0:(Z_0,S_0)\rightarrow (X\ni P)$ be a toric blow-up, where ${\text {Exc}}g_0=S_0$ is an irreducible divisor and $g_0(S_0)=P$. Assume that there exists a curve $\Gamma _0\subset S_0$ such that $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ is a plt triple (see Definition 4.9). Such triples are classified in Proposition 4.7 and are divided into the five types: A, $D_l$, $E_6$, $E_7$ and $E_8$.

Fig. 4

Case of Point. Construction in ${\mathbb Q}$-factorial case

Remark 5.2

There exists an irreducible reduced Weil divisor $\Omega$ on X such that $\Omega _{Z_0}|_{S_0}=\Gamma _0$. The surface $\Omega$ has a log terminal singularity at the point P. A singularity type coincides with a type of the triple $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$. In particular, if $\psi$ is a G–semi-invariant polynomial in ${\mathbb C}^3$ determining $\Omega$ then Du Val singularity $\{\psi =0\}\subset ({\mathbb C}^3 \ni 0)$ is of the same type.

The following lemma gives a restriction on the triple $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ in the case of terminal singularities.

Lemma 5.3

Let $(X\ni P)$ be a terminal singularity, that is, it is of type $\frac{1}{r}(-1,-q,1)$, where $\gcd (r,q)=1$ and $1\le q\le r$. Write ${\text {Diff}}_{S_0}(0)=\sum _{i=1}^3\frac{d_i-1}{d_i}D_i$, where $D_i$ are the closures of corresponding one-dimensional orbits of the toric surface $S_0$. Then $\gcd (d_i,d_j)=1$ for $i\ne j$.

Proof

It is sufficient to prove that the singularities of $Z_0$ are cyclic. Consider the cone $\sigma$ determining the singularity $(X\ni P)$ (see Example 2.2 (1)). By $(w_1,w_2,w_3)$ denote the primitive vector defining the blow-up $g_0$. Then $Z_0$ is covered by three affine charts with the singularities of types $\frac{1}{w_3}(-w_1,-w_2,1)$, $\frac{1}{rw_2-qw_3}(-w_1+uw_2+vw_3,-uw_2-vw_3,1)$ and $\frac{1}{rw_1-w_3}(-w_1,qw_1-w_2,1)$, where $uq+vr=1$ and u, $v\in {\mathbb Z}$.   $\square$

According to Proposition 4.7 the curve $\Gamma _0$ is locally a toric subvariety of $Z_0$ in every sufficiently small analytic neighborhood of each point of $\Gamma _0$. Note also that $Z_0$ is a smooth variety at a general point of $\Gamma _0$.

Let $h_0:(Y_0,\widetilde{S}_1)\rightarrow (Z_0\supset \Gamma _0)$ be an arbitrary blow-up of the curve $\Gamma _0$ with an unique exceptional divisor (${\text {Exc}}h_0=\widetilde{S}_1$) for which the following three conditions are satisfied.

(1) The morphism $h_0$ is locally toric at every point of $\Gamma _0$. In particular, $\widetilde{S}_0\cong S_0$, $\rho (\widetilde{S}_0)=1$.

(2) Let $H_0$ be a general hyperplane section of $Z_0$ passing through the general point $Q_0\in \Gamma _0$. Then the morphism $h_0$ induces a weighted blow-up of the smooth point $(H_0\ni Q_0)$ with weights $(\beta ^1_0,\beta ^2_0)$.

(3) $h_0^*S_0=\widetilde{S}_0+\beta ^2_0\widetilde{S}_1$.

The set of all possible blow-ups $h_0$ is denoted by $\mathcal H_0$. The morphism $h'_0$ gives the divisorial contraction $h'_0:Y_0\rightarrow Z_1$ which contracts the divisor $\widetilde{S}_0$ to a point. We obtain a non-toric blow-up $g_1:(Z_1,S_1)\rightarrow (X\ni P)$, where ${\text {Exc}}g_1=S_1$ is an irreducible divisor and $g_1(S_1)=P$.

Lemma 5.4

Let $\widetilde{\Gamma }_0=\widetilde{S}_0\cap \widetilde{S}_1$. Then

$$ (\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}=\beta ^1_0\frac{\big (K_{S_0}+{\text {Diff}}_{S_0}(0)\big )\cdot \Gamma _0}{a(S_0,0)+1} - \beta ^2_0(\Gamma _0^2)_{S_0}. $$

Proof

This formula follows from the following equalities

$$\begin{aligned} (\widetilde{\Gamma }_0^2)_{\widetilde{S}_1} =&\beta ^1_0\widetilde{S}_0\cdot \widetilde{\Gamma }_0=\beta ^1_0(S_0\cdot \Gamma _0- \beta ^2_0\widetilde{S}_1\cdot \widetilde{\Gamma }_0)= \beta ^1_0 S_0\cdot \Gamma _0 -\\&\, - \beta ^2_0(\widetilde{\Gamma }_0^2)_{\widetilde{S}_0}=\beta ^1_0 S_0\cdot \Gamma _0 -\beta ^2_0(\Gamma _0^2)_{S_0} = \\ = \beta ^1_0&((K_{Z_0}+S_0)\cdot \Gamma _0)/(a(S_0,0)+1) - \beta ^2_0(\Gamma _0^2)_{S_0}. \end{aligned}$$

   $\square$

In next Proposition 5.5 we will describe the pair $(S_1,{\text {Diff}}_{S_1}(0))$. The surface $\widetilde{S}_1$ is a conic bundle with $\rho (\widetilde{S}_1)=2$, in particular, every geometric fiber is irreducible. If we contract the section $\widetilde{\Gamma }_0=\widetilde{S}_0\cap \widetilde{S}_1$ of $\widetilde{S}_1$ then we obtain the surface $S_1$. The curve $\Gamma _0$ passes through a finite number of the singular points $Q_1,\ldots ,Q_r$ of $Z_0$ ($r\le 3$), and by $\widetilde{F}_1,\ldots ,\widetilde{F}_r$ denote the fibers of $\widetilde{S}_1$ over these points. In small analytic neighborhoods of a general point of $\widetilde{\Gamma }_0$ and a general point of some section $\widetilde{E}_0$ the variety $Y_0$ has the singularities of types ${\mathbb C}^1\times \frac{1}{\beta ^1_0}(-\beta ^2_0,1)$ and ${\mathbb C}^1\times \frac{1}{\beta ^2_0}(-\beta ^1_0,1)$ respectively. By $F_1,\ldots ,F_r$, $E_0$ denote the transforms of $\widetilde{F}_1,\ldots ,\widetilde{F}_r$, $\widetilde{E}_0$ on the surface $S_1$ respectively. The empty circles are $\widetilde{F}_1,\ldots ,\widetilde{F}_r$ in the figures of Proposition 5.5. The singularities of $\widetilde{S}_1$ are into ovals. Note that the self-intersection index $(\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}$ was calculated in Lemma 5.4.

Proposition 5.5

Depending on a type of the triple $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ we have the following structure of $(S_1,{\text {Diff}}_{S_1}(0))$.

(1) Type A (Fig. 5),

Fig. 5

Type A

and

$$ {\text {Diff}}_{S_1}(0)=\frac{k_1-1}{k_1}F_1+\frac{k_2-1}{k_2}F_2+\frac{\beta ^2_0-1}{\beta ^2_0}E_0. $$

The pair $(S_1,{\text {Diff}}_{S_1}(0))$ is toric.

(2) Type $D_l$ $(l\ge 4)$ (Fig. 6),

Fig. 6

Type $D_l$

and

$$ {\text {Diff}}_{S_1}(0)=\frac{k_1-1}{k_1}F_1+\frac{k_2-1}{k_2}F_2+\frac{k_2-1}{k_2}F_3+ \frac{\beta ^2_0-1}{\beta ^2_0}E_0. $$

(3) Type $E_6$ (Fig. 7),

Fig. 7

Type $E_6$

and

$$ {\text {Diff}}_{S_1}(0)=\frac{k_1-1}{k_1}F_1+\frac{k_2-1}{k_2}F_2+\frac{k_3-1}{k_3}F_3+ \frac{\beta ^2_0-1}{\beta ^2_0}E_0. $$

(4) Type $E_7$, (Fig. 8)

Fig. 8

Type $E_7$

and

$$ {\text {Diff}}_{S_1}(0)=\frac{k_1-1}{k_1}F_1+\frac{k_2-1}{k_2}F_2+\frac{k_3-1}{k_3}F_3+ \frac{\beta ^2_0-1}{\beta ^2_0}E_0. $$

(5) Type $E_8$, (Fig. 9)

Fig. 9

Type $E_8$

and

$$ {\text {Diff}}_{S_1}(0)=\frac{k_1-1}{k_1}F_1+\frac{k_2-1}{k_2}F_2+\frac{k_3-1}{k_3}F_3+ \frac{\beta ^2_0-1}{\beta ^2_0}E_0. $$

The pair $(S_1, {\text {Diff}}_{S_1}(0))$ is klt, therefore $g_1:(Z_1,S_1)\rightarrow (X\ni P)$ is a non-toric plt blow-up.

In cases A, $D_l$, $E_6$, $E_7$ and $E_8$ we have a non-plt 1-, 2-, 3-, 4- and 6-complement of $(S_1,{\text {Diff}}_{S_1}(0))$ respectively.

Proof

By the construction, the morphism $h_0|_{\widetilde{S}_1}:\widetilde{S}_1\rightarrow \Gamma _0$ is locally toric. Therefore, the surface $\widetilde{S}_1$ has either no singularities in a fiber or only two singularities of types $\frac{1}{r_1}(1,b_1)$ and $\frac{1}{r_1}(1,-b_1)$. Let us show the local calculations. Consider the singularity at the point $Q_1$ of $Z_0$ such that the curve $\Gamma _0$ contains it. Let the cone $\langle e_1,e_2,e_3\rangle$ determines locally the variety $Z_0$ in some analytical neighborhood of $Q_1$, $\Gamma _0=V(\langle e_2,e_3\rangle )$ and $S_0=V(\langle e_3\rangle )$. According to Proposition 4.7 we may assume $e_1=(1,0,0)$. We locally have $Y_0=T_N(\Delta ')$, where

$$ \Delta '=\{\langle \beta ,e_1,e_2 \rangle , \langle \beta ,e_1,e_3 \rangle ,\ \text {their faces}\}, $$

$\beta =\beta ^1_0e_2+\beta ^2_0e_3$ and $N\cong {\mathbb Z}^3$. Note that $V(\langle \beta \rangle )=\widetilde{S}_1$ and $\widetilde{F}_1=V(\langle \beta , e_1 \rangle )$ is the fiber of $\widetilde{S}_1$ over the point $Q_1$. Write $(Z_0\ni Q_1)\cong ({\mathbb C}^3\ni 0)/G$, $(Y_0\ni Q_1')\cong ({\mathbb C}^3\ni 0)/G_1$, $(Y_0\ni Q_1'')\cong ({\mathbb C}^3\ni 0)/G_2$, where $Q_1'=\widetilde{F}_1\cap \widetilde{E}_0$, $Q_1''=\widetilde{F}_1\cap \widetilde{S}_0$, and G, $G_1$, $G_2$ are the abelian groups acting freely in codimension 1. Hence, $\beta ^2_0|G|=|G_1|$ and $\beta ^1_0|G|=|G_2|$.

Finally, a corresponding complement of the pair $(E_0, {\text {Diff}}_{E_0}({\text {Diff}}_{S_1}(0)))$ is extended to a required complement of $(S_1, {\text {Diff}}_{S_1}(0))$ by Proposition 1.17.   $\square$

Second step. Assume that there exists a curve $\Gamma _1\subset S_1$ with the following two properties: (1) $K_{S_1}+{\text {Diff}}_{S_1}(0)+\Gamma _1$ is an anti-ample divisor, $h_0:(\Gamma _1)_{\widetilde{S}_1}\rightarrow \Gamma _0$ is a surjective morphism and (2) $\Gamma _1$ is not a center of any blow-up of ${\mathcal H_0}$, in particular, if $(S_1, {\text {Diff}}_{S_1}(0))$ is a toric pair then $\Gamma _1$ is its non-toric subvariety. For convenience, we put $\widetilde{\Gamma }_1=(\Gamma _1)_{\widetilde{S}_1}$.

Lemma 5.6

The triples $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ and $(S_1,{\text {Diff}}_{S_1}(0),\Gamma _1)$ are of type A. Moreover, $\Gamma _1\sim E_0+F_j$ for some index j and $\beta ^2_0{=}1$ (that is, $E_0\not \subset {\text {Supp}}({\text {Diff}}_{S_1}(0)))$.

Proof

Let us remember that the pairs $(S_1,{\text {Diff}}_{S_1}(0))$ were classified in Proposition 5.5, and we will use the same notation.

Put $M=(K_{\widetilde{S}_1}+{\text {Diff}}_{\widetilde{S}_1}(0)+\widetilde{\Gamma }_1)\cdot \widetilde{E}_0$. Note that $M<0$. There are two possibilities:

(1) $\widetilde{\Gamma }_1\sim \widetilde{E}_0$, $\widetilde{E}_0\subset {\text {Supp}}({\text {Diff}}_{\widetilde{S}_1}(0))$ and $\widetilde{\Gamma }_1\not = \widetilde{E}_0$;

(2) $\widetilde{\Gamma }_1\not \sim \widetilde{E}_0$, $\widetilde{\Gamma }_1\sim a_0\widetilde{E}_0+\sum _{i=1}^r a_i\widetilde{F}_i$, where $a_i\in {\mathbb Z}_{\ge 0}$ and $a_0\ge 1$.

Suppose that the triple $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ does not have type A. We will prove that it is impossible. Proposition 4.7 and Lemma 5.4 imply that $(\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}<- \beta ^2_0(\Gamma _0^2)_{S_0}\le - \beta ^2_0\le -1$. Hence the proper transform of $\widetilde{\Gamma }_0$ has the self-intersection index $\le -2$ on the minimal resolution of $\widetilde{S}_1$. Consider possibility (1). Then $M=-2+\deg ({\text {Diff}}_{\widetilde{E}_0}(0))+\frac{1}{2}\widetilde{E}_0^2=1-\sum _{i=1}^3\frac{1}{n_i}+\frac{1}{2}\widetilde{E}_0^2$, where $n_i\ge 2$ for all i. Since the linear system $|\widetilde{E}_0|$ is movable then $\widetilde{E}_0^2=\widetilde{E}_0\cdot \widetilde{\Gamma }_1\ge \frac{1}{n_{i_1}}+\frac{1}{n_{i_2}}$ (it is possible that $i_1=i_2$), and hence $M\ge 0$. Consider possibility (2). If $a_i\ge 1$ for some $i\ge 1$ then it is obvious that $M\ge 0$. Therefore we have to consider the last case $\widetilde{\Gamma }_1\sim a_0\widetilde{E}_0$, where $a_0\ge 2$. Arguing as in possibility (1) and in its notation we have $\widetilde{E}_0^2=\frac{1}{a_0}\widetilde{E}_0\cdot \widetilde{\Gamma }_1\ge \frac{2}{a_0}\sum _{k=1}^{a_0} \frac{1}{n_{i_k}}$, where $i_k\in \{1,2,3\}$, and hence $M\ge 0$.

Suppose that the triple $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ is of type A. We will prove that possibility (1) is not realized, and $a_0=1$, $r=1$, $a_1=1$ in possibility (2).

Let $m_i=r_i/k_i$ be an index of the singularity at the point $\widetilde{F}_i\cap \widetilde{E}_0\in \widetilde{S}_1$, where $i=1,2$. Lemma 5.4 implies that

$$\begin{aligned} (\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}<- \beta ^2_0(\Gamma _0^2)_{S_0}\le - \beta ^2_0\Big (\frac{1}{m_1k_1}+\frac{1}{m_2k_2}\Big ). \end{aligned}$$

(1)

The morphism $h'_0|_{\widetilde{S}_1}:\widetilde{S}_1\rightarrow S_1$ contracts $\widetilde{\Gamma }_0$ to a point of type $\frac{1}{m_3}(m_1,m_2)$ and $h'_0|_{\widetilde{S}_1}$ is a toric blow-up corresponding to the weights $(m_1,m_2)$. Hence

$$\begin{aligned} (\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}=-\frac{m_3}{m_1m_2}. \end{aligned}$$

(2)

Therefore $m_3>\beta ^2_0(m_1/k_2+m_2/k_1)$. The toric surface $S_1$ is completely determined by the triple $(m_1,m_2,m_3)$. For possibility (1) (recall that $\beta _0^2\ge 2$) we obtain the contradiction

$$\begin{aligned} M\ge -2+&\deg \Big ({\text {Diff}}_{\widetilde{E}_0}\Big (\frac{k_1-1}{k_1}\widetilde{F}_1+\frac{k_2-1}{k_2}\widetilde{F}_2\Big )\Big )+\frac{1}{2}\widetilde{E}_0^2=\\ =&-\frac{1}{m_1k_1}-\frac{1}{m_2k_2}+\frac{m_3}{2m_1m_2}>0. \end{aligned}$$

The same calculations for possibility (2) imply $a_0=1$, and since $\widetilde{\Gamma }_1$ is an irreducible curve that the same calculations imply $r=1$ and $a_1=1$.

In order to prove the lemma we must prove only that the plt triple $(S_1,{\text {Diff}}_{S_1}(0),\Gamma _1)$ is of type A. Assuming the converse: its type differs from type A. For instance, let us consider Case 6) of Proposition 4.7, the other cases are considered similarly. Thus $(S_1,{\text {Diff}}_{S_1}(0),\Gamma _1)=({\mathbb P}_{x_1x_2x_3}(2b_2+1,b_2,1),\frac{1}{2}\{x_1=0\},{\mathcal O}_{S_1}(2b_2+1))$, where $b_2\ge 2$. Since $\widetilde{S}_1\rightarrow \Gamma _0$ is a toric conic bundle then there are one possibility only: $\widetilde{S}_1\rightarrow S_1$ is the weighted blow-up of singularity of type $\frac{1}{b_2}(1,1)$ at the point (0 : 1 : 0) with the weights $(2b_2+1,1)$. Now $(\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}=-\frac{b_2}{2b_2+1}$ by equality (2) and $(\widetilde{\Gamma }_0^2)_{\widetilde{S}_1}\le -(\frac{1}{2}+\frac{1}{2b_2+1})$ by inequality (1). This contradiction concludes the proof.   $\square$

Remark 5.7

A klt singularity is called weakly exceptional if there exists its unique plt blow-up (see [13, 19]). A two-dimensional klt singularity is weakly exceptional if and only if it is of type ${\mathbb D}_n$, ${\mathbb E}_6$, ${\mathbb E}_7$ or ${\mathbb E}_8$. Lemma 5.6 shows the interesting correspondence of the types.

Let $h_1:(Y_1,(S_2)_{Y_1})\rightarrow (Y_0\supset \widetilde{\Gamma }_1)$ be a blow-up of the curve $\widetilde{\Gamma }_1$ with an unique exceptional divisor (${\text {Exc}}h_1=(S_2)_{Y_1}$), $(S_1)_{Y_1}\cong (S_1)_{Y_0}$ and the same structure as $h_0$. The set of all possible blow-ups $h_1$ is denoted by $\mathcal H_1$.

By Proposition 4.7 there is 1-complement of $K_{S_1}+{\text {Diff}}_{S_1}(0)+\widetilde{\Gamma }_1$ that extends to 1-complement of $K_{Z_1}+S_1$. Therefore we have 1-complement $K_{Y_0}+\widetilde{S}_1+\widetilde{S}_0+(D_1)_{Y_0}\sim 0$. Since $(D_1)_X=(\psi =0\subset ({\mathbb C}^3\ni 0))/G$ we can slightly change the function $\psi$ keeping all properties. Therefore there is at least a pencil of $(D_1)_{Y_1}$ by proof of Proposition 4.4.1 [22], and we can assume that $a((S_2)_{Y_1}, (D_1)_X)=-1$.

If $a(S_0, (D_1)_X)\ge 0$ then $S_0\cdot (D_1)_{Z_0}\ge 2\Gamma _0$, hence $K_{S_0}+{\text {Diff}}_{S_0}((D_1)_{Z_0})$ is nef by Proposition 4.7 and $a(S_0, (D_1)_X)\le -1$.

So we have 1-complement $K_{Y_1}+(S_2)_{Y_1}+(S_1)_{Y_1}+(S_0)_{Y_1}+(D_1)_{Y_1}\sim 0$. By the cone theorem we have:

(1) there exists an divisorial contraction $h'_{1,1}:Y_1\rightarrow Y_{1,1}$ of $(S_1)_{Y_1}$ onto a curve, $(S_2)_{Y_1}\cong (S_2)_{Y_{1,1}}$;

(2) apply $K_{Y_{1,1}}+(S_0)_{Y_{1,1}}+(S_2)_{Y_{1,1}}$-MMP to contract small extremal ray by a small contraction $\varphi _{1,1}$. Put ${\text {Exc}}\varphi _{1,1}=(F_0)_{Y_{1,1}}$. Let $\varphi ^+_{1,1}$ be a log flip of $\varphi _{1,1}$, ${\text {Exc}}\varphi ^+_{1,1}=(F^+_0)_{Y_{1,2}}$, $h'_{1,2}:Y_{1,1}\dashrightarrow Y_{1,2}$ be a corresponding birational map;

(3) there exists a divisorial contraction $h'_{1,3}:Y_{1,2}\rightarrow Z_2$ of $(S_0)_{Y_{1,2}}$ to a point.

Thus we obtain a birational map $h'_1{=}h'_{1,3}\circ h'_{1,2}\circ h'_{1,1}:Y_1\dashrightarrow Z_2$. Since $(D_1)_{Y_{1,1}}\cdot (F_0)_{Y_{1,1}}=-(K_{Y_{1,1}}+(S_0)_{Y_{1,1}}+(S_2)_{Y_{1,1}})\cdot (F_0)_{Y_{1,1}}>0$, $(D_1)_{Y_{1,1}}$ contains a some fiber of $(S_2)_{Y_{1,1}}$ and $(D_1)_{Y_{1,1}}\not \supset (F_0)_{Y_{1,1}}$ by Proposition 4.7, then the divisor $(D_1)_{Z_2}$ contains the fiber $(F^+_0)_{Z_2}$ and $((S_2)_{Z_2}, {\text {Diff}}_{(S_2)_{Z_2}}(0))$ is a toric pair by Shokurov’s criterion on the characterization of toric varieties [26]. We obtain a non-toric blow-up $g_2:(Z_2,S_2)\rightarrow (X\ni P)$.

We prove the following proposition.

Proposition 5.8

The pair $(S_2,{\text {Diff}}_{S_2}(0))$ is toric (1-complementary) with the structure described in Proposition 5.5 (Type A), $g_2$ is a non-toric plt blow-up.

Third step. Assume that there exists a curve $\Gamma _2\subset S_2$ with the following two properties: (1) $K_{S_2}+{\text {Diff}}_{S_2}(0)+\Gamma _2$ is an anti-ample divisor, $h_0\circ h_1:(\Gamma _2)_{Y_1}\rightarrow \Gamma _0$ is a surjective morphism and (2) $\Gamma _2$ is not a center of any blow-up of ${\mathcal H_1}$, in particular, $\Gamma _2$ is a non-toric subvariety of $(S_2, {\text {Diff}}_{S_2}(0))$.

Proposition 5.9

There is no any blow-up $h_2:(Y_2, (S_3)_{Y_2})\rightarrow (Y_1\supset (\Gamma _2)_{Y_1})$ of the curve $(\Gamma _2)_{Y_1}$ with unique exceptional divisor such that $(S_3)_{Y_2}$ is realized by some plt blow-up $g_3:Z_3\rightarrow (X\ni P)$.

Proof

Assume the converse. Repeat the procedure described in Diagram 4, but with one change, replace the blow-up $g_0:Z_0\rightarrow X$ by the blow-up $g_1:Z_1\rightarrow X$. Therefore, returning to the main procedure, we can assume that there is 1-complement $K_{Y_2}+(S_3)_{Y_2}+(S_2)_{Y_2}+(S_1)_{Y_2}+(S_0)_{Y_2}+(D_2)_{Y_2}\sim 0$. Apply MMP to contract $S_1$ and $S_2$. Let $Y_2\dashrightarrow Y_{2,2}$ be a corresponding birational map. If $(S_0)_{Y_{2,2}}$ contains one fiber of $(S_3)_{Y_{2,2}}$ then $(S_1)_{Y_2}$ and $(S_0)_{Y_2}$ contain a fiber of $(S_3)_{Y_2}$, a contradiction with log canonicity. Therefore $(S_0)_{Y_{2,2}}$ contains two fibers of $(S_3)_{Y_{2,2}}$. Then we obtain the contradiction $(K_{(S_3)_{Y_{2,2}}}+{\text {Diff}}_{(S_3)_{Y_{2,2}}}((S_0)_{Y_{2,2}}+(D_2)_{Y_{2,2}}))\cdot C>0$, where C is any section of the conic bundle $(S_3)_{Y_{2,2}}$.   $\square$

(A2). Let $(X\ni P)$ be a non-${\mathbb Q}$-factorial terminal toric three-dimensional singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$.

Let $f:(Y, E)\rightarrow (X\ni P)$ be some non-toric plt blow-up. Let $\varphi _i:X_i\rightarrow (X\ni P)$ be two ${\mathbb Q}$-factorializations, ${\text {Exc}}\varphi _i=C_i$ ($i=1, 2$). Let $\psi _i:(Y_i, E_i)\rightarrow (X_i\ni Q_i)$ be a plt blow-up for some i such that $E_i$ and E define the same discrete valuation of the function field $\mathcal K(X)$, $Q_i$ is a point. The blow-up $\psi _i$ was constructed in the previous case of ${\mathbb Q}$-factorial singularities, $\rho (E_i)=1$.

Let $Y_i\dashrightarrow \overline{Y}_i$ be a log flip for the curve $(C_i)_{Y_i}$. Considering another value of i we see that $-(E_i)_{\overline{Y}_i}$ is ample. Therefore $\overline{Y}_i=Y$ and $\rho (E)=2$.

We give another construction and prove that $(E,{\text {Diff}}_E(0))$ is a toric pair by the procedure illustrated on the next diagram (Fig. 10) and defined below.

Fig. 10

Case of Point. Construction in non-${\mathbb Q}$-factorial case

First step. Let $g_0:(Z_0,S_0)\rightarrow (X\ni P)$ be a toric plt blow-up, where ${\text {Exc}}g_0=S_0$ and $g_0(S_0)=P$ (see Definition 4.1 and its notation). Assume that there exists a curve $\Gamma _0\subset S_0$ such that $(S_0,{\text {Diff}}_{S_0}(0),\Gamma _0)$ is a plt triple (see Definition 4.9). Such triples are classified in Proposition 4.8.

Remark 5.10

Note that there exists the divisor $\Omega =\{x_2+\gamma x_1^{w_2/w_1}+\ldots =0\}|_X$ such that $\Omega _{Z}|_S=\Gamma _0$, and it has Du Val singularity of type ${\mathbb A}_{w_2/w_1}$, where $\gamma \ne 0$.

Let $h_0:(Y_0,\widetilde{S}_1)\rightarrow (Z_0\supset \Gamma _0)$ be an arbitrary blow-up of the curve $\Gamma _0$ with an unique exceptional divisor (${\text {Exc}}h_0=\widetilde{S}_1$) as in case (A1). The set of all possible blow-ups $h_0$ is denoted by $\mathcal H_0$.

There are two possibilities. The first possibility is as follows. There is a divisorial contraction of $\widetilde{S}_0$ to a curve: $h'_0:Y_0\rightarrow Z_1$, and we obtain a non-toric plt blow-up $g_1:(Z_1,S_1)\rightarrow (X\ni P)$, where ${\text {Exc}}g_1=S_1$ and $g_1(S_1)=P$. The pair $(S_1, {\text {Diff}}_{S_1}(0))$ is toric as in Proposition 5.5 (1).

The second possibility is when the first possibility is not realized. The curves $(C_{13})_{Y_0}$ and $(C_{23})_{Y_0}$ (see Definition 4.1) generate extremal rays of $\overline{{\text {NE}}}(Y_0/X)$ that give small contractions. Let us contract the second one and $h'_{0,1}:Y_0\dashrightarrow Y_{0,1}$ be a log flip. Let $h'_{0,2}:Y_{0,1}\rightarrow Z_1$ be a divisorial contraction of $(S_0)_{Y_{0,1}}$ to a point. Thus we obtain a birational map $h'_0=h'_{0,2}\circ h'_{0,1}:Y_0\dashrightarrow Z_1$. As in case (A1) 1-complement $K_{S_0}+C_{13}+C_{23}+\Gamma _0$ of $K_{S_0}+{\text {Diff}}_{S_0}(0)$ extends to 1-complement $K_{Z_0}+S_0+(D_0)_{Z_0}$ such that $a((S_1)_{Y_0}, (D_0)_{Z_0}+S_0)=-1$. Therefore the divisor ${\text {Diff}}_{S_1}((D_0)_{Z_1})$ consists of four curves and is 1-complement of $K_{S_1}+{\text {Diff}}_{S_1}(0)$. By Shokurov’s criterion on the characterization of toric varieties $(S_1, {\text {Diff}}_{S_1}(0))$ is a toric pair. Thus $g_1:Z_1\rightarrow (X\ni P)$ is a non-toric plt blow-up.

Second step. Assume that there exists a curve $\Gamma _1\subset S_1$ with the following two properties: (1) $K_{S_1}+{\text {Diff}}_{S_1}(0)+\Gamma _1$ is an anti-ample divisor, $h_0:(\Gamma _1)_{\widetilde{S}_1}\rightarrow \Gamma _0$ is a surjective morphism and (2) $\Gamma _1$ is not a center of any blow-up of ${\mathcal H_0}$, $\Gamma _1$ is a non-toric subvariety of $(S_1, {\text {Diff}}_{S_1}(0))$.

The self-intersection index $\Gamma _0^2$ is calculated by Proposition 4.8. Lemmas 5.4 and 5.6 are also true in this case. So we have 1-complement $K_{Y_1}+(S_2)_{Y_1}+(S_1)_{Y_1}+(S_0)_{Y_1}+(D_1)_{Y_1}\sim 0$. By the cone theorem we have:

(1) there exists an divisorial contraction $h'_{1,1}:Y_1\rightarrow Y_{1,1}$ of $(S_1)_{Y_1}$ onto a curve, $(S_2)_{Y_1}\cong (S_2)_{Y_{1,1}}$;

(2) apply $K_{Y_{1,1}}+(S_0)_{Y_{1,1}}+(S_2)_{Y_{1,1}}$-MMP to contract small extremal ray, let $h'_{1,2}:Y_{1,1}\dashrightarrow Y_{1,2}$ be a corresponding log flip;

(3) apply $K_{Y_{1,2}}+(S_0)_{Y_{1,2}}+(S_2)_{Y_{1,2}}$-MMP to contract either small extremal ray or the divisor $(S_0)_{Y_{1,2}}$ onto a curve; we obtain a birational map $h'_{1,3}:Y_{1,2}\dashrightarrow Y_{1,3}$ or a morphism $h'_{1,4}:Y_{1,3}\rightarrow Z_2$ respectively;

(4) in the first case of (3) there exists a divisorial contraction $h'_{1,3}:Y_{1,3}\rightarrow Z_2$ of $(S_0)_{Y_{1,2}}$ to a point.

Thus we obtain a birational map $h'_1:Y_1\dashrightarrow Z_2$ and a non-toric blow-up $g_2:(Z_2,S_2)\rightarrow (X\ni P)$. The pair $(S_2, {\text {Diff}}_{S_2}(0))$ is toric by the same arguments as in case (A1).

We prove the following proposition.

Proposition 5.11

The pair $(S_i,{\text {Diff}}_{S_i}(0))$ is klt and toric (1-complementary), $\rho (S_i)=2$, $g_i$ is a non-toric plt blow-up for $i=1, 2$.

Example 5.12

In this case we will construct examples of non-toric canonical blow-ups and prove that they are not terminal blow-ups. Depending on a type of $(X\ni P)$ there are two Cases (B1) and (B2).

(B1). Let $(X\ni P)\cong ({\mathbb C}_{x_1x_2x_3}^3\ni 0)$. Let us consider a weighted blow-up $g:(Z,S)\rightarrow (X\ni P)$ with weights $(w_1,w_2,w_3)$ such that $g(S)=P$ (that is, $w_i>0$ for all $i=1,2,3$), where $\gcd (w_1,w_2,w_3)=1$. Write $(w_1,w_2,w_3)=(a_1q_2q_3, a_2q_1q_3,a_3q_1q_2)$, where $q_i=\gcd (w_k,w_l)$ and i, k, l are mutually distinct indices from 1 to 3. Then

$$ \Big (S,{\text {Diff}}_S(0)\Big )\cong \Big ({\mathbb P}_{x_1x_2x_3}\big (a_1,a_2,a_3\big ),\sum _{i=1}^3 \frac{q_i-1}{q_i}\{x_i=0\}\Big ). $$

Assume that g is a canonical blow-up.

Proposition 5.13

Let the curve $\Gamma$ be a non-toric subvariety of $(S,{\text {Diff}}_S(0))$. Assume that $\Gamma$ does not contain any center of canonical singularities of Z and $-(K_S+{\text {Diff}}_S(0)+\Gamma )$ is an ample divisor. Then we have one of the following possibilities for weights $(w_1,w_2,w_3)$ up to permutation of coordinates.

Type $({\mathbb A})$. $(w_1,w_2,w_3)=(a_1q_3,a_2q_3,1)$, $\Gamma \sim {\mathcal O}_S(a_1+a_2)$.

Type $({\mathbb D})$. $(w_1,w_2,w_3){=}(l,l-1,2)$, $(l+1,l,1)$, (l, l, 1) and $\Gamma \sim {\mathcal O}_S(l)$, ${\mathcal O}_S(2l)$, ${\mathcal O}_S(2)$ respectively, where $l\ge 2$.

Type $({\mathbb E}_6)$. $(w_1,w_2,w_3)=(3,2,2)$, (6, 4, 3), (5, 3, 2), (4, 2, 1) and $\Gamma \sim {\mathcal O}_S(3)$, ${\mathcal O}_S(2)$, ${\mathcal O}_S(9)$, ${\mathcal O}_S(3)$ respectively.

Type $({\mathbb E}_7)$. $(w_1,w_2,w_3)=(3,2,2)$, (6, 4, 3), (9, 6, 4), (3, 3, 1), (5, 4, 2), (7, 5, 3), (5, 3, 2) and $\Gamma \sim {\mathcal O}_S(3)$, ${\mathcal O}_S(2)$, ${\mathcal O}_S(3)$, ${\mathcal O}_S(2)$, ${\mathcal O}_S(5)$, ${\mathcal O}_S(14)$, ${\mathcal O}_S(6)$ respectively.

Type $({\mathbb E}_8)$. $(w_1,w_2,w_3)=(3,2,2)$, (6, 4, 3), (9, 6, 4), (12, 8, 5), (15, 10, 6), (5, 4, 2), (10, 7, 4), (8, 5, 3) and $\Gamma \sim {\mathcal O}_S(3)$, ${\mathcal O}_S(2)$, ${\mathcal O}_S(3)$, ${\mathcal O}_S(6)$, ${\mathcal O}_S(1)$, ${\mathcal O}_S(5)$, ${\mathcal O}_S(10)$, ${\mathcal O}_S(15)$ respectively.

In all possibilities there is Du Val element $\Omega _Z\in |-K_Z|$ such that $\Omega _Z|_S=\Gamma +\sum _{i=1}^r\gamma _i\Gamma _i$. Moreover, $\Omega _Z|_S=\Gamma$, except the two possibilities: $(l+1,l,1)$, $\Gamma \sim {\mathcal O}_S(2l) ($type ${\mathbb D})$ and (5, 3, 2), $\Gamma \sim {\mathcal O}_S(6) ($type ${\mathbb E}_7)$. In these two possibilities we have $\Omega _Z|_S=\Gamma +\Gamma _1$, where $\Gamma _1\sim {\mathcal O}_S(1)$ and ${\mathcal O}_S(3)$ respectively.

Proof

The proof follows from Proposition 2.6 by enumeration of cases.   $\square$

Remark 5.14

Proposition 5.13 is similar to Proposition 4.7. Note that there is one-to-one correspondence between the sets $(w_1,w_2,w_3,\Gamma )$ and the exceptional curves of minimal resolution of Du Val singularity $(\Omega \ni P)$, where $\Omega =g(\Omega _Z)$. Types in Proposition 5.13 correspond to Du Val types of the singularity $(\Omega \ni P)$.

By Theorem 1.6 there exists a divisorial contraction $h:(\widetilde{Y},\widetilde{E})\rightarrow (Z\supset \Gamma )$ for any weights $(\beta _1,1)$ such that

(1) ${\text {Exc}}h=\widetilde{E}$ is an irreducible divisor and $h(\widetilde{E})=\Gamma$;

(2) the morphism h is locally toric for a general point of $\Gamma$;

(3) if H is a general hyperplane section passing through the general point $Q\in \Gamma$, then h induces the weighted blow-up of the smooth point $(H\ni Q)$ with weights $(\beta _1,1)$;

(4) $h^*S=\widetilde{S}+\widetilde{E}$ and $h^*\Omega _{Z}=\Omega _{\widetilde{Y}}+\beta _1\widetilde{E}$.

Apply $K_{\widetilde{Y}}+\Omega _{\widetilde{Y}}+\varepsilon \widetilde{S}$–MMP. Since $\rho (\widetilde{Y}/X)=2$ and $K_{\widetilde{Y}}+\Omega _{\widetilde{Y}}+\varepsilon \widetilde{S}\equiv \varepsilon \widetilde{S}$ over X, then we obtain a sequence of log flips $\widetilde{Y}\dashrightarrow \overline{Y}$, and after it we obtain the divisorial contraction $h':\overline{Y}\rightarrow Y$ which contracts the proper transform $\overline{S}$ of $\widetilde{S}$.

Thus we obtain a required non-toric blow-up $f:(Y,E)\rightarrow (X\ni P)$, where ${\text {Exc}}f=E$ is an irreducible divisor and $f(E)=P$. Since $K_Y+\Omega _Y=f^*(K_X+\Omega )$ then f is a canonical blow-up.

Finally let us prove that f is a non-terminal blow-up, that is, the singularities of Y are non-terminal. We must prove only that the center of $\overline{S}$ on Y does not lie in $\Omega _Y$, since $0=a(S,\Omega )$. Let $\widetilde{Y}=\overline{Y}_1\dashrightarrow \overline{Y}_2\dashrightarrow \ldots \dashrightarrow \overline{Y}_n=\overline{Y}$ be a decomposition of log flip sequence into elementary steps. If $\Omega _{\overline{Y}_i}$ is a nef divisor then by the base point free theorem [9] the linear system $|m\Omega _{\overline{Y}_i}|$ gives the birational contraction $h'$ for $m\gg 0$. It contracts the proper transform of $\widetilde{S}$ to a point, $i=n$, and this completes the proof. Suppose that $\Omega _{\overline{Y}_i}$ is not a nef divisor. The cone $\overline{{\text {NE}}}(\overline{Y}_i/X)$ is generated by two extremal rays. By $Q_i$, $R_i$ denote them, and to be definite, assume that the ray $R_i$ determines the next step of MMP. By construction, we have $\Omega _{\overline{Y}_i}\cdot Q_i>0$, and hence $-K_{\overline{Y}_i}\cdot R_i=\Omega _{\overline{Y}_i}\cdot R_i<0$. Since $K_{\overline{Y}_i}\cdot R_i>0$ and the singularities of MMP are canonical, then the ray $R_i$ gives a log flip (that is, $i<n$), and after it we have $\Omega _{\overline{Y}_{i+1}}\cdot Q_{i+1}>0$. At the end we obtain that $\Omega _{\overline{Y}_j}$ is a nef divisor for some j. This completes the proof.

(B2). Let $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. Let us consider a toric canonical blow-up $g:(Z,S)\rightarrow (X\ni P)$ (see Proposition 2.6 (3)).

Proposition 5.15

Let a curve $\Gamma$ be a non-toric subvariety of $(S,{\text {Diff}}_S(0))$. Assume that $\Gamma$ does not contain any center of canonical singularities of Z and $-(K_S+{\text {Diff}}_S(0)+\Gamma +\Gamma ')$ is an ample divisor, where $\Gamma '$ is some effective ${\mathbb Q}$-divisor. Then $w_1=1$ and $\Gamma \sim {\mathcal O}_{{\mathbb P}(w_1,w_2,w_3,w_4)}(w_2)|_S$ up to permutation of coordinates. There exists Du Val element $\Omega _Z\in |-K_Z|$ such that $\Omega _Z|_S=\Gamma$. In particular, $-(K_S+{\text {Diff}}_S(0)+\Gamma )$ is an ample divisor and $(\Omega \ni P)$ is Du Val singularity of type ${\mathbb A}_{w_2}$, where $\Omega =g(\Omega _Z)$.

Proof

The proof follows from Proposition 2.6 (3).   $\square$

Now we can apply the construction of Case $\mathbf{(B1)}$.

Another construction of same non-toric canonical blow-ups is the following one. Consider a ${\mathbb Q}$-factorialization $g:\widetilde{X}\rightarrow X$ and $\widetilde{T}={\text {Exc}}g$. By G denote the center of E on $\widetilde{X}$. Applying (if necessary) a flop $\widetilde{X}\dashrightarrow \widetilde{X}^+$ we may assume that G is a point. Let us apply the above mentioned construction in Case $\mathbf{(B1)}$ for singularity $(\widetilde{X}\ni G)$. We obtain a non-toric canonical blow-up $f:Y\rightarrow \widetilde{X}$. Let $Y\dashrightarrow Y^+$ be a log flip for the curve $T_Y$. Thus we obtain a non-toric canonical blow-up $f^+:(Y^+,E^+)\rightarrow (X\ni P)$, where $E^+={\text {Exc}}f^+$ and $f^+(E^+)=P$.

6 Main Theorems. Case of Point

Example 6.1

Let $(X\ni P)\cong ({\mathbb C}_{x_1x_2x_3}^3\ni 0)$. Let us consider the weighted blow-up $g:(Z,S)\rightarrow (X\ni P)$ with the weights (15, 10, 6). Then

$$ \Big (S,{\text {Diff}}_S(0)\Big )\cong \Big ({\mathbb P}^2,\frac{1}{2}L_1+\frac{2}{3}L_2+\frac{4}{5}L_3\Big ), $$

where $L_i$ are the straight lines, and the divisor $\sum L_i$ is a complement to open toric orbit of S.

Let $\Omega =\{x_1^2+x_2^3+x_3^5=0\}\subset (X\ni P)$ be a divisor with Du Val singularity of type ${\mathbb E}_8$. Then $L=\Omega _Z|_S$ is a straight line. Put $P_i=L_i\cap L$. Then the points $P_i$ are non-toric subvarieties of $(S,{\text {Diff}}_S(0))$.

The main difference of structure of non-toric canonical blow-ups from the structure of non-toric plt blow-ups is shown in the following statements.

(1) We have $P_i\in {\text {CS}}(Z,\Omega _Z)$ for every i. Thus $P_i$ are the centers of some non-toric canonical blow-ups of $(X\ni P)$, that is, there exists the canonical blow-up $(Y,E_i)\rightarrow (X\ni P)$ such that the center of $E_i$ on Z is the point $P_i$ for every i.

(2) The points $P_i$ are not the centers of any non-toric plt blow-ups of $(X\ni P)$. The proof of this fact is given in Theorem 6.2.

The origin of this difference is that S is not (locally) Cartier divisor at the points $P_i$ (cf. Theorem 2.13).

The straight line $L\in {\text {CS}}(Z,\Omega _Z)$ is a center of some non-toric canonical and plt blow-ups of $(X\ni P)$. As might appear at first sight the class of non-toric canonical blow-ups is much wider than the class of non-toric plt blow-ups, but it is not true. To construct the non-toric canonical blow-ups, some necessary conditions used implicitly in this example must be satisfied. Namely, g is a canonical blow-up, $a(S,\Omega )=0$, the straight line L does not contain any center of canonical singularities of Z.

Theorem 6.2

Let $f:(Y,E) \rightarrow (X \ni P)$ be a plt blow-up of three-dimensional toric terminal singularity, where $f(E)=P$. Then, either f is a toric morphism, or f is a non-toric morphism described in Sect. 5.

Proof

Let f be a non-toric morphism (up to analytical isomorphism). Let $D_Y\in |-n(K_Y+E)|$ be a general element for $n\gg 0$. Put $D_X=f(D_Y)$ and $d=\frac{1}{n}$. The pair $(X,dD_X)$ is log canonical, $a(E,dD_X)=-1$ and E is a unique exceptional divisor with discrepancy $-1$.

Let $(X\ni P)$ be a ${\mathbb Q}$–factorial singularity. According to the construction of partial resolution of $(X,dD_X)$ (see Definition 2.7) and Criterion 2.8 there exists a toric divisorial contraction $g:Z\rightarrow X$ such that it is dominated by partial resolution of $(X,dD_X)$ (up to toric log flips), and one of the following Cases I and II occurs.

Case I. The exceptional set ${\text {Exc}}g=S$ is an irreducible divisor, the divisors S and E define the different discrete valuations of the function field $\mathcal K(X)$, and $g(S)=P$. By $\Gamma$ denote the center of E on the surface S. Then the center $\Gamma$ is a non-toric subvariety of Z. In the other words $\Gamma$ is a non-toric subvariety of $(S,{\text {Diff}}_S(0))$. If $\Gamma$ is a point then we assume that it does not lie on any one-dimensional orbit of the surface S (up to analytical isomorphism $(X\ni P)$ of course).

Case II. The variety Z is ${\mathbb Q}$-gorenstein, hence it is ${\mathbb Q}$-factorial. The exceptional set ${\text {Exc}}g=S_1\cup S_2$ is the union of two exceptional irreducible divisors, $S_1$, $S_2$ and E define mutually distinct discrete valuations of the function field $\mathcal K(X)$ and $g(S_1)=g(S_2)=P$. To be definite, let $\rho (S_1)=1$, $\rho (S_2)=2$, and $C=S_1\cap S_2$ is a closure of one-dimensional orbit of Z. By $\Gamma$ denote the center of E on Z. In this case $\Gamma$ is a point and a non-toric subvariety of $(S_1,{\text {Diff}}_{S_1}(0))$, $\Gamma \in C$, and the curve C has the coefficient 1 in the divisor ${\text {Diff}}_{S_1}(S_2+dD_Z)$. Mori cone $\overline{{\text {NE}}}(Z/X)$ is generated by two extremal rays, denote them by $R_1$ and $R_2$. To be definite, let $R_1$ gives the divisorial contraction which contracts the divisor $S_1$ to some point $P_1$. Considering toric blow-ups of $P_1$ we may assume that ${\text {Diff}}_{S_1}(S_2+dD_Z)$ is a boundary in some analytical neighborhood of the point $\Gamma$.

If $R_2$ gives the divisorial contraction which contracts the divisor $S_2$ (onto curve) then it is Case IIa. If $R_2$ gives a small flipping contraction then it is Case IIb.

Let us consider Case IIb in more detail. Let $Z\dashrightarrow Z^+$ be a toric log flip induced by $R_2$. The corresponding objects on $Z^+$ are denoted by the index $^+$. For the toric divisorial contraction $g^+:Z^+\rightarrow X$ we have $\rho (S^+_1)=2$, $\rho (S^+_2)=1$. Note that the point $\Gamma ^+\in C^+=S_1^+\cap S_2^+$ of E on $Z^+$ can be a toric subvariety of $(S^+_2,{\text {Diff}}_{S^+_2}(0))$. The morphism $g^+$ is dominated by partial resolution of $(X,dD_X)$ (up to toric log flips), and the curve $C^+$ has the coefficient 1 in the divisor ${\text {Diff}}_{S_2^+}(S_1^++dD_{Z^+})$.

Note that the equality $g({\text {Exc}}g)=P$ is proved similarly to Theorem 2.12 in both Cases I and II.

Now, according to Sect. 5 the following lemma implies the proof of theorem (for ${\mathbb Q}$–factorial singularities).   $\square$

Lemma 6.3

It is possible Case ${\text {I}}$ only. Moreover, $\Gamma$ is a curve and $K_S+{\text {Diff}}_S(0)+\Gamma$ is a plt divisor.

Proof

Let us consider Case I. Write

$$ K_Z+dD_Z+aS=g^*\big (K_X+dD_X\big ), $$

where $a<1$. Hence

$$ a\big (E,S+dD_Z\big )< a\big (E,aS+dD_Z\big )=-1. $$

Therefore $\Gamma \subset {\text {LCS}}(S,{\text {Diff}}_S(dD_Z))$ and $-(K_S+{\text {Diff}}_S(dD_Z))$ is an ample divisor.

Assume that $\Gamma$ is a (irreducible) curve. We must prove that $K_S+{\text {Diff}}_S(0)+\Gamma$ is a plt divisor. Assume the converse. By the adjunction formula, $\Gamma$ is a smooth curve, and by connectedness lemma the divisor $K_S+{\text {Diff}}_S(0)+\Gamma$ is not a plt one at unique point denoted by G. The point G is a toric subvariety of $(S,{\text {Diff}}_S(0))$ by Theorem 4.2. Moreover, the curve $\Gamma$ is locally a non-toric subvariety at the point G only. According to the construction of partial resolution [27] there exists the divisorial toric contraction $\widehat{g}:\widehat{Z}\rightarrow Z$ such that ${\text {Exc}}\widehat{g}=S_2$ is an irreducible divisor, $\widehat{g}(S_2)=G$ and the following two conditions are satisfied.

(1). Put $S_1=S_{\widehat{Z}}$ and $C=S_1\cap S_2$. Let $c(\Gamma )$ be the log canonical threshold of $\Gamma$ for the pair $(S,{\text {Diff}}_S(0))$. Then ${\widehat{g}}|_{S_1}:S_1\rightarrow S$ is the inductive toric blow-up of $K_S+{\text {Diff}}_S(0)+c(\Gamma )\Gamma$ (see Theorems 1.10 and 2.12), and the point $\widehat{G}=C\cap \Gamma _{S_1}$ is a non-toric subvariety of $(S_2,{\text {Diff}}_{S_2}(0))$.

(2). The divisor ${\text {Diff}}_{S_2}(dD_{\widehat{Z}}+S_1)$ is a boundary at the point $\widehat{G}$.

Let H be a general hyperplane section of large degree passing through the point P. Then we have $a(S_i,dD_X+hH)=-1$ and $a(S_j,dD_X+hH)>-1$ for some $h>0$, $i\ne j$. If $i=1$ and $j=2$ then we have the contradiction with Theorem 4.2 for the pair $(S_2,{\text {Diff}}_{S_2}(dD_{\widehat{Z}}+S_1))$. Hence, we may assume that $i=2$ and $j=1$. Mori cone $\overline{{\text {NE}}}(\widehat{Z}/X)$ is generated by two rays, denote them by $\widehat{R}_1$ and $\widehat{R}_2$. To be definite, let $\widehat{R}_2$ gives the contraction $\widehat{g}$.

At first assume that $\widehat{R}_1$ gives the contraction $g_1:\widehat{Z}\rightarrow Z_1$ which contracts $S_1$ (onto a curve). The contraction $g_1$ is an isomorphism for the surface $S_2$, therefore we denote $g_1(S_2)$ by $S_2$ again for convenience. If ${\text {Diff}}_{S_2}(dD_{Z_1})$ is a boundary then we have the contradiction with Theorem 4.2 applied for the pair $(S_2,{\text {Diff}}_{S_2}(dD_{Z_1}))$. If it is not a boundary then we have the following contradiction

$$\begin{aligned}&\qquad \, \qquad \, \, 0>(1+a(S_1,dD_X+hH))S_1\cdot C_0=\\ {}&\qquad \, \qquad = (K_{S_1}+{\text {Diff}}_{S_1}(dD_{\widehat{Z}}+S_2+hH_{\widehat{Z}}))\cdot C_0\ge \\ \ge&(K_{S_1}+{\text {Diff}}_{S_1}(0)'+\Gamma _{S_1}+C+C_0)\cdot C_0\ge (-F_1-F_2+\Gamma _{S_1})\cdot C_0\ge 0, \end{aligned}$$

where $C_0$ is the closure of one-dimensional orbit of $S_1$, having zero-intersection with C, and $F_1$, $F_2$ are the two toric fibers (the closures of corresponding one-dimensional toric orbits) of the toric conic bundle $S_1\rightarrow g_1(S_1)$, and the divisor ${\text {Diff}}_{S_1}(0)'$ is a part of ${\text {Diff}}_{S_1}(0)$ provided that we equate to zero the coefficients of C and $C_0$ in ${\text {Diff}}_{S_1}(0)$.

At last assume that $\widehat{R}_1$ gives a flipping contraction. Let $\widehat{Z}\dashrightarrow \widehat{Z}^+$ be a corresponding toric log flip. The corresponding objects on $\widehat{Z}^+$ are denoted by the index $^+$. If the point $\widehat{G}^+$ is a non-toric subvariety of $(S_1^+,{\text {Diff}}_{S_1^+}(0))$ then we have the contradiction with Theorem 4.2 applied for the pair $(S_1^+,{\text {Diff}}_{S_1^+}(S_2^+)+\widehat{\Gamma }^+)$. Therefore we can assume that the point $G^+$ is a toric subvariety. If the curve $\widehat{\Gamma }^+$ is a non-toric subvariety of $(S_1^+,{\text {Diff}}_{S_1^+}(0))$, then by the inversion of adjunction the pair $(S_1^+,{\text {Diff}}_{S_1^+}(S_2^+)+\widehat{\Gamma }^+)$ is plt outside $\widehat{G}^+$, and we have the contradiction with Proposition 4.7. Thus we have proved that $\widehat{\Gamma }^+$ and $G^+$ are the toric subvarieties of $(S_1^+,{\text {Diff}}_{S_1^+}(0))$. In particular, $S_1^+\cong {\mathbb P}(1,r_1,r_2)$, where $\gcd (r_1,r_2)=1$ and $(\widehat{\Gamma }^+)^2=r_1/r_2$. Considering the divisor $D(\delta )=(d-\delta )D+h(\delta )H$ for some $\delta \ge 0$ and $h(\delta )>0$ ($h(0)=1$) instead of the divisor $D(0)=dD$, we may assume that the whole construction is satisfied and $a(E,D(\delta ))=-1$.

Let ${\text {Diff}}_{S_2}(D(\delta )-a(S_1,D(\delta ))S_1)\ge 0$ (for example, it holds if $a(S_1,D(\delta ))<0$). Replacing the divisor H by other general divisor with $\widehat{G}\in {\text {Supp}}(H_{\widehat{Z}})$, we may assume that the three following conditions are satisfied: (1) ${\text {Diff}}_{S_2}(D(\delta )-a(S_1,D(\delta ))S_1)\ge 0$; (2) $\widehat{G}$ is a center of ${\text {LCS}}(\widehat{Z},D(\delta )_{\widehat{Z}}-a(S_1,D(\delta ))S_1-a(S_2,D(\delta ))S_2)$; (3) $a(S_2,D(\delta ))>-1$. We obtain the contradiction with Theorem 4.2 for the pair $(S_2,{\text {Diff}}_{S_2}(D(\delta )-a(S_1,D(\delta ))S_1))$.

Let ${\text {Diff}}_{S_2}(D(\delta )-a(S_1,D(\delta ))S_1)$ is not an effective divisor. The curve $\widehat{\Gamma }^+$ is locally a toric subvariety in some analytical neighborhood of every point of $\widehat{Z}^+$, therefore there exists a blow-up $\overline{g}:(\overline{Z}\supset \overline{S}_3)\rightarrow (\widehat{Z}^+\supset \widehat{\Gamma }^+)$, where ${\text {Exc}}\overline{g}=\overline{S}_3$ is an irreducible divisor such that $\overline{g}(\overline{S}_3)=\widehat{\Gamma }^+$ and the following three conditions are satisfied.

(A) The morphism $\overline{g}$ is locally a toric one at every point of $\widehat{\Gamma }^+$, in particular, $\overline{S}_1\cong S_1$.

(B) Let H be a general hyperplane section of $\widehat{Z}^+$ passing through the general point $\widehat{Q}\in \widehat{\Gamma }^+$. Then $\overline{g}$ induces a weighted blow-up of $(H\ni \widehat{Q})$ with weights $(\beta _1,\beta _2)$, and $\overline{g}^*S_1^+=\overline{S}_1+\beta _2\overline{S}_3$.

(C) Either the divisors $\overline{S}_3$ and E define the same discrete valuation of the function field $\mathcal K(X)$ (Case C1), or the curve $\overline{\Gamma }\subset \overline{S}_3$ being the center of E on $\overline{Z}$ is a non-toric subvariety of $(\overline{S}_3,{\text {Diff}}_{\overline{S}_3}(0))$ (Case C2).

By $\overline{C}_0$ and $\overline{F}$ denote zero-section and a general fiber of $\overline{S}_3$ respectively.

Let us consider Case C1. Then $\overline{D}(\delta )|_{\overline{S}_3}\sim _{{\mathbb Q}} a\overline{C}_0+b\overline{F}$ by the generality of D, where $b\ge 0$ and $a=2+a(S_1,D(\delta ))/\beta _1-\frac{\beta _2-1}{\beta _2}-\frac{\beta _1-1}{\beta _1}\ge 1+\frac{1}{\beta _2}$. We obtain the contradiction (the calculations are similar to Lemma 5.4 and Proposition 5.5)

$$\begin{aligned} 0=&(K_{\overline{S}_3}+{\text {Diff}}_{\overline{S}_3}(\overline{D}(\delta )+\overline{S}_2^+-a(S_1,D(\delta ))\overline{S}_1^+))\cdot \overline{C}_0\ge \\ {}&\, \ge -2+1+\frac{r_2-1}{r_2}+ \overline{C}_0^2 > (r_1-1)/r_2\ge 0. \end{aligned}$$

Let us consider Case C2. If $a(\overline{S}_3,D(\delta ))\le -1$ then we require the condition $a(\overline{S}_3,D(\delta ))=-1$ to be satisfied instead of the condition $a(E,D(\delta ))=-1$ in the construction of $D(\delta )$, and we obtain similar contradiction as in Case C1. Therefore we may assume that $a(\overline{S}_3,D(\delta ))>-1$. Then $\overline{\Gamma }\sim a\overline{C}_0+b\overline{F}$, where either $a\ge 1$, $b\ge 1$, or $a\ge 2$, $b\ge 0$, or $a=1$, $b=0$, $\overline{\Gamma }\ne \overline{C}_0$, $\beta _2\ge 2$. Continuing this line of reasoning, we have the same contradictions for any possibility of $\overline{\Gamma }$.

Now assume that $\Gamma$ is a point. Theorem 4.2 implies that ${\text {Diff}}_S(dD_Z)$ is not a boundary in any analytical neighborhood of $\Gamma$. Moreover, there is unique curve passing through $\Gamma$ with the coefficient $\ge 1$ in the divisor ${\text {Diff}}_S(dD_Z)$. It is clear that it is smooth at the point $\Gamma$, it is a non-toric subvariety of $(S,{\text {Diff}}_S(0))$ and denote it by T.

Let us prove that $(S,{\text {Diff}}_S(0)+T)$ is a plt pair. Let H be a general hyperplane section of large degree passing through the point P such that $\Gamma \in H_Z$. As above by Theorem 4.2, there exist some rational numbers $0<\delta <d$, $h>0$ and the divisor $D'=(d-\delta )D_X+hH$ such that $(X,D')$ is a log canonical pair, ${\text {LCS}}(Z,D'_Z-a(S,D')S)=T$ and $\Gamma$ is a center of $(Z,D'_Z-a(S,D')S)$. Moreover, we may assume that there are not another centers differing from $\Gamma$ and T by connectedness lemma. Now, according to the standard Kawamata’s perturbation trick, there exists an effective ${\mathbb Q}$-divisor $D''$ on X such that the curve T is unique minimal center of $(Z,D''_Z-a(S,D'')S)$. So, by the previous statement proved (when $\Gamma$ is a curve) $(S,{\text {Diff}}_S(0)+T)$ is a plt pair.

Let us consider the blow-up $\overline{g}:(\overline{Z}\supset \overline{S}_3)\rightarrow (Z\supset T)$ for the pair $(X,D')$ which is similar to the blow-up $\overline{g}:(\overline{Z}\supset \overline{S}_3)\rightarrow (\widehat{Z}^+\supset \widehat{\Gamma }^+)$, where ${\text {Exc}}\overline{g}=\overline{S}_3$. Let $\overline{\Gamma }\subset \overline{Z}$ be a center of E. There are two cases $\overline{\Gamma }=\overline{F}$, $\overline{\Gamma }$ is a point, where $\overline{F}$ is a fiber over the point $\Gamma$. Applying Lemma 4.4 if $\Gamma$ is a point, we obtain the contradiction in same way as above

$$ 0=(K_{\overline{S}_3}+{\text {Diff}}_{\overline{S}_3}(\overline{D'}-a(S,D')\overline{S}))\cdot \overline{C}_0>0. $$

Let us prove that Case II is impossible. Let H be a general hyperplane section of large degree passing through the point P. Then we have $a(S_i,dD_X+hH)=-1$ and $a(S_j,dD_X+hH)>-1$ for some $h>0$.

Let us introduce the following notation: let $M=\sum m_iM_i$ be the divisor decomposition on irreducible components, then we put $M^b=\sum _{i:m_i>1}M_i+\sum _{i:m_i\le 1}m_iM_i$.

If $i=2$ and $j=1$ then we obtain the contradiction with Theorem 4.2 for the pair $(S_1,{\text {Diff}}_{S_1}(dD_Z+S_2)^b)$. Therefore $i=1$ and $j=2$.

Let us consider Case IIb. If $\Gamma ^+$ is a non-toric subvariety of $(S_2^+,{\text {Diff}}_{S_2^+}(0))$ then we obtain the contradiction with Theorem 4.2 for the pair $(S_2^+,{\text {Diff}}_{S_2^+}(dD_{Z^+}+S_1^+)^b)$. Therefore we assume that $\Gamma ^+$ is a toric subvariety of $(S_2^+,{\text {Diff}}_{S_2^+}(0))$. The similar (related) case have been considered, when $\Gamma$ was a curve, therefore we do not repeat its complete description. By construction, the curve $C^+\subset S^+_1$ is exceptional and contains at most one singularity of $S^+_1$. Since the pair $(S^+_1,{\text {Diff}}_{S_1^+}(dD_{Z^+}+hH_{Z^+})$ is not log canonical at the point $\Gamma ^+$, then $(dD_{Z^+}+hH_{Z^+})\cdot C^+=1+\sigma$, where $\sigma >0$. Since the divisor $-K_{S_1^+}$ is a sum of four one-dimensional orbit closures, then

$$\begin{aligned}&\, \, \, a(S^+_2,dD_{Z^+}+hH_{Z^+})S_2^+\cdot C^+=\\ {}&=(K_{S_1^+}+{\text {Diff}}_{S_1^+}(dD_{Z^+}+hH_{Z^+}))\cdot C^+\ge \\ {}&\, \ge -(C^+)^2_{S_1^+}-1-\frac{1}{r}_1+1+\sigma \ge \sigma >0. \end{aligned}$$

Since $S_2^+\cdot C^+<0$ then $a(S^+_2,dD_{Z^+}+hH_{Z^+})<0$. Now, to obtain the contradiction with Theorem 4.2 for the pair $(S_1,{\text {Diff}}_{S_1}(dD_{Z}+hH_{Z}-a(S_2,dD+hH)S_2)^b)$, it is sufficient to decrease the coefficient h slightly (then $a(S_1,dD+hH)>-1$).

Let us consider Case IIa. Let $g_1:Z\rightarrow Z_1$ be a contraction of $R_2$. The contraction $g_1$ is an isomorphism for the surface $S_1$, therefore we denote $g_1(S_1)$ by $S_1$ again for convenience. If the divisor ${\text {Diff}}_{S_1}(dD_{Z_1})$ is a boundary then we have the contradiction with Theorem 4.2 for the pair $(S_1,{\text {Diff}}_{S_1}(dD_{Z_1}))$, and if it is not a boundary then we have the following contradiction

$$\begin{aligned}&\, \, \, 0>(1+a(S_2,dD_X+hH))S_2\cdot C_0=\\ {}&\, =(K_{S_2}+{\text {Diff}}_{S_2}(dD_Z+S_1+hH_Z))\cdot C_0\ge \\&\ge (K_{S_2}+{\text {Diff}}_{S_2}(0)'+F+C+C_0)\cdot C_0\ge 0, \end{aligned}$$

where $C_0$ is the closure of one-dimensional orbit of $S_2$ having zero-intersection with C, and F is a general fiber of the conic bundle $S_2\rightarrow g_1(S_2)$, and the divisor ${\text {Diff}}_{S_2}(0)'$ is a part of ${\text {Diff}}_{S_2}(0)$ provided that we equate to zero the coefficients of C and $C_0$ in ${\text {Diff}}_{S_2}(0)$. Note that the equality $(D_Z|_{S_2}\cdot C)_{\Gamma }\ge 1$ have been applied here (see Lemma 4.4); it is true since $(S_2,C+D_Z|_{S_2})$ is not a plt pair at the point $\Gamma$ by the construction.   $\square$

Let $(X\ni P)$ be a non-${\mathbb Q}$–factorial singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. We repeat the arguments given in Sect. 5. Let $g:\widetilde{X}\rightarrow X$ be a ${\mathbb Q}$-factorialization and let $C={\text {Exc}}g\cong {\mathbb P}^1$. Note that $\widetilde{X}$ is a smooth variety. By G denote the center of E on $\widetilde{X}$. If G is a point then it is a toric subvariety, and hence the main theorem is reduced to the case of ${\mathbb Q}$-factorial singularities. If $G=C$ then we consider the flop $\widetilde{X}\dashrightarrow \widetilde{X}^+$, and we may assume that G is a point by replacing $\widetilde{X}$ by $\widetilde{X}^+$.

Theorem 6.4

Let $f:(Y,E) \rightarrow (X \ni P)$ be a plt blow-up of three-dimensional toric ${\mathbb Q}$–factorial singularity, where $f(E)=P$. Then, either f is a toric morphism, or f is a non-toric morphism described in Sect. 5.

Proof

We can repeat the proof of Theorem 6.2 without any changes in our case. Lemma 5.3 gives some restrictions, when $(X\ni P)$ is a terminal singularity, but it is not used in what follows.   $\square$

Theorem 6.5

Let $f:(Y,E)\rightarrow (X\ni P)$ be a canonical blow-up of three-dimensional toric terminal singularity, where $f(E)=P$. Then, either f is a toric morphism (see Proposition 2.6), or f is a non-toric morphism described in Sect. 5.

Proof

Let f be a non-toric morphism (up to analytical isomorphism). Let $D_Y\in |-nK_Y|$ be a general element for $n\gg 0$. Put $D_X=f(D_Y)$ and $d=\frac{1}{n}$. The pair $(X,dD_X)$ has canonical singularities and $a(E,dD_X)=0$.

Let $(X\ni P)$ be a ${\mathbb Q}$–factorial singularity. There is one of two Cases I and II described in the proof of Theorem 6.2. We will use the notation from the proof of Theorem 6.2. According to Sect. 5 the following proposition implies the proof of theorem for ${\mathbb Q}$–factorial singularities.   $\square$

Proposition 6.6

There exists a toric blow-up g such that we have Case I always, the center $\Gamma$ is a curve, $a(S,dD_X)=0$ and $(X\ni P)$ is a smooth point, in particular, g is a canonical blow-up.

Proof

Let us consider Case II. We may assume that $C\not \subset {\text {Supp}}({\text {Sing}}Z)$. Actually, by taking toric blow-ups with the center C we obtain either the requirement, or Case I (that is, there is some blow-up g such that the center of E is a curve and a non-toric subvariety of corresponding exceptional divisor). Therefore $S_1$ and $S_2$ are Cartier divisors at the point $\Gamma$. Therefore we have

$$ a(E,S_i+dD_Z)\le a(E,-a(S_i,dD_X)S_i+dD_Z)-1\le -1 $$

for $i=1,2$

Let H be a general hyperplane section of large degree passing through the point P and let $\Gamma \in H_Z$. For any $\delta >0$ there exists a number $h(\delta )>0$ such that $(X,D(\delta )=(d-\delta )D_X+h(\delta )H)$ is a log canonical and not plt pair. Let $D_Z|_S=\sum d_iD^S_i$ be a decomposition on the irreducible components ($S=S_1+S_2$). If it is necessary we replace the divisor $D_X$ by $D'_X$ in order to $D'_Z|_S=\sum _{i:\Gamma \in D^S_i} d_iD^S_i$. By the generality of H and connectedness lemma, there exists $\delta >0$ with the following two properties.

(1) The pair $(X,D(\delta ))$ defines a plt blow-up $(Y(\delta ),E(\delta ))\rightarrow (X\ni P)$.

(2) By T denote the center of $E(\delta )$ on Z. Then, either $T=\Gamma$, or T is a curve provided that $T\subset S_2$ and $\Gamma \in T$ (note that case $T\subset S_1$ is impossible, since it was proved in Case I of Theorem 6.2).

Let $T=\Gamma$. Then we have Case II of Theorem 6.2, but it was proved that this case is impossible.

Let T be a curve and let $\psi :Z\rightarrow Z'$ be a contraction of $R_1$. The morphism $\psi$ contracts the divisor $S_1$ to the point $P_1$. By construction, $K_{S'_2}+{\text {Diff}}_{S'_2}(0)+T_{S'_2}$ is not a plt divisor at the point $P_1$, and it was proved in Case I of Theorem 6.2 that this case is impossible.

Let us consider Case I. Write $K_Z+dD_Z=g^*(K_X+dD_X)+a(S,dD_X)S$, where $a(S,dD_X)\ge 0$. Since S is Cartier divisor at a general point of $\Gamma$ then

$$ a(E,S+dD_Z)\le a(E,-a(S,dD_X)S+dD_Z)-1=-1. $$

Hence $\Gamma \subset {\text {LCS}}(S,{\text {Diff}}_S(dD_Z))$.

Let $a(S,dD_X)=0$. Then Z has canonical singularities.

Assume that $\Gamma$ is a curve. Then $(X\ni P)$ is a smooth point by Lemma 6.7, which is of independent interest.   $\square$

Lemma 6.7

Let $g:(Z,S)\rightarrow (X\ni P)$ be a toric canonical blow-up of three-dimensional ${\mathbb Q}$-factorial terminal toric singularity. Assume that there exists a curve $\Gamma \subset S$ such that it is a non-toric subvariety of $(S,{\text {Diff}}_S(0))$, and it does not contain any center of canonical singularities of Z. Let $-(K_S+{\text {Diff}}_S(0)+\Gamma )$ be an ample divisor. Assume that there exists a divisor $D'_Z\in |-mK_Z|$ for some $m\in {\mathbb Z}_{>0}$ such that $\big (Z,\frac{1}{m}D'_Z\big )$ is a canonical pair and $\big (\frac{1}{m}D'_Z\big )|_S=\Gamma +\sum \gamma _i\Gamma _i$, where $\gamma _i\ge 0$ for all i. Then $(X\ni P)$ is a smooth point.

Proof

Assume the converse. We suppose that the reader knows the proof of Proposition 2.6 (2), and we use its terminology. We have $a(S,0)=\frac{1}{r}(w_3+rw_2-qw_3+rw_1-w_3)-1$. If $a(S,0)=\frac{1}{r}$ then we have a contradiction obviously. Therefore we suppose that $a(S,0)>\frac{1}{r}$. For some $j\in \{1,2,3\}$ we have the inequality $\frac{1}{r}\ge a(S,0)/N_j$ and one of the two following requirements: either $P_j\in {\text {CS}}(Z)$, or the singularity at the point $P_j$ is of type $\frac{1}{N_j}(1,-1,0)$, where $N_j\ge 2$, $N_1=w_3$, $N_2=rw_1-w_3$, $N_3=rw_2-qw_3$.

The non-toric curve $\Gamma$ is conveniently represented as $\Gamma =D_Z\cap S$, where $D=(\psi (x_1,x_2,x_3)=0)/{\mathbb Z}_r\subset ({\mathbb C}^3\ni 0)/{\mathbb Z}_r(-1,-q,1)$ and $\psi$ is a quasihomogeneous polynomial with respect to $(N_1,N_2,N_3)$.

Then $P_j\in \Gamma$, the singularity is of type $\frac{1}{N_j}(1,-1,0)$ at the point $P_j$ and $N_j/r\ge 1$. Let us prove it. Let $D'=g(D'_Z)$. If $P_j\not \in \Gamma$ then we have the contradiction $a(S,\frac{1}{m}D')<a(S,0)-N_j/r\le 0$, since $\Gamma$ is a non-toric subvariety. Let $P_j\in \Gamma$. Then $P_j\not \in {\text {CS}}(Z)$, and if $N_j/r<1$, then we have the contradiction $a(S,\frac{1}{m}D')\le N_j/r-1<0$ since $\Gamma$ is a non-toric subvariety.

Assume that Case (2A) of Proposition 2.6 takes place. Then $j=3$. Since $N_3>\max \{N_1,N_2\}$ then the singularity must be isolated at the point $P_3$. We obtain the contradiction. It is not hard to prove that Case (2B) of Proposition 2.6 is impossible.   $\square$

Assume that $\Gamma$ is a point. Then ${\text {Diff}}_S(dD_X)$ is a boundary, and hence we obtain the contradiction with Theorem 4.2 for the pair $(S,{\text {Diff}}_S(dD_X))$ and the point $\Gamma$.

Let $a(S,dD_X)>0$. We will obtain a contradiction. Note that the number of exceptional divisors with discrepancy 0 is finite for the pair $(X,dD_X)$. Now we will carry out the procedure consisting of the two steps: (i1) replacing $dD_X$ by $D(\delta )$ and (i2) replacing $(X,dD_X)$ by other pair with canonical singularities (the variety X is replaced by other variety also). As the result of finite number of steps of this procedure we will obtain a contradiction. Let $H_1$ be a general hyperplane section of large degree containing the center of S on X (at this first step the point P is this center, and note that this center can be a curve after replacing X as a result of step (i2)). Also we require that $(H_1)_Z|_S \subset S$ is an irreducible reduced subvariety (curve) not containing any zero-dimensional orbit of S. This last condition is necessary to our procedure terminates obviously after a finite number of steps.

Let us consider the numbers $\delta \ge 0$, $h(\delta )\ge 0$ and the divisor $D(\delta )=(d-\delta )D_X+h(\delta )H_1$ such that $(X,D(\delta ))$ has canonical singularities, $\Gamma$ is a center of canonical singularities of $(Z,D(\delta )_Z-a(S,D(\delta ))S)$, and one of the two following conditions are satisfied: either (a1) $a(S,D(\delta ))=0$ or (a2) $a(S,D(\delta ))>0$ and there exists a center of canonical singularities different from $\Gamma$ for the pair $(Z,D(\delta )_Z-a(S,D(\delta ))S)$. Take the maximal number $\delta$ with such properties. By E again (for convenience) we denote some exceptional divisor with discrepancy 0 for $(X,D(\delta ))$ such that its center is $\Gamma$ on Z. It is step (i1).

Let $a(S,D(\delta ))=0$ and $\Gamma$ be a curve. By the above statement $(X\ni P)$ is a smooth point. We claim that $h(\delta )=0$, and thus we have the contradiction. Let us prove it. Consider the general point Q of $\Gamma$ and the general (smooth) hyperplane section H passing through this point. Then $(H\ni Q,(D(\delta )_Z)|_H)$ has canonical non-terminal singularities. This is equivalent to ${\text {mult}}_Q(D(\delta )_Z)|_H=1$. Let us apply the construction of non-toric canonical blow-ups from Sect. 5 to the curve $\Gamma$ provided that $\beta _1=1$. As the result we obtain the non-toric canonical non-terminal blow-up $(Y'',E'')\rightarrow (X\ni P)$. By the above $a(E'',D(\delta ))=0$. Since $\Gamma \not \subset (H_1)_Z$ then the divisor $(H_1)_{Y''}$ contains the center of canonical singularities of $Y''$ (see Sect. 5) always. Therefore $h(\delta )=0$.

Let $a(S,D(\delta ))=0$ and $\Gamma$ be a point. Then ${\text {Diff}}_S(D(\delta ))$ is a boundary and we have the contradiction with Theorem 4.2.

Let $a(S,D(\delta ))>0$. Let $\widehat{X}\rightarrow X$ be a log resolution of $(X,D(\delta ))$. Let us consider the set $\mathcal E$ consisting of all exceptional divisors $E'$ on $\widehat{X}$ with the two conditions: (1) $E'$ can be realized by some toric blow-up of $(X\ni P)$ and (2) $a(E',D(\delta ))=0$.

Let $\mathcal E=\emptyset$. Hence, if $T\in {\text {CS}}(Z,D(\delta )_Z-a(S,D(\delta ))S)$ and T is a curve, then T is a non-toric subvariety of $(S,{\text {Diff}}_S(0))$. Let us consider the variety $T\in {\text {CS}}(Z,D(\delta )_Z-a(S,D(\delta ))S)$ which is the maximal obstruction to increase a coefficient $\delta$, that is, if put $\Gamma =T$ then we can more increase the coefficient $\delta$ as the result of step (i1). If T is a curve then we consider T instead of $\Gamma$ and repeat the first step (i1) to increase the coefficient $\delta$ (for the sake to be definite, we denote the curve T by $\Gamma$). If T is a non-toric point lying on some toric orbit, then we are in Case II. We have proved that Case II is reduced to Case I, besides we can assume that we consider the pair $(X,D(\delta ))$ for some $\delta >0$. If T is a point not lying on any toric orbit then we can consider the point T instead of $\Gamma$ and increase $\delta$ as the result of step (i1). If T is a toric point then we can consider the point T instead of $\Gamma$ and increase $\delta$ and repeat the procedure from the beginning with the same notation.

Let $\mathcal E\ne \emptyset$. Let us consider the toric divisorial contraction $g_1:Z_1\rightarrow (X\ni P)$ which realizes the set $\mathcal E$ exactly. In particular, $K_{Z_1}+D(\delta )_{Z_1}=g_1^*(K_X+D(\delta ))$. Let $P_1$ be a center of E on $Z_1$. Let us consider locally the pair $(Z_1\supset P_1,D_1=D(\delta )_{Z_1})$ instead of $(X\ni P,D(\delta ))$. It is step i2). Let us repeat the whole procedure. We obtain a new divisor $D_1(\delta )$ on $Z_1$. Let $a(S,D_1(\delta ))=0$. If the center of S on $Z_1$ is a point then we have the contradiction as above. If the center of S on $Z_1$ is a closure of one-dimensional toric orbit then we have the similar contradiction, but we must use the results of Sect. 3 (Example 3.6 and Theorem 3.9) to prove $h(\delta )=0$. Let $a(S,D_1(\delta ))>0$. The case $\mathcal E=\emptyset$ is considered as above (the set $\mathcal E$ will be another one). In the case $\mathcal E\ne \emptyset$ we obtain a toric divisorial contraction $g_2:Z_2\rightarrow (Z_1\supset P_1)$, which is constructed similarly to the construction of $g_1$. After it let us repeat the whole procedure. By construction of partial resolution of $(X,dD_X)$ we obtain some pair $(Z_k,D_k(\delta ))$ in a finite numbers of steps such that $a(S,D_k(\delta ))=0$, and hence we have the contradiction.

Let $(X\ni P)$ be a non-${\mathbb Q}$–factorial singularity, that is, $(X\ni P)\cong (\{x_1x_2+x_3x_4=0\}\subset ({\mathbb C}^4_{x_1x_2x_3x_4},0))$. According to Sect. 5 it is sufficient to prove that the analog of Proposition 6.6 is satisfied for this singularity. Arguing as above in Theorem 6.2, the required statement is reduced to the case of ${\mathbb Q}$-factorial singularities, this concludes the proof.   $\square$

Corollary 6.8

Under the same assumption as in Theorem 6.5 the two following statements are satisfied:

(1) [2, 6, 8] if f is a terminal blow-up then f is a toric morphism (see Proposition 2.6);

(2) if f is a non-toric morphism then an index of $(X\ni P)$ is equal to 1.   $\square$