Keywords

1 Introduction

For a long time, convolutional neural networks (CNNs) have been widely used in various applications, such as image classification [4, 14], image retrieval [17, 19], semantic segmentation [5, 9], and clothing recommendation [10, 24]. Classical CNNs focus on the problems where a data instance can be represented in a regular grid structure [1], e.g., an image. With a regular structure, filters can directly be applied to extract effective features for model generation. However, many problems involve irregular structures in nature, and these datasets are commonly modeled as irregular graph structures, such as social relation analysis. As a result, generalized CNNs have been rapidly developed for irregular graph structures from single-relational and even multi-relational data instances, see, e.g., [1,2,3, 8].

Earlier, Bruna et al. extended the classical convolution operator based on the spectral representation of graphs for generalized CNNs [1]. Extending the work in [1], Defferrard et al. proposed a computationally efficient method to perform convolution operations on graphs [2]. Subsequently, Kipf and Welling considered the classical graph-based semi-supervised learning (SSL) problems, where the objective is to predict labels for unlabeled nodes based on labeled nodes, see e.g., [25, 26]. They then developed graph convolutional networks (GCNs) for graph-based SSL problems [8]. Further, Veličković et al. added self-attention layers to reweight edges of graphs [20]. Jiang et al. then showed performance improvement by combining Kipf and Welling’s GCNs and their edge reweighting method [6]. Recently, Rong et al. studied edge removal and showed the effectiveness on preventing over-smoothing [21]. Yu et al. presented graph-revised convolutional networks (GRCNs), which are capable of adding new edges and reweighting edges [23].

While most works resorted to edge-based refinement, this paper further explores the domain of node addition. Node addition allows nodes with similar features to share information together and reduce noisy information. This paper further considers edge reweighting so as to determine proper weights for edges adjacent to the added nodes, and remove noisy edges. Overall, this paper presents a simple but effective extension of GCNs in [8] by node addition and edge reweighting, for graph-based SSL problems. Compared to [6, 20], node addition considers the addition of new nodes and new edges to original graphs, while the two works focused on reweighting the edges existing in the original graphs. In contrast to [23], the proposed approach further considers the addition of new nodes and the removal of noisy edges. Overall, this paper has three main contributions as follows:

  • To the best of our knowledge, this paper presents the first work on adding new nodes for graph-based CNNs on SSL problems.

  • This paper presents a new method to reweight edges and even to remove noisy edges of a given graph. Besides, the method benefits node addition by determining proper weights for edges adjacent to the new nodes.

  • We conduct experiments on four datasets to validate the effectiveness of the proposed approach on node classification.

The remainder of this paper is organized as follows. Section 2 reviews the GCN method for graph-based SSL problems. Section 3 details the proposed approach. Section 4 evaluates the performance of the proposed approach. Section 5 concludes this paper.

2 Background

This section briefly reviews the SSL of using the GCN method in [8]. Let G(V, E) be a graph with nodes V and edges \(E \subseteq V \times V\). An adjacency matrix \(A\in \mathbb {R}^{|V|\times |V|}\) provides a representation of whether pairs of nodes in G contain edges connecting them, where |V| is the number of nodes of graph G. Typically, \(A_{ij}=1\) if the nodes i and j are adjacent, and \(A_{ij}=0\) otherwise. We are given a feature matrix \(X=(x_1, x_2, ..., x_n)\in \mathbb {R}^{n\times p}\) for n instances, where \(x_i\) is the feature vector of instance i, and p is the dimension of a feature vector. For SSL, each node of graph G is associated with the feature vector of an instance, and thus, \(|V|=n\). The adjacency matrix, A, is associated with the relationship between pairs of the instances, e.g., similarity. We let \(Y\in \mathbb {R}^{n\times c}\) be a label matrix and L be the set of nodes with labels, where \(Y_{ij}=1\) if \(i\in L\) and the label of \(x_i\) is j, and \(Y_{ij}=0\) otherwise.

Given X, A, Y, and L, as the inputs for SSL, an r-layer GCN method performs layer-wise propagation as follows.

$$\begin{aligned} H^{(u+1)}=\sigma (\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(u)}W^{(u)}), \end{aligned}$$
(1)

where \(H^{(0)}=X\), \(u=0,1,...,(r -1)\) is a layer index, \(\tilde{A}=A+I\) means to add a self-loop of every node, \(I\in \mathbb {R}^{n\times n}\) is the identify matrix, \(\tilde{D}\in \mathbb {R}^{n\times n}\) is a diagonal matrix with \(\tilde{D}_{ii}=\sum _{j=1}^{n}\tilde{A}_{ij}\), \(W^{(u)}\) is the weight matrix that is going to be learned for the u-th layer, and \(\sigma (.)\) is an activation function, e.g., \(\textrm{ReLU}(.)\). It is worth mentioning that \(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}\) is a symmetric normalization for \(\tilde{A}\). If we let \(\hat{A} =\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}\), then \(\hat{A}_{ij}\) can be viewed as the weight of edge that connects the nodes associating to \(x_i\) and \(x_j\) of graph G. Note that the output of the propagation is defined as,

$$\begin{aligned} Z=\textrm{softmax}(H^{(r)}W^{(r)}), \end{aligned}$$
(2)

where \(Z\in \mathbb {R}^{n\times c}\). Row \(Z_i\) refers to the prediction of the node associating to \(x_i\) for the c classes. Finally, the GCN method defines the loss function as,

$$\begin{aligned} \zeta _{\textrm{pred}} =-\sum _{i\in L}\sum _{j=1}^{c} \left( Y_{ij}\textrm{ln}Z_{ij}\right) , \end{aligned}$$
(3)

to measure how good or bad the model does.

3 Proposed Approach

Fig. 1.
figure 1

Overall flow of the proposed approach.

Full size image

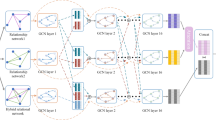
Figure 1 outlines the proposed approach. We first group the given nodes into several clusters, followed by adding a new node for each cluster. In each time we add a new node into a cluster, we also connect the new node to the nodes in the same cluster by adding new edges. More details about the node addition will be presented in Sect. 3.1. After adding the new nodes and edges, we will obtain a new graph. To combine edge reweighting with the GCN method, we add a parameter that will be learned for each node of the new graph, and then modify the GCN method partially. More details about edge reweighting will be presented in Sect. 3.2. Subsequently, the resultant network is used to produce a classification result. To make the performance less sensitive to clustering results, we will repeat the above process several times, and take the average of their classification results as the final results.

3.1 Node Addition

In real-world applications, inputs for SSL might be incomplete or contain noisy data. The goal of node addition is to reduce the influence of the imperfect inputs. More specifically, the motivation of node addition is twofold: (1) it is expected that nodes with similar features can share information together and also reduce noise by averaging, and (2) adding edges for isolated nodes or even ordinary nodes is capable of increasing the performance of SSL. Considering the two, we intend to provide a communication center that connects nodes with similar features, and helps information sharing.

Fig. 2.
figure 2

Illustration of node addition. (a) Suppose that nodes associated with \(\{x_1, x_2, x_3, x_4\}\) are grouped together, and nodes associated with \(\{x_5, x_6, x_7\}\) are grouped together. (b) For each cluster, a new node is added. (c) For each cluster, new edges are added. Each new node will be acted as a communication center of the nodes within the same cluster.

Full size image

For node addition, we group nodes of graph G into clusters, based on the features associated with the nodes, so that nodes with similar features can be assigned to the same cluster. For each cluster, we then add a node in it, where the feature of the new node is set to be the average of the features of the original nodes in the cluster. That is, the new node is placed at the center of the cluster. In each time we add a new node for a cluster, we also add an edge between the new node and each of the original nodes in the cluster. Figure 2 illustrates the idea, where seven nodes that are associated with seven instances, say \(\{x_1, x_2, ..., x_7\}\), respectively.

So far, we have built a communication center by adding a new node and some edges, for each cluster of nodes with similar features. Note that the number of nodes added and the number of edges added in graph G are equal to the number of clusters and the total number of nodes in graph G, respectively. Because node addition changes graph G, we will use the superscript, \('\), for the notations associated with the new graph. For example, \(G'(V', E')\) is the new graph, \(X'\in \mathbb {R}^{n'\times p}\) is the new feature matrix, and \(A'\in \mathbb {R}^{n'\times n'}\) is the new adjacency matrix, where \(n'\) is the number of nodes in graph \(G'\), and obviously \((n' - n)\) is the number of nodes added into G. Note that entries of \(A'\) are either zeros or one. Intuitively, no two features are exactly the same for most cases, and thus it is expected that weights of edges incident to the communication centers could properly be assigned. The assignment of proper weights will be covered in the scope of our edge reweighting method. Later in Sect. 3.2, we will generate a weighted adjacency matrix from \(A'\), and then do edge reweighting.

For practical implementation, we use k-means clustering, and we apply a simple heuristic as follows. We randomly pick m (\(m=5\) in this paper) distinct numbers from 0 to n/10 as the candidates of the k-value, where we set n/10 as a bound because we do not intend to generate too many small-size clusters. After clustering, there can be a few nodes far from the center of each cluster. Mostly, it is beneficial to refine the clustering result. We thus calculate the average distance between each point in a cluster to the cluster center. For each cluster, we then remove nodes from the cluster if their distances to the cluster center are greater than the average distance of the cluster. Finally, we update the cluster center based on the remaining nodes of each cluster. Note that we do not remove nodes from the graph. We only refine the clustering result. In addition, node addition places the new nodes on the updated centers, and adds the new edges only for the remaining nodes.

For each of the m candidates of the k-value, we will go through the GCN optimization flow shown in Fig. 1. Eventually, we can get m different results. Because it is difficult to find a proper k-value for a given graph, we take the average of the m results for the prediction result.

3.2 Edge Reweighting

This section reviews layer-wise propagation first, and details the implementation of edge reweighting afterward. Based on graph \(G'\), Eq. (1) can directly be rewritten as,

$$\begin{aligned} H'^{(u+1)}=\sigma (\tilde{D}'^{-\frac{1}{2}}\tilde{A}'\tilde{D}'^{-\frac{1}{2}}H'^{(u)}W'^{(u)}). \end{aligned}$$
(4)

In Eq. (4), we can see that the operation, \(\hat{A}'=\tilde{D}'^{-\frac{1}{2}}\tilde{A}'\tilde{D}'^{-\frac{1}{2}}\), normalizes \(\tilde{A}'\) in a symmetric way. More specifically, the operation assigns a weight for each edge considering the degrees of nodes in graph \(G'\). Generally, the operation is used when edges of graph \(G'\) are undirected, i.e., \(A'\) is symmetric. \(\hat{A'}\) will be symmetric if \(A'\) is symmetric. If edges of graph \(G'\) are directed, the operation can be replaced with \(\hat{A}'=D'^{-1}\tilde{A}'\), so that each row in \(\hat{A'}\) sums to one. That is, weights of edges pointing from each node sums to one. In many cases, \(\hat{A}'\) will not be symmetric if edges of graph \(G'\) are directed.

Edge reweighting will view the given graph, i.e., \(G'\), as a directed graph. Typically, an undirected graph can be converted into a directed graph by replacing the undirected edge between each pair of nodes with two directed edges in opposite direction. Practically, if edges of the initial graph, i.e., graph G, are directed, we will use two directed edges to connect a new node to each of the original nodes in the same cluster for the stage of node addition. Then for Eq. (4), we will replace \(\tilde{D}'^{-\frac{1}{2}}\tilde{A}'\tilde{D}'^{-\frac{1}{2}}\) with \(D'^{-1}\tilde{A}'\). Note that if edges of the initial graph are undirected, we will not make any change for Eq. (4). It is worth mentioning that our edge reweighting method has two advantages. Firstly, we can consider only the edges pointing from (or to) a node at each time, and thus drastically reduce the complexity of reweighting. Secondly, our method can not only be applied to undirected graphs, but also directed graphs. Note that no matter whether edges of graph G (and thus, graph \(G'\)) are directed or undirected, the methods introduced below can be applied and are exactly the same.

Given graph \(G'\), we create a vector \(b=(b_1, b_2, ..., b_{n'})^T\in \mathbb {R}^{n'\times 1}\), as parameters to be learned. Each parameter is assigned to exactly a node of graph \(G'\). The parameter of a node will be added to the weight of every edge pointing from the node. Formally, we generate an adjacency matrix, say \(B\in \mathbb {R}^{n'\times n'}\), where

$$\begin{aligned} B_{ij}=\textrm{max}(\hat{A}'_{ij}+b_i, 0),\forall i, (i, j)\in E'. \end{aligned}$$
(5)

Note that \(b_i\) can be negative, and \(\textrm{max}(.)\) forces negative values to be zero. If \(B_{ij}\) equals zero, there is no edge pointing from node i to node j. That is, some edges can be removed if \(b_i\) is negative. We then do normalization by \(\hat{B}=D'^{-1}B\) so that weights of edges points from each node sums to one. If \(b_i\) is positive and \(b_i\) is much greater than any of \(\hat{A}'_{ij}\) with \((i, j)\in E'\), normalization can make all of the values of \(\hat{B}_{ij}\) with \((i, j)\in E'\) be almost the same. That is, parameters \(\{b_1, b_2, ..., b_{n'}\}\) can be used to reduce the difference of edge weights or remove some edges of graph \(G'\).

The resultant layer-wise propagation is as follows:

$$\begin{aligned} H'^{(u+1)}=\sigma (\hat{B}H'^{(u)}W'^{(u)}). \end{aligned}$$
(6)

Similar to [6, 12], we then define the loss function used to optimize the parameters as,

$$\begin{aligned} \zeta _{\textrm{graph}} =(1-\lambda )\sum _{i,j=1}^{n'} \left( \big \Vert x_i-x_j\big \Vert _2^2\hat{B}_{ij}\right) +\lambda \sum _{i,j=1}^{n'}\hat{B}_{ij}^2, \end{aligned}$$
(7)

where the former encourages nodes with larger distance in features to have smaller weights, the latter tries to remove noisy edges, and \(1\ge \lambda \ge 0\) is a constant used to control the relative importance between the two terms. Finally, the loss function of our approach is set to be \(\zeta _{\textrm{pred}} + \beta \zeta _{\textrm{graph}}\), where \(\beta \ge 0\) is also a constant used to control the relative importance. Empirically, \(\lambda \) and \(\beta \) are set to be 0.9 and 0.1, respectively.

4 Experiments

Table 1. Statistics of four publicly available datasets.
Full size table
Table 2. Comparison the accuracy (%) of the GCN, GAT, GLCN, GRCN, and our models, on the datasets.
Full size table

We implemented the proposed approach based on PyTorch [13] and scikit-learn [15]. For comparative studies, we evaluated the performance of (1) the GCN model [8], (2) the GAT model [20], (3) the GLCN model [6], (4) the GRCN model [23], (5) our extension on the GCN model, and (6) our extension on the GRCN model. Note that all of the models used the same optimizer (i.e., Adam [7]), learning rates, weight decays, and the number of hidden units, based on the settings of GRCN. All of them were also based on PyTorch. It is worth mentioning that the GLCN model was implemented by ourselves, because we did not find its PyTorch implementation. For evaluation, we conducted experiments based on four publicly available datasets from [11] and [18]. The statistics of the datasets are shown in Table 1.

In Table 1, column “#Nodes” lists the number of nodes, “#Features” the dimension of each feature vector, “#Edges” the number of edges, and “#Classes” the number of classes for classification. The preparation of the datasets is the same as [22], where 20 instances of each class were used for training data. Overall, there were 500 and 1, 000 instances used for validation data and testing data, respectively. There were 20 and 30 instances of each class used for training data and validation data, respectively. For testing data, the classes and instances were first removed if the number of instances of a class is smaller than 50. The remaining data were used as the testing data.

Table 2 shows the experimental results. For each dataset, we reported the average results over five runs with random splits on training, validation, and testing data (the data numbers were kept the same). As can be seen, our extensions achieved better performance than the other models. Based on the results, we can see that adding edges on existing graphs (i.e., GRCN and Ours) is helpful to achieve better performance than the others in most cases. Consider our extensions on GCNs and GRCNs. We noticed that combining the edges added by GRCNs and the edges by our approach mostly improved the performance. However, some edges might become noisy for accuracy, see, the result on the PubMed dataset.

Fig. 3.
figure 3

Case study of refining clustering results or not to our extension on GCNs on the Photo dataset. Note that the dotted line shows the accuracy of a baseline, where no clustering is used (i.e., \(k=0\), for k-means clustering).

Full size image

Remind that in Sect. 3.1, we not only refine the clustering results, but also take the average of several optimized results, so as to make our performance less sensitive to the quality and the k-values of k-means clustering. Figure 3 shows the result of a case study that compares our extension on GCNs of refining clustering results or not on the Photo dataset. As can be seen, node addition by clustering improved the accuracy in most cases, no matter if the refinement was used or not. Further, we can see that the refinement created a smoothing effect for most k-values. Numerically, the refinement reduced the standard deviations from 0.008 to 0.005, while the average accuracy values were almost the same, i.e., 91.11% to 91.10%. The refinement did reduce the sensitivity to the k-values of the clustering.

5 Conclusion

This paper has presented a simple but effective extension of GCNs for semi-supervised node classification. The extension is not limited to undirected graphs; it can also be applied to directed graphs. Node addition provides communication centers for nodes to share information together. Edge reweighting not only reweights edges, but also removes noisy edges for high performance. Future works include the node removal and dynamic graph modification for GCNs.