Abstract
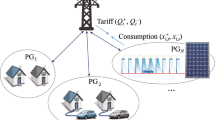
This paper investigated an electricity control strategy to minimize the electrical peak demand of a microgrid system composed of households. Each household can install a distributed generation system by applying for the subsidy program that the central grid system operator (GSO) encourages. The distributed generation system includes an electricity storage system and residential electricity generators such as photovoltaics and wind turbines. Each consumer seeks to arrange an appropriate schedule that minimizes the overall cost including electricity bills, investment costs, and penalty costs incurred by consumer dissatisfaction. Simultaneously, the GSO wants to minimize the peak demand among households. To address the problem, this paper developed a mixed-integer bilevel programming (MIBP) model. An exact algorithm based on consumer behavior is developed to attain optimal solutions for optimistic consumers. Numerical experiments are presented to illustrate the practical use of the model in the applications.
This research was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning [Grant no. NRF-2019R1A2C2084616].
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Electricity consumption has rapidly increased globally over the last few decades. The ever-growing electricity demand affects the stability of electricity grids. If the demand exceeds the capacity reserved by power generators in the grid, critical failures such as overloads of power transmitters or blackout may happen. Hence, it is important to manage the consumption demand so that it can be controlled against the maximum capacity of the grid. The highest demand that occurs over a specified time period is called peak demand. Especially in South Korea, daily peak demand has shown a relatively higher growth rate than the daily average electricity consumption [1]. This trend shows that the peak demand is getting closer to the maximum capacity and that demand within any given day fluctuates significantly. A simple solution is to add a new generator to the grid (i.e., supply-side management) to avoid the peak demand exceeding the maximum capacity. However, the construction of new baseload generation sources, such as nuclear and coal plants, can be a significant financial burden for the grid system operator (GSO). In addition, the simple expansion of grid generators can cause a low utilization rate for some generators.
Another way to deal with the problem of the supply-demand imbalance is demand-side management. In demand-side management, the GSO can level off a fluctuating demand or reduce the peak demand by rewarding (or penalizing) users depending on conditions. If the program proposed by the GSO makes it reasonable for users to change their electricity usage patterns, the realized demand will help match supply and demand as a response to the program. Another way to manage the demand side is to reduce a residential microgrid system by installing small decentralized generators on the grid. If a consumer has a small decentralized generator from renewable energy sources (RES) such as wind turbines and photovoltaics, the consumer in the microgrid system can generate electricity, save electricity for his or her energy storage system (ESS), and trade the surplus electricity within an energy market. With these functions, consumers should control their electricity usage according to the pre-announced central electricity planning strategy. Both the GSO and individual consumers can benefit from such a microgrid system. The GSO can reduce the peak electricity demand level and contribute to decreased carbon emissions by financially supporting consumers in building their RES-based generators. Consumers can save on their electricity bills by generating electricity themselves at lower costs and by making a profit by selling electricity credits that have been locally generated.
However, constructing a microgrid system with financial assistance from the GSO provokes decentralized decisions that assume electricity usage in households is scheduled after the GSO makes its decisions regarding subsidization.
Therefore, the following consecutive questions arise:
-
What is the optimal proportion of GSO subsidies for investments in RES-based generators and ESS to reduce peak demand in microgrid systems?
-
How should the GSO decide whether or not to install RES and ESS?
-
What is the optimal schedule for the electrical appliances installed?
In the microgrid system, participants constitute a Stackelberg leader-follower game, especially in bilevel programming, where consumers’ lower-level programs are embedded in the GSO’s upper-level program [2, 3]. The bilevel program deals with decision-making in various sectors such as the electricity generation market and the chemical industries, where network members interact with each other in a supply chain, but not in a cooperative manner [4].
The proposed mixed-integer bilevel programming (MIBP) generalizes the classical bilevel programming setup by considering binary decisions about investments in RES and ESS at a lower level. To the best of our knowledge, there is no existing research that integrates individual electricity strategies with GSO subsidization. In this study, we develop a solution algorithm for an MIBP that includes discrete decisions based on optimistic consumers–an algorithm that although it has been treated as generally intractable [5]. The performance of the algorithm is evaluated with randomly generated instances.
The remainder of this paper is organized as follows. Section 2 describe the problem and introduce the MIBP model. Section 3 propose an algorithm based on optimistic consumers. In Sect. 4, numerical experiments are conducted. Finally, conclusions are presented in Sect. 5.
2 Problem Definition and Mathematical Formulation
The proposed MIBP consists of a GSO’s linear program and consumers’ mixed-integer linear program. In the MIBP, we assume that the GSO is the leader and each consumer is the follower. The detailed assumptions of the MIBP are defined as follows: (1) the total time is divided into identical time slots; (2) consumers can install the RES and ESS simultaneously with subsidies from the central GSO; (3) energy potential of RES is predetermined; and (4) electricity loads of appliances are deterministic; The following are the notations used in the MIBP.
Sets
- N :
-
set of consumers
- \(A_{1}^{i}\) :
-
set of basic appliances
- \(A_{2}^{i}\) :
-
set of schedule-based appliances
- \(A_{3}^{i}\) :
-
set of model-based appliances
- \(A^{i}\) :
-
set of all appliances (\(A^{i}=A_{1}^{i}\bigcup A_{2}^{i}\bigcup A_{3}^{i}\))
- T :
-
set of finite time slots
- \(P_{a}^{i}\) :
-
set of predetermined pattern for using schedule-based appliance a
Parameters
\(l_{a}\) | length of operation time of appliance a | \(\forall a\in A^{i}\) |
\(E_{a}\) | electricity required for the operation of appliance a per one hour | \(\forall a\in A^{i}\) |
\(\overline{E}_{a}\) | maximum electricity of appliance a used per one hour | \(\forall a\in A^{i}\) |
\(\underline{E}_{a}\) | minimum electricity of appliance a used per one hour | \(\forall a\in A^{i}\) |
\(\pi \) | amortized cost of investment in the RES and ESS | |
\(\tilde{e}_{at}\) | electricity demand of appliance a at time t | \(\forall a\in A^{i}\), \(\forall t\in T\) |
\(\alpha \) | minimum requirements of consumers’ utilization | |
\(c_t\) | unit supply cost of consumer at time t | \(\forall t\in T\) |
\(p_t\) | electricity price from the consumer at time t | \(\forall t\in T\) |
\(\epsilon ^{dis}\) | efficiency when electricity is discharged from the ESS | |
\(\epsilon ^{cha}\) | efficiency when electricity is charged to the ESS | |
\(C_t^{out}\) | outside centigrade degree at time t | \(\forall t\in T\) |
Decision variables
\(e_{it}\) | quantity of electricity used at time t | \(\forall i\in N\), \(\forall t\in T \) |
\(e_{iat}\) | quantity of electricity of appliance a used at time t | \(\forall i\in N\), \(\forall a\in A\), \(\forall t\in T\) |
\(e_{it}^{in}\) | inbound quantity of electricity from a supplier at time t | \(\forall t\in T\) |
\(e_{it}^{out}\) | outbound quantity of electricity to a supplier at time t | \(\forall t\in T\) |
\(e_{it}^{cha}\) | quantity of electricity charged in ESS at time t | \(\forall t\in T\) |
\(e_{it}^{dis}\) | quantity of electricity discharged in ESS at time t | \(\forall t\in T\) |
\(e_{it}^{gen}\) | quantity of electricity generated by RES at time t | \(\forall i\in N\), \(\forall t\in T\) |
\(u_{it}\) | utilization of user at time t | \(\forall i\in N\), \(\forall t\in T\) |
\(x_{i}\) | 1, if a consumer invests in ESS and RES; 0, otherwise. | \(\forall i\in N\) |
y | proportion of subsidies | |
\(\lambda _{iap}\) | 1, if predefined schedule p is selected for appliance a; | \(\forall i\in N\), \(\forall a\in A_{2i}\) |
0, otherwise. | \(\forall p\in P_{a}^{i}\) | |
\(C_{it}^{in}\) | inside centigrade degree at time t | \(\forall i\in N\), \(\forall t\in T\) |
The leader’s and follower’s optimization problems are presented separately below.
2.1 Leader’s Upper-Level Problem
When the capacity of baseload generation sources is given, the GSO decide the percentage of subsidies for followers, as well as a time-varying electricity pricing schedule. The two objectives of the leader’s problem are to minimize the maximum peak demands among households and to minimize the cost of the subsidy. The relevant mathematical formulation is developed as follows:
Objective function (1) simultaneously minimizes the peak demand and the subsidy required for individuals. Constraint (2) defines the range of proportion of subsidy over investment cost \(\pi \). Constraint (3) represents the optimal electricity load profile of individual consumers which will be presented in Sect. 2.2.
2.2 Follower’s Lower-Level Problem
In the follower’s problem, we assume three types of appliances in households. A type-1 appliance is a machine required for daily use (e.g., refrigerators). A type-2 appliance is used based on schedules. (e.g., televisions) Patterns of using each schedule-based machine are predetermined by the users and are known and have been established in this study. A type-3 appliance is a model-based machine. Model-based machines operate to maintain comfortable living environments (e.g., air conditioners and electric heaters). The formulations for the lower-level problem are referred to [6].
Objective Function. In the residential microgrid system, consumer \(i \in N\) wants to minimize the overall cost of electricity bills, investment costs, and deductions from the GSO’s subsidy support.
The objective function (4) minimizes the summation composed of electricity bills, the revenue generated from selling surplus electricity to the power market, and subsidies from the GSO. In the operation of RES and ESS, we assume that the quantity of electricity charged (or discharged) is limited by capacity.
Constraints for RES and ESS. In the operation of RES and ESS, we assume that the quantity of electricity charged (or discharged) is limited by the capacity \(\overline{B}\).
Constraint (5) mandates that the energy level in ESS at time t should be non-negative and lower than the maximum capacity of ESS. Constraint (6) is the balance equation of electricity, which can be traded with an electricity provider, transferred to the ESS, and generated by RES in the residential area. Constraints (7)–(9) ensure that it is possible to sell energy and store energy only if the RES and ESS are determined to be installed by a consumer. Constraint (10) aggregates the entire electricity load from the operation of appliances at time t.
Constraint for Type-1 Appliances. A type-1 appliance always requires a certain energy level, which is given. For instance, a refrigerator needs a specific level of energy to maintain a low temperature.
Constraint (11) indicates that energy is consumed regularly in an appliance a at a time slot t.
Constraints for Type-2 Appliances. An appliance that belongs to a type-2 category is only operated within a consumer’s preferred time \(t\in [\underline{T}_a,\overline{T}_a]\). Two constraints are required for a type-2 appliance:
Constraints (12) and (13) ensure that only one predefined schedule can be determined, based on its association with an appliance, where \(E_{apt}\) is the electricity load of the appliance at time slot t relevant to schedule p.
Constraints for Type-3 Appliances
Constraints (14) and (15) describe energy demanded in order to adjust for environmental conditions such as temperature and humidity at a given time slot. Constraint (14) represents a physical model that expresses the relationship between environmental conditions and electricity consumption. Constraint (15) stipulates that the electricity load of an application should be within the operating range. Constraint (16) represents that the environmental condition over time should be within the desirable condition range.
Constraints on a Consumer’s Dissatisfaction
In the microgrid system, a consumer’s dissatisfaction level is calculated by the predefined dissatisfaction level of schedule p. Constraint (17) defines the dissatisfaction level at time t. Constraint (18) stipulates that the aggregated dissatisfaction level is lower than or equal to the given level. Constraints (19) and (20) define decision variables.
3 Solution Strategy
It is obvious that a consumer should install the equipment by applying for the subsidy program if the profit from operating ESS and RES is greater than the cost of installing ESS and RES. Using this fact, one can obtain the threshold proportion of a subsidy. If decision variable y is equal to the threshold, the consumer is indifferent about installing ESS and RES. If it is assumed that consumers always choose to install the equipment to reduce peak demand (optimistic), we can easily find the global optimal solution. In our problem, Pareto points correspond to peak demand for a whole grid system and subsidy support. If we predetermine y as the threshold that spurs a household to adopt the program, the dominating Pareto point is determined by calculating all the schedules of consumers and the total subsidies. An algorithm for obtaining the Pareto curve is presented in Algorithm 1.

4 Computational Experiments
To demonstrate the proposed solution algorithm for solving the MIBP model, we consider a case study on a hypothetical grid system [6]. There are 27 households that can switch their existing energy consumption system to a microgrid system. We refer to an instance of the single microgrid system as baseline data [6]. By changing three sets of data, such as (i) minimum satisfaction level, (ii) RES-based generation potential, and (iii) energy consumption style with three levels, such as “low,” “moderate,” and “high,” a total of 27 instances corresponding to the households are obtained. For (i), \(\alpha \) is set by 0.9, 0.7, and 0.5. For (ii), \(G_t^{max}\) is changed to 80%, 100%, and 120%. For (iii), energy loads of type-1 appliances are changed to 90%, 100%, and 110% and the set of type-2 appliances used in one household is set according to its level of (iii). Table 1 shows input data for type-2 appliances. All consumers use “\(a_1^{Type2}\)” and “\(a_2^{Type2}\)” appliances. Consumers in a “moderate” level of (iii) additionally operate a “\(a_3^{Type2}\)” appliance. Consumers in a “high” level of (iii) use all the appliance types.
We assume that the investment cost for installing ESS and RES is $20,938. To amortize the investment cost of the equipment, we consider the capital charge factor for the land, assuming the interest rate of 8% and a lifetime of 5 years. Thereby the equivalent daily cost of the investment cost is set to 14.15 ($/day). The electricity cost and price are assumed to be constant and are set to 3.5 ($/kWh) and 2.8 ($/kWh), respectively.
To validate that the capacity of ESS affects the reduction of peak demand, we conducted experiments by changing the capacity of ESS to 1.8 kWh (small), 2.4 kWh (medium), and 3.0 kWh (large). The results can be found in Fig. 1. The results show that the Pareto frontier obtained for a large capacity of consumption dominates other Pareto frontiers. This means that increasing the capacity of ESS is effective in reducing peak demand.
5 Conclusions
We investigated Stackelberg-game-based modeling and optimization for reducing peak demand for a microgrid system. In order to find the optimal solution for optimistic consumers, we developed an exact algorithm. Computational experiments show that the algorithm gets the Pareto frontier of the MIBP model within reasonable time limits. A sensitivity analysis was conducted to validate the effect of ESS capacity on peak demand.
References
Ministry of Trade, Industry, and Energy: The 8th Basic Plan for Long-term electiricity Supply and Demand, Korea (2017)
Von Stackelberg, H.: Market Structure and Equilibrium. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-12586-7
Dempe, S., Kalashnikov, V., Pérez-Valdés, G. A., Kalashnykova, N.: Bilevel Programming Problems. Springer, Berlin (2015). https://doi.org/10.1007/978-3-662-45827-3
Sinha, A., Malo, P., Deb, K.: A review on bilevel optimization: from classical to evolutionary approaches and applications. IEEE Trans. Evol. Comput. 22(2), 276–295 (2018). https://doi.org/10.1109/TEVC.2017.2712906
Vicente, L., Savard, G., Judice, J.: Discrete linear bilevel programming problem. J. Optim. Theory Appl. 89(3), 597–614 (1996). https://doi.org/10.1007/BF02275351
Tsui, K.M., Chan, S.C.: Demand response optimization for smart home scheduling under real-time pricing. IEEE Trans. Smart Grid 3(4), 1812–1821 (2012). https://doi.org/10.1109/TSG.2012.2218835
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 IFIP International Federation for Information Processing
About this paper
Cite this paper
Woo, YB., Moon, I. (2022). Bilevel Programming for Reducing Peak Demand of a Microgrid System. In: Kim, D.Y., von Cieminski, G., Romero, D. (eds) Advances in Production Management Systems. Smart Manufacturing and Logistics Systems: Turning Ideas into Action. APMS 2022. IFIP Advances in Information and Communication Technology, vol 663. Springer, Cham. https://doi.org/10.1007/978-3-031-16407-1_55
Download citation
DOI: https://doi.org/10.1007/978-3-031-16407-1_55
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-16406-4
Online ISBN: 978-3-031-16407-1
eBook Packages: Computer ScienceComputer Science (R0)