Provably Secure Reflection Ciphers

Abstract

This paper provides the first analysis of reflection ciphers such as Prince from a provable security viewpoint.

As a first contribution, we initiate the study of key-alternating reflection ciphers in the ideal permutation model. Specifically, we prove the security of the two-round case and give matching attacks. The resulting security bound takes form $\mathcal {O}(qp^2/2^{2n}+q^2/2^n)$, where $q$ is the number of construction evaluations and $p$ is the number of direct adversarial queries to the underlying permutation. Since the two-round construction already achieves an interesting security lower bound, this result can also be of interest for the construction of reflection ciphers based on a single public permutation.

Our second contribution is a generic key-length extension method for reflection ciphers. It provides an attractive alternative to the FX construction, which is used by Prince and other concrete key-alternating reflection ciphers. We show that our construction leads to better security with minimal changes to existing designs. The security proof is in the ideal cipher model and relies on a reduction to the two-round Even-Mansour cipher with a single round key. In order to obtain the desired result, we sharpen the bad-transcript analysis and consequently improve the best-known bounds for the single-key Even-Mansour cipher with two rounds. This improvement is enabled by a new sum-capture theorem that is of independent interest.

1 Introduction

Cryptographers have long been fascinated by self-inverse, or almost self-inverse, encryption schemes. For example, the Enigma rotor machine has the surprising property that its encryption and decryption operations are identical. This feature, enabled by the middle reflector or Umkehrwalze, made the encryption device considerably more compact.

Although the reflector ultimately contributed to the demise of Enigma, the use of self-inverse structures was not abandoned and persists in modern cryptography. Feistel ciphers such as the DES, for instance, are equal to their own inverse up to a reordering of the round keys. Despite this property, it was later shown by Luby and Rackoff [28] and follow-up work that the generic Feistel construction is indeed sound.

Many traditional key-alternating ciphers also use involutions, i.e. self-inverse functions, as their components in order to keep the hardware implementation costs for encryption and decryption similar and to save area. The block ciphers anubis [3], khazad [4] and noekeon [16] are early examples of this strategy. Key-alternating ciphers have been extensively analyzed from the perspective of provable security [7, 13, 20, 21, 25], with results demonstrating their resistance against generic attacks. The provable security of key-alternating ciphers based on an involution instead of permutations has been studied by Lee [26].

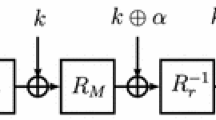
At ASIACRYPT 2012, Borghoff et al. [8] introduced the block cipher Prince as an alternative approach to minimizing the overhead of supporting both efficient encryption and decryption. Prince has the following reflection property: decryption is the same as encryption using a related key. This feature is achieved by using the structure shown in Fig. 1, which we will call the key-alternating reflection cipher. Although the use of both permutations and their inverse risks increasing area requirements, this is not a concern for the low-latency use-case that Prince aims for. Indeed, Prince targets fully unrolled hardware implementations that encrypt a plaintext in a single cycle.

Fig. 1.

A 2r-round key-alternating reflection cipher based on r public permutations $\pi _1, \ldots , \pi _r$ and $2r+2$ keys $K_1, \ldots , K_{2r+2}$. Various key-schedules are possible. In the Prince core cipher $K_1 = \ldots = K_{r + 1}$ and $K_{r + 2} = \ldots = K_{2r + 2} \oplus \alpha$ for some constant $\alpha \ne 0$. The reflector $\mathcal R$ is an involution.

Following increased interest in lightweight cryptography, and low-latency encryption in particular, several other key-alternating reflection ciphers were subsequently proposed. For example, Princess [10] and Prince v2 [11] are variants of Prince. The tweakable block ciphers Mantis [5] and Qarma [1] combine the key-alternating reflection cipher structure with involutive components and target applications such as memory encryption.

Despite their widespread use, the generic security of key-alternating reflection ciphers has not been analyzed from a provable security viewpoint. This stands in sharp contrast to Feistel ciphers and traditional key-alternating ciphers, which have been a regular subject of study in symmetric-key provably security. This is remarkable, since it is natural to wonder whether or not the additional structure of reflection ciphers leads to generic flaws.

Related Work. The block cipher Prince has been extensively analyzed from a cryptanalytic point of view, see for instance the results of the Prince cryptanalysis challenge which ran between 2014 and 2016 [9]. Boura et al. [10] discuss the choice of the reflector $\mathcal {R}$ and the key-schedule of general key-alternating reflection ciphers.

No results, for any number of rounds or any kind of key-schedule, are known about the provable security of key-alternating reflection ciphers. The study of traditional key-alternating ciphers, in contrast, goes back to Even and Mansour [20] for one round. The analysis of multiple rounds was initiated by Bogdanov et al. [7] and continued in [13, 21, 25]. Their results consider the case with independent round keys. For the two-round case, the security with three equal keys was shown by Chen et al. [12] at CRYPTO 2014.

Despite the lack of results about the provable security of key-alternating reflection ciphers, the design of Prince does rely on results from provable security for the purpose of key-length extension. Specifically, Prince uses a variant of the FX construction [24] to extend the key-length of its 64-bit core reflection cipher from 64 to 128 bits. This construction is shown in Fig. 2. The designers of Prince prove that, under the strong assumption that $E^*$ is an ideal reflection cipher, the resulting construction is secure up to the tradeoff curve $pq = 2^{128}$ with p the number of queries to $E^*$ and q the number of construction queries. Mantis uses the same approach to key-length extension.

Fig. 2.

The structure of Prince and Mantis, with secret keys $K$ and $L$, and $E$ a block cipher. The map $\sigma$ is an invertible linear map and $\mathcal R$ is a linear involution.

Although the construction in Fig. 2 can offer reasonable security when the number of construction queries q is limited, it has been observed that the security margin offered by the $pq = 2^{128}$ tradeoff may be less comfortable than expected. In particular, at EUROCRYPT 2015, Dinur [18] proposed new time-memory-data tradeoff attacks against Prince. Recently, Prince v2 [11] was proposed with the explicit goal of obtaining improved security with minimal changes to the original design. The approach taken by Prince v2 is to use alternating round keys, i.e. $K_{2i - 1} = K_1$ and $K_{2i} = K_2$ for $i = 1, \ldots , r$ in Fig. 1. They also slightly modify the reflector $\mathcal R$.

Contribution. The contribution of this paper is twofold. First, we initiate the study of the provable security of key-alternating reflection ciphers. Second, we provide a simple and generic key-extension method for reflection ciphers that achieves much better security than the FX construction.

For the first contribution, we analyze the security of the two-round variant of the general construction from Fig. 1 in the ideal permutation model. Specifically, our results focus on the case with a linear reflector $\mathcal R$ and two alternating round keys (i.e. $K_3 = K_1$, $K_4 = K_2$), similar to the Prince v2 construction. Decryption is then the same as encryption up to swapping of the keys $K_1$ and $K_2$. We denote this construction by $\textsf{KARC}2$. Our Theorem 1 shows that any adaptive distinguisher making p primitive queries and q construction queries to $\textsf{KARC}2$ achieves an advantage of at most $\mathcal {O}(p^2q/2^{2n} + q^2/2^n)$. In Sect. 3.2, alternative key-schedules are discussed, and we show that reducing the number of round keys is nontrivial and even results in insecure constructions for many natural choices of the key-schedule.

The $\textsf{KARC}2$ construction is the first generic reflection cipher construction with a security proof. This resolves the first case of a problem of intrinsic theoretical interest, similar to the study of key-alternating ciphers. From a more practical perspective, the result limits the power of generic attacks and motivates the general soundness of a widely used construction.

Although $\textsf{KARC}2$ achieves only birthday-bound security with respect to the number of construction queries q, the best tradeoff between primitive and construction queries satisfies $p^2 q = 2^{2n}$. Since the amount of data q is often limited in practice, the latter tradeoff is usually dominant. Hence, we believe the $\textsf{KARC}2$ construction could also be instantiated directly with concrete reduced-round permutations to build an attractive reflection cipher. Although many permutations are only designed to be efficient in the forward direction, there are exceptions such as Friet [32].

In Sect. 4, we show that Theorem 1 is tight for general choices of the reflector $\mathcal R$, by providing two matching generic attacks. The first attack is information-theoretic and shows that the tradeoff curve $p^2 q = 2^{2n}$ cannot be improved. The second attack is a variant of the mirror slide attack of Dunkelman, Keller and Shamir [19]. It uses $\mathcal {O}(2^{n/2})$ construction queries and has a similar time-complexity. The advantage achieved by the attack is lower bounded in Theorem 2, thereby showing that the $q^2/2^n$ term in Theorem 1 can not be avoided in general. Although this may suggest that the reflector $\mathcal R$ is not that important from a generic viewpoint, it is important from the viewpoint of dedicated cryptanalysis (when all permutations are instantiated). Another reason for considering $\mathcal R$ is simply that all practical reflection ciphers have such a layer, and we want our results to say something about their generic security.

The proof of Theorem 1 is given in Sect. 5. It relies on Patarin’s H-coefficient technique [13, 29]. The good transcript analysis resembles ideas of the first iteration of Patarin’s mirror theory [30, 31], but additional difficulties appear due to the fact that the underlying permutation can be queried by the distinguisher. Note that the framework of Chen et al. [14] relies on mirror theory for two independent permutations, so it cannot be applied to $\textsf{KARC}2$, which requires the single permutation variant of mirror theory. For the secret permutation case, different techniques can be used in order to obtain domain separation [17, 30]. In our proof, the domain separation is covered by a bad event, which leads to the $q^2/2^n$ term in the final security bound. The proof, like many proofs in provable security, is in an idealized model. The assumption that the primitive is ideal will never be satisfied in practice. For this reason, it is good practice to complement the provable security analysis (which rules out generic attacks) with dedicated cryptanalysis when all components are instantiated.

Our second contribution is a general method to extend the key-length of reflections ciphers, similar to the FX construction shown in Fig. 2, but achieving much better security. Specifically, our proposal is to add the keys K and $\sigma (K)$ again before and after the reflector $\mathcal R$ respectively. For this construction, we model the block cipher E as an ideal cipher. Our Theorem 7 shows that any distinguisher making adaptively chosen plaintext and ciphertext queries to this construction achieves an advantage of at most $\smash {\widetilde{\mathcal {O}}}(p\sqrt{q}/2^{n + k})$, with n the block size and k the key-length of the ideal cipher.

The proof of Theorem 7 is by a reduction to the security of the two-round Even-Mansour cipher with a single key. However, in order to be able to prove that $p^2 q = 2^{2(n + k)}$ is the optimal tradeoff for our ideal cipher construction, we had to sharpen the analysis of two-round Even-Mansour by Chen et al. [12]. Hence, as a side-result that is of independent interest, we improve the best known bounds for the two-round Even-Mansour cipher with identical round keys. Figure 3 shows the difference between our new bound and the bound of Chen et al.. This result is presented in Theorem 3.

Fig. 3.

Comparison between the result of Chen et al. [12] for 2-round Even-Mansour and Theorem 3. The lines correspond to an advantage upper bound equal to one.

The proof of Theorem 3 is given in Sect. 6. Our improvement over the result of Chen et al. [12] is due to a sharpening of their bad-transcript analysis. This sharpening is made possible by an improved sum-capture theorem, which we present in Theorem 5 and prove in Sect. 6.1. Our sharpened sum-capture theorem is also of independent interest, as it is applicable to all other proofs relying on this result. In a nutshell, the new result removes the unnecessary discrepancy between the best-known sum-capture theorems for random functions and random permutations. Hence, we are able to avoid a term of order $p^2\sqrt{pq}/2^{2n}$ in the security bound. A detailed discussion of this result is given in Sect. 6.

Section 7 presents our ideal cipher construction and the proof of Theorem 7. When applied to Prince or Mantis, we obtain a reflection cipher with an optimal tradeoff of $p^2q = 2^{256}$. This should be compared to the tradeoff curve $pq = 2^{128}$ for the FX construction. Hence, our construction can tolerate far more construction queries before becoming insecure. Compared to the dedicated construction Prince v2, it has the advantage of introducing a more minimalist change. In addition, Prince v2 does not completely preserve the reflection property of Prince due to the changes it introduces in the reflector $\mathcal R$.

Future Work. Our work opens up several directions for interesting future research. Currently, our results only apply when two independent keys are used. Several difficulties in using a single key are discussed in Sect. 3.2, but we believe that using a nonlinear involution $\sigma$ could resolve these issues. However, this seems to require novel proof techniques, as the sum-capture theorem requires linear mappings. Likewise, it is an open question to categorize all strong linear key schedules using two independent master keys.

Another challenging problem is that the mirror slide attack from Sect. 4.2 suggests that a good choice of the reflector may improve the security of $\textsf{KARC}2$, in the sense that the birthday bound term $q^2/2^n$ can be avoided. However, proving this seems difficult with state-of-the-art techniques.

A third tantalizing open problem is to generalize our results to a larger number of rounds. Namely, for $r>1$, can we find sufficient conditions on the key-schedule such that the $2r$-round key-alternating reflection cipher achieves tight security?

It would also be interesting to reduce the time complexity of attacks against the $\textsf{KARC}2$ construction (potentially down to $\smash {\widetilde{\mathcal {O}}}(2^{2n/3})$). Note that the analogous problem for two-round Even-Mansour cipher is also open, with the best attack due to Leurent and Sibleyras [27] having a time-complexity of $\mathcal {O}(2^{n}/\sqrt{n})$.

Another possible future research direction is to design tweakable reflection ciphers from public random permutations. Finally, it could be interesting to study the related key security of $\textsf{KARC}2$ – apart from the intentional reflection relation, and to perform cryptanalysis of concrete instances of the $\textsf{KARC}2$ construction.

2 Preliminaries

For a non-negative integer n, the set of bitstrings of length n will be denoted by $\{0,1\}^{n}$. For any two bitstrings $X, Y \in \{0,1\}^{n}$, we denote their bitwise exclusive-or as the bitstring $X \oplus Y \in \{0,1\}^{n}$.

For any finite set $\mathcal {S}$, the notation $S \xleftarrow {\$} \mathcal {S}$ indicates that S is a random variable uniformly distributed on $\mathcal {S}$. In particular, $\textrm{Perm}(n)$ denotes the set of all permutations on $\{0,1\}^{n}$ and $\smash {\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)}$ defines $\pi$ as a uniform random permutation. For a list of input-output tuples $\mathcal {Q}_\pi =\{(x_1,y_1),\dots \}$, we denote by $\pi \vdash \mathcal {Q}_\pi$ the event that the permutation $\pi$ is consistent with the queries-response tuples in $\mathcal {Q}_\pi$, i.e. that $\pi (x)=y$ for all $(x,y)\in \mathcal {Q}_\pi$.

Finally, for any non-negative integers $b \le a$, the falling factorial of a with respect to b will be denoted by $(a)_b$. The value $(a)_b$ is equal to the number of injections from a set of size b to a set of size a. In particular,

$$\begin{aligned} (a)_b = {\left\{ \begin{array}{ll} 1 &{} \text {if}~b = 0,\\ a(a-1)\dots (a-b+1) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

2.1 Block Ciphers

For non-negative integers k and n, a block cipher is a function $F:\{0,1\}^{k}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$, such that for every fixed key $K \in \{0,1\}^{k}$, the function $F_K(\cdot )=F(K,\cdot )$ is a permutation on $\{0,1\}^{n}$. The inverse of $F_K$ will be denoted by $F_K^{-1}(\cdot )=F^{-1}(K,\cdot )$.

We will consider block ciphers F based on r public random permutations $\smash {\pi _1,\ldots ,\pi _r\xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)}$. Our analysis of such constructions will use the strong pseudorandom permutation (sprp) security notion. Specifically, let $\mathcal {D}$ be a distinguisher with bi-directional access to either $(F_K[\pi _1,\dots ,\pi _r],\pi _1,\dots ,\pi _r)$ for secret key $\smash {K\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{k}}$, or $(\pi ,\pi _1,\dots ,\pi _r)$ for $\smash {\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)}$. The goal of $\mathcal {D}$ is to determine which oracle it was given access to and its advantage with respect to this task is defined as

$$\begin{aligned} \textbf{Adv}_{F}^{\textrm{sprp}}(\mathcal {D}) = \left|\Pr \left[ \mathcal {D}^{F_K^{\pm }[\pi _1,\ldots ,\pi _r], \pi _1^{\pm },\dots ,\pi _r^{\pm }} = 1\right] -\right. \left. \Pr \left[ \mathcal {D}^{\pi ^{\pm }, \pi _1^{\pm },\dots ,\pi _r^{\pm }} = 1\right] \right|\,. \end{aligned}$$

It is possible to build a new block cipher F from an ideal cipher E. The sprp security notion carries over to this case, but the distinguisher $\mathcal {D}$ is given access to the ideal cipher E rather than to r random permutations. This means that $\mathcal {D}$ can query the random permutations $F(K, \cdot )$ or its inverse for any chosen key K. Formally, let $\mathcal {D}$ be a distinguisher with bi-directional access to either $(F_K[E], E)$ for a secret key $\smash {K \xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}}$, or $(\pi , E)$ with $\smash {\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)}$. The sprp-advantage of $\mathcal {D}$ against F is defined as

$$\begin{aligned} \textbf{Adv}_{F}^{\textrm{sprp}}(\mathcal {D}) = \left|\Pr \left[ \mathcal {D}^{F_K^{\pm }[E], E^{\pm }} = 1\right] -\right. \left. \Pr \left[ \mathcal {D}^{\pi ^{\pm }, E^{\pm }} = 1\right] \right|\,. \end{aligned}$$

Here $\mathcal {D}^\mathcal {O}$ denotes the value returned by $\mathcal {D}$ when interacting with the oracle $\mathcal {O}$ and the superscript ± indicates that the distinguisher has bi-directional access.

2.2 Patarin’s H-Coefficient Technique

We use the H-coefficient technique of Patarin [29], and our description of it follows the modernization of Chen and Steinberger [13].

Consider a deterministic distinguisher $\mathcal {D}$ that is given access to either a real world oracle $\mathcal {O}$ or an ideal world oracle $\mathcal {P}$. The distinguisher’s goal is to determine which oracle it is given access to and we denote its advantage by

$$\begin{aligned} \textbf{Adv}_{}^{\mathrm {}}(\mathcal {D}) = \left|\Pr \left[ \mathcal {D}^{\mathcal {O}} = 1\right] - \Pr \left[ \mathcal {D}^{\mathcal {P}} = 1\right] \right|\,. \end{aligned}$$

The query-response tuples learned by $\mathcal {D}$ during its interaction with the oracle $\mathcal {O}$ or $\mathcal {P}$ can be summarized in a transcript $\tau$. Let $X_{\mathcal {O}}$ (respectively $X_{\mathcal {P}}$) be a random variable equal to transcript produced by the interaction between $\mathcal {D}$ and $\mathcal {O}$ (respectively $\mathcal {P}$). A particular transcript $\tau$ is called attainable if $\Pr [ X_{\mathcal {P}} = \tau ] > 0$ and the set of all attainable transcripts is denoted by $\mathcal {T}$.

Lemma 1

(H-coefficient technique). Let $\mathcal {D}$ be any deterministic distinguisher. Define a partition $\mathcal {T}= \mathcal {T}_{\textrm{good}}\cup \mathcal {T}_{\textrm{bad}}$, where $\mathcal {T}_{\textrm{good}}$ is the subset of attainable transcripts $\mathcal {T}$ which contains all the “good” transcripts and $\mathcal {T}_{\textrm{bad}}$ is the subset with all the “bad” transcripts. If there exists an $\epsilon \ge 0$ such that for all attainable $\tau \in \mathcal {T}_{\textrm{good}}$,

$$\begin{aligned} \frac{\Pr [ X_{\mathcal {O}} = \tau ]}{\Pr [ X_{\mathcal {P}} = \tau ]} \ge 1-\epsilon \,, \end{aligned}$$

then $\textbf{Adv}_{}^{\mathrm {}}(\mathcal {D}) \le \epsilon + \Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}]$.

3 Construction Based on a Public Permutation

In this section, we consider the two-round variant of the general construction shown in Fig. 1. In particular, as shown in Fig. 4, we consider the case with $K_3 = K_1$ and $K_4 = K_2$ and a linear reflector $\mathcal R$. This case is of particular interest because it is both a natural choice for the key-schedule, and one which is used by concrete reflection ciphers such as Prince v2 [11]. A few alternative choices of the key-schedule are discussed in Sect. 3.2 below.

Fig. 4.

The $\textsf{KARC}2$ construction based on a public permutation $\pi$ and with secret keys $K_1$ and $K_2$.

The construction shown in Fig. 4 will be referred to as $\textsf{KARC}2$, for key-alternating reflection cipher with two rounds. Formally, let n be a positive integer, $\pi \in \textrm{Perm}(n)$, and $\mathcal R:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$ a linear involution. The generic construction $\textsf{KARC}2 :\{0,1\}^{2n}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ is defined as

$$\begin{aligned} \textsf{KARC}2 _{K_1, K_2}[\pi ](M) = \pi ^{-1}(\mathcal R(\pi (M\oplus K_1)\oplus K_2) \oplus K_1) \oplus K_2\,. \end{aligned}$$

The $\textsf{KARC}2$ construction has the following reflection property:

$$\begin{aligned} \big (\textsf{KARC}2 _{K_1, K_2}[\pi ]\big )^{-1} = \textsf{KARC}2 _{K_2, K_1}[\pi ] \end{aligned}$$

The security of $\textsf{KARC}2$ is discussed in Sect. 3.1.

3.1 Security Lower Bound

In Sect. 5, we prove the following security bound for $\textsf{KARC}2$. As will be shown in Sect. 4, it is also the case that this bound is tight for general choices of the reflector $\mathcal R$, i.e., there are specific $\mathcal R$ (such as the identity) with a matching attack.

Theorem 1

Let n be a positive integer, $\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$ and $K_1, K_2 \xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$. Let $\mathcal R$ be a linear involution on $\{0,1\}^{n}$. For any distinguisher $\mathcal {D}$ for $\textsf{KARC}2 _{K_1, K_2}[\pi ]$ making at most q construction queries, and at most p primitive queries to $\pi ^{\pm }$ such that $p+2q < 2^{n - 1}$, we have

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}2}^{\textrm{sprp}}(\mathcal {D}) \le \frac{3qp^2}{2^{2n}} + \frac{q^2}{2^{n}} + \frac{4q^{3/2}}{2^{n}} + \frac{4q(p+2q)(p+2q+1)}{2^{2n}}\,. \end{aligned}$$

On the one hand, Theorem 1 ‘only’ shows that $\textsf{KARC}2$ achieves birthday-bound security with respect to the number of construction queries q. On the other hand, it also shows that the best possible tradeoff curve between construction and primitive queries is $p^2 q = 2^{2n}$ up to a small constant. This is much better than the typical birthday-bound tradeoff $pq = 2^{n}$. This result is especially important since in practice the number of construction queries is usually limited by the application. The number of primitive queries, however, is only limited by the computational power of the adversary.

The attacks that will be presented in Sect. 4 show that the term $q^2/2^n$ cannot be avoided unless the reflector $\mathcal R$ is carefully chosen. However, for any linear involution $\mathcal R$, there is an attack with advantage approximately $2^{-n/2}$ using $q = 2^{n / 2}$ construction queries and no primitive queries. Hence, some terms independent of p cannot be avoided. It will also be shown that the term $p^2 q/2^{2n}$ is tight from an information-theoretic point of view, but we are not aware of any attacks achieving the $p^2 q = 2^{2n}$ tradeoff with reasonable time complexity.

3.2 Variants

The choice of the key-schedule in Fig. 4 is not the only possibility. One tempting option is to further reduce the number keys by setting $K_2 = \sigma (K_1)$ for some involution $\sigma$. However, when $\sigma$ is linear, this construction would not even be secure up to $q^2/2^n$ for general choices of $\mathcal R$. The reason is that $K_1 \oplus K_2 = K_1 \oplus \sigma (K_1)$ can then no longer be uniform random, and this significantly facilitates the attack presented in Sect. 4.2 below. Indeed, one has the following result.

Lemma 2

Let n be a positive integer and $\sigma : \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ a linear involution. Then $\sigma$ has at least $2^{n/2}$ fixed points and the image of $\sigma \oplus \textsf{id}$, where $\textsf{id}$ is the identity function, contains at most $2^{n / 2}$ distinct values.

Proof

Since $f = \sigma \oplus \textsf{id}$ is linear, the cardinality of its image is $2^{\dim (\textrm{im}f)}$. Furthermore, $f^2 = 0$, so $\textrm{im}(f) \subseteq \ker (f)$ and

$$\begin{aligned} \dim (\textrm{im}f) \le \dim (\ker f) = n - \dim (\textrm{im}f)\,. \end{aligned}$$

It follows that $\dim (\textrm{im}f) \le n/2$. The claim about the number of fixed points follows from the observation that the fixed points of $\sigma$ are precisely the elements of $\ker f$.    $\square$

Due to the above issue, we focus on constructions with two keys. The case of one key, which necessarily requires either a special choice of $\mathcal R$ or a nonlinear $\sigma$, will be left as interesting (but likely challenging) future work. However, even with two keys, several constructions are possible. For example, Boura et al. [10] propose general key-schedules in which the third and fourth key-addition in Fig. 4 (counting from the left) are replaced by $F_2(K_1, K_2)$ and $F_1(K_1, K_2)$ respectively, where $F_1$ and $F_2$ are (possibly nonlinear) functions. The construction we analyze is arguably the simplest secure case: $F_1(K_1, K_2) = K_1$ and $F_2(K_1, K_2) = K_2$.

4 Attacks on the Public Permutation Construction

This section shows that the security bound in Theorem 1 is essentially tight by providing two matching generic attacks. The first attack is only information theoretic and has no practical significance: it shows that the tradeoff curve $p^2 q = 2^{2n}$ between the number of construction queries q and the number of primitive queries p can be achieved with a time-complexity of $\mathcal {O}(2^{2n})$. The second attack only uses construction queries and corresponds to the $q^2 / 2^n$ term in Theorem 1. Contrary to the first attack, the time-complexity of the second attack is limited to $\smash {\widetilde{\mathcal {O}}}(2^{n/2})$ operations.

4.1 Information Theoretic Attack

Suppose the attacker makes 2q construction queries and p primitive queries with inputs-output pairs denoted by $(u_1, v_1), \ldots , (u_p, v_p)$. If $p^2q = 2^{2n}$, then the expected number of plaintext-ciphertext pairs (M, C) and primitive query indices (i, j) such that

$$\begin{aligned} \begin{aligned} M \oplus K_1&= u_i \\ C \oplus K_2&= u_j \,, \end{aligned} \end{aligned}$$

(1)

is equal to two. Whenever the above conditions hold, one also has $\mathcal R(v_i) \oplus v_j = K_1 \oplus \mathcal R(K_2)$. This suggests the following method for obtaining the keys $K_1$ and $K_2$. For each possible choice of $K_1$ and $K_2$, the adversary proceeds as follows:

• (i) Identify the pairs (M, C) and (i, j) for which a collision of type (1) occurs.

• (ii) For each of the cases identified in step i , check that $\mathcal R(v_i) \oplus v_j = K_1 \oplus \mathcal R(K_2)$. If this relation holds for all pairs that were identified, add $(K_1, K_2)$ to a list of candidate keys.

Since the expected number of pairs satisfying (1) is equal to two, each incorrect key $(K_1, K_2)$ has an average probability of $1/2^{2n}$ of being accepted. Hence, the adversary obtains a list of a constant number of candidate keys. These candidate keys can be checked using a few additional queries.

The attack sketched above is purely information theoretic and does not account for the computational cost of the procedure. Since the attack uses $\mathcal {O}(2^{2n})$ table lookups, it indeed has no practical significance. Nevertheless, it shows that the $p^2 q / 2^{2n}$ term in Theorem 1 cannot be avoided.

Finding attacks with lower computational cost is left for future work and we believe this is an interesting problem, as the situation for the two-round Even-Mansour cipher is similar. In that case, the best known attack is due to Leurent and Sibleyras [27] and has a time-complexity of $\mathcal {O}(2^n / \sqrt{n})$ [27]. Their attack is based on a reduction to the 3-XOR problem. However, since the $\textsf{KARC}2$ construction has two keys, this approach does not help to reduce the time-complexity below $\mathcal {O}(2^n)$.

4.2 Mirror Slide Attack

The second attack is a variant of the mirror slide attack of Dunkelman, Keller and Shamir [19]. The attack is applicable whenever $\mathcal R$ has many fixed points and recovers the value of $K_1 \oplus K_2$.

The original mirror slide attack is applicable to the one-round Even-Mansour cipher with an involutive permutation. To apply a similar technique to $\textsf{KARC}2$, we let

$$\begin{aligned} \mathcal I(x) = \pi ^{-1}(K_1 \oplus \mathcal R(K_2) \oplus \mathcal R(\pi (x)))\,. \end{aligned}$$

The $\textsf{KARC}2$ construction can then be written as $M \mapsto \mathcal {I}(x \oplus K_1) \oplus K_2$. In general, $\mathcal I$ is not an involution since

$$\begin{aligned} \mathcal I^{-1}(x) = \pi ^{-1}(K_2 \oplus \mathcal R(K_1) \oplus \mathcal R(\pi (x)))\,. \end{aligned}$$

Nevertheless, the equation above shows that $\mathcal I$ is an involution iff $K_1 \oplus K_2$ is a fixed point of the reflector $\mathcal R$. Since by Lemma 2 any linear involution has at least $2^{n/2}$ fixed points, the mirror slide attack is applicable for a fraction of at least $2^{-n/2}$ weak keys. However, if $\mathcal R{}$ is chosen as the identity map, then all keys are weak.

The attack is based on the following observation. Let (M, C) and $(M^*, C^*)$ be two input-output pairs for the construction such that $M \oplus C^* = K_1 \oplus K_2$ with $K_1 \oplus K_2$ a fixed point of $\mathcal R{}$. Since $M \oplus K_1 = C^{*} \oplus K_2$, it then follows that

$$\begin{aligned} M^* = K_1 \oplus \mathcal I^{-1}(C^* \oplus K_2) = K_1 \oplus \mathcal I(M \oplus K_1) = K_1 \oplus K_2 \oplus C\,. \end{aligned}$$

The attack itself is then simple: choose $\varTheta (2^{n/2})$ distinct values $M_1, M_2, \ldots$ and $C_1, C_2, \ldots$. With high probability, there exist indices $i \ne j$ such that $M_i \oplus C_j = K_1 \oplus K_2 = M_j \oplus C_i$. Furthermore, since the expected number of collisions is small, one obtains a short list of candidates for $K_1 \oplus K_2$.

Theorem 2 gives a lower bound on the advantage of a distinguisher based on the same principle. Hence, the security lower bound in Theorem 1 is tight in the sense that the $\mathcal {O}(q^2/2^n)$ term cannot be avoided for some choices of $\mathcal R$. Finding matching attacks when $\mathcal R$ has only $2^{n/2}$ fixed points, or improving the security lower bound in this case, will be left as future work.

Theorem 2

(Mirror slide attack). Let $n \ge 2$ be an even integer, $\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$, and $K_1,K_2\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$. Let $\mathcal R$ be a linear involution on $\{0,1\}^{n}$ with $\ell \ge 4$ fixed points. There exists a distinguisher $\mathcal {D}$ for $\textsf{KARC}2 _{K_1, K_2}[\pi ]$ making $3\cdot 2^{n/2} + 1$ construction queries such that

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}2}^{\textrm{sprp}}(\mathcal {D}) \ge \frac{\ell }{2^n} - \frac{4}{2^{n}}\,. \end{aligned}$$

Proof

Let $\varDelta$ be an arbitrary constant which is zero on the first n/2 bits, such as $\varDelta = 0^{n - 1}\Vert 1$. The distinguisher $\mathcal {D}$ follows the approach described above, but using a slightly different approach to make the attack deterministic in the real world (assuming $K_1 \oplus K_2$ is a fixed point of $\mathcal R$). Specifically, $\mathcal {D}$ operates as follows:

• (i) For $i=1,\dots ,2^{n/2}$, query $M_i = \langle i\rangle _{n/2}\parallel 0^{n/2}$ to obtain its encryption $C_i$. Likewise, query $\smash {\widetilde{M}_i} = M_i \oplus \varDelta$ to obtain its encryption $\smash {\widetilde{C}}_i$.

• (ii) For $i=1,\dots ,2^{n/2}$, query $C_i^* = 0^{n/2}\parallel \langle i\rangle _{n/2}$ to obtain $M^*_i$. Likewise, define $\smash {\widetilde{C}^*_i} = C_i \oplus \varDelta$ and denote the corresponding plaintext by $\smash {\widetilde{M}}^*_i$.

• (iii) If there exists a pair of indices (i, j) such that $M_i \oplus C^*_j = M^*_i \oplus C_j$ and $\smash {\widetilde{M}}_i \oplus \smash {\widetilde{C}}^*_j = \smash {\widetilde{M}}^*_i \oplus \smash {\widetilde{C}}_j$, then output $1$. Otherwise, output $0$.

Since in step ii only $2^{n/2} + 1$ new queries are made, the total number of queries made is $3\cdot 2^{n/2} + 1$. The distinguisher’s advantage satisfies

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}2}^{\textrm{sprp}}(\mathcal {D})&= \left|\Pr \left[ \mathcal {D}^{\textsf{KARC}2 _{K_1,K_2}^{\pm }[\mathcal R{}, \pi ], \pi ^{\pm }} = 1\right] -\right. \left. \Pr \left[ \mathcal {D}^{\pi _I^{\pm }, \pi ^{\pm }} = 1\right] \right|\,. \end{aligned}$$

Suppose that $K_1 \oplus K_2$ is a fixed point of $\mathcal R$. In the real world, there is a unique pair $(i, j)$ such that $M_i \oplus C_j^* = K_1 \oplus K_2$. It then also holds that $(M_i \oplus \varDelta ) \oplus (C_j^* \oplus \varDelta ) = K_1 \oplus K_2$. Hence, as detailed in the explanation of the mirror slide attack above, the following two events then necessarily hold:

$$\begin{aligned} A_{i, j} : \qquad M_i \oplus C^*_j&= M^*_j \oplus C_i\\ B_{i, j} : \qquad \widetilde{M}_i \oplus \widetilde{C}^*_j&= \widetilde{M}^*_j \oplus \widetilde{C}_i\,. \end{aligned}$$

Thus, since the number of fixed points of $\mathcal R{}$ is $\ell$,

$$\begin{aligned} \Pr \left[ \mathcal {D}^{\textsf{KARC}2 _{K_1,K_2}^\pm [\mathcal R{}, \pi ], \pi ^{\pm }} = 1\right] \ge \ell / 2^n\,. \end{aligned}$$

For the ideal world, we have

$$\begin{aligned} \Pr \left[ \mathcal {D}^{\pi _I^{\pm }, \pi ^{\pm }} = 1\right] = \Pr \left[ \bigvee _{i,j}\; A_{i,j} \wedge B_{i,j}\right] \le 2^n\Pr \left[ A_{1,1} \wedge B_{1,1}\right] \le \frac{4}{2^{n}}\,. \end{aligned}$$

Hence, the result follows provided that $\ell \ge 4$.

5 Security Proof for the Public Permutation Construction

In this section we prove Theorem 1. Let $K_1,K_2\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$ and $\pi _I,\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$. Consider any computationally unbounded and deterministic distinguisher $\mathcal {D}$ with access to the oracles $(\textsf{KARC}2 _{K_1,K_2}^{\pm }[\pi ], \pi ^{\pm })$ in the real world and $(\pi _I^{\pm }, \pi ^{\pm })$ in the ideal world.

The distinguisher makes $q$ construction queries to $\textsf{KARC}2 _{K_1,K_2}^{\pm }[\pi ]$ or $\pi _I^{\pm }$, and these are summarized in a transcript of the form $\tau _0=\{(M_1,C_1),\ldots ,(M_q,C_q)\}$. It also makes $p$ primitive queries to $\pi ^{\pm }$, and these are summarized in the transcript $\tau _1=\{(u_1,v_1),\dots ,(u_p,v_p)\}$. Without loss of generality, it can be assumed that the distinguisher does not make duplicate construction or primitive queries.

After $\mathcal {D}$’s interaction with the oracles, but before it outputs its decision, we disclose the keys $K_1$ and $K_2$ to the distinguisher. This can only increase its advantage. In the real world, these are the keys used in the construction. In the ideal world, $K_1$ and $K_2$ are dummy keys drawn uniformly at random. The complete view is denoted by $\tau =(\tau _0,\tau _1,K_1,K_2)$.

5.1 Bad Events

Throughout the proof, let $U = \{u~|~(u,v)\in \tau _1\}$ and $V = \{v~|~(u,v)\in \tau _1\}$. Recall that $\mathcal R:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$ is an involution, i.e. $\mathcal R^{-1} = \mathcal R$. We say that $\tau \in \mathcal {T}_{\textrm{bad}}$ if and only if there exist construction queries $(M_i,C_i),(M_{j},C_{j})\in \tau _0$ and primitive queries $(u,v),(u',v')\in \tau _1$ such that one of the following conditions holds:

$$\begin{aligned} \textrm{bad}_1:&M_j \oplus C_{i} = K_1\oplus K_2\,,\end{aligned}$$

(2)

$$\begin{aligned} \textrm{bad}_2:&M_j \oplus u = K_1 \; \text {and} \; C_j \oplus u' = K_2\,,\end{aligned}$$

(3)

$$\begin{aligned} \textrm{bad}_3:&M_j \oplus u = K_1 \; \text {and} \; \mathcal R(v)\oplus v' = K_1\oplus \mathcal R(K_2)\,,\end{aligned}$$

(4)

$$\begin{aligned} \textrm{bad}_4:&C_j \;\oplus u' = K_2 \; \text {and} \; v\oplus \mathcal R(v')= \mathcal R(K_1) \oplus K_2\,, \end{aligned}$$

(5)

When $p < q$, we also need the following two bad events for our good transcripts analysis:

$$\begin{aligned} \textrm{bad}_5:&\alpha _1 = |\{(M_j,C_j)\in \tau _0~|~M_j \oplus K_1 \in U\}|\ge \sqrt{q}\,,\end{aligned}$$

(6)

$$\begin{aligned} \textrm{bad}_6:&\alpha _2 = |\{(M_j,C_j)\in \tau _0~|~C_j\; \oplus K_2 \in U\}|\ge \sqrt{q}\,. \end{aligned}$$

(7)

Any attainable transcript $\tau$ for which $\tau \notin \mathcal {T}_{\textrm{bad}}$ will be called a good transcript.

We give an informal explanation of the definition of the first four bad events. The first bad event is necessary to exclude the mirror slide attack that was described in Sect. 4.2. The second bad event is exploited by the information-theoretic attack from Sect. 4.1. The motivation behind $\textrm{bad}_3$ and $\textrm{bad}_4$ is similar. In fact, note that $\mathcal R(v)\oplus v' = K_1\oplus \mathcal R(K_2)$ in $\textrm{bad}_3$ and $v\oplus \mathcal R(v')= \mathcal R(K_1) \oplus K_2$ in $\textrm{bad}_4$ express the same equation. In the real world, if $\textrm{bad}_1$ does not hold, then every construction query $j$ induces exactly two evaluations $(u,v),(u',v')$ of the underlying public permutation $\pi$, and these two pairs satisfy

$$\begin{aligned} M_j \oplus u&= K_1\,,\\ C_j\; \oplus u'&= K_2\,,\\ \mathcal R(v)\oplus v'&= K_1\oplus \mathcal R(K_2)\,. \end{aligned}$$

Clearly, u and $u'$ are fixed by $M_j$ (if in the forward direction) or $C_j$ (if in the inverse direction) and $K_1, K_2$, but there is “freedom” in the value $\mathcal R(v)\oplus v'$. If it happens to be that the distinguisher queried u, i.e., that $(u,v)\in \tau _1$, the construction query also fixes the input-output tuple $(u',v')$. However, in the ideal world, there is no such dependency. This means that if the adversary queries $u=M_j\oplus K_1$ and $u'=C_j \oplus K_2$ to $\pi$, with high probability the third equation would not hold. An identical reasoning applies for the case where the distinguisher happened to have set any other two out of three equations.

5.2 Probability of Bad Events in the Ideal World

We want to bound the probability $\Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}]$ that an ideal world transcript $\tau$ satisfies either of (2)–(7). Therefore, by the union bound, the probability that $X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}$ can be bounded as

$$\begin{aligned} \Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}] \le \sum _{i=1}^{6}\Pr [\textrm{bad}_i]\,. \end{aligned}$$

1$^{st}$ Bad Event. We first consider the bad event $\textrm{bad}_1$. Here, we rely on the randomness of $K_1\oplus K_2$. Since $K_1$ and $K_2$ are dummy keys generated independently of $\tau _0$ and $\tau _1$, the probability that (2) holds for fixed i and j is $1/2^{n}$. Summing over $q^2$ possible choices of the pair $(i, j)$, we have

$$\begin{aligned} \Pr [\textrm{bad}_1] \le \frac{q^2}{2^{n}}\,. \end{aligned}$$

2$^{nd}$ Bad Event. We now consider the event $\textrm{bad}_2$. For any construction query $(M_j,C_j)\in \tau _0$ and any primitive queries $(u,v)$ and $(u',v')$, the only randomness in the first equation of (3) is $K_1$ and the only randomness in the second equation is $K_2$. This means that the event that one of the equations defining $\textrm{bad}_2$ holds is independent of the event that the other one holds. Since the keys $\smash {K_1,K_2 \xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}}$ are dummy keys generated independently of $\tau _0$ and $\tau _1$, the probability that $\textrm{bad}_2$ holds for a fixed choice of $j$, $(u,v)$, and $(u',v')$ is $1/2^{2n}$. Summing over the $q$ possible construction queries and $p^2$ possible pairs of primitive queries, we get

$$\begin{aligned} \Pr [\textrm{bad}_2] \le \frac{qp^2}{2^{2n}}\,. \end{aligned}$$

3$^{rd}$ Bad Event. Next, we consider the bad event $\textrm{bad}_3$. Note that in the second equation of (4), we can replace $K_1$ by $M_j\oplus u$. Hence, the only randomness in the first equation is $K_1$ and the only randomness in the second equation (conditional on the first) is $K_2$. The events that one of the equations defining $\textrm{bad}_2$ holds is therefore independent of the other. Summed over $q$ possible construction queries and $p^2$ possible pairs of primitive queries, we get

$$\begin{aligned} \Pr [\textrm{bad}_3] \le \frac{qp^2}{2^{2n}}\,. \end{aligned}$$

4$^{th}$ Bad Event. The same reasoning as in the case of $\textrm{bad}_3$ applies to $\textrm{bad}_4$. Hence, it also holds that $\Pr [\textrm{bad}_4] \le qp^2 / 2^{2n}$.

5$^{th}$ Bad Event. Finally, if $p < q$, we also consider the bad event $\textrm{bad}_5$. Note that $\alpha _1$ is a random variable over the random choice of $K_1$, and it is independent of $K_2$. Furthermore, by the uniformity of $K_1$,

$$\begin{aligned} \mathbb {E}[\alpha _1] = \sum _{j = 1}^q \sum _{u \in U} \Pr [M_j\oplus K_1 = u] = \frac{qp}{2^n}, \end{aligned}$$

Hence, by Markov’s inequality and because we only consider this event for $p < q$,

$$\begin{aligned} \Pr [\textrm{bad}_5] \le \frac{\sqrt{q} p}{2^n} \le \frac{q^{3/2}}{2^n}\,. \end{aligned}$$

6$^{th}$ Bad Event. The analysis of the last bad event is similarly to that of $\textrm{bad}_5$. Hence, we also have $\Pr [\textrm{bad}_6] \le q^{3/2} / 2^n$.

Conclusion. Summing the probabilities of the bad events, we get

$$\begin{aligned} \Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}] \le \frac{3qp^2}{2^{2n}} + \frac{q^2}{2^{n}} + \frac{2q^{3/2}}{2^n}\,. \end{aligned}$$

(8)

This concludes the analysis of the bad transcripts in the ideal world.

5.3 Ratio for Good Transcripts

Before we continue with the proof, we present the following lemma, which will be useful in the good transcript analysis.

Lemma 3

Let $a,b,c \ge 0$ and $N \ge 1$ be integers such that $2a+b\le N/2$ and $2a+c+1\le N/2$. Then

$$\begin{aligned} \prod _{i=1}^{a}\frac{(N-i)(N-b-c-3i)}{(N-b-2i)(N-c-2i-1)} \ge 1-\frac{4a(2a + b)(2a+c+1)}{N^{2}} \end{aligned}$$

Proof

One has

$$\begin{aligned}&\prod _{i=1}^{a}\frac{(N-i)(N-b-c-3i)}{(N-b-2i)(N-c-2i-1)}\\&\qquad \ge \prod _{i=1}^{a}\frac{N^2-N(b+c+4i)-N}{N^2-N(b+c+4i+1)+(b+2i)(c+2i+1)}\\&\qquad =\prod _{i=1}^{a}\Big (1-\frac{(b+2i)(c+2i+1)}{N^2-N(b+c+4i+1)+(b+2i)(c+2i+1)}\Big )\\&\qquad =\prod _{i=1}^{a}\Big (1-\frac{(b+2i)(c+2i+1)}{(N-b-2i)(N-c-2i-1)}\Big )\\&\qquad \ge 1-\frac{a(2a+b)(2a+c+1)}{(N-b-2a)(N-c-2a-1)}\\&\qquad \ge 1-\frac{4a(2a+b)(2a+c+1)}{N^{2}}\,, \end{aligned}$$

where for the last inequality we used $2a+b\le N/2$ and $2a+c+1\le N/2$.    $\square$

Consider an attainable transcript $\tau \in \mathcal {T}_{\textrm{good}}$. We now lower bound $\Pr [ X_{\mathcal {O}} = \tau ]$ and compute $\Pr [ X_{\mathcal {P}} = \tau ]$ in order to obtain a lower bound for the ratio of these probabilities. For the ideal world oracle $\mathcal {P}$, the probability of any good transcript $\tau$ is equal to

$$\begin{aligned} \Pr [ X_{\mathcal {P}} = \tau ]&= \frac{1}{2^{2n}}\cdot \frac{(2^n-p)!}{2^{n}!}\cdot \frac{(2^n-q)!}{2^n!}\\&= \frac{1}{2^{2n}}\cdot \frac{1}{(2^{n})_{p}}\cdot \frac{1}{(2^{n})_{q}}\,. \end{aligned}$$

The first factor is due to the number of possible keys $K_1$ and $K_2$. The second and third factors correspond to the probability that the uniform random permutations $\pi$ and $\pi _I$ are consistent with the transcripts $\tau _1$ and $\tau _0$ respectively.

Similarly, the real world oracle $\mathcal {O}$ is compatible with a good transcript $\tau$ if and only if it is compatible with $\tau _0$ and $\tau _1$. Hence,

$$\begin{aligned} \Pr [ X_{\mathcal {O}} = \tau ]&= \frac{1}{2^{2n}}\cdot \frac{1}{(2^{n})_{p}}\cdot \Pr [\textsf{KARC}2 _{K_1,K_2}^{\pm }[\pi ]\vdash \tau _0\mid \pi \vdash \tau _1]\,, \end{aligned}$$

where the probability is taken with respect to $\smash {\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)}$ and conditional on the keys. As before, the first factor corresponds to the number of possible keys $K_1$ and $K_2$. The second factor is the probability that $\pi$ is consistent with $\tau _1$. The third factor is the probability that the construction $\textsf{KARC}2 _{K_1,K_2}^{\pm }[\pi ]$ is consistent with $\tau _0$, given the keys $K_1,K_2$, and given that $\pi$ is compliant with $\tau _1$.

If we let $\rho (\tau )=\Pr [\textsf{KARC}2 _{K_1,K_2}^{\pm }[\pi ]\vdash \tau _0\mid \pi \vdash \tau _1]$, then from the above we obtain that

$$\begin{aligned} \frac{\Pr [ X_{\mathcal {O}} =\tau ]}{\Pr [ X_{\mathcal {P}} =\tau ]} = (2^{n})_{q}\,\rho (\tau )\,. \end{aligned}$$

(9)

In order to bound $\rho (\tau )$, we re-group the construction queries in $\tau _0$ according to their collisions with the primitive queries:

$$\begin{aligned} Q_{U_1}&= \{(M_j,C_j)\in \tau _0~|~M_j\oplus K_1\in U\}\,,\\ Q_{U_2}&= \{(M_j,C_j)\in \tau _0~|~C_j \oplus K_2\in U\}\,,\\ Q_0&= \{(M_j,C_j)\in \tau _0~|~M_j\oplus K_1, C_j\oplus K_2\notin U\}\,. \end{aligned}$$

By definition, $\alpha _1 = \left|Q_{U_1}\right|$ and $\alpha _2 = \left|Q_{U_2}\right|$. Also note that $Q_{U_1}\cap Q_{U_2}=\emptyset$ by $\lnot \textrm{bad}_2$, $Q_{U_1}\cap Q_0=\emptyset$ and $Q_{U_2}\cap Q_0=\emptyset$ by the definition of $Q_{U_1}$, $Q_{U_2}$, and $Q_0$. Denote respectively by $E_1$, $E_2$, and $E_0$ the events that $\textsf{KARC}2 _{K_1,K_2}^{\pm }[\pi ]\vdash Q_{U_1}$, $Q_{U_2}$, and $Q_0$ such that

$$\begin{aligned} \rho (\tau ) = \Pr [E_1\wedge E_2\mid \pi \vdash \tau _1] \Pr [E_0\mid E_1\wedge E_2\wedge \pi \vdash \tau _1]\,. \end{aligned}$$

(10)

Lower Bounding $\Pr [E_1\wedge E_2\mid \pi \vdash \tau _1].$ The consistency condition $\pi \vdash \tau _1$ already defines exactly $p$ distinct input-output relations for $\pi$. We know that for each $(M_j,C_j)\in Q_{U_1}$, there is an unique $(u,v)\in \tau _1$ such that $M_j\oplus K_1 = u$, and $\pi (M_j\oplus K_1)=v$. We define

$$\begin{aligned} \tilde{V}_2&= \{\mathcal R(\pi (M_j\oplus K_1)\oplus K_2)\oplus K_1:(M_j,C_j)\in Q_{U_1}\}\,,\\ \tilde{U}_2&= \{C_j\oplus K_2:(M_j,C_j)\in Q_{U_1}\}\,. \end{aligned}$$

Similarly, for each $(M_j,C_j)\in Q_{U_2}$, there is a unique $(u,v)\in \tau _1$ such that $C_j\oplus K_2 = u$, and $\pi (C_j\oplus K_2) = v$. Again, define

$$\begin{aligned} \tilde{V}_1&= \{\mathcal R(\pi (C_j\oplus K_2)\oplus K_1)\oplus K_2~|~(M_j,C_j)\in Q_{U_2}\}\,,\\ \tilde{U}_1&= \{M_j\oplus K_1~|~(M_j,C_j)\in Q_{U_2}\}\,. \end{aligned}$$

Note that all values in $\tilde{U}_1$ and all values in $\tilde{V}_2$ are distinct since the $M_j$’s are distinct, and all values in $\tilde{U}_2$ and all values in $\tilde{V}_1$ are distinct since the $C_j$’s are distinct. We also have $\tilde{U}_1\cap \tilde{U}_2=\tilde{V}_1\cap \tilde{V}_2=\emptyset$ by $\lnot \textrm{bad}_1$, $U\cap \tilde{U}_1 = U\cap \tilde{U}_2=\emptyset$ by $\lnot \textrm{bad}_2$, $V\cap \tilde{V}_2=\emptyset$ by $\lnot \textrm{bad}_3$, and $V\cap \tilde{V}_1=\emptyset$ by $\lnot \textrm{bad}_4$. Hence, the events $E_1$ and $E_2$ define exactly $\alpha = |Q_{U_1}| + |Q_{U_2}|$ new and distinct input-output pairs of $\pi$ and it follows that

$$\begin{aligned} \Pr [E_1\wedge E_2\mid \pi \vdash \tau _1] = \frac{1}{(2^n-p)_{\alpha }}\,. \end{aligned}$$

(11)

Lower Bounding $\Pr [E_0\mid E_1\wedge E_2\wedge \pi \vdash \tau _1]$. The conditions $\pi \vdash \tau _1$, $E_1$ and $E_2$ now define exactly $p' = |U \cup \tilde{U}_1 \cup \tilde{U}_2| = |V \cup \tilde{V}_1 \cup \tilde{V}_2| = p + \alpha$ distinct input-output pairs of $\pi$. Our goal now is to count the number of new distinct input-output relations for $\pi$ induced by the event $E_0$. Recall that the event $E_0$ holds if and only if the reflection cipher is consistent with the construction queries in $Q_0$, i.e. $\textsf{KARC}2 _{K_1,K_2}[\pi ] \vdash Q_0$. The queries in $Q_0$ can be labeled as

$$\begin{aligned} Q_0=\{(M_{l_1},C_{l_1}),\dots ,(M_{l_{q'}},C_{l_{q'}})\}\,, \end{aligned}$$

where $q' = \left|Q_0\right|=q-\alpha$ is the total number of these queries.

The event $E_0$ defines exactly $2q'$ relations for $\pi$ of the form $\pi (\bar{u}_{2i - 1}) = \bar{v}_{2i - 1}$ and $\pi (\bar{u}_{2i}) = \bar{v}_{2i}$, where $\bar{u}_{2i - 1} = M_{l_i} \oplus K_1$ and $\bar{u}_{2i} = C_{l_i} \oplus K_2$ for $i = 1, \ldots , q'$. By the definition of $Q_0$ and because $\textrm{bad}_1$ does not hold for good transcripts, it follows that

$$\begin{aligned} \{\bar{u}_1, \ldots , \bar{u}_{2q'}\} \not \subseteq U \cup \tilde{U}_1 \cup \tilde{U}_2\,. \end{aligned}$$

Hence, taking into account that $\pi$ is a permutation, the values $\bar{v}_1, \ldots , \bar{v}_{2q'}$ must satisfy the following conditions (for $i = 1, \ldots , q'$) in the real world:

• (1) $\mathcal R(\bar{v}_{2i - 1}) \oplus \bar{v}_{2i} = K_1 \oplus \mathcal R(K_2)$.

• (2) The variables $\bar{v}_{2i-1}$ additionally satisfy:

  • (a) $\bar{v}_{2i-1}\notin V\cup \tilde{V}_1\cup \tilde{V}_2$,

  • (b) $\bar{v}_{2i-1}\notin \{\bar{v}_{1},\dots ,\bar{v}_{2i - 2}\}$ if $i > 1$.

• (3) The variables $\bar{v}_{2i}$ additionally satisfy:

  • (a) $\bar{v}_{2i}\notin V\cup \tilde{V}_1\cup \tilde{V}_2$,

  • (b) $\bar{v}_{2i}\notin \{\bar{v}_{1},\bar{v}_{3},\dots ,\bar{v}_{2i - 1}\}$ if $i > 1$.

Observe that whenever conditions (1) and (2b) are satisfied, then it also holds that $\bar{v}_{2i}\notin \{\bar{v}_{2},\bar{v}_{4},\dots ,\bar{v}_{2i - 2}\}$, since $K_1 \oplus \mathcal R(K_2)$ is a fixed value. It follows that conditions (1), (2b) and (3b) ensure that the values $\bar{v}_1, \ldots , \bar{v}_{2q'}$ are distinct.

For any positive integer $m \le q'$, let $N_{m}$ denote the number of distinct tuples $(\bar{v}_{1},\dots ,\bar{v}_{2m})$ satisfying the conditions above for $i = 1, \ldots , m$. In particular, for each of the $N_{q'}$ possible consistent choices of $(\bar{v}_1, \ldots , \bar{v}_{2q'})$, the event $E_0$ is equivalent to exactly $2q'$ new input-output relations for $\pi$. Hence,

$$\begin{aligned} \Pr [E_0\mid E_1\wedge E_2\wedge \pi \vdash \tau _1]&= \frac{N_{q'}}{(2^n-p')_{2q'}}\,. \end{aligned}$$

(12)

Below, a recursive formula for $N_{m}$ in terms of $N_{m - 1}$ will be determined. This formula leads to a lower bound for $N_{m} / N_{m - 1}$. Finally, in order to lower bound $N_{q'}$, the following telescoping product will be used ($N_0 = 1$):

$$\begin{aligned} N_{q'} = \prod _{m = 1}^{q'} \frac{N_{m}}{N_{m - 1}}\,. \end{aligned}$$

(13)

Define $R_m$ as the set of all tuples $(\bar{v}_1, \ldots , \bar{v}_{2m})$ that satisfy all conditions above for $i = 1, \ldots , m - 1$ and satisfy condition (1) for $i = m$, but not  (2) and (3) . It is easy to see that $|R_m| = 2^n N_{m - 1}$.

Furthermore, let $S_m$ be the set of values $(\bar{v}_1, \ldots , \bar{v}_{2m})$ also satisfying all conditions for $i = 1, \ldots , m - 1$, and additionally satisfying (1) and (2) but not (3) for $i = m$. Define $T_m$ analogously but with values satisfying  (1) and  (3) but not  (2) for $i = m$. The set of complete solutions can then be written as $R_m \setminus (S_m \cup T_m)$. Hence, by the union bound,

$$\begin{aligned} N_{2m + 2} = |R_m \setminus (S_m \cup T_m)| = |R_m| - |S_m \cup T_m| \ge |R_m| - |S_m| - |T_m|\,. \end{aligned}$$

(14)

Since any $(\bar{v}_1, \ldots , \bar{v}_{2m}) \in S_m$ satisfies $\bar{v}_{2m - 1} \in \{\bar{v}_1, \ldots , \bar{v}_{2m - 2}\} \cup V_1 \cup \tilde{V}_1 \cup \tilde{V}_2$, one has that $|S_m| \le (p' + 2m - 2)N_{m - 1}$. Similarly, $|T_m| \le (p' + m - 1)N_{m-1}$. Hence, substituting these inequalities and $|R_m| = 2^n N_{m-1}$ in (14) and dividing out $N_{m-1}$ yields

$$\begin{aligned} \frac{N_{m}}{N_{m - 1}} \ge 2^n - (p' + 2m - 2) - (p' + m - 1) = 2^n - 2p' - 3m + 3\,. \end{aligned}$$

Using the telescoping product (13), it follows that

$$\begin{aligned} N_{q'} \ge \prod _{m = 1}^{q'} (2^n - 2p' - 3m + 3) \ge \prod _{i = 0}^{q'-1} (2^n - 2p' - 3i)\,. \end{aligned}$$

Combining (10), (11) and (12), we obtain

$$\begin{aligned} \frac{\Pr [ X_{\mathcal {O}} =\tau ]}{\Pr [ X_{\mathcal {P}} =\tau ]}&\ge N_{q'}\,\frac{(2^n)_q}{(2^n-p')_{2q'}\,(2^n-p)_{\alpha }}\nonumber \\&\ge \underbrace{N_{q'}\frac{(2^n)_{q'}}{(2^n-p')_{2q'}}}_{A} \cdot \underbrace{\frac{(2^n - q')_{\alpha }}{(2^n-p)_{\alpha }}}_{B}\,. \end{aligned}$$

(15)

Plugging in the lower bound for $N_{q'}$ in A yields

$$\begin{aligned} A&\ge \frac{\prod _{i=0}^{q'-1}(2^n-i)(2^n-2p'-3i)}{(2^n-p')_{2q'}}\nonumber \\&\ge \prod _{i=0}^{q'-1}\frac{(2^n-i)(2^n-2p'-3i)}{(2^n-p'-2i)(2^n-p'-2i-1)}\nonumber \\&\ge 1-\frac{4q'(p'+2q')(p'+2q'+1)}{2^{2n}}\nonumber \\&\ge 1-\frac{4q(p+2q)(p+2q+1)}{2^{2n}}\,, \end{aligned}$$

(16)

where we used Lemma 3 with $a=q'$ and $b=c=p'$, and the fact that $q'\le q$ and $p'+2q'+1\le p+2q+1\le 2^n/2$.

Next, we consider the factor $B$ in (15). Note that for $p\ge q\ge q'$ and using the fact that $q=q'+\alpha$, we have $B\ge 1$. For $p<q$, we have

$$\begin{aligned} B \ge \frac{(2^n - q')_{\alpha }}{2^{\alpha n}} \ge \Bigg (\frac{2^n - q}{2^{n}}\Bigg )^{\alpha } \ge 1 - \frac{2q^{3/2}}{2^{n}}\,, \end{aligned}$$

(17)

where we used $\alpha = \alpha _1 + \alpha _2\le 2\sqrt{q}$, which is due to $\lnot \textrm{bad}_5$, and $\lnot \textrm{bad}_6$.

Conclusion. From (15), (16), and (17) we conclude that

$$\begin{aligned} \frac{\Pr [ X_{\mathcal {O}} =\tau ]}{\Pr [ X_{\mathcal {P}} =\tau ]} \ge 1 - \frac{4q(p+2q)(p+2q+1)}{2^{2n}} - \frac{2q^{3/2}}{2^{n}}=: 1-\epsilon \,, \end{aligned}$$

using $(1-x)(1-y) \ge 1-x-y$.

5.4 Conclusion

Using Patarin’s H-Coefficient technique (Lemma 1), we obtain

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}2}^{\textrm{sprp}}(\mathcal {D}) \le \frac{3qp^2}{2^{2n+1}} + \frac{q^2}{2^{n}} + \frac{4q(p+2q)(p+2q+1)}{2^{2n}} + \frac{4q^{3/2}}{2^{n}}\,. \end{aligned}$$

6 Sharpened Analysis of Two-Round Even-Mansour

As an intermediate result that will be used to prove the security of our ideal cipher construction, we consider the following single-key variant of the 2-round Even-Mansour cipher. For any positive integer n, let $\pi _1, \pi _2\in \textrm{Perm}(n)$, and let $\gamma _1,\gamma _2:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$ be arbitrary invertible linear maps on $\{0,1\}^{n}$ with respect to $\oplus$. Define the generic construction $\textsf{EMIP} {2}:\{0,1\}^{n}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ as

$$\begin{aligned} \textsf{EMIP} {2}_{K}[\pi _1,\pi _2](M) = \pi _2(\pi _1(M\oplus K)\oplus \gamma _1(K) ) \oplus \gamma _2(K)\,. \end{aligned}$$

Chen et al. [12] showed that for $\gamma _1 = \gamma _2 = \textsf{id}$, $\textsf{EMIP}$ 2 is secure up to $\widetilde{\mathcal {O}}(2^{2n/3})$ queries. In this section, the following sharpened result will be shown. The result is sharper because, as explained below, our proof avoids the term $p^2\sqrt{qp}/2^{2n}$ in the bad transcript analysis. The latter term can play an important role when $p$ is large. The difference between Theorem 3 and the result of Chen et al. is illustrated in Fig. 3 in the introduction.

Theorem 3

Let $n \ge 4$ be an integer, let $\smash {K \xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}}$ and $\smash {\pi _1,\pi _2\xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)}$ independent and uniform random permutations. Let $\mathcal {D}$ be any distinguisher for $\textsf{EMIP} {2}_{K}[\pi _1, \pi _2]$ making at most $q > 1$ construction queries, at most p primitive queries to $\pi _1^{\pm }$ and at most p primitive queries to $\pi _2^{\pm }$. For all $q < 2^{n - 1}$ or $q = 2^{n}$, we have

$$\begin{aligned} \textbf{Adv}_{\textsf{EMIP} {2}}^{\textrm{sprp}}(\mathcal {D}) \le \frac{12}{2^{2c - n}} + \frac{7qp^2}{2^{2n}} + \frac{6\sqrt{3cqp^2}}{2^n}\,, \end{aligned}$$

with $c > 0$ an arbitrary real number.

We prove Theorem 3 in Sect. 6.2. The bad transcript analysis of Chen et al. [12] relies on a sum-capture theorem. The sharpened bound in Theorem 3 is due to a sharpening of this result. Several variants of the sum-capture theorem exist for different situations [12, 15]. These results build on the work of Babai [2] and Steinberger [33]. Typically, a sum-capture theorem states that for a random subset $Z$ of $\{0,1\}^{n}$ of size $q$, the quantity

$$\begin{aligned} \mu (Z,A,B) = \left|\{(z,a,b)\in Z\times A\times B:z = a\oplus b\}\right| \end{aligned}$$

is not much larger than $q\,\left|A\right|\,\left|B\right|/2^{n}$ for any possible choice of A and B, except with negligible probability. In our setting, $Z$ will consist of query-response tuples from a permutation, i.e. Z consists of values $u_i \oplus v_i$ where $\{(u_1,v_1),\dots ,(u_q,v_q)\}$ is a permutation transcript. For this case, Chen et al. [12] proved the following result.

Theorem 4

(Chen et al. [12]). Let $\varGamma$ be an invertible linear map on the $\mathbb {F}_2$-vector space $\{0,1\}^{n}$. Let $\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$, let $\mathcal {D}$ be some probabilistic algorithm making exactly $q$ distinct two-sided adaptive queries to $\pi$. Let $Z = \{(u_1, v_1), \ldots , (u_q, v_q)\}$ be the transcript of the interaction of $\mathcal {D}$ with $\pi$, which consists of $q \ge 1$ pairs such that either $v_i = \pi (u_i)$ or $u_i = \pi (v_i)$ for all $i = 1, \ldots , q$. For any two subsets $A,B\subseteq \{0,1\}^{n}$, let

$$\begin{aligned} \mu (Z,A,B) = \left|\{((u,v),a,b)\in Z\times A\times B:u\oplus a = \varGamma (v\oplus b)\}\right|\,. \end{aligned}$$

Then, for $9n\le q\le 2^{n-1}$, we have

$$\begin{aligned} \Pr \left[ \mu (Z,A,B) \ge \frac{q\left|A\right|\left|B\right|}{2^n} + \frac{2q^2\sqrt{\left|A\right|\left|B\right|}}{2^n} + 3\sqrt{nq\left|A\right|\left|B\right|} \right] \le \frac{2}{2^n}\,. \end{aligned}$$

In Sect. 6.1, we prove the following sharpened and simplified version of their result. For $c = n$, the bound in the theorem below is essentially identical to the one given in the sum-capture theorem of Cogliati et al. [15, Lemma 1] for the case where Z results from the interaction with a random function. Hence, our result removes the unnecessary discrepancy between the sum-capture theorems for random functions and random permutations.

Theorem 5

(Sum-capture theorem). Let $\varGamma$ be an invertible linear map on the $\mathbb {F}_2$-vector space $\{0,1\}^{n}$. Let $\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$, and let $\mathcal {D}$ be some probabilistic algorithm making exactly $q$ distinct two-sided adaptive queries to $\pi$. Let $Z = \{(u_1, v_1), \ldots , (u_q, v_q)\}$ be the transcript of the interaction of $\mathcal {D}$ with $\pi$, which consists of $q \ge 1$ pairs such that either $v_i = \pi (u_i)$ or $u_i = \pi (v_i)$ for all $i = 1, \ldots , q$. For any two subsets $A,B\subseteq \{0,1\}^{n}$, let

$$\begin{aligned} \mu (Z,A,B) = \left|\{((u,v),a,b)\in Z\times A\times B:u\oplus a = \varGamma (v\oplus b)\}\right|\,. \end{aligned}$$

For any real number $c > 0$, it then holds that

$$\begin{aligned} \Pr \left[ \mu (Z,A,B) \ge \frac{q\left|A\right|\left|B\right|}{2^n} + 2\sqrt{3 c q\left|A\right|\left|B\right|} \right] \le \frac{4}{2^{2c - n}}\,. \end{aligned}$$

As can be seen by comparing Theorem 4 and Theorem 5, our version of the sum-capture theorem does not contain the term $2q^2\sqrt{\left|A\right|\left|B\right|}/2^n$ and avoids the condition $9n\le q\le 2^{n-1}$. This eliminates the terms $2q^2p/2^{2n}$ and $4p^2\sqrt{qp}/2^{2n}$ in our bad transcript analysis. The latter term can play an important role when $p$ is large.

6.1 Proof of the Sharpened Sum-Capture Theorem

For a subset Z of $\{0,1\}^{n} \times \{0,1\}^{n}$ and an invertible linear map $\varGamma$ of the $\mathbb {F}_2$-vector space $\{0,1\}^{n}$, we define the quantity

$$\begin{aligned} \varPhi _\varGamma (Z) = \max _{\begin{array}{c} \alpha \in \{0,1\}^{n}\\ \alpha \ne 0 \end{array}} \Big |\sum _{(x, y) \in Z} (-1)^{\langle \alpha , x\rangle \oplus {} \langle \alpha , \varGamma (y)\rangle }\Big |\,. \end{aligned}$$

In the expression above, $\langle \alpha , x\rangle = \oplus _{i = 1}^n \alpha _i x_i$ denotes the standard dot product between bitstrings of length n. The following lemma was proven by Chen et al. [12], but in the statement of their result they replaced the smaller quantity $\varPhi _\varGamma (Z)$ by the quantity

$$\begin{aligned} \varPhi (Z) = \max _{\begin{array}{c} \alpha , \beta \in \{0,1\}^{n}\\ \alpha , \beta \ne 0 \end{array}} \Big |\sum _{(x, y) \in Z} (-1)^{\langle \alpha , x\rangle \oplus {} \langle \beta , y\rangle } \Big |\ge \varPhi _\varGamma (Z)\,. \end{aligned}$$

However, their proof carries over essentially completely.

Lemma 4

(Chen et al. [12]). Let $\varGamma$ be an automorphism of the $\mathbb {F}_2$-vector space $\{0,1\}^{n}$. For all sets $Z \subseteq \{0,1\}^{n} \times \{0,1\}^{n}$ and $A, B \subseteq \{0,1\}^{n}$, define

$$\begin{aligned} \mu (Z,A,B) = \left|\{((u,v),a,b)\in Z\times A\times B:u\oplus a = \varGamma (v\oplus b)\}\right|\,. \end{aligned}$$

Then it holds that

$$\begin{aligned} \mu (Z,A,B) \le \frac{|Z|\,|A|\,|B|}{2^n} + \varPhi _\varGamma (Z) \sqrt{|A|\,|B|}\,. \end{aligned}$$

In order to obtain the simplified sum-capture theorem, it suffices to compute a tail bound for the quantity $\varPhi _\varGamma (Z)$. Our improvement over the result of Chen et al. is enabled by the following theorem of Hoeffding [22], which is stated for the special case of zero-mean uniformly bounded populations below.

Theorem 6

(Hoeffding [22]). If $x_1, x_2, \ldots , x_q$ is a random sample without replacement from a finite population (multiset) $\{\{c_1, c_2, \ldots , c_N\}\}$ such that $a \le c_i \le b$ for all $i = 1, \ldots , N$ and $\sum _{i = 1}^N c_i = 0$, then for all $\delta > 0$, it holds that

$$\begin{aligned} \Pr \Bigg [\sum _{i = 1}^q x_i \ge \sqrt{q} \delta \Bigg ] \le \exp \left( \frac{-2\delta ^2}{(b - a)^2}\right) \,. \end{aligned}$$

Theorem 6 is precisely the same bound as the classical Hoeffding inequality for sampling with replacement [22, Theorem 2]. It is not surprising that the same result should be true for sampling without replacement, since the latter tends to decrease variability. To prove Theorem 6, Hoeffding first showed that the average of any continuous convex function of $\sum _{i = 1}^q x_i$ is less than the same function of an equivalent sum involving random variables sampled with replacement. The result then follows by applying this argument for the exponential function (which is clearly convex) and by using Markov’s inequality.

Lemma 5

Let $\pi \xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$ and let $\mathcal {D}$ be some probabilistic algorithm making exactly $q$ distinct two-sided adaptive queries to $\pi$. Let $Z = \{(u_1, v_1), \ldots , (u_q, v_q)\}$ be the transcript of the interaction of $\mathcal {D}$ with $\pi$, which consists of $q \ge 1$ pairs such that $v_i = \pi (u_i)$ or $u_i = \pi (v_i)$. For any real number $c > 0$, the tail of $\varPhi _\varGamma (Z)$ can be bounded as

$$\begin{aligned} \Pr [\varPhi _\varGamma (Z) \ge 2\sqrt{3cq}] \le \frac{4}{2^{2c - n}}\,. \end{aligned}$$

Proof

By swapping inputs and outputs where necessary for $i = 1, \ldots , q$, there exist pairs $(x_i, y_i)$ such that $y_i = \pi (x_i)$ and

$$\begin{aligned} \varPhi _\varGamma (Z) = \max _{\begin{array}{c} \alpha \in \{0,1\}^{n}\\ \alpha \ne 0 \end{array}} \Big |\sum _{i = 1}^{q} (-1)^{\langle \alpha , x_i\rangle \oplus {} \langle \alpha , \varGamma (y_i)\rangle }\Big |\,. \end{aligned}$$

For any $\alpha \ne 0$ the values $z_i = \langle \alpha , \varGamma (y_i)\rangle$ with $i = 1, \ldots , q$ are random samples without replacement from a population consisting of $2^{n-1}$ values 0 and $2^{n-1}$ values 1. Indeed, any nonzero linear combination of the output bits of a uniform random permutation is a uniform random balanced Boolean function and no queries to $\pi$ can be repeated. Furthermore, due to the fact that $\pi$ is a uniform random permutation, $z_1, \ldots , z_q$ are independent of $x_1, \ldots , x_q$. Hence, consider the sum

$$\begin{aligned} S_\alpha = \sum _{i = 1}^{q} (-1)^{\langle \alpha , x_i\rangle }\,(-1)^{z_i}\,. \end{aligned}$$

Note that $S_\alpha$ is a symmetric random variable and $\mathbb {E} [S_\alpha ] = 0$. Applying the union bound¹ and Theorem 6 to the terms with positive and negative coefficients separately gives the tail bound

$$\begin{aligned} \Pr {\big [|S_\alpha | \ge \delta \sqrt{q}~|~x_1, \ldots , x_q\big ]} \le 4\,e^{-\delta ^2 / 8}\,. \end{aligned}$$

The law of total probability then directly yields the upper bound $\Pr {\big [|S_\alpha | \ge } {\delta \sqrt{q}\big ]} \le 4\,e^{-\delta ^2 / 8}$. By the union bound,

$$\begin{aligned} \Pr {[\varPhi _\varGamma (Z) \ge \delta \sqrt{q}]} = \Pr {\big [\max _{\alpha \ne 0}|S_\alpha | \ge \delta \sqrt{q}\big ]} \le 2^{n + 2}\,e^{-\delta ^2 / 8}\,. \end{aligned}$$

Let $\delta = 2\sqrt{3c} > 4\sqrt{\ln 2^{c}}$ for $c > 0$, then

$$\begin{aligned} \Pr {[\varPhi _\varGamma (Z) \ge 2\sqrt{3cq}]} \le 2^{n + 2}\,e^{-2\ln 2^{c}} = \frac{4}{2^{2c - n}}\,. \end{aligned}$$

This concludes the proof.   $\square$

6.2 Proof of Theorem 3

In this section we prove Theorem 3. Let $K\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$ and $\pi _I,\pi _1,\pi _2\xleftarrow {{\scriptscriptstyle \$}}\textrm{Perm}(n)$. Consider any computationally unbounded and deterministic distinguisher $\mathcal {D}$ with access to the oracles $(\textsf{EMIP} {2}_K^{\pm }[\pi _1,\pi _2], \pi _1^{\pm }, \pi _2^{\pm })$ in the real world and $(\pi _I^{\pm }, \pi _1^{\pm }, \pi _2^{\pm })$ in the ideal world.

The distinguisher makes $q$ construction queries to $\textsf{EMIP} {2}_K^{\pm }[\pi _1,\pi _2]$ or $\pi _I^{\pm }$, and these are summarized in a transcript of the form $\tau _0=\{(M_1,C_1),\ldots ,(M_q,C_q)\}$. It also makes $p$ primitive queries to $\pi _1^{\pm }$, and $p$ primitive queries to $\pi _2^{\pm }$, these are respectively summarized in the transcript $\tau _1=\{(u_1,v_1),\dots ,(u_p,v_p)\}$ and $\tau _2=\{(x_1,y_1),\dots ,(x_p,y_p)\}$. Without loss of generality, it can be assumed that the distinguisher does not make duplicate construction or primitive queries.

After $\mathcal {D}$’s interaction with the oracles, but before it outputs its decision, we disclose the key $K$ to the distinguisher. In the real world, this is the key used in the construction. In the ideal world, $K$ is a dummy key that is drawn uniformly at random. The complete view is denoted by $\tau =(\tau _0,\tau _1,\tau _2,K)$.

Bad Events. We say that $\tau \in \mathcal {T}_{\textrm{bad}}$ if and only if there exist a construction query $(M_j,C_j)\in \tau _0$ and primitive queries $(u,v)\in \tau _1$ and $(x,y)\in \tau _2$ such that one of the following conditions holds:

$$\begin{aligned} \textrm{bad}_1:&M_j \oplus u=K \; \text {and} \; C_j \oplus y=\gamma _2(K)\,,\end{aligned}$$

(18)

$$\begin{aligned} \textrm{bad}_2:&M_j \oplus u=K \; \text {and} \; v\oplus x=\gamma _1(K)\,,\end{aligned}$$

(19)

$$\begin{aligned} \textrm{bad}_3:&C_j \oplus y=\gamma _2(K) \; \text {and} \; v\oplus x=\gamma _1(K)\,. \end{aligned}$$

(20)

Any attainable transcript $\tau$ for which $\tau \notin \mathcal {T}_{\textrm{bad}}$ will be called a good transcript.

Probability of Bad Events in the Ideal World. We want to bound the probability $\Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}]$ that an ideal world transcript $\tau$ satisfies either of (18)-(20). Therefore, the probability that $X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}$ is given by

$$\begin{aligned} \Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}] \le \Pr [\textrm{bad}_1] + \Pr [\textrm{bad}_2] + \Pr [\textrm{bad}_3]\,. \end{aligned}$$

Throughout the proof, let $U = \{u~|~(u,v)\in \tau _1\}$, $V = \{v~|~(u,v)\in \tau _1\}$, $X = \{x~|~(x,y)\in \tau _2\}$ and $Y = \{y~|~(x,y)\in \tau _2\}$. In addition, denote

$$\begin{aligned} \varOmega _1&= \left|\big \{\big (j,(u,v),(x,y)\big )~|~M_j\oplus u = \gamma _2^{-1}(C_j\oplus y)\big \}\right|\,,\\ \varOmega _2&= \left|\big \{\big (j,(u,v),(x,y)\big )~|~M_j \oplus u = \gamma _1^{-1}(v\oplus x)\big \}\right|\,,\\ \varOmega _3&= \left|\big \{\big (j,(u,v),(x,y)\big )~|~C_j\;\oplus y = \gamma _2\circ \gamma _1^{-1}(v\oplus x)\big \}\right|\,. \end{aligned}$$

In the ideal world, $\varOmega _1$, $\varOmega _2$, and $\varOmega _3$ only depend on $\pi _1$, $\pi _2$ and $\pi$, and not on the key $K\xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}$, which is drawn uniformly at random at the end of the interaction. For any $i\in \{1,2,3\}$ and $\lambda _i > 0$ a real constant, we have

$$\begin{aligned} \Pr [\textrm{bad}_i] \le \Pr [\varOmega _i \ge \lambda _i] + \frac{\lambda _i}{2^n}\,. \end{aligned}$$

To upper bound the first term above, the sharpened sum-capture theorem (Theorem 5) will be used. This application of the sum-capture theorem will also rely on the linearity of $\gamma _1$ and $\gamma _2$.

1$^{st}$ Bad Event. The first bad event can be rewritten as $M_j\oplus u = \gamma _2^{-1}(C_j)\oplus \gamma _2^{-1}(y) = K$. To apply the sum-capture lemma, define

$$\begin{aligned} Z_1&= \{M_j \oplus \gamma _2^{-1}(C_j)~|~(M_j,C_j)\in \tau _0\}\,,\\ A_1&= U\,,\\ B_1&= \{\gamma _2^{-1}(y)~|~y\in Y\}\,. \end{aligned}$$

Since $\gamma _2^{-1}$ is a permutation, Lemma 4 can be applied with $\varOmega _1 = \mu (Z_1,A_1,B_1)$,

$$\begin{aligned} \Pr \left[ \mu (Z_1,A_1,B_1) \ge \frac{qp^2}{2^n} + 2\sqrt{3cqp^2} \right] \le \frac{4}{2^{2c - n}}\,. \end{aligned}$$

We thus set $\lambda _1= qp^2 / 2^n + 2\sqrt{3cqp^2}$ and obtain

$$\begin{aligned} \Pr [\textrm{bad}_1] \le \frac{4}{2^{2c - n}} + \frac{qp^2}{2^{2n}} + \frac{2\sqrt{3cqp^2}}{2^n}\,. \end{aligned}$$

2$^{nd}$ Bad Event. For $i=2$, we rewrite $\textrm{bad}_2$ as $M_j \oplus u = \gamma _1^{-1}(v)\oplus \gamma _1^{-1}(x) = K$, and we define

$$\begin{aligned} Z_2&= \{u \oplus \gamma _1^{-1}(v)~|~(u,v)\in \tau _1\}\,,\\ A_2&= \{M_j~|~(M_j,C_j)\in \tau _0\}\,,\\ B_2&= \{\gamma _1^{-1}(x)~|~x\in X\}\,. \end{aligned}$$

Then, since $\gamma _1^{-1}$ is a permutation, we can apply Lemma 4 with $\varOmega _2 = \mu (Z_2,A_2,B_2)$,

$$\begin{aligned} \Pr \left[ \mu (Z_2,A_2,B_2) \ge \frac{qp^2}{2^n} + 2\sqrt{3cqp^2} \right] \le \frac{4}{2^{2c - n}}\,. \end{aligned}$$

We thus set $\lambda _2= qp^2 / 2^n + 2\sqrt{3cqp^2}$ and obtain

$$\begin{aligned} \Pr [\textrm{bad}_2] \le \frac{4}{2^{c - 2n}} + \frac{qp^2}{2^{2n}} + \frac{2\sqrt{3cqp^2}}{2^n}\,. \end{aligned}$$

3$^{rd}$ Bad Event. For $i=3$, we rewrite $\textrm{bad}_3$ as $C_j \oplus y = \gamma _2\circ \gamma _1^{-1}(v)\oplus \gamma _2\circ \gamma _1^{-1}(x) = \gamma _2(K)$ and we define

$$\begin{aligned} Z_3&= \{\gamma _2\circ \gamma _1^{-1}(x) \oplus y~|~(x,y)\in \tau _2\}\,,\\ A_3&= \{C_j~|~(M_j,C_j)\in \tau _1\}\,,\\ B_3&= \{\gamma _2\circ \gamma _1^{-1}(v)~|~v\in V\}\,. \end{aligned}$$

Then, since $\gamma _2\circ \gamma _1^{-1}$ is a permutation, we can apply Lemma 4 with $\varOmega _3 = \mu (Z_3,A_3,B_3)$,

$$\begin{aligned} \Pr \left[ \mu (Z_3,A_3,B_3) \ge \frac{qp^2}{2^n} + 2\sqrt{3cqp^2} \right] \le \frac{4}{2^{2c - n}}\,. \end{aligned}$$

We thus set $\lambda _3= qp^2 / 2^n + \sqrt{5nqp^2}$ and obtain

$$\begin{aligned} \Pr [\textrm{bad}_3] \le \frac{4}{2^{2c - n}} + \frac{qp^2}{2^{2n}} + \frac{2\sqrt{3cqp^2}}{2^n}\,. \end{aligned}$$

Conclusion. Summing the probabilities of the three bad events, we get

$$\begin{aligned} \Pr [ X_{\mathcal {P}} \in \mathcal {T}_{\textrm{bad}}] \le \frac{12}{2^{2c - n}} + \frac{3qp^2}{2^{2n}} + \frac{6\sqrt{3cqp^2}}{2^n}\,. \end{aligned}$$

(21)

Probability Ratio for Good Transcripts. Since our bad events are the same as in the analysis of Chen et al. [12], their analysis of the good transcript ratio can be recycled. In particular, their Lemma 8 (i) implies that for any good transcript $\tau$ and any integers q and p such that $2q + 2p \le 2^n$,

$$\begin{aligned} \frac{\Pr [ X_{\mathcal {O}} = \tau ]}{\Pr [ X_{\mathcal {P}} \in \tau ]} \ge 1 - \frac{4qp^2}{2^{2n}}\,. \end{aligned}$$

However, the above bound is trivial whenever $p \ge 2^{n - 1} / \sqrt{q}$. Hence, $2q + 2p \le 2^{n} / \sqrt{q} + 2q$ and for $n \ge 4$ this is lower than $2^n$ whenever $q > 1$ and $q < 2^{n-1}$. Furthermore, by [12, Lemma 8 (ii)], the result also holds for $q = 2^n$.

Conclusion. Using Patarin’s H-Coefficient technique (Lemma 1), we obtain

$$\begin{aligned} \textbf{Adv}_{\textsf{EMIP} {2}}^{\textrm{sprp}}(\mathcal {D}) \le \frac{12}{2^{2c - n}} + \frac{3qp^2}{2^{2n}} + \frac{6\sqrt{3cqp^2}}{2^n} + \frac{4qp^2}{2^{2n}}\,. \end{aligned}$$

7 Construction Based on an Ideal Cipher

We now turn to our second reflection cipher construction, which is illustrated in Fig. 5 below. Theorem 7 will show that, for an n-bit ideal block cipher with a k-bit key, this construction achieves a $\smash {\widetilde{\mathcal {O}}}(p\sqrt{q}/2^{n + k})$ security bound. The proof of this result is based on a reduction to our sharpened security bound for the two-round Even-Mansour cipher from Theorem 3.

Fig. 5.

The $\textsf{KARC}\text {-}\textsf{IC}$ construction uses two secret keys $K$ and $L$, and a block cipher $E$. The reflector $\mathcal R$ is a fixed linear involution and $\sigma$ is an invertible linear map. To obtain a pure reflection property with respect to both keys, $\sigma$ should be an involution.

Although the construction in Fig. 5 is based on the more powerful ideal cipher model, it is of considerable practical interest. Indeed, block-ciphers such as Prince [8], Mantis [5] and Qarma [1] are designed to support a 64 bit block size with 128 bit keys (internally split into two 64 bit keys), and claim a security tradeoff of $pq = 2^{128}$.

In the case of Prince and Mantis, this is achieved by instantiating the XEX-construction [23] with an ideal reflection cipher. Their construction is shown in Fig. 2 (in the introduction). Importantly, although this achieves the desired tradeoff, the construction of the ideal reflection cipher $E^*$ in Prince and Mantis closely follows our proposed construction: the only difference is the presence of key-additions in the middle layer of our construction. Hence, by minimally modifying Prince and Mantis, our results show that an improved security tradeoff of $pq^2 = 2^{256}$ can be achieved. However, it should be stressed that our results only establish security against generic attacks. Careful analysis by cryptanalysts remains necessary, even for minor changes such as the one proposed by our construction. For instance, in the case of Mantis, reduced-round nonlinear invariant attacks have been discovered [6]. The presence of key additions in the middle could provide additional flexibility to propagate the invariant property over more rounds. We believe a detailed analysis of this case would make for interesting future work.

The design of Qarma follows a very similar approach to our construction. In fact, Avanzi [1] remarks that the true security of the Qarma construction is likely to exceed the claimed $pq = 2^n$ trade-off. Our results corroborate this to some extent. However, our Theorem 7 is not directly applicable because Qarma uses a nonlinear reflector $\mathcal R$ between the middle key-additions. Analyzing the security of such construction would be possible if the sum-capture theorem could be extended to allow for nonlinearity. This is an interesting problem by itself.

Before giving Theorem 7 and its proof, we formalize our second construction. For any positive integers n and k, let E be a block cipher with key $L \in \{0,1\}^{k}$, and let $K \in \{0,1\}^{n}$ be a second construction key. Furthermore let $\mathcal R$ be a linear involution and $\sigma$ an invertible linear map on $\{0,1\}^{n}$ such that $\textrm{id} + \mathcal R\,\circ \,\sigma$ is invertible. The generic construction $\textsf{KARC}\text {-}\textsf{IC} {2}:\{0,1\}^{n+k}\times \{0,1\}^{n}\rightarrow \{0,1\}^{n}$ is defined by

$$\begin{aligned} \textsf{KARC}\text {-}\textsf{IC} {2}_{K, L}[E](M) = E^{-1}_{L + \alpha }(\mathcal R(E_{L}(M\oplus K)\oplus K)\oplus \sigma (K)) \oplus \sigma (K)\,, \end{aligned}$$

(22)

with $\alpha \in \{0,1\}^{k}$ a nonzero constant. The condition that $\textrm{id} + \mathcal R\circ \sigma$ is invertible is an important one, since Theorem 3 requires that $\gamma _2$ is invertible. Note that this condition is equivalent to the requirement that $\mathcal R\circ \sigma$ does not have any fixed points. The security of $\textsf{KARC}\text {-}\textsf{IC}$ 2 is given in Theorem 7, which can be proven by a reduction to the security of $\textsf{EMIP}$ 2.

Theorem 7

For any positive integers $n \ge 2$ and k, let $\smash {K \xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{n}}$ and $\smash {L \xleftarrow {{\scriptscriptstyle \$}}\{0,1\}^{k}}$ be uniform random keys and E an ideal cipher. If $\mathcal {D}$ is any distinguisher for $\textsf{KARC}\text {-}\textsf{IC} {2}_{K, L}[E]$ making at most $q > 1$ construction queries, and at most p primitive queries to $E^{\pm }$, then for all $q < 2^{n - 1}$ or $q = 2^n$ it holds that:

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}\text {-}\textsf{IC} {2}}^{\textrm{sprp}}(\mathcal {D}) \le \frac{12}{2^{n + k}} + 9\sqrt{2n + k}\;\frac{\sqrt{q}\,p}{2^{n + k}}\,. \end{aligned}$$

Proof

Enumerate all $\ell = 2^k$ possible ideal cipher keys as $L_1, \ldots , L_{\ell }$. Suppose the distinguisher $\mathcal {D}$ makes $p_{1, i}$ queries to $E^{\pm 1}$ with key $L_i$. Likewise, let $p_{2, i}$ denote the number of queries to $E^{\pm 1}$ with key $L_i \oplus \alpha$. For convenience, let $p_i = \max \{p_{1, i}, p_{2, i}\}$ be the maximum number of queries made for either $L_i$ or $L_i \oplus \alpha$. Since the total number of queries is equal to p, we have

$$\begin{aligned} \sum _{i = 1}^{\ell } p_i \le \sum _{i = 1}^{\ell } p_{1, i} + p_{2, i} = 2p\,. \end{aligned}$$

It follows from the law of total probability and the triangle inequality that

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}\text {-}\textsf{IC} {2}}^{\textrm{sprp}}(\mathcal {D}) \le \sum _{i = 1}^{\ell } \frac{1}{\ell }\,\textbf{Adv}_{\textsf{KARC}\text {-}\textsf{IC} {2}_{K, L_i}[E]}^{\textrm{sprp}}(\mathcal {D}) \,. \end{aligned}$$

Let $\mathcal {D}_i$ be a distinguisher running $\mathcal {D}$ to play the indistinguishability game against the $\textsf{EMIP} {2}_K[\pi _1, \pi _2]$ construction with $\pi _1 = E_{L_i}$ and $\pi _2 = E^{-1}_{L_i \oplus \alpha }$ using $p_{1, i}$ primitive queries to $\pi _1$, $p_{2, i}$ primitive queries to $\pi _2$ and q construction queries. In order to do this, $\mathcal {D}_i$ simulates $\mathcal {D}$’s queries to E whenever the key is different from $L_i$ or $L_i \oplus \alpha$. A standard hybrid argument then shows that

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}\text {-}\textsf{IC} {2}_{K, L_i}[E]}^{\textrm{sprp}}(\mathcal {D}) \le \textbf{Adv}_{\textsf{EMIP} {2}_{K}[E_{L_i}, E^{-1}_{L_i + \alpha }]}^{\textrm{sprp}}(\mathcal {D}_i) \,. \end{aligned}$$

Since $L_i \ne L_i \oplus \alpha$, the permutations $\pi _1$ and $\pi _2$ are indeed independent and uniform random. Hence, Theorem 3 (with $c = n + k/2$) yields the upper bound

$$\begin{aligned} \textbf{Adv}_{\textsf{EMIP} {2}_{K_1}[E_{L_i}, E^{-1}_{L_i + \alpha }]}^{\textrm{sprp}}(\mathcal {D}_i)&\le \frac{12}{2^{n + k}} + \frac{7qp_i^2}{2^{2n}} + 6\sqrt{3(n + k/2)}\frac{\sqrt{q}\,p_i}{2^n}\\&\le \frac{12}{2^{n + k}} + (6\sqrt{3(n + k/2)} + \sqrt{7})\frac{\sqrt{q}\,p_i}{2^n}\\&\le \frac{12}{2^{n + k}} + 9\sqrt{2n + k}\;\frac{\sqrt{q}\,p_i}{2^n}\,, \end{aligned}$$

where the second inequality follows from $x^2 \le x$ for all $x \in [0, 1]$. Hence, it follows that

$$\begin{aligned} \textbf{Adv}_{\textsf{KARC}\text {-}\textsf{IC} {2}}^{\textrm{sprp}}(\mathcal {D}) \le \frac{12}{2^{n + k}} + 9\sqrt{2n + k}\;\frac{\sqrt{q}\,p}{2^{n + k}}\,. \end{aligned}$$

This concludes the proof.   $\square$

To apply Theorem 7 to Prince, it remains to show that the linear map $\mathcal R\circ \sigma$ does not have any fixed points when $\mathcal R$ is the linear reflector and $\sigma$ the whitening-key orthomorphism² of Prince. Specifically, $\sigma : \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ is defined by

$$\begin{aligned} \sigma (x) = (x \ggg 1) \oplus (x \gg 63)\,. \end{aligned}$$

(23)

One can verify that $\textrm{rank}(\textrm{id} + \mathcal R\circ \sigma ) = 64$. That is, $\mathcal R\circ \sigma$ does not have any fixed points.

Observe that the $\sigma$ defined by (23) is not an involution. Hence, the Prince decryption algorithm is not the exactly same as the encryption algorithm: K and $\sigma (K)$ must also be swapped. Our construction preserves the same property, but we note that it is also possible to choose an involution $\sigma$ such that $\mathcal R\circ \sigma$ does not have any fixed points. In this case, decryption and encryption are purely related by the coupling map $(K, L) \mapsto (\sigma (K), L \oplus \alpha )$.

However, since the block cipher E used in Prince starts by xoring L to the state, using an involution $\sigma$ has the potential downside that $(K + L, \sigma (K) + L)$ is no longer jointly uniform for uniform random keys K and L. Indeed, for any linear involution $\sigma$, it holds that $\textrm{rank}(\textrm{id} + \sigma ) \le n/2$. This may facilitate partial key guessing. Again, this illustrates the importance of performing additional cryptanalysis when instantiating our (or, more generally, any) generic construction.