Stable Rotational Orbits of Base-Excited Pendula System

Abstract

The dynamics of a harmonically base-excited two pendula system, is investigated for the practical application of energy harvesting from rotatory motions [1, 2]. The central aim of this study is to identify system parameter ranges for which pendulum rotations exist. The external harmonic excitation amplitude and frequency, and the difference in pendulums lengths are the system parameters which have been varied thresholds. Bifurcation analysis has been performed for the identification of values beyond which rotations exist, and the study of corresponding bifurcation points has been conducted with computational tool ABESPOL, developed at the Centre for Applied Dynamics Research (CADR) of the University of Aberdeen [3]. Direct simulations and one-parameter continuation analysis were performed with ABESPOL and some results were corroborated with direct numerical integration in Matlab, based on a Runge-Kutta algorithm. One parameter continuation results showed complex bifurcation scenarios for antiphase rotatory motions, presenting evidence of existence and form of representation. Further results showed that pendulum rotations, in phase and antiphase, co-exist with oscillatory motions. Therefore, the basins of attraction have been computed, enabling attractors to be targeted so as to enable antiphase rotatory motion.

University of Aberdeen and Curtin University Alliance

1 Introduction

The application of pendula systems for energy harvesting from ambient vibration has been extensively investigated in the past years by the Centre for Applied Dynamics and Research (CADR), University of Aberdeen. The motivation to harvest energy from sea waves led to novel concept of rotational coupled parametric pendulum for their application to Wave Energy Converters (WEC). Previous studies [4] proved the superiority of rotatory over oscillatory pendulum responses with regards to energy harvesting. Therefore, further understanding of system parameters and physics governing pendula rotatory motions are needed to enable rotations for a two-pendula parametrically excited system. The dynamics of a vertically excited parametric pendulum was studied by Clifford and Bishop [5] and the experimental research on this matter was conducted by Alevras et al. [6] to achieve rotations from a single parametric pendulum. Moreover, stochastic excitations were also considered by Andreeva et al. [7] for the specific application to sea waves energy harvesting. Further studies by Garira and Bishop [8] as well as Horton [9] limited the stability of pendula rotations, and associated period-1 rotations with saddle node bifurcations. Further studies from Lenci et al. [10] also presented saddle node bifurcations, with the birth of pendulum rotatory responses, identified by a perturbation method. The robustness of rotational solutions in terms of dynamics integrity was consolidated in later work [11]. Moreover, a classification of the double pendulum states of equilibrium, oscillations and rotations considering Lyapunov exponent was made by Dudkoski et al. [12], and the existence of self-sustained rotations was identified by Klimina, Lokshin and Samsonor [13].

This study is based on previous experimental studies of a two-pendula system coupled to an elastic base presented by Najdecka et al. under periodic [1] and stochastic excitation [14]. The analysis to identify rotational orbits in both pendulums excited parametrically and system parameters boundaries are studied by Marzal et al. [2]. The system parameters that will be considered in subsequent sections are length of pendulums, amplitude and excitation frequency.

The rest of the paper is organised as follows. Section 2 describes the physical model of the two-pendula system coupled to a common elastic base and harmonically excited in the vertical direction. System dynamic responses were obtained from direct numerical integration. Bifurcation analysis based on one-parameter continuation in the subsequent section is compared to system qualitative responses predicted by Runge-Kutta algorithm, Sect. 3. Concluding remarks are shown in Sect. 4, presenting the outcomes from the study.

2 Physical and Mathematical Modelling

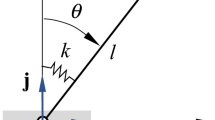
The physical system, which can be deployed for energy harvesting, was analysed in the form of time histories and bifurcation diagrams by Najdecka, Kapitaniak and Wiercigroch [1], based on two parametric pendulums mounted on a flexible, common supporting structure excited in the vertical direction by a common harmonic force $R_{y}$, where ($R_{y}$ = Asin($\varOmega$t)). Figure 1(a) shows the experimental rig used for model validation and experimental data acquisition. The two pendulums are able to rotate independently, and the aluminium elastic base sustains both pendulums, allowing their synchronization. Figure 1(b) shows typical phase plane responses when both pendulums are synchronized in antiphase rotatory motion, and also when the responses are close to heteroclinic cycles. Data presenting Pendulum 1 is drawn in black while that of Pendulum 2, in red. Therefore, the system is comprised of three masses: the supporting structure, M, and the two bob masses, $m_{1}$ and $m_{2}$ of pendulum 1 and pendulum 2 respectively; $l_{1}$ and $l_{2}$ represent the pendulum lengths and $c_{\theta }$ denotes the damping coefficient. $k_{x},k_{y},c_{x}$ and $c_{y}$ represent the total stiffness and damping properties of the supporting structure in the x and y directions. The system is modelled with four-degrees-of-freedom where X and Y denote the horizontal and vertical displacements respectively, and $\theta _{1}$ and $\theta _{2}$ depict the angular displacement of Pendulum 1 and 2 respectively measured from the vertical.

Fig. 1.

(a) Two-pendula experimental rig. (b) Phase plane of typical rotatory and nearly heteroclinic orbit for Pendulum 1 (black) and Pendulum 2 (red).

The system governing equations of motion have been derived by the Lagrangian method for equal masses ($m_{1}=m_{2}=m$), and $l_{1}=l$ and $l_{2}=l+\delta$; the equations of motion are expressed in the form $\boldsymbol{M u+C u+ K u=f(\theta _{1},\theta _{2})}$ where $\boldsymbol{u=(X,Y,\theta _{1},\theta _{2})^{T}}$ and f contains the nonlinear terms. The equations of motion in the dimensionless form can be written as follows:

$$\begin{aligned} \begin{aligned} x ^{\prime \prime } +&\gamma _{x}x^{\prime }+\alpha _{x} x\\&= -a[\theta _{1}^{\prime \prime }cos(\theta _{1})-(\theta _{1}^{\prime })^2sin(\theta _{1})]-a\left( 1+\dfrac{\delta }{l}\right) [\theta _{2}^{\prime \prime }cos(\theta _{2})-(\theta _{2}^{\prime })^2sin(\theta _{2})], \end{aligned} \end{aligned}$$

(1)

$$\begin{aligned} \begin{aligned} y ^{\prime \prime } +&\gamma _{y}(y^{\prime }-\omega pcos(\omega \tau ))+\alpha _{y}[y-psin(\omega \tau )]\\&= -a[\theta _{1}^{\prime \prime }sin(\theta _{1})+(\theta _{1}^{\prime })^2cos(\theta _{1})]-a\left( 1+\dfrac{\delta }{l}\right) [\theta _{2}^{\prime \prime }sin(\theta _{2})+(\theta _{2}^{\prime })^2cos(\theta _{2})], \end{aligned} \end{aligned}$$

(2)

$$\begin{aligned} \theta _{1}^{\prime \prime }+\dfrac{\gamma _{\theta }}{l}\theta _{1}^{\prime }=-x^{\prime \prime }cos(\theta _{1})-[1-\omega ^{2}psin(\omega \tau )]sin(\theta _{1}), \end{aligned}$$

(3)

$$\begin{aligned} \theta _{2}^{\prime \prime }+\dfrac{\gamma _{\theta }}{(l+\delta )}\theta _{2}^{\prime }=-x^{\prime \prime }lcos(\theta _{2})\left( \dfrac{1}{l+\delta }\right) -[1-\omega ^{2}plsin(\omega \tau )]sin(\theta _{2}). \end{aligned}$$

(4)

where ’ denotes differenciation with respect to the non-dimensionalized time $\tau$ and the non-dimensionalised parameters and variables are,

$x=\dfrac{X}{l}$, $\gamma _{x}=\dfrac{c_{x}}{(M+2m)\omega _{n}}$, $\alpha _{x}=\dfrac{k_{x}}{(M+2m)\omega _{n}^2}$, $a=\dfrac{m}{M+2m}$, $\omega =\dfrac{\varOmega }{\omega _{n}}$,

$p=\dfrac{A}{l}$, $\gamma _{\theta }=\dfrac{c_\theta }{m\omega _{n}}$, $y=\dfrac{Y}{l}$, $\gamma _{y}=\dfrac{c_{y}}{(M+2m)\omega _{n}}$, $\alpha _{y}=\dfrac{k_{y}}{(M+2m)\omega _{n}^2}$.

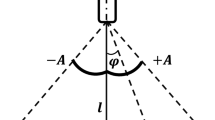
Equations (1) to (4) were non-dimensionalised with respect to a linear natural frequency, and solved by direct numerical integration to obtain a form of exact solution based on initial conditions initial conditions of $x(0)=x^{\prime }(0)=0$, $\theta _{1}(0)=1.5708$, $\theta _{1}^{\prime }(0)=2.5$, $\theta _{2}(0)=0.5708$ and $\theta _{2}^{\prime }(0)=-2.5$. To give an overview of system qualitative responses, a three-dimensional graph was constructed for the three parameters in this study, which are the non-dimensionalised amplitude and frequency of the wave excitation, represented as p and $\omega$, respectively and the parameter mismatch $\delta$, describing the difference between pendulum lengths. System qualitative responses in the three-dimensional graph, were differentiated by colour. Pendulum 1 is oscillating, and Pendulum 2 is rotating, the plot colour is yellow. If Pendulum 1 is rotating and Pendulum 2 is oscillating, the plot is green. For both pendulums oscillating, black is used. Red is deployed for both pendulums rotating. Figure 2(b) present typical phase planes and trajectories, corresponding to different system qualitative responses.

Fig. 2.

Dynamical system responses, where yellow indicated Pendulum 1 oscillations and Pendulum 2 rotations, green denotes Pendulum 1 rotations and Pendulum 2 oscillations, black implies oscillations and red corresponds to rotations for ranges of system parameters of (a) $\delta$ $\in$ [00.06], $\omega$ $\in$ [1.9 2.2] and p$\in$[0.05 1.4]. (b) Area of future bifurcation analysis constrained between $\delta$ $\in$[00.06], $\omega$ $\in$ [1.9 2.2] and p$\in$ [0.05 1.5] and a selection of time histories and phase portraits for both pendulums.

Direct numerical integration predict the existence of rotations for amplitude values of p tending towards zero or larger values close to 1.4, when the frequency, $\omega$, is 2.1. Values close to zero amplitude were studied further and identified to be values close to 0.05 when frequencies, $\omega$, target between 2.0 and 2.2. The parameter mismatch $\delta$ ranged between 0.00 and 0.06. To identify the parameter values beyond which rotations cease to exist, a bifurcation analysis was performed with the computational tool ABESPOL [3] to identify attractors to be targeted in practice. This was based on the approach of continuation.

Fig. 3.

Bifurcation analysis using path following with system initial conditions are $x(0)=x^{\prime }(0)=0$, $\theta _{1}(0)=1.5708$, $\theta _{1}^{\prime }(0)=2.5$, $\theta _{2}(0)=0.5708$ and $\theta _{2}^{\prime }(0) = -2.5$. Case for $\omega$ = 2.00 and $\delta$ = 0.00 from p = [0 1.40000]. Stable and unstable solutions are presented in green and red respectively, saddle node bifurcations are represented as red dots. (a) and (b) Pendulum 1 and 2 bifurcation diagrams.

3 Bifurcation Analysis

To identify the ranges of parameter values for which rotations occur, numerical continuation was performed. One parameter numerical continuation has been performed with ABESPOL, which connects with the continuation core, COCO [17].

In addition, direct simulation has been carried out for values of p, $\omega$ and $\delta$ within the ranges computed by direct numerical integration. Results were shown in Fig. 2. The results obtained have been summarized for the case of $\omega =2.00$ and $\delta =0.00$ and one parameter continuation was implemented for $p\in$ [0.01274 1.40000]. Figure 3 present the results obtained from one parameter continuation as well as the direct simulations required to initialize the continuations for each pendulum. Stable solutions are presented in green, and red lines correspond to unstable solutions. For both pendulums, the coexistence of phase rotations, antiphase rotations and oscillations has been identified. Basins of attraction are required to identify rotational motions for both pendulums so as to apply to energy harvesting. Some example phase planes are presented for antiphase and oscillatory motions, to prove the existence of this type of motion. Pendulum 1 experienced a saddle node bifurcation for the antiphase rotational motion, $p=0.012739$, and a period doubling bifurcation at $p= 0.42600$ for $\omega =2.00$ and $\delta =0.00$. For Pendulum 2, only one saddle node was detected for antiphase rotations at $p=0.012739$. Only the first saddle node bifurcation is located at the limiting values of system parameter values. These values distinguish between stable and unstable orbits. Further work would extend the identification of boundaries separating rotational and oscillatory motions.

4 Concluding Remarks

This paper studied a coupled pendula system excited vertically to identify ranges of system parameters for which pendulums exhibit stable rotations. This can be applied to wave energy harvesting in a novel WEC concept. Direct numerical integration showing that rotations for both pendulums exist when p $\rightarrow$ 0 and p $\rightarrow$ 1.4 for $\omega$ = 2.10 and $\delta \in$ [0.00 0.06], and more specifically for ranges of p$\in$ [0.0500 0.500], $\omega \in$ [1.90 2.20] and $\delta \in$ [0.00 0.06], where p and $\omega$ denote non-dimesionalized amplitude and frequency of excitation respectively; whereas $\delta$ describes the difference in pendulum lengths.

Numerical continuation in ABESPOL has identified bifurcation scenarios and attractors to be targeted in the practice, and helped to identify ranges of system parameters for both Pendulum 1 and Pendulum 2. The analysis conducted for p $\in$ [0.012739 1.4], $\omega$ = 2.00 and $\delta$ = 0.00 has located a saddle node bifurcation at p = 0.012739 and period doubling bifurcations at p = 0.42600 for antiphase rotation. Oscillations coexist with anti-phase rotations for values of smaller than $p=0.32000$. Chaotic oscillations coexist with period-2 oscillations for both Pendulum 1 and Pendulum 2.