State Identification and Verification with Satisfaction

Abstract

We use SAT-solving to construct adaptive distinguishing sequences and unique input/output sequences for finite state machines in the flavour of Mealy machines. These sequences solve the state identification and state verification problems respectively. Preliminary experiments evaluate our implementation and show that this approach via SAT-solving works well and is able to find many short sequences.

1 Introduction

In a paper by Lee and Yannakakis [LY94], the notion of adaptive distinguishing sequence (ADS) is developed. Such a sequence is a (single) experiment which can determine exactly in which state a given finite state machine (FSM) is. The experiment consists of input symbols for the FSM, which may depend on the outputs of the FSM observed so far (making it adaptive). The goal of the experiment is to determine exactly in which state the given FSM is at the start of the experiment (making it distinguishing). We use the formalism of Mealy machines to model FSMs; but the techniques can also be adapted to Moore machines and DFAs. Whether such an experiment exists for the whole machine can be decided efficiently. In the special case where we have prior knowledge that the machine is in one of two states, such a sequence always exists and can also be found efficiently. Despite these positive results, the general problem is hard:

Theorem

[LY94, Theorem 3.4]. Given an FSM and a set of possible initial states, it is PSpace-complete to tell whether there is an experiment that identifies the initial state.

Nonetheless, the problem is of practical interest. For instance, the $\textsf{L}\!^\sharp$ algorithm [VGRW22] learns an opaque FSM based on its input/output behaviour, that is without having access to the internal transition structure. It does so by successively exhibiting distinct states in the FSM that differ in their behaviour, that is, states that are provably apart. Whenever a longer trace of the FSM is observed, the algorithm has to identify whether this leads to the same state as one of the exhibited states so far. Hence, it would be useful if there is a single experiment from which we could determine in which state the FSM is. In such a learning algorithm, the queries are often the bottleneck, since they interact with embedded devices with restricted communication speed. So even though the learning can be done in polynomial time, it may be worth some extra computation to reduce the query size or the number of resets.

In this paper, we will use SAT solvers to construct two types of experiments: adaptive distinguishing sequences and unique input/output sequences. The problem of deciding the existence of these sequences is PSpace-complete. Our motivation typically asks for short experiments, and so we will fix a bound (polynomial in the size of the automaton). This bound ensures that the problem is in NP and so a reduction to SAT is possible. This preference towards short experiments is perfectly in line with the setting of learning where one can run multiple short experiments instead of a single long one.

Dedication

This paper is dedicated to Frits Vaandrager who was our supervisor and co-author.

Frits was the first author’s PhD supervisor: In the very first week of my PhD, he gave me a very well-defined task: read the paper by Lee and Yannakakis [LY94] and implement their algorithm. This was a fun start of my research and brought us useful insights in the area of model learning. I am very thankful to Frits that he gave me such interesting problems at the start.

Frits is the supervisor of the second author’s postdoc studies: since starting in Nijmegen, Frits introduced me to the realm of automata learning and testing. Those numerous research discussions finally led to the $\textsf{L}\!^\sharp$ algorithm [VGRW22], which makes great use of adaptive (and ordinary) distinguishing sequences.

Now, we once again return to those basic concepts of finite state machines, as there is still more to discover about adaptive distinguishing sequences and unique input/output sequences.

2 State Identification and Verification

As commonly done in (software) engineering, we model the systems of interest as (deterministic) finite state machines for a fixed finite input alphabet I and output alphabet O.

Definition 2.1

A finite state machine M (FSM) consists of

• 1. a finite set Q, called the state space,

• 2. a function $\delta :Q \times I \rightarrow Q$, called the transition function, and

• 3. a function $\lambda :Q \times I \rightarrow O$, called the output function.

For states $q,q'\in Q$, we write $q\xrightarrow {a/o} q'$ to denote $\delta (q,a) = q'$ and $\lambda (q,a) = o$, we call a the input and o the output of the transition. An example FSM is visualized in Fig. 1a on page page 4. We do not require a specified initial state in the definition of FSM since it is not relevant for the task of state identification and verification. In fact, in this task, we are given an FSM in some unknown state and need to derive from the I/O behaviour, in which state the FSM is.

Definition 2.2

The transition and output functions for an FSM inductively extend to words:

$$\begin{aligned} \delta&:Q \times I^* \rightarrow Q;&\delta ^*(q, \epsilon )&{:}{=}q;&\delta ^*(q, aw)&{:}{=}\delta ^*(\delta (q, a), w) \\ \lambda&:Q \times I^* \rightarrow O^*;&\lambda ^*(q, \epsilon )&{:}{=}\epsilon ;&\lambda ^*(q, aw)&{:}{=}\lambda (q, a) \cdot \lambda ^*(\delta (q, a), w) \end{aligned}$$

The semantics, i.e. observable behaviour, of a state $q \in Q$ are given as a function $\llbracket {q} \rrbracket :I^* \rightarrow O^*$ defined as

$$\begin{aligned} \llbracket {q} \rrbracket (w) {:}{=}\lambda ^*(q, w) \,. \end{aligned}$$

Two states $q_1$ and $q_2$ are apart [GJ21], i.e., have different observable behaviour, written $w\vdash q_1\mathbin {\#}q_2$, if $w\in I^*$ is an input word on which their semantics differ:

$$ \llbracket {q_1} \rrbracket (w) \ne \llbracket {q_2} \rrbracket (w). $$

Since we are only concerned with observable behaviour, we assume that machines are minimal, meaning that all distinct states in the given FSM are apart.

2.1 Testing Problems

We are in a setting where we are provided with a known machine M but do not know in which state it currently is:

• State identification: The task is to determine the state the M currently is in. We are allowed to interact with the M by inputting symbols from I and observing the output O. It is fine if those tests alter the current state of M. It is our task to determine the state M was in when we were presented it.

• State verification: Given a distinguished state $q\in Q$, the task is to verify whether the FSM is in q.

In either problem, there is no way of resetting the machine. The experiment may consist of multiple inputs and may depend on the previously produced outputs of the machine. In the present paper we focus on state identification and verification since they appear as important subtasks in model learning (also called machine identification) and in conformance testing and fault detection; a survey on these problems is given by Lee and Yannakakis [LY96]¹.

2.2 Separating and Distinguishing Sequences

The solutions of the state identification and verification problems boil down to finding clever input sequences such that the output allows us to reason about the states traversed:

Definition 2.3

For a machine M, a word $w\in I^*$ is

• 1. a separating sequence for two states $p, q \in Q$ if $w \vdash p \mathbin {\#}q$.

• 2. a unique input/output sequence (UIO) of a state $p \in Q$ if $w \vdash p \mathbin {\#}q$ for all other states $q \in Q$.

• 3. a preset distinguishing sequence (PDS) if $w \vdash p \mathbin {\#}q$ for all distinct states $p, q \in Q$.

Fig. 1.

Example of an FSM with inputs $I = \{i,j\}$ and outputs $O=\{e,o\}$ in which all states are pairwise apart.

Note how each definition requires $w \vdash p \mathbin {\#}q$, with the only difference being the quantification over p and q. This also means that a PDS is automatically a UIO and a UIO is automatically a separating sequence. See Fig. 1b for examples of separating sequences.

Separating sequences can be found very efficiently [SMJ16]. Unfortunately, both UIO sequences and PDSs are very hard to find:

Theorem

[LY94]. It is PSpace-complete to decide if a given machine has a PDS and it is PSpace-complete to decide whether a given state in a given machine has a UIO.

Under the assumption that NP $\ne$ PSpace, this PSpace-completeness implies that these sequences are not bounded by any polynomial (otherwise we could find them in NP time).

To overcome this hardness, Lee and Yannakakis looked more closely at the adaptive distinguishing sequence. In this sequence of inputs, the choice of input may depend on the output of the machine for the earlier inputs. It is a decision tree rather than just a sequence. The adaptive nature makes it so that after each letter a (possibly) smaller set of states is relevant, and so it becomes easier to continue the experiment.

Definition 2.4

We fix a machine M. An adaptive distinguishing sequence (ADS) is a rooted tree T of which the internal nodes are labelled with input symbols $a \in I$, the edges are labelled with output symbols $o \in O$, and the leaves are labelled with states $q \in Q$, such that:

• all edges leaving a certain node have distinct output symbols, and

• reading the inputs and outputs while following the path to a leaf labelled q, results in words $w \in I^*$ and $v \in O^*$ such that $\lambda (q, w) = v$.

Such a tree is called an adaptive distinguishing sequence for M if each state $q \in Q$ has a corresponding leaf.

Theorem

[LY94, Theorem 3.1]. Deciding whether a machine has an ADS can be done in polynomial time.

Example 2.5

We consider the example from Fig. 1a and show that there is no ADS for M. If the ADS would start with i (i.e. i in the root node), then it cannot distinguish w and z because $\delta (w, i) = \delta (z, i)$ and $\lambda (w, i) = \lambda (z, i)$. Similarly, starting with j fails to distinguish y and w. Thus, there is no ADS for the entire FSM of Fig. 1a. However, we can distinguish states for a smaller subset, for example the tree depicted in Fig. 1c distinguishes $\{x, y, z\}$ (and also $\{x, y, w\}$).

A preset distinguishing sequence is also an adaptive distinguishing sequence. And when one follows the root to a leaf in an ADS for the FSM, one obtains a UIO for the state labelled by the leaf. So the existence of these types of sequences are ordered:

$$ \text {PDS} ~\implies ~\text {ADS} \text { (for { M})} ~\implies ~\text {UIOs (for all states)} $$

None of the converse implications holds in general: For a minimal FSM M, all pairs of states have a separating sequence, but not every state may have a UIO. Even if every state has a UIO, there may be no ADS for M. And even if there is an ADS, there may be no PDS.

These sequences are related by the testing problems mentioned above. If an ADS exists for the entire FSM, then state identification can be solved with it. Similarly, state verification can be solved with UIO sequences if they exist.

2.3 Identification in a Subset of States

In the context of model learning, we may have additional insight about the FSM in state identification and verification. Given a (partly unknown) machine M in an unknown state, we may already exclude some states based on previous observations, leading to the simplified version of the state identification task:

• Local state identification: Given a known machine M that is currently in a state in the subset $Q_0\subseteq Q$, the task is to identify the current state exactly.

For $Q_0 = Q$, this is the original problem posed above, and if we have only two states (i.e., $Q_0 = \{p, q\}$), then identification problem can be solved with separating sequences. For the general problem where $Q_0$ is an arbitrary subset of Q, we adjust the previous sequence definitions:

Definition 2.6

For a machine M and a subset $Q_0 \subseteq Q$, an $Q_0$-local adaptive distinguishing sequence is an ADS that mentions all states $p \in Q_0$ in its leaves. Likewise, an $Q_0$-local UIO of a state p is a sequence w such that $w \dashv p \mathbin {\#}q$ for all $q \in Q_0$ other than p.

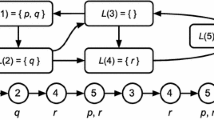
Surprisingly, finding an ADS for $Q_0$ is PSpace-complete, that is, harder than finding an ADS for $Q_0 = Q$, visualized in Fig. 2. This comes from the fact that even if there is no ADS for the full state set Q, there may be one for a subset. An example for such an FSM is depicted in Fig. 1a which does not have an ADS for $Q = \{w,x,y,z\}$ but for the subset $Q_0 = \{x,y,z\}$ (Fig. 1c).

Fig. 2.

The general problem of finding ADSs is PSpace-complete. But at the extreme cases, where $Q_0$ consists of either two states or all states, the problem is in P.

3 Reduction to SAT Solving

SAT solving is concerned with the problem of finding a satisfying assignment for a boolean propositional formula. This is a fundamental problem in computer science and enjoys a lot of applications [BHvMW09]. Although the problem is NP-complete, there exist implementations which work very well in practice.

Most solvers require the input to be in conjunctive normal form (CNF), which is a conjunction of clauses. In turn, a clause is a disjunction of literals, where a literal is a proposition variable or a negation of a proposition variable. Every formula has an equivalent formula in CNF. For instance, we often deal with an implication such as

$$\begin{aligned} (x_1 \wedge \cdots \wedge x_k) \implies y \end{aligned}$$

which is equivalent to the clause

$$\begin{aligned} \lnot x_1 \vee \cdots \vee \lnot x_k \vee y \,. \end{aligned}$$

When the conversion to CNF is straightforward (which is the case for implications), we only present the original formula.

Some care is required when turning arbitrary formulas into CNF, as the formula can get substantially bigger. In order to avoid very big CNF formulas, it is sometimes beneficial to introduce auxiliary variables, as we will later do.

Cardinality Constraints. It is very common to require that at most one of a set of literals is satisfied, and such a constraint is called a cardinality constraint. Such constraints can be encoded directly in CNF in a variety of ways, we use the following definitions:

$$\begin{aligned}&{{\,\mathrm{\textsf {at-least-1}}\,}}(x_1, \ldots , x_n) {:}{=}(x_1 \vee \cdots \vee x_n) \\&{{\,\mathrm{\textsf {at-most-1}}\,}}(x_1, \ldots , x_n) {:}{=}\bigwedge _{i \ne j} (\lnot x_i \vee \lnot x_j) \\&\,\, {{\,\mathrm{\textsf {exactly-1}}\,}}(x_1, \ldots , x_n) {:}{=}{{\,\mathrm{\textsf {at-least-1}}\,}}(x_1, \ldots , x_n) \wedge {{\,\mathrm{\textsf {at-most-1}}\,}}(x_1, \ldots , x_n) \end{aligned}$$

Non-boolean Variables. Often, we want to express not just boolean values, but a variable x with a bounded domain such as $\{1, \ldots , k\}$. We do this with a one-hot encoding (also called direct encoding or sparse encoding), meaning that we introduce k variables $x_1, \ldots , x_k$, where $x_i$ means that x has value i. This works in conjunction with the constraint ${{\,\mathrm{\textsf {exactly-1}}\,}}(x_1, \ldots , x_k)$.

As a convention, we use subscripts for indices used in a one-hot encoding and superscripts otherwise. For example, when we guess a word of length l from an alphabet I, we introduce the variables $x^i_a$ for $1 \le i \le l$ and $a \in I$.

We will now translate the problem of finding UIO sequences and ADSs into SAT. We will encode these problems directly in CNF.

3.1 State Verification via UIO Sequences

We fix a machine M with state space Q and a state $q_0 \in Q$. Our task is to find a UIO sequence for $q_0$, bounded by a length l.

The encoding of finding a UIO sequence of length l is quite straightforward: We guess the sequence, and determine the outputs of all the states when provided with this sequence, and check that those outputs differ in at least one place with the output of $q_0$.

Encoding. We introduce the variables listed in Table 1². We could, theoretically, encode everything in propositional logic with only the variables $\mathfrak {a}^{q_0, i}_{a}$. However, by introducing the other variables, the resulting CNF formula is much smaller and easier to construct.

Table 1. Variables for the encoding of the UIO sequence for a fixed state $q_0$.

One-Hot Encoded Variables. For all the one-hot encoded variables, we require that exactly one variable is satisfied.

$$\begin{aligned}&\bigwedge _{1 \le i \le l} {{\,\mathrm{\textsf {exactly-1}}\,}}(\{ \mathfrak {a}^{q_0, i}_{a} \mid a \in I \}) \\ \wedge&\bigwedge _{q \in Q} \bigwedge _{0 \le i \le l} {{\,\mathrm{\textsf {exactly-1}}\,}}(\{ \mathfrak {s}^{q, i}_{q'} \mid q' \in Q \}) \\ \wedge&\bigwedge _{q \in Q} \bigwedge _{0 \le i \le l} {{\,\mathrm{\textsf {exactly-1}}\,}}(\{ \mathfrak {o}^{q, i}_{o} \mid o \in O \}) \end{aligned}$$

Successor States and Output. If the state q is in state $q'$ after i symbols, it should output $\lambda (q', a)$ on the current symbol a:

$$\begin{aligned} \bigwedge _{q \in Q} \bigwedge _{1 \le i \le l} \bigwedge _{a \in I} \big ( \mathfrak {s}^{q, i-1}_{q'} \wedge \mathfrak {a}^{q_0, i}_{a} \implies \mathfrak {o}^{q, i}_{\lambda (q', a)} \big ) \end{aligned}$$

Similarly, we encode that the successor state is consistent with the guessed word:

$$\begin{aligned} \bigwedge _{q \in Q} \bigwedge _{1 \le i \le l} \bigwedge _{a \in I} \big ( \mathfrak {s}^{q, i-1}_{q'} \wedge \mathfrak {a}^{q_0, i}_{a} \implies \mathfrak {s}^{q, i}_{\delta (q', a)} \big ) \end{aligned}$$

In the above formulas, when $i=1$, we use a new variable $\mathfrak {s}^{q, 0}_{q'}$ as short-hand notation for

$$ \mathfrak {s}^{q, 0}_{q'} := {\left\{ \begin{array}{ll} \top &{}\text {if }q=q'\\ \bot &{}\text {if }q\ne q'.\\ \end{array}\right. } $$

Differences. So far, we have encoded a word and the according outputs starting from each state. In order to find UIOs, we need that the outputs of $q_0$ are different from the outputs of others states q (at some index i). First we encode what it means for a difference to occur, using the variables $\mathfrak {d}^{q', i}$:

$$\begin{aligned} \bigwedge _{q' \in Q \setminus \{q_0\}} \bigwedge _{1 \le i \le l} \bigwedge _{o \in O} \big ( \mathfrak {d}^{q', i} \wedge \mathfrak {o}^{q_0, i}_{o} \implies \lnot \mathfrak {o}^{q', i}_{o} \big ) \end{aligned}$$

In words this reads: if a difference is claimed (i.e., $\mathfrak {d}^{q, i}$ is guessed to be true), and if $q_0$ outputs o, then $q'$ may not do so. We do not need to encode the converse direction explicitly.

Finally, we require at least one difference for each state:

$$\begin{aligned} \bigwedge _{q' \in Q \setminus \{q_0\}} {{\,\mathrm{\textsf {at-least-1}}\,}}\big (\mathfrak {d}^{q', 1}, \mathfrak {d}^{q', 2}, \ldots , \mathfrak {d}^{q', l} \big ) \end{aligned}$$

Putting it Together. Denote the conjunction of all above clauses by

$$\begin{aligned} {{\,\mathrm{\textsf{UIO}}\,}}(M, l, q_0) \,. \end{aligned}$$

Lemma 3.1

Given a machine M, a length l, and a state $q_0$, the CNF formula ${{\,\mathrm{\textsf{UIO}}\,}}(M, l, q_0)$ is satisfiable if and only if $q_0$ has a UIO sequence of length l.

Improvements. In order to keep the above encoding simple, we have omitted the following improvements from the above presentation. The improvements are explained in more detail in the implementation.

Only Encode Reachable States. As presented, the variables $\mathfrak {s}^{q, i}_{q'}$ are created for all $q' \in Q$. This is unnecessary, and only the states reachable from q in exactly i steps have to be considered. Similarly for the outputs.

Searching Multiple UIOs. In many situations, we may want to find UIO sequences for multiple states. It is then beneficial to re-use most of the constructed formula. This can be achieved with incremental SAT-solving [ES03b].

Extending UIOs to Obtain New UIOs. If a UIO sequence w for state q has been found, then this could possibly lead to UIO sequences for predecessors of q. Namely, if $q'$ is a state with a transition $q' \xrightarrow {a/o} q$ and the input/output pair (a, o) is unique among the predecessors of q, then aw is a UIO sequence for $q'$.

To use this idea, we define the UIO implication graph as follows. The nodes are the states in Q, and there is an edge from q to $q'$ if a UIO sequence for q can be extended (by 1 symbol) to a UIO for $q'$. This graph can be precomputed and many UIOs can be found by traversing this graph. Note, however, that the found UIOs may not be of minimal length.

Incrementing the Length. The presented encoding works with a fixed bound. It is useful to start with a low bound and increment this bound one-by-one. This way, we can find short UIOs for many states, and only need to construct large formulas for the states which have no short UIOs.

3.2 State Identification via Adaptive Distinguishing Sequences

If we want to identify the current state of an FSM, we can construct an ADS for a fixed machine M with states Q in a similar way. We fix a subset $Q_0 \subseteq Q$ of potential initial states and a bound l on the length of the sequence. (The length of an ADS is the depth of the tree.)

The encoding of an ADS is less straightforward than for UIO sequences, because we are not searching for a single word, but for a tree structure. To tackle this problem, we recall a remark by Lee and Yannakakis [LY96, Section IV.A] which relates adaptive distinguishing sequences to sets of sequences:

“[..] we can satisfy the separation property with all sets $Z_i$ being singletons if and only if A has an adaptive distinguishing sequence.”

The sets $Z_i$ contain sequences, and if there exists an ADS, these sets are singletons. So, instead of searching for a tree, we may as well search for one sequence per state (together with additional requirements). We rephrase this result in the following lemma.

Lemma 3.2

The following are in one-to-one correspondence:

• 1. An adaptive distinguishing sequence for $Q_0\subseteq Q$

• 2. A map $f:Q_0\rightarrow I^*$ such that for all $q,q'\in Q_0$ with $q\ne q'$:

  • (a) $f(q)\vdash q\mathbin {\#}q'$ (i.e. f(q) is a $Q_0$-local UIO for q).

  • (b) if wa is a prefix of f(q) and $\llbracket {q} \rrbracket (w) = \llbracket {q'} \rrbracket (w)$, then wa is also a prefix of $f(q')$.

Proof (Sketch)

Given an ADS for $Q_0$, define $f:Q_0\rightarrow I^*$ as the map that sends $q\in Q_0$ to word $v\in I^*$ on the internal nodes leading to q in the ADS. This map satisfies the two properties: (a) For $q'\in Q_0$ with $q\ne q'$, the definition of ADS implies $\llbracket {q} \rrbracket (v)\ne \llbracket {q'} \rrbracket (v)$. (b) If wa is a prefix of v, and $\llbracket {q} \rrbracket (w) = \llbracket {q'} \rrbracket (w)$, then $q'$ must also be in the subtree of the ADS to which w leads and whose node is labelled a.

Conversely, we can recursively build an ADS from such a map $f:Q_0\rightarrow I^*$: if $|Q_0| < 2$ the ADS is trivial. If $Q_0$ has at least two elements there must be some $a\in I$ that is the prefix of all f(q), $q\in Q_0$ by (b). Thus, the root is labelled a and it has a subtree for each element of $\{\llbracket {q} \rrbracket (i)\mid q\in Q_0\}\subseteq O$. The subtree reached via $o\in O$ is recursively constructed for $Q_0' := \{q\in Q_0\mid \llbracket {q} \rrbracket (a) = o\}$ and $f':Q_0'\rightarrow I^*$, $f'(q) = w$ with $aw=f(q)$.    $\square$

Encoding. We introduce the variables listed in Table 2. The encoding is similar to that of UIO sequences. There is one crucial difference: here every state q has an associated word f(q) in the sense of Lemma 3.2. In order to achive that these words describe a tree, these input words f(q), $f(q')$ for different states $q,q'$ must be the same, as long as the two states also produce the same output symbols, as described by the condition in Lemma 3.2.

Table 2. Variables used for the ADS encoding

One-Hot Encoded Variables. We again start by requiring that every one-hot encoded variable has exactly one value enabled:

$$\begin{aligned}&\bigwedge _{q \in Q_0} \bigwedge _{1 \le i \le l} {{\,\mathrm{\textsf {exactly-1}}\,}}(\{ \mathfrak {a}^{q, i}_{a} \mid a \in I \}) \\ \wedge&\bigwedge _{q \in Q_0} \bigwedge _{0 \le i \le l} {{\,\mathrm{\textsf {exactly-1}}\,}}(\{ \mathfrak {s}^{q, i}_{q'} \mid q' \in Q \}) \\ \wedge&\bigwedge _{q \in Q_0} \bigwedge _{0 \le i \le l} {{\,\mathrm{\textsf {exactly-1}}\,}}(\{ \mathfrak {o}^{q, i}_{o} \mid o \in O \}) \end{aligned}$$

Successor States and Outputs. Similarly to the UIO sequences, we require that the guessed successor states and outputs are consistent with the transition and output function:

$$\begin{aligned} \bigwedge _{q \in Q_0} \bigwedge _{1 \le i \le l} \bigwedge _{q' \in Q} \bigwedge _{a \in I} \big ( \mathfrak {s}^{q, i-1}_{q'} \wedge \mathfrak {a}^{q, i}_{a} \implies \mathfrak {s}^{q, i}_{\delta (q', a)} \big ) \wedge \big ( \mathfrak {s}^{q, i-1}_{q'} \wedge \mathfrak {a}^{q, i}_{a} \implies \mathfrak {o}^{q, i}_{\lambda (q', a)} \big ) \end{aligned}$$

Differences. If the solver claims one of the $\mathfrak {d}^{q, q', i}$ to be true, then there must be an actual difference in output:

$$\begin{aligned} \bigwedge _{q \ne q' \in Q_0} \bigwedge _{1 \le i \le l} \bigwedge _{o \in O} \big ( \mathfrak {d}^{q, q', i} \wedge \mathfrak {o}^{q, i}_{o} \implies \lnot \mathfrak {o}^{q', i}_{o} \big ) \end{aligned}$$

And we encode the fact that there is at least one difference for each pairs of states $q, q' \in Q_0$.

$$\begin{aligned} \bigwedge _{q \ne q' \in Q_0} {{\,\mathrm{\textsf {at-least-1}}\,}}\big (\mathfrak {d}^{q, q', 1}, \mathfrak {d}^{q, q', 2}, \ldots , \mathfrak {d}^{q, q', l} \big ) \end{aligned}$$

Shared Prefixes. Finally, we have to assert that the words of two states are the same as long as there is no observed difference in output. First, we encode the “closure” of difference:

$$\begin{aligned} \bigwedge _{q \ne q' \in Q_0} \big ( \overline{\mathfrak {d}}^{q, q', 1} \implies \mathfrak {d}^{q, q', 1} \big ) \wedge \bigwedge _{2 \le i \le l} \big ( \overline{\mathfrak {d}}^{q, q', i} \implies (\mathfrak {d}^{q, q', i} \vee \overline{\mathfrak {d}}^{q, q', i-1}) \big ) \end{aligned}$$

In words this means that $\overline{\mathfrak {d}}^{q, q', j}$ may only hold true if some difference $\mathfrak {d}^{q, q', i}$ holds true earlier (i.e., for some $i \le j$). (We only need to encode one direction of the implication.)

Second, states must use the same inputs as long as $\overline{\mathfrak {d}}^{q, q', i}$ is still false. Note that the first symbols are always equal.

$$\begin{aligned} \bigwedge _{q \ne q' \in Q_0} \bigwedge _{a \in I} \big ( \mathfrak {a}^{q, 1}_{a} \implies \mathfrak {a}^{q', 1}_{a} \big ) \wedge \bigwedge _{2 \le i \le l} \big ( \lnot \overline{\mathfrak {d}}^{q, q', i-1} \wedge \mathfrak {a}^{q, i}_{a} \implies \mathfrak {a}^{q', i}_{a} \big ) \end{aligned}$$

Putting it Together. Denote the conjunction of the above clauses by

$$\begin{aligned} {{\,\mathrm{\textsf{ADS}}\,}}(M, l, Q_0) \,. \end{aligned}$$

Lemma 3.3

Given a machine M, a length $l\in \mathbb {N}$ and a subset $Q_0$, the formula ${{\,\mathrm{\textsf{ADS}}\,}}(M, l, Q_0)$ is satisfiable if and only if there exists an ADS for $Q_0$ of depth l.

Improvements. Some of the same improvements mentioned for the UIO sequence apply here as well. Nevertheless, there is one interesting optimization specifically for the ADS problem.

Encoding Distinct Successors. As long as two states $q, q'\in Q_0$ produce the same outputs for an input word $w\in I^*$, i.e. a path in the ADS, the states must not transition to the same state $\delta (q,w) = \delta (q', w)$, because this would make the states indistinguishable. In the Lee and Yannakakis algorithm, this is called validity of a split or transition. Every ADS has this validity property, so the ADS found by the solver will also have this property. We can encode this property explicitly to help the solver to prune the search. The following clauses state that as long as there is no difference and one state transitions to $q''$, then the other state is not allowed to transition to $q''$.

$$\begin{aligned} \bigwedge _{q \ne q' \in Q_0} \bigwedge _{2 \le i \le l} \bigwedge _{q'' \in Q} \big ( \lnot \overline{\mathfrak {d}}^{q, q', i-1} \wedge \mathfrak {s}^{q, i}_{q''} \implies \lnot \mathfrak {s}^{q', i}_{q''} \big ) \end{aligned}$$

In one instance, the solving time was reduced from 90 min to a mere 2 min. It is not unlikely that other such redundant clauses can be added to improve the runtime.

4 Preliminary Experimental Results

4.1 Implementation

The encoding is implemented in Python and the solving is done through the PySAT package [IMM18]. This package supports several SAT solvers, such as MiniSat [ES03a], Glucose [AS09]. The implementation can be found at

https://github.com/Jaxan/satuio

Throughout the experiments, the SAT solver we use is Glucose3, as this worked well enough on some preliminary tests. PySAT also allows different encodings for the cardinality constraints as explained in Sect. 3. We stick to the default encoding provided by PySAT, which is based on sequential counters [Sin05].

The experiments are run on a 2020 MacBook Air (with an M1 chip) on a single core. We use Python version 3.10.2 and PySAT version 0.1.7.dev16.

4.2 Benchmarks

We use finite state machines from the open automata wiki [NSVK18]. This wiki contains many models from a variety of real-world domains, such as internet communication protocols, smart cards, and embedded systems. We pick the following two sets of models.

Small Models from Protocols. We have picked the models which are learned from the DTLS implementations [FJM+20] and MQTT implementations [TAB17] with fewer than 50 states. Both DTLS and MQTT are internet protocols with many (open source) implementations. These are state machines with fewer than 50 states and have between 6 and 11 inputs.

Big Model from an Embedded System. In order to test the scalability of the encoding, we use the biggest model from the automata wiki, which is the ESM controller [SMVJ15]. This is a state machine in control of printer hardware and has 3410 states and 78 inputs. This was used in a case study for automata learning, and the automata wiki also includes the intermediate hypotheses, which we use as a family of models of increasing size.

4.3 UIO Experiments

For the UIO sequences, we will compare our efficiency to an algorithm by Naik [Nai97]. We only have implemented their base algorithm, which is a non-trivial enumerative search. It searches UIO sequences for all states at the same time, returning sequences as it finds them.

Fig. 3.

Results for the small benchmark, comparing and (timeout = 3 s). The number of UIOs found as fraction of the state space is plotted left and the average length of the found UIOs is plotted right. Note that there may be several models with the same number of states.

Fig. 4.

Results for the big benchmark, comparing and (timeout = 10 min). The number of UIOs found as fraction of the state space is plotted left and the average length of the found UIOs is plotted right.

For each small benchmark, we run both algorithms with a time limit of 3 s. For the bigger benchmarks, we set a time limit of 10 min. We report how many UIOs each algorithm finds within that time. Note that some models have states without UIO sequences, meaning that a search may take a very long time (as the upper bound on the length is exponential). This is the reason it is necessary to set a time bound, even for the small models. Also note that both algorithms search in a non-deterministic way, and so one can be lucky or unlucky in specific instances.

The results are shown in Figs. 3 and 4. In almost all instances, our algorithm was able to find more UIO sequences than the baseline algorithm. However, the baseline algorithm results, on average, in shorter sequences. This may be because it finds fewer, or because it finds the shortest ones first.

We also note that our tool can often find UIO sequences for all states for the small models in a short time (3 s) and that the UIO sequences are generally short. In the big benchmark, the found UIO sequences are still relatively short, but after the first five models, we do not find UIO sequences for all states. This is partly because not every state has a UIO sequence, and partly because it is becoming computationally harder to find them when the number of states increase.

4.4 ADS Experiments

For the ADS we do not have an alternative implementation. So we include some experiments to see how well the SAT solving scales. We only run the algorithm for the big benchmark with 3410 states and 78 inputs. (This machine does not admit an ADS for all states.) For the set of potential initial states, $Q_0$, we pick a random subset of specified size and set the bound (i.e., depth of the tree) to be 7.

Fig. 5.

Finding ADSs for a random subset $Q_0$, of increasing size. The state machine used here is the big benchmark with 3410 states and 78 inputs. The indicate satisfiability and the indicate unsatisfiability.

Figure 5 shows the runtime for finding an ADS of given size in the big benchmark. We observe that for small sets $Q_0$ the solver is able to find adaptive distinguishing sequences in mere seconds. But already for 120 states (which is a small fraction of the total 3410 states), the algorithm needs almost a full minute to find an ADS or to prove unsatisfiability.

We also observe that bigger sets $Q_0$ more often lead to unsatisfiability. For these sets, a bigger bound could provide an ADS, at the cost of more computation time. Interestingly, we see that the solver can prove unsatisfiability a bit faster than satisfiability.

5 Conclusions and Future Work

We have presented and evaluated a reduction of UIO and ADS computation to satisfiability checking of CNF formulae, such that the ADS and UIO can be determined from the satisfying assignment of the formula. The experiments show that the reduction is able to find many UIO sequences and ADSs. For the UIO sequences it is competitive with a non-trivial search algorithm by Naik [Nai97]. Unfortunately, for the larger benchmark, the computation time is still rather large. The experiments also show that, if sequences are found, they are often short, even in larger models.

The reduction may add some overhead compared to direct implementations for searching these sequences, but it is a versatile solution. The high level encoding into logic allows us to change the requirements easily, without having to integrate these changes in a search algorithm. One such variation is an extension to partiality, meaning that the FSM might have an unknown behaviour for certain input letters $a \in I$. This is the setting in the $\textsf{L}\!^\sharp$ learning algorithm [VGRW22], where all observations are gathered in a tree, which happens to be a partial FSM. Here, the partiality expresses that the behaviour for certain inputs is still unknown, as those inputs have not yet been tested. We are optimistic that the our generic encoding techniques can also help finding adaptive distinguishing sequences for partial Mealy machines and other flavours of finite-state machines that arise in the future.