Active Automata Learning as Black-Box Search and Lazy Partition Refinement

Abstract

We present a unifying formalization of active automata learning algorithms in the MAT model, including a new, efficient, and simple technique for the analysis of counterexamples during learning: $L^{\!\lambda }$ is the first active automata learning algorithm that does not add sub-strings of counterexamples to the underlying data structure for observations but instead performs black-box search and partition refinement. We analyze the worst case complexity in terms of membership queries and equivalence queries and evaluate the presented learning algorithm on benchmark instances from the Automata Wiki, comparing its performance against efficient implementations of some learning algorithms from LearnLib.

1 Introduction

Active automata learning has gained a lot of traction as a formal analysis method for black-box models in the previous decade [19]. We provide a detailed account of the first half of the decade in a dedicated survey paper [8]. The second half of the decade saw extensions to new automata models, e.g. to symbolic automata [4] and one-timer automata [20], applications, e.g., in model checking network protocols [5], and algorithmic advances, e.g., an SMT-based learning algorithm [17]. We cannot do the development of the field adequate justice in a couple of paragraphs, and hence will not even attempt to.

What has remained elusive for a long time is a simple and generic formalization of active automata learning and a lower bound result. Frits Vaandrager and coauthors have recently presented active automata learning in the framework of apartness [21], providing a nice formalization of the long established intuition that active automata learning is about distinguishing states.

We continue in this vein and show that it is sufficient to remember which states to distinguish while disregarding the concrete evidence for their apartness: In this paper on the occasion of Frits Vaandrager’s $60^{th}$ birthday, we present a unifying formalization of active automata learning algorithms in the MAT model for finite state acceptors, Moore machines, and Mealy machines and develop a new, efficient, and simple technique for the analysis of counterexamples during learning. The $L^{\!\lambda }$ ($\lambda$ for lazy) algorithm is—to the best of our knowledge—the first active automata learning algorithm that does not add sub-strings of counterexamples to the underlying data structure for observations but instead performs black-box search and lazy partition refinement, based on information extracted from a counterexample.

We establish the correctness of the presented framework in a series of straightforward lemmas. The presented proofs do not rely on concrete underlying data structures, which will hopefully facilitate easy adaptation of the algorithmic ideas to other (richer) classes of models. We analyze the worst case complexity in terms of membership queries and equivalence queries and evaluate the presented learning algorithm on benchmark instances from the Automata Wiki¹, comparing its performance against efficient implementations of some learning algorithms from LearnLib [11]. We still cannot provide a lower bound but we certainly hope that the $L^{\!\lambda }$ is one step on the way to such a bound.

Outline. The remainder of the paper is structured as follows. We present a unifying view on regular languages, finite state acceptors, and Mealy machines in the next section, before recapitulating the MAT learning model and existing learning algorithms in Sect. 3. Our main contribution, the $L^{\!\lambda }$ learning algorithm, is presented in Sect. 4 and demonstrated in Sect. 5. Results of the performance evaluation are discussed in Sect. 6.

2 Regular Languages and Automata

We start with a brief unifying recapitulation of different finite automata models. For some fix finite alphabet $\varSigma$, we usually use a to denote a symbol from that alphabet, and u, v, w for words in $\varSigma ^{*}$. For empty word $\epsilon$, let $\varSigma ^{+} = \varSigma ^{*} \setminus \{ \epsilon \}$. We use symbols like words in concatenation uv (or $u\cdot v$ for emphasis) where $uv=u_1\cdots u_m \cdot v_1 \cdots v_n$ for $u=u_1 \cdots u_m$ and $v=v_1 \cdots v_n$. Finally, we use $u_{[i,j]}$ for $1\le i\le j \le |u|$ as a shorthand for the sub-word $u_i \cdots u_j$ of u.

Definition 1

A Deterministic Finite Automaton (DFA) is a tuple $\langle Q, q_0, \varSigma , \delta \rangle$ where Q is a finite nonempty set of states, $q_0 \in Q$ is the initial state, $\varSigma$ is a finite alphabet, and $\delta : Q \times \varSigma \rightarrow Q$ is the transition function.

We extend $\delta$ to words in the natural way by defining $\delta (q, \epsilon ) =q$ for the empty word $\epsilon$ and $\delta (q, ua) = \delta (\delta (q,u), a)$ for $u\in \varSigma ^{*}$ and $a\in \varSigma$.

We can generally distinguish automata that associate output or acceptance with states (i.e., finite state acceptors and Moore machines) from those that associate output with transitions (i.e., Mealy machines).

Definition 2

A Moore machine is a tuple $\langle Q, q_0, \varSigma , \varOmega , \delta , \lambda \rangle$ where $\langle Q, q_0, \varSigma , \delta \rangle$ is a DFA, $\varOmega$ is a finite set of outputs, and $\lambda : Q \rightarrow \varOmega$ is the state output function.

A Moore machine $M=\langle Q, q_0, \varSigma , \varOmega , \delta , \lambda \rangle$ maps words $w\in \varSigma ^*$ to outputs $o\in \varOmega$ through the semantic function $S^{*}_A:\varSigma ^* \rightarrow \varOmega$, which we define as $S^{*}_M =_{def} \lambda \circ \delta$.

Definition 3

A finite state acceptor (FSA) is a tuple $\langle Q, q_0, \varSigma , \delta , F \rangle$ defining a Moore machine $\langle Q, q_0, \varSigma , \{ 0,1 \}, \delta , \lambda \rangle$ in which $\lambda : Q \rightarrow \{ 0,1 \}$ marks the set of accepting states ($\lambda (q) = 1$ iff $q\in F$).

An FSA $F=\langle Q, q_0, \varSigma , \delta , \lambda \rangle$ accepts a regular language $L_F \subseteq \varSigma ^*$: for $w\in \varSigma ^*$ let $w \in L_F$ iff $S^{*}_F(w) = 1$, i.e., if $\delta (w) \in F$.

Definition 4

A Mealy machine is a tuple $\langle Q, q_0, \varSigma , \varOmega , \delta , \lambda \rangle$ where $\langle Q, q_0, \varSigma , \delta \rangle$ is a DFA, $\varOmega$ is a finite set of outputs, and $\lambda : Q \times \varSigma \rightarrow \varOmega$ is the transition output function.

A Mealy machine $M=\langle Q, q_0, \varSigma , \varOmega , \delta , \lambda \rangle$ maps words $w\in \varSigma ^{+}$ to outputs $o\in \varOmega$ through the semantic function $S^{+}_M:\varSigma ^{+} \rightarrow \varOmega$, which we define as $S^{+}_M(ua) =_{def} \lambda (\delta (u) ,a)$ for $u\in \varSigma ^*$ and $a\in \varSigma$.

Residuals and Congruences. For some DFA $A=\langle Q, q_0, \varSigma , \delta \rangle$ and state $q\in Q$, the q-residual DFA A|q is the automaton $\langle Q, q, \varSigma , \delta \rangle$, in which we make q the initial state. The automaton A|q represents the behavior of A after reaching state q.

The concept of residuals extends to regular languages and semantic functions: For a Moore machine $M=\langle Q, q_0, \varSigma , \{ 0,1 \}, \delta , \lambda \rangle$ and some word $u\in \varSigma ^*$, let $q=\delta (u)$ and M|q with semantic function $S^{*}_{M|q}$. As $S^{*}_{M|q}(w) = S^{*}_{M}(u\cdot w)$ for $w \in \varSigma ^*$, we omit M|q and write $u^{-1}S^{*}_{M}$ for the residual semantic function of $S^{*}_M$ after u. We can then define a congruence relation $\equiv _S$ on the set $\varSigma ^*$ of words: for words $u,v \in \varSigma ^*$ let $u \equiv _Sv$ iff $u^{-1}S^{*}_{M} = v^{-1}S^{*}_{M}$. For regular languages, this congruence is the well-known Nerode-relation [14]. For a Mealy machine M, we can make an analogous construction using its semantic function $S^{+}_M$ and the set of words $\varSigma ^{+}$ [18].

Canonical Automata. Congruence relations are the basis for constructing canonical automata models. A semantic function $S^{*}$ can be represented as a finite automaton if $\equiv _S$ is of finite index. The canonical automaton for any such $S$ over some alphabet $\varSigma$ is the automaton $A_S= \langle Q, q_0, \varSigma , \delta \rangle$ with one state in Q for every class of $\equiv _S$ and $q_0$ the state for $\epsilon$. The transition function is defined using the congruence as $\delta ([u]_S, a) = [ua]_S$ for $u\in \varSigma ^*$, $a\in \varSigma$, where $[u]_S$ denotes the class of u in $\equiv _S$. For a semantic function $S^{*}:\varSigma ^{*}\rightarrow \varOmega$, the canonical Moore machine $M_S$ (or FSA in the case of $\varOmega =\{ 0,1 \}$) is the automaton $\langle Q, q_0, \varSigma , \varOmega , \delta , \lambda \rangle$ with $\langle Q, q_0, \varSigma , \delta \rangle$ as above and $\lambda ([u])=_{def} S^{*}(u)$ for $u\in \varSigma ^*$. For a semantic function $S^{+}:\varSigma ^{*}\rightarrow \varOmega$, the canonical Mealy machine $M_S$ is the automaton $\langle Q, q_0, \varSigma , \varOmega , \delta , \lambda \rangle$ with $\langle Q, q_0, \varSigma , \delta \rangle$ as above and $\lambda ([u], a)=_{def} S^{+}(ua)$ for $u\in \varSigma ^*$ and $a\in \varSigma$.

3 MAT Learning

Active automata learning [2] is concerned with the problem of inferring an automaton model for an unknown semantic function $\mathcal {L}$ over some alphabet $\varSigma$.

Fig. 1.

Active Automata Learning Algorithms. Cells (One Suffix of CE) and (One Prefix of CE) contain more algorithms than shown. For (One Prefix of CE): complexities pertain to Kearns/Vazirani not to cell. We compare number of membership queries (MQ) and number of input symbols (IS).

MAT Model. Active learning is often formulated as a cooperative game between a learner and a teacher. The task of the learner is to learn a model of some unknown semantic function $\mathcal {L}$. The teacher assists the learner by answering two kinds of queries:

• Membership queries ask for the value of $\mathcal {L}$ for a single word $w\in \varSigma ^*$. The teacher answers these queries with $\mathcal {L}(w)$.

• Equivalence queries ask if a candidate function, represented as a finite hypothesis automaton $\mathcal {H}$, is equal to $\mathcal {L}$. If $\mathcal {H}$ is not equal to $\mathcal {L}$, the teacher will provide a counterexample: a word w for which $\mathcal {H}(w) \ne \mathcal {L}(w)$.

The teacher in this model is called a minimally adequate teacher (MAT) and the learning model is hence often referred to as MAT learning.

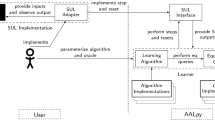
Dana Angluin originally presented the MAT learning model along with a first learning algorithm [2]. With the MAT learning model, she introduced an abstraction that enabled the separation of concerns (constructing stable preliminary models and checking the correctness of these models). This enabled an algorithmic pattern that allowed the formulation and optimization of learning algorithms. The $L^*$ learning algorithm for regular languages and corresponding sequence of lemmas showing the correctness of the algorithms have served as a basis for learning algorithms inferring more complex classes of concepts, e.g., symbolic automata [4] and register automata [1, 9]. The $L^{*}$ algorithms and all other MAT learning algorithms that have been discovered subsequently mimic the construction of canonic automata, using a finite set $Sp\subset \varSigma ^*$ of short prefixes for representing classes of $\equiv _S$ and a set $V\subset \varSigma ^{*}$ (resp. $V\subset \varSigma ^{+}$ for Mealy machines) of suffixes for distinguishing classes of $\equiv _\mathcal {L}$: for all $u,u'\in \varSigma ^{*}$ with $u \not \equiv _\mathcal {L}u'$ exists $v\in \varSigma ^{*}$ (resp. $v\in \varSigma ^{+}$ for Mealy machines) with $\mathcal {L}(uv) \ne \mathcal {L}(u'v)$. Membership queries and equivalence queries are used for finding new short prefixes and distinguishing suffixes.

All known active learning algorithms fall into one of two classes, as is shown in Fig. 1: The first class comprises algorithms that search for new short prefixes and construct new suffixes incrementally through observable inconsistencies between residual semantic functions of prefixes [2, 12], relying on the following observation.

Proposition 1

(New short prefix [2, 12]). Every counterexample w has a prefix $w'$ for which $w' \equiv _\mathcal {H}u$ for some $u\in Sp$ while $w'a \not \equiv _\mathcal {H}ua$ for some $a\in \varSigma$, proven by some $v\in V$ for which $\mathcal {L}(w'av) \ne \mathcal {L}(uav)$.

In algorithms of this class, the word $w'$ is used as a new short prefix and a av will subsequently (while refining the current hypothesis) be constructed as a new suffix, documenting $w' \not \equiv _\mathcal {H}u$.

The second group of algorithms searches for new suffixes and identifies new short prefixes through corresponding observable differences (so-called unclosedness) [7, 15, 16, 18, 21].

Proposition 2

(New suffix [16]). A counterexample w has a suffix v that distinguishes two words $ua \equiv _\mathcal {H}u'$ with $u, u'\in Sp$ and $a\in \varSigma$ through $\mathcal {L}(uav) \ne \mathcal {L}(u'v)$.

The suffix v of the counterexample is used as a new distinguishing suffix and ua will subsequently become a new short prefix.

Algorithms in the first group produce a suffix-closed set of suffixes but are prone to adding unnecessarily long prefixes of counterexamples as short prefixes. Algorithms in the second group produce a prefix-closed set of short prefixes but are generally vulnerable to using unnecessarily long distinguishing suffixes.

Both groups can be further sub-divided into algorithms that add one prefix (or suffix) of a counterexample to the observations and ones that use all prefixes and suffixes. As can be seen in Fig. 1, moving toward the left or to the top in the groups, improves the worst-case number of membership queries and symbol complexity of algorithms. We could further subdivide the left cell in the middle row to distinguish by underlying data structure, which does not have an impact on the worst case but in practice has a significant impact.

The TTT algorithm [10], though belonging to the second group, is the first algorithm that produces a prefix-closed set of short prefixes and a suffix-closed set of suffixes, albeit, at the expense of using long suffixes as preliminary distinguishing suffixes in cases where incremental construction of a new suffix is not immediately possible.

The $L^{\!\lambda }$ algorithm that we present in the next section extends upon ideas from both classes of algorithms: it constructs a prefix-closed set of short prefixes and a suffix-closed set of suffixes without any intermediate artifacts. It is thus the first algorithm that belongs to the top left group in Fig. 1.

4 The $L^{\!\lambda }$ Algorithm

We present the $L^{\!\lambda }$ learning algorithm in the unifying framework of semantic functions and without using a concrete data structure. The idea of an abstract data structure that unifies arguments for implementations based on observation tables and for implementations based on discrimination trees is inspired by partition refinement and was also used by Balcázar et al. [3] as a basis for their unified overview of active automata learning algorithms for FSAs.

Abstract Data Structure. The learner maintains a prefix-closed set $Sp\subset \varSigma ^{*}$ of words (so-called $short prefixes$) to represent equivalence classes of $\equiv _S$. In order to mimic the definition of the transition function in the construction of the canonic automaton, she will maintain a set $U= Sp\cup Sp\cdot \varSigma$ of prefixes that cover transitions between equivalence classes. She also maintains a partitioning of $U$ into a pack of components $\mathcal {B}= \{ B_0, B_1, \ldots \}$, i.e., such that $U=_{def} \bigcup _{B\in \mathcal {B}} (B)$, ensuring that, every time she submits a hypothesis $\mathcal {H}$ to an equivalence query, each component contains exactly one short prefix.

Two prefixes $u,u' \in U$ are equivalent w.r.t. $\mathcal {B}$, denoted by $u \equiv _\mathcal {B}u'$ iff they are in the same component. For every component $B$, the learner maintains a set $V_B$ of suffixes such that prefixes $u,u'\in B$ are not distinguished by $V_B$, i.e., such that $S(uv)=S(u'v)$ for $v\in V_B$. For $u \in B$ and $u \not \equiv _\mathcal {B}u'$, on the other hand, the set $V_\mathcal {B}$ contains at least one suffix v for which $S(uv)\ne S(u'v)$, distinguishing $[u]$ from $[u']$ in $\equiv _S$ and the components of u and $u'$ in $\mathcal {B}$. She initializes the observation pack $\mathcal {B}$ with a single component $B^{\epsilon }=\{ \epsilon \}$ and an empty set of $Sp=\emptyset$. The initial set of suffixes $V_B^{\epsilon }$ is initialized as $\{ \epsilon \}$ when inferring Moore machine models or finite state acceptors and as $\varSigma$ when inferring Mealy machine models—reflecting how residuals are defined for semantic functions $\mathcal {L}^{*}$ and $\mathcal {L}^{+}$.

The learner performs the following two main operations, detailed in Procedure Expand and Procedure Refine, on this data structure.

• Expand. Similar to a search on the states of an automaton, the learner will expand the set $Sp$ of short prefixes with a word u from the set $U\setminus Sp$ of prefixes whenever she can prove that u belongs to an equivalence class of $\equiv _S$ which is not yet represented in $Sp$. The set $U$ is extended accordingly and a new set of suffixes is introduced in such a case.

• Refine. Similar to partition refinement, the learner will refine a class $B$ of $\mathcal {B}$ whenever she finds that two short prefixes $u',u''\in B$ do not belong to the same class of $\equiv _S$. This is the case if for some $a\in \varSigma$ she has already established that $u'a \not \equiv _\mathcal {B}u''a$. The learner can then identify a suffix v that distinguishes $u'a$ from $u''a$ and she uses av to distinguish $u'$ from $u''$.

Conjectures and Equivalence Queries. At certain points during learning, the learner computes a conjecture $\mathcal {H}= \langle Q, q_0, \varSigma , \varOmega , \delta _\mathcal {H}, \lambda _\mathcal {H} \rangle$ where

• Q contains a state $q_{B}$ for every class $B$ of $\mathcal {B}$,

• $q_0 = q_{B^{\epsilon }}$ is the initial state,

• $\delta _\mathcal {H}(q_{B},a) = q_{B'}$ for $Sp\cap B= \{ u \}$, $a\in \varSigma$, and $B' \ni ua$,

• $\varOmega$ is the set of observed outputs, and

in the case of an unknown semantic function $\mathcal {L}^{*}$, the output function is defined as $\lambda _\mathcal {H}(q_{B})= \mathcal {L}^{*}(u)$ for $Sp\cap B= \{ u \}$. In the case of an unknown semantic function $\mathcal {L}^{+}$, the output function is defined as $\lambda _\mathcal {H}(q_{B}, a)= \mathcal {L}^{+}(ua)$ for $Sp\cap B= \{ u \}$ and $a \in \varSigma$.²

Conjectured automata are well-defined as they are only constructed when every component contains exactly one short prefix as we will show below and since $\epsilon$ is an element (resp. $\varSigma$ is a subset) of every set of suffixes. The conjecture $\mathcal {H}$ is then submitted to an equivalence query. In case $\mathcal {H}$ equals $\mathcal {L}$, the teacher acknowledges this and learning ends with the correct model. Otherwise, the learner receives a counterexample w for which $\mathcal {L}(w) \ne \mathcal {H}(w)$.

Analyzing Counterexamples. Counterexamples are used to find prefixes in the set $U$ from equivalence classes of $\equiv _S$ that are not represented in the set of short prefixes yet. As long as the hypothesis is not equivalent to $\mathcal {L}$, the set $U$ must contain a word $ua \in B\setminus Sp$ such that for some suffix $v\in \varSigma ^+$ and a short prefix $u' \in B\cap Sp$ it holds that $\mathcal {L}(ua\cdot v) \ne \mathcal {L}(u' \cdot v)$. The algorithms find such a ua by binary search on the counterexample and adds ua to the set of short prefixes.

For longer v, adding ua to the short prefixes may not immediately lead to an inconsistency with corresponding new suffix, and subsequent refinement. Intuitively, more steps ahead may be required until the difference in behavior becomes detectable with the current sets of distinguishing suffixes. In such cases, multiple new short prefixes can be derived from a counterexample and one of the two words uav and $u'v$ is a guaranteed counterexamples until ua and $u'$ are refined into two different components, as we will show.

The Learning Algorithm. The abstract $L^{\!\lambda }$ algorithm is shown in Algorithm 1. The algorithms starts by initializing the set of prefixes with $\epsilon$, the access sequence of the initial state. The set of suffixes is initialized to $\{ \epsilon \}$ in the case of FSAs or Moore machines, distinguishing states by their associated output, and to the empty set in the case of Mealy machines. The observations are initialized by expanding $\epsilon$ as the basis for an initial conjecture. Then the algorithm proceeds by searching for counterexamples. As long as a counterexample w exists, the algorithm initializes a set of candidate counterexamples with w and iterates the following steps until exhausted. First, a new short prefix and two new candidate counterexamples are generated from one of the candidate counterexamples. Then, consistency of observations is checked. Inconsistent observations for two short prefixes lead to a new suffix and refinement.

While the abstract $L^{\!\lambda }$ algorithm can be presented without assuming details about the underlying data structure, we have to specify special cases for inferring Mealy machine models in two lines of the algorithm: when initializing the set of suffixes, and when checking consistency. Since it is not guaranteed that a symbol $a\in \varSigma$ is in the set of suffixes, we have to add corresponding consistency checks. On the other hand, this (to the best of our knowledge) manifests the first active automata learning algorithm for Mealy machines that can use an observation table as a data structure and does not add all alphabet symbols as suffixes to the table.

Correctness and Complexity. We present technical details and arguments for the correctness of the approach in the following two lemmas where we use $As(w)$ as a shorthand for the set $B\cap Sp$ of short prefixes in $B\in \mathcal {B}$ corresponding to state $q_B = \delta _\mathcal {H}(w)$, reached by w in $\mathcal {H}$.

Fig. 2.

Replacing prefixes of a counterexamples with short prefixes. For semantic function $\mathcal {L}$ and hypothesis $\mathcal {H}$ it is guaranteed that for symbol $w_m$ of the counterexample the conjecture is correct by the definition of the output function $\lambda$.

Lemma 1

A counterexample w of length m has a prefix $w_{1} \ldots w_{i-1}$ with $i < m$ such that for some $u \in As(w_{1} \cdots w_{i})$ and it holds that

• 1. $uw_{i+1}$ is not a short-prefix, i.e., $uw_{i+1} \not \in Sp$, and

• 2. $uw_{i+1}$ should become a short-prefix since $uw_{i+1} ~ \not \equiv _S~ u'$, as witnessed by $\mathcal {L}(uw_{i+1} \cdot w_{i+2}\cdots w_m) \ne \mathcal {L}(u' \cdot w_{i+2} \cdots w_m)$, for all $u' \in As(u \cdot w_{i+1})$.

Proof

The argument is almost identical to the one presented by Rivest and Schapire in their proof of the existence of a distinguishing suffix in a counterexample [16]. The idea of the argument is visualized in Fig. 2. We analyze decompositions $w=w_{[1,i]} \cdot w_{[i+1,m]}$ of the counterexample where $w_{[i,j]}=w_i \cdots w_j$ for $0 \le i \le j \le m$ and with $w_{[0,0]} = \epsilon$. Since w is a counterexample, it must hold that

$$\mathcal {L}(\epsilon \cdot w_{[1,m]}) = \mathcal {L}(w) ~ \ne ~ \mathcal {H}(w) = \mathcal {L}(u' \cdot w_{[m,m]})$$

for all $u' \in As(w_{[1,m-1]})$. As a consequence, there must be some index $1\le i < m$ at which for some $u \in As(w_{[0,i-1]})$ and all $u' \in As(w_{[0,i]})$

$$\mathcal {L}(u \cdot w_{[i,m]}) \ne \mathcal {L}(u' \cdot w_{[i+1,m]}).$$

The word $uw_{i}$ is obviously not a short-prefix but should be a short-prefix: the stated inequality implies $uw_{i} \not \equiv _\mathcal {L}u'$ since $u \cdot w_{[i,m]} = uw_{i} \cdot w_{i+1}\cdots w_m$ and $u' w_{[i+1,m]} = u'\cdot w_{i+1}\cdots w_m$.    $\square$

Lemma 2

Analyzing a counterexample leads to refinement and after the analysis every component has one short prefix.

Proof

We perform a case analysis. A counterexample w leads to new word ua at index i and witnesses $uav, u'v$ for $u' \in As({ua})$. Suffix v proves that ua is not $\equiv _{\mathcal {L}}$-equivalent to any $u'$. We can distinguish two basic cases:

• 1) Immediate Refinement. Short prefix ua leads to immediate refinement. There is one short prefix per component.

• 2) No Immediate Refinement. If no refinement happens, then $\mathcal {H}$ does not change and w is still counterexample. Still, there is progress: w cannot be split again at index i since ua was added to $Sp$. Moreover, we obtain witnesses $uav, u'v$, one of which will be a counterexample until ua and $u'$ are refined into different components.

As a consequence, we have one access sequence per component after processing a counterexample.    $\square$

After the lemmas we have proven, correctness of $L^{\!\lambda }$ is trivial: Every counterexample will lead to at least one new short prefix for which it can be proven that it is not $\equiv _{\mathcal {L}}$-equivalent to any existing short prefix. Hypothesis construction guarantees that $\mathcal {H}(w) = \mathcal {L}(w)$ for $ua \in U$, that $|As(ua)|=1$, and (at least for the final model) that for $u'\in As(ua)$ it holds that $ua \equiv _{\mathcal {L}} u'$—this generalizes to $\varSigma ^{*}$ or $\varSigma ^{+}$ by induction.

As for query complexity and symbol complexity, for a target $\mathcal {L}$ with k input symbols, n states in the canonic automaton for $L$, and counterexamples of length m or shorter $L^{\!\lambda }$ uses O(kn) prefixes and O(n) suffixes in the observations. The algorithm performs a binary search on counterexamples, and during processing of counterexamples, components may have more than one access sequence, requiring O(n) tests per analyzed index of the counterexample in the worst case. This yields the following theorem.

Theorem 1

Algorithm $L^{\!\lambda }$ learns $\mathcal {L}^{*}$ with $O(kn^2 + n^2 log(m))$ membership queries and O(n) equivalence queries.    $\square$

Since words in the observations are of length in O(n), we obtain the following corollary on the symbol complexity of $L^{\!\lambda }$.

Corollary 1

The symbol complexity of Algorithm $L^{\!\lambda }$ is $O(kn^3 + n^2 m \, log(m))$.

   $\square$

Comparing the obtained worst-case complexities with the results displayed in Fig. 1, relying on refinements can increase the queries for analyzing counterexamples in cases when refinement does not occur immediately. While we construct such a case in the next section, we were not able to observe delayed refinement in any of the experiments on models of real systems reported in Sect. 6. On the other hand, the symbol complexity associated with observations used for constructing hypothesis automata does not depend on the length of counterexamples for $L^{\!\lambda }$, which can be observed in experiments.

Fig. 3.

Canonical FSA of target language.

5 Demonstration

For the sake of simplicity, we assume an observation table as a data structure in the presentation of this demonstration example.³ Rows of an observation table are labeled with prefixes from $U$, columns are labeled with suffixes. We use a single big set V that distinguishes all components pairwisely. The cell in row u and column v holds the value of $S(u\cdot v)$. We demonstrate how the learning algorithm infers the canonical FSA for a target language shown in Fig. 3.

The learning algorithm starts by expanding $\epsilon$, adding it to the set of short prefixes (depicted as the upper set of rows in the table) and adds prefixes a and b. As $S(a \cdot \epsilon ) \ne S(\epsilon \cdot \epsilon )$, prefix a becomes a short prefix as well and is expanded by adding prefixes aa and ab. Now the observations become stable. The corresponding observation table resulting hypothesis are shown in Fig. 4, marked as Obs 1 and Hyp 1.

Fig. 4.

Observation table and hypothesis at time of first equivalence query (no. 1), when bbbabbaaa is no longer a counterexample (no. 2), and final observation table (no. 3).

Now, let us assume that the counterexample find the counterexample bbbabbaaa, which is in the target language but not accepted by the hypothesis. The learner discovers that she can split the counterexample as $\epsilon b\cdot bbabbaaa$, which is still a counterexample, but when she replaces prefix $\epsilon b$ by its only access sequence a, the word $a \cdot bbabbaaa$ is not a counterexample. Hence, she expands b and adds words bbbabbaaa and abbabbaaa to the pool of potential counterexamples.

The expansion does not lead to a refinement. Another analysis of the counterexample yields the split $aa \cdot aa$, where short prefix a is one access sequence of the prefix bbbabb of the counterexample. While $aa\cdot aa$ is still a counterexample, none ob the words in $\{ a,b \} \cdot \{ aa \}$ are. Expanding aa (and the set of candidate counterexamples) still does not lead to a refinement. The next analysis results in the split $aaa \cdot a$ (aa now being one of the access sequences for the prefix bbbabba) of the counterexample. Since none of the words in $\{ a,b,aa \} \cdot \{ a \}$ is a counterexample, prefix aaa is expanded (along with the set of candidate counterexamples), finally leading to a sequence of refinements, adding suffixes a, aa, and aaa and generating components for aa, aaa and aaaa. The corresponding observation table and hypothesis are shown as Obs 2 and Hyp 2 in Fig. 4.

At this point, the word bbbabbaaa stops being a counterexample but candidate word abbabbaaa has become a counterexample. Analyzing this new counterexample, the learner splits it into $aab\cdot baaa$, which is a counterexample (abba has access sequence aa). For the next index $aa \cdot baaa$ is not a counterexample. Expanding aab yields refinements, adding suffixes baaa and bbaaa, generating the remaining components and resulting in observation table Obs 3, which is equivalent to the canonical DFA.

We can observe the two particular features discussed in the previous section. First: in a round of learning, all expansions eventually lead to refinements. Second: when analyzing counterexamples, components may contain a growing number of short prefixes until all refinements are performed.

6 Evaluation

We evaluate the performance of the presented algorithm in three series of experiments on the benchmark set from the Automata Wiki [13]. We implemented four versions of the new algorithm in LearnLib, two based on an observation table (for FSAs and for Mealy Machines), and two based on a discrimination tree. We use the Mealy variants, denoted $L^{\!\lambda }_{DT}$ and $L^{\!\lambda }_{Obs}$ in our experiments and compare these variants against Mealy variants of learning algorithms implemented in LearnLib [11], namely TTT [10], Observation Packs [7], ADT [6], Kearns/Vazirani [12], Rivest/Schapire [16], and $L^{*}$ [2].

In the first series of experiments, we evaluate all algorithms on the m106.dot model from the Automata Wiki and vary the length of counterexamples, enabling a basic comparison of algorithms of the different groups shown in Fig. 1. Counterexamples are generated using a heuristic that tries to find counterexamples of a certain length cannot be shortened trivially (i.e., such that prefixes of a counterexample are not counterexamples).

In the second series, we compare the subset of the most efficient learning algorithms (TTT, Observation Packs, and $L^{\!\lambda }_{DT}$) on several benchmarks instances from the Automata Wiki, namely:

$$\begin{aligned}&learnresult\_new\_Rand\_500\_10-15\_MC\_fix.dot&(R500), \\&mosquitto\_\_two\_client\_will\_retain.dot&(Mosq), \\&OpenSSH.dot&(SSH), \\&TCP\_Windows8\_Server.dot&(TCP), \\&m95.dot&(M95). \end{aligned}$$

As a third series of experiments, we reproduce the results presented by Frits and his coauthors in their TACAS 2022 [21] paper and add the new $L^{\!\lambda }_{DT}$ learning algorithm to the analysis. We also replace Rivest and Schapire’s learning algorithm by ObservationPacks to generate data on the effect of using adaptive distinguishing sequences: The ADT algorithm, the first learning algorithm that used adaptive distinguishing sequences [6], is algorithmically closest related to ObservationPacks. This lets us compare the two pairs $L^{\#}$, $L^{\#}_{ADS}$ and ObservationPacks, ADT.

All experiments were computed on a 3, 2 GHz 6-Core Intel Core i7 Mac mini (2018) with 32 GB of RAM. LearnLib is executed in a Java virtual machine with 32 GB heap memory. We report averages and standard deviations from 10 executions of every experiment.

Fig. 5.

Membership queries, input symbols used in membership queries, equivalence queries, and actual length of generated counterexamples for learning m106.dot from the Automata Wiki with different learning algorithms and different counterexample lengths. $L^*$ did not terminate successfully in most cases for a targeted counterexample length of 400.

Figure 5 shows the results from the first series of experiments. We report membership queries, equivalence queries, actual length of generated counterexamples, and number of input symbols used in membership queries.

The data shows that $L^{*}$ and the algorithm by Kearns and Vazirani are impacted by the length of counterexamples with respect to membership queries and input symbols. $L^{*}$ adds all prefixes of counterexamples to the observation table. Kearns and Vazirani perform a linear forward search over a counterexample. Moreover, we can observe that in relation to the other algorithms $L^{\!\lambda }_{DT}$, TTT, and ObservationPacks use virtually equally many membership queries and input symbols (we take a closer look in the second series of experiments) and that on this benchmark instance not adding all alphabet symbols to the set of suffixes leads to a significant reduction in membership queries and symbols for $L^{\!\lambda }_{Obs}$ compared to Rivest and Schapire’s algorithm.

For equivalence queries we observe that in our limited experiments all algorithms are invariant to the length of counterexamples. The $L^{*}$ algorithm that adds all prefixes of counterexamples to the observation table needs the fewest number of equivalence queries, followed by Rivest and Schapire’s algorithm that uses an observation table, too (and hence uses found distinguishing suffixes globally), and the $L^{\!\lambda }_{Obs}$ algorithm, which uses an observation table but initializes the set of suffixes as $\emptyset$, leading to more equivalence queries than the other two algorithms require. Among the algorithms that are based on decision trees, the algorithm of Kearns and Vazirani uses more equivalence than the other algorithms consistently since it is the only algorithm that (in it’s original version) will not analyze counterexamples exhaustively. The fact that ObservationPacks, TTT, and $L^{\!\lambda }_{DT}$ use virtually the same number of equivalence queries seems to indicate that the additional witnesses used by $L^{\!\lambda }_{DT}$ do not provide an advantage on this benchmark instance.

The actual length of counterexamples shows that the target length rather serves as an upper bound over the length of experiment—likely since it is hard for our randomized implementation to find long counterexamples for early (small) hypothesis models.

Fig. 6.

Membership queries and input symbols for $L^{\!\lambda }_{DT}$, TTT, and ObservationPacks on several systems from the Automata Wiki.

Figure 6 shows the results from the second series of experiments. We report membership queries and number of input symbols used in membership queries for $L^{\!\lambda }_{DT}$, TTT, and ObservationPacks on five benchmark instances from the Automata Wiki for counterexamples of (targeted) length 100. ObservationPacks and $L^{\!\lambda }_{DT}$ use fewer membership queries than TTT, which exchanges long suffixes during learning by shorter ones, resulting in additional queries (we observe $10\%$ to $30\%$ overhead compared to $L^{\!\lambda }_{DT}$). ObservationPacks in many cases uses significantly fewer membership queries than the other two algorithms. This can be explained by the fact that in LearnLib, in contrast to our presentation here, Mealy machines semantics is modeled as $\varSigma ^{+} \mapsto \varOmega ^{+}$ making long suffixes more likely to distinguish many prefixes. Considering the number of input symbols, the ObservationPacks algorithm is influenced most by long counterexamples as the algorithm uses suffixes of counterexamples directly. $L^{\!\lambda }_{DT}$ and TTT use a significantly smaller amount of input symbols on most examples, with a visible edge for $L^{\!\lambda }_{DT}$ which (in contrast to TTT) does not rely on intermediate suffixes.

Fig. 7.

Input Symbols and resets for $L^{\!\lambda }_{DT}$, TTT, ObservationPacks, ADT, $L^{\#}$, and $L^{\#}_{ADS}$ on experiments from TACAS 2022 [21].

Figure 7 shows the results from the third series of experiments.⁴ The $L^{\!\lambda }_{DT}$ narrowly but consistently outperforms the other learning algorithms that do not use adaptive distinguishing sequences. As in the second series of experiments, the ObservationPacks performs worst since it uses long suffixes of counterexamples in the observations. The two learning algorithms that use adaptive distinguishing sequences improve significantly upon the corresponding variants without adaptive distinguishing sequences (ADT vs. ObservationPacks and $L^{\#}_{ADS}$ vs. $L^{\#}$), yielding the question if similar improvements could be realized for TTT and $L^{\!\lambda }_{DT}$. A detailed account of the integration of distinguishing sequences is beyond the scope of this paper. We refer readers to [21] instead.

7 Conclusion

We have presented the abstract $L^{\!\lambda }$ learning algorithm along with four implementations (for finite state acceptors and Mealy machines, as well as based on an observation table, and based on a decision tree). The defining characteristic of the $L^{\!\lambda }$ algorithm is that no sub-strings of counterexamples are used in the algorithm’s main data structure, resulting in new worst-case complexities for membership queries and input symbols. We show that, though the obtained worst-case complexities are slightly worse than the lowest existing worst-case complexities, the algorithm seems to outperform existing learning algorithms in practice.