Keywords

1 Introduction

Limitations of silicon based computing, like Moore’s Law and environmental reasons for higher integration of green computing have refueled the interest and effort put in the field of unconventional computing. Namely, specific features of physical, chemical and living systems are exploited to perform some types of computations [1]. The use of material in the liquid state for building computing systems is not a new concept, however, it still sounds alien to most of computer scientists [5]. Despite that, there are plenty prototypes build in laboratories that employ liquids to perform computations. The use of the liquids can be to carry signals, accommodate chemical reactions or actuate mechanical parts as an element of the calculations [5].

A well established medium that is utilized in several laboratory based experiments is the Belousov-Zhabotinsky (BZ) reaction [53, 54]. This class of reactions is characterized by non-equilibrium thermodynamics that are the result of interactions between the activating and inhibiting species within the liquid solution [11]. Because of these dynamics, the reactions are ideal for use as a computational substrate. One of the first experiments to prove the suitability of BZ as a computational substrate was the successful replication of the diode on the medium [7]. Moreover, more complicated architectures were developed, like counters [24] and logic gates [45]. While, these experiments proved the concept that BZ medium can be utilized as the building block of a massively parallel computational medium, some other experiments targeted on computation beyond the use of classical von Neumann architectures. For instance, the use of a light-sensitive variant of the BZ solution to perform image processing [36] and more recently, the use of mechanical parts to build an array of programmable BZ cells that have achieved in memory computation, performing pattern recognition as a chemical auto-encoder [40].

The robustness of these unconventional computing machines is attributed to the fact that they are comprised by several elementary units that can be affected by and interchange signals internally or/and to their environment, in order to acquire, retain and process information [44]. This definition makes them ideal systems to be mimicked by Cellular Automata (CAs). CAs are models of physical systems that incorporate localized interactions, whereas space and time are defined in a discrete form [52]. In order to define a CA, the simulated plane is divided in a grid of cells, where each cell is described by an ensemble of parameters, namely its state, and a local rule that determines how the state of each cell is updated based on the neighboring cells’ states. Usually the rule is the same for all the cells in the grid and they update their states in a synchronous manner [17, 35], although, spatial inhomogeneity in the rule can be inserted and asynchronous updating of the local rule. The process of using CAs to simulate physical systems is in agreement with the present concept of unified space and time, as well as implementing the cutting-edge notion of in-memory computation. This is conceived by representing the memory as the state of the CA cell and the processing unit as the local rule of the grid [8].

There are numerous examples of successful explanation and simulation of real world phenomena by CAs [17, 26]. For instance, they were utilized as robust tools to extensively analyze and effortlessly imitate the dynamical wave propagation in chemical media [18, 27, 37, 38, 51]. These models enabled the analysis of the dispersion and curvature of wave patterns [22], the wave dynamics associated with turbulence [27] and anisotropic media [41]. Nonetheless, CAs are suitable tools to approximate the solution of partial differential equations (PDEs) and it has been established that they can easily represent high complexity in the initialization, constrains and anisotropies of PDEs [43, 47].

This study investigates the transformation of the Oregonator equations used to simulate light-sensitive BZ reactions into a local rule for CAs. In particular, the Oregonator is a very simple model of chemical dynamics of the BZ reaction oscillations [20, 25, 53, 54]. It was developed by Field and Noise [21] at the University of Oregon and consists of five elementary chemical stoichiometries. This network was obtained by reconstructing BZ’s complex chemical reaction mechanism while the reduction is carried out using standard methods of chemical dynamics, in particular the approximation of the step ratio. The successful corresponding CA tool is then utilized to inform the development of light masks that can be used so that the reservoir performs the desired logic functionality. As examples here, the classic AND logic gate and a combinatorial one were demonstrated.

2 Methods for Simulation of Chemical Gates

The dynamics of the BZ reaction that is affected by light intensity can be determined by the Oregonator equation set with two variables [10, 21]. These two variables represent the concentrations of excitation (u) and refractory (v) components in the chemical solution. Namely, the equations are:

$$\begin{aligned} \frac{\partial u}{\partial t}= & {} \frac{1}{\epsilon } (u - u^2 - (f v + \phi )\frac{u-q}{u+q}) + D_u \nabla ^2 u \nonumber \\ \frac{\partial v}{\partial t}= & {} u - v \end{aligned}$$
(1)

where u and v as mentioned previously are the activating/excitation and the inhibiting/refractory ingredients of BZ reaction, respectively. The time scale for the conversion of u to v is expressed as the \(\epsilon \) parameter. The stoichiometric coefficient of the reaction is expressed as f, whereas, the proportional modulation between activation and inhibition of the ingredients is expressed by the parameter q. Also, the development of the inhibiting ingredient can be affected by the \(\phi \) parameter, a fact that is employed to represent the photo-sensitivity of the BZ. Namely, the parameter \(\phi \) can be associated with the illumination intensity of the specific area and, as a result, alter the speed of the inhibiting ingredient development. More specifically, the lower the parameter \(\phi \) is, the lower the speed of the inhibiting ingredient is developed and, as a result, the BZ medium becomes more excitable.

The use of CAs for the numerical approximation of differential equations was studied and confirmed [16, 28, 30, 47, 48] as a powerful technique in order to provide significant speed up. Given the fact that CAs are viable alternatives of solving PDEs, the Oregonator equations were expressed in a CA format to study a photo-sensitive BZ medium and its application in unconventional computations.

This CA model has been developed and tested previously [15, 49, 50], and proved to replicate the results of previous models and actual chemical experiments with appropriate accuracy. It is based on a discrete grid that divides the area of interest in identical cells. These cells are characterized by a specific state each, which are updated in a synchronous fashion based on a local rule. The local rule takes into account the states of the current cell and all the cells in its neighborhood. From the two most renown neighborhoods for CAs in two dimensions, the von Neumann was utilized here. Namely, the center, north, south, east and west adjacent cells form a group that informs the updating of the local rule.

The cells that represent the laboratory area are defined by the following state:

$$\begin{aligned} ST_{i, j}^{t}=\left\{ {AA}_{i, j}, {U}_{i, j}^{t}, {V}_{i, j}^{t}, {\varPhi }_{i, j}\right\} \end{aligned}$$
(2)

where \({AA}_{i, j}\) is a constant parameter that symbolizes the sectors that can be accessed by the chemical waves, i.e. sets the barriers of the computing architecture. Also, parameters \({U}_{i, j}^{t}\) and \({V}_{i, j}^{t}\) symbolize the aggregation of the excitation and refractory ingredients, respectively, of the simulated sector as the (i, j) cell on the time interval t. The final parameter of the state, defined as \(\varPhi \), symbolizes the intensity of light in the appropriate cell (i, j) that affects the speed of development of the refractory ingredient, which is similar to the parameter \(\phi \) used in Eq. (1).

Utilizing the technique of the three point central difference approximation:

$$\begin{aligned} {\frac{{{d}^{2}g}}{{dx}^{2}}} \bigg |_{x}= \frac{g(x+\varDelta x) -2g(x) +g(x-\varDelta x)}{\varDelta x^{2}} \end{aligned}$$
(3)

and the set of the Oregonator equations (Eq. 1), the local rule is obtained as in the following:

$$\begin{aligned} {U}_{i, j}^{t+1}= & {} \frac{\varDelta t}{\epsilon } ({U}_{i, j}^{t} - {{U}_{i, j}^{t}}^2 - (f {V}_{i, j}^{t} + {\varPhi }_{i, j})\frac{{U}_{i, j}^{t}-q}{{U}_{i, j}^{t}+q}) \nonumber \\+ & {} \frac{\varDelta t D_u}{{\varDelta x} ^2}({U}_{i-1, j}^{t} +{U}_{i+1, j}^{t} +{U}_{i, j-1}^{t}+ {U}_{i, j+1}^{t}-4*{U}_{i, j}^{t})) + {U}_{i, j}^{t} \nonumber \\ {V}_{i, j}^{t+1}= & {} \varDelta t [{U}_{i, j}^{t} - {V}_{i, j}^{t}] +{V}_{i, j}^{t} \end{aligned}$$
(4)

To initialize the architecture of the chemical gate and set its functionality, each parameter of the state of the CA cells were set to the following values for \(t=0\). For the area availability parameter, \({AA}_{i, j}=1\) represents a section where the chemical waves can not reach, whereas \({AA}_{i, j}=0\) represents a section that is part that is accessible by the chemicals. To express the inputs of the chemical gates, in these specific areas where logic values are considered HIGH the concentration of the excitation ingredient is set to the maximum values, namely \({U}_{i, j}^{t=0} = 1\). For the rest of the areas, the concentration of both ingredients are set to zero. Finally, the parameter that expresses the controllability by light intensity, \({\varPhi }_{i, j}\) is equal with 0.088 for sections simulating excitable areas, whereas equal with 0.091 for sections simulating sub-excitable areas.

Fig. 1.
figure 1

(a) Chemical medium representation. wave front evolution for (b) excitable and (c) sub-excitable medium.

Full size image

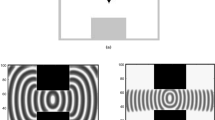
The aforementioned values of excitability control were based on previous works [4, 50] where the simulations provided similar results to actual experiments. The traversing of the chemical waves in the simulated area for a sub-excitable and an excitable medium are compared in Fig. 1. This example is performed on a \(100\times 100\) cells grid, where the available area is illustrated with white color, whereas the unavailable area with grey color. An initial source of the wave fronts is defined as an ensemble of cells (here defined as an area of \(5\times 1\) cells) that were set with an initial parameter \({U}_{i, j}^{t=0} = 1\) and indicated by a black arrow. The difference of the traverse of wave fronts on an excitable and a sub-excitable medium can be realized in Figs. 1(b) and (c), respectively. The advance of the wave fronts in Fig. 1(b) and (c) is depicted in grey scale, whereas the unavailable area in black color. In the case of the excitable medium (Fig. 1(b)) it is apparent that the wave front is inflated around the whole available area after reaching a wider channel. On the other hand, in the case of the sub-excitable medium (Fig. 1(c)), the formation of the waves on the wider channel resembles the formation of the narrow channel where it was initiated. This can imitate the ballistic features of entities used in collision based computing [2, 3]. Thus, a similar approach is utilized to implement logic circuits.

Fig. 2.
figure 2

AND logic gate (a) medium configuration and (b–d) simulation results.

Full size image
Fig. 3.
figure 3

Combinatorial logic gate (a) medium configuration and (b–d) simulation results.

Full size image

3 Results

Having as main goal to simulate the potential computational capabilities of the chemical medium, two gates were demonstrated with the CA-based described earlier Oregonator model, namely a classic AND and one with combinatorial logic gate. For triggering the input signals, the \({U}_{i, j}^{t=0}\) ingredient was set to 1 for a column of \(10\times 1\) cells on the respective input channel. To provide a clear view of the wave front, the presented figures were considered as snapshots of every 500 time-steps of the simulation and not as the results on the final time-step of the simulation.

The AND gate was designed as depicted in Fig. 2(a) configuration, where the inputs, outputs and the light mask are properly illustrated. This is a two-input gate and only when both inputs are HIGH (“1”), the gate output requests to be HIGH, as can be realized in Fig. 2(d) through the merging of the two wave fronts that results to a unified one able to travel forward to the proper output channel. On the contrary, when only one of the proposed inputs is present, the wave front is not able to overcome the sub-excitable medium areas and, as a result, it is slowly decreasing till it dies out (Figs. 2(b) and (c)). Consequently, the light sensitive BZ logic gate acts as a constraint to the wave propagation. The truth table of AND gate is achieved in the experiments as shown in Fig. 2 owing to the topology of light illumination, given that the (“00”) case is again omitted since no wave front would be propagated in the medium.

As next step, the emergence of increased complexity in logic functions, within the same grid of \(200\times 500\) cells used for the basic logic gate, was attempted. The presented gate of Fig. 3(a) is able to perform two logic functions at the same time, utilizing the illustrated light mask. The simulations for every input combinations were successfully performed (Figs. 3(b), (c) and (d)), verifying that the results comply with the theoretical background for the \(F_U=\overline{A}{B}\) and \(F_L=A\overline{B}\) functions of the upper and lower output channel, respectively.

In the aftermath, in case of cascading such gates, the formation of more complex functions can be achieved. For example, a XOR gate can be formed if both outputs of the combinatorial gate are connected to the inputs of an OR gate. Considering that XOR gate can be the “SUM” output of a half-adder, along with an AND gate representing the “CARRY” output, a complete computing system can be achieved.

In the view of the forgoing, there is a novel nano-electronic device suitable for the successful representation of CA models in hardware, and in particular for chemical logic gates, namely memristor device [46] able to perform effectively in-memory computations taking leverage of its inherent characteristics of non-volatility, high density and low power consumption. In more details, memristor is a two terminal nanoelectronic device with resistance controlled by an applied voltage signal across its terminals, and depended on its state’s history [19]. It presents certain similarities with the notion of unified memory and computation architecture in one physical unit like CAs while, at the same time, memristors are successfully implemented in a grid like manner as switching nodes on nano-crossbars. Moreover, memristors have been efficiently coupled with the CA notion resulting to the notion of memristive cellular automata [6, 29, 31,32,33,34, 39, 42]. Towards this path, memristors have been utilized for implementing a coupling between excitable elements [9, 23] that are able to propagate wave fronts. Also, simplified MRLC and MRC circuits have been presented in literature that mimic the behaviour of the chemical waves propagation and interaction in order to perform logic computations [12,13,14]. The resulting unconventional logic gates as well as their nano-electronic representation through the memristors’ oscillating networks in crossbar topologies incorporate basic principles of CA theory, like emergent computation, inherent parallelism, reprogrammability and neighborhood consideration.

Concerning the first approach, an implementation of a reaction-diffusion-based (RD-based) excitable medium is foreseen incorporating memristive devices into the nano-electronic circuit. These RD circuitries are able to perform CA-like computations of RD systems using nano-electronic elements that emulate chemical reactions. Having a rectangular or hexagonal grid of such RC cells coupled with each other through their neighboring connections via appropriate devices can result to a 2-D spatial chemical dissipation and wave propagation to the medium. The diffusion coupling of the RD-based excitable medium is modeled with the memristor nanodevices by changing their switching state when the excitable waves are propagating towards them. Both 1-D and 2-D RD models can be foreseen, showcasing the velocity change of the propagating excitable wave directly linked to the conductance change.

In the case of the latest approach, the wave propagation of a BZ membrane is presented thought the transmission-line-equivalent of appropriate nano-electronic circuits. A memristor is incorporated in these cells in order to expand the local non-linearity of BZ medium. The wave propagation is occurring through an applied voltage stimulus, which is transmitted to the neighboring cells of the proposed grid. In order to simplify the circuit, a corresponding memristor-based with elements unit can be utilized finally able to perform oscillations even with the inductor element is removed. Neighboring cells are connected using a power supply module that can activate their oscillation and effectively perform the wave propagation though the medium. Suitable simulations of chemical logic gates have been already presented in the corresponding literature for the successful evaluation of the discussed approaches enabling chemical computing with nano-electronic circuits.

4 Conclusions

In this work, chemical logic gates simulation was efficiently performed by utilizing the concept of CA in combination with the Oregonator model. In particular, chemical medium light sensitivity was taken into consideration and exploited to demonstrate various logic gates. Simulations for classic logic gate like the AND one, as well as for more complex and combinatorial functions were adequately delivered proving the correct functionality of the proposed model.