Abstract
This paper revisits Key-Policy Attribute-Based Encryption (KP-ABE), allowing delegation of keys, traceability of compromised keys, and key anonymity, as additional properties.
Whereas delegation of rights has been addressed in the seminal paper by Goyal et al. in 2006, introducing KP-ABE, this feature has almost been neglected in all subsequent works in favor of better security levels. However, in multi-device scenarios, this is quite important to allow users to independently authorize their own devices, and thus to delegate their initial rights with possibly more restrictions to their everyday-use devices. But then, one may also require tracing capabilities in case of corrupted devices and anonymity for the users and their devices.
To this aim, we define a new variant of KP-ABE including delegation, with switchable attributes, in both the ciphertexts and the keys, and new indistinguishability properties. We then provide a concrete and efficient instantiation with adaptive security under the sole SXDH assumption in the standard model. We eventually explain how this new primitive can address all our initial goals.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Multi-device scenarios have become prevalent in recent years, as it is now quite usual for people to own multiple phones and computers for personal and professional purposes. Users manage multiple applications across different devices, which brings forth new kinds of requirements. One must be able to granularly control what each of his devices can do for numerous applications, with a cost that is minimal for the user and the overall system. In particular, it is expected that one can control what each of its devices can access, for example restricting the rights to read sensitive documents from a professional laptop or phone during travel. Furthermore, if one suspects a key to be compromised, it should be possible to trace and change it without impacting the service. At the same time, these operations must happen transparently between different devices from the perspective of the user. This means each device should be autonomously configurable with regards to interactions with a central authority or to other devices. Eventually, one may also expect the delegated keys to be unlinkable, for some kind of anonymity for the users, even when devices are explored or corrupted by an adversary.
Usual current authentication means defining a unique account for the user, providing the same access-rights to all the devices, is equivalent to a key-cloning approach, where the user clones his key in every device. In this case, all the devices of the same user are easily linked together, from their keys. This also prevents countermeasures against specific devices.
Key-Policy Attribute-Based Encryption (KP-ABE), in the seminal paper of Goyal et al. [7], offers interesting solutions to these issues. Indeed, a policy is embedded inside each user’s private key, any user can finely-tune the policy for each of his devices when delegating his keys, for any more restrictive policy. Besides, since keys become different in each device, one could expect to trace and revoke keys independently. However, delegation and tracing capabilities might look contradictory with current approaches, as explained below. But we bridge this gap and we also suggest complementing these features with a certain level of unlinkability between the different keys of a single user in order to better protect the privacy of users.
1.1 Related Work
Attribute-Based Encryption (ABE) has first been proposed in the paper by Goyal et al. [7]. In an ABE system, on the one hand, there is a policy \(\mathcal {P}\) and, on the other hand, there are some attributes \((A_i)_i\), and one can decrypt a ciphertext with a key if the policy \(\mathcal {P}\) is satisfied on the attributes \((A_i)_i\). They formally defined two approaches: Key-Policy Attribute-Based Encryption (KP-ABE), where the policy is specified in the decryption key and the attributes are associated to the ciphertext; Ciphertext-Policy Attribute-Based Encryption (CP-ABE), where the policy is specified in the ciphertext and the attributes are associated to the decryption key.
In their paper, they proposed a concrete construction of KP-ABE, for any monotonous access structure defined by a policy expressed as an access-tree with threshold internal gates and leaves associated to attributes. Attributes in the ciphertext are among a large universe \(\mathcal {U}\) (not polynomially bounded). Given an access-tree \(\mathcal {T}\) embedded in a private key, and a set of attributes \(\varGamma \subset \mathcal {U}\) associated to a ciphertext, one can decrypt if and only if \(\varGamma \) satisfies \(\mathcal {T}\). Furthermore, they laid down the bases for delegation of users’ private keys: one can delegate a new key, associated with a more restrictive access-tree.
This first paper on KP-ABE allows fine-grained access-control for multiple devices, dealing with delegation of keys for more restrictive policies. However, their approach for delegation of keys is conflictual with traceability. Indeed, on the one hand, for delegation to work properly, users must be given enough information in the public key to be able to produce valid delegated keys. On the other hand, for the tracing process to be effective in a black-box way, attackers must not be able to detect it. From our knowledge, this natural tension between the two features is in all the existing literature.
Predicate Encryption/Inner-Product Encryption (IPE) were used by Okamoto and Takashima [13,14,15], together with LSSS: the receiver can read the message if a predicate is satisfied on some information in the decryption key and in the ciphertext. Inner-product encryption (where the predicate checks whether the vectors embedded in the key and in the ciphertext are orthogonal) is the major tool. Their technique of Dual Pairing Vector Space (DPVS) provided two major advantages in KP-ABE applications: whereas previous constructions were only secure against selective attacks (the attributes in the challenge ciphertext were known before the publication of the keys), this technique allowed full security (a.k.a. adaptive security, where the attributes in the challenge ciphertext are chosen at the challenge-query time). In addition, it allows the notion of attribute-hiding (from [8]) where no information leaks about the attributes associated to the ciphertext, except for the fact that they are accepted or not by the policies in the keys. It gets closer to our goals, as tracing might become undetectable. However, it does not seem any longer compatible with delegation, as the security proofs require all the key generation material to remain a secret information for the key issuer only.
As follow-up works, Chen et al. [3, 4] designed multiple systems for IPE, with adaptive security, and explored full attribute-hiding with weaker assumptions and shorter ciphertexts and secret keys than in the previous work of Okamoto-Takashima. However, it does not fit our expectations on delegation, for the same reasons. On the other hand, Attrapadung also proposed new ABE schemes based on Pair Encoding Systems, which allow for all possible predicates and large universes [1], but this deals neither with delegation nor with any kind of attribute-hiding, as we would need.
1.2 Contributions
Since the approach of [14] is close to our goal, with attribute-hiding that seems promising for traceability, we extend the original construction to make it compatible with delegation. We propose and prove, in the full version [6], a simple variant that handles delegation with adaptive security under the SXDH assumption. Then, we target delegatable KP-ABE with some additional attribute-hiding property in the ciphertext to allow undetectable tracing.
To this aim, we first detail one of the main limitation we have to overcome in order to get delegation and traceability: with the original approach of [7], attributes associated to the ciphertext are explicitly stated as elements in the ciphertext. Removing some attributes can thus allow to single out specific private keys, but this is a public process, and thus incompatible with any tracing procedure, that would then be detectable by the adversary. To prevent that, our first contribution is the new primitive: Switchable-Attribute Key-Policy Attribute-Based Encryption (SA-KP-ABE), where one can invalidate some attributes in the ciphertext, without removing them. More precisely, we will bring new properties to the attributes in ciphertexts (for undetectable tracing) but also symmetrically to the leaves in keys (for anonymity).
In a \(\textsf {SA}\hbox {-}\textsf {KP}\hbox {-}\textsf {ABE} \) scheme, attributes in a ciphertext and leaves in an access-tree \(\mathcal {T}\) defining the policy in a key can be switched in two different states: Attributes can be set to valid or invalid in a ciphertext at encryption time, using a secret encryption key. We then denote
 , the set of attributes for a ciphertext, as the disjoint union of valid and invalid attributes; Leaves can be set to passive or active in the access-tree in a key at key generation time, using the master secret key. We also denote
, the set of attributes for a ciphertext, as the disjoint union of valid and invalid attributes; Leaves can be set to passive or active in the access-tree in a key at key generation time, using the master secret key. We also denote
 , the set of leaves, as the disjoint union of passive and active leaves. A set of valid/invalid attributes
, the set of leaves, as the disjoint union of passive and active leaves. A set of valid/invalid attributes
 is accepted by an access-tree \(\mathcal {T}\) with passive/active leaves
is accepted by an access-tree \(\mathcal {T}\) with passive/active leaves
 , if the tree \(\mathcal {T}\) is accepting when all the leaves in \(\mathcal {L}\) associated to an attribute in \(\varGamma \) are set to True, except if the leaf is active (in \(\mathcal {L}_a\)) and the associated attribute invalid (in \(\varGamma _i\)). As already presented above, passive/active leaves in \(\mathcal {L}\) are decided during the Key Generation procedure by the authority, using the master secret key. Then the keys are given to the users. During the Encryption procedure, a ciphertext is generated for attributes in \(\varGamma \), but one might specify some attributes to be invalid by using a secret tracing key, which virtually and secretly switches some active leaves to False. Passive leaves are not impacted by invalid attributes.
, if the tree \(\mathcal {T}\) is accepting when all the leaves in \(\mathcal {L}\) associated to an attribute in \(\varGamma \) are set to True, except if the leaf is active (in \(\mathcal {L}_a\)) and the associated attribute invalid (in \(\varGamma _i\)). As already presented above, passive/active leaves in \(\mathcal {L}\) are decided during the Key Generation procedure by the authority, using the master secret key. Then the keys are given to the users. During the Encryption procedure, a ciphertext is generated for attributes in \(\varGamma \), but one might specify some attributes to be invalid by using a secret tracing key, which virtually and secretly switches some active leaves to False. Passive leaves are not impacted by invalid attributes.
A second contribution is a concrete and efficient instantiation of SA-KP-ABE, with security proofs under the SXDH assumption. We eventually explain how one can deal with delegatable and traceable KP-ABE from such a primitive. As shown on Fig. 1, our scheme is the first one that can combine both delegation and traceability of keys for KP-ABE. Computational assumptions are recalled in the next section and in the full version [6].
Our first simple construction (in the full version [6]) following the initial proof from [14], only allows a polynomial-size universe for the attributes involved in the policy, encoded as a Boolean access-tree. This is due to a limited theorem with static attributes in the change of basis in the DPVS framework (see the next section). The latter construction will allow an unbounded universe for the attributes, with an adaptive variant in the change of basis (see Theorem 3). This result is of independent interest.
Discussions. Our setting bears common characteristics with recent \(\textsf {KP}\hbox {-}\textsf {ABE} \) approaches, but with major differences. First, Waters [16] introduced the Dual System Encryption (DSE) technique, to improve the security level of \(\textsf {KP}\hbox {-}\textsf {ABE} \), from selective security in [7] to adaptive security. In DSE, keys and ciphertexts can be set semi-functional, which is in the same vein as our active leaves in keys and invalid attributes in ciphertexts. However, DSE solely uses semi-functional keys and ciphertexts during the simulation, in the security proof, while our construction exploits them in the real-life construction. The security proof thus needs another layer of tricks.
Second, the attribute-hiding notions are strong properties that have been well studied in different IPE works. However, one does not need to achieve such a strong result for tracing: Our (Distinct) Attribute-Indistinguishability is properly tailored for KP-ABE and tracing.
Finally, we detail the advantage of our solution over a generic KEM approach that would combine a Delegatable KP-ABE and a black-box traitor-tracing scheme. This generic solution works if one is not looking for optimal bounds on collusion-resistance during tracing: The main issue with such a use of two independent schemes is that for each user, the KP-ABE key and the traitor-tracing key are not linked. As a consequence, the encryptions of the ABE part and the tracing part are done independently. The colluding users can all try to defeat the traitor tracing without restriction: the collusion-resistance for tracing in the global scheme will exactly be the collusion-resistance of the traitor tracing scheme. On the other hand, our construction will leverage the collusion-resistance of KP-ABE to improve the collusion-resistance of tracing: only players non-revoked by the KP-ABE part can try to defeat the traitor tracing part. Hence, during tracing, one can revoke arbitrary users thanks to the policy/attributes part. This allows to lower the number of active traitors, possibly keeping them below the collusion-resistance of the traitor tracing scheme, so that tracing remains effective.
2 Preliminaries
We will make use of a pairing-friendly setting \(\mathcal {G}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_t,e,G_1,G_2,q)\), with a bilinear map e from \(\mathbb {G}_1 \times \mathbb {G}_2\) into \(\mathbb {G}_t\), and \(G_1\) (respectively \(G_2\)) is a generator of \(\mathbb {G}_1\) (respectively \(\mathbb {G}_2\)). We will use additive notation for \(\mathbb {G}_1\) and \(\mathbb {G}_2\), and multiplicative notation in \(\mathbb {G}_t\).
Definition 1
(Decisional Diffie-Hellman Assumption). The DDH assumption in \(\mathbb {G}\), of prime order q with generator G, states that no algorithm can efficiently distinguish the two distributions
And we will denote by \(\mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}}(T)\) the best advantage an algorithm can get in distinguishing the two distributions within time bounded by T. Eventually, we will make the following more general Symmetric eXternal Diffie-Hellman (SXDH) Assumption which makes the DDH assumptions in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\). Then, we define \(\mathsf {Adv}_\mathcal {G}^\mathsf {sxdh}(T) = \max \{\mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_1}(T), \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_2}(T)\}\).
2.1 Dual Pairing Vector Spaces
We review the main points on Dual Pairing Vector Spaces (DPVS) to help following the intuition provided in this paper. Though not necessary for the comprehension of the paper, the full details are provided in the full version [6]. DPVS have been used for schemes with adaptive security [9, 12, 13, 15] in the same vein as Dual System Encryption (DSE) [16], in prime-order groups under the DLIN assumption. In [10], and some subsequence works, DSE was defined using pairings on composite-order elliptic curves. Then, prime-order groups have been used, for efficiency reasons, first with the DLIN assumption and then with the SXDH assumption [5]. In all theses situations, one exploited indistinguishability of sub-groups or sub-spaces. While we could have used any of them, the latter prime-order groups with the SXDH assumption lead to much more compact and efficient constructions.
In this paper, we thus use the SXDH assumption in a pairing-friendly setting \(\mathcal {G}\), with the additional law between elements \({\mathbf {X}}\in \mathbb {G}_1^n\) and \({\mathbf {Y}}\in \mathbb {G}_2^n\): \({\mathbf {X}}\times {\mathbf {Y}}{\mathop {=}\limits ^{\textsf {\tiny def}}}\prod _i e({\mathbf {X}}_i,{\mathbf {Y}}_i)\). If \({\mathbf {X}}= (X_i)_i = {\vec {x}}\cdot G_1\in \mathbb {G}_1^n\) and \({\mathbf {Y}}= (Y_i)_i = {\vec {y}}\cdot G_2\in \mathbb {G}_2^n\): \(({\vec {x}}\cdot G_1) \times ({\vec {y}}\cdot G_2) = {\mathbf {X}}\times {\mathbf {Y}}= {\prod }_i e(X_i,Y_i) = g_t^{\langle {\vec {x}},{\vec {y}} \rangle }\), where \(g_t = e(G_1,G_2)\) and \(\langle {\vec {x}},{\vec {y}} \rangle \) is the inner product between vectors \({\vec {x}}\) and \({\vec {y}}\).
From any basis \(\mathcal {B}= ({\vec {b}}_i)_i\) of \(\mathbb {Z}_q^n\), we can define the basis \(\mathbb {B}= ({\mathbf {b}}_i)_i\) of \(\mathbb {G}_1^n\), where \({\mathbf {b}}_i = {\vec {b}}_i \cdot G_1\). Such a basis \(\mathcal {B}\) is equivalent to a random invertible matrix \(B{\mathop {\leftarrow }\limits ^{{}_\$}}\text{ GL}_n(\mathbb {Z}_q)\), the matrix with \({\vec {b}}_i\) as its i-th row. If we additionally use \(\mathbb {B}^* = ({\mathbf {b}}^*_i)_i\), the basis of \(\mathbb {G}_2^n\) associated to the matrix \(B' = (B^{-1})^\top \), as \(B \cdot {B'}^\top = I_n\), \({\mathbf {b}}_i \times {\mathbf {b}}^*_j = ({\vec {b}}_i \cdot G_1) \times ({\vec {b}}'_j \cdot G_2) = g_t^{\langle {\vec {b}}_i, {\vec {b}}'_j \rangle } = g_t^{\delta _{i,j}}\), where \(\delta _{i,j} = 1\) if \(i=j\) and \(\delta _{i,j} = 0\) otherwise, for \(i,j\in \{1,\ldots ,n\}\): \(\mathbb {B}\) and \(\mathbb {B}^*\) are called Dual Orthogonal Bases. A pairing-friendly setting \(\mathcal {G}\) with such dual orthogonal bases \(\mathbb {B}\) and \(\mathbb {B}^*\) of size n is called a Dual Pairing Vector Space.
2.2 Change of Basis
Let us consider the basis \(\mathbb {U}= ({\mathbf {u}}_i)_i\) of \(\mathbb {G}^n\) associated to a random matrix \(U\in \text{ GL}_n(\mathbb {Z}_q)\), and the basis \(\mathbb {B}= ({\mathbf {b}}_i)_i\) of \(\mathbb {G}^n\) associated to the product matrix BU, for any \(B\in \text{ GL}_n(\mathbb {Z}_q)\). For a vector \({\vec {x}}\in \mathbb {Z}_q^n\), we denote \(({\vec {x}})_\mathbb {B}= {\sum }_i x_i \cdot {\mathbf {b}}_i\). Then, \(({\vec {x}})_\mathbb {B}= ({\vec {y}})_\mathbb {U}\) where \({\vec {y}}= {\vec {x}}\cdot B\). Hence, \(({\vec {x}})_\mathbb {B}= ({\vec {x}}\cdot B)_\mathbb {U}\) and \(({\vec {x}}\cdot B^{-1})_\mathbb {B}= ({\vec {x}})_\mathbb {U}\) where we denote \(\mathbb {B}{\mathop {=}\limits ^{\textsf {\tiny def}}}B \cdot \mathbb {U}\). For any invertible matrix B, if \(\mathbb {U}\) is a random basis, then \(\mathbb {B}= B\cdot \mathbb {U}\) is also a random basis. Furthermore, if we consider the random dual orthogonal bases \(\mathbb {U}= ({\mathbf {u}}_i)_i\) and \(\mathbb {U}^* = ({\mathbf {u}}^*_i)_i\) of \(\mathbb {G}_1^n\) and \(\mathbb {G}_2^n\) respectively associated to a matrix U (which means that \(\mathbb {U}\) is associated to the matrix U and \(\mathbb {U}^*\) is associated to the matrix \(U' = (U^{-1})^\top \)): the bases \(\mathbb {B}= B\cdot \mathbb {U}\) and \(\mathbb {B}^* = B' \cdot \mathbb {U}^*\), where \(B' = (B^{-1})^\top \), are also random dual orthogonal bases:
All the security proofs will exploit changes of bases, from one game to another game, with two kinds of changes: formal or computational.
Formal Change of Basis, where we start from two dual orthogonal bases \(\mathbb {U}\) and \(\mathbb {U}^*\) of dimension 2, and set
then,
In practice, this change of basis makes \({\mathbf {b}}_1 = {\mathbf {u}}_1+{\mathbf {u}}_2\), \({\mathbf {b}}_2 = {\mathbf {u}}_2\), \({\mathbf {b}}^*_1 = {\mathbf {u}}^*_1\), \({\mathbf {b}}^*_2 = -{\mathbf {u}}^*_1 + {\mathbf {u}}^*_2\). If \({\mathbf {u}}_1/{\mathbf {b}}_1\) and \({\mathbf {u}}^*_2/{\mathbf {b}}^*_2\) are kept private, the adversary cannot know whether we are using \((\mathbb {U},\mathbb {U}^*)\) or \((\mathbb {B},\mathbb {B}^*)\). This will be used to duplicate some component, from a game to another game, as shown in the above Example (2).
Computational Change of Basis, where we define vectors in a dual orthogonal basis \((\mathbb {U},\mathbb {U}^*)\) of dimension 2. From a Diffie-Hellman challenge \((a\cdot G_1, b\cdot G_1, c\cdot G_1)\), where \(c = ab + \tau \bmod q\) with either \(\tau = 0\) or \(\tau {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}^*_q\), one can set
then, in basis \((\mathbb {B},\mathbb {B}^*)\), we implicitly define
where \(\tau \) can be either 0 or random, according to the Diffie-Hellman challenge. And the two situations are indistinguishable. We should however note that in this case, \({\mathbf {b}}^*_2\) cannot be computed, as \(a\cdot G_2\) is not known. This will not be a problem if this element is not provided to the adversary.
Partial Change of Basis: in the constructions, bases will be of higher dimension, but we will often only change a few basis vectors. We will then specify the vectors as indices to the change of basis matrix: in a space of dimension n,
means that only the two first coordinates are impacted, and thus \({\mathbf {b}}_1,{\mathbf {b}}_2\) and \({\mathbf {b}}_1^*,{\mathbf {b}}_2^*\). We complete the matrices B and \(B'\) with the identity matrix: \({\mathbf {b}}_i = {\mathbf {u}}_i\) and \({\mathbf {b}}^*_i = {\mathbf {u}}^*_i\), for \(i\ge 3\).
2.3 Particular Changes
The security proofs will rely on specific indistinguishable modifications that we detail here. We will demonstrate the first of them to give the intuition of the methodology to the reader. A full demonstration for the other modifications can be found in the full version [6]. These results hold under the DDH assumption in \(\mathbb {G}_1\), (but it can also be applied in \(\mathbb {G}_2\)), on random dual orthogonal bases \(\mathbb {B}\) and \(\mathbb {B}^*\).
With the above change of basis provided in Eq. (4), we can compute \(\mathbb {B}= ({\mathbf {b}}_i)_i\), as we know \(a\cdot G_1\) and all the scalars in U:
Hence, to compute \({\mathbf {b}}_i\), one needs all the scalars in U, but only the group elements \(B_{i,j}\cdot G_1\), and so \(G_1\) and \(a\cdot G_1\). This is the same for \(\mathbb {B}^*\), except for the vector \({\mathbf {b}}^*_2\) as \(a \cdot G_2\) is missing. One can thus publish \(\mathbb {B}\) and \(\mathbb {B}^*\backslash \{{\mathbf {b}}^*_2\}\).
Indistinguishability of Sub-spaces (3). As already remarked, for such a fixed matrix B, if \(\mathbb {U}\) is random, so is \(\mathbb {B}\) too, and \(({\vec {x}})_\mathbb {B}= ({\vec {x}}\cdot B)_\mathbb {U}\), so \(({\vec {x}})_\mathbb {U}= ({\vec {x}}\cdot B^{-1})_\mathbb {B}\). Note that \(B^{-1} = {B'}^\top \). So, \((b,c,0, \ldots , 0)_\mathbb {U}= (b,c-ab,0,\ldots ,0)_\mathbb {B}\), then
where \(\tau \) can be either 0 or random. Note that whereas we cannot compute \({\mathbf {b}}^*_2\), this does not exclude this second component in the computed vectors, as we can use \((y_1, \ldots , y_n)_{\mathbb {U}^*} = (y_1 + a y_2, y_2, \ldots , y_n)_{\mathbb {B}^*}\).
Theorem 2
Under the DDH Assumption in \(\mathbb {G}_1\), for random dual orthogonal bases \(\mathbb {B}\) and \(\mathbb {B}^*\), once having seen \(\mathbb {B}\) and \(\mathbb {B}^*\backslash \{{\mathbf {b}}^*_2\}\), and any vector \((y_1, y_2, \ldots , y_n)_{\mathbb {B}^*}\), for any \(y_2,\ldots ,y_n\in \mathbb {Z}_q\), but unknown random \(y_1{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), one cannot distinguish \((x_1,x'_2,x_3, \ldots , x_n)_\mathbb {B}\) and \((x_1,x_2,x_3, \ldots , x_n)_\mathbb {B}\), for any \(x_2,\ldots ,x_n\in \mathbb {Z}_q\), but unknown random \(x_1,x'_2{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\).
Some scalar coordinates can be chosen (and thus definitely known) by the adversary, whereas some other must be random. Eventually the adversary only sees the vectors in \(\mathbb {G}_1^n\) and \(\mathbb {G}_2^n\). We now directly state two other properties for which the demonstration (which works similarly as the SubSpace-Ind one) can be found in the full version [6].
-
Swap-Ind Property, on \((\mathbb {B},\mathbb {B}^*)_{1,2,3}\): from the view of \(\mathbb {B}\) and \(\mathbb {B}^*\backslash \{{\mathbf {b}}^*_1,{\mathbf {b}}^*_2\}\), and the vector \((y_1, y_1, y_3, \ldots , y_n)_{\mathbb {B}^*}\), for any \(y_1,y_3,\ldots ,y_n\in \mathbb {Z}_q\), one cannot distinguish the vectors \((x_1,0, x_3,x_4, \ldots , x_n)_\mathbb {B}\) and \((0,x_1,x_3,x_4, \ldots , x_n)_\mathbb {B}\), for any \(x_1,x_4,\ldots ,x_n\in \mathbb {Z}_q\), but unknown random \(x_3{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\).
-
(Static) Index-Ind Property, on \((\mathbb {B},\mathbb {B}^*)_{1,2,3}\): from the view of \(\mathbb {B}\) and \(\mathbb {B}^*\backslash \{{\mathbf {b}}^*_3\}\), for fixed \(t\ne p\in \mathbb {Z}_q\), and the \((\pi \cdot (t, -1), y_3, \ldots , y_n)_{\mathbb {B}^*}\), for any \(y_3,\ldots ,y_n\in \mathbb {Z}_q\), but unknown random \(\pi {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), one cannot distinguish \((\sigma \cdot (1,p), x_3,x_4, \ldots , x_n)_\mathbb {B}\) and \((\sigma \cdot (1,p), x'_3,x_4, \ldots , x_n)_\mathbb {B}\), for any \(x'_3,x_3,x_4,\ldots ,x_n\in \mathbb {Z}_q\), but unknown random \(\sigma {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\).
We stress that, in this static version, t and p must be fixed, and known before the simulation starts in the security analysis, as they will appear in the matrix B. In the Okamoto-Takashima’s constructions [13, 15], such values t and p were for bounded names of attributes. In the following, we want to consider unbounded attributes, we thus conclude this section with an adaptive version, where t and p do not need to be known in advance, from a large universe:
Theorem 3
(Adaptive Index-Ind Property). Under the DDH Assumption in \(\mathbb {G}_1\), for random dual orthogonal bases \(\mathbb {B}\) and \(\mathbb {B}^*\), once having seen \(\mathbb {B}\) and \(\mathbb {B}^*\backslash \{{\mathbf {b}}^*_3\}\), and \((\pi \cdot (t, -1), y_3, 0,0, y_6,\ldots ,y_n)_{\mathbb {B}^*}\), for any \(t, y_3, y_6,\ldots ,y_n\in \mathbb {Z}_q\), but unknown random \(\pi {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), one cannot distinguish \((\sigma \cdot (1,p), x_3, 0,0, x_6,\ldots ,x_n)_\mathbb {B}\) and \((\sigma \cdot (1,p), x'_3,0,0, x_6,\ldots ,x_n)_\mathbb {B}\), for any \(x_3,x'_3,x_6,\ldots ,x_n\in \mathbb {Z}_q\), and \(p\ne t\), but unknown random \(\sigma {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), with an advantage better than \(8\times \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_1}(T) + 4 \times \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_2}(T)\), where T is the running time of the adversary.
Proof
For the sake of simplicity, we will prove indistinguishability between \((\sigma \cdot (1,p), 0, 0,0)_\mathbb {B}\) and \((\sigma \cdot (1,p), x_3,0,0)_\mathbb {B}\), in dimension 5 only, instead of n. Additional components could be chosen by the adversary. Applied twice, we obtain the above theorem. The proof follows a sequence of games.
-
\(\mathbf {Game}\, \mathbf {G_0}{} \mathbf{:}\) The adversary can choose \(p\ne t\) and \(x_3,y_3\) in \(\mathbb {Z}_q\), but \(\pi ,\sigma {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\) are unknown to it:
$$\begin{aligned} {\mathbf {k}}^* = (\pi (t,-1), y_3, 0, 0)_{\mathbb {B}^*}&\qquad \qquad \quad {\mathbf {c}}_0 = (\sigma (1,p), 0, 0, 0)_{\mathbb {B}} \\&\qquad \qquad \quad {\mathbf {c}}_1 = (\sigma (1,p), x_3, 0,0)_{\mathbb {B}} \end{aligned}$$Vectors \(({\mathbf {b}}_1,{\mathbf {b}}_2,{\mathbf {b}}_3,{\mathbf {b}}^*_1,{\mathbf {b}}^*_2)\) and \(({\mathbf {c}}_b,{\mathbf {k}}^*)\) are provided to the adversary that must decide on b: \(\mathsf {Adv}_{\mathbf {0}}\) is its advantage in correctly guessing b. Only \({\mathbf {k}}^*\) and \({\mathbf {c}}_0\) will be modified in the following games, so that eventually \({\mathbf {c}}_0 = {\mathbf {c}}_1\) in the last game, which leads to perfect indistinguishability.
-
\(\mathbf {Game}\, \mathbf {G_1}{} \mathbf{:}\) We replicate the first sub-vector \((t,-1)\), with \(\rho {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), in the hidden components: \({\mathbf {k}}^* = (\pi (t,-1), y_3, \rho (t,-1))_{\mathbb {B}^*}\). To show the indistinguishability, one applies the SubSpace-Ind property on \((\mathbb {B}^*,\mathbb {B})_{1,2,4,5}\). Indeed, we can consider a triple \((a\cdot G_2, b\cdot G_2, c\cdot G_2)\), where \(c=ab+\tau \bmod q\) with either \(\tau = 0\) or random, which are indistinguishable under the DDH assumption in \(\mathbb {G}_2\). Let us assume we start from random dual orthogonal bases \((\mathbb {V},\mathbb {V}^*)\). We define
$$\begin{aligned} B'&= \left( \begin{array}{cccc} 1 &{} 0 &{} a &{} 0 \\ 0 &{} 1 &{} 0 &{} a \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) _{1,2,4,5}&B&= \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0 \\ -a &{} 0 &{} 1 &{} 0 \\ 0 &{} -a &{} 0 &{} 1 \end{array} \right) _{1,2,4,5}&\mathbb {B}^*&= B' \cdot \mathbb {V}^*&\mathbb {B}&= B \cdot \mathbb {V}\end{aligned}$$The vectors \({\mathbf {b}}_4, {\mathbf {b}}_5\) can not be computed, but they are hidden from the adversary’s view, and are not used in any vector. We compute the new vectors:
$$\begin{aligned} {\mathbf {k}}^*&= (b (t,-1), y_3, c (t,-1))_{\mathbb {V}^*} \qquad \qquad \qquad {\mathbf {c}}_0 = (\sigma (1,p), 0, 0, 0)_{\mathbb {B}} \\&= (b (t,-1), y_3, (c-ab) (t,-1)_{\mathbb {B}^*} \\&= (b (t,-1), y_3, \tau (t,-1)_{\mathbb {B}^*} \end{aligned}$$One can note that when \(\tau =0\), this is the previous game, and when \(\tau \) random, we are in the new game, with \(\pi =b\) and \(\rho = \tau \): \(\mathsf {Adv}_{0} - \mathsf {Adv}_{{1}} \le \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_2}(T)\).
-
\(\mathbf {Game}\, \mathbf {G_2}{} \mathbf{:}\) We replicate the non-orthogonal sub-vector (1, p), with \(\theta {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\):
$$\begin{aligned} {\mathbf {k}}^*&= (\pi (t,-1), y_3, \rho (t,-1))_{\mathbb {B}^*}&{\mathbf {c}}_0&= (\sigma (1,p), 0, \theta (1,p))_{\mathbb {B}} \end{aligned}$$To show the indistinguishability, one applies the SubSpace-Ind property on \((\mathbb {B},\mathbb {B}^*)_{1,2,4,5}\). Indeed, we can consider a triple \((a\cdot G_1, b\cdot G_1, c\cdot G_1)\), where \(c=ab+\tau \bmod q\) with either \(\tau = 0\) or random, which are indistinguishable under the DDH assumption in \(\mathbb {G}_1\). Let us assume we start from random dual orthogonal bases \((\mathbb {V},\mathbb {V}^*)\). Then we define the matrices
$$\begin{aligned} B&= \left( \begin{array}{cccc} 1 &{} 0 &{} a &{} 0 \\ 0 &{} 1 &{} 0 &{} a \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) _{1,2,4,5}&B'&= \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0 \\ -a &{} 0 &{} 1 &{} 0 \\ 0 &{} -a &{} 0 &{} 1 \end{array} \right) _{1,2,4,5}&\mathbb {B}&= B \cdot \mathbb {V}&\mathbb {B}^*&= B' \cdot \mathbb {V}^* \end{aligned}$$The vectors \({\mathbf {b}}^*_4, {\mathbf {b}}^*_5\) can not be computed, but they are hidden from the adversary’s view. We compute the new vectors in \(\mathbb {V}\) and \(\mathbb {V}^*\):
$$\begin{aligned} {\mathbf {c}}_0&= (b (1,p), 0, c (1,p))_{\mathbb {V}} \qquad \qquad \quad {\mathbf {k}}^* = (\pi ' (t,-1), y_3, \rho (t,-1))_{\mathbb {V}^*} \\&= (b (1,p), 0, (c-ab) (1,p))_{\mathbb {B}} \qquad \quad \, = ((\pi ' + a\rho ) (t,-1), y_3, \rho (t,-1))_{\mathbb {B}^*} \\&= (b (1,p), 0, \tau (1,p))_{\mathbb {B}} \end{aligned}$$One can note that when \(\tau =0\), this is the previous game, and when \(\tau \) random, we are in the new game, with \(\pi =\pi '+a\rho \), \(\sigma =b\), and \(\theta = \tau \): \(\mathsf {Adv}_{{1}} - \mathsf {Adv}_{{2}} \le \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_1}(T)\).
-
\(\mathbf {Game}\, \mathbf {G_3}{} \mathbf{:}\) We randomize the two non-orthogonal sub-vectors, with random scalars \(u_1,u_2,v_1,v_2{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\):
$$\begin{aligned} {\mathbf {k}}^*&= (\pi (t,-1), y_3, u_1,u_2)_{\mathbb {B}^*}&{\mathbf {c}}_0&= (\sigma (1,p), 0, v_1,v_2)_{\mathbb {B}} \end{aligned}$$To show the indistinguishability, one makes a formal change of basis on \((\mathbb {B}^*,\mathbb {B})_{4,5}\), with a random unitary matrix Z, with \(z_1z_4-z_2z_3=1\):
$$\begin{aligned} B'&= Z = \left( \begin{array}{cc} z_1 &{} z_2 \\ z_3 &{} z_4 \end{array} \right) _{4,5}&B&= \left( \begin{array}{cccc} z_4 &{} -z_3 \\ -z_2 &{} z_1 \end{array} \right) _{4,5}&\mathbb {B}^*&= B' \cdot \mathbb {V}^*&\mathbb {B}&= B \cdot \mathbb {V}\end{aligned}$$This only impacts the hidden vectors \(({\mathbf {b}}_4, {\mathbf {b}}_5)\), \(({\mathbf {b}}^*_4, {\mathbf {b}}^*_5)\). If one defines \({\mathbf {k}}^*\) and \({\mathbf {c}}_0\) in \((\mathbb {V}^*,\mathbb {V})\), this translates in \((\mathbb {B}^*,\mathbb {B})\):
$$\begin{aligned} {\mathbf {k}}^*&= (\pi (t,-1), y_3, \rho (t,-1))_{\mathbb {V}^*} = (\pi (t,-1), y_3, \rho (t z_1 - z_3, t z_2 - z_4))_{\mathbb {B}^*} \\ {\mathbf {c}}_0&= (\sigma (1,p), 0, \theta (1,p))_{\mathbb {V}} = (\sigma (1,p), 0, \theta (z_4 - p z_2, -z_3 + p z_1))_{\mathbb {B}} \end{aligned}$$Let us consider random \(u_1,u_2,v_1,v_2{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\), and solve the system in \(z_1,z_2,z_3,z_4\). This system admits a unique solution, if and only if \(t\ne p\). And with random \(\rho ,\theta \), and random unitary matrix Z,
$$\begin{aligned} {\mathbf {k}}^*&= (\pi (t,-1), y_3, u_1,u_2)_{\mathbb {B}^*}&{\mathbf {c}}_0&= (\sigma (1,p), 0, v_1,v_2)_{\mathbb {B}} \end{aligned}$$with random scalars \(u_1,u_2,v_1,v_2{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\). In bases \((\mathbb {V},\mathbb {V}^*)\), we are in the previous game, and in bases \((\mathbb {B},\mathbb {B}^*)\), we are in the new game, if \(p\ne t\): \(\mathsf {Adv}_{{2}} = \mathsf {Adv}_{{3}}\).
-
\(\mathbf {Game}\, \mathbf {G_4}{} \mathbf{:}\) We now randomize the third component in \({\mathbf {c}}_0\):
$$\begin{aligned} {\mathbf {k}}^*&= (\pi (t,-1), y_3, u_1,u_2)_{\mathbb {B}^*}&{\mathbf {c}}_0&= (\sigma (1,p), x_3, v_1,v_2)_{\mathbb {B}} \end{aligned}$$To show the indistinguishability, one applies the SubSpace-Ind property on \((\mathbb {B},\mathbb {B}^*)_{4,3}\). Indeed, we can consider a triple \((a\cdot G_1, b\cdot G_1, c\cdot G_1)\), where \(c=ab+\tau \bmod q\) with either \(\tau = 0\) or \(\tau = x_3\), which are indistinguishable under the DDH assumption in \(\mathbb {G}_1\). Let us assume we start from random dual orthogonal bases \((\mathbb {V},\mathbb {V}^*)\). Then we define the matrices
$$\begin{aligned} B&= \left( \begin{array}{cc} 1 &{} 0 \\ a &{} 1 \end{array} \right) _{3,4}&B'&= \left( \begin{array}{cc} 1 &{} -a \\ 0 &{} 1 \end{array} \right) _{3,4}&\mathbb {B}&= B \cdot \mathbb {V}&\mathbb {B}^*&= B' \cdot \mathbb {V}^* \end{aligned}$$The vectors \({\mathbf {b}}^*_3\) can not be computed, but it is not into the adversary’s view. We compute the new vectors:
$$\begin{aligned} {\mathbf {k}}^*&= (\pi (t,-1), y_3, u'_1, u_2)_{\mathbb {V}^*} \qquad \qquad \quad {\mathbf {c}}_0= (\sigma (1,p), c, b, v_2)_{\mathbb {V}} \\&= (\pi (t,-1), y_3, u'_1+ay_3, u_2)_{\mathbb {B}^*}\qquad \quad \,\, = (\sigma (1,p), c-ab, b, v_2)_{\mathbb {B}} \\&\qquad \quad \qquad \quad \qquad \quad \qquad \qquad \quad \qquad \quad = (\sigma (1,p), \tau , b, v_2)_{\mathbb {B}} \end{aligned}$$One can note that when \(\tau =0\), this is the previous game, and when \(\tau =x_3\), we are in the new game, with \(v_1=b\) and \(u_1 = u'_1 + ay_3\): \(\mathsf {Adv}_{{3}} - \mathsf {Adv}_{{4}} \le 2\times \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_1}(T)\), by applying twice the Diffie-Hellman indistinguishability game.
We can undo successively games \(\mathbf {G}_{{3}}\), \(\mathbf {G}_{{2}}\), and \(\mathbf {G}_{{1}}\) to get, after a gap bounded by \(\mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_1}(t) + \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_2}(t)\): \({\mathbf {k}}^* = (\pi (t,-1), y_3, 0,0)_{\mathbb {B}^*}\) and \({\mathbf {c}}_0 = (\sigma (1,p), x_3, 0, 0)_{\mathbb {B}}\). In this game, the advantage of any adversary is 0. The global difference of advantages is bounded by \(4\cdot \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_1}(T) + 2 \cdot \mathsf {Adv}^\mathsf {ddh}_{\mathbb {G}_2}(T)\), which concludes the proof.
3 Key-Policy ABE with Switchable Attributes
Classical definitions and properties for KP-ABE, and more details about policies, are reviewed in the full version [6], following [7]. We recall here the main notions on labeled access-trees as a secret sharing to embed a policy in keys.
3.1 Policy Definition
Access Trees. As in the seminal paper [7], we will consider an access-tree \(\mathcal {T}\) to model the policy on attributes in an unbounded universe \(\mathcal {U}\), but with only AND and OR gates instead of more general threshold gates: an AND-gate being an n-out-of-n gate, whereas an OR-gate is a 1-out-of-n gate. This is also a particular case of the more general LSSS technique. Nevertheless, such an access-tree with only AND and OR gates is as expressive as with any threshold gates or LSSS. For any monotonic policy, we define our access-tree in the following way: \(\mathcal {T}\) is a rooted labeled tree from the root \(\rho \), with internal nodes associated to AND and OR gates and leaves associated to attributes. More precisely, for each leaf \(\lambda \in \mathcal {L}\), \(A(\lambda )\in \mathcal {U}\) is an attribute, and any internal node \(\nu \in \mathcal {N}\) is labeled with a gate \(G(\nu )\in \{\textsf {AND},\textsf {OR} \}\) as an AND or an OR gate to be satisfied among the children in \(\mathsf {children}(\nu )\). We will implicitly consider that any access-tree \(\mathcal {T}\) is associated to the attribute-labeling A of the leaves and the gate-labeling G of the nodes. For any leaf \(\lambda \in \mathcal {L}\) of \(\mathcal {T}\) or internal node \(\nu \in \mathcal {N}\backslash \{\rho \}\), the function \(\mathsf {parent}\) links to the parent node: \(\nu \in \mathsf {children}(\mathsf {parent}(\nu ))\) and \(\lambda \in \mathsf {children}(\mathsf {parent}(\lambda ))\).
On a given list \(\varGamma \subseteq \mathcal {U}\) of attributes, each leaf \(\lambda \in \mathcal {L}\) is either satisfied (considered or set to True), if \(A(\lambda )\in \varGamma \), or not (ignored or set to False) otherwise: we will denote \(\mathcal {L}_\varGamma \) the restriction of \(\mathcal {L}\) to the satisfied leaves in the tree \(\mathcal {T}\) (corresponding to an attribute in \(\varGamma \)). Then, for each internal node \(\nu \), one checks whether all children (AND-gate) or at least one of the children (OR-gate) are satisfied, from the attributes associated to the leaves, and then \(\nu \) is itself satisfied or not. By induction, if for each node \(\nu \) we denote \(\mathcal {T}_\nu \) the subtree rooted at the node \(\nu \), \(\mathcal {T}= \mathcal {T}_\rho \). A leaf \(\lambda \in \mathcal {L}\) is satisfied if \(\lambda \in \mathcal {L}_\varGamma \) then, recursively, \(\mathcal {T}_\nu \) is satisfied if the AND/OR-gate associated to \(\nu \) via \(G(\nu )\) is satisfied with respect to status of the children in \(\mathsf {children}(\nu )\): we denote \(\mathcal {T}_\nu (\varGamma ) = 1\) when the subtree is satisfied, and 0 otherwise:
Evaluation Pruned Trees. In the above definition, we considered an access-tree \(\mathcal {T}\) on leaves \(\mathcal {L}\) and a set \(\varGamma \) of attributes, with the satisfiability \(\mathcal {T}(\varGamma )=1\) where the predicate defined by \(\mathcal {T}\) is true when all the leaves \(\lambda \in \mathcal {L}_\varGamma \) are set to True. A \(\varGamma \)-evaluation tree \(\mathcal {T}' \subset \mathcal {T}\) is a pruned version of \(\mathcal {T}\), where one children only is kept to OR-gate nodes, down to the leaves, so that \(\mathcal {T}'(\varGamma )=1\). Basically, we keep a skeleton with only necessary True leaves to evaluate the internal nodes up to the root. We will denote \(\textsf {EPT}(\mathcal {T},\varGamma )\) the set of all the evaluation pruned trees of \(\mathcal {T}\) with respect to \(\varGamma \). \(\textsf {EPT}(\mathcal {T},\varGamma )\) is non-empty if and only if \(\mathcal {T}(\varGamma )=1\).
Figure 2 gives an illustration of such an access-tree for a policy: when the colored leaves \(\{\lambda _1,\lambda _3,\lambda _5,\lambda _8,\lambda _9,\lambda _{10}\}\) are True, the tree is satisfied, and there are two possible evaluation pruned trees: down to the leaves \(\{\lambda _1,\lambda _3,\lambda _5,\lambda _8\}\) or \(\{\lambda _1,\lambda _3,\lambda _5,\lambda _9,\lambda _{10}\}\).
Partial Order on Policies. Delegation will only be possible for a more restrictive access-tree, or a less accessible tree \(\mathcal {T}'\), than \(\mathcal {T}\) with the following partial order: \(\mathcal {T}' \le \mathcal {T}\), if and only if for any subset \(\varGamma \) of attributes, \(\mathcal {T}'(\varGamma )=1 \Longrightarrow \mathcal {T}(\varGamma )=1\). In our case of access-trees, a more restrictive access-tree is, for each node \(\nu \): if \(G(\nu ) = \textsf {AND} \), one or more children are added (i.e., more constraints); if \(G(\nu ) = \textsf {OR} \), one or more children are removed (i.e., less flexibility); the node \(\nu \) is moved one level below as a child of an AND-gate at node \(\nu '\), with additional sub-trees as children to this AND-gate (i.e., more constraints).
3.2 Labeling of Access-Trees
Labeled Access-Trees. We will label such trees with integers so that some labels on the leaves will be enough/necessary (according to the policy) to recover the labels above, up to the root, as illustrated on Fig. 3.
Definition 4
(Random y-Labeling). For an access-tree \(\mathcal {T}\) and any \(y\in \mathbb {Z}_p\), the probabilistic algorithm \(\varLambda _y(\mathcal {T})\) sets \(a_\rho \leftarrow y\) for the root, and then in a top-down manner, for each internal node \(\nu \), starting from the root: if \(G(\nu )=\textsf {AND} \), with n children, a random n-out-of-n sharing of \(a_\nu \) is associated to each children; if \(G(\nu )=\textsf {OR} \), with n children, each children is associated to the value \(a_\nu \).
Algorithm \(\varLambda _y(\mathcal {T})\) outputs \(\varLambda _y = (a_\lambda )_{\lambda \in \mathcal {L}}\), for all the leaves \(\lambda \in \mathcal {L}\) of the tree \(\mathcal {T}\). Because of the linearity, from any y-labeling \((a_\lambda )_\lambda \) of the tree \(\mathcal {T}\), and a random z-labeling \((b_\lambda )_\lambda \) of \(\mathcal {T}\), the sum \((a_\lambda +b_\lambda )_\lambda \) is a random \((y+z)\)-labeling of \(\mathcal {T}\). In particular, from any y-labeling \((a_\lambda )_\lambda \) of \(\mathcal {T}\), and a random zero-labeling \((b_\lambda )_\lambda \) of \(\mathcal {T}\), the values \(c_\lambda \leftarrow a_\lambda + b_\lambda \) provide a random y-labeling of \(\mathcal {T}\).
Labels on leaves are a secret sharing of the root that allows reconstruction of the secret if and only if the policy is satisfied, as explained below:
Properties of Labelings. For an acceptable set \(\varGamma \) for \(\mathcal {T}\) and a labeling \(\varLambda _y\) of \(\mathcal {T}\) for a random y, given only \((a_\lambda )_{\lambda \in \mathcal {L}_\varGamma }\), one can reconstruct \(y = a_\rho \). Indeed, as \(\mathcal {T}(\varGamma )=1\), we use an evaluation pruned tree \(\mathcal {T}'\in \textsf {EPT}(\mathcal {T},\varGamma )\). Then, in a bottom-up way, starting from the leaves, one can compute the labels of all the internal nodes, up to the root.
On the other hand, when \(\mathcal {T}(\varGamma )=0\), with a random labeling \(\varLambda _y\) of \(\mathcal {T}\) for a random y, given only \((a_\lambda )_{\lambda \in \mathcal {L}_\varGamma }\), y is unpredictable: for any \(y,y'\in \mathbb {Z}_p\), \(\mathcal {D}_y\) and \(\mathcal {D}_{y'}\) are perfectly indistinguishable, where \(\mathcal {D}_y = \{(a_\lambda )_{\lambda \in \mathcal {L}_\varGamma }, (a_\lambda )_\lambda {\mathop {\leftarrow }\limits ^{{}_\$}}\varLambda _y(\mathcal {T})\}\). Intuitively, given \((a_\lambda )_{\lambda \in \mathcal {L}_\varGamma }\), as \(\mathcal {T}(\varGamma )=0\), one can complete the labeling so that the label of the root is any y.
For our notion of Attribute-Indistinguishability, we need to identify a specific property called independent leaves, which describes leaves for which the secret share leaks no information in any of the other leaves in the access-tree.
Definition 5
(Independent Leaves). Given an access-tree \(\mathcal {T}\) and a set \(\varGamma \) so that \(\mathcal {T}(\varGamma )=0\), we call independent leaves, in \(\mathcal {L}_\varGamma \) with respect to \(\mathcal {T}\), the leaves \(\mu \) such that, given only \((a_\lambda )_{\lambda \in \mathcal {L}_\varGamma \backslash \{\mu \}}\), \(a_\mu \) is unpredictable: for any y, the two distributions \(\mathcal {D}^\$_y(\varGamma ) = \{(a_\lambda )_{\lambda \in \mathcal {L}_\varGamma }\}\) and \(\mathcal {D}_y(\varGamma ,\mu ) = \{(b_\mu ) \cup (a_\lambda )_{\lambda \in \mathcal {L}_\varGamma \backslash \{\mu \}} \}\) are perfectly indistinguishable, where \((a_\lambda )_\lambda {\mathop {\leftarrow }\limits ^{{}_\$}}\varLambda _y(\mathcal {T})\) and \(b_\mu {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_p\).
With the illustration on Fig. 3, with non-satisfied tree, when only colored leaves are set to True, leaves \(\lambda _3\) and \(\lambda _5\) are independent among the True leaves \(\{\lambda _3,\lambda _5,\lambda _8,\lambda _9,\lambda _{10}\}\). But leaves \(\lambda _8\), \(\lambda _9\) and \(\lambda _{10}\) are not independent as \(a_{\lambda _8} = a_{\lambda _9}+a_{\lambda _{10}} \bmod 7\) for any random labeling. Intuitively, given \((a_\lambda )_{\lambda \in \mathcal {L}_\varGamma \backslash \{\mu \}}\) and any \(a_\mu \), one can complete it into a valid labeling (with any random root label y as \(\mathcal {T}(\varGamma )=0\)), for \(\mu \in \{3,5\}\), but not for \(\mu \in \{8,9,10\}\).
3.3 Switchable Leaves and Attributes
For a Key-Policy ABE with Switchable Attributes (SA-KP-ABE), leaves in the access-tree can be made active or passive, and attributes in the ciphertext can be made valid or invalid. We thus enhance the access-tree \(\mathcal {T}\) into \({\tilde{\mathcal {T}}}= (\mathcal {T},\mathcal {L}_a,\mathcal {L}_p)\), where the implicit set of leaves
 is now the explicit disjoint union of the active-leaf and passive-leaf sets. Similarly, a ciphertext will be associated to the pair \((\varGamma _v,\varGamma _i)\), also referred as a disjoint union
is now the explicit disjoint union of the active-leaf and passive-leaf sets. Similarly, a ciphertext will be associated to the pair \((\varGamma _v,\varGamma _i)\), also referred as a disjoint union
 , of the valid-attribute and invalid-attribute sets.
, of the valid-attribute and invalid-attribute sets.
We note \({\tilde{\mathcal {T}}}(\varGamma _v,\varGamma _i) = 1\) if there is an evaluation pruned tree \(\mathcal {T}'\) of \(\mathcal {T}\) that is satisfied by
 (i.e., \(\mathcal {T}' \in \textsf {EPT}(\mathcal {T},\varGamma )\)), with the additional condition that all the active leaves in \(\mathcal {T}'\) correspond only to valid attributes in \(\varGamma _v\): \(\exists \mathcal {T}'\in \textsf {EPT}(\mathcal {T},\varGamma ), \forall \lambda \in \mathcal {T}' \cap \mathcal {L}_a\), \(A(\lambda ) \in \varGamma _v\). In other words, this means that an invalid attribute in the ciphertext should be considered as inexistent for active leaves, but only for those leaves.
(i.e., \(\mathcal {T}' \in \textsf {EPT}(\mathcal {T},\varGamma )\)), with the additional condition that all the active leaves in \(\mathcal {T}'\) correspond only to valid attributes in \(\varGamma _v\): \(\exists \mathcal {T}'\in \textsf {EPT}(\mathcal {T},\varGamma ), \forall \lambda \in \mathcal {T}' \cap \mathcal {L}_a\), \(A(\lambda ) \in \varGamma _v\). In other words, this means that an invalid attribute in the ciphertext should be considered as inexistent for active leaves, but only for those leaves.
We also have to enhance the partial order on \(\mathcal {T}\) to \({\tilde{\mathcal {T}}}\), so that we can deal with delegation: \({\tilde{\mathcal {T}}}' = (\mathcal {T}',\mathcal {L}'_a,\mathcal {L}'_p) \le {\tilde{\mathcal {T}}}= (\mathcal {T},\mathcal {L}_a,\mathcal {L}_p)\) if and only if \(\mathcal {T}' \le \mathcal {T}\), \(\mathcal {L}'_a \cap \mathcal {L}_p = \mathcal {L}'_p \cap \mathcal {L}_a = \emptyset \) and \(\mathcal {L}'_a \subseteq \mathcal {L}_a\). More concretely, \(\mathcal {T}'\) must be more restrictive, existing leaves cannot change their passive or active status, and new leaves can only be passive.
3.4 Key-Policy Attribute-Based Encapsulation with Switchable Attributes
We can now define the algorithms of an SA-KP-ABE, with the usual description of Key Encapsulation Mechanism, that consists in generating an ephemeral key K and its encapsulation C. The encryption of the actual message under the key K, using a symmetric encryption scheme is then appended to C. We will however call C the ciphertext, and K the encapsulated key in C. In our definitions, there are two secret keys: the master secret key \(\mathsf {MK}\) for the generation of users’ keys, and the secret key \(\mathsf {SK}\) for running the advanced encapsulation with invalid attributes:
-
\(\mathsf {Setup}(1^\kappa )\). From the security parameter \(\kappa \), the algorithm defines all the global parameters \(\mathsf {PK}\), the secret key \(\mathsf {SK}\) and the master secret key \(\mathsf {MK}\);
-
\(\mathsf {KeyGen}(\mathsf {MK}, {\tilde{\mathcal {T}}})\). The algorithm outputs a key \(\mathsf {dk}_{\tilde{\mathcal {T}}}\) which enables the user to decapsulate keys generated under a set of attributes
 if and only if \({\tilde{\mathcal {T}}}(\varGamma _v,\varGamma _i) = 1\);
if and only if \({\tilde{\mathcal {T}}}(\varGamma _v,\varGamma _i) = 1\); -
\(\mathsf {Delegate}(\mathsf {dk}_{\tilde{\mathcal {T}}},{\tilde{\mathcal {T}}}')\). Given a key \(\mathsf {dk}_{\tilde{\mathcal {T}}}\), generated from either the \(\mathsf {KeyGen}\) or the \(\mathsf {Delegate}\) algorithms, for a policy \({\tilde{\mathcal {T}}}\) and a more restrictive policy \({\tilde{\mathcal {T}}}' \le {\tilde{\mathcal {T}}}\), the algorithm outputs a decryption key \(\mathsf {dk}_{\mathcal {T}'}\);
-
\(\mathsf {Encaps}(\mathsf {PK},\varGamma )\). For a set \(\varGamma \) of (valid only) attributes, the algorithm generates the ciphertext C and an encapsulated key K;
-
\(\mathsf {Encaps}^*(\mathsf {SK},\varGamma _v,\varGamma _i)\). For a pair \((\varGamma _v,\varGamma _i)\) of disjoint sets of valid/invalid attributes, the algorithm generates the ciphertext C and an encapsulated key K;
-
\(\mathsf {Decaps}(\mathsf {dk}_{\tilde{\mathcal {T}}},C)\). Given the key \(\mathsf {dk}_{\tilde{\mathcal {T}}}\) from either \(\mathsf {KeyGen}\) or \(\mathsf {Delegate}\), and the ciphertext C, the algorithm outputs the encapsulated key K.
We stress that fresh keys (from the \(\mathsf {KeyGen}\) algorithm) and delegated keys (from the \(\mathsf {Delegate}\) algorithm) are of the same form, and can both be used for decryption and can both be delegated. This allows multi-hop delegation.
On the other hand, one can note the difference between \(\mathsf {Encaps}\) with \(\mathsf {PK}\) and \(\mathsf {Encaps}^*\) with \(\mathsf {SK}\), where the former runs the latter on the pair \((\varGamma ,\emptyset )\). And as \(\varGamma _i=\emptyset \), the public key is enough. This is thus still a public-key encryption scheme when only valid attributes are in the ciphertext, but the invalidation of some attributes require the secret key \(\mathsf {SK}\). For the advanced reader, this will lead to secret-key traceability, as only the owner of \(\mathsf {SK}\) will be able to invalidate attributes for the tracing procedure (as explained in Sect. 5). For correctness, the \(\mathsf {Decaps}\) algorithm should output the encapsulated key K if and only if C has been generated for a pair \((\varGamma _v,\varGamma _i)\) that satisfies the policy \({\tilde{\mathcal {T}}}\) of the decryption key \(\mathsf {dk}_{\tilde{\mathcal {T}}}\): \({\tilde{\mathcal {T}}}(\varGamma _v,\varGamma _i) = 1\). The following security notion enforces this property. But some other indistinguishability notions need to be defined in order to be able to exploit these switchable attributes in more complex protocols.
3.5 Security Notions
For the sake of simplicity, we focus on one-challenge definitions (one encapsulation with Real-or-Random encapsulated key, one user key with Real-or-All-Passive leaves, and one encapsulation with Real-or-All-Valid attributes), in the same vein as the Find-then-Guess security game. But the adversary could generate additional values, as they can either be publicly generated or an oracle is available. Then, the definitions can be turned into multi-challenge security games, with an hybrid proof, as explained in [2].
Definition 6
(Delegation-Indistinguishability for SA-KP-ABE). \(\textsf {Del}\hbox {-}\textsf {IND}\) security for SA-KP-ABE is defined by the following game:
-
Initialize: The challenger runs the \(\mathsf {Setup}\) algorithm of SA-KP-ABE and gives the public parameters \(\mathsf {PK}\) to the adversary;
-
Oracles: The following oracles can be called in any order and any number of times, except for \(\mathsf {RoREncaps}\) which can be called only once.
-
\(\mathsf {OKeyGen}({\tilde{\mathcal {T}}})\): this models a \(\mathsf {KeyGen}\)-query for any access-tree \({\tilde{\mathcal {T}}}= (\mathcal {T},\mathcal {L}_a,\mathcal {L}_p)\). It generates the decryption key but only outputs the index k of the key;
-
\(\mathsf {ODelegate}(k,{\tilde{\mathcal {T}}}')\): this models a \(\mathsf {Delegate}\)-query for any more restrictive access-tree \({\tilde{\mathcal {T}}}' \le {\tilde{\mathcal {T}}}\), for the k-indexed generated decryption key for \({\tilde{\mathcal {T}}}\). It generates the decryption key but only outputs the index \(k'\) of the new key;
-
\(\mathsf {OGetKey}(k)\): the adversary gets back the k-indexed decryption key generated by \(\mathsf {OKeyGen}\) or \(\mathsf {ODelegate}\) oracles;
-
\(\mathsf {OEncaps}(\varGamma _v,\varGamma _i)\): The adversary may be allowed to issue \(\mathsf {Encaps}^*\)-queries, with \((K,C)\leftarrow \mathsf {Encaps}^*(\mathsf {SK},\varGamma _v,\varGamma _i)\), and C is returned;
-
\(\mathsf {RoREncaps}(\varGamma _v,\varGamma _i)\): The adversary submits a unique real-or-random encapsulation query on a set of attributes
 . The challenger asks for an encapsulation query on \((\varGamma _v,\varGamma _i)\) and receives \((K_0,C)\). It also generates a random key \(K_1\). It eventually flips a random coin b, and outputs \((K_b,C)\) to the adversary;
. The challenger asks for an encapsulation query on \((\varGamma _v,\varGamma _i)\) and receives \((K_0,C)\). It also generates a random key \(K_1\). It eventually flips a random coin b, and outputs \((K_b,C)\) to the adversary;
-
-
Finalize(\(b'\)): The adversary outputs a guess \(b'\) for b. If for some access-tree \({\tilde{\mathcal {T}}}'\) corresponding to a key asked to the \(\mathsf {OGetKey}\)-oracle, \({\tilde{\mathcal {T}}}'(\varGamma _v,\varGamma _i)=1\), on the challenge set \((\varGamma _v,\varGamma _i)\), \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), otherwise one sets \(\beta = b'\). One outputs \(\beta \).
\(\mathsf {Adv}^{\mathsf {del}\hbox {-}\mathsf {ind}}(\mathcal {A})\) denotes the advantage of an adversary \(\mathcal {A}\) in this game.
In the basic form of Del-IND-security, where \(\mathsf {Encaps}^*\) encapsulations are not available, the \(\mathsf {RoREncaps}\)-oracle only allows \(\varGamma _i=\emptyset \), and no \(\mathsf {OEncaps}\)-oracle is available. But as \(\mathsf {Encaps}\) (with \(\varGamma _i=\emptyset \)) is a public-key algorithm, the adversary can generate valid ciphertexts by himself. We will call it “Del-IND-security for \(\mathsf {Encaps}\)”. For the more advanced security level, \(\mathsf {RoREncaps}\)-query will be allowed on any pair \((\varGamma _v,\varGamma _i)\), with the additional \(\mathsf {OEncaps}\)-oracle. We will call it “Del-IND-security for \(\mathsf {Encaps}^*\)”.
With these disjoint unions of
 and
and
 , we will also consider some indistinguishability notions on \((\mathcal {L}_a,\mathcal {L}_p)\) and \((\varGamma _v,\varGamma _i)\), about which leaves are active or passive in
, we will also consider some indistinguishability notions on \((\mathcal {L}_a,\mathcal {L}_p)\) and \((\varGamma _v,\varGamma _i)\), about which leaves are active or passive in
 for a given key, and which attributes are valid or invalid in
for a given key, and which attributes are valid or invalid in
 for a given ciphertext. The former will be the key-indistinguishability, whereas the latter will be attribute-indistinguishability. Again, as \(\mathsf {Encaps}\) is public-key, the adversary can generate valid encapsulations by himself. However, we may provide access to an \(\mathsf {OEncaps}\)-oracle to allow \(\mathsf {Encaps}^*\) queries, but with constraints in the final step, to exclude trivial attacks against key-indistinguishability. Similarly there will be constraints in the final step on the \(\mathsf {OKeyGen}/\mathsf {ODelegate}\)-queries for the attribute-indistinguishability.
for a given ciphertext. The former will be the key-indistinguishability, whereas the latter will be attribute-indistinguishability. Again, as \(\mathsf {Encaps}\) is public-key, the adversary can generate valid encapsulations by himself. However, we may provide access to an \(\mathsf {OEncaps}\)-oracle to allow \(\mathsf {Encaps}^*\) queries, but with constraints in the final step, to exclude trivial attacks against key-indistinguishability. Similarly there will be constraints in the final step on the \(\mathsf {OKeyGen}/\mathsf {ODelegate}\)-queries for the attribute-indistinguishability.
Definition 7
(Key-Indistinguishability). \(\textsf {Key}\hbox {-}\textsf {IND}\) security for SA-KP-ABE is defined by the following game:
-
Initialize: The challenger runs the \(\mathsf {Setup}\) algorithm of SA-KP-ABE and gives the public parameters \(\mathsf {PK}\) to the adversary;
-
Oracles: \(\mathsf {OKeyGen}({\tilde{\mathcal {T}}})\), \(\mathsf {ODelegate}(k,{\tilde{\mathcal {T}}}')\), \(\mathsf {OGetKey}(k)\), \(\mathsf {OEncaps}(\varGamma _v,\varGamma _i)\), and
-
\(\mathsf {RoAPKeyGen}({\tilde{\mathcal {T}}})\): The adversary submits one Real or All-Passive \(\mathsf {KeyGen}\)-query for any access structure \({\tilde{\mathcal {T}}}\) of its choice, with a list
 of active and passive leaves, and gets \(\mathsf {dk}_{0} = \mathsf {KeyGen}(\mathsf {MK},(\mathcal {T},\mathcal {L}_a,\mathcal {L}_p))\) or \(\mathsf {dk}_{1} = \mathsf {KeyGen}(\mathsf {MK}, (\mathcal {T}, \emptyset , \mathcal {L}))\). It eventually flips a random coin b, and outputs \(\mathsf {dk}_b\) to the adversary;
of active and passive leaves, and gets \(\mathsf {dk}_{0} = \mathsf {KeyGen}(\mathsf {MK},(\mathcal {T},\mathcal {L}_a,\mathcal {L}_p))\) or \(\mathsf {dk}_{1} = \mathsf {KeyGen}(\mathsf {MK}, (\mathcal {T}, \emptyset , \mathcal {L}))\). It eventually flips a random coin b, and outputs \(\mathsf {dk}_b\) to the adversary;
-
-
Finalize(\(b'\)): The adversary outputs a guess \(b'\) for b. If for some \((\varGamma _v,\varGamma _i)\) asked to the \(\mathsf {OEncaps}\)-oracle,
 , for the challenge access-tree \(\mathcal {T}\) where
, for the challenge access-tree \(\mathcal {T}\) where
 , \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), otherwise one sets \(\beta = b'\). One outputs \(\beta \).
, \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), otherwise one sets \(\beta = b'\). One outputs \(\beta \).
\(\mathsf {Adv}^{\mathsf {key}\hbox {-}\mathsf {ind}}(\mathcal {A})\) denotes the advantage of an adversary \(\mathcal {A}\) in this game.
In this first definition, the constraints in the finalize step require the adversary not to ask for an encapsulation on attributes that would be accepted by the policy with all-passive attributes in the leaves.
A second version deals with accepting policies: it allows encapsulations on attributes that would be accepted by the policy with all-passive leaves in the challenge key, until attributes associated to the active leaves in the challenge key and invalid attributes in the ciphertexts are distinct. Hence, the Distinct Key-Indistinguishability (\(\textsf {dKey}\hbox {-}\textsf {IND}\)) where Finalize(\(b'\)) reads: The adversary outputs a guess \(b'\) for b. If some active leaf \(\lambda \in \mathcal {L}_a\) from the challenge key corresponds to some invalid attribute \(t\in \varGamma _i\) in an \(\mathsf {OEncaps}\)-query, then set \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), otherwise set \(\beta = b'\). One outputs \(\beta \).
Definition 8
(Attribute-Indistinguishability). \(\textsf {Att}\hbox {-}\textsf {IND}\) security for SA-KP-ABE is defined by the following game:
-
Initialize: The challenger runs the \(\mathsf {Setup}\) algorithm of SA-KP-ABE and gives the public parameters \(\mathsf {PK}\) to the adversary;
-
Oracles: \(\mathsf {OKeyGen}({\tilde{\mathcal {T}}})\), \(\mathsf {ODelegate}(k,{\tilde{\mathcal {T}}}')\), \(\mathsf {OGetKey}(k)\), \(\mathsf {OEncaps}(\varGamma _v,\varGamma _i)\), and
-
\(\mathsf {RoAVEncaps}(\varGamma _v, \varGamma _i)\): The adversary submits one Real-or-All-Valid encapsulation query on distinct sets of attributes \((\varGamma _v, \varGamma _i)\). The challenger generates \((K,C) \leftarrow \mathsf {Encaps}^*(\mathsf {SK},\varGamma _v, \varGamma _i)\) as the real case, if \(b=0\), or
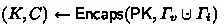 as the all-valid case, if \(b=1\), and outputs C to the adversary;
as the all-valid case, if \(b=1\), and outputs C to the adversary;
-
-
Finalize(\(b'\)): The adversary outputs a guess \(b'\) for b. If for some access-tree \({\tilde{\mathcal {T}}}'\) corresponding to a key asked to the \(\mathsf {OGetKey}\)-oracle,
 , on the challenge set \((\varGamma _v,\varGamma _i)\), \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), else one sets \(\beta = b'\). One outputs \(\beta \).
, on the challenge set \((\varGamma _v,\varGamma _i)\), \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), else one sets \(\beta = b'\). One outputs \(\beta \).
\(\mathsf {Adv}^{\mathsf {att}\hbox {-}\mathsf {ind}}(\mathcal {A})\) denotes the advantage of an adversary \(\mathcal {A}\) in this game.
This definition is a kind of attribute-hiding, where a user with keys for access-trees that are not satisfied by
 cannot distinguish valid from invalid attributes in the ciphertext.
cannot distinguish valid from invalid attributes in the ciphertext.
As above on key-indistinguishability, this first definition excludes accepting policies on the challenge ciphertext. However, for tracing, one also needs to deal with ciphertexts on accepting policies. More precisely, we must allow keys and a challenge ciphertext that would be accepted in the all-valid case, and still have indistinguishability, until attributes associated to the active leaves in the keys and invalid attributes in the challenge ciphertext are distinct. Hence, the Distinct Attribute-Indistinguishability (\(\textsf {dAtt}\hbox {-}\textsf {IND}\)) where Finalize(\(b'\)) reads: The adversary outputs a guess \(b'\) for b. If some attribute \(t\in \varGamma _i\) from the challenge query corresponds to some active leaf \(\lambda \in \mathcal {L}'_a\) in a \(\mathsf {OGetKey}\)-query, then set \(\beta {\mathop {\leftarrow }\limits ^{{}_\$}}\{0,1\}\), otherwise set \(\beta = b'\). One outputs \(\beta \).
4 Our SA-KP-ABE Scheme
4.1 Description of Our KP-ABE with Switchable Attributes
We extend the basic KP-ABE scheme proven in the full version [6], with leaves that can be made active or passive in a decryption key, and some attributes can be made valid or invalid in a ciphertext, and prove that it still achieves the Del-IND-security. For our construction, we will use two DPVS, of dimensions 3 and 9 respectively, in a pairing-friendly setting \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_t,e,G_1,G_2,q)\), using the notations introduced in Sect. 2.1. Essentially, we introduce a 7-th component to deal with switchable attributes. The two new basis-vectors \({\mathbf {d}}_7\) and \({\mathbf {d}}^*_7\) are in the secret key \(\mathsf {SK}\) and the master secret key \(\mathsf {MK}\) respectively. The two additional 8-th and 9-th components are to deal with the unbounded universe of attributes, to be able to use the adaptive Index-Ind property (see Theorem 3), instead of the static one. These additional components are hidden, and for the proof only:
-
\(\mathsf {Setup}(1^\kappa )\). The algorithm chooses two random dual orthogonal bases
$$\begin{aligned} \mathbb {B}&= ({\mathbf {b}}_1,{\mathbf {b}}_2,{\mathbf {b}}_3)&\mathbb {B}^*&= ({\mathbf {b}}^*_1,{\mathbf {b}}^*_2,{\mathbf {b}}^*_3)&\mathbb {D}&= ({\mathbf {d}}_1,\ldots , {\mathbf {d}}_9)&\mathbb {D}^*&= ({\mathbf {d}}^*_1,\ldots , {\mathbf {d}}^*_9). \end{aligned}$$It sets the public parameters \(\mathsf {PK}= \{ ({\mathbf {b}}_1, {\mathbf {b}}_3, {\mathbf {b}}^*_1), ({\mathbf {d}}_1,{\mathbf {d}}_2,{\mathbf {d}}_3,{\mathbf {d}}^*_1,{\mathbf {d}}^*_2,{\mathbf {d}}^*_3) \}\), whereas the master secret key is \(\mathsf {MK}= \{ {\mathbf {b}}^*_3, {\mathbf {d}}^*_7 \}\) and the secret key is \(\mathsf {SK}= \{ {\mathbf {d}}_7 \}\). Other basis vectors are kept hidden.
-
\(\mathsf {KeyGen}(\mathsf {MK}, {\tilde{\mathcal {T}}})\). For an extended access-tree \({\tilde{\mathcal {T}}}= (\mathcal {T},\mathcal {L}_a,\mathcal {L}_p)\), the algorithm first chooses a random \(a_0{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), and a random \(a_0\)-labeling \((a_\lambda )_\lambda \) of the access-tree \(\mathcal {T}\), and builds the key:
$$\begin{aligned} {\mathbf {k}}^*_0&= (a_0,0,1)_{\mathbb {B}^*}&{\mathbf {k}}^*_\lambda&= (\pi _\lambda (1,t_\lambda ), a_\lambda , 0,0,0,r_\lambda ,0,0)_{\mathbb {D}^*} \end{aligned}$$for all the leaves \(\lambda \), where \(t_\lambda = A(\lambda )\), \(\pi _\lambda {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\), and \(r_\lambda {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}^*_q\) if \(\lambda \) is an active leaf in the key \((\lambda \in \mathcal {L}_a)\) or else \(r_\lambda = 0\) for a passive leaf \((\lambda \in \mathcal {L}_p)\). The decryption key \(\mathsf {dk}_{\tilde{\mathcal {T}}}\) is then \(({\mathbf {k}}^*_0, ({\mathbf {k}}^*_\lambda )_\lambda )\).
-
\(\mathsf {Delegate}(\mathsf {dk}_{\tilde{\mathcal {T}}}, {\tilde{\mathcal {T}}}')\). Given a private key for a tree \({\tilde{\mathcal {T}}}\) and a more restrictive subtree \({\tilde{\mathcal {T}}}' \le {\tilde{\mathcal {T}}}\), the algorithm creates a delegated key \(\mathsf {dk}_{{\tilde{\mathcal {T}}}'}\). It chooses a random \(a'_0{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\) and a random \(a'_0\)-labeling \((a'_\lambda )_\lambda \) of \(\mathcal {T}'\); Then, it updates \({\mathbf {k}}^*_0 \leftarrow {\mathbf {k}}^*_0 + (a'_0,0,0)_{\mathbb {B}^*}\); It sets \({\mathbf {k}}^*_\lambda \leftarrow (\pi '_\lambda \cdot (1,t_\lambda ),a'_\lambda ,0,0,0,0,0,0)_{\mathbb {B}^*}\) for a new leaf, or updates \({\mathbf {k}}^*_\lambda \leftarrow {\mathbf {k}}^*_\lambda + (\pi '_\lambda \cdot (1,t_\lambda ),a'_\lambda ,0,0,0,0,0,0)_{\mathbb {B}^*}\) for an old leaf, with \(\pi '_\lambda {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\).
-
\(\mathsf {Encaps}(\mathsf {PK},\varGamma )\). For a set \(\varGamma \) of attributes, the algorithm first chooses random scalars \(\omega , \xi {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\). It then sets \(K = g_t^\xi \) and generates the ciphertext \(C = ({\mathbf {c}}_0, ({\mathbf {c}}_t)_{t\in \varGamma })\) where
$$\begin{aligned} {\mathbf {c}}_0&= (\omega ,0,\xi )_{\mathbb {B}}&{\mathbf {c}}_t&= (\sigma _t (t, -1), \omega , 0,0,0,0,0,0)_{\mathbb {D}} \end{aligned}$$for all the attributes \(t\in \varGamma \), with \(\sigma _t {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\).
-
\(\mathsf {Encaps}^*(\mathsf {SK},(\varGamma _v, \varGamma _i))\). For a disjoint union
 of sets of attributes (\(\varGamma _v\) is the set of valid attributes and \(\varGamma _i\) is the set of invalid attributes), the algorithm first chooses random scalars \(\omega , \xi {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\). It then sets \(K = g_t^\xi \) and generates the ciphertext
of sets of attributes (\(\varGamma _v\) is the set of valid attributes and \(\varGamma _i\) is the set of invalid attributes), the algorithm first chooses random scalars \(\omega , \xi {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\). It then sets \(K = g_t^\xi \) and generates the ciphertext
 where $$\begin{aligned} {\mathbf {c}}_0&= (\omega ,0,\xi )_{\mathbb {B}}&{\mathbf {c}}_t&= (\sigma _t (t, -1), \omega ,0,0,0,u_t,0,0)_{\mathbb {D}} \end{aligned}$$
where $$\begin{aligned} {\mathbf {c}}_0&= (\omega ,0,\xi )_{\mathbb {B}}&{\mathbf {c}}_t&= (\sigma _t (t, -1), \omega ,0,0,0,u_t,0,0)_{\mathbb {D}} \end{aligned}$$for all the attributes
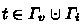 , \(\sigma _t {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\) and \(u_t {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}^*_q\) if \(t\in \varGamma _i\) or \(u_t = 0\) if \(t\in \varGamma _v\).
, \(\sigma _t {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}_q\) and \(u_t {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {Z}^*_q\) if \(t\in \varGamma _i\) or \(u_t = 0\) if \(t\in \varGamma _v\). -
\(\mathsf {Decaps}(\mathsf {dk}_{\tilde{\mathcal {T}}},C)\). The algorithm first selects an evaluation pruned tree \(\mathcal {T}'\) of \(\mathcal {T}\) that is satisfied by \(\varGamma = \varGamma _v \cup \varGamma _i\), such that any leaf \(\lambda \) in \(\mathcal {T}'\) is either passive in the key \((\lambda \in \mathcal {L}_p)\) or associated to a valid attribute in the ciphertext \((t_\lambda \in \varGamma _v)\). This means that the labels \(a_\lambda \) for all the leaves \(\lambda \) in \(\mathcal {T}'\) allow to reconstruct \(a_0\) by simple additions, where \(t = t_\lambda \):
$$\begin{aligned} {\mathbf {c}}_t \times {\mathbf {k}}^*_\lambda&= g_t^{ \sigma _t \cdot \pi _\lambda \cdot \langle (t,-1), (1, t_\lambda ) \rangle + \omega \cdot a_\lambda + u_t \cdot r_\lambda } = g_t^{\omega \cdot a_\lambda }, \end{aligned}$$as \(u_t = 0\) or \(r_\lambda =0\). Hence, the algorithm can derive \(g_t^{\omega \cdot a_0}\). From \({\mathbf {c}}_0\) and \({\mathbf {k}}^*_0\), it can also compute \({\mathbf {c}}_0 \times {\mathbf {k}}^*_0 = g_t^{ \omega \cdot a_0 + \xi }\), which then easily leads to \(K = g_t^{\xi }\).
First, note that the delegation works as \({\mathbf {b}}^*_1\), \({\mathbf {d}}^*_1,{\mathbf {d}}^*_2,{\mathbf {d}}^*_3\) are public. This allows to create a new key for \({\tilde{\mathcal {T}}}' \le {\tilde{\mathcal {T}}}\). But as \({\mathbf {d}}^*_7\) is not known, any new leaf is necessarily passive, and an active existing leaf in the original key cannot be converted to passive, and vice-versa. Indeed, all the randomnesses are fresh, except for the last components \(r_\lambda \) that remain unchanged: this is perfectly consistent with the definition of \({\tilde{\mathcal {T}}}' \le {\tilde{\mathcal {T}}}\).
Second, in encapsulation, for invalidating a contribution \({\mathbf {c}}_t\) in the ciphertext with a non-zero \(u_t\), for \(t\in \varGamma _i\), one needs to know \({\mathbf {d}}_7\), hence the \(\mathsf {Encaps}^*\) that requires \(\mathsf {SK}\), whereas \(\mathsf {Encaps}\) with \(\varGamma _i=\emptyset \) just needs \(\mathsf {PK}\).
Eventually, we stress that in the above decryption, one can recover \(g_t^{\omega \cdot a_0}\) if and only if there is an evaluation pruned tree \(\mathcal {T}'\) of \(\mathcal {T}\) that is satisfied by \(\varGamma \) and the active leaves in \({\tilde{\mathcal {T}}}'\) correspond to valid attributes in \(\varGamma _v\) (used during the encapsulation). And this holds if and only if \({\tilde{\mathcal {T}}}(\varGamma _v,\varGamma _i) = 1\).
4.2 \(\textsf {Del}\hbox {-}\textsf {IND}\)-Security of Our SA-KP-ABE for \(\mathsf {Encaps}\)
For this security notion, we first consider only valid contributions in the challenge ciphertext, with indistinguishability of the \(\mathsf {Encaps}\) algorithm. Which means that \(\varGamma _i=\emptyset \) in the challenge pair. And the security result holds even if the vector \({\mathbf {d}}_7\) is made public:
Theorem 9
Our SA-KP-ABE scheme is \(\textsf {Del}\hbox {-}\textsf {IND}\) for \(\mathsf {Encaps}\) (with only valid attributes in the challenge ciphertext), even if \({\mathbf {d}}_7\) is public.
The proof essentially reduces to the \(\textsf {IND}\)-security result of the KP-ABE scheme, and is available in the full version [6]. We present an overview of the proof, as the structure of the first games is common among most of our proofs. The global sequence of games is described on Fig. 4, where \(({\mathbf {c}}_0, ({\mathbf {c}}_t))\) is the challenge ciphertext for all the attributes \(t\in \varGamma \), and \(({\mathbf {k}}^*_{\ell ,0}, ({\mathbf {k}}^*_{\ell ,\lambda }))\) are the keys, for \(1\le \ell \le K\), and \(\lambda \in \mathcal {L}_\ell \) for each \(\ell \)-query, with active and passive leaves.
In the two first games \(G_1\) and \(G_2\), one is preparing the floor with a random \(\tau \) and random masks \(z_t\) in the ciphertexts \({\mathbf {c}}_t\) (actually, the challenge ciphertext corresponding to the attribute t). Note that until the actual challenge query is asked, one does not exactly know the attributes in \(\varGamma \) (as we are in the adaptive-set setting), thus we will decide on the random mask \(z_t\), where t is virtually associated to the number of the attribute in their order of apparition in the security game. The main step is to get to Game \(G_3\), starting with an additional labeling \((s_{\ell ,0},(s_{\ell ,\lambda })_\lambda )\), using hybrid games that begins from Game \(G_2\). To do this, the new labelling is added in each \(\ell \)-th key, then each label is masked by the random \(z_t\) for each attribute t. One then exploits the limitations expected from the adversary in the security game: the adversary cannot ask keys on access-trees \(\mathcal {T}\) such that \(\mathcal {T}(\varGamma )=1\), for the challenge set \(\varGamma \). This limitation translates into the value \(s_{\ell ,0}\) being unpredictable for the adversary with regards to \((s_{\ell ,\lambda })_\lambda \), as for each key requested by the adversary, there is at least one \(s_{\ell ,\lambda }\) by lack of a corresponding ciphertext. Thus, we can replace \(s_{\ell ,0}\) by a random independent \(r_{\ell ,0}\) without giving any advantage to the adversary. To formally mask the shares \(s_{\ell ,\lambda }\), we need another level of hybrid games: we will change all the keys associated with a specific attribute \(\lambda \) at the same time, by using the Adaptive \(\textsf {Index}\hbox {-}\textsf {Ind} \) technique. This allows us to mask the \(s_{\ell ,\lambda }\) share in each key with \(z_t\), one \(\lambda \) at a time inside the \(\ell \)-th key.
Simulation of delegation can just be done by using the key generation algorithm, making sure we use the same randomness for all the keys delegated from the same one. As the vector \({\mathbf {d}}^*_7\) is known to the simulator, this is easy. As \({\mathbf {d}}_7\) is public, the adversary can run by himself both \(\mathsf {Encaps}\) and \(\mathsf {Encaps}^*\).
We stress that our construction makes more basis vectors public, than in the schemes from [15], as only \({\mathbf {b}}^*_3\) is for the key issuer. This makes the proof more tricky, but this is the reason why we can deal with delegation for any user.
4.3 \(\textsf {Del}\hbox {-}\textsf {IND}\)-Security of Our SA-KP-ABE for \(\mathsf {Encaps}^*\)
We now study the full indistinguishability of the ciphertext generated by an \(\mathsf {Encaps}^*\) challenge, with delegated keys. The intuition is that when \(u_t \cdot r_{\ell ,\lambda } \ne 0\), the share \(a_{\ell ,\lambda }\) in \(g_t^{\omega \cdot a_{\ell ,\lambda } + u_t \cdot r_{\ell ,\lambda }}\) is hidden, but we have to formally prove it.
The main issue in this proof is the need to anticipate whether \(u_t \cdot r_{\ell ,\lambda } = 0\) or not when simulating the keys, and the challenge ciphertext as well (even before knowing the exact query \((\varGamma _v,\varGamma _i)\)). Without being in the selective-set setting where both \(\varGamma _v\) and \(\varGamma _i\) would have to be specified before generating the public parameters \(\mathsf {PK}\), we ask to know disjoint super-sets \(A_v, A_i \subseteq \mathcal {U}\) of attributes. Then, in the challenge ciphertext query, we will ask that \(\varGamma _v \subseteq A_v\) and \(\varGamma _i\subseteq A_i\). We will call this setting the semi-adaptive super-set setting, where the super-sets have to be specified before the first decryption keys are issued. Furthermore, the set of attributes
 used in the real challenge query is only specified at the moment of the challenge, as in the adaptive setting.
used in the real challenge query is only specified at the moment of the challenge, as in the adaptive setting.
For this proof, \({\mathbf {d}}_7\) must be kept secret (cannot be provided to the adversary). We will thus give access to an \(\mathsf {Encaps}^*\) oracle. We then need to simulate it.
Theorem 10
Our SA-KP-ABE scheme is \(\textsf {Del}\hbox {-}\textsf {IND}\) for \(\mathsf {Encaps}^*\), in the semi-adaptive super-set setting (where \(A_v, A_i \subseteq \mathcal {U}\) so that \(\varGamma _v \subseteq A_v\) and \(\varGamma _i\subseteq A_i\) are specified before asking for keys).
We stress that the semi-adaptive super-set setting is much stronger than the selective-set setting where the adversary would have to specify both \(\varGamma _v\) and \(\varGamma _i\) before the setup. Here, only super-sets have to be specified, and just before the first key-query. The adversary is thus given much more power.
The full proof can be found in the full version [6], we provide some hints, that extend the above sketch: we only consider keys that are really provided to the adversary, and thus delegated keys. They can be generated as fresh keys except for the \(r_\lambda \)’s that have to be the same for leaves in keys delegated from the same initial key. However, in order to randomize \(s_{\ell ,0}\) once all of the shares have been masked, one cannot directly conclude that \(s_{\ell ,0}\) is independent from the view of the adversary: we only know \({\tilde{\mathcal {T}}}_\ell (\varGamma _v,\varGamma _i) = 0\), but not necessarily
 , as in the previous proof.
, as in the previous proof.
To this aim, we revisit this gap with an additional sequence where we focus on the k-th key and the challenge ciphertext. In that sequence, we first prepare with additional random values \(y_{\ell ,\lambda }\) in all the keys, with the same repetition properties as the \(r_{\ell ,\lambda }\). Thereafter, in another sub-sequence of games on the attributes, we can use the Swap-Ind property to completely randomize \(s_{k,\lambda }\) when \(u_{t_{k,\lambda }} \cdot r_{k,\lambda } \ne 0\). Hence, the \(s_{k,\lambda }\) are unknown either when \(z_{t_{k,\lambda }}\) is not known (the corresponding element is not provided in the challenge ciphertext) or this is a random \(s'_{k,\lambda }\) when \(u_{t_{k,\lambda }} \cdot r_{k,\lambda } \ne 0\). The property of the access-tree then makes \(s_{k,0}\) perfectly unpredictable, which can be replaced by a random independent \(r_{k,0}\).
4.4 Distinct Indistinguishability Properties
We first claim easy results, for which the proofs are symmetrical:
Theorem 11
Our SA-KP-ABE scheme is \(\textsf {dKey}\hbox {-}\textsf {IND}\), even if \({\mathbf {d}}^*_7\) is public.
Theorem 12
Our SA-KP-ABE scheme is \(\textsf {dAtt}\hbox {-}\textsf {IND}\), even if \({\mathbf {d}}_7\) is public.
Both proofs can be found in the full version [6]. In these alternative variants, all the invalid attributes in all the queried ciphertexts do not correspond to any active leaf in the challenge keys (for \(\textsf {dKey}\hbox {-}\textsf {IND}\)) or all active leaves in all the queried keys do not correspond to any invalid attribute in the challenge ciphertext (for \(\textsf {dAtt}\hbox {-}\textsf {IND}\)). Then, we can gradually replace all the real keys by all-passive in the former proof or all the real ciphertexts by all-valid in the latter proof.
4.5 Attribute-Indistinguishability
Theorem 13
Our SA-KP-ABE scheme is \(\textsf {Att}\hbox {-}\textsf {IND}\), even if \({\mathbf {d}}_7\) is public, if all the active keys correspond to independent leaves with respect to the set of attributes
 in the challenge ciphertext.
in the challenge ciphertext.
The proof can be found in the full version [6]. This is an important result with respect to our target application of tracing, combined with possible revocation. Indeed, with such a result, if a user is excluded independently of the tracing procedure (the policy would reject him even if all his passive leaves match valid attributes in the ciphertext), he will not be able to detect whether there are invalid attributes in the ciphertext and thus that the ciphertext is from a tracing procedure. This gives us a strong resistance to collusion.
5 Application to Tracing
In our Traitor-Tracing approach, any user would be given a key associated to a word in a traceable code at key generation time. To embed a word inside a key, the key generation authority only needs to create a new policy for a user with policy \(\mathcal {T}\): the new policy will be a root \(\textsf {AND} \) gate, that connects the original access-tree \(\mathcal {T}\) as one child, and a word-based access-tree composed of active leaves as another child, as illustrated on Fig. 5.
From there, the tracing authority, using the secret key \(\mathsf {SK}\), could trace any Pirate Decoder by invalidating attributes associated to the positions in words, one position at a time. Since an adversary cannot know whether attributes are valid or invalid, until it is not impacted by the invalid attributes (thanks to the Distinct Attribute-Indistinguishability), he will answer each queries of the tracer, when it is able to do it, effectively revealing the bits of his word on each position, until the tracer finds his complete word, to eventually trace back the traitors, from the traceable-code properties. Furthermore, thanks to the Attribute-Indistinguishability (not Distinct), a traitor that has been identified by the tracing authority can be removed from the target set at tracing time, and can thus no longer participate in the coalition, as it will be excluded from the policy, whatever the valid/invalid attributes. We stress that the secret key \(\mathsf {SK}\) is required for invalidating some attributes, and so for the tracing. We thus have secret-key black-box traceability. More details are given in the full version [6].
6 Conclusion
We have designed a KP-ABE scheme that allows an authority to generate keys with specific policies for each user, so that these users can thereafter delegate their keys for any more restrictive rights. Thanks to the (Distinct) Attribute-Indistinguishability and Attribute-Indistinguishability, it can also include key material for tracing a compromised key involved in a pirate device while limiting the size of collusions. In addition, with Key-Indistinguishability on active leaves and perfect randomization on passive leaves, one achieves a strong level of anonymity: one cannot detect whether two keys have been delegated by the same original key.
References
Attrapadung, N., Tomida, J.: Unbounded dynamic predicate compositions in ABE from standard assumptions. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12493, pp. 405–436. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64840-4_14
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th FOCS, pp. 394–403. IEEE Computer Society Press, October 1997. https://doi.org/10.1109/SFCS.1997.646128
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Chen, J., Gong, J., Wee, H.: Improved inner-product encryption with adaptive security and full attribute-hiding. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11273, pp. 673–702. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_23
Chen, J., Lim, H.W., Ling, S., Wang, H., Wee, H.: Shorter IBE and signatures via asymmetric pairings. In: Abdalla, M., Lange, T. (eds.) Pairing 2012. LNCS, vol. 7708, pp. 122–140. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36334-4_8
Delerablée, C., Gouriou, L., Pointcheval, D.: Key-policy ABE with delegation of rights. Cryptology ePrint Archive, Report 2021/867 (2021). https://eprint.iacr.org/2021/867
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. https://doi.org/10.1145/1180405.1180418. Available as Cryptology ePrint Archive Report 2006/309
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_4
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_27
Liu, Z., Wong, D.S.: Practical ciphertext-policy attribute-based encryption: traitor tracing, revocation, and large universe. In: Malkin, T., Kolesnikov, V., Lewko, A.B., Polychronakis, M. (eds.) ACNS 2015. LNCS, vol. 9092, pp. 127–146. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-28166-7_7
Okamoto, T., Takashima, K.: Homomorphic encryption and signatures from vector decomposition. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 57–74. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85538-5_4
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Okamoto, T., Takashima, K.: Adaptively attribute-hiding (hierarchical) inner product encryption. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 591–608. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_35
Okamoto, T., Takashima, K.: Fully secure unbounded inner-product and attribute-based encryption. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 349–366. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_22
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Acknowledgment
This work was supported in part by the French ANR Project ANR-19-CE39-0011 PRESTO.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Delerablée, C., Gouriou, L., Pointcheval, D. (2022). Key-Policy ABE with Switchable Attributes. In: Galdi, C., Jarecki, S. (eds) Security and Cryptography for Networks. SCN 2022. Lecture Notes in Computer Science, vol 13409. Springer, Cham. https://doi.org/10.1007/978-3-031-14791-3_7
Download citation
DOI: https://doi.org/10.1007/978-3-031-14791-3_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-14790-6
Online ISBN: 978-3-031-14791-3
eBook Packages: Computer ScienceComputer Science (R0)








 if and only if
if and only if  . The challenger asks for an encapsulation query on
. The challenger asks for an encapsulation query on  of active and passive leaves, and gets
of active and passive leaves, and gets  , for the challenge access-tree
, for the challenge access-tree  ,
, 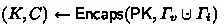 as the all-valid case, if
as the all-valid case, if  , on the challenge set
, on the challenge set  of sets of attributes (
of sets of attributes ( where
where 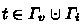 ,
, 
