Keywords

1 Introduction

The transport of molecular oxygen throughout the body is primarily realised by blood cells in the cardiovascular system [1]. The final destination of oxygen is the cytochrome c oxidase (COX), a protein embedded in the inner mitochondrial membrane, where oxygen is consumed in the energy conversion cycle. The binding site for oxygen is located at the center of the inner mitochondrial membrane [2]. Passive diffusive transport through several membranes, including the plasma membrane, is responsible for the last steps of oxygen from blood cells to the COX binding site. Cancer cells are known to show hypoxia which can fluctuate across the tumour cell, and tumour oxygenation can enhance radiation therapy of cancer cells [3]. Interestingly, nerve cell axons are surrounded by myelin, which is composed of stacked membrane bilayers containing large fractions of cholesterol, phospholipids, and glycolipids [4, 5]. Understanding the mechanisms of oxygen pathways from capillaries to tissue mitochondria is thus important for completely unraveling the physiological role of oxygen [6].

In this paper, a bottom-up approach will be used to study the role of membranes starting from the molecular scale. Phospholipid membranes form a barrier for oxygen, but the oxygen solubility in the phospholipid tail region is higher than in water, such that a high concentration of oxygen is found in the hydrophobic matrix [7, 8]. This high partitioning toward the membrane suggests that the omnipresence of phospholipid membranes provides the cell with an oxygen reservoir. Therefore, this paper wants to establish the view that a phospholipid membrane has a dual function: slowing oxygen transport, while also storing oxygen. Moreover, the inhomogeneity and anisotropy of the membrane facilitate oxygen transport in the interleaflet region of a lipid bilayer, compared to the transport orthogonal to the membrane surface [9]. The interleaflet space of bilayers can thus form a connected network of efficient diffusive pathways throughout the cell. The timely delivery of oxygen is especially important in the brain and the peripheral nervous system. This paper will in addition investigate how stacked membranes can serve as an oxygen reservoir in the nervous system, given a certain partial oxygen pressure.

In the methods section, kinetic modelling based on the Smoluchowski equation is introduced. It is explained how kinetic parameters were extracted from previous molecular dynamics (MD) simulations. The kinetic parameters will be used to predict the steady-state oxygen distribution given an oxygen gradient. In the results and discussion section, the enhancement in oxygen storage due to the stacking will be computed, where the number of stacked bilayers is varied. The conclusion section summarises our findings.

2 Methodology

Smoluchowski Equation for Transport

Due to the membrane’s inhomogeneity along the membrane’s normal (z-coordinate, Fig. 1), the oxygen concentration c is z-dependent. It relates to the free energy profile F(z) =  − kBTlnc(z), with kB the Boltzmann constant and T the temperature. Diffusive transport through an inhomogeneous medium is governed by the Smoluchowski equation, which is determined by the free energy F(z) and diffusion D(z) profiles [10]. Discretisation in N bins along z transforms the Smoluchowski equation into a set of linearly coupled equations, which can be summarised by a rate model with rate matrix R

Fig. 1
A diagram of a stimulation box that has 3 layers, water, bilayer, and water. Two graphs plot free energy and diffusivity versus z. Graphs B and C form u and w-like curves.

MD simulations of the (POPC) membrane. (a) Simulation box with indication of the z-axis. For clarity, water and phospholipid molecules are shaded in the right part of the box with one high-lighted POPC molecule (ball-and-stick) and red oxygen molecules (van der Waals spheres). (b) Free energy F(z) in units kBT. (c) Diffusivity D(z). F(z) and D(z) were obtained from Bayesian analysis of the MD trajectories

Full size image
$$ \frac{\partial {c}_i(t)}{\partial t}=\sum \limits_N^{j=1}{R}_{ij}{c}_j(t), $$
(1)

where ci(t) is the concentration in bin i at time t, and where the kinetic parameters in the rate matrix R are uniquely determined by the F(z) and D(z) profiles [10]. In this work, we will solve the rate equations with different profiles, representing different stacked bilayers.

Construction of the Rate Model from Molecular Simulations

Bayesian analysis (BA) of MD trajectories at the atomic scale can be used to obtain the F and D profiles – and thus the rate matrix R – of a membrane [9,10,11]. In practice, the transitions observed in conventional MD trajectories are compared to the transitions expected by the rate model with a proposed rate matrix R. A Monte Carlo procedure is then used to extract the rate matrix with the highest likelihood of producing the observed MD trajectories.

Previously published MD simulations and their F and D profiles are used in this work to investigate the storage capacity of stacked bilayers. The considered membranes are a homogeneous 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) bilayer (see Fig. 1) and a model system for inner mitochondrial membrane (labeled MITO) from Ref. [9]. MD simulations were run with the CHARMM36 force field at 310 K with a simulation box containing 72 lipid molecules, as depicted in Fig. 1a [12, 13]. The z-axis was discretised into 100 bins (\( (z \bigoplus 0.68^-) \)), and BA was performed on the oxygen trajectories, resulting in the F and D profiles shown in Fig. 1b, c.

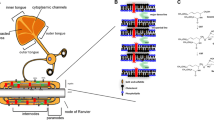
In a next step, the single-membrane profiles are extended to artificially construct the F and D profiles of n stacked membranes by concatenating the membrane part of the profiles n times, to imitate myelin sheaths (Fig. 2a). The following three configurations are compared (Fig. 2b):

  1. 1.

    A water layer without any membrane (Fig. 2b top), representing oxygen diffusion to the mitochondria without shielding of membranes.

  2. 2.

    A single bilayer and water (Fig. 2b centre).

  3. 3.

    A series of n stacked bilayers (Fig. 2b bottom), representing myelin sheaths.

The oxygen storage S is measured under an oxygen gradient (see below), which gives S(0), S(1) and S(n) for the setups with zero, one, and n bilayers, respectively. The amount of water is varied in setup 1 and setup 2 to match the size of setup 3, as is depicted in Figs. 2b. This allows for comparison between equally sized configurations in the results and discussion section. The stacking periodicity d can be increased to simulate a more disorganised structure with a larger aqueous phase between the membrane layers.

Fig. 2
Two schematic diagrams. Diagram 1 illustrates stacks of phospholipids and oxygen molecules that make up a myelin sheath. Diagram 2 displays three setups with steady-state boundary conditions.

(a) Myelin sheaths wrapped around a neural cell consist of stacked membranes [5]. (b) Considered configurations with steady-state boundary conditions: c = c* to the left and c = 0 to the right. Setup 1 is pure water, setup 2 has one bilayer, setup 3 has n bilayers (depicted is n = 5). Stacking periodicity d is indicated with arrow

Full size image

Steady-State Solution Under Oxygen Gradient

The oxygen storage S in the membranes is measured under an oxygen gradient, where one side (to the left in Fig. 2) has a partial oxygen pressure and the other side (to the right of Fig. 2) has zero partial oxygen pressure, referring to full depletion of oxygen by COX. The concentration profile is assumed to have reached the steady-state regime, where the concentration no longer changes over time, but a net oxygen flux might still occur.

We solve the rate model (Eq. 1) for the steady-state solution, i.e., the right hand side of Eq. 1 vanishes, with bin 1 (to the left) at fixed concentration c1 = c* and bin N (to the right) at fixed concentration cN = 0, for all times t. This is done by constructing the vector v of length N − 2, which has all elements equal to zero except for its first element v1 =  − R2, 1. The rate matrix is stripped of its first and Nth rows and columns, to form the cropped rate matrix R' [14]. The steady-state concentration \( {c}_i^{SS} \) in each bin i is then obtained by matrix multiplication of R' and the vector v, and scaling with the concentration c*,

$$ {c}_i^{ss}=\Big\{{\displaystyle \begin{array}{cc}{c}^{\ast },& i=1\\ {}{c}^{\ast}\sum \limits_{j=2}^{N-1}{\left[{R}^{\prime -1}\right]}_{i-1,j-1}{v}_j,& i=2,\dots, N-1\\ {}0,& i=N\end{array}} $$
(2)

where R’−1 is the matrix inverse of R'. Finally, the storage capacity S corresponding to a concentration profile c(z) is computed by integrating over the concentration profile and multiplying with the membrane surface area A,

$$ S=A\int c(z) dz\approx A\sum \limits_i{c}_i\varDelta z $$
(3)

where in the second equation, the integral was approximated by the discretisation with bin width Δz.

3 Results and Discussion

First, we calculated the concentration profile under an oxygen gradient (Eq. 2) in the setups without bilayer, with one bilayer, and with n stacked bilayers. The steady-state profiles for the POPC membrane are shown for n = 5 in Fig. 3a. The setup of pure water gives a simple linear slope (black line), while the presence of a membrane clearly introduces a high peak in oxygen concentration (blue dashed line). Increasing the number of stacked membranes creates additional peaks (green line), whose height drops linearly with each additional peak.

Fig. 3
Two graphs illustrate steady-state concentration and enhancement. Graph A displays decreasing trends for the water, 1 P O P C membrane, and 5 P O P C membranes. Graph B displays increasing trends for P O P C and M I T O.

(a) Steady-state concentration profile under oxygen gradient (in units c*) with c = c* to the left and c = 0 to the right, for n = 5. Setup 1 with only water (black), setup 2 with 1 POPC membrane (blue dashed) and setup 3 with n = 5 stacked POPC membranes (green), as shown in Fig. 2b. (b) Stacking enhancement E(n) = S(n)/S(1) is the ratio of storage capacity between n stacked bilayers and one bilayer, under a steady-state oxygen gradient over the membrane(s). S(1) and S(n) correspond to setup 2 and setup 3 in Fig. 2, respectively

Full size image

The stacking enhancement of adding bilayers is quantified by E(n) = S(n)/S(1), which is the ratio between storage in n stacked bilayers versus storage in 1 bilayer (setup 2 and setup 3 in Fig. 2). The membrane area A (Eq. 3) drops out of this ratio, and E(n) has no unit. Fig. 3b depicts the stacking enhancement E(n) for the POPC and MITO membranes, which shows that the stacking enhancement increases with the number n of stacked membranes. This indeed suggests that myelin sheaths may function as a reservoir for oxygen storage in the nervous system, making oxygen readily available to COX in the nearby mitochondria.

Interestingly, stacked bilayers not only have more peaks in Fig. 3a, but the first peak of the stacked bilayers (green) is also higher compared to the case of a single bilayer (blue dashed). This again favours the enhancement in stacked membranes compared to a single bilayer. The higher peak is explained by the fact that the nearby second peak also provides a source of oxygen.

Moreover, the slope of the curve in Fig. 3b becomes less steep with increasing n, meaning that stacking an additional membrane onto a thick layer of stacked membranes has less impact. In other words, stacking a 51st membrane on top of 50 stacked membranes has less impact on the stacking enhancement than stacking an 11th membrane on top of 10 stacked membranes. Therefore, it seems plausible that, for a certain stacking number, a trade-off may be reached between stacking enhancement and the extent of the physical space occupied by the membranes. Indeed, in electron microscopy images, myelin sheaths often consist of about 10–300 bilayers but not thousands [5].

The storage efficiency also depends on the intrinsic storage capacity of a single bilayer. The ratio S(1)/S(0) is a measure for the content in a single bilayer compared to a slab of pure water with the same dimension. For POPC, this ratio amounts to S(1)/S(0) ≈ 8 in the steady-state regime using a membrane thickness of approximately 5.2 nm. Because of the linearity of the rate model and the symmetry of the considered setups, we can conclude that the latter ratio is equivalent to the ratio of storage in a membrane versus storage in the water phase in equilibrium. This is also known as the membrane partitioning constant Km, of which the study was initiated over a century ago with Overton’s rule. In short, S(1)/S(0) = Km = cmem/cwat, with cmem and cwat the equilibrium oxygen concentration in the membrane and water phase, respectively.

Concretely, the POPC membrane stores about 8 times more oxygen molecules than can be stored in pure water. For example, let us assume a partial oxygen pressure of ~10 mmHg, which lies in the reported 10–34 mmHg range for brain tissue [15]. At atmospheric pressure and body temperature, the partial oxygen pressure is 159 mmHg, and the solubility of oxygen in water is approximately 7.187 mg/L [16]. Therefore, the 10 mmHg partial oxygen pressure corresponds to an oxygen concentration of (10/159) · 7.187 mg/L = 0.45 mg/L. Next, the steady-state profile over 10 stacked POPC membranes under this oxygen gradient (c* = 0.45 mg/L to the left of the stack, while c = 0 to the right of the stack) is computed with Eq. 2, and similarly for pure water. Finally, the storage per area (S/A) follows from Eq. 3, resulting in about 1791/μm2 oxygen molecules available in the membrane stack, compared to 226/μm2 oxygen molecules in a similarly sized slab of water.

Next, it is tested how the bilayer spacing influences the enhancement provided by the stacked membranes. The pathophysiology of cancer cells may show abnormal microvasculature and defective microcirculatory function, such as an increase in interstitial fluid [17, 18]. Moreover, abnormal myelination can also occur following trauma to a central nervous system tract, where myelin sheath swelling and decompaction have been observed, even in myelin that is spatially separated from the primary injury [19, 20]. Here, structural loss in the membrane stacking is modeled by increasing the thickness of the aqueous phase between the stacked bilayers. These additional water layers will decrease the total permeability [21], but they might also affect the storage capacity. Fig. 4 shows the enhancement S(n)/S(0) for n = 10 stacked bilayers, comparing the storage in 10 bilayers with the storage in pure water, while the stacking periodicity d (indicated in Fig. 2b) is gradually increased. At the left of the figure, the periodicity d = 5.2 nm corresponds to 10 stacked POPC membranes without additional water, as was simulated in Fig. 3b. Figure 4 clearly shows that an increase in stacking periodicity d can cause a strong decrease in the storage enhancement by the stacked bilayers, indicating that additional water between the myelin layers affects the storage efficiency in a negative way. This can be understood by comparing the contributions to the total storage by the membrane and by the interstitial water. The oxygen storage in water becomes larger for increasing d, simply because there is more interstitial water. In contrast, the oxygen storage in the membranes is fairly independent of d. Thus, for increasing periodicity d, the relative contribution of the bilayers to the total oxygen storage becomes smaller, and consequently a highly distorted membrane stack will gradually lose its function as a compact oxygen reservoir.

Fig. 4
A graph plots S of 10 divided by S of 0 versus d in nanometers. It illustrates a concave up, decreasing curve that starts at (6, 8) and ends at (19, 3). The values are approximated.

Enhancement S(n)/S(0) in stacked membranes for n = 10, as a function of stacking periodicity d

Full size image

4 Conclusion

A phospholipid membrane has a higher solubility for molecular oxygen compared to pure water. By calculating the steady-state concentration over a membrane under an oxygen gradient, we have shown that the oxygen storage capacity S can be even more enhanced by stacking multiple bilayers, as is the case in myelin sheaths of axons in the nervous system. The stacking enhancement levels out when many membranes are stacked, meaning that beyond a certain number of stacked membranes, stacking even more would have limited efficiency. This could explain why myelin sheaths appear to consist of 10–300 stacked bilayers but not thousands. Finally, the enhancement is negatively affected by an increase of the aqueous phase between the bilayers, which can for instance occur in cancer cells with more disordered stacking geometry.