Abstract
We study the local and (bipartite) entanglement Rényi entropies of the free Fermi gas in multi-dimensional Euclidean space  in thermal equilibrium. We prove positivity of the entanglement entropies with Rényi index γ ≤ 1 for all temperatures T > 0. Furthermore, for general γ > 0 we establish the asymptotics of the entropies for large T and large scaling parameter α > 0 for two different regimes—for fixed chemical potential
in thermal equilibrium. We prove positivity of the entanglement entropies with Rényi index γ ≤ 1 for all temperatures T > 0. Furthermore, for general γ > 0 we establish the asymptotics of the entropies for large T and large scaling parameter α > 0 for two different regimes—for fixed chemical potential  and also for fixed particle density ρ > 0. In particular, we thereby provide the last remaining building block for a complete proof of our low- and high-temperature results presented (for γ = 1) in J. Phys. A: Math. Theor. 49, 30LT04 (2016); [Corrigendum. 50, 129501 (2017)], but being supported there only by the basic proof ideas.
and also for fixed particle density ρ > 0. In particular, we thereby provide the last remaining building block for a complete proof of our low- and high-temperature results presented (for γ = 1) in J. Phys. A: Math. Theor. 49, 30LT04 (2016); [Corrigendum. 50, 129501 (2017)], but being supported there only by the basic proof ideas.
In memory of Harold Widom (1932–2021)
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Non-smooth functions of Wiener–Hopf operators
- Asymptotic trace formulas
- Rényi (entanglement) entropy of fermionic equilibrium states
Mathematics Subject Classification (2020)
1 Introduction
This section briefly describes the physical background, introduces the most important mathematical definitions, and provides a summary of the main results.
1.1 Physical Background
Over the last decades the so-called entanglement entropy (EE) has become a useful single-number quantifier of non-classical correlations between subsystems of a composite quantum-mechanical system [1, 14]. For example, one may imagine a macroscopically large system consisting of a huge number of particles in the state of thermal equilibrium at some (absolute) temperature T ≥ 0. All the particles inside some bounded spatial region Λ may then be considered to constitute one subsystem and the particles outside of Λ another one. The corresponding EE, more precisely the spatially bipartite thermal EE, now quantifies, to some extent, how strongly these two subsystems are correlated “across the interface” between Λ and its complement.
In the simplified situation where the particles do not dynamically interact with each other, such as in the ideal gas or, slightly more general, in the free gas, all possible correlations are entirely due to either the Bose–Einstein or the (Pauli–) Fermi–Dirac statistics by the assumed indistinguishability of the (point-like and spinless) particles.The present study is devoted to the latter case. Accordingly, we consider the free Fermi gas [3, 7, 10] infinitely extended in the Euclidean space  of an arbitrary dimension d ≥ 1. Although the fermions neither interact with each other nor with any externally applied field, their EE remains a complicated function of the region
of an arbitrary dimension d ≥ 1. Although the fermions neither interact with each other nor with any externally applied field, their EE remains a complicated function of the region  which is difficult to study by analytical methods. In general one can only hope for estimates and asymptotic results for its (physically interesting) growth when Λ is replaced with αΛ where the scaling parameter α > 0 becomes large. A decisive progress towards the understanding of the growth of the EE at T = 0, in other words of the ground-state EE, is due to Gioev and Klich [11, 12]. They observed, remarkably enough, that this growth is related to a conjecture of Harold Widom [28, 31] about the quasi-classical Szegő-type asymptotics for traces of (smooth) functions of multi-dimensional versions of truncated Wiener–Hopf operators with discontinuous symbols. After Widom’s conjecture had been proved by one of us [21, 23] the gate stood open to confirm [16] the precise (leading) large-scale growth conjectured in [12] and, in addition, to establish its extension from the von Neumann EE to the whole one-parameter family of (quantum) Rényi EE’s.
which is difficult to study by analytical methods. In general one can only hope for estimates and asymptotic results for its (physically interesting) growth when Λ is replaced with αΛ where the scaling parameter α > 0 becomes large. A decisive progress towards the understanding of the growth of the EE at T = 0, in other words of the ground-state EE, is due to Gioev and Klich [11, 12]. They observed, remarkably enough, that this growth is related to a conjecture of Harold Widom [28, 31] about the quasi-classical Szegő-type asymptotics for traces of (smooth) functions of multi-dimensional versions of truncated Wiener–Hopf operators with discontinuous symbols. After Widom’s conjecture had been proved by one of us [21, 23] the gate stood open to confirm [16] the precise (leading) large-scale growth conjectured in [12] and, in addition, to establish its extension from the von Neumann EE to the whole one-parameter family of (quantum) Rényi EE’s.
In the present study we only consider the case of a true thermal state characterized by a strictly positive temperature T > 0 (and a chemical potential  or, equivalently, a spatial particle-number density ρ > 0). On the one hand, the case T > 0 is simpler, because the Fermi function
\(E\mapsto 1/\big (1+\exp (E/T)\big )\) on the real line
or, equivalently, a spatial particle-number density ρ > 0). On the one hand, the case T > 0 is simpler, because the Fermi function
\(E\mapsto 1/\big (1+\exp (E/T)\big )\) on the real line  is smooth in contrast to its zero-temperature limit, the Heaviside unit-step function. On the other hand, a reasonable definition of the EE (see (8)) is more complicated, because the thermal state is not a pure state. Nevertheless, due to the presence of the “smoothing parameter” T > 0 the leading asymptotic growth of the EE as α →∞, is determined by an asymptotic coefficient again going back to Widom [27, 30], see also [8, 19]. We introduce it in (17) and denote it by \(\mathcal B\).
is smooth in contrast to its zero-temperature limit, the Heaviside unit-step function. On the other hand, a reasonable definition of the EE (see (8)) is more complicated, because the thermal state is not a pure state. Nevertheless, due to the presence of the “smoothing parameter” T > 0 the leading asymptotic growth of the EE as α →∞, is determined by an asymptotic coefficient again going back to Widom [27, 30], see also [8, 19]. We introduce it in (17) and denote it by \(\mathcal B\).
From a physical point of view it is interesting to study the scaling asymptotics α →∞ as the temperature T varies. The emerging double asymptotics of the EE and of the coefficient \(\mathcal B\) are not simple to analyze and hard to guess by heuristic arguments. For low temperatures, that is, small T > 0, this analysis has been performed in [18] for d = 1 and in [25] for d ≥ 2 yielding a result consistent with that for T = 0 in [12, 16].
At high temperatures quantum effects become weaker and the free Fermi gas should exhibit properties of the corresponding classical free gas without correlations (for fixed particle density). In particular, the ideal Fermi gas [3, 10] should behave like the Maxwell–Boltzmann gas, the time-honored “germ cell” of statistical mechanics. Hence the main purpose of our study is to determine the precise two-parameter asymptotics of the EE as α →∞ and T →∞.
1.2 Pseudo-Differential Operators and Entropies
At first we introduce the translation invariant pseudo-differential operatorFootnote 1

Here the smooth real-valued function a is its underlying symbol, u is an arbitrary complex-valued Schwartz function, and α > 0 is the scaling parameter. Informally, one may think of \( \operatorname {\mathrm {{Op}}}_\alpha (a)\) as the function a(−(i∕α)∇) of the gradient operator  , that is, the vector of partial derivatives with respect to x = (x
1, x
2, …, x
d).
, that is, the vector of partial derivatives with respect to x = (x
1, x
2, …, x
d).
The main role will be played by the truncated Wiener–Hopf operator

where χ
Λ is the (multiplication operator corresponding to the) indicator function of the “truncating” open set  . Clearly, for a bounded symbol a the operators \( \operatorname {\mathrm {{Op}}}_\alpha (a)\) and W
α(a;Λ) are bounded on the Hilbert space
. Clearly, for a bounded symbol a the operators \( \operatorname {\mathrm {{Op}}}_\alpha (a)\) and W
α(a;Λ) are bounded on the Hilbert space  . Given a test function
. Given a test function
 , we are interested in the operator f(W
α(a, Λ)) and in the operator difference
, we are interested in the operator f(W
α(a, Λ)) and in the operator difference

where the symbol f ∘ a is the composition of f and a defined by  .
.
For a bounded Λ and suitable a and f both operators on the right-hand side of (2) belong individually to the trace class. Remarkably, its difference does so even for a large class of unbounded Λ, see Condition 2.1 and Proposition 2.6 below. Our analysis of the scaling behavior of the entropies will be based on the asymptotics for the trace of D α(a, Λ;f) as α →∞. The reciprocal parameter α −1 can be naturally viewed as the Planck constant, and hence the limit α →∞ can be regarded as the quasi-classical limit. By a straightforward change of variables the operator (2) is seen to be unitarily equivalent to D 1(a, αΛ;f), so that α →∞ can be interpreted also as a spatial large-scale limit. In our large-scale applications it is either α itself or a certain combination of α with the temperature T that will become large.
The macroscopic thermal equilibrium state of the free Fermi gas depends, first of all, on its (classical) single-particle Hamiltonian  , sometimes also called the energy-momentum (dispersion) relation. The minimal conditions that we impose on h are as follows. We assume that h is smooth in the sense that
, sometimes also called the energy-momentum (dispersion) relation. The minimal conditions that we impose on h are as follows. We assume that h is smooth in the sense that  and that it satisfies the bounds
and that it satisfies the bounds

for some constant m > 0. Here  and the notations \(\partial _{\boldsymbol \xi }^n\), \(\lesssim \) , ≳ are defined at the end of the Introduction.
and the notations \(\partial _{\boldsymbol \xi }^n\), \(\lesssim \) , ≳ are defined at the end of the Introduction.
For given h, temperature T > 0, and chemical potential  we introduce the Fermi symbol as the composition of the Fermi function and the “shifted” Hamiltonian h − μ by
we introduce the Fermi symbol as the composition of the Fermi function and the “shifted” Hamiltonian h − μ by

Next, we introduce the (bounded and continuous) entropy function
 for each Rényi index
γ > 0. For γ ≠ 1 it is defined by
for each Rényi index
γ > 0. For γ ≠ 1 it is defined by

and for γ = 1, the von Neumann case, it is given by the point-wise limit

Finally, we define the (Rényi) local entropy associated with a bounded region Λ as the trace

and the (Rényi) entanglement entropy (EE) for the bipartition  as
as

This definition is motivated by the notion of mutual information, see e.g. [1, Eq. (9)]. The conditions (3) guarantee that these entropies are well-defined, see the paragraph after Proposition 2.6. In formula (8) either Λ or its complement  is assumed to be bounded, see Sect. 2 for details. It is useful to observe, as in (26) of [17], that the local entropy (7) can be expressed as
is assumed to be bounded, see Sect. 2 for details. It is useful to observe, as in (26) of [17], that the local entropy (7) can be expressed as
Here |Λ| is the volume (Lebesgue measure) of the bounded region Λ and

is the spatial entropy density. For γ = 1 it is the usual thermal entropy density [3, 7].
1.3 Summary of the Main Results
Our first result is of non-asymptotic nature. In Sect. 3 we explore concavity properties of the function η γ. First we notice that η γ is concave on the unit interval [0, 1] for all γ ∈ (0, 2], so that for a bounded Λ one can use a Jensen-type trace inequality to establish a lower bound for the local entropy (7) in terms of the entropy density (10), see Theorem 3.3. For the EE (8) this argument is not applicable, but we observe that η γ for γ ∈ (0, 1] is even operator concave so that the Davis operator inequality (32) implies the positivity of the EE for γ ∈ (0, 1] (including the most important case γ = 1 corresponding to the von Neumann EE), see Theorem 3.5. We do not know whether the EE is positive for γ ∈ (1, 2]. Later on however, we will see that the EE for γ ∈ (1, 2] is positive at least for large T, see Remark 2 and 5 in Sect. 6.3.
The other main objective of the present paper is to study the asymptotics of Hγ(T, μ;αΛ) as α →∞ and T →∞. For this, we have to impose conditions on the Hamiltonian h stronger than those in (3), see Sect. 5.1. In particular, h should be asymptotically homogeneous as |ξ|→∞. We distinguish between two high-temperature cases: the case of a constant chemical potential  and the case where the mean particle density
and the case where the mean particle density

being finite by (3), is (asymptotically) fixed to a prescribed constant ρ > 0, as T becomes large. The latter case implies that the chemical potential effectively becomes a function of T (and ρ) in the sense that
This corresponds to the quasi-classical limit of the free Fermi gas at fixed particle density. Indeed, since the so-called integrated density of states

of the single-particle Hamiltonian h, evaluated at T, tends to infinity as T →∞, one has \(\rho /\mathcal N(T)\to 0\). In physical terms, the spatial density of the number of particles is much smaller than that of the number of occupiable single-particle states with (eigen)energies below T, when T is sufficiently large. Therefore the restrictions by the Pauli exclusion principle are negligible.
Our results on the high-temperature scaling asymptotics are presented in Theorem 6.1 (for constant μ) and in Theorem 6.3 (for constant ρ). We postpone the discussion of these theorems until Sect. 6. Here we only mention two important facts: a) in both regimes the asymptotics still hold if T →∞ and the scaling parameter α is fixed, e.g. α = 1, b) the EE with Rényi index γ > 2 becomes negative for fixed particle density at high temperature; the same happens for fixed chemical potential at large γ. This suggests that values γ > 2 are only of limited physical interest.
The main asymptotic orders as α →∞ and T →∞ have been presented (without precise pre-factors and proofs) in [17], in the cases of fixed μ and fixed ρ, for γ = 1 and all d ≥ 1. Here we provide complete proofs for all γ > 0, but concentrate on the multi-dimensional case d ≥ 2. The case d = 1 is not considered for lack of space.
The paper is organized as follows. In Sect. 2 we present the basic information such as our conditions on the truncating region and the definition of the asymptotic coefficient \(\mathcal B\). Section 2 also contains the results, borrowed mostly from [26], that are used throughout the paper. In Sect. 3 we study the concavity of the function η γ and investigate the positivity of the corresponding entanglement entropy. In Sect. 4 we derive elementary trace-class bounds for some abstract bounded (self-adjoint) operators. These bounds are based on estimates for quasi-commutators of the form f(A)J − Jf(B) with bounded J, bounded self-adjoint A, B, and suitable functions f. By using such bounds in Sect. 5 we obtain the large α and T asymptotics for the trace of the operator D α(p T, Λ;f) with a symbol p T modeling the Fermi symbol (4) in the fixed μ or fixed ρ regimes. In Sect. 6 we collect our results on the high-temperature asymptotics for the EE (8), see Theorems 6.1 and 6.3. Their proofs are directly based on the formulas obtained in Sect. 5. In Sect. 6.3 we also comment on the asymptotics of the local entropy (7). The Appendix contains a short calculation clarifying the structure of the Fermi symbol when the mean particle density is fixed as T →∞.
Throughout the paper we adopt the following standard notations. For two positive numbers (or functions) X and Y , possibly depending on parameters, we write \(X\lesssim Y\) (or Y ≳ X) if X ≤ CY with some constant C ≥ 0 independent of those parameters. If \(X\lesssim Y\) and X ≳ Y , then we write X ≍ Y . To avoid confusion we often make explicit comments on the nature of the (implicit) constants in the bounds. For multiple partial derivatives we use the notation \(\partial _{\boldsymbol \xi }^n := \partial _{\xi _1}^{n_1}\partial _{\xi _2}^{n_2}\cdots \partial _{\xi _d}^{n_d}\) for a vector  and a multi-index
and a multi-index  of order
of order  . By B(z, R) we mean the open ball in
. By B(z, R) we mean the open ball in  with center
with center  and radius R > 0. We also use the weight function
and radius R > 0. We also use the weight function  for any vector
for any vector  .
.
The notation \(\mathfrak S_p\), p ∈ (0, ∞), is used for the Schatten–von Neumann classes of compact operators on a complex separable Hilbert space \(\mathcal H\), see e.g. [6, Chapter 11]. By definition, the operator A belongs to \(\mathfrak S_p\) if  . The functional ∥⋅∥p on \(\mathfrak S_p\) is a norm if p ≥ 1 and a quasi-norm if p < 1. Apart from Sect. 4, where the space \(\mathcal H\) is arbitrary, we assume that
. The functional ∥⋅∥p on \(\mathfrak S_p\) is a norm if p ≥ 1 and a quasi-norm if p < 1. Apart from Sect. 4, where the space \(\mathcal H\) is arbitrary, we assume that  .
.
We dedicate this paper to the memory of Harold Widom (1932–2021). His ground-breaking results on the asymptotic expansions for traces of pseudo-differential operators have been highly influential to many researchers including us. Without his results the present contribution and our previous ones to the study of fermionic entanglement entropy would have been unthinkable. We are deeply indebted to Widom’s ingenious insights. All three of us had the honor and pleasure of meeting him at a memorable workshop in March 2017 hosted by the American Institute of Mathematics (AIM) in San Jose, California, USA.
2 Basic Definitions and Basic Facts
In this section we collect some definitions and facts from [26] concerning the trace of (2) and its asymptotic evaluation. They are instrumental in the proof of our main asymptotic results corresponding to a = a T,μ and f = η γ. Throughout the rest of the paper we always assume d ≥ 2 for the spatial dimension.
2.1 Conditions on the Truncating Region Λ
We call an open and connected set  a Lipschitz domain, if it can be described locally as the epigraph of a Lipschitz function, see [22, 23] for details. We call Λ a Lipschitz region, if it is a union of finitely many Lipschitz domains such that their closures are pair-wise disjoint. From now on we always assume that Λ satisfies the following condition. Nevertheless, for convenience we will often mention it.
a Lipschitz domain, if it can be described locally as the epigraph of a Lipschitz function, see [22, 23] for details. We call Λ a Lipschitz region, if it is a union of finitely many Lipschitz domains such that their closures are pair-wise disjoint. From now on we always assume that Λ satisfies the following condition. Nevertheless, for convenience we will often mention it.
Condition 2.1
-
1.
The set
 is a Lipschitz region, and either Λ or
is a Lipschitz region, and either Λ or
 is bounded.
is bounded.
-
2.
The boundary (surface) ∂Λ is piece-wise C 1 -smooth.
We note that Λ and  satisfy Condition 2.1 simultaneously.
satisfy Condition 2.1 simultaneously.
2.2 The Asymptotic Coefficient \(\mathcal B\) and Its Basic Properties
We assume the real-valued symbol to be smooth in the sense that  and satisfies the decay condition
and satisfies the decay condition
for all  and all
and all  with some implicit constants that may depend on n.
with some implicit constants that may depend on n.
Before stating the leading asymptotic formula for \( \operatorname {\mathrm {{tr}}} D_\alpha (a, \varLambda ; f)\) as α →∞, we need to introduce the corresponding asymptotic coefficient. For a function  and any
and any  we consider the integral
we consider the integral

It is well-defined for any Hölder continuous f. And it is positive if f is also concave.
For every unit vector  we define a functional of the symbol a by the principal-value integral:
we define a functional of the symbol a by the principal-value integral:

Finally we define the main asymptotic coefficient by

where n x is the (unit outward) normal vector at the point x ∈ ∂Λ and σ is the canonical (d − 1)-dimensional area measure on the boundary surface ∂Λ.
For functions  with bounded second derivative and for a symbol a obeying the condition (14) the integral (16) exists in the usual sense and is bounded uniformly in e. Hence (17) is also finite, see [26, Section 3]. However, in order to accommodate the entropy function η
γ we allow for test functions being non-smooth in the sense of the following condition.
with bounded second derivative and for a symbol a obeying the condition (14) the integral (16) exists in the usual sense and is bounded uniformly in e. Hence (17) is also finite, see [26, Section 3]. However, in order to accommodate the entropy function η
γ we allow for test functions being non-smooth in the sense of the following condition.
Condition 2.2
The function f is in
 , where
, where
 is a finite set of its singular points. Moreover, for some δ > 0 and all R > 0 the function f = f
(0)
and its first two derivatives satisfy the bounds
is a finite set of its singular points. Moreover, for some δ > 0 and all R > 0 the function f = f
(0)
and its first two derivatives satisfy the bounds
for all \(t\in [-R, R]\setminus \mathcal T\) with an implicit constant that may depend on R.
Under this condition \(\mathcal B(a, \partial \varLambda ; f)\) is finite:
Proposition 2.3 ([26, Corollary 3.4])
Let the set Λ satisfy Condition 2.1 and let the function f satisfy Condition 2.2 with δ > 0. Finally, let the symbol a satisfy (14), but this time with some \(\beta > d\,\max \{1, 1/\delta \}\) . Then the coefficient \(\mathcal B(a, \partial \varLambda ; f)\) is finite.
We point out a few simple properties of this coefficient.
Remark 2.4
-
1.
Since \(\mathcal A(a, \mathbf e; f) = \mathcal A(a, -\mathbf e; f)\), the coefficients \(\mathcal B\) for the regions Λ and
 coincide.
coincide. -
2.
By definition (15), the coefficient (17) is positive for concave functions f and negative for convex ones. For example, the function η γ with γ ∈ (0, 2] is concave on the interval [0, 1] (see Lemma 3.1) so that \(\mathcal B(a, \partial \varLambda ; \eta _\gamma )\ge 0\) for symbols a taking values only in [0, 1], like the Fermi symbol a T,μ.
-
3.
If the symbol a is spherically symmetric (for example, by spherical symmetry of the Hamiltonian h in a T,μ), then the surface area |∂Λ| factors out of \(\mathcal B(a, \partial \varLambda ; f)\). Nevertheless, the remaining integral is still hard to compute for general a and f. See, however, Remark 2 in Sect. 6.3 for Gaussian a and quadratic f.
A less obvious property of the coefficient \(\mathcal B(a, \partial \varLambda ; f)\) is its continuity in the symbol a. Since it is important for our purposes, we state a corresponding result. In the next and subsequent assertions we consider a one-parameter family of symbols {a 0, a λ}, λ > 0, all of them satisfying (14) with some \(\beta > d\,\max \{1,\delta ^{-1}\}\), uniformly in λ, and point-wise convergence a λ → a 0 as λ ↓ 0.
Proposition 2.5 ([26, Corollary 3.5])
Let the set Λ and the function f be as in Proposition 2.3 . Then
2.3 The Asymptotics for \( \operatorname {\mathrm {{tr}}} D_\alpha (a, \varLambda ; f)\) as α →∞
Now we are in a position to state the required asymptotic facts.
Proposition 2.6 ([26, Theorem 2.3])
Let the set Λ, the function f, and the symbol a be as in Proposition 2.3 . Then the operator D α(a, Λ;f) is of trace class and
This limit is uniform in the class of symbols a that satisfy (14) with the same implicit constants.
Proposition 2.6 ensures the existence of the entropies (7) and (8). In fact, assume that Λ satisfies Condition 2.1 and that the Hamiltonian h in the Fermi symbol a
T,μ of (4) is as specified in (3). Then a
T,μ satisfies (14) for all T > 0 and  . Moreover, the function η
γ satisfies Condition 2.2 for all γ > 0 with arbitrary \(\delta < \min \{1, \gamma \}\) and the set \(\mathcal T = \{0, 1\}\). Thus, due to Proposition 2.6, the operators D
1(a
T,μ, Λ;η
γ) and
. Moreover, the function η
γ satisfies Condition 2.2 for all γ > 0 with arbitrary \(\delta < \min \{1, \gamma \}\) and the set \(\mathcal T = \{0, 1\}\). Thus, due to Proposition 2.6, the operators D
1(a
T,μ, Λ;η
γ) and  are of trace class, so that the entanglement entropy (8) is finite. If we additionally assume that Λ is bounded, then by (9) also the local entropy (7) is finite.
are of trace class, so that the entanglement entropy (8) is finite. If we additionally assume that Λ is bounded, then by (9) also the local entropy (7) is finite.
Proposition 2.6 was also used in [26] to determine the scaling asymptotics for the entanglement entropy at fixed temperature. To study the high-temperature regime, we need the continuity of this result in the symbol a:
Corollary 2.7
Let the set Λ and the function f be as in Proposition 2.3 . Then
where the limits α →∞ and λ → 0 are taken simultaneously.
Proof
According to Proposition 2.6,
uniformly in λ. Together with (19) this leads to (20). □
The next two propositions describe the asymptotics for “small” symbols.
Proposition 2.8 ([26, Theorem 2.5])
Let the set Λ satisfy Condition
2.1
and let f
0
be the function defined by f
0(t) := M|t|δ
with real constants M and δ > 0. Finally, suppose that the function
 satisfies the conditions
satisfies the conditions
Then
In the next proposition we consider instead of the homogeneous function f 0 the function η defined by

which still leads to an asymptotically homogeneous behavior.
Proposition 2.9 ([26, Theorem 2.6])
Let the set Λ satisfy Condition
2.1
and suppose that the function
 satisfies the conditions
satisfies the conditions
Then
We note that under any of the assumptions (21) and (23) the function f satisfies Condition 2.2 with \(\mathcal T = \{0\}\). For assumption (21) (resp. (23) ) the condition (18) holds with the constant δ from (21) (resp. arbitrary δ < 1).
The asymptotic results listed above are useful, but, as they stand, not directly applicable for our purposes. This is because our symbol of main interest, the Fermi symbol (4), depends on the two parameters T and μ, and in the course of our analysis in Sect. 5 we naturally come across certain “effective” symbols that do not satisfy conditions like (14) uniformly in these parameters. However, we overcome this problem by considering a wider class of symbols, called multi-scale symbols in [18, Section 3].
2.4 Multi-Scale Symbols
We consider symbols  for which there exist two continuous functions τ and v on
for which there exist two continuous functions τ and v on  with τ > 0, v > 0, v bounded, and such that
with τ > 0, v > 0, v bounded, and such that

with implicit constants independent of ξ. It is natural to call τ the scale (function) and v the amplitude (function). The scale τ is assumed to be globally Lipschitz continuous with Lipschitz constant \(\mathcal L<1\), that is,

Under this assumption the amplitude v is assumed to satisfy the bounds
with implicit constants independent of ξ and ξ ′. It is useful to think of τ and v as (functional) parameters. They, in turn, may depend on other parameters, e.g. numerical ones like α and T. For example, the results in the previous subsections are based on the assumption that a satisfies (14), which translates into (24) with τ(ξ) = 1 and v(ξ) = 〈ξ〉−β. On the other hand, in Sect. 5 we encounter amplitudes and scales depending on the temperature T.
Actually, we will only need the following result involving multi-scale symbols. As mentioned in the Introduction, ∥ ⋅ ∥p denotes the (quasi-)norm in the Schatten-von Neumann class \(\mathfrak S_p\) of compact operators. Below the underlying Hilbert space is  .
.
Proposition 2.10 ([18, Lemma 3.4])
Let the set Λ satisfy Condition 2.1 and let the functions τ and v be as described above. Suppose that the symbol a satisfies (24) and that the conditions

hold. Then for any q ∈ (0, 1] we have

This bound is uniform in the symbols a satisfying (24) with the same implicit constants.
We will make use of (28) in Sect. 5 by combining it with bounds obtained in Sect. 4.
3 The Positivity of Certain Entanglement Entropies
Given the organization of the paper, this section is a kind of interlude. It turns out that the property given by its title is present if the underlying entropy function η
γ, as defined in (5) and (6), is operator concave (when restricted from the real line  to its unit interval [0, 1]). Since this and related results are not of asymptotic character, we assume in this section α = 1 for the scaling parameter.
to its unit interval [0, 1]). Since this and related results are not of asymptotic character, we assume in this section α = 1 for the scaling parameter.
3.1 Concavity of the Entropy Function η γ for γ ≤ 2
We prove the property given by the title of this subsection and then establish consequences for the corresponding local and entanglement entropies. The next lemma is elementary.
Lemma 3.1
The entropy function η γ is concave on the interval [0, 1] if γ ∈ (0, 2], and neither convave nor convex if γ > 2.
Proof
By the continuity of η γ on [0, 1] its enough to check the sign of the second derivative of η γ on the open interval (0, 1). For γ = 1 we simply have \(\eta _1^{\prime \prime }(t) = - t^{-1}(1-t)^{-1}<0\) so that η 1 is concave. For γ ≠ 1 we use the formula
For γ < 1 the right-hand side is obviously negative for all t ∈ (0, 1). For γ = 2 it simply equals − 8t(1 − t) < 0. If γ > 2, then (29) implies ηγ(0) = γ∕(γ − 1) > 0 and ηγ(1∕2) = −4γ < 0. Hence η γ is neither concave nor convex.
It remains to consider the case γ ∈ (1, 2). We rewrite (29) as

for any  . Our claim g
p(t) ≥ 0 is equivalent to
. Our claim g
p(t) ≥ 0 is equivalent to
Using the abbreviation

the (elementary example of the) Young inequality
for a = [t(1 − t)]1−p , u = (1 − p)−1 and b = 1, v = p −1 yields
Since this coincides with (30), the proof is complete. □
The just established concavity is useful to find a lower bound on the local entropy (7) with γ ≤ 2, which is greater than the obvious bound 0. To this end, we recall a formulation [15, Theorem A.1] of an abstract Jensen-type trace inequality dating back to Berezin [5].
Proposition 3.2
Let
\(\mathcal H\)
be a complex separable Hilbert space, P an orthogonal projection on
\(\mathcal H\)
, A a self-adjoint operator on
\(\mathcal H\)
with its spectrum contained in the interval
 , and
, and
 a concave function. Finally, let
a concave function. Finally, let
 be of trace class and PAP compact. Then
\( \operatorname {\mathrm {{tr}}}\varDelta \ge 0\)
. If Δ and PAP are of trace class, than also the following trace inequality is valid:
be of trace class and PAP compact. Then
\( \operatorname {\mathrm {{tr}}}\varDelta \ge 0\)
. If Δ and PAP are of trace class, than also the following trace inequality is valid:
(If 0∉I, then the operator f(PAP) is understood to act on the subspace \(P\mathcal H\) ).
The following result is a corollary to Proposition 3.2.
Theorem 3.3
Let
 be bounded and satisfy Condition
2.1
. Assume that the Hamiltonian h satisfies (3) and that γ ∈ (0, 2]. Then the local entropy (7) obeys the inequality
be bounded and satisfy Condition
2.1
. Assume that the Hamiltonian h satisfies (3) and that γ ∈ (0, 2]. Then the local entropy (7) obeys the inequality
where s γ(T, μ) is the entropy density (10).
Proof
We use Proposition 3.2 with \(A = \operatorname {\mathrm {{Op}}}_1(a_{T, \mu })\), P = χ
Λ, and the concave function f = η
γ. Since  and PAP has ϱ(T, μ)|Λ|, see (11), as its finite trace, Proposition 3.2 is indeed applicable and yields \( \operatorname {\mathrm {{tr}}} D_1(a, \varLambda ; \eta _\gamma )\ge 0\). By (9) this entails (31). □
and PAP has ϱ(T, μ)|Λ|, see (11), as its finite trace, Proposition 3.2 is indeed applicable and yields \( \operatorname {\mathrm {{tr}}} D_1(a, \varLambda ; \eta _\gamma )\ge 0\). By (9) this entails (31). □
We stress that Proposition 3.2 cannot be applied if the set Λ is unbounded, since in this case the operator \(\chi _\varLambda \operatorname {\mathrm {{Op}}}_\alpha (a_{T, \mu })\chi _\varLambda \) is not necessarily compact. Thus Theorem 3.3 cannot be used to determine the sign of the entanglement entropy (8). But, fortunately, we can use the rather strong property as given by the title of the following subsection.
3.2 Operator Concavity of the Entropy Function η γ for γ ≤ 1
For the general background of this genre we recommend Simon’s comprehensive book [20]. Let \(\mathcal H\) be a complex separable Hilbert space of infinite dimension and {A, B} an arbitrary pair of bounded self-adjoint operators on \(\mathcal H\) with spectra in an interval  . A continuous function
. A continuous function  is called (decreasing) operator monotone if the (operator) inequality f(A) ≥ f(B) holds whenever A ≥ B. Likewise it is called operator concave if f(λA + (1 − λ)B) ≥ λf(A) + (1 − λ)f(B) holds for all λ ∈ [0, 1]. It is called operator convex if − f is operator concave. Of course, every operator monotone (operator concave) function is monotone (concave). We are going to use the following standard examples, see [2]:
is called (decreasing) operator monotone if the (operator) inequality f(A) ≥ f(B) holds whenever A ≥ B. Likewise it is called operator concave if f(λA + (1 − λ)B) ≥ λf(A) + (1 − λ)f(B) holds for all λ ∈ [0, 1]. It is called operator convex if − f is operator concave. Of course, every operator monotone (operator concave) function is monotone (concave). We are going to use the following standard examples, see [2]:
-
1.
The function t↦t p, t ∈ [0, ∞), is operator monotone and operator concave if p ∈ (0, 1].
-
2.
The function \(t\mapsto \ln (t)\), t ∈ (0, ∞), is operator monotone and operator concave.
-
3.
The function \(t\mapsto -t\ln (t)\), t ∈ [0, ∞), is operator concave.
Any operator concave function f satisfies [9, 13] the following Davis operator inequality for all bounded self-adjoint operators A with spectrum in I and all orthogonal projections P on \(\mathcal H\):
If 0∉I, then the operator f(PAP) is understood to act on the subspace \(P\mathcal H\). If 0 ∈ I and f(0) = 0, then (32) may be shortened to f(PAP) ≥ Pf(A)P.
Lemma 3.4
If γ ∈ (0, 1], then η γ is operator concave on the interval [0, 1].
Proof
It suffices to consider self-adjoint operators A and B with  . Assume first that γ < 1. The function
. Assume first that γ < 1. The function  is operator concave on [0, 1] (by example 1 above) and the logarithm is operator monotone on (0, 1] (example 2). Thus for all λ ∈ [0, 1] we have
is operator concave on [0, 1] (by example 1 above) and the logarithm is operator monotone on (0, 1] (example 2). Thus for all λ ∈ [0, 1] we have
Now, since the logarithm is also operator concave on (0, 1] (again example 2), the right-hand side is larger than or equal to
Hence η
γ, for γ < 1, is operator concave on (0, 1] and, by continuity, on [0, 1]. For γ = 1 we proceed more directly and use that  is operator concave on [0, 1] (example 3).This immediately implies that η
1(t) = g(t) + g(1 − t) is also operator concave on [0, 1]. □
is operator concave on [0, 1] (example 3).This immediately implies that η
1(t) = g(t) + g(1 − t) is also operator concave on [0, 1]. □
Now we can use the inequality (32) with f = η γ (for γ ∈ (0, 1]), P = χ Λ, and \(A= \operatorname {\mathrm {{Op}}}_1(a_{T,\mu })\). Combining this with Proposition 2.6 yields the following result.
Theorem 3.5
Let
 satisfy Condition
2.1
. Assume that the Hamiltonian h is as in (3) and that γ ∈ (0, 1]. Then both operators D
1(a
T,μ, Λ;η
γ) and
satisfy Condition
2.1
. Assume that the Hamiltonian h is as in (3) and that γ ∈ (0, 1]. Then both operators D
1(a
T,μ, Λ;η
γ) and
 are not only of trace class, but also positive. Hence the entanglement entropy (8) is positive.
are not only of trace class, but also positive. Hence the entanglement entropy (8) is positive.
This method cannot be used for the EE with γ > 1 because of the following negative result.
Theorem 3.6
If γ > 1, then η γ is not operator concave on the interval [0, 1].
Proof
For convenience, instead of η γ we consider the function

Our objective is to show that g γ is not operator convex on [−1∕2, 1∕2]. If g γ were operator convex, then by [4, Corollary 1], g γ would be analytic on the complex plane with cuts along the half-lines (−∞, −1∕2) and (1∕2, ∞). Let us prove that such an analytic continuation of g γ is impossible. To this end, let u = iy∕2 with y > 0. Then
so that
Since γ > 1, there exists a finite y 0 > 0 such that \(\gamma \tan ^{-1}(y_0) = \pi /2\), so that the right-hand side of (33) changes sign at y = y 0. This implies that the function g γ has a branching point at u = iy 0∕2, and hence cannot be analytic in the whole upper half-plane. This proves that g γ is not operator convex, as claimed. □
4 Quasi-Commutator Bounds
In this section we collect some bounds for the Schatten–von Neumann classes \(\mathfrak S_p\), p ∈ (0, ∞), of compact operators on a complex separable Hilbert space \(\mathcal H\), see e.g. [6, Chapter 11]. As mentioned at the end of the Introduction, the functional  defines a norm for p ≥ 1 and a quasi-norm for p < 1. It satisfies the following “triangle inequality”:
defines a norm for p ≥ 1 and a quasi-norm for p < 1. It satisfies the following “triangle inequality”:
This inequality is used systematically in what follows. The main part is played by estimates for quasi-commutators f(A)J − Jf(B) with bounded J and bounded self-adjoint A, B. The following fact is adapted from [24, Theorem 2.4].
Proposition 4.1
Suppose that f satisfies Condition 2.2 with some δ > 0. Let A, B be two bounded self-adjoint operators and let J be a bounded operator. Suppose that \(AJ-JB\in \mathfrak S_q\) where q satisfies \(0 < q < \min \{1, \delta \}\) . Then
with a constant independent of the operators A, B, J. This constant in (35) may depend on the set \(\mathcal T\) in Condition 2.2 , and is uniform in the functions satisfying (18) with the same implicit constants.
Actually, [24, Theorem 2.4] provides bounds of the type (35) in arbitrary (quasi-) normed operator ideals of compact operators and gives a more precise dependence on the constants related to the function f. For the present paper (35) is sufficient.
All subsequent bounds involving the function f are uniform in f in the sense specified in Proposition 4.1. We are going to apply Proposition 4.1 to obtain various bounds for the operator difference  with an orthogonal projection P.
with an orthogonal projection P.
Corollary 4.2
Let the function f and the parameter q be as in Proposition 4.1 . Let A, B be bounded self-adjoint operators and let J be a bounded operator such that
Then
and
The implicit constants in these bounds depend on the norms ∥A∥, ∥B∥, and ∥J∥, but they are uniform in the operators A, B, J whose norms are bounded by the same constants. They are also uniform in the functions f in the sense specified in Proposition 4.1.
Proof
The proof is based mainly on the bound (35). The assumption (36) considerably simplifies the calculations, and we use it without further comments.
For the proof of (37) we carry out the estimate for the first term on the left-hand side only, as the second one can be treated in the same way. We rewrite
Then we use (35) and (34) to estimate the first term on the right-hand side,
For the second term on the right-hand side of (39) we also use (35) and (34):
Adding up the above two estimates we get (37).
In order to prove (38) we first estimate the difference
Then we use (35) to estimate the first term on the right-hand side as follows
To estimate the second and the third term on the right-hand side of (40), we notice that \(\|f(A)\|\lesssim 1\), \(\|f(B)\|\lesssim 1\) uniformly in the operators A, B and in the function f. Consequently,
To summarize, the difference (40) has an upper bound like the one in the claim (38).
Finally we are going to derive such a bound also for the difference analogous to (40):
In view of (36), the first term on the right-hand side vanishes, and hence
By combining this with the upper bound on (40) and using the triangle inequality for the trace norm we arrive at (38). □
Corollary 4.3
Under the assumptions of Corollary
4.2
(with
 being the identity operator) we have
being the identity operator) we have

This bound is uniform in A, B, J and in the function f in the same sense as in Corollary 4.2.
Proof
We observe

and apply Corollary 4.2. □
5 High-Temperature Analysis
The purpose of this section is to obtain the large α and large T asymptotics for the trace of the operator D α(p T, Λ;f) with the symbol p T of (46), modeling the Fermi symbol (4) for large T. Throughout the section we assume that the function f satisfies Condition 2.2 with some δ > 0 and recall that this condition is guaranteed by assumption (21) as well as by assumption (23). We also continue to assume that the truncating region Λ satisfies Condition 2.1. Since Λ is always fixed, we omit it from the notation and simply write D α(p T;f) and \(\mathcal B(p_T; f)\). Recall that d ≥ 2 throughout.
5.1 Further Conditions on the Single-Particle Hamiltonian h
So far we assumed that the Hamiltonian h satisfies (3) with some m > 0. Now we need to impose on h more restrictive conditions. We assume that  and that for some constant \(m\in \mathbb N\), the following bounds hold:
and that for some constant \(m\in \mathbb N\), the following bounds hold:

Furthermore, we assume that there exists a function  which is homogeneous of degree 2m (that is, h
∞(t
ξ) = t
2m
h
∞(ξ) for all
which is homogeneous of degree 2m (that is, h
∞(t
ξ) = t
2m
h
∞(ξ) for all  and all t > 0), such that
and all t > 0), such that
The function h ∞ is assumed to be non-degenerate in the sense that

Homogeneity and non-degeneracy of h
∞ imply that h
∞≥ 0. It is clear that the conditions (42), (43) and (44) imply that h satisfies (3) with the constant m from (42). It is important to emphasize that from now on the constant m > 0 is supposed to be integer. This guarantees that the function h
∞ belongs to  which enables application of the results in Subsection 2.3 to the limiting symbols \((1+\mathrm {e}^{h_\infty })^{-1}\) and \(\mathrm {e}^{-h_\infty }\) featured in Sect. 6.
which enables application of the results in Subsection 2.3 to the limiting symbols \((1+\mathrm {e}^{h_\infty })^{-1}\) and \(\mathrm {e}^{-h_\infty }\) featured in Sect. 6.
5.2 Modeling the Fermi Symbol
Given two positive continuous functions T↦ϕ T ≥ 0 and T↦ω T > 0 on the temperature half-line [1, ∞) with the properties
we generalize the Fermi symbol a T,μ of (4) to the symbol p T by the definition

We also consider its “high-temperature limit” p ∞ naturally defined by

Theorem 5.1
Let p T be the symbol defined in (46). Then
as αT 1∕2m →∞ and T →∞.
We also consider the operator D α(λ T p T;f) with the symbol λ T p T, where λ T > 0 is, for the time being, an arbitrary continuous function of T that tends to zero as T →∞.
Theorem 5.2
Let f 0 be as in Proposition 2.8 and η be as in (22). Assume that αT 1∕2m →∞ and T →∞. Then the following implications hold:
-
1.
If
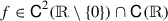 satisfies (21), then
$$\displaystyle \begin{aligned} \lim \big(\alpha T^{\frac{1}{2m}}\big)^{1-d}\lambda_T^{-\delta} \operatorname{\mathrm{{tr}}} D_\alpha(\lambda_T p_T; f) = \mathcal B(p_\infty; f_0)\,. \end{aligned} $$(49)
satisfies (21), then
$$\displaystyle \begin{aligned} \lim \big(\alpha T^{\frac{1}{2m}}\big)^{1-d}\lambda_T^{-\delta} \operatorname{\mathrm{{tr}}} D_\alpha(\lambda_T p_T; f) = \mathcal B(p_\infty; f_0)\,. \end{aligned} $$(49) -
2.
If
 satisfies (23), then
$$\displaystyle \begin{aligned} \lim \big(\alpha T^{\frac{1}{2m}}\big)^{1-d}\lambda_T^{-1} \operatorname{\mathrm{{tr}}} D_\alpha(\lambda_T\, p_T; f) = \mathcal B(p_\infty; \eta)\,.\end{aligned} $$(50)
satisfies (23), then
$$\displaystyle \begin{aligned} \lim \big(\alpha T^{\frac{1}{2m}}\big)^{1-d}\lambda_T^{-1} \operatorname{\mathrm{{tr}}} D_\alpha(\lambda_T\, p_T; f) = \mathcal B(p_\infty; \eta)\,.\end{aligned} $$(50)
To prove these two theorems we compare the operator D
α for two different symbols defined as follows. Firstly, we pick an arbitrary real-valued “cut-off” function  with w(ξ) = 0 if |ξ|≤ 1 and w(ξ) = 1 if |ξ|≥ 2. Moreover, we define two scaled versions of w by
with w(ξ) = 0 if |ξ|≤ 1 and w(ξ) = 1 if |ξ|≥ 2. Moreover, we define two scaled versions of w by

so that \(w_T \widetilde w_T = \widetilde w_T\). For a fixed number r ∈ (0, 1] we now consider the operators
They fulfill (36) and their (uniform) norms are uniformly bounded in T. Thus we can use Corollary 4.3 for the proof of the following “comparison lemma”:
Lemma 5.3
Assume that T ≳ 1 and \(\alpha (r T)^{\frac {1}{2m}}\gtrsim 1\) for a fixed r ∈ (0, 1]. Then, using (51), we have the trace norm estimate
with an implicit constant independent of α, T, and r.
Proof
Let us estimate the right-hand side of (41) and start with a bound for ∥[J, P]∥q, q ≤ 1. Since  , we use Proposition 2.10 with \(a = 1-\widetilde w_{rT}\). This symbol satisfies (24) with scale and amplitude functions
, we use Proposition 2.10 with \(a = 1-\widetilde w_{rT}\). This symbol satisfies (24) with scale and amplitude functions

with an arbitrary β > 0. Now we assume that βq > d. The conditions (25) and (26) are obviously satisfied, and hence Proposition 2.10 is applicable. We estimate the integral on the right-hand side of (28) as follows:

Thus, under our assumptions on α, T, and r the condition (27) is satisfied, and hence, by (28), we have
Estimating  and
and  is somewhat trickier. For the first commutator we are going to use Proposition 2.10 with the symbol \(a = (1-\widetilde w_{rT})p_T\). At first we estimate the derivatives of eh(ξ)∕T for \(|\boldsymbol \xi |\le 4(rT)^{\frac {1}{2m}}\) using (42):
is somewhat trickier. For the first commutator we are going to use Proposition 2.10 with the symbol \(a = (1-\widetilde w_{rT})p_T\). At first we estimate the derivatives of eh(ξ)∕T for \(|\boldsymbol \xi |\le 4(rT)^{\frac {1}{2m}}\) using (42):

Furthermore,
Therefore, we obtain from (46) that
with an arbitrary β > d∕q. Consequently, the symbol a satisfies (24) with the scale and amplitude

Again the conditions (25), (26), and (27) are satisfied, and we can use Proposition 2.10 to produce the bound

Thus by (28),

The bound for the commutator  is proved in the same way. Substituting the above bounds into the statement (41) of Corollary 4.3, we get the claimed estimate (52). □
is proved in the same way. Substituting the above bounds into the statement (41) of Corollary 4.3, we get the claimed estimate (52). □
A useful consequence of this fact is the following continuity statement:
Corollary 5.4
With the function w r defined in (51) and the symbol p ∞ defined in (47) we have
Proof
We apply Lemma 5.3 with h = h ∞, T = 1, and the constant functions ω ≡ ω ∞ and ϕ ≡ ϕ ∞. Then, for αr ≳ 1,
Therefore,
Now, we use Proposition 2.6 to obtain the estimate
This leads to (53), as claimed. □
We already have a result on the continuity of the asymptotic coefficient, see Proposition 2.5. However, this proposition is not applicable to the truncated symbol w r p T, since its derivatives are not bounded uniformly in r > 0. This explains why we need Corollary 5.4.
The next lemma provides the same asymptotics as in Theorems 5.1 and 5.2, but this time for w rT p T instead of p T. We recall that λ T > 0 obeys λ T → 0 as T →∞.
Lemma 5.5
Assume that r ∈ (0, 1] is fixed and that \(\alpha T^{\frac {1}{2m}}\to \infty , T\to \infty \) . Then
If f satisfies (21), then
If f satisfies (23), then
Proof
By a straightforward change of variables in definition (1), we obtain
where

Thanks to the condition (43), for all ξ ≠ 0, we have as T →∞:
Assuming that T ≳ 1, an elementary calculation using (42) leads to the bounds

with ν > 0 from (44) and implicit constants depending on the number r ∈ (0, 1]. Since b T satisfies (57) uniformly in T ≳ 1, we obtain by Corollary 2.7 that
By the above change of variables, this leads to (54). Formulas (55) and (56) follow along the same lines from Propositions 2.8 and 2.9. □
Proof (Of Theorem 5.1)
We begin by estimating as follows:
By (52) and (54) we then obtain
where the upper limit is taken as \( \alpha T^{\frac {1}{2m}}\to \infty \), T →∞. Taking r → 0 and using (53) we arrive at (48). □
Proof (Of Theorem 5.2)
We recall that the only singular point of the function f is t = 0. We assume that f satisfies (21), so that for all t ≠ 0,
Consequently, the function  ,
,  , satisfies the same inequalities with the same constants. Now we can apply the argument in the previous proof to the operator
, satisfies the same inequalities with the same constants. Now we can apply the argument in the previous proof to the operator
More precisely, we estimate as follows
By (52) and (55) we then obtain
where \(\limsup \) is taken as \( \alpha T^{\frac {1}{2m}}\to \infty \), T →∞. Taking r → 0 and using (53) we obtain (49).
Now we assume that f satisfies (23). We use (59) with δ = 1 and f 0 replaced by η. Then
As before, the last term on the right-hand side tends to zero due to (53). The second term vanishes as \( \alpha T^{\frac {1}{2m}}\to \infty \), T →∞ due to (56). To estimate the first term we represent f = η + g, so that g satisfies (58) with δ = 1. Therefore,
where  and
and  . As in the previous calculation, the second term is estimated with the help of (52) by \(r^{\frac {d-1}{2m}}\). Since \(\tilde \eta _T(t) = \eta (t) - t\ln (\lambda _T)\) and the operator difference (2) vanishes for linear functions f, we have
. As in the previous calculation, the second term is estimated with the help of (52) by \(r^{\frac {d-1}{2m}}\). Since \(\tilde \eta _T(t) = \eta (t) - t\ln (\lambda _T)\) and the operator difference (2) vanishes for linear functions f, we have
The function η from (22) satisfies (58) for all δ < 1, and hence by (52) the above difference is again estimated by \(r^{\frac {d-1}{2m}}\). This entails (50) and the proof of Theorem 5.2 is complete. □
6 Main Results on the High-Temperature Asymptotics
In this section we adapt Theorems 5.1 and 5.2 to two different asymptotic regimes of the entanglement entropy (8), when the temperature becomes large. This is straightforward for the (first) regime of a fixed chemical potential μ, since we work from the outset within the grand-canonical formalism [3, 7] for an indefinite number of particles. For the (second) regime of a fixed particle density ρ it is slightly more involved, but physically often more interesting. Both results will be discussed in some detail in Sect. 6.3.
6.1 Case of a Fixed Chemical Potential μ
Since the Fermi symbol a T,μ of (4) equals p T of (46) with ϕ T = 1 and \(\omega _T =\exp (-\mu /T)\), the limit symbol in this case is obviously \(p_\infty = (1+\mathrm {e}^{h_\infty })^{-1}\). For the function f we take η γ which satisfies Condition 2.2 with \(\mathcal T= \{0, 1\}\) and an arbitrary \(\delta < \min \{1, \gamma \}\). Thus, by combining definition (8), Remark 2.4(1), and Theorem 5.1 we obtain:
Theorem 6.1
Let the truncating region Λ satisfy Condition 2.1 . Then we have,
for any fixed
 , as
\(\alpha T^{\frac {1}{2m}}\to \infty \)
and T →∞.
, as
\(\alpha T^{\frac {1}{2m}}\to \infty \)
and T →∞.
6.2 Case of a Fixed Particle Density ρ
In this case we have to find a function T↦μ ρ(T) satisfying (12) for a fixed constant ρ > 0. According to the Appendix we have for any such function
with the function T↦λ T given explicitly by

This implies for the Fermi symbol at fixed ρ the formula
where p T is given by (46) with
By (61) and (62) we clearly have ϕ T → 0 and ω T → 1 as T →∞. Hence the limit symbol is the classical “Boltzmann factor” corresponding to h ∞:

To study the symbol \(a_{T, \mu _\rho (T)}\) we use Theorem 5.2 with f = η γ. For a start we need to understand the behavior of η γ(t) for small t. Since this behavior depends on γ, we need to distinguish five different regimes for its value. To state the result in a unified way for all values, we define a parameter δ γ and a pair of functions {f γ, \(\eta _\gamma ^{\mathrm {eff}}\)} on the interval [0,1] in Table 1.
The next lemma shows that \(\eta _\gamma ^{\mathrm {eff}}\) describes the effective asymptotic contribution of f γ as t ↓ 0.
Lemma 6.2
Let the parameter δ γ and the functions f γ, \(\eta _\gamma ^{\mathrm {eff}}\) on the interval (0, 1) be as defined in Table 1 . Then the following three asymptotic relations hold:
Proof
For γ ≠ 1 we expand η γ at t = 0 to obtain
The notation g(t) = O(t
b) means that \(|g^{(k)}(t)|\lesssim t^{b-k}\), for all  . This expansion leads to the claim (66) for all γ∉{1, 2}. For γ = 2 the expansion (67) is insufficient since the terms with t
2 cancel out. By including the third-order term explicitly we find \(\eta _2(t) = 2t - \frac {4}{3} t^3 + O(t^4)\) and obtain (66) for γ = 2. Finally, for γ = 1 we have \(\eta _1(t) =-t\ln (|t|) + t + O(t^2)\) which again leads to (66). □
. This expansion leads to the claim (66) for all γ∉{1, 2}. For γ = 2 the expansion (67) is insufficient since the terms with t
2 cancel out. By including the third-order term explicitly we find \(\eta _2(t) = 2t - \frac {4}{3} t^3 + O(t^4)\) and obtain (66) for γ = 2. Finally, for γ = 1 we have \(\eta _1(t) =-t\ln (|t|) + t + O(t^2)\) which again leads to (66). □
Now we are in a position to state and prove our second main result for the scaling of the entanglement entropy.
Theorem 6.3
Let the truncating region Λ satisfy Condition 2.1 . For a fixed number ρ > 0 let T↦μ ρ(T) be a function satisfying (12) and ϰ be as defined in (62). Finally, let δ γ and \(\eta _\gamma ^{\mathrm {eff}}\) be as defined in Table 1 . Then we have the asymptotic relation
as \(\alpha T^{\frac {1}{2m}}\to \infty \,\, \mathit{\mbox{and}}\,\,T\to \infty \).
Proof
We replace the symbol \(a_{T, \mu _\rho (T)}\) with λ T p T as specified in (64). Furthermore, since the operator difference (2) vanishes for linear functions f, we have
As the function f γ satisfies the condition (66), we can use Theorem 5.2 which gives
as \(\alpha T^{\frac {1}{2m}}\to \infty \) and T →∞, where p
∞ is given by (65). The same formula holds for the region  . The claimed formula (68) now follows from definition (8), Remark 2.4(1), (62), and (63). □
. The claimed formula (68) now follows from definition (8), Remark 2.4(1), (62), and (63). □
6.3 Concluding Remarks
-
1.
We have proved the positivity of the EE for Rényi index γ ≤ 1, see Theorem 3.5. For bounded Λ we have actually a somewhat stronger statement, namely:
$$\displaystyle \begin{aligned} 0\le \mathrm{S}_{\gamma}(T,\mu; \varLambda)-s_\gamma(T, \mu) |\varLambda|\le \mathrm{H}_{\gamma}(T,\mu;\varLambda), \quad \gamma \le 1\,. \end{aligned}$$Here the first inequality for the local entropy is due to Theorem 31 and holds even for γ ≤ 2. The second one follows by combining (8), (9), and Theorem 3.5.
Although Theorem 3.5 ensures the positivity of the EE only for γ ≤ 1, the asymptotic coefficient \(\mathcal B(a_{T, \mu },\partial \varLambda ; \eta _\gamma )\) is positive for all γ ≤ 2 and all
 , T > 0, see Remark 2.4(2). It is an open question however whether the positivity of the EE extends to all γ ≤ 2.
, T > 0, see Remark 2.4(2). It is an open question however whether the positivity of the EE extends to all γ ≤ 2. -
2.
In case of a fixed ρ (Theorem 6.3) and γ ≤ 2, the function \(\eta _\gamma ^{\mathrm {eff}}\) in Table 1 is strictly concave on [0, 1], and since h ∞ > 0, the coefficient \(\mathcal B\big ( \mathrm {e}^{-h_\infty }, \partial \varLambda ; \eta _\gamma ^{\mathrm {eff}}\big )\) is strictly positive. On the other hand, if γ > 2, then \(\eta _\gamma ^{\mathrm {eff}}\) is strictly convex so that this coefficient is strictly negative. This change of sign, unexpected by us, suggests that our definition (8) of the EE is somewhat unphysical for γ > 2. In passing we note that \(\mathcal B\big ( \mathrm {e}^{-h_\infty }, \partial \varLambda ; \eta _\gamma ^{\mathrm {eff}}\big )\) for γ > 2 can be computed rather explicitly. Indeed, since \(\eta _\gamma ^{\mathrm {eff}}(t) = \gamma (2(\gamma -1))^{-1}\ t^2\) it is easy to calculate the function (15):
$$\displaystyle \begin{aligned} U\big(u,v;\eta_\gamma^{\mathrm{eff}}\big) = -\frac{\gamma}{2(\gamma-1)} (u-v)^2\,,\quad \gamma>2\,. \end{aligned}$$This observation and the use of Parseval’s identity, as in the proof of Proposition 1 in [29], enables us to find the coefficient (16) and hence (17) in terms of the Fourier transform of \(\exp (-h_\infty )\). In particular, for the quadratic “asymptotic” Hamiltonian h ∞(ξ) = |ξ|2∕2 (which includes the Hamiltonian of the ideal Fermi gas) we obtain the formula
$$\displaystyle \begin{aligned} \mathcal B\big( \mathrm{e}^{-h_\infty}, \partial\varLambda; \eta_\gamma^{\mathrm{eff}}\big) = - \frac{\gamma}{\gamma-1} 2^{-d-3} \pi^{-(d+1)/2} |\partial\varLambda|\,,\quad \gamma>2\,. \end{aligned}$$ -
3.
For γ < 2 the function \(\eta _\gamma ^{\mathrm {eff}}\) is exactly the classical entropy function of the Maxwell–Boltzmann gas. This confirms our expectations stated in the Introduction. This conclusion does not hold for γ ≥ 2.
-
4.
In case of a fixed μ (Theorem 6.1), and γ ≤ 2, we know that the coefficient \(\mathcal B_\gamma : = \mathcal B(p_\infty ,\partial \varLambda ;\eta _\gamma )\), \(p_\infty = (1+\exp (h_\infty ))^{-1}\), on right-hand side of (60) is positive. Here we indicate that \(\mathcal B_\gamma \) should become negative for large γ. Indeed, we calculate the point-wise limit:

This function is (strictly) convex on [0, 1∕2] and also on [0, 1∕2], but not on the whole interval [0, 1]. Since by our assumptions in Sect. 5.1 h ∞≥ 0, we have p ∞≤ 1∕2, and hence
$$\displaystyle \begin{aligned} \mathcal B_\infty = \mathcal B(p_\infty, \partial\varLambda; -\ln(1-\cdot))<0\,. \end{aligned}$$Thus, assuming continuity of \(\mathcal B_\gamma \) as a function of γ > 0 we can claim that there is a value γ 0 > 2 such that \(\mathcal B_{\gamma _0} = 0\) and \(\mathcal B_\gamma < 0\) for all finite γ > γ 0.
One can be more specific about the value of \(\mathcal B_\infty \). Namely, for u, v ∈ [0, 1∕2] we have
$$\displaystyle \begin{aligned} U \big(u,v;\eta_\infty\big) &= - U\big(u,v;\ln(1-\cdot)\big) = - U\big(1-u,1-v;\ln(\cdot)\big) \\ &= -\frac{1}{2} \big(\ln(1-u) - \ln(1-v)\big)^2\,. \end{aligned} $$The last step is an elementary calculation (see [29]) that reconfirms the negativity of U. With
 we get $$\displaystyle \begin{aligned} U\big(p_\infty(\boldsymbol\xi), p_\infty(\boldsymbol\xi + t\mathbf{e}); \eta_\infty\big) = -\frac{1}{2}\big(b(\boldsymbol\xi) - b(\boldsymbol\xi+t\mathbf{e})\big)^2\,. \end{aligned}$$
we get $$\displaystyle \begin{aligned} U\big(p_\infty(\boldsymbol\xi), p_\infty(\boldsymbol\xi + t\mathbf{e}); \eta_\infty\big) = -\frac{1}{2}\big(b(\boldsymbol\xi) - b(\boldsymbol\xi+t\mathbf{e})\big)^2\,. \end{aligned}$$Similarly to Remark 2, the coefficient \(\mathcal B_\infty \) can be found in terms of the Fourier transform of the symbol b. In particular, in the case h ∞(ξ) = |ξ|2∕2 the coefficient \(\mathcal B_\infty \) can be computed explicitly:
$$\displaystyle \begin{aligned} \mathcal B((1+\exp(h_\infty))^{-1},\partial\varLambda;\eta_\infty) = - \frac{1}{2}(2\pi)^{-(d+1)/2} \varSigma(d) |\partial\varLambda|\,, \end{aligned}$$where
 [Numerically we find e.g. Σ(2) ≈ 0.19798 and Σ(3) ≈ 0.15419]. We omit the details.
[Numerically we find e.g. Σ(2) ≈ 0.19798 and Σ(3) ≈ 0.15419]. We omit the details. -
5.
In both high-temperature regimes (fixed μ or fixed ρ) the scaling parameter α may be fixed to, say, α = 1. Thus the truncating set αΛ is fixed and only the temperature T tends to infinity.
-
6.
Using the relation (9) and Theorem 5.1 one can also derive appropriate asymptotic formulas for the local entropy. For example, assuming that μ is fixed, as in Theorem 6.1, we easily obtain the asymptotic relation
$$\displaystyle \begin{aligned} \lim\big(\alpha T^{\textstyle\frac{1}{2m}}\big)^{1-d}\, \big[\mathrm{S}_{\gamma}(T,\mu;\alpha\varLambda) - \alpha^d s_\gamma(T, \mu)\,|\varLambda|\big] = \mathcal B\big((1+\mathrm{e}^{h_\infty})^{-1}, \partial\varLambda; \eta_\gamma\big)\,, \end{aligned} $$as \(\alpha T^{\frac {1}{2m}}\,\to \infty \) and T →∞. However, in order to obtain from this formula a proper asymptotic expansion for the local entropy, one needs to find an expansion for the entropy density s γ(T, μ) as T →∞. A convenient starting point for its derivation could be, for example, the representation (10.8) in [18].
An analogous formula can be written down for the case of a fixed ρ. The inequality \(\mathcal B\big (\mathrm {e}^{-h_\infty }, \partial \varLambda ;\eta _\gamma ^{\mathrm {eff}}\big )<0\) for γ > 2 would then imply that the local entropy obeys for large T the bound Sγ(T, μ ρ(T);Λ) < s γ(T, μ ρ(T))|Λ|, instead of (31) which is valid for all γ ≤ 2 and all T > 0.
References
L. Amico, R. Fazio, A. Osterloh, V. Vedral, Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008)
T. Ando, Concavity of certain maps on positive definite matrices and applications to Hadamard products. Linear Algebra Appl. 26, 203–241 (1979)
R. Balian, From Microphysics to Macrophysics II (Springer, Berlin, 1992)
J. Bendat, S. Sherman, Monotone and convex operator functions. Trans. Am. Math. Soc. 79, 58–71 (1955)
F.A. Berezin, Convex operator functions. Math. USSR Sbornik 17, 269–277 (1972) [Russian original: Mat. Sbornik (N.S.) 88, 268–276 (1972)]
M.S. Birman, M.Z. Solomjak, Spectral Theory of Self-Adjoint Operators in Hilbert Space (Reidel, Dordrecht, 1987). [Translated from the 1980 Russian original by S. Khrushchëv and V. Peller]
O. Bratteli, D.W. Robinson, Operator Algebras and Quantum Statistical Mechanics, vol. 2, 2nd edn. (Springer, Berlin, 1997)
A.M. Budylin, V.S. Buslaev, On the asymptotic behaviour of the spectral characteristics of an integral operator with a difference kernel on expanding domains, in Differential Equations, Spectral Theory, Wave Propagation. Probl. Mat. Fiz., vol. 13 (Leningrad University, Leningrad, 1991), pp. 16–60 [in Russian]
C. Davis, A Schwarz inequality for convex operator functions. Proc. Am. Math. Soc. 8, 42–44 (1957)
E. Fermi, Zur Quantelung des idealen einatomigen Gases. Z. Physik 36, 902–912 (1926)
D. Gioev, Szegő limit theorem for operators with discontinuous symbols and applications to entanglement entropy. Int. Math. Res. Not. 2006, 95181, 23 pp. (2006)
D. Gioev, I. Klich, Entanglement entropy of fermions in any dimension and the Widom conjecture. Phys. Rev. Lett. 96, 100503, 4 pp. (2006)
F. Hansen, G.K. Pedersen, Jensen’s operator inequality. Bull. Lond. Math. Soc. 35, 553–564 (2003)
R. Horodecki, P. Horodecki, M. Horodecki, K. Horodecki, Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009)
A. Laptev, Y. Safarov, Szegő type limit theorems. J. Funct. Anal. 138, 544–559 (1996)
H. Leschke, A.V. Sobolev, W. Spitzer, Scaling of Rényi entanglement entropies of the free Fermi-gas ground state: a rigorous proof. Phys. Rev. Lett. 112, 160403, 5 pp. (2014)
H. Leschke, A.V. Sobolev, W. Spitzer, Large-scale behaviour of local and entanglement entropy of the free Fermi gas at any temperature. J. Phys. A: Math. Theor. 49, 30LT04, 9 pp. (2016); Corrigendum. 50, 129501, 1 p. (2017)
H. Leschke, A.V. Sobolev, W. Spitzer, Trace formulas for Wiener–Hopf operators with applications to entropies of free fermionic equilibrium states. J. Funct. Anal. 273, 1049–1094 (2017)
R. Roccaforte, Asymptotic expansions of traces for certain convolution operators. Trans. Am. Math. Soc. 285, 581–602 (1984)
B. Simon: Loewner’s Theorem on Monotone Matrix Functions (Springer Nature, Cham, 2019)
A.V. Sobolev, Pseudo-Differential Operators with Discontinuous Symbols: Widom’s Conjecture. Mem. Am. Math. Soc. 222(1043), vi+104 pp. (AMS, Providence, 2013)
A.V. Sobolev, On the Schatten–von Neumann properties of some pseudo-differential operators. J. Funct. Anal. 266, 5886–5911 (2014)
A.V. Sobolev, Wiener–Hopf operators in higher dimensions: the Widom conjecture for piece-wise smooth domains. Integr. Equ. Oper. Theory 81, 435–449 (2015)
A.V. Sobolev, Functions of self-adjoint operators in ideals of compact operators. J. Lond. Math. Soc. (2) 95, 157–176 (2017)
A.V. Sobolev, Quasi-classical asymptotics for functions of Wiener–Hopf operators: smooth versus non-smooth symbols. Geom. Funct. Anal. 27, 676–725 (2017)
A.V. Sobolev, On Szegő formulas for truncated Wiener–Hopf operators. Integr. Equ. Oper. Theory 91, 1, 28 pp. (2019)
H. Widom, A theorem on translation kernels in n dimensions. Trans. Am. Math. Soc. 94, 170–180 (1960)
H. Widom, On a class of integral operators with discontinuous symbol, in Toeplitz Centennial, ed. by I. Gohberg, Operator Theory: Advances and Applications, vol. 4 (Birkhäuser, Basel, 1982), pp. 477–500
H. Widom, A trace formula for Wiener–Hopf operators. J. Oper. Theory 8, 279–298 (1982)
H. Widom, Asymptotic Expansions for Pseudodifferential Operators on Bounded Domains. Lecture Notes in Mathematics, vol. 1152 (Springer, Berlin, 1985)
H. Widom, On a class of integral operators on a half-space with discontinuous symbol. J. Funct. Anal. 88, 166–193 (1990)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: The Fermi Symbol for Fixed ρ and Large T
Appendix: The Fermi Symbol for Fixed ρ and Large T
Our main aim is to derive formula (61) for a Hamiltonian h as specified in Sect. 5.1. After a change of variables and replacing μ with μ ρ(T) formula (11) for the mean particle density takes the form

Since \(T^{-1} h(T^{\frac {1}{2m}}\boldsymbol \xi )\to h_\infty (\boldsymbol \xi )\) as T →∞, for each ξ ≠ 0, the condition (12) requires that \(\exp \big (-\mu _\rho (T)/T\big )\to \infty \). Consequently,
where ϰ is defined in (62). Using (12), this leads to (61).
As explained in the Introduction, the high-temperature limit under the condition (12) corresponds to the Maxwell–Boltzmann gas limit. This fact can be conveniently restated in terms of the so-called fugacity  as follows. By (43) the integrated density of states \(\mathcal N(T)\) of (13), satisfies for large T the relation \(\mathcal N(T)\asymp T^{\frac {d}{2m}}\). So (61) implies \(z_\rho (T)\asymp \rho \, \mathcal N(T)^{-1}\to 0\).
as follows. By (43) the integrated density of states \(\mathcal N(T)\) of (13), satisfies for large T the relation \(\mathcal N(T)\asymp T^{\frac {d}{2m}}\). So (61) implies \(z_\rho (T)\asymp \rho \, \mathcal N(T)^{-1}\to 0\).
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Leschke, H., Sobolev, A.V., Spitzer, W. (2022). Rényi Entropies of the Free Fermi Gas in Multi-Dimensional Space at High Temperature. In: Basor, E., Böttcher, A., Ehrhardt, T., Tracy, C.A. (eds) Toeplitz Operators and Random Matrices. Operator Theory: Advances and Applications, vol 289. Birkhäuser, Cham. https://doi.org/10.1007/978-3-031-13851-5_21
Download citation
DOI: https://doi.org/10.1007/978-3-031-13851-5_21
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-031-13850-8
Online ISBN: 978-3-031-13851-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



 is a Lipschitz region, and either Λ or
is a Lipschitz region, and either Λ or
 is bounded.
is bounded.
 coincide.
coincide.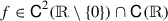 satisfies (
satisfies ( satisfies (
satisfies ( , T > 0, see Remark
, T > 0, see Remark 
 we get
we get  [Numerically we find e.g. Σ(2) ≈ 0.19798 and Σ(3) ≈ 0.15419]. We omit the details.
[Numerically we find e.g. Σ(2) ≈ 0.19798 and Σ(3) ≈ 0.15419]. We omit the details.