Abstract
Recently, offset quadrature amplitude modulation (OQAM) based filter bank multicarrier (FBMC), due to its reduced out-of-band (OOB) emission, has attracted significant research interests for replacing orthogonal frequency division multiplexing (OFDM) in future wireless communication systems. This chapter analyses and design FBMC-OQAM waveform based multiple-input multiple-output (MIMO) and multi-user massive MIMO systems. It begins by describing key features and differences of FBMC waveform over the widely popular OFDM waveform, followed by the discussion over key challenges in designing FBMC based MIMO and massive MIMO systems. A semi-blind (SB) channel state information (CSI) estimation scheme, which enhances the performance with a limited pilot overhead, is developed for MIMO-FBMC system along with its Cramer-Rao lower bound (CRLB) for benchmarking the performance. To compare the performance of FBMC and OFDM waveforms in the uplink transmission, the achievable sum-rates are derived for multi-user (MU) massive MIMO technology relying on FBMC waveform with maximum ratio combining (MRC) and zero-forcing (ZF) receivers. The corresponding power scaling laws for MU massive MIMO-FBMC are also found. It is shown that in practical impairments such as carrier frequency offset, massive MIMO-FBMC systems significantly outperform their OFDM counterparts.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
Recently, offset quadrature amplitude modulation (OQAM)-based filter bank multicarrier (FBMC), due to its reduced out-of-band (OOB) emission, has attracted significant research interests for replacing orthogonal frequency division multiplexing (OFDM) in future wireless communication systems. This chapter analyses and designs FBMC-OQAM waveform-based multiple-input multiple-output (MIMO) and multi-user massive MIMO systems. It begins by describing key features and differences of FBMC waveform over the widely popular OFDM waveform, followed by the discussion over key challenges in designing FBMC-based MIMO and massive MIMO systems. A semi-blind (SB) channel state information (CSI) estimation scheme, which enhances the performance with a limited pilot overhead, is developed for MIMO-FBMC system along with its Cramer-Rao lower bound (CRLB) for benchmarking the performance. To compare the performance of FBMC and OFDM waveforms in the uplink transmission, the achievable sum rates are derived for multi-user (MU) massive MIMO technology relying on FBMC waveform with maximum ratio combining (MRC) and zero-forcing (ZF) receivers. The corresponding power scaling laws for MU massive MIMO-FBMC are also found. It is shown that in practical impairments such as carrier frequency offset, massive MIMO-FBMC systems significantly outperform their OFDM counterparts.
3.1 Introduction
From the past two decades, orthogonal frequency division multiplexing (OFDM) has enjoyed its widespread dominance in broadband wired [1] and wireless [2] communication systems. OFDM waveform has been widely embraced in digital subscriber lines (DSL) standards, as well as wireless standards such as the third-generation partnership program long-term evolution (3GPP-LTE), IEEE 802.16, IEEE 802.11, LTE-Advanced and 5G-New Radio (NR). The key advantages of OFDM signalling are (i) orthogonality among subcarriers allows synthesis and analysis of the transmit and receive signals using computationally efficient inverse fast Fourier transform (IFFT) and FFT blocks, respectively; (ii) the use of cyclic prefix (CP) guarantees one-tap equalization; and (iii) trivial amalgamation with multiple-input multiple-output (MIMO) and massive MIMO technologies. Fifth-generation (5G) communications systems are characterised by a wide range of use cases such as enhanced Machine Type Communications (eMTC), Ultra-Reliable Low latency Communications (URLLC) and enhanced Mobile BroadBand (eMBB) [3]. In order to cope with a large number of applications, future communication systems require a flexible time-frequency resource allocation. The 3GPP body has yet again adopted OFDM (with some minor changes) for 5G wireless communication systems. OFDM shapes each of its subcarrier using a rectangular window, which results in a sinc-shaped frequency localization. As soon as the synchronization in OFDM is lost, the time-domain rectangular pulse shape associated with synthesised subcarriers at the transmitter and analysed subcarriers at the receiver, due to its relatively higher out-of-band (OOB) emission, results in significant leakage of signal power among the band of neighbourhood users [4]. Thus, OFDM-based systems are sensitive to practical impairments such as carrier frequency offset and timing offset, especially in vehicular scenarios where tracking Doppler shifts of different user equipments is challenging. For instance, achieving perfect synchronization in the uplink of orthogonal frequency division multiple access (OFDMA) may not be possible. This happens because each of the users transmits independently from different locations. Attaining synchronization in OFDM-based cognitive radio systems is even more challenging, because primary and secondary users transmit independently and may be operating on distinct standards [5, 6].
In view of the above observations, researchers are motivated to investigate new multicarrier modulation schemes for future wireless communication systems. Such schemes, while outperforming existing solutions in terms of OOB emission, should also ensure similar efficiency and robustness as OFDM. In this context, engineers in Alcatel-Lucent Bell Laboratories have investigated a waveform called universal filtered multicarrier (UFMC) [7], wherein a set of subcarriers assigned to a node are processed through a filter to minimize the multi-node interference. This technique, due to degraded orthogonality among the subcarrier in the existence of multipath fading, results in a performance loss [8]. The second popular waveform is generalized frequency division multiplexing (GFDM), proposed in [9]. In GFDM, each subcarrier is shaped using a well frequency-time (FT) localized filter in circular fashion such that one CP is attached to a block of N d information bearing symbols that are dispersed over N subcarriers and N d∕N symbol instants [9].
Another potential waveform candidate for future wireless communication systems is based on filter bank multicarrier (FBMC) operation [10]. Contrary to the time-domain rectangular pulse with sinc-shaped frequency localization in OFDM, subcarriers in FBMC are synthesised and analysed using a bank of well FT localized modulated and demodulated filters, respectively. There are several variants of FBMC in the existing literature, namely, staggered multi-tone (SMT), filtered multi-tone (FMT) and cosine-modulated multi-tone (CMT) [10]. FMT, which has been evolved particularly for DSL [11], is designed using the classic frequency division multiplexing (FDM) operation, wherein the subcarriers band are made unconnected by introducing guard bands. Thus, FMT is a bandwidth inefficient signalling scheme. In contrast, both SMT and CMT, by allowing overlapping of adjacent subcarriers, offer maximum bandwidth efficiency [10]. To carry pulse amplitude modulated (PAM) symbols, overlapped vestigial side-band (VSB) modulated signals are staggered in CMT. On the other side, signalling in SMT is designed using staggering of overlapping double side-band modulated format to carry quadrature amplitude modulated (QAM) symbols, whose real and imaginary parts are time-offset by one half of a symbol duration. A formal mathematical relationship between CMT and SMT has been derived in [12]. Since the VSB modulation in CMT requires Hilbert transform, its implementation is more complex than SMT. In the literature, SMT is popularly known as offset quadrature amplitude modulation (OQAM)-based OFDM (OFDM-OQAM) or FBMC-OQAM.
Figure 3.1a,b show a section of OFDM and FBMC-OQAM filter banks, respectively. The subchannel index therein corresponds to the frequency axis with unity subcarrier spacing. The subcarrier orthogonality for the OFDM filter bank in Fig. 3.1a can be observed through the zero crossings at the integer multiple of subcarrier spacing where only one subchannel is non-zero. As shown in Fig. 3.1a, OFDM filter bank has significantly higher OOB emission due to the sinc-shaped spectrum of the rectangular prototype filter. Therefore, performance of OFDM-based systems degrades severely in the presence of synchronization error due to carrier frequency offset (CFO) and timing offset. On the other hand, as can be observed from Fig. 3.1b, only adjacent subcarriers are overlapping in FBMC-OQAM due to the associated well frequency-time localized prototype filter. Thus, one can separate the adjacent bands by inserting an empty subcarrier between them. Furthermore, the sharp prototype filter in FBMC-OQAM significantly lowers down the OOB emission and relaxes the stringent synchronization requirement in such systems [14]. Additionally, these sharp filters also avoid the need for CP that is otherwise required in OFDM to remove inter-symbol-interference (ISI). This increases the spectral efficiency of FBMC-OQAM-based systems. The implementation of FBMC-OQAM can be realised using a computationally efficient polyphase structure [15]. Furthermore, for relatively low frequency-selective channels, FBMC-OQAM can be efficiently coupled to MIMO technology [16]. Additionally, the concept of GFDM can also be extended to FBMC-OQAM [17, 18]. The resulting signalling format from this amalgamation is called circular FBMC (C-FBMC). The references [19] and [4], respectively, show the benefits of FBMC-OQAM waveform over its OFDM counterpart in the uplink of multi-user (MU) networks and cognitive radios. In the light of the above-listed benefits of FBMC-OQAM, and its ability to address the shortcomings of OFDM by using sharp pulse shaping, FBMC-OQAM has recently received significant research interests [16, 20,21,22,23], which reflect that FBMC-OQAM is a compelling signalling technique for future wireless communication systems. The aim of this chapter is, therefore, to analyse and design FBMC-OQAM-based multiple-input multiple-output (MIMO) and multi-user massive MIMO systems. For brevity, FBMC-OQAM is referred to as FBMC in the sequel.
Section of a filter bank. (a) OFDM and (b) FBMC-OQAM relying on Phydyas filter [13] with a overlapping factor 4
The subcarrier in FBMC waveform, unlike OFDM, is orthogonal in the real domain only [15]. The resulting intrinsic interference challenges amalgamation of FBMC signalling with future mobile communication systems. Furthermore, the overlapping of FBMC symbols in the time-domain poses additional challenges. For example, FBMC channel state information (CSI) estimation needs the placement of zeros between the adjacent training symbols [24]. Thus, one has to carefully compute the intrinsic interference for constructing the virtual training symbols at the receiver. Moreover, one also needs to find the optimal number of zeros required to avoid overdesign/underdesign of FBMC systems. In light of the above challenges, it is not always feasible to use the existing solutions or corresponding analysis for OFDM-based systems, while designing FBMC aided future wireless systems.
3.2 Organization of Chapter
The next section discusses single-input single-output (SISO) and MIMO-FBMC system models and the key differences between OFDM and FBMC waveforms. Section 3.4 demonstrates a semi-blind channel estimator for MIMO-FBMC systems. Section 3.5 demonstrates and compares the performance of FBMC and OFDM waveforms in the uplink transmission of MU massive MIMO systems. Section 3.6 concludes the chapter and provides future directions.
3.3 FBMC System Model
The continuous-time baseband FBMC transmitted signal is expressed as [15, 25]
where d m,n are real-valued OQAM symbols at the mth subcarrier and the nth symbol instant. The parameter N symbolises the number of subcarriers. The FBMC basis function χ m,n(t) is defined as
where T is the QAM symbol duration, F = 1∕T is the spacing between two consecutive subcarriers, T∕2 is the offset between the in-phase and quadrature parts of a QAM symbol and p(t) is the symmetrical real-valued pulse, which is different from the rectangular pulse in OFDM. The phase factor ϕ m,n is defined as modulo π, for example, ϕ m,n = (π∕2)(m + n) [15]. The real OQAM symbols d m,n are drawn from the spatially and temporally independent and identically distributed (i.i.d.) in-phase and quadrature components of a QAM symbol c m,n as follows:
Each component OQAM symbols d m,2n and d m,2n+1 is of duration T∕2. Let \(\mathbb {E}[c_{m,n}c_{m,n}^{\ast }]=2P_d\), which implies that \(\mathbb {E}[d_{m,n}d_{m,n}^{\ast }]=P_d\). In the presence of ideal channel without noise, the FBMC demodulation at subcarrier index \(\bar {m}\) and symbol instant \(\bar {n}\) is performed using the matched filtering operation as shown below [15]
Thus, in order to recover OQAM symbols d m,n at the receiver, the basis functions χ m,n(t) satisfy the following real-field orthogonality condition
where \(\delta _{m,\bar {m}}\) is the Kronecker delta with \(\delta _{m,\bar {m}}=1\) if \(m=\bar {m}\) and zero otherwise.
Since N complex valued symbols are transmitted in T time interval, T s = T∕N is the critical sampling interval. The discrete-time FBMC baseband transmitted signal is obtained by sampling s(t) with the sampling rate 1∕T s. The causal discrete-time prototype pulse p[k] of length L p is obtained by truncating p(t) from − (L p∕2)T s to (L p∕2)T s and delaying it by ((L p − 1)∕2)T s. The discrete-time baseband signal is obtained by sampling s(t) at t = kT s as
The discrete-time basis function χ m,n[k] is defined as
The equivalent real-field orthogonality in the discrete domain for reconstructing real OQAM symbols d m,n is given as
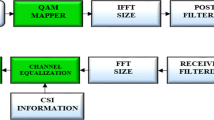
Figure 3.2a,b shows the discrete-time baseband model for the FBMC transmitter and receiver, respectively. The main dissimilarities between FBMC and OFDM waveforms lie (i) in the selection of pulse-shaping filter p[k] and (ii) in the property the former accepted OQAM symbols instead of QAM symbols. The function Φ(⋅) in Fig. 3.2a performs the operations described in (3.3) and (3.4) for the even and odd indexed subcarriers. This operation is reversed at the receiver using the function Φ−1(⋅). The other blocks are self-explanatory. Let the quantity \(\xi ^{\bar {m},\bar {n}}_{m,n}=\sum _{k=-\infty }^{+\infty }\chi _{m,n}[k]\chi _{\bar {m},\bar {n}}^{*}[k]\). Thus, it follows from (3.9) that
where \(\langle \xi \rangle ^{\bar {m},\bar {n}}_{m,n}=\Im \{\sum _{k=-\infty }^{+\infty }\chi _{m,n}[k]\chi _{\bar {m},\bar {n}}^{*}[k]\}\) extracts the imaginary part of the cross correlation between the basis functions [26]. The signal received at the SISO-FBMC receiver is
where h[k] denotes impulse response of an L h-tap channel. The scaler quantity η[k] is an additive white Gaussian noise (AWGN) with mean zero and variance \(\sigma ^{2}_{\eta }\). At the receive, the FBMC signal is demodulated at frequency index \(\bar {m}\) and symbol instant \(\bar {n}\) by matching it with the basis function \(\chi _{\bar {m},\bar {n}}[k]\) as [15]
By substituting s[k], \(\chi _{\bar {m},\bar {n}}[k]\) and y[k] from (3.7), (3.8) and (3.11), respectively, in the above expression, \(y_{\bar {m},\bar {n}}\) is expanded as
where \(\eta _{\bar {m},\bar {n}}=\sum _{k=-\infty }^{+\infty } \eta [k] \chi _{\bar {m},\bar {n}}^{\ast }[k]\) is the demodulated noise which obeys Gaussian distribution with mean
The covariance between \(\eta _{\bar {m},\bar {n}}\) and η m,n is computed as
The noise at FT index \((\bar {m},\bar {n})\) is thus correlated. This correlation, however, is negligible because of the associated sharp prototype filters for pulse shaping in FBMC [24]. The duration of the prototype pulse p[k] in FBMC is typically chosen as an integer multiple of the symbol time T. Thus, the pulse duration is significantly larger than the channel delay spread, i.e. L p = k 0 N >> L h. For example, references [24, 26] set k 0 to be 4. This implies that the bandwidth of the pulse-shaping filter p[k] is significantly lower than the channel coherence bandwidth. As a result, the impulse response p[k] of prototype filter in time has negligible variations over the channel delay spread. Therefore, as described in [24, 26]
Upon employing the above result, the expression for y[k] in (3.13) can be simplified as
where
symbolises channel frequency response (CFR) for the mth subcarrier. The channel h[k] is considered to be quasi-static throughout the chapter. Separating the desired and undesired terms in (3.16), one obtains

3.3.1 Data Detection
To begin with, let the transmission channel be ideal, i.e. h[k] = δ[k]. Thus, the CFR \(H_{\bar {m}}=1\), and it follows from (3.18) that
It follows from (3.10) that the quantity \(\sum _{(m,n)\neq (\bar {m},\bar {n})}^{} d_{m,n} \langle \xi \rangle ^{\bar {m},\bar {n}}_{m,n}\) is real in nature. Consequently, OQAM symbol \(d_{\bar {m},\bar {n}}\) at the receiver can be estimated as
In practice, channel h[k] is not ideal. Therefore, as shown in Fig. 3.2b, equalization operation is performed before detecting OQAM symbols. By performing the ZF equalization in (3.18), the estimate of OQAM symbol at the subcarrier \(\bar {m}\) and symbol instant \(\bar {n}\) is
where the quantity
is called the intrinsic interference in FBMC systems. Since the quantity \(\frac {H_{m}}{H_{\bar {m}}}\) is complex, \(\Re \big \{jI_{\bar {m},\bar {n}}\big \}\neq 0\). The term \(\Re \big \{jI_{\bar {m},\bar {n}}\big \}\) characterises the ISI and inter-carrier-interference (ICI) between the transmitted OQAM symbols. This is unlike OFDM systems wherein the former is suppressed using the CP and the latter is mitigated using the orthogonality among the subcarriers. It sounds difficult to obtain a reliable estimate of the OQAM symbol \(d_{\bar {m},\bar {n}}\) at this stage. However, introduction of few approximations by exploiting the inherent properties of FBMC systems leads to a reliable estimate of OQAM symbols as follows. The interference evaluation in (3.22) can be recast as
where the symbol \(\Omega _{\bar {m},\bar {n}}\) symbolises the neighbourhood of the desired symbol at subcarrier-symbol time index \((\bar {m},\bar {n})\) by excluding the index \((\bar {m},\bar {n})\). Since prototype filter p[k] in FBMC is well localized both in frequency and time, the interference due to the FT points (m, n) outside the neighbourhood \(\Omega _{\bar {m},\bar {n}}\) is negligible since \(\langle \xi \rangle ^{\bar {m},\bar {n}}_{m,n}\big |{ }_{(m,n)\not \in \Omega _{\bar {m},\bar {n}}}\approx 0\) [26]. Furthermore, since the subcarrier bandwidth is significantly smaller than the coherence bandwidth of channel, the CFR is well approximated by a constant over the neighbourhood \(\Omega _{\bar {m},\bar {n}}\) [26]. Typically, due to the associated sharp pulse-shaping filters in FBMC, the interference mainly arises from the first-order neighbourhood \(\Omega _{\bar {m},\bar {n}}=\{(\bar {m}\pm 1,\bar {n}\pm 1),(\bar {m},\bar {n}\pm 1),(\bar {m}\pm 1,\bar {n})\}\). Upon using the above inherent properties of FBMC systems, the intrinsic interference in (3.23) is well approximated as
which also implies that \(\Re \{j\tilde {I}_{\bar {m},\bar {n}}\}\approx 0\). Employing the above result in (3.18), the received symbol \(y_{\bar {m},\bar {n}}\) at the FT index \((\bar {m},\bar {n})\) can be recast as
Here the term \(b_{\bar {m},\bar {n}}=d_{\bar {m},\bar {n}}+jI_{\bar {m},\bar {n}}\) is known as virtual symbol, which is the summation of the desired symbol \(d_{\bar {m},\bar {n}}\) and the corresponding interference component \(I_{\bar {m},\bar {n}}\). The model in (3.25) is widely popular with the name interference approximation model (IAM) [26], because it utilizes the property that each FBMC symbol interferes with the symbols in its small FT neighbourhood, over which the CFR can be approximated to a constant. With zero mean i.i.d. OQAM symbols, each of power P d, \(I_{\bar {m},\bar {n}}\) has a mean zero and power \(\mathbb {E}[|I_{\bar {m},\bar {n}}|{ }^{2}]\approx P_d\) [27]. Furthermore, the OQAM symbol \(d_{\bar {m},\bar {n}}\) and the interference term \(I_{\bar {m},\bar {n}}\) are zero mean independent. The virtual symbol \(b_{\bar {m},\bar {n}}\) thus has mean zero and power
Following Fig. 3.2b, one can obtain a reliable estimate of OQAM symbols using the model in (3.25) as follows:
The function \(\Phi ^{-1}(\hat {d}_{\bar {m},\bar {n}})\) in Fig. 3.2b at the \(\bar {m}\)th subcarrier, by combining the estimated OQAM symbols \(\hat {d}_{m,2n}\) and \(\hat {d}_{m,2n+1}\), obtains the estimate \(\hat {c}_{m,n}\) of complex-valued QAM symbol as follows
The SISO-FBMC system model discussed above can be easily extended to MIMO with N t transmit and N r receive antennas. Similar to (3.7), the FBMC baseband signal s t[k] at the tth transmit antenna is expressed as
where 1 ≤ t ≤ N t, and \(d^{t}_{m,n}\) is an OQAM symbol transmitted by tth antenna at the frequency-time point (m, n). The signal at the rth antenna of FBMC receiver is expressed as
The scaler h r, t[k] above symbolises an L h-tap channel impulse response between the tth transmit and the rth receive antenna pair. The noise η r[k] at the rth receive antenna obeys \(\mathcal {C}\mathcal {N}(0,\sigma ^{2}_{\eta })\). Following the procedure described in the SISO-FBMC system, the received signal on the rth antenna at subcarrier \(\bar {m}\) and symbol instant \(\bar {n}\)th, after passing through the receive filter bank, is obtained as
where the complex quantity \(H^{r,t}_{\bar {m}}\) symbolises the CFR between the tth transmit and the rth receive antenna pair at the \(\bar {m}\)th subcarrier and is computed as \(H^{r,t}_{\bar {m}}=\sum _{l=0}^{L_{h}-1}h^{r,t}[l]e^{-j2\pi \bar {m}l/N}\). The demodulated noise \(\eta ^{r}_{\bar {m},\bar {n}}=\sum _{k=-\infty }^{+\infty }\eta ^{r}[k]\ \chi _{\bar {m},\bar {n}}^{\ast }[k]\) obeys \(\mathcal {C}\mathcal {N}(0,\sigma ^{2}_{\eta })\). The term \(b^{t}_{\bar {m},\bar {n}} = d^{t}_{\bar {m},\bar {n}}+jI^{t}_{\bar {m},\bar {n}}\) is the virtual symbol for the tth transmit antenna, where the associated intrinsic interference \(I^{t}_{\bar {m},\bar {n}}\) is given as
For mathematical ease, (3.31) can be written in vector form as
where the vector \(\boldsymbol {\eta }_{\bar {m},\bar {n}}=[\eta ^{1}_{\bar {m},\bar {n}},\eta ^{2}_{\bar {m},\bar {n}}, \ldots ,\eta ^{N_{r}}_{\bar {m},\bar {n}}]^{T}\in \mathbb {C}^{N_{r}\times 1}\) comprises noise with the covariance matrix \(\mathbb {E}[\boldsymbol {\eta }_{\bar {m},\bar {n}}\boldsymbol {\eta }_{\bar {m},\bar {n}}^{H}]=\sigma ^{2}_{\eta }{\mathbf {I}}_{N_{r}}\) and \({\mathbf {y}}_{\bar {m},\bar {n}}=[y^{1}_{\bar {m},\bar {n}},y^{2}_{\bar {m},\bar {n}},\ldots ,y^{N_{r}}_{\bar {m},\bar {n}}]^{T}\in \mathbb {C}^{N_{r}\times 1}\) is the observation symbol vector across N r receive antennas. The virtual symbol vector \({\mathbf {b}}_{\bar {m},\bar {n}}=[b^{1}_{\bar {m},\bar {n}}, b^{2}_{\bar {m},\bar {n}},\ldots ,b^{N_{t}}_{\bar {m},\bar {n}}]^{T}\in \mathbb {C}^{N_{t}\times 1}\) has a covariance matrix \(\mathbb {E}[{\mathbf {b}}_{\bar {m},\bar {n}}{\mathbf {b}}_{\bar {m},\bar {n}}^{H}]\approx 2P_{d}{\mathbf {I}}_{N_{t}}\). The (r, t)th element of the MIMO CFR matrix \({\mathbf {H}}_{\bar {m}}\in \mathbb {C}^{N_{r}\times N_{t}}\) at the \(\bar {m}\)th subcarrier is given as \(H_{\bar {m}}^{r,t}\). The observed symbols \(y^{1}_{m,n}, y^{2}_{m,n},\cdots ,y^{N_{r}}_{m,n}\) are equalized, followed by the operation \(\Re (\cdot )\), which pulls out the estimate of OQAM symbols from the estimated virtual data vector \(\hat {\mathbf {b}}_{m,n}=[\hat {b}^{1}_{m,n},\hat {b}^{2}_{m,n},\cdots ,\hat {b}^{N_{t}}_{m,n}]^{T}\). Finally, the vectors \(\hat {\mathbf {d}}_{m,2n}=[\hat {d}^{1}_{m,2n},\hat {d}^{2}_{m,2n},\cdots ,\hat {d}^{N_{t}}_{m,2n}]^{T}\) and \(\hat {\mathbf {d}}_{m,2n+1}=[\hat {d}^{1}_{m,2n+1},\hat {d}^{2}_{m,2n+1},\cdots ,\hat {d}^{N_{t}}_{m,2n+1}]^{T}\) on each subcarrier are clubbed together for constructing QAM symbol vector as
3.4 MIMO-FBMC Semi-Blind CSI Estimation
Channel state information (CSI) at receiver is typically acquired using pilot symbols, which do not carry information, and therefore, transmission of pilot symbols results in spectral efficiency loss. Due to the diversity gain offered by MIMO technology, the required signal-to-noise-ratio (SNR) for the desired bit-error-rate performance decreases. In such low SNR regimes, pilot-based CSI estimation methods demand large overheads for providing a reliable CSI estimate. Therefore, this section aims to develop a semi-blind channel estimation scheme for FBMC-based MIMO technology by exploiting the pilot symbols along with statistical properties of the information symbols. This results in a significant reduction in the mean square error (MSE) in comparison to its conventional pilot-based counterpart.
3.4.1 Review of Existing Works
There has been a significant research progress in the area of channel estimation for MIMO-FBMC systems. Reference [28] extended the concept of IAM model-based CFR estimation for FBMC-aided MIMO systems and proposed least squares (LS) estimator. Rottenberg et al. in [29] investigated a linear minimum mean square error (MMSE) CFR estimation approach for the downlink of a distributed MIMO-FBMC technology. Reference [30] described a method for pilot sequence design for the IAM model-based CSI estimation by employing zero-correlation zone sequences in MIMO-FBMC systems. Javaudin et al. designed a scattered pilot-based CSI estimator for MIMO-FBMC systems in [31]. The authors in [32] analysed the performance of the IAM model-based MMSE and LS CSI estimations for MIMO-FBMC waveform in the existence of imperfect channel correlations. Reference [24] provided a comprehensive review on training-based approaches for CSI estimation in FBMC-based SISO and MIMO systems. References [16, 33,34,35] designed training-based time-domain CSI estimation algorithms for MIMO-FBMC systems over a high frequency selective channel. Lin et al. in [36] designed a pilot-based compressive sensing technique in the time domain for MIMO-FBMC CSI estimation by utilising the generalized approximate message passing algorithm.
A key drawback of the above treatises is to employ only pilot symbols for CSI estimation, which leads to a decrease in the spectral efficiency. To avoid this shortcoming, the FBMC literature has developed blind CSI estimation schemes, which do not need pilot symbols for estimation [37, Chapter 11]. Blind schemes, however, are usually computationally expansive and affected by poor convergence. For example, the authors in [38] investigated a blind CSI estimation technique for SISO-FBMC systems by utilising the cyclostationarity induced by the overlapping nature of pulse-shaping filters. The proposed technique therein demands a large number of data symbols to provide a reliable CSI estimate, and its performance deteriorates with an increase in the pulse-shaping filters’ length. Savaux et al. in [39] designed blind equalization for FBMC-based SISO waveform by utilizing the concept of constant norm. The technique therein is restricted for square QAM constellations, and similar to [38], its convergence needs a large data length.
In presence of the above observations, semi-blind schemes, which significantly improve CSI estimation accuracy by utilising both statistical characteristics of the underlying system and a small training overhead, present a viable alternative to both pilot-based and blind CSI estimation methods. Authors in [40] conceived a semi-blind CSI estimation scheme for FBMC-based SISO systems, wherein the CSI magnitude and phase are estimated blindly by exploiting the subcarrier power and the spatial-sign covariance matrix, respectively, and pilot symbols are utilised to mitigate the sign ambiguity arising from the blind CSI estimation algorithm. The MSE of the blind estimation in [40] is sensitive to frame length, and therefore, its performance deteriorates as the frame length decreases [41]. Kofidis et al. in [42] proposed a tensor-based scheme for semi-blind CSI estimation and data detection for FBMC-based MIMO systems by using canonical polyadic decomposition (CPD). The results presented therein are restricted to a single-input multiple-output (SIMO)-FBMC system, because the CPD model is not always identifiable. Due to the effectiveness and improved performance of semi-blind schemes, this section develops a different semi-blind technique for CSI estimation in FBMC-based MIMO systems by exploiting both pilot and the statistical properties of data symbols. Contrary to the pilot-based CSI estimation schemes in [24, 26, 28,29,30,31, 33, 36, 43,44,45,46], the semi-blind MIMO-FBMC scheme leverages the pilot symbols along with blind data symbols for estimating the unitary and whitening components of the channel matrix H m. It is thus offered significantly lower MSE than the existing IAM model-based LS CSI estimation scheme that utilises only pilot symbols. The Cramer-Rao lower bounds (CRLBs) are derived to quantify the MSE gain of the semi-blind method over the pilot-based techniques.
3.4.2 Semi-Blind MIMO-FBMC Channel Estimator
Let the tth antenna transmit L 0 symbols on each of the subcarriers, as shown in the frame in Fig. 3.3. Each frame consists of M pilot symbols to be utilised for estimating CSI. The N d symbols at the end of the frame carry data. Unlike OFDM, adjacent time-domain FBMC symbols interfere with each other because of the overlapping of the pulse-shaping filters. Thus, z zeros are placed between the adjacent pilot symbols to mitigate the ISI [24, 26]. Due to the inter-frame time gap commonly used in wireless systems, one does not need to insert zeros in the beginning of the frame [24]. The effect of varying z on the MSE of the semi-blind and conventional pilot-based CSI estimation schemes is shown later using simulations, which demonstrates that employing z = 1 is sufficient for reducing the ISI to a tolerable level. This implies that MIMO-FBMC frame with zeros employs 2M OQAM symbols on each of the subcarriers for CSI estimation, which is equivalent to M QAM symbols [24]. The channel estimation pilot overhead in MIMO-FBMC is therefore same as that of MIMO-OFDM systems [47].
As shown in Fig. 3.3, the pilot symbols are located at n = i(1 + z) for 0 ≤ i ≤ M − 1. Evaluating (3.33) at these instants and stacking the resulting observations, one gets
Here the virtual pilot matrix \({\mathbf {B}}_{\bar {m}}=[{\mathbf {b}}_{\bar {m},0},{\mathbf {b}}_{\bar {m},(1+z)},\ldots , {\mathbf {b}}_{\bar {m},(M-1)(1+z)}]\in \mathbb {C}^{N_{t}\times M}\), the observation matrix \({\mathbf {Y}}_{\bar {m}}=[{\mathbf {y}}_{\bar {m},0}, {\mathbf {y}}_{\bar {m},(1+z)},\ldots , {\mathbf {y}}_{\bar {m},(M-1)(1+z)}]\in \mathbb {C}^{N_{r}\times M}\) and the noise matrix \(\boldsymbol {\eta }_{\bar {m}}=[\boldsymbol {\eta }_{\bar {m},0}, \boldsymbol {\eta }_{\bar {m},(1+z)},\ldots , \boldsymbol {\eta }_{\bar {m},(M-1)(1+z)}]\in \mathbb {C}^{N_{r}\times M}\). Let the elements of the CFR matrix \({\mathbf {H}}_{\bar {m}}\) obey \(\mathcal {C}\mathcal {N}(0,\sigma ^{2}_h)\). The tth component of the pilot vector \({\mathbf {b}}_{\bar {m},i(1+z)}\in \mathbb {C}^{N_{t}\times 1}\) is obtained as \(b^{t}_{\bar {m},i(1+z)}=d^{t}_{\bar {m},i(1+z)}+jI^{t}_{\bar {m},i(1+z)}\), where the interference \(I^{t}_{\bar {m},i(1+z)}\) is obtained as
The MIMO-FBMC channel matrix \({\mathbf {H}}_{\bar {m}}\) of size N r × N t with N r ≥ N t can be decomposed as
where \({\mathbf {Q}}_{\bar {m}}\in \mathbb {C}^{N_{t}\times N_{t}}\) and \({\mathbf {W}}_{\bar {m}}\in \mathbb {C}^{N_{r}\times N_{t}}\), and for \(0\leq \bar {m}\leq N-1\), are referred to as unitary (complex rotation) and the whitening (decorrelating) matrices, respectively.Footnote 1 Being a unitary matrix, \({\mathbf {Q}}_{\bar {m}}\) satisfies the constraint \({\mathbf {Q}}_{\bar {m}}{\mathbf {Q}}_{\bar {m}}^{H}={\mathbf {Q}}_{\bar {m}}^{H}{\mathbf {Q}}_{\bar {m}}={\mathbf {I}}_{N_{t}}\). Thus, it follows from (3.37) that
The semi-blind CSI estimation scheme works on the principle that the whitening matrix \({\mathbf {W}}_{\bar {m}}\) can be estimated by exploiting the second-order statistical characteristics of N d = L 0 − M(1 + z) data symbols in Fig. 3.3, and the unitary matrix \({\mathbf {Q}}_{\bar {m}}\) can be estimated using the M pilot symbols in the frame. The matrix \({\mathbf {Q}}_{\bar {m}}\) is parameterized by a few parameters. It can therefore be estimated accurately with a limited pilot overhead. On the other side, estimation of \({\mathbf {W}}_{\bar {m}}\) blindly using statistical properties of data symbols significantly enhances accuracy of the CSI estimation.
The covariance matrix \({\mathbf {R}}_{{\mathbf {y}}_{\bar {m}}{\mathbf {y}}_{\bar {m}}}\in \mathbb {C}^{N_r\times N_r}=\mathbb {E}\big [{\mathbf {y}}_{\bar {m},\bar {n}}{\mathbf {y}}_{\bar {m},\bar {n}}^{H}\big ]\) of the observation vectors \({\mathbf {y}}_{\bar {m},\bar {n}}\) in (3.33) is calculated as
The above results follow from the identities \(\mathbb {E}[{\mathbf {b}}_{\bar {m},\bar {n}}{\mathbf {b}}_{\bar {m},\bar {n}}^{H}]=2P_{d}{\mathbf {I}}_{N_{t}}\) and \(\mathbb {E}[\boldsymbol {\eta }_{\bar {m},\bar {n}}\boldsymbol {\eta }_{\bar {m},\bar {n}}^{H}]=\sigma ^{2}_{\eta }{\mathbf {I}}_{N_{r}}\). One can rewrite (3.39) as
The whitening matrix \({\mathbf {W}}_{\bar {m}}\) can now be estimated blindly as
The matrices \(\widehat {\boldsymbol {\Sigma }}_{\bar {m}}\) and \(\widehat {\mathbf {U}}_{\bar {m}}\) are calculated using SVD as given below:
The matrix \(\widehat {\mathbf {R}}_{{\mathbf {y}}_{\bar {m}}{\mathbf {y}}_{\bar {m}}}\) above, which represents the estimate of \({\mathbf {R}}_{{\mathbf {y}}_{\bar {m}}{\mathbf {y}}_{\bar {m}}}\), is obtained by using the observation vectors \({\mathbf {y}}_{\bar {m},\bar {n}}\) for M(1 + z) ≤ n ≤ L 0 as \(\widehat {\mathbf {R}}_{{\mathbf {y}}_{\bar {m}}{\mathbf {y}}_{\bar {m}}}=\frac {1}{N_{d}}\sum _{\bar {n}=M(1+z)}^{L_0}{\mathbf {y}}_{\bar {m},\bar {n}}{\mathbf {y}}_{\bar {m},\bar {n}}^{H}\). Note that the estimate \(\widehat {\mathbf {R}}_{{\mathbf {y}}_{\bar {m}}{\mathbf {y}}_{\bar {m}}}\rightarrow {\mathbf {R}}_{{\mathbf {y}}_{\bar {m}}{\mathbf {y}}_{\bar {m}}}\) with high probability as N d increases [48]. After obtaining the estimate of \({\mathbf {W}}_{\bar {m}}\), the estimate of the unitary matrix \({\mathbf {Q}}_{\bar {m}}\) is obtained as a solution of the following optimization problem:
For an orthogonal pilot matrix \({\mathbf {B}}_{\bar {m}}\) \(({\mathbf {B}}_{\bar {m}}{\mathbf {B}}^{H}_{\bar {m}}=2P_{d}M{\mathbf {I}}_{N_{t}})\) [49], the solution of the optimization problem above is expressed as [50]
The matrices \(\widehat {\mathbf {U}}_{{\mathbf {Q}}_{\bar {m}}}\) and \(\widehat {\mathbf {V}}_{{\mathbf {Q}}_{\bar {m}}}\) above are obtained using the SVD as follows:
Upon employing the estimate of whitening and unitary matrices, the semi-blind estimate of CSI matrix \( {\mathbf {H}}_{\bar {m}}\) is obtained as
Let \(\mathbb {H}\in \mathbb {C}^{N_{r}\times NN_{t}}\) be the MIMO channel matrix, which is obtained as
The semi-blind estimate of \(\mathbb {H}\) can be calculated as
The algorithmic form of the semi-blind scheme is given in Algorithm 1.
Algorithm 1: Algorithmic form of the semi-blind estimator

3.4.3 MSE Gain of the Semi-Blind Estimate over the LS Estimate
From (3.35), the pilot-based LS estimate of the CSI matrix \({\mathbf {H}}_{\bar {m}}\) is given as
One can obtain the LS estimate of the MIMO CSI matrix \({\mathbf {H}}_{\bar {m}}\) as [24]
Here the operation \({\mathbf {B}}_{\bar {m}}^{\dagger }={\mathbf {B}}_{\bar {m}}^{H}\big ({\mathbf {B}}_{\bar {m}}{\mathbf {B}}_{\bar {m}}^{H}\big )^{-1}\) gives the pseudo-inverse of \({\mathbf {B}}_{\bar {m}}\) [51]. As shown in [52], the MSE of the LS CSI estimator is
It is worth mentioning that the CRLB of the LS estimator equals the channel estimation error covariance, because \(\widehat {\mathbf {H}}_{\text{LS},\bar {m}}\) is the minimum variance unbiased estimate. The LS estimate of the MIMO CSI matrix in (3.47) is
The MSE in \(\mathbb {H}_{\text{LS}}\) is calculated as
The CRLB for the channel estimation per parameter using the LS CSI estimator is determined as \( \frac {\sigma ^{2}_{\eta }NN_{t}N_{r}}{2P_{d}M}\big (\frac {1}{N_{t}N_{r}}\big )\), which can be seen to remain unchanged with N t and N r.
Coming to the semi-blind estimator, the unitary matrix \({\mathbf {Q}}_{\bar {m}}\) constrained as \({\mathbf {Q}}_{\bar {m}}^{H}{\mathbf {Q}}_{\bar {m}}={\mathbf {I}}_{N_{t}}\). Thus, one can utilize the constrained CRLB framework in [53] for benchmarking the MSE of the semi-blind estimator. To begin with, the whitening matrix \({\mathbf {W}}_{\bar {m}}\) can be assumed to be known at the receiver. This assumption, as shown in [52], holds well with the transmission of a few hundred OQAM data symbols, because the accuracy for estimating the matrix \({\mathbf {W}}_{\bar {m}}\) is sufficiently high. It follows from [52] that CRLB for the MSE of the semi-blind estimator for (l, k)th element \({\mathbf {H}}_{\bar {m}}(k,l)\) of the CSI matrix \({\mathbf {H}}_{\bar {m}}\) is expressed as
where \({\mathbf {Q}}_{\bar {m}}(l,j)\) and \({\mathbf {S}}_{\bar {m}}(k,i)\), respectively, represent the (l, j)th element of \({\mathbf {Q}}_{\bar {m}}\) the (k, i)th element of \({\mathbf {S}}_{\bar {m}}\). It is important to note that the weighting factor \(\sigma ^{2}_{\bar {m},i}/(\sigma ^{2}_{\bar {m},j}+\sigma ^{2}_{\bar {m},i})\) gives the net reduction in the CSI estimation error in comparison to that of the pilot-aided LS CSI estimator. Furthermore, it follows from [50] that the minimum error for estimating \({\mathbf {H}}_{\bar {m}}\) by using the semi-blind technique is bounded as
where \(N_{\theta }=N_{t}^{2}\) gives the number of real parameters required to parameterize \({\mathbf {Q}}_{\bar {m}}\) [54]. It also implies that when the estimation of the whitening matrix \({\mathbf {W}}_{\bar {m}}\) is performed accurately by using the blind information of data symbols, the CSI matrix \({\mathbf {H}}_{\bar {m}}={\mathbf {W}}_{\bar {m}}{\mathbf {Q}}^{H}_{\bar {m}}\) also requires estimation of only \(N_{t}^{2}\) parameters. These parameters can be estimated with high degree of accuracy by using a limited pilot overhead. The constraint CRLB for the estimation of the CSI matrix in (3.48) is given as
The CRLB for CSI estimation per parameter is \(\geq \frac {\sigma ^{2}_{\eta }NN_{t}^{2}}{4P_{d}M}\big (\frac {1}{N_{t}N_{r}}\big )\), which reduces with increasing the number of receive antennas N r. Upon using (3.53) and (3.50), the MSE gain of the semi-blind technique over the pilot-based LS technique is
Since N r ≥ N t, it is immediately clear that \(\frac {2N_{r}}{N_{t}}\geq 2\). It follows from (3.54) that for square MIMO-FBMC system that has N r = N t, the semi-blind technique outperforms the LS technique up to 3 dB. Furthermore, the MSE gain \(\mathcal {G}\) can be increased by increasing the number of receive antennas N r.
Figure 3.4a shows numerical results to verify MSE gain of the semi-blind (SB) technique over the conventional LS scheme quantified in (3.54). For this study, an N t × N r MIMO-FBMC system with the number of subcarriers N = 128 is considered over a type A Rayleigh fading channel for vehicular scenarios that has L h = 6 taps, with the delay profile (in ns) 0, 310, 710, 1090, 1730, 2510 and power profile (in dB) 0.0, −1.0, −9.0, −10.0, −15.0, −20.0 between the (t, r)th transmit-receive antenna pair. The isotropic orthogonal transform algorithm (IOTA) prototype pulse [15] of duration 4T is used for pulse shaping in FBMC system. Pilot and data symbols are drawn from the real and imaginary parts of 4-QAM symbols. The SNR on each subcarrier is calculated as \(2P_{d}/\sigma ^{2}_{\eta }\). It can be seen from Fig. 3.4a that the semi-blind CSI estimation technique for 2 × 4 and 2 × 6 MIMO-FBMC systems can be observed to provide MSE gain of 6 dB and 7.78 dB over the pilot only LS CSI estimator, respectively. This happens because the MSE per parameter for the latter does not change with N r, whereas it decreases with N r for the former. This NMSE trend validates the CRLB analysis presented in Section 3.4.3. It is also seen that both SB and LS techniques achieve their respective CRLBs.
(a) MSE gain of the semi-blind (SB) CSI estimator (perfect \({\mathbf {W}}_{\bar {m}}\)) over the pilot-aided LS CSI estimator with N = 128, z = 3 and M = N t = 2 and (b) MSE comparison of the SB (perfect and imperfect \({\mathbf {W}}_{\bar {m}}\)) and LS CSI estimators with N r = 4, M = N t = 2 and N d = 320
Figure 3.4b shows the NMSE as a function SNR for the SB and LS CSI estimators. The graphs in the presence of perfect and imperfect knowledge of whitening matrix are marked as Perf W m and Imperf W m, respectively. For the Perf W m case, \({\mathbf {W}}_{\bar {m}}={\mathbf {S}}_{\bar {m}}\boldsymbol {\Gamma }_{\bar {m}}\), where \({\mathbf {S}}_{\bar {m}}\boldsymbol {\Gamma }_{\bar {m}}{\mathbf {Q}}^{H}_{\bar {m}}\) is obtained using the SVD of the CSI matrix \({\mathbf {H}}_{\bar {m}}\). For the Imperf \({\mathbf {W}}_{\bar {m}}\) case, \({\mathbf {W}}_{\bar {m}}\) is estimated using the second-order statistical characteristics of N d = 320 OQAM data symbols. The SB CSI estimator in the presence of imperfect \({\mathbf {W}}_{\bar {m}}\) can be seen to perform close to its perfect \({\mathbf {W}}_{\bar {m}}\) counterpart. It can also be seen that the NMSE of both the LS and SB techniques with z = 1 floors at high SNR. This happens because the ISI between the pilot symbols dominates at the high SNR. As z increases to 3, both the CSI estimation methods receiver NMSE improvement due to the reduced effect of the ISI. Furthermore, the SB CSI estimator in the presence of imperfect \({\mathbf {W}}_{\bar {m}}\) achieves a performance close to its CRLB. This shows that fixing z = 3 gives the ideal spectral efficiency versus NMSE trade-off, because the CRLB is nothing but the best possible estimation performance of an estimator.
3.5 Performance of FBMC Waveform in Uplink of Massive MIMO
In recent years, massive MIMO technology has received widespread popularity because of its ability to support a large number of users with high throughput [55]. By using a few hundred antennas at the base station, the massive MIMO technology achieves the favourable propagation, which mitigates the co-channel interference by employing linear receivers, namely, ZF, MMSE and maximum ratio combining (MRC). This leads to a significant enhancement in spectral efficiency. OFDM is being used with massive MIMO technology for 5G deployment. However, OFDM-based systems are susceptible to practical impairments associated with carrier and timing offsets, particularly in the uplink wherein it is difficult to track the Doppler spreads experienced by different users [5, 6]. The aim of this section is to analyse the uplink performance of FBMC waveform in the context of MU massive MIMO technology.
3.5.1 Review of Existing Works
Reference [56] showed that the signal-to-interference-plus-noise ratio (SINR) of FBMC waveform-based massive MIMO technology over frequency-selective channel saturates to a deterministic value that depends on the correlation between the channel impulse responses and weights of multi-antenna combining taps. Aminjavaheri et al. in [21] developed an equalizer to mitigate the SINR saturation in [56]. References [57, 58] compared OFDM and FBMC waveforms in the massive MIMO setup and highlight the benefits of the latter over the former in terms of (i) sensitivity to CFO; (ii) peak-to-average power ratio; and (iii) increased bandwidth efficiency. The work in [22] used the FBMC waveform for the uplink transmission in massive MIMO technology and derived the MSE of the estimated symbols for the MMSE, ZF and matched filtering receivers. Reference [49] derived the uplink achievable rate for FBMC-based multi-user multi-cell massive MIMO systems relying on the ZF and MRC receivers. The pertinent power scaling laws in the existence of perfect and imperfect receiver CSIs have also been derived therein. Recently, reference [59] investigated the uplink sum rate performance of multi-cell massive MIMO-FBMC systems over Rician fading channels. The studies reviewed above show that FBMC waveform in the context of massive MIMO technology has got significant attention. This section analyses the performance of FBMC waveform in the uplink of MU massive MIMO technology, in terms of uplink sum rates of the MRC and ZF receivers in the existence of perfect and imperfect CSIs. The lower bounds on the uplink sum rates of the MRC and ZF receivers are also derived, followed by the corresponding power scaling laws. Numerical examples are presented to (i) verify the analysis and (ii) compare the performance of OFDM- and FBMC-based MU massive MIMO technologies.
3.5.2 Massive MIMO-FBMC System Model
An uplink of FBMC waveform-based single-cell MU massive MIMO technology is considered that has N subcarriers, U single-antenna users and a BS comprising L antennas with 1 ≪ U ≪ L. The U users communicate to the BS using the same time-frequency resources. An OQAM symbol transmitted by the uth user at FT index (m, n) is denoted by \(d^{u}_{m,n}\). The OQAM symbols are generated from QAM symbols as per the rules given in (3.3) and (3.4). The in-phase and quadrature components of QAM symbol \(c^{u}_{m,n}\) are assumed to be spatially and temporally i.i.d. with power P d. This implies that \(\mathbb {E}\big [d^{u}_{m,n}\left (d^{u}_{m,n}\right )^{\ast }\big ]=P_{d}\) and \(\mathbb {E}\big [c^{u}_{m,n}\left (c^{u}_{m,n}\right )^{\ast }\big ]=2P_{d}\). The signal on the lth BS antenna at frequency index \(\bar {m}\) and symbol instant \(\bar {n}\) is obtained as
where the complex quantity \(G^{l,u}_{\bar {m}}=\sum _{k=0}^{L_{h}-1}g^{l,u}[k]e^{-j2\pi \bar {m}k/N}\), between the uth user in the cell and the lth antenna of the base station, represents the CFR at subcarrier \(\bar {m}\). The term g l, u[k] is the corresponding L h-tap channel impulse response. The demodulated noise \(\eta ^{l}_{\bar {m},\bar {n}}\) at the lth BS antenna obeys \(\mathcal {C}\mathcal {N}(0,\sigma ^{2}_{\eta })\). The quantity \(b^{u}_{\bar {m},\bar {n}} = d^{u}_{\bar {m},\bar {n}}+j I^{u}_{\bar {m},\bar {n}}\) is the virtual symbol for the uth user. The interference \(I^{u}_{\bar {m},\bar {n}}\) is expressed by (3.24). For convenience, (3.55) can be expressed in vector form as
where \({\mathbf {y}}_{\bar {m},\bar {n}}=[y^{1}_{\bar {m},\bar {n}},y^{2}_{\bar {m},\bar {n}},\ldots ,y^{L}_{\bar {m},\bar {n}}]^{T}\in \mathbb {C}^{L\times 1}\) comprises observed symbols across L antennas of the BS, while \(\boldsymbol {\eta }_{\bar {m},\bar {n}}=[\eta ^{1}_{\bar {m},\bar {n}},\eta ^{2}_{\bar {m},\bar {n}}, \ldots ,\eta ^{L}_{\bar {m},\bar {n}}]^{T}\in \mathbb {C}^{L\times 1}\) is the noise vector such that \(\mathbb {E}[\boldsymbol {\eta }_{\bar {m},\bar {n}}\boldsymbol {\eta }_{\bar {m},\bar {n}}^{H}]=\sigma ^{2}_{\eta }{\mathbf {I}}_{L}\). The vector \({\mathbf {b}}_{\bar {m},\bar {n}}=[b^{1}_{\bar {m},\bar {n}}, b^{2}_{\bar {m},\bar {n}},\ldots ,b^{U}_{\bar {m},\bar {n}}]^{T}\in \mathbb {C}^{U\times 1}\) consists of virtual symbol of the U users such that \({\mathbb {E}}[{\mathbf {b}}_{\bar {m},\bar {n}}{\mathbf {b}}^{H}_{\bar {m},\bar {n}}]\approx 2P_{d}{\mathbf {I}}_{U}\). The matrix \({\mathbf {G}}_{\bar {m}}=[{\mathbf {g}}^{1}_{\bar {m}},{\mathbf {g}}^{2}_{\bar {m}},\ldots ,{\mathbf {g}}^{U}_{\bar {m}}]\in \mathbb {C}^{L\times U}\) is the CSI matrix between the U users in the cell and the base station. The matrix \({\mathbf {G}}_{\bar {m}}\) is commonly modelled as [60]
where the diagonal matrix \(\mathbf {D}=\text{diag}(\beta ^{1},\beta ^{2},\cdots ,\beta ^{U})\in \mathbb {R}^{U\times U}\) with β u being the large-scale fading coefficient for the uth user. The quantity β u, which remains same for many coherence time intervals, can be assumed to be known at the base station. Also, it is assumed to be independent from BS antennas and subcarriers. The matrix \({\mathbf {H}}_{\bar {m}}=[{\mathbf {h}}^{1}_{\bar {m}},{\mathbf {h}}^{2}_{\bar {m}},\ldots ,{\mathbf {h}}^{U}_{\bar {m}}]\in \mathbb {C}^{L\times U}\) consists of small-scale fading factors from the U users in the cell to the base station. The entries of \({\mathbf {H}}_{\bar {m}}\) are i.i.d. as \(\mathcal {C}\mathcal {N}(0,1)\).
3.5.3 Uplink Sum Rate for Massive MIMO-FBMC with Imperfect CSI
The combiner matrix \({\mathbf {A}}_{\bar {m}}\) for the ZF and MRC receivers, which are widely used due to their low complexity and linear nature, is
OQAM symbols at output of the combiner \({\mathbf {A}}_{\bar {m}}\) are obtained as \(\hat {\mathbf {d}}^u_{\bar {m},\bar {n}}=\Re \left \{{\mathbf {A}}^H_{\bar {m}}{\mathbf {y}}_{\bar {m},\bar {n}}\right \}\). The CSI matrix \({\mathbf {G}}_{\bar {m}}\), in practice, is estimated at the BS using pilot symbols. Reference [49] derived the uplink achievable rate for FBMC-based multi-user multi-cell massive MIMO systems by considering the effect of pilot contamination. This chapter considers single-cell multi-user massive MIMO-FBMC systems, wherein users transmit orthogonal pilot symbols for channel estimation at the base station. Thus, there is no pilot contamination. Let each user in the cell transmit M pilot symbols on each subcarrier for uplink channel estimation, as shown in Fig. 3.3. As explained in [49], the pilot-aided MMSE estimate of channel at subcarrier \(\bar {m}\) from the uth user to the BS is obtained as
where \({\mathbf {y}}^{u}_{\bar {m}}\) is the L × 1 observed pilot vector at the subcarrier \(\bar {m}\) of the uth user and P p = 2P d M represents the pilot power. Let \({\mathbf {e}}^{u}_{\bar {m}}={\mathbf {g}}^{u}_{\bar {m}}-\hat {\mathbf {g}}^{u}_{\bar {m}}\) be the channel estimation error vector for the uth user. One can show that
3.5.3.1 MRC Receiver
Employing \({\mathbf {g}}^{u}_{\bar {m}}=\hat {\mathbf {g}}^{u}_{\bar {m}}+{\mathbf {e}}^{u}_{\bar {m}}\), the expression in (3.56) can be expanded as
The OQAM symbol estimate at subcarrier \(\bar {m}\) and symbol index \(\bar {n}\) for the uth user at the output of MRC receiver can be formulated as
Here the noise-plus-interference \(v^{u,\text{mrc}}_{\bar {m},\bar {n}}\) is
Upon employing (3.34), the QAM symbol estimate at the MRC receiver output is
where we have \(c^{u}_{\bar {m},\bar {n}}={d}^{u}_{\bar {m},2\bar {n}}+j{d}^{u}_{\bar {m},2\bar {n}+1}\) and \(\tilde {v}^{u,\text{mrc}}_{\bar {m},\bar {n}}=v^{u,\text{mrc}}_{\bar {m},2\bar {n}}+jv^{u,\text{mrc}}_{\bar {m},2\bar {n}+1}\) when \(\bar {m}\) is even, and for odd \(\bar {m}\), \(c^{u}_{\bar {m},\bar {n}}={d}^{u}_{\bar {m},2\bar {n}+1}+j{d}^{u}_{\bar {m},2\bar {n}}\) and \(\tilde {v}^{u,\text{mrc}}_{\bar {m},\bar {n}}=v^{u,\text{mrc}}_{\bar {m},2\bar {n}+1}+jv^{u,\text{mrc}}_{\bar {m},2\bar {n}}\). As shown in [49], the uth user SINR at subcarrier \(\bar {m}\) in the existence of imperfect knowledge of channel is determined as
where the random variable \(\tilde {\mathbf {g}}^{j}_{\bar {m}}\) obeys \(\tilde {\mathbf {g}}^{j}_{\bar {m}}=(\hat {\mathbf {g}}^{u}_{\bar {m}})^{H}\hat {\mathbf {g}}^{j}_{\bar {m}}/\left \lVert \hat {\mathbf {g}}^{u}_{\bar {m}}\right \rVert \). The uplink rate for the uth user is determined as
Upon utilizing Jensen’s inequality \(\mathbb {E}[f(x)]\geq f(\mathbb {E}[x])\) along with the convexity of \(\text{log}(1+\frac {1}{x})\), as shown in [49], the uplink rate of the uth user is lower bounded as
By setting \(2P_{d}=E_{u}/\sqrt {L}\) for a fixed E u, and L →∞, one obtains
3.5.3.2 ZF Receiver
The estimated OQAM symbol vector at the output of ZF receiver in the existence of imperfect channel knowledge is given as
Here the noise plus interference vector \({\mathbf {v}}^{\text{zf}}_{\bar {m},\bar {n}}=\Re \big \{\hat {\mathbf {G}}^{\dagger }_{\bar {m}}\sum _{j=1}^{U}{\mathbf {e}}^{j}_{\bar {m}}b^{j}_{\bar {m},\bar {n}}+\hat {\mathbf {G}}^{\dagger }_{\bar {m}}\boldsymbol {\eta }_{\bar {m},\bar {n}}\big \}\). It follows from [49] that the SINR for the uth user can be determined as
The operation \(\big [\big (\hat {\mathbf {G}}^{H}_{\bar {m}}\hat {\mathbf {G}}_{\bar {m}}\big )^{-1}\big ]_{u,u}\) above extracts the uth diagonal element of the matrix \(\big (\hat {\mathbf {G}}^{H}_{\bar {m}}\hat {\mathbf {G}}_{\bar {m}}\big )^{-1}\). As given in [49], the uplink rate of the ZF receiver for the uth user is lower bound as
Note that for \(2P_{d}=E_{u}/\sqrt {L}\) and L →∞, \(\tilde {\mathcal {R}}^{u,\text{zf}}_{\bar {m},\text{IP}}\rightarrow \mathcal {R}^{u,\text{zf}}_{\bar {m},\text{IP}}\). It is important to note that similar to OFDM-based massive MIMO systems, the uplink power scaling laws also hold for their FBMC counterparts in the existence of imperfect channel knowledge.
3.5.4 Uplink Sum Rate for Massive MIMO-FBMC with Perfect CSI
The uplink rate for the ZF and MRC receiver processing at the BS in the existence of perfect channel knowledge can be derived as special case of their imperfect CSI counterparts as follows.
3.5.4.1 MRC Receiver
The SINR at the output of the MRC receiver for the uth user is
The lower bound on the uplink rate is
It is easy to verify that for 2P d = E u∕L and L →∞, the lower-bound \(\tilde {\mathcal {R}}^{u,\text{mrc}}_{\bar {m},\text{P}}\rightarrow \mathcal {R}^{u,\text{mrc}}_{\bar {m},\text{P}}\).
3.5.4.2 ZF Receiver
The ZF receiver SINR at the \(\bar {m}\)th subcarrier of the uth user is derived as
The above rate is lower bound as \(\mathcal {R}^{u,\text{zf}}_{\bar {m},\text{P}}= \mathbb {E}\big [\text{log}_{2}(1+\Upsilon ^{u,\text{zf}}_{\bar {m},\text{P}})\big ]\) is
If 2P d = E u∕L and L grows large, one obtains \(\tilde {\mathcal {R}}^{u,\text{zf}}_{\bar {m},\text{P}}\xrightarrow []{L\rightarrow \infty }\text{log}_{2}\left (1+{E_{u}\beta ^{u}}/{\sigma ^{2}_{\eta }}\right ). \) It is observed that similar to the OFDM-based massive MIMO systems, the uplink power scaling laws also hold for massive MIMO-FBMC systems in the existing of perfect channel knowledge at the base station.
Figure 3.5a,b demonstrate the performance of FBMC and OFDM waveforms in the uplink of massive MIMO technology. FBMC waveform with N = 128 subcarriers is considered. Pilot and data symbols are drawn from the in-phase and quadrature components of 4-QAM constellation. Each of the subcarriers in FBMC is shaped using the IOTA filter [15] of length 4T. The matrix D comprises large-scale fading coefficients β u (for 1 ≤ u ≤ U), which depend on geographical position of users in the cell as well as radio frequency of EM waves. These coefficients remain constant for multiple coherence intervals [60]. The coefficients β u, for 1 ≤ u ≤ U, are typically modelled as β u = z u∕(r u∕r h)ν [60], where z u is a log-normal random variable for the uth user with a standard deviation σ z, r u is the distance between the uth user and the BS and ν is the path loss exponent. The large-scale fading matrix D = diag[0.749, 0.045, 0.246, 0.121, 0.125, 0.142, 0.635, 0.256] [61] is a snapshot of the above model with σ z = 8 dB, ν = 3.8, r h = 100 metres and r u = 1000 metres. The small-scale fading channel from each user to the base station is considered to be complex Gaussian of length L h = 6 with uniform power delay profile. Each user transmits M = U number of OQAM pilot symbols on each subcarrier for channel estimation. The noise variance \(\sigma ^{2}_{\eta }\) is assumed to be 1. With this assumption, the transmit power per user can be interpreted as normalized transmit SNR, and hence it is dimensionless. There are U = 8 single antenna users in the cell.
Uplink performance comparison of FBMC- and OFDM-based massive MIMO technologies: (a) Uplink sum rate as a function of the number of BS antennas in the existence of imperfect and perfect knowledge of channel with power per user 2P d = 10 dB and (b) SER versus normalized CFO with perfect knowledge of channel, power per user 2P d = −5 dB, L = 64, L h = 2 and β u = 1 for 1 ≤ u ≤ U
Figure 3.5a shows that the uplink sum rates achieved by the ZF and MRC receivers agree to their respective lower bounds in the existence of imperfect and perfect channel knowledge. It can be seen that that the uplink sum rates of the FBMC-based MU massive MIMO system coincide with their OFDM counterparts. It is also observed that the ZF receiver outperforms the MRC receiver, especially in the high SNR regime. However, in comparison to the latter, the former costs more in terms of computational complexity. The results in Fig. 3.5a are plotted in the existence of perfect synchronization. However, in the existence of synchronization errors due to practical impairments such as CFO, as shown in Fig. 3.5b, the symbol error rate (SER) of an OFDM-based massive MIMO system degrades severely in comparison to its FBMC counterpart. This happens because the OFDM waveform experiences significant ICI due to the sinc-shaped frequency localization of the rectangular pulse shaping, whereas FBMC waveform, due to associated well time-frequency localized pulse-shaping filter, experience significantly lower ICI, which makes FBMC waveform robust against practical impairments.
3.6 Conclusions and Future Directions
This chapter designed and analysed FBMC-OQAM-based MIMO and massive MIMO systems. For improving the accuracy of CSI at the receiver with limited pilot overhead, a semi-blind (SB) MIMO-FBMC CSI estimation scheme was developed. The SB technique exploited both the pilot symbols and the second-order statistical information of data symbols. The NMSE gain of the SB scheme over the LS increases with the number of receive antennas. It was also demonstrated that the SB scheme achieves its CRLB.
This chapter also analysed the uplink performance of FBMC waveform in multi-user massive MIMO systems in the existence of both perfect and imperfect knowledge of channel. The uplink sum rates and their corresponding lower bounds were derived for massive MIMO-FBMC systems relying on the MRC and ZF receiver processing at the base station with/without perfect CSI. For both the receivers, the derived lower bounds on the achievable uplink sum rate were seen to closely agree with their respective simulated rates. Furthermore, the uplink power scaling laws, similar to OFDM waveform, were seen to exist for FBMC-based massive MIMO systems. It was also shown that OFDM- and FBMC-based massive MIMO systems achieve the same uplink performance in the existence of perfect synchronization. However, in the existence of practical impairments such as CFO, FBMC-based massive MIMO systems were seen to vastly outperform their OFDM counterparts.
The future works may investigate semi-blind scheme for highly frequency-selective and/or time-selective channels. Future research may present an analysis for characterising the performance of FBMC-based massive MIMO systems in time-selective channels. Future research may also analyse performance of FBMC waveform in the downlink of massive MIMO by considering the effect of multi-user precoding, which poses additional challenges. Future lines of this work can also investigate performance of FBMC signalling in other state-of-the-art technologies like millimetre wave, intelligent reflecting surfaces (IRS) and Internet of Things (IoT).
Notes
- 1.
Let the singular value decomposition (SVD) of \({\mathbf {H}}_{\bar {m}}\) be expressed as \(\text{SVD}({\mathbf {H}}_{\bar {m}})={\mathbf {S}}_{\bar {m}}\boldsymbol {\Gamma }_{\bar {m}}{\mathbf {Q}}_{\bar {m}}^{H}\). It is clear that one possible choice for \({\mathbf {W}}_{\bar {m}}={\mathbf {S}}_{\bar {m}}\boldsymbol {\Gamma }_{\bar {m}}\) and the unitary matrix can be set as \({\mathbf {Q}}_{\bar {m}}\). It implies that the whitening unitary decomposition in (3.37) is guaranteed to exist.
References
T. Starr, J.M. Cioffi, P.J. Silverman, Understanding Digital Subscriber Line Technology (Prentice Hall PTR, Hoboken, 1999)
R.V. Nee, R. Prasad, OFDM for Wireless Multimedia Communications (Artech House Inc., Norwood, 2000)
S. Schwarz, T. Philosof, M. Rupp, Signal processing challenges in cellular-assisted vehicular communications: efforts and developments within 3GPP LTE and beyond. IEEE Signal Process. Mag. 34(2), 47–59 (2017)
B. Farhang-Boroujeny, R. Kempter, Multicarrier communication techniques for spectrum sensing and communication in cognitive radios. IEEE Commun. Mag. 46(4), 80–85 (2008)
T. Pollet, M.V. Bladel, M. Moeneclaey, BER sensitivity of OFDM systems to carrier frequency offset and wiener phase noise. IEEE Trans. Commun. 43(234), 191–193 (1995)
M. Morelli, C.J. Kuo, M. Pun, Synchronization techniques for orthogonal frequency division multiple access (OFDMA): a tutorial review. Proc. IEEE 95(7), 1394–1427 (2007)
V. Vakilian, T. Wild, F. Schaich, S. ten Brink, J. Frigon, Universal-filtered multi-carrier technique for wireless systems beyond LTE, in Workshops Proceedings of the Global Communications Conference, GLOBECOM, Atlanta, December 9–13 (2013), pp. 223–228
B. Farhang-Boroujeny, H. Moradi, OFDM inspired waveforms for 5G. IEEE Commun. Surv. Tutorials 18(4), 2474–2492 (2016)
N. Michailow, M. Matthe, I.S. Gaspar, A.N. Caldevilla, L.L. Mendes, A. Festag, G.P. Fettweis, Generalized frequency division multiplexing for 5th generation cellular networks. IEEE Trans. Commun. 62(9), 3045–3061 (2014)
B. Farhang-Boroujeny, OFDM versus filter bank multicarrier. IEEE Signal Process. Mag. 28(3), 92–112 (2011)
G. Cherubini, E. Eleftheriou, S. Ölçer, Filtered multitone modulation for very high-speed digital subscriber lines. IEEE J. Select. Areas Commun. 20(5), 1016–1028 (2002)
B. Farhang-Boroujeny, C.H.G. Yuen, Cosine modulated and offset QAM filter bank multicarrier techniques: a continuous-time prospect. EURASIP J. Adv. Sig. Proc. 2010 (2010)
M.G. Bellanger, Specification and design of a prototype filter for filter bank based multicarrier transmission, in Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2001, 7–11 May, 2001, Salt Palace Convention Center, Salt Lake City (2001), pp. 2417–2420
A. Aminjavaheri, A. Farhang, A. RezazadehReyhani, B. Farhang-Boroujeny, Impact of timing and frequency offsets on multicarrier waveform candidates for 5G, in IEEE Signal Processing and Signal Processing Education Workshop, SP/SPE 2015, Salt Lake City, August 9–12 (2015), pp. 178–183
P. Siohan, C. Siclet, N. Lacaille, Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Trans. Signal Proces. 50(5), 1170–1183 (2002)
A.I. Pérez-Neira, M. Caus, R. Zakaria, D.L. Ruyet, E. Kofidis, M. Haardt, X. Mestre, Y. Cheng, MIMO signal processing in offset-QAM based filter bank multicarrier systems. IEEE Trans. Signal Proces. 64(21), 5733–5762 (2016)
M.J. Abdoli, M. Jia, J. Ma, Weighted circularly convolved filtering in OFDM/OQAM, in 24th IEEE Annual International Symposium on Personal, Indoor, and Mobile Radio Communications, PIMRC 2013, London, September 8–11 (2013), pp. 657–661
H. Lin, P. Siohan, Multi-carrier modulation analysis and WCP-COQAM proposal. EURASIP J. Adv. Sig. Proc. 2014, 79 (2014)
H.S. Sourck, Y. Wu, J.W.M. Bergmans, S. Sadri, B. Farhang-Boroujeny, Complexity and performance comparison of filter bank multicarrier and OFDM in uplink of multicarrier multiple access networks. IEEE Trans. Signal Proces. 59(4), 1907–1912 (2011)
R. Nissel, S. Schwarz, M. Rupp, Filter bank multicarrier modulation schemes for future mobile communications. IEEE J. Select. Areas Commun. 35(8), 1768–1782 (2017)
A. Aminjavaheri, A. Farhang, B. Farhang-Boroujeny, Filter bank multicarrier in massive MIMO: analysis and channel equalization. IEEE Trans. Signal Proces. 66(15), 3987–4000 (2018)
F. Rottenberg, X. Mestre, F. Horlin, J. Louveaux, Performance analysis of linear receivers for uplink massive MIMO FBMC-OQAM systems. IEEE Trans. Signal Proces. 66(3), 830–842 (2018)
S. Srivastava, P. Singh, A.K. Jagannatham, A. Karandikar, L. Hanzo, Bayesian learning-based doubly-selective sparse channel estimation for millimeter wave hybrid MIMO-FBMC-OQAM systems. IEEE Trans. Commun. 69(1), 529–543 (2021)
E. Kofidis, D. Katselis, A.A. Rontogiannis, S. Theodoridis, Preamble-based channel estimation in OFDM/OQAM systems: a review. Signal Proces. 93(7), 2038–2054 (2013)
P. Singh, K. Vasudevan, Preamble-based synchronization for OFDM/OQAM systems in AWGN channel, in 4th IEEE International Conference on Signal Processing and Integrated Networks (SPIN) (2017), pp. 60–65
C. Lélé, J. Javaudin, R. Legouable, A. Skrzypczak, P. Siohan, Channel estimation methods for preamble-based OFDM/OQAM modulations. Eur. Trans. Telecommun. 19(7), 741–750 (2008)
P. Singh, R. Budhiraja, K. Vasudevan, SER analysis of MMSE combining for MIMO FBMC-OQAM systems with imperfect CSI. IEEE Commun. Lett. 23(2), 226–229 (2019)
E. Kofidis, D. Katselis, Preamble-based channel estimation in MIMO-OFDM/OQAM systems, in IEEE International Conference on Signal and Image Processing Applications, ICSIPA, Kuala Lumpur, 16–18 November (2011), pp. 579–584
F. Rottenberg, Y. Medjahdi, E. Kofidis, J. Louveaux, Preamble-based channel estimation in asynchronous FBMC-OQAM distributed MIMO systems, in International Symposium on Wireless Communication Systems (ISWCS), Belgium, 25–28, August (2015), pp. 566–570
S. Hu, Z. L. Liu, Y. L. Guan, C. Jin, Y. Huang, J. Wu, Training sequence design for efficient channel estimation in MIMO-FBMC systems. IEEE Access 5, 4747–4758 (2017)
J.-P. Javaudin, Y. Jiang, Channel estimation in MIMO OFDM/OQAM, in IEEE 9th Workshop on Signal Processing Advances in Wireless Communications, SPAWC (2008), pp. 266–270
P. Singh, K. Vasudevan, MIMO-FBMC channel estimation with limited, and imperfect knowledge of channel correlations, in National Conference on Communications, NCC, Bangalore, February 20–23 (2019), pp. 1–6
E. Kofidis, Preamble-based estimation of highly frequency selective channels in MIMO-FBMC/OQAM systems, in Proceedings of the 21th European Wireless Conference (VDE, Berlin, 2015), pp. 1–6
P. Singh, K. Vasudevan, Time domain channel estimation for MIMO-FBMC/OQAM systems. Wirel. Person. Commun. 108(4), 2159–2178 (2019)
P. Singh, E. Sharma, K. Vasudevan, R. Budhiraja, CFO and channel estimation for frequency selective MIMO-FBMC/OQAM systems. IEEE Wirel. Commun. Lett. 7(5), 844–847 (2018)
M. Lin, Y. Li, L. Xiao, J. Wang, A compressive sensing channel estimation for MIMO FBMC/OQAM system. Wirel. Person. Commun., 1–16 (2017)
M. Renfors, X. Mestre, E. Kofidis, F. Bader, Orthogonal Waveforms and Filter Banks for Future Communication Systems (Academic Press, Cambridge, 2017)
H. Bölcskei, P. Duhamel, R. Hleiss, A subspace-based approach to blind channel identification in pulse shaping OFDM/OQAM systems. IEEE Trans. Signal Proces. 49(7), 1594–1598 (2001)
V. Savaux, F. Bader, J. Palicot, OFDM/OQAM blind equalization using CNA approach. IEEE Trans. Signal Proces. 64(9), 2324–2333 (2016)
W. Hou, B. Champagne, Semiblind channel estimation for OFDM/OQAM systems. IEEE Signal Process. Lett. 22(4), 400–403 (2015)
B. Su, Semiblind channel estimation for OFDM/OQAM systems assisted by zero-valued pilots, in IEEE International Conference on Digital Signal Processing, Singapore, July 21–24 (2015), pp. 393–397
E. Kofidis, C. Chatzichristos, A.L.F. de Almeida, Joint channel estimation/data detection in MIMO-FBMC/OQAM systems – A tensor-based approach, in 25th European Signal Processing Conference, EUSIPCO 2017, Kos (2017), pp. 420–424
J.-M. Choi, Y. Oh, H. Lee, J.-S. Seo, Pilot-aided channel estimation utilizing intrinsic interference for FBMC/OQAM systems. IEEE Trans. Broadcast. 63(4), 644–655 (2017)
H. Lin, P. Siohan, Robust channel estimation for OFDM/OQAM. IEEE Commun. Lett. 13(10), 724–726 (2009)
V. Savaux, F. Bader, Y. Louët, A joint MMSE channel and noise variance estimation for OFDM/OQAM modulation. IEEE Trans. Commun. 63(11), 4254–4266 (2015)
D. Katselis, E. Kofidis, A.A. Rontogiannis, S. Theodoridis, Preamble-based channel estimation for CP-OFDM and OFDM/OQAM systems: a comparative study. IEEE Trans. Signal Proces. 58(5), 2911–2916 (2010)
M.J.F. García, E. Biglieri, G. Taricco, Frequency-domain channel estimation in MIMO-OFDM, in 12th European Signal Processing Conference, Vienna, September 6–10 (2004), pp. 1869–1872
R. Vershynin, How close is the sample covariance matrix to the actual covariance matrix?. J. Theoret. Probab. 25(3), 655–686 (2012)
P. Singh, H.B. Mishra, A.K. Jagannatham, K. Vasudevan, L. Hanzo, Uplink sum-rate and power scaling laws for multi-user massive MIMO-FBMC systems. IEEE Trans. Commun. 68(1), 161–176 (2020)
A.K. Jagannatham, B.D. Rao, Whitening-rotation-based semi-blind MIMO channel estimation. IEEE Trans. Signal Proces. 54(3), 861–869 (2006)
K.B. Petersen, M.S. Pedersen et al., The matrix cookbook. Tech. Univ. Denmark 7, 15 (2008)
P. Singh, H.B. Mishra, A.K. Jagannatham, K. Vasudevan, Semi-blind, training, and data-aided channel estimation schemes for MIMO-FBMC-OQAM systems. IEEE Trans. Signal Proces. 67(18), 4668–4682 (2019)
A.K. Jagannatham, B.D. Rao, Cramér-Rao lower bound for constrained complex parameters. IEEE Signal Proces. Lett. 11(11), 875–878 (2004)
J.C. Roh, B.D. Rao, Efficient feedback methods for MIMO channels based on parameterization. IEEE Trans. Wirel. Commun. 6(1), 282–292 (2007)
T.L. Marzetta, E.G. Larsson, H. Yang, H.Q. Ngo, Fundamentals of Massive MIMO (Cambridge University Press, Cambridge, 2016)
A. Aminjavaheri, A. Farhang, L.E. Doyle, B. Farhang-Boroujeny, Prototype filter design for FBMC in massive MIMO channels, in IEEE International Conference on Communications, ICC, Paris, May 21–25 (2017), pp. 1–6
A. Farhang, N. Marchetti, L.E. Doyle, B. Farhang-Boroujeny, Filter bank multicarrier for massive MIMO, in IEEE 80th Vehicular Technology Conference, VTC Fall, Vancouver, September 14–17 (2014), pp. 1–7
A. Aminjavaheri, A. Farhang, N. Marchetti, L.E. Doyle, B. Farhang-Boroujeny, Frequency spreading equalization in multicarrier massive MIMO, in Workshop Proceedings of the IEEE International Conference on Communication, ICC, June 8–12 (2015), pp. 1292–1297
S. Singh, P. Singh, S. Sahu, K. Vasudevan, H.B. Mishra, Uplink transmission in MU multi-cell massive MIMO-FBMC systems over ricean fading, in 94th IEEE Vehicular Technology Conference, VTC Fall 2021, Norman, September 27–30 (2021), pp. 1–6
H.Q. Ngo, E.G. Larsson, T.L. Marzetta, Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 61(4), 1436–1449 (2013)
Y. Dai, X. Dong, Power allocation for multi-pair massive MIMO two-way AF relaying with linear processing. IEEE Trans. Wirel. Commun. 15(9), 5932–5946 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Singh, P., Sharma, E. (2023). FBMC: A Waveform Candidate for Beyond 5G. In: Matin, M.A. (eds) A Glimpse Beyond 5G in Wireless Networks. Signals and Communication Technology. Springer, Cham. https://doi.org/10.1007/978-3-031-13786-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-13786-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13785-3
Online ISBN: 978-3-031-13786-0
eBook Packages: Computer ScienceComputer Science (R0)