1 Model Order Reduction for Gas and Energy Networks

Computer-based simulation of gas transport in pipeline networks has been an industrial as well as academic field of interest since the earliest scientific computing systems [5]. Especially, the transient simulation of gas flow and the dynamic gas network behavior are the pinnacle discipline in this regard. The MATLAB-based morgen—Model Order Reduction for Gas and Energy Networks—platformFootnote 1 continues this research by providing a modular open-source software simulation stack for the comparison and benchmarking of models (discretizations), solvers (time steppers), and reductors (model reduction algorithms) [3]. Beyond selecting apposite simulator components or ranking model reduction methods, an overall goal is the acceleration of forward simulations, so that many-query tasks relying thereon, such as optimization, control or uncertainty quantification, benefit in terms of performance. In this work, we summarize and enhance the foundational work of [3] with additional details, and accompany version 1.1 of morgen.

1.1 Modules Overview

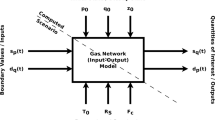
The morgen platform is organized into modules: models, solvers, reductors, networks and tests. The networks module holds topology and scenario data, and the tests module defines the simulation and model reduction experiments, thus, we summarize the currently available core modules: models, solvers, and reductors. The models module assembles a semi-discrete input-output system from a network topology. Currently, two spatially discrete models are included (Table 1). The solvers module computes a time-discrete output trajectory from a model and a scenario. Six solvers are provided in the current version (Table 2). The reductors module compresses a model given a solver and (generic training) scenario. All in all, 23 reductors organized in four classes are available (Table 3).

Table 1 Available models in morgen in version 1.1
Full size table
Table 2 Available solvers in morgen in version 1.1
Full size table
Table 3 Available reductors in morgen in version 1.1
Full size table

2 Enhanced Functionality

In this section, we discuss some of the new properties of the morgen 1.1 platform. Specifically, one aspect of each core module (model, solver, reductor) is addressed.

2.1 Gravity Term

One component of the gas pipeline model, particularly of the retarding forces in the mass-flux equation, is the gravity term, which accounts for increase or decrease in momentum due to an incline in a pipeline section. In [2], this gravity term is modeled in great detail, as it does not only consider a height difference between the pipe’s end points, as morgen does, but also the height profile for the full run of the pipe (see [2, Fig. 11]). Both approaches are justified, depending on the aimed accuracy of the model, as discussed in [1]. Such pipeline height profiles can be included into morgen by supplying a pipe as sequence of virtual pipes, each connecting two subsequent local height extrema. In morgen 1.1, the gravity term is configurable so it is computable based on the dynamic pressure, static pressure or not at all, whereas the static gravity term, based on the steady-state was newly added.

2.2 Explicit Solvers

In [3], the classic explicit 4th order Runge-Kutta method rk4 was tested, as it was employed in earlier works. Yet we found it to be not suitable for gas network simulations. In [4], an explicit Runge-Kutta method from [9, Sec. 4] was suggested for this application. The Butcher tableau for this explicit 5-stage, 2nd order low-storage scheme with increased stability, is given by:

0

     

\(\frac {1}{4}\)

\(\frac {1}{4}\)

    

\(\frac {1}{6}\)

0

\(\frac {1}{6}\)

   

\(\frac {3}{8}\)

0

0

\(\frac {3}{8}\)

  

\(\frac {1}{2}\)

0

0

0

\(\frac {1}{2}\)

 
 

0

0

0

0

1

This additional solver rk2hyp, as well as a 4th order Runge-Kutta method with increased hyperbolic stability limit from [6, Sec. 4.1] (rk4hyp), were added to morgen 1.1 and tested against various test problems. Both increased-stability solvers allow larger time steps then rk4, specifically in conjunction with the ode_end model, but compared to the implicit-explicit solvers imex1 and imex2, they are still not fully competitive. However, these explicit methods could be interesting for new implicit-explicit or predictor-corrector methods.

2.3 Gain Matching

An important quality for certain applications of model reduction, such as electrical circuits, is the preservation of the steady-state gain (also known as DC gain), which is the output for zero frequency input. First, we clarify that we are not discussing the actual steady-state gain of the reduced order model, due to the centering around the steady-state and hence, the steady-state gain match [3, Sec. 3]. Yet, there can still be an output error for a constant input on top of the steady-state input, which is relevant due to the assumed low-frequency boundary values. Since there is an interpretation of gas networks as circuits [8], we consider this reduced model property, which induces two questions: How to compute the steady-state gain, and how to correct a gain mismatch? The former is answered by [10], stating that for a linear port-Hamiltonian model, with components as in [3, Sec. 2.9], the gain S is computable by:

$$\displaystyle \begin{aligned} S = C Q^{-1} B, \end{aligned}$$

with input matrix B, output matrix C, and energy storage matrix Q. Since the models are nonlinear and do not have to be port-Hamiltonian, but comprise the same model components, the above formula can still be applied albeit yielding only an approximation. The per-port gain mismatch D ∗ is then computed by the difference of full and reduced-order model (reduced-order quantities are denoted by ⋅r) gain:

$$\displaystyle \begin{aligned} D_* := (C Q^{-1} B) - (C_r Q_r^{-1} B_r), \end{aligned}$$

which can then be used to correct the reduced-order model gain by adding D ∗ as a feedthrough matrix to the output function, as described in the gain matching procedure in [7]. We included this approximate gain matching test to morgen 1.1.

The gain correction was tested with all reductors (Table 3). For all reductors, the correction was about the level of 10−5, see Tables f and g in Fig. 1, except for the bpod_ro method, for which the gain correction fully deteriorates the reduced model. Thus, the improvement of reduced-order models is small at best. This is not unexpected, considering the gas network model is hyperbolic: A single pipeline, or more generally an input-output system based on a first-order hyperbolic partial differential equation, has the transport property which expresses as a delay in observable outputs of controllable inputs. Hence, an immediate effect of inputs to outputs (circumventing the system dynamics), i.e. by a feedthrough term, is typically not needed.

Fig. 1
figure 1

Visualization of the test scenario, model reduction errors between FOM (full-order model) and ROM (reduced-order model), MORscore, and gain errors of the tested ROMs for the hypothetical network [5, Part 2] (left side) and actual network [5, Part 3] (right side). Computed with MATLAB 2021a. See [3, Sec. 6] for a description of the plot presentation

Full size image

3 Numerical Experiments

We extend the numerical experiments in [3], by reimplementing the results from [5], specifically, we test the hypothetical network [5, Part 2], and the actual network [5, Part 3], which are both tree networks, on their associated scenarios.

Six structured empirical-Gramian-based Galerkin reductors are tested on the port-Hamiltonian endpoint model and the first order implicit-explicit solver. The results are presented in Fig. 1. In line with other experiments, the eds_ro_l reductor yields the most accurate results.

4 Next-Gen Gas Network Simulation

For the newly tested features we conclude that currently, explicit solvers do not seem a viable option to simulate gas networks, while gain matching offers only minor accuracy improvements; yet, the new static gravity term is more robust with respect to model reduction and is henceforth the default setting in morgen.

Overall, based on the comparisons in [3] and this work’s numerical results, we currently recommend a port-Hamiltonian model, an implicit-explicit solver, and a Galerkin reductor. Thus, the endpoint discretization, first order IMEX time stepper, and the structured empirical dominant subspaces reductor make a promising model-solver-reductor ensemble for the next generation of transient gas network simulators. Future extensions of the morgen platform will refine this recommendation.