Keywords

1 Introduction

The Galveston Bay Recovery Study (GBRS) survey was conducted to study the impact of Hurricane Ike, which had made landfall at Galveston Bay on September 13, 2008. The survey took place in Chambers County and Galveston County in Texas. Galveston County includes Galveston Island and the Bolivar Peninsula, with Goat Island just to the north. The hurricane caused severe damage, particularly on the Bolivar Peninsula and Goat Island, but also on Galveston Island and further into the Bay.

With the intention of gathering data close to the time of the disaster, the investigators were able to design a three-wave longitudinal survey of which Wave 1 went into the field about two months after Hurricane Ike. Wave 1 continued until March 24, 2009. Wave 2 was a half-hour follow-up intended to be conducted two to three months after the initial interview. Wave 3 was a full follow-up survey intended to be conducted about a year after the first interview (University of Michigan Survey Research Center/Institute for Social Research 2010). The sampling design was a two-stage area sample of households from address-based frames, while interviewing took place by telephone. The main goal was to characterize trajectories and determinants of post-disaster mental health outcomes, such as Post-Traumatic Stress Disorder (PTSD), as measured through a severity score computed from responses to a 17-item scale (Pietrzak et al. 2013). Another aim (Gruebner et al. 2016a,b) was to use spatial analysis to identify patterns of mental health and wellness, and their predictors, across the geographic area in the aftermath of the disaster.

With a view to incorporating the complex features of the sampling design, Anthopolos et al. (2020) have proposed a Bayesian growth mixture model, where the three-wave trajectory of the log of the PTSD severity score is modelled within latent classes. The modelling of latent class membership is multilevel because of the clustering of the sample, and incorporates spatial dependence across adjacent clusters. Sampling design variables such as household size and auxiliary information on the frames are incorporated as covariates. Inference concerning the cluster-level variance components of latent class membership is part of the purpose.

The aim of this paper is to implement a frequentist approach to incorporating complex sampling design features in a more basic repeated measures analysis of the same data, where inference concerning the cluster-level variance components for the log PTSD severity score itself is envisaged. The complex sampling design features are incorporated using pairwise likelihood using the approach of Rao et al. (2013) and Yi et al. (2016).

Section 2 will describe the sampling design in detail. Sections 3 and 4 will document the construction of survey weights and the derivation of the inclusion probabilities required for the illustrative analyses. Section 5 specifies the spatial multilevel model under consideration. Sections 6 and 7 present a standard Bayesian analysis and the proposed frequentist analysis, respectively. Section 8 discusses the advantages and disadvantages of the two approaches, with reference to the ways in which they use the information in the sampling design and the weights.

2 Sampling Design

The following description is taken from Valliant et al. (2009) and University of Michigan Survey Research Center/Institute for Social Research (2010).

There were two sampling frames. One frame was the Experian Gold list for Galveston and Chambers Counties, purchased from the credit reporting agency Experian. This list had demographic information that could be used in an attempt to identify households and persons with higher probability of experiencing PTSD in the short or long run, based on earlier studies. A score was then constructed by the SRC to classify most of the households as high risk or low risk (or with insufficient data to determine) for PTSD after a disaster. The other frame was an area probability frame created by field staff listing procedures. Its coverage was more comprehensive, for example, including growth since the 2000 Census.

For the GBRS survey, FEMA maps of the flooding in the Galveston area immediately after Hurricane Ike and Census 2000 data were used to divide the two-county area into five geographic strata:

  • Stratum 1: Galveston Island and the Bolivar Peninsula, which suffered storm surge damage

  • Stratum 2: Flooded areas of the mainland

  • Stratum 3: Non-flooded areas of the mainland which had relatively high rates of poverty in the 2000 Census

  • Stratum 4: Non-flooded, non-poverty areas east of Route 146 (and thus close to the Bay)

  • Stratum 5: Non-flooded, non-poverty areas west of Route 146 and the remainder of Chambers County (not flooded for the most part)

Within strata, the researchers constructed area segments composed of census blocks from the 2000 Census. Eighty (80) of these were to be selected. It was initially decided that the relative sampling rates in the strata would be 4, 4, 2, 2, and 1, so that Stratum 1 and Stratum 2 would be oversampled, while Stratum 5 would be undersampled. Implementing these rates resulted in an allocation of area segments to strata of 42, 4, 16, 4, and 14. Within strata, the area segments were selected with probability proportional to a size measure, namely the number of occupied housing units in the 2000 census.

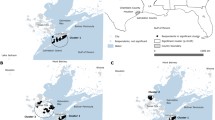
Three of the selected segments in Stratum 1 were in an area (the Bolivar Peninsula) that received extensive damage and could not be field-listed. Thus the final numbers of segments represented in the strata samples are 39, 4, 16, 4 and 14; or 77 in all. Figure 1 shows the locations of the census tracts of the sampled area segments, coloured according to stratum, superimposed on a map of population density from the 2000 Census. From this map it is apparent that the sample is taken from areas of higher population density.

Fig. 1
figure 1

Census blocks of the sampled area segments superimposed on a map of population density from the 2000 Census

Full size image

The area field listing included many housing units present in the area which did not appear on the Experian frame, and there were many cases where the same housing unit was recorded differently on the two frames. Within selected area segments, it was decided to use the Experian list as the primary sampling frame. Households therein were subdivided in each geographic stratum into High Risk for PTSD and Other (low risk or not determinable). The High Risk group was sampled at a rate 1.5 times that of the Other group. A separate sample was then taken from the subset of the area field frame listings which did not appear on the Experian frame. Whether this was the case could not always be determined perfectly: in some apartment buildings, there were cases that had a chance of selection on both frames. In the end, there were 124 Wave 1 interviews that came from the area frame (all coded as other for the risk variable) and 534 from the Experian frame.

In a first phase of sampling, selected households where it was possible to make contact were rostered, and in each, a member was selected at random from among those who were 18 years of age or older at the time of selection. Respondent locating was a major part of the effort, and this task was sent first to an outside vendor for internet locating of respondents, to be followed by in-person tracking.

In a second phase of sampling of households not responding in the first fieldwork period, cases from the first released sample, either in tracking or never contacted, were considered for further effort aimed at completing an interview. Of 489 eligible cases, 250 were selected.

Overall there were 2116 selected housing units, 420 of which were determined to be out of scope, and 658 of which resulted in a completed interview. Twenty (20) of the selected respondents were judged ineligible. Thus the Wave 1 response rate was approximately 40%. Weighted re-interview rates were 81.4% at Wave 2 and 73.3% at Wave 3.

3 Survey Weights

Survey weights were constructed for the GBRS survey data. Only the Wave 1 weights will be described here. The process is described in Valliant et al. (2009). The initial household weight was calculated as the reciprocal of the intended household inclusion probability, taking into account risk status (High Risk for PTSD or Other), the possibility of inclusion in both frames, and phase of sampling.

Consideration of phase of sampling leads to high variability of the initial household weight within strata.

The household weight was then adjusted for non-response, as follows. Contact, screening, and main interview completion were modelled in terms of housing unit characteristics: observed damage to the unit, observed destruction of the unit, stratum, Bolivar indicator, Experian indicator, High Damage Area indicator, Median Year Housing Units Built (an area segment variable), Ever a Refusal (15% of household refusals were converted), and Number of Calls.

Four adjustment strata were created, and weights were adjusted by the mean predicted contact, screening, and interview propensities in their adjustment strata. A few non-response adjustment factors were very large, and the corresponding weights were trimmed, with the reduction in weights being distributed across the other cases.

For each individual respondent, the person-level weight was the product of the non-response-adjusted household weight and the number of adults aged 18 or over in the household.

4 Inferring Inclusion Probabilities from the Weights

In the data file the household weights and person weights were provided, giving us the unconditional inclusion probability for each household and for each individual. For an illustrative design-based multilevel analysis, we needed to assign an estimated inclusion probability to each sampled area segment, and an estimated inclusion probability to each sampled individual, conditional on their area segment being sampled. The sampling of area segments was done using probability proportional to size sampling, where size was the 2000 census number of occupied housing units in the area segment. We were able to obtain an approximate value of the size of an area segment by summing the year 2000 occupied housing unit numbers of the census blocks of sampled households within the area segment, and adjusting the sum upward so that the totals over area segments in the strata would match known numbers. This produced an estimated size variable \(\hat {N}_{hj}\) for each Stratum h and area segment j. It should be noted that the designers of the sampling plan would have had access to the true size values.

If we denote the initial household weight for household k in area segment j and Stratum h by w hjk, we can write the reciprocal of w hjk as

$$\displaystyle \begin{aligned} \pi_{k \mid hj} \pi_{j \mid h}, \end{aligned} $$
(1)

where π j∣h is the needed area segment inclusion probability and π k∣hj is the design inclusion probability of household k within sampled area segment j in Stratum h. The value of π k∣hj depends on the risk stratum (High Risk for PTSD vs Other) of the household.

The High Risk for PTSD vs Other variable is not included on the data set. However, within many area segments, the lower household weights follow a pattern: the lowest weights are about 2/3 of the next lowest weights. Thus it appears that the lowest weights may correspond to deliberate oversampling, and we have assumed that they belong to households that were sampled at a rate of 1.5 times the “usual” rate in the area segment. We have also noted that within strata, the inclusion probabilities for households from the area frame were a fixed multiple of the inclusion probability of lower risk households from the Experian frame. Using these facts, together with information about the inclusion probabilities for the second phase samples, and additional assumptions, we have assigned a value of the High Risk indicator to each household.

Except for some extreme values due to the second phase of sampling, the initial household weights are not highly variable within area segments, and we approximated household inclusion probabilities by assuming simple random sampling within risk indicator value to begin with. Let a hj (to be estimated) be N hj times the sampling rate for lower risk households in area segment j of stratum h, where N hj is the number of census 2000 occupied housing units in the area segment (the “size” of the area segment), so that for household k, the probability of inclusion π k∣hj is \(1.5^{\delta _{hjk}} a_{hj}/N_{hj}\) where δ hjk = 1 if household k is of High Risk for PTSD, and 0 otherwise. Suppose the number of sampled households in the area segment is n hj. Let the proportion of those households that appear (from their weights) to be High Risk for PTSD be \(\hat {p}_{hj}\). Then a hj can be estimated from the equation

$$\displaystyle \begin{aligned} n_{hj} = \hat{p}_{hj}(1.5\hat{a}_{hj}) + (1-\hat{p}_{hj})\hat{a}_{hj}. \end{aligned} $$
(2)

This gives a preliminary estimate of N hj π k∣hj for each household k in the sample in area segment j.

Taking this estimate and multiplying by initial household weight, i.e., the reciprocal of the expression in (1), we computed a household-specific preliminary estimate of π j∣h∕N hj. We averaged these over the households with non-extreme weights in area segment j to estimate π j∣h∕N hj. We multiplied by \(\hat {N}_{hj}\) and took the minimum of the result and 1 to obtain an approximate value of π j∣h for each area segment j.

We then estimated the post-nonresponse inclusion probability for a household, given inclusion of its area segment, as the reciprocal of (the non-response adjusted household weight times the approximate value of the area segment inclusion probability). If we set aside three area segments with unusually high inclusion probabilities in Stratum 1, the average estimated area segment inclusion probabilities in the five strata are, respectively, 0.516, 0.689, 0.239, 0.260, and 0.113. The relative values of these are not very different from those of the initial target sampling rates, which were to be proportional to 4, 4, 2, 2, and 1.

These calculations allowed us to construct, for illustrative purposes, approximate decompositions of the person-level inclusion probabilities as follows:

$$\displaystyle \begin{aligned}\pi_{hjki} = \pi_{j \mid h}\pi_{k \mid hj}\pi_{i \mid hjk},\end{aligned}$$

where π i∣hjk is the reciprocal of the number of people aged 18 or over in household k. In what follows it will be convenient most of the time so suppress the stratum index h and combine the selection of household and person, writing the inclusion probability of person i of area segment j as

$$\displaystyle \begin{aligned} \pi_{ji} = \pi_{j}\pi_{i \mid j}. \end{aligned} $$
(3)

5 Spatial Multilevel Model

Let the outcome variable y jit be the logarithm of self-reported Post-Traumatic Stress Disorder (PTSD) severity score for resident i living in sampling cluster j at Wave t, t = 1, 2, 3. The sampling clusters are taken to be the area segments. We suppress notation for the sampling stratum h and the household k for simplicity. The PTSD severity scores were calculated as the sum of responses to 17 symptoms of PTSD, such as “repeated, disturbing memories of Hurricane Ike,” using the Checklist-Specific version (PCL-S) (Blanchard et al. 1996) with each symptom rated from 1 (not at all) to 5 (extremely). Questions were asked in reference to the period since the hurricane at Wave 1, and the period since the previous interview at Waves 2 and 3. Let x ji be the row vector of p covariates of interest for resident i in cluster j, potentially including age, gender, ethnicity, highest education completed, pre-disaster trauma exposure, pre-disaster PTSD, pre-disaster depression, hurricane-related trauma and stressors, peri-event reactions, and community-level social assets (Gruebner et al. 2016a). The model for the outcome variable could also depend on the sampling design through the sampling stratum, and through determinants of w ij, such as a smooth function of the logarithm of the size variable (the number of occupied housing units in the sampled census blocks of the area segment); the risk indicator for the household; the number of adult members of the household; and a function of the household non-response adjustment (Anthopolos et al. 2020). We have used all of these except the function of the size variable, this being omitted to keep the covariate space relatively simple.

The goal of this modelling approach is to examine risk factors, analytically and visually, associated with post-disaster scores of PTSD after accounting for longitudinal dependence, spatial correlation and the complex survey design. We propose a three-level model, where the three levels are the spatial cluster (the area segment), the individual within a cluster, and the survey wave within an individual. By an extension of notation j is the identifier of the adjusted census tract (CT) containing cluster j. Adjusted CTs were defined as follows: if two or more area segments (clusters) were in one official CT, the CT was split based on the number of area segments within it so that each area segment is in just one adjusted CT; if a CT has no area segment within it, that CT is combined with the nearest adjusted CT; thus after adjustment, the whole study area has the same number of adjusted CTs as the number of area segments.

The model for the outcome variable can be written as follows:

$$\displaystyle \begin{aligned}y_{jit} | \mu_{jit} \sim N(\mu_{jit}, \sigma_{c}^{2})\end{aligned}$$
$$\displaystyle \begin{aligned}\mu_{jit} = \alpha_{0ji} + \gamma_{02}I(t = 2) + \gamma_{03}I(t=3)\end{aligned}$$
$$\displaystyle \begin{aligned}\alpha_{0ji} = \beta_{0j} + \mathbf x_{ji} \beta + v_{0ji}\end{aligned}$$
$$\displaystyle \begin{aligned}v_{0ji} \sim N(0, \sigma_{v0}^{2})\end{aligned}$$
$$\displaystyle \begin{aligned}\beta_{0j} = \gamma_{00} + w_{0j}+ u_{0j}\end{aligned}$$
$$\displaystyle \begin{aligned}w_{0j} \sim N(0, \sigma_{w0}^{2}),\end{aligned}$$

where μ jit is the expected value for individual i in area segment j at Wave t, and \(\sigma _{c}^{2}\) is the within person variance component; the individual level intercept α 0ji depends on the covariates, and has an individual level variance component \(\sigma _{v0}^{2}\); its area segment level intercept β 0j has the sum of two error terms, a spatially correlated term u 0j and an i.i.d. error term w 0j with variance component equal to \(\sigma _{w0}^{2}\).

For the spatially correlated error term of the area segment level intercept a relatively simple choice is the intrinsic conditional autoregressive (ICAR) prior (Besag et al. 1991):

$$\displaystyle \begin{aligned} u_{0j}|u_{0j'}, j' \in \text{ne}(j) \sim N \left ( \bar{u}_{0j}, \frac{\sigma_{u0}^{2}}{n_j} \right ), \end{aligned} $$
(4)

where ne(j) is the set of adjusted CTs which are neighbours of Area j, n j is the number of such neighbours, and \(\bar {u}_{0j}\) is the mean of the neighbouring spatial random effects.

In this spatial multilevel model, we model the spatial dependence of clusters by the neighbourhood structure. Adjusted CTs are considered to be neighbours if they have a boundary edge or a corner in common.

A Note on Identifiability

An important reason for application of a multilevel spatial model is to try to estimate the response variable cluster means and to map them. Separating the cluster random effects into spatially correlated and independent parts can also be of interest, and that means not only estimating the variance components \(\sigma _{c}^{2}\), \(\sigma _{v0}^{2}\), \(\sigma _{w0}^{2}\), and \(\sigma _{u0}^{2}\) but also estimating (in a Bayesian analysis) or predicting (in a frequentist analysis) w 0j and u 0j. With the model of this section and the kind of data available from the Galveston Bay Recovery Study, the variance components are identifiable in a frequentist likelihood analysis, or in the composite likelihood approach of Sect. 7. The quantities β 0j and γ 00 are also estimable if the β 0j are constrained to have mean value 0. However, the separation of the random effect w 0j + u 0j into its two components is not identifiable in these contexts. (The Bayesian analysis of Sect. 6 would allow such a separation because of the prior assumption on the variance components.) See Eberly and Carlin (2000) and Best et al. (2005) for discussions of this non-identifiability of spatial and random effects.

Leroux et al. (1999) and MacNab (2003) proposed a different model for b 0j = w 0j + u 0j under which this total cluster random effect can be estimated, as well as a parameter λ that expresses the extent of spatial dependence of the cluster means. In this model, the covariance of b 0j and \(b_{0j^\prime }\) is the jj ′-th element of the matrix \([\sigma _{w0}^{2}+\sigma _{u0}^{2}][\lambda (D- A)+(1-\lambda )I]^{-1}\) where D is the diagonal matrix with j-th entry equal to n j, the number of neighbours of area segment j; A is the adjacency matrix for the area segment clusters; and I is the identity matrix. Our method in this paper could be adapted to working with this parameterization.

6 A Bayesian Analysis

If a Bayesian approach is taken, for example, using WINBUGS, the following prior distributions for the parameters may be adopted:

$$\displaystyle \begin{aligned}\gamma_{02} \sim N(0, 1000); \; \gamma_{03} \sim N(0, 1000); \; \beta \sim MVN(0, 1000*I),\end{aligned}$$

where I is the identity matrix with the same number of rows as the dimension of x ij and the component standard deviations σ c, σ u0, σ v0 and σ w0 have a Cauchy(25) distribution, where Cauchy(h) signifies a half-Cauchy distribution with scale parameter h. The parameter γ 00 is given an improper uniform prior. All parameters are a priori independent. In all analyses in this paper, we assume dropout is not informative.

The results of the Bayesian analysis are displayed in Table 1. The level of PTSD is seen to decrease after Wave 1, and to rise a little between Wave 2 and Wave 3. The level of PTSD tends to be higher among females, and to increase with age; it is higher for minorities; higher for people with PTSD prior to Hurricane Ike; higher for people with Ike-related trauma; higher for people with peri-event emotional reactions. The components of variance \(\sigma _{c}^{2}\) and \(\sigma _{v0}^{2}\) are estimated at 0.047 and 0.046, respectively, while the estimates of \(\sigma _{u0}^{2}\) and \(\sigma _{w0}^{2}\) are much smaller, and the posterior 2.50% quantiles of these last two variance components are very close to 0, suggesting that the variability within and between individuals dominates the area segment level variability.

Table 1 Results of the Bayesian analysis
Full size table

Figures 2 and 3 display, respectively, the estimated cluster-level mean fixed effects and the estimated cluster-level random effects u 0 + w 0. (See Fig. 1 for comparison of the areas of high and low predicted PTSD severity with the stratum definitions.) The cluster-level mean fixed effects are the average, taken over sample members of the cluster at baseline, of the regression function with the coefficients replaced by their posterior mean values.

Fig. 2
figure 2

Estimated cluster-level mean fixed effects of PTSD severity score

Full size image
Fig. 3
figure 3

Estimated cluster-level random effects of PTSD severity score

Full size image

The estimated mean fixed effects have higher variability about their overall mean than do the estimated random effects. For the mean fixed effects, the values are mainly as expected given the characteristics of their strata. For example, higher values for the average predicted PTSD severity score are found in Stratum 1, in the eastern part of Galveston Island and Bolivar Island, and in some areas of Stratum 3, while lower values appear in parts of Stratum 5. The random effects also appear higher in Stratum 1.

7 Frequentist Composite Likelihood Analysis

For a frequentist analysis, we consider adapting the weighted pairwise composite likelihood approach of Rao et al. (2013) and Yi et al. (2016). The idea in outline is as follows.

  • Find (approximately) unbiased census estimating function terms for individual y values (for mean function parameters) and pairs of y values (for variance parameters).

  • Combine them appropriately so that the combinations become maximum pairwise composite likelihood equations under the Gaussian model of Sect. 5.

  • Estimate the census estimating functions by weighted sample estimating functions, and find their roots for point estimation.

7.1 Estimating Function System for Mean Parameters

For the mean parameters, the estimating function system could be a survey weighted GEE system:

$$\displaystyle \begin{aligned} \sum_{j}\sum_{i}w_{ji}X_{ji}(\varSigma_r)^{-1}(y_{ji.} - M_{ji.}), \end{aligned} $$
(5)

where M jit = γ 00 + x ji β + γ 02 I(t = 2) + γ 03 I(t = 3) is the marginal mean of y jit, and y ji. − M ji. is the vector of observed y jit minus the corresponding M jit; X ji is a (p + 3) × 3 matrix with columns equal to the transposes of (x ji, 1, 1, 1), (x ji, 0, 1, 0) and (x ji, 0, 0, 1); and Σ r is an exchangeable working correlation matrix, with 1’s on the diagonal and with off-diagonal entries equal to a single correlation parameter ρ. The residuals are \(\hat {z}_{jit} = y_{jit} - \hat {M}_{jit}.\)

We note that the corresponding census estimating equation system is sub-optimal because the working covariance structure assumes independence of individuals, rather than the two-level model. Fitting this model using SUDAAN allows the stratification and two-stage design to be taken into account in estimation and testing hypotheses for the mean function parameters. This use of SUDAAN requires that the working correlation matrix be either exchangeable or independent.

7.2 Decomposition of the Error Term

The variance of

$$\displaystyle \begin{aligned}z_{jit} = y_{jit} - M_{jit} = e_{jit}+v_{0ij}+ w_{0j}+u_{0j}\end{aligned}$$

is

$$\displaystyle \begin{aligned}\sigma^{2}_{c}+ \sigma^{2}_{v0} + \sigma^{2}_{w0}+ \sigma^{2}_{uj},\end{aligned}$$

where \(\sigma ^{2}_{uj}\) is the (unconditional) variance of u 0j under the ICAR model.

The covariance of z jit and \(z_{j^{\prime }i^{\prime }t^{\prime }}\) is the (unconditional) covariance of u 0j, \(u_{0j^{\prime }}\) under the ICAR model. This is expressible as \(C_{ujj^{\prime }}\), the jj ′-th element of the matrix \(\sigma _{u0}^{2}(D- A)^{-1}\) (generalized inverse) where D is the diagonal matrix with j-th entry equal to n j, the number of neighbours of area segment j; and A is the adjacency matrix for the area segment clusters.

7.3 Estimating Equation System for Variance Components

If z jit = y jit − M jit, and s j denotes the sample of respondents in cluster j, the estimating equation system for the variance components can be written as:

$$\displaystyle \begin{aligned} \sum_{j}w_{j}\sum_{i \in s(j)}w_{i \mid j}\sum_{t=1}^{3}(z_{jit}^{2}-v_{1j})= 0, \end{aligned} $$
(6)
$$\displaystyle \begin{aligned} \sum_{j}w_{j}\sum_{i \in s(j)}w_{i \mid j}\sum_{t=1}^{3}\sum_{t^{\prime}<t}(z_{jit}z_{jit^{\prime}}-v_{2j})= 0, \end{aligned} $$
(7)
$$\displaystyle \begin{aligned} \sum_{j}w_{j}\sum_{i^{\prime} < i} \sum_{\in s(j)}w_{ii^{\prime} \mid j}\sum_{t=1}^{3}\sum_{t^{\prime}=1}^{3}(z_{jit}z_{ji^{\prime}t^{\prime}}-v_{3j})= 0, \end{aligned} $$
(8)

and

$$\displaystyle \begin{aligned} \sum_{h}\sum_{j^{\prime}<j \in S_{h}}w_{jj^{\prime}}\sum_{i^{\prime} \in s(j^{\prime})}\sum_{i \in s(j)} w_{i^{\prime} \mid j^{\prime}} w_{i \mid j}\sum_{t=1}^{3}\sum_{t^{\prime}=1}^{3}(z_{jit}z_{j^{\prime}i^{\prime}t^{\prime}}-C_{jj^{\prime}})= 0. \end{aligned} $$
(9)

In Eqs. (6)–(8), the notation ∑j signifies \(\sum _{h}\sum _{j \in S_{h}}\), where S h denotes Stratum h. In the system of equations (6)–(9)

$$\displaystyle \begin{aligned}v_{1j} = \sigma^{2}_{uj} + \sigma^{2}_{w0} +\sigma^{2}_{v0}+\sigma^{2}_{c}\end{aligned}$$
$$\displaystyle \begin{aligned}v_{2j} = \sigma^{2}_{uj} + \sigma^{2}_{w0} +\sigma^{2}_{v0}\end{aligned}$$
$$\displaystyle \begin{aligned}v_{3j} = \sigma^{2}_{uj} + \sigma^{2}_{w0}\end{aligned}$$
$$\displaystyle \begin{aligned}C_{ujj^{\prime}} = c_{jj^{\prime}}\sigma_{u0}^{2}\end{aligned}$$

and \(c_{jj^{\prime }}\) is a known constant.

The solutions to (5) and to (6)–(9) have closed forms:

$$\displaystyle \begin{aligned} \hat{\sigma}^{2}_{u0} = \frac{\sum_{h}\sum_{j^{\prime}<j \in S_{h}}w_{jj^{\prime}}\sum_{i^{\prime} \in s(j^{\prime})}\sum_{i \in s(j)} w_{i^{\prime} \mid j^{\prime}} w_{i \mid j}\sum_{t=1}^{3}\sum_{t^{\prime}=1}^{3}I_{it}I_{i^{\prime}t^{\prime}}z_{jit}z_{j^{\prime}i^{\prime}t^{\prime}}}{\sum_{h}\sum_{j^{\prime}<j \in S_{h}}w_{jj^{\prime}}\sum_{i^{\prime} \in s(j^{\prime})}\sum_{i \in s(j)} w_{i^{\prime} \mid j^{\prime}} w_{i \mid j}\ell_{i}\ell_{i^{\prime}}c_{jj^{\prime}}} \end{aligned} $$
(10)
$$\displaystyle \begin{aligned} \hat{\sigma}^{2}_{w0} = \frac{\sum_{j}w_{j}\sum_{i \in s(j)}\sum_{i^{\prime} < i \in s(j)}w_{ii^{\prime} \mid j}\sum_{t=1}^{3}\sum_{t^{\prime}=1}^{3}I_{it}I_{i^{\prime}t^{\prime}}(z_{jit}z_{ji^{\prime}t^{\prime}}-a_{j}\hat{\sigma}^{2}_{u0})}{\sum_{j}w_{j}\sum_{i \in s(j)}\sum_{i^{\prime} < i \in s(j)}w_{ii^{\prime} \mid j}\ell_{i}\ell_{i^{\prime}}} \end{aligned} $$
(11)
$$\displaystyle \begin{aligned} \hat{\sigma}^{2}_{v0} = \frac{\sum_{j}w_{j}\sum_{i \in s(j)}w_{i \mid j}\sum_{t=1}^{3}\sum_{t^{\prime}<t}I_{it}I_{it^{\prime}}(z_{jit}z_{jit^{\prime}}- a_{j}\hat{\sigma}^{2}_{u0})}{\sum_{j}w_{j}\sum_{i \in s(j)}w_{i \mid j}\ell_{i}(\ell_{i} - 1)/2} - \hat{\sigma}^{2}_{w0} \end{aligned} $$
(12)
$$\displaystyle \begin{aligned} \hat{\sigma}^{2}_{c} = \frac{\sum_{j}w_{j}\sum_{i \in s(j)}w_{i \mid j}\sum_{t=1}^{3}I_{it}(z_{jit}^{2}-a_{j}\hat{\sigma}^{2}_{u0})}{\sum_{j}w_{j}\sum_{i \in s(j)}w_{i \mid j}\ell_{i}} - \hat{\sigma}^{2}_{w0} - \hat{\sigma}^{2}_{v0}. \end{aligned} $$
(13)

where I it is the indicator function for i having an interview at t, and ℓ i is the number of interviews of i.

7.4 Point Estimation

In a design-based analysis taking the weights to be the reciprocals of the corresponding inclusion probabilities, inclusion probabilities are needed for area segments j and for individuals within area segments i∣j. Joint inclusion probabilities are needed for area segments jj ′ and for individuals within area segments ii ′∣j.

To illustrate the method with the GBRS data, having reconstructed inclusion probabilities from partial information on the data file as described in Section 4, we have used a Hájek approximation (Hájek et al. 1964) for the joint inclusion probabilities:

$$\displaystyle \begin{aligned}\pi_{ab} \simeq \pi_{a}\pi_{b}\left [1 - \frac{(1-\pi_{a})(1-\pi_{b})}{\sum_{a \in sample}(1-\pi_{a})}\right ].\end{aligned}$$

The paper by Haziza et al. (2008) gives an account of this and other joint inclusion approximations that can be used in variance estimation, including the one by Hartley and Rao (1962).

The residuals z jit = y jit − M jit were estimated using SUDAAN; the results of the SUDAAN analysis are displayed in Table 2:

Table 2 Results of the GEE analysis
Full size table

In (5), the design weight for y ji. minus its marginal mean is the design weight for individual i in cluster j. This was taken to be the reciprocal of π i∣j π j as approximated in Sect. 4. These design weights were also applied in (13) and (12).

In (11), the design weight for \(z_{ji^{\prime }t^{\prime }}z_{jit}\) minus its marginal mean was taken to be the reciprocal of \(\pi _{j}\pi _{i i^{\prime } \mid j}\), where the second factor is the joint inclusion probability of i and i ′, given that cluster j is included. The second factor was taken to be the product of the reciprocals of the numbers of adults in their households, times the joint inclusion probabilities of their households, given that cluster j is included. This last factor was calculated by a Hájek approximation from the individual conditional inclusion probabilities. Finally, in (10), the weight \(w_{jj^\prime }\) was taken to be the reciprocal of the Hájek approximation to the joint cluster inclusion probability \(\pi _{jj^\prime }\).

The point estimates of the first two variance components from the Galveston Bay data are \(\hat {\sigma }^{2}_{c} = 0.0381\) and \(\hat {\sigma }^{2}_{v0} = 0.0314\). The sum of \(\hat {\sigma }^{2}_{u0}\) and \(\hat {\sigma }^{2}_{w0}\), the total cluster-level variance component, is estimated at 0.0023, indicating that in this data set, the within cluster (between person) and within person variances dominate. We note that the sample has not been designed to facilitate a spatial analysis with the multilevel model of Sect. 5, and that the model itself may be too simple to apply well to the whole area.

The point estimates of variance components are somewhat smaller than those arising from the Bayesian analysis, but despite the high variability of the survey weights, the relative values from the frequentist analysis are similar.

There is good agreement between the estimates in Tables 1 and 2. Considering exclusion of zero from a nominal 95% interval as evidence of a non-zero effect, there are only four variables (average social support, average collective efficacy and the two education variables) where the inferences are different. It should be noted that, although the GEE point estimation is sub-optimal, the standard errors from the GEE analysis do take into account the clustering and (through the design weights) the unequal probability sampling in the sampling design, and not surprisingly the SEs for the GEE analysis tend to be a little larger than the SDs of the Bayesian analysis.

7.5 Uncertainty Estimation

There are several methods that can be contemplated for the estimation of uncertainty in the point estimates arising from the system (5) and (6)–(8) or the system (5) and (10)–(13).

Applying a classical design-based approach would require the use of third and fourth order approximate inclusion probabilities. More appealing would be a model-based estimator of the mean-squared error of the design-based point estimators, using a sandwich estimation technique, described next in a simpler case.

Suppose \(\hat {\theta }\) is the solution of the estimating equation

$$\displaystyle \begin{aligned}\sum_{i \in s} w_{i}\phi_{i}(y_{i}, \theta),\end{aligned}$$

where under the model for the observations y i, the terms ϕ i(y i, θ) are correlated, with a correlation structure having parameters ρ. Then consider the Taylor series expression for the estimation error:

$$\displaystyle \begin{aligned}\hat{\theta} - \theta \simeq \left ( \sum_{i \in s} w_{i}\frac{\partial \phi_{i}}{\partial \theta} \right )^{-1} \sum _{i \in s}w_{i} \phi_{i}.\end{aligned}$$

The square of the left-hand side can be expressed as

$$\displaystyle \begin{aligned}(\hat{\theta} - \theta)^{2} = \left ( \sum_{i \in s} w_{i}\frac{\partial \phi_{i}}{\partial \theta} \right )^{-1} \sum_{i}\sum_{i^{\prime}}w_{i}w_{i^{\prime}}\phi_{i}\phi_{i^{\prime}} \left ( \sum_{i \in s} w_{i}\frac{\partial \phi_{i}}{\partial \theta} \right )^{-1}. \end{aligned}$$

The factor in the middle can be replaced by its expectation in terms of the ρ parameters. The estimator of the variance of \(\hat {\theta }\) could be the same expression evaluated at \(\hat {\theta }\) and \(\hat {\rho }\).

Another possible approach would be to treat the expressions in the left-hand sides for the sample-based maximum pairwise composite likelihood equations as analogous to the score function in a corresponding Gaussian model for the generation of the observations, as developed in the case of a simpler random effects model by Thompson et al. (2022). In that case, applying an adjustment to the curvature of the corresponding log likelihood along the lines of that proposed by Ribatet et al. (2012) would make the pairwise log likelihood equations information unbiased and bring the inference based on them closer to that of a Bayesian analysis.

8 Discussion and Conclusions

We have outlined a frequentist design-based approach to estimation of the parameters of a multilevel repeated measures model with a continuous outcome, using data from a complex stratified three stage sampling design. The method uses the sample data to estimate population pairwise composite likelihood estimating functions. We have applied it to complex survey data from the Galveston Bay Recovery Study. In this application, the point estimates are broadly similar to those obtained from a Bayesian analysis of the same model.

Besides availability in software, important advantages of the Bayesian approach are the capacity to estimate the parameters of complex models and the principled expression of uncertainty through posterior distributions and credible intervals. From the frequentist perspective, a disadvantage of some Bayesian approaches is a requirement for knowledge of the variables influencing the sampling design, and the form of that influence. Incorporating this knowledge in the model accounts for the way in which the sampling design may distort the population relationships of interest. Other Bayesian approaches, such as the one used by Anthopolos et al. (2020), and used in Sect. 6, summarize the design features by including in the model the sample weights as covariates. When we include the survey design variables in the model, the interpretation of covariates of interest is altered, and may be changed in ways that do not align with scientific investigation.

The design-based frequentist approach attempts to address directly and compensate for this distortion. An advantage of this approach is that it can be applied in a straightforward manner to simple analytic uses of complex survey data with the use of a single set of survey weights supplied with the data. With this approach, there is also a natural extension to account for missing data by multiplying the baseline weight of someone who has responded at Wave t by the reciprocal of the probability of remaining in the sample up to that wave. Disadvantages are that the method as applied in this paper requires linear or quadratic estimating functions and that the variance components at the cluster-level tend to be weakly estimable.

We recommend the use of both methods for comparison in simple analytic uses of the data.