Symbolic Execution: Foundations, Techniques, Applications, and Future Perspectives

Abstract

Symbolic Execution (SE) enables a precise, deep program exploration by executing programs with symbolic inputs. Traditionally, the SE community is divided into the rarely interacting sub-communities of bug finders and program provers. This has led to independent developments of related techniques, and biased surveys and foundational papers. As both communities focused on their specific problems, the foundations of SE as a whole were not sufficiently studied. We attempt an unbiased account on the foundations, central techniques, current applications, and future perspectives of SE. We first describe essential design elements of symbolic executors, supported by implementations in a digital companion volume. We recap a semantic framework, and derive from it a—yet unpublished—automatic testing approach for SE engines. Second, we introduce SE techniques ranging from concolic execution over compositional SE to state merging. Third, we discuss applications of SE, including test generation, program verification, and symbolic debugging. Finally, we address the future. Google’s OSS-Fuzz project routinely detects thousands of bugs in hundreds of major open source projects. What can symbolic execution contribute to future software verification in the presence of such competition?

1 Introduction

It is no secret that every non-trivial software product contains bugs, and not just a few: A data analytics company reported in 2015 [7] that on average, a developer creates 70 bugs per 100 lines of code, of which 15 survive until the software is shipped to customers. In a recent, global survey among 950 developers [74], 88% of the participants stated that bugs and errors are frequently detected and reported by the actual users of the product, rather than being detected by tests or monitoring tools. In the same survey, more than a third of developers (37%) declared that they spend more than quarter of their time fixing bugs instead of “doing their job.”

These numbers indicate that testing with manually written test cases alone is insufficient for effective and sustainable software verification: First, it is notoriously hard to come up with the right inputs to ensure well-enough coverage of all semantic features implemented in code. The fact that a test suite achieves a high syntactic code coverage, which is hard enough to accomplish, does unfortunately not imply that all bugs are found. Second, developers already spend much of their time testing and fixing bugs. In the above survey, 43% of the developers complained that testing is one of the major “pain points” in software development.

Clearly, there is a need for automated bug finding strategies. A simple, yet surprisingly effective, idea is to run programs with random inputs. When following this idea on the system level, it is called (blackbox) fuzz testing (or fuzzing) [65], while on the unit level, the label Property-Based Testing (PBT) [24] is customary.

Random approaches, however, struggle with covering parts of programs that are only reachable by few inputs only. For example, it is hard to randomly produce a structured input (such as an XML file or a C program), a magic value, or a value for a given checksum. Furthermore, even if code is covered, we might miss a bug: The expression a // (b + c) only raises a ZeroDivisionError if both b and c are 0. Generally, it can be difficult to choose “suitable” failure-inducing values, even when massively generating random inputs.

Symbolic Execution (SE) [2, 8, 19, 58] provides a solution by executing programs with symbolic inputs. Since a (potentially constrained) symbolic value represents many values from the concrete domain, this allows to explore the program for any possible input. Whenever the execution depends on the concrete value of a symbolic input (e.g., when executing an if statement), SE follows all or only a subset of possible paths, each of which is identified by a unique path condition.

The integration of SE into fuzzing techniques yields so-called white-box, or constraint-based, fuzzers [20, 38,39,40, 69, 87, 93]. Especially at the unit level, SE can even exhaustively explore all possible paths (which usually requires auxiliary specifications), and prove that a property holds for all possible inputs [2, 52].

Since its formation, the SE community has been split into two distinct sub communities dedicating their work either to test generation or program proving. The term “Symbolic Execution” has been coined by King [58] in 1976, who applied it to program testing. Independently, Burstall [19] proposed a program proving technique in 1974, which is based on “hand simulation” of programs—essentially, nothing different than SE. This community separation still persists today. In this chapter, we attempt a holistic approach to Symbolic Execution, explaining foundations, technical aspects, applications, and the future of SE from both perspectives.

This chapter combines aspects of a survey paper with a guide to implementing a symbolic interpreter. Moreover, especially Sect. 6 on the future of SE is based on personal opinions and judgments, which is more characteristic of an essay than of a research paper. We hope to provide useful theoretical and practical insights into the nature of SE, and to inspire impactful discussions.

We begin in Sect. 3 by addressing central design choices in symbolic executors. Especially for this chapter, we implemented a symbolic interpreter for minipy, a Python subset. Section 2 introduces the minipy language itself. When suitable, we enrich our explanations with implementation details. We continue with a frequently neglected aspect: The semantic foundations of SE. Special attention is paid to the properties an SE engine has to satisfy to be useful for its intended application (testing vs. proving). We introduce all four existing works on the topic, one of which we discuss in-depth. In the course of this, we derive a novel technique for automated testing of SE engines which has not been published before.

We discuss selected SE techniques in Sect. 4. For example, we derive a concolic interpreter from the baseline symbolic interpreter in just eight lines of code. We implemented most techniques as extensions of our symbolic interpreter.

In Sect. 5, we describe current trends in four application scenarios. Apart from the most popular ones, namely test generation and program proving, we also cover symbolic debugging and model checking of abstract programs.

Finally, we take a look at the future of SE. The probabilistic analysis in [13] indicates that systematic testing approaches like SE need to become significantly faster to compete with randomized approaches such as coverage-guided fuzzers. Otherwise, we can expect to reach the same level of confidence about a program’s correctness more quickly when using random test generators instead of symbolic executors. What does this imply for the role of SE in future software verification?

2 Minipy

All our examples and implementations target the programming language minipy, a statically typed, imperative, proper subset of the Python language. It supports Booleans, integers, and integer tuples, first-order functions, assignments, and , , , , , , , and statements. Excluded are, e.g., classes and objects, strings, floats, nested function definitions and lambdas, comprehensions and generators, for loops, and the raise statement. Expressions are pure in minipy (without side effects other than raised exceptions), since we have no heap and omitted Python’s global keyword.

An example minipy program is the linear search routine in Listing 1. The values of x and y after execution are 2 and -1, respectively. The implementation uses an block after the loop, which is executed whenever the loop completes normally—i.e., not due to the statement in Line 5, executed if needle has been found. The type annotations in Line 1 are mandatory in minipy; thus, the type of a variable can always be determined either from the type of the right-hand side of an initial assignment, or from the annotations in function signatures.

We constructed a concrete interpreter for minipy. It consists of functions of the shape for evaluating expressions, and for executing statements. The environment consists of a store mapping variables to values and a repository of function implementations (e.g., len). The evaluation functions return a value and leave the environment unchanged; the execution functions only have side effects: They may change the environment, and complete abruptly. Abrupt completion due to returns, breaks, and continues is signaled by special exception types.

3 Foundations

We can focus on two aspects when studying the principles of SE. First, we consider how SE engines are implemented. We distinguish static symbolic interpreters, e.g., angr [80], KeY  [2], KLEE [20], and S$^2$E [23], and approaches dynamically executing the program.¹ The PEF tool [10], e.g., extracts symbolic constraints using proxy objects; QSYM [93] by a runtime instrumentation, and SYMCC [69] by compiling directives maintaining path constraints directly into the target program.

The second aspect addresses the semantics of SE, i.e., what does and should SE compute? Test generators compute an underapproximation of all possible final program states. In case one of these is an error state, e.g., crashes or does not satisfy an assertion, there is always a corresponding concrete, fault-inducing input (a test case). Program proving tools, on the other hand, overapproximate the state space. Thus, the absence of any erroneous state in the analysis result implies the absence of such states in the reachable state space, which results in a program proof.

We begin this section by providing a scheme to characterize SE engines. At the same time, we describe how to implement a relatively simple symbolic interpreter for minipy (Sect. 3.1). We decided on implementing a static executor since this allows investigating both over- and underapproximating SE variants (e.g., in Sect. 4 we integrate (overapproximating) loop invariants, and turn the interpreter into an underapproximating concolic interpreter with only a few lines of code). In Sect. 3.2, we then introduce a semantic framework for Symbolic Execution. Finally, in Sect. 3.3, we derive an automatic testing technique for SE engines from this formal framework. To the best of our knowledge, this is only the second approach addressing the verification of SE engines using automated testing, and the first which can address multi-path and overapproximating SE in a meaningful way.

3.1 Designing a Symbolic Interpreter

Table 1. Characteristics of SE engines.

To describe implementation aspects of an SE engine in a structured way, we extracted characteristics for distinguishing them (displayed in Table 1) by comparing different kinds of engines from the literature. This catalog is definitely incomplete. Yet, we think that it is sufficiently precise to contextualize most engines; and we did not find any satisfying alternative in the literature.

In the following, we step through the catalog and briefly explain the individual characteristics. We describe how our implemented baseline symbolic interpreter fits into this scheme, and provide chosen implementation details.

Implementation Type. We distinguish SE engines that statically interpret programs from those that dynamically execute them. Among the interpretation-based approaches, we distinguish those that retain multiple paths in memory and those that only keep a single path. An example for the latter would be an interpretation-based concolic executor.

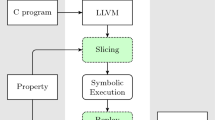
As a baseline for further studies, we implemented a multi-path symbolic minipy interpreter, with the concrete interpreter serving as a reference. The interpreter keeps all execution tree leaves discovered so far in memory (which is not necessarily required from a multi-path engine). What is more, it also retains all intermediate execution states, such that the output is a full Symbolic Execution Tree (SET). An example SET for the linear search program in Listing 1, automatically produced by our implemented framework, is shown in Fig. 1. The nodes of the tree are Symbolic Execution States (SESs) consisting of (1) a path condition, which is a set of closed formulas (path constraints) over program variables, (2) a symbolic store, a mapping of program variables to symbolic expressions over program variables, and (3) a program counter pointing to the next statement to execute. Assignments update the store, while case distinctions (such as while and if statements) update path constraints. Together, path condition, store, and program counter determine the concrete states represented by an SES. We formalize this semantics in Sect. 3.2.

The following definition assumes sets $PVars$ of program variables, $Expr$ of (arithmetic, boolean, or sequence) expressions, and $Fml$ of formulas over program variables. We formalize symbolic stores as partial mappings $PVars \hookrightarrow Expr$ and use the shorthand $SymStores$ for the set of all these mappings.

Definition 1 (Symbolic Execution State)

A Symbolic Execution State (SES) is a triple $( Constr , Store , PC )$ of (1) a set of path constraints $Constr \subseteq Fml$, the path condition, (2) a mapping $Store \in SymStores$ of program variables to symbolic expressions, the symbolic store, and (3) a program counter $PC$ pointing to the next statement to execute. We omit $PC$ if it is empty. SESs is the set of all $SEStates$.

Fig. 1.

SET of the linear search program in Listing 1 with one loop unrolling.

The structure of our symbolic interpreter aligns with the concrete minipy interpreter. Environments are now symbolic environments, consisting of a set of path constraints in addition to the (symbolic) store and built-in function repository. Execution functions are side-effect free and produce SETs instead of manipulating environments. Expressions evaluate to conditioned symbolic values, since the evaluation of the same expression, e.g., x // y, may result in a value (e.g., 4 for $\texttt {x}=4$ and $\texttt {y}=2$) or in an exception (e.g., for $\texttt {y}=0$). In Sect. 3.1, we explain how we concretely represent symbolic expressions and constraints.

As an example, we discuss the symbolic execution of if statements. As usual, the concrete code is available at [84]. First, we evaluate the guard expression. Since this can result in multiple conditioned values, we loop over all values and attached constraints. If an evaluation result is unsatisfiable with the current path condition, it is not considered; if the evaluation resulted in an exceptional result, we set the “abrupt completion” flag of the symbolic environment to the returned exception.

If evaluating the guard resulted in a value, we compute the symbolic environments for the then and else branch. We only add the subtrees for these branches if they are satisfiable to avoid the execution of infeasible paths. Finally, the then and else blocks are executed and added to the result SET; if there is no else branch, we add the corresponding environment without program counter.

An alternative to implementing symbolic transitions in code, as we did in our symbolic interpreter, is encoding them as a set of small-step rules in a domain-specific language. This is the approach followed by the KeY SE engine [2].

In Sect. 3.1, we discuss satisfiability checking for symbolic environments. Next, we focus on the representation of constraints and symbolic values.

Representation of Constraints and Values. The choice of how to express symbolic values and constraints in an SE engine usually goes hand in hand with the choice of the used constraint solver (which we discuss in the next section). When using an off-the-shelf solver, one is ultimately bound to its available theories. However, there are two styles of embedding the language of symbolic values and constraints, namely a deep and a shallow approach [35, 88]. In a deep embedding, one defines dedicated Abstract Syntax Trees (ASTs) for values and constraints, and formalizes specialized operations on those in terms of the solver theories. Shallow embeddings directly encode the embedded language in terms of already available data structures. Both approaches have advantages and disadvantages: Deep embeddings offer more flexibility, but require the definition of new theories, which can be non-trivial and give rise to inconsistencies. Shallow embeddings, on the other hand, are simpler and allow re-using pre-defined theories, but can come at the cost of a reduced expressiveness. A different approach followed, e.g., by the KeY  [2] engine, is the development of a specialized solver with home-grown theories. This approach offers most flexibility, but is costly to implement and decouples the engine from advances of general-purpose solvers.

Our symbolic interpreter is based on a shallow embedding into the Z3 SMT solver [66]. Integer types are mapped to z3.ArithRef expressions, constraints and Booleans to z3.BoolRef, and tuples to sequences of sort z3.SeqRef. This—easy to implement—approach restricts us to non-nested tuples, since nested sequences are not supported in Z3. For a complete support of minipy’s language features, we would have to resort to a deeper embedding into Z3.

Constraint Solving. Constraint solving plays a crucial role in SE engines [8]: Constraints are checked when evaluating path feasibility, simplifying symbolic stores, or verifying assertions. Usually, path constraints are eagerly checked to rule out the exploration of infeasible paths. However, this can be expensive in the presence of many complex constraints (e.g., nonlinear arithmetics). Engler and Dunbar [30] propose a lazier approach to constraint solving. If a constraint cannot be quickly solved, they defer its evaluation to a later point (e.g., when an error has been found). Only then, feasibility is checked with higher timeout thresholds.

Few systems (e.g., KeY) implement own solvers. Most symbolic executors, however, use off-the-shelf solvers like Z3. To alleviate the overhead imposed by constraint solving, some systems preprocess constraints before querying the solver. KLEE [20], e.g., reduces expressions with rewriting optimizations, and re-uses previous solutions by caching counterexamples. Systems like QSYM [93] resort to “optimistic” solving, which is an unsound technique only considering partial path conditions. Since QSYM is a hybrid fuzzer combining a random generator and a symbolic executor, generating “unsound” inputs (which do not conform to the path they are generated for) is not a big problem, since the fuzzing component will quickly detect whether the input is worthwhile or not by concrete execution (and, e.g., collecting coverage data). The Fuzzy-Sat system [15] analyzes constraints collected during SE and, based on that, performs smart mutations (a concept known from the fuzzing domain) of known solutions for partial constraints to create satisfying inputs faster.

Frequently, SMT solvers time out, and fail to provide a definitive answer at all. We use Z3 as a default solver, and discovered that its behavior can be highly non-deterministic: For a given unsatisfiable formula, we either received a timeout or a quick, correct answer, depending on the order of the constraints in a formula, or the value of an initial seed value, or whether Z3 is run in parallel mode.²

We follow a pragmatic approach to deal with Z3’s incompleteness: Whenever a Z3 call returns “timeout,” we query another solver, in this case KeY, which is run inside a small service to reduce bootstrapping costs. KeY is significantly slower than Z3 in the average case (fractions of seconds vs. multiple seconds), but is stable (behaves deterministically), and it features a powerful theory of sequences, which behaves well together with arithmetic constraints.

Treatment of Loops and Recursion. Loops and recursion require special attention in SE. Consider, e.g., the execution of the body of the find function in Listing 1. If haystack is a symbolic value such that we do not know its length, the number of times an engine should execute the body of the while loop until the loop guard becomes unsatisfiable is unknown. There are three main ways to address this issue (which also apply to recursive functions). First, we can impose a fixed bound on the number of loop executions and unroll the loop that many times. This is the procedure implemented in our baseline symbolic interpreter. For example, in Fig. 1, we only unrolled the loop one time. If we increase the threshold by one, we obtain two additional leaves in the SET, one for the case where needle has been found, and one for the case where it has not. Second, one can use loop invariants [49]. A loop invariant is a summary of the loop’s behavior that holds independently from the number of loop iterations. For example, an invariant for Listing 1 is that i does not grow beyond the size of haystack. Instead of executing the actual loop body, one can then step over a loop and add its invariant to the path condition. Although much research has been conducted in the area of automatic loop invariant inference [17, 31, 33, 60, 81], those specifications are mostly manually annotated, turning specification into a main bottleneck of invariant-based approaches [2]. In Sect. 3.1, we show how to integrate invariants into the baseline symbolic interpreter, turning it into a tool that can be used for program proving. Finally, loops are naturally addressed by concolic SE engines, where the execution is guided by concrete inputs. Then, the loop is executed as many times as it would have been under concrete execution. In Sect. 4.1, we derive a concolic tester from the baseline interpreter with minimal effort.

Treatment of Calls. Analogously to loops, there are two ways of executing calls in SE: Either, one can inline and symbolically execute the function body, or take a summary (depending on the context also called contract) of the function’s behavior and add this abstraction to the path condition. If their code is unavailable, we cannot inline function bodies (e.g., for a system call). Usually, specifying a contract is one option. Yet, this is problematic when analyzing of systems with many calls to unspecified libraries. Furthermore, it might not even be possible. Godefroid [36] names as a simple example an if statement with guard containing an error location in its then branch. To reach that location, we have to find two symbolic values x and y such that x is the hash value of y. If hash is a cryptographic hash function, it has been designed exactly to prevent such reasoning, and we cannot expect to come up with a contract for hash (and even less to obtain a usable path constraint from SE without contracts). Concolic execution does not provide a direct solution this time, either: While we can concretely execute any function call, we will not obtain a constraint from it.

A pragmatic approach in dynamic (i.e., integrating elements from concrete execution) SE is to switch between concrete and symbolic execution whenever adequate (see, e.g., [23, 38]). When reaching the if statement of the program above, for example, it is easy to decide whether the equation holds by choosing random concrete values for x and y satisfying the above precondition, and continue symbolically executing and collecting constraints from then on. What is more, we can fix the value of y only, compute its hash, and choose the value of x such that it does (not) satisfy the comparison. We discuss this approach in Sect. 4.2.

The baseline symbolic interpreter inlines function calls. It does so in a “non-transparent” way (inspired by the concrete minipy interpreter): Whenever we reach a function definition, we add a continuation to the functions repository. When evaluating a call, the continuation is retrieved and passed the current symbolic environment and symbolic arguments, and returns an EvalExprResult. In the computed SET, the execution steps inside the function body are thus not communicated. In the digital companion volume [84], we extend the baseline interpreter with a technique for transparent inlining; in Sect. 3.1, we show how to integrate function summaries.

Path Explosion Countermeasures. Path explosion is a major, if not the most serious, obstacle for SE [8, 22, 91]. It is caused by an exponential growth of feasible paths in particular in the presence of loops, but also of more innocuous constructs like if statements (e.g., if they occur right at the beginning of a substantially sized routine). Auxiliary specifications, i.e., loop invariants and function summaries which we already mentioned before, effectively reduce the state space. While loop invariants and full functional contracts generally have to be annotated manually, there do exist approaches inferring function summaries from cached previous executions in the context of dynamic SE (e.g., [5]).

Subsumption techniques drop paths that are similar (possibly after an abstraction step) to previously visited paths. Anand et al. [6], e.g., summarize heap objects (e.g., linked lists and arrays) with techniques known from shape analysis to decide whether two states are to be considered equal. Another line of work (see, e.g., [63]) distinguishes a subset of possible program locations considered “interesting,” e.g., because of the annotation with an assert statement. When an execution does not reach an interesting location, intermediate locations are tagged with path constraints. Whenever such a label is visited another time, there are two options: Either, the current path condition is implied by the label. In that case, this execution path is dropped, since we can be sure that it will not reach an interesting location. In the other case, either an interesting location is eventually reached, or the label is refined using an interpolation technique summarizing previous unsuccessful paths at a position.

State merging [46, 61, 76, 78, 82] is a flexible and powerful technique for mitigating path explosion. The idea is to bring together SESs with the same program counter (e.g., after the execution of an if statement) by computing a summary of the path constraints and stores of the input states. This summary can be fully precise, e.g., using If-Then-Else terms, underapproximating (omitting one input state in the most extreme case), or overapproximating (e.g., using an abstract domain).

Our baseline symbolic interpreter does not implement any countermeasure to path explosion. However, we extend it with contracts and state merging in Sect. 4.

3.2 Semantic Foundations of Symbolic Execution

Despite the popularity of SE as a program analysis technique, there are only few works dedicated to the semantics and correctness of SE. This could be because most SE approaches focus on test generation, and deep formal definitions and proofs are less prevalent in that area than in formal verification. Furthermore, every experienced user of SE has a solid intuition about the intended working of the symbolic analysis, and thus might not have felt the need to make it formal.

We know of four works on the semantic foundations of SE: One from the 90s [59] and three relatively recent ones [12, 62, 82], published between 2017 to 2020.

Kneuper [59] distinguishes fully precise SE, which exactly captures the set of all execution paths, and weak SE, which overapproximates it. Intuitively, the weak variant can be used in program proving, and the fully precise one in testing. Yet, fully precise SE is generally out of reach; Kneuper does not consider underapproximation. The frameworks by Lucanu et al. [62] and de Boer and Bonsangue [12] relate symbolic and concrete execution via simulation relations; they do not consider the semantics of individual SESs. Lucanu et al. [62] define two properties of SE. Coverage is the property that for every concrete execution, there is a corresponding feasible symbolic one. Precision means that for every feasible symbolic execution, there is a corresponding concrete one. De Boer and Bonsangue argue from a program proving point of view. Their property corresponding to “coverage” of [62] is named completeness, and soundness for “precision.”

In [82], we provided a framework based on the semantics of individual SESs, which represent many concrete states. A transition is precise if the output SESs represent at most the concrete states represented by the input SESs, and exhaustive if the outputs represent at least the states represented by the inputs. Other than [12, 62], this is a big-step system not considering paths and intermediate states. We think that coverage/completeness from [12, 62] imply exhaustiveness, and precision/soundness “our” precision. Kneuper’s weak SE is exhaustive/complete/has full coverage, while fully precise SE is additionally precise/sound.

In the following, we present a simplified account of the framework from [82]. Apart from personal taste, the focus on the input-output behavior of symbolic transitions allows us to derive a novel technique for automatically testing SE engines in Sect. 3.3. The only other work we know of on testing symbolic executors [56] only tests precision, and struggles (resorts to comparatively weak oracles) with testing multi-path engines. We think that the focus on paths, and not the semantics of states, binds such approaches to precision and single-path scenarios; the state-based big step semantics allows addressing these shortcomings. The framework from [82] is based on the concept of concretizations of symbolic stores and SESs. Intuitively, a symbolic store represents up to infinitely many concrete states. For example, the store $Store$ mapping the variable $\texttt {x}$ to $2\cdot \texttt {y}$ represents all concrete states where $\texttt {x}$ is even. Given any concrete input, we can concretize $Store$ to a concrete state by interpreting variables in the range of $Store$ within the concrete state. If $\sigma (\texttt {y})=-3$, e.g., the concretization of $Store$ w.r.t. $\sigma$ maps $\texttt {x}$ to $-6$.

Definition 2 (Concretization of Symbolic Stores)

Let $ConcrStates$ denote all concrete execution states (sets of pairs of variables and concrete values). The symbolic store concretization function $concr _ store : SymStores \times ConcrStates \rightarrow ConcrStates$ maps a symbolic store $Store$ and a concrete state $\sigma$ to a concrete state $\sigma '\in ConcrStates$ such that (1) for all $\texttt {x}\in PVars$ in the domain of $Store$, $\sigma '(\texttt {x})$ equals the right-hand side of $\texttt {x}$ in Store when evaluating all occurring program variables in $\sigma$, and (2) $\sigma (\texttt {y})=\sigma '(\texttt {y})$ for all other program variables y not in the domain of $Store$.

The concretization of symbolic stores is extended to SESs by first checking whether the given concrete store satisfies the path condition; if this is not the case, the concretization is empty. Otherwise, it equals the concretization of the store. Consider the constraint $\texttt {y}>0$. Then, the concretization of $(\{\texttt {y}>0\}, Store )$ w.r.t. $\sigma$ (where $Store$ and $\sigma$ are as before) is $\emptyset$. For $\sigma '(\texttt {y})=3$, on the other hand, we obtain a singleton set with a concrete state mapping $\texttt {x}$ to $6$. Additionally, we can take into account program counters by executing the program at the indicated location starting in the concretization of the store. The execution result is then the concretization.

Definition 3 (Concretization of SESs)

Let, for every minipy program $p$, $\rho (p)$ be a (concrete) transition relation relating all pairs $\sigma ,\sigma '$ such that executing $p$ in the state $\sigma \in ConcrStates$ results in the state $\sigma '\in ConcrStates$. Then, the concretization function $concr : SEStates \times ConcrStates \rightarrow 2^{ ConcrStates }$ maps an SES $( Constr , Store , PC )$ and a concrete state $\sigma \in ConcrStates$ (1) to the empty set $\emptyset$ if either $Constr$ does not hold in $\sigma$, or there is no $\sigma '$ such that $( concr _ store ( Store , \sigma ),\sigma ')\in \rho ( PC )$, or otherwise (2) the singleton set $\{\sigma '\}$ such that $( concr _ store ( Store , \sigma ),\sigma ')\in \rho ( PC )$.

Consider the SES $s=(\{\texttt {1}\in \texttt {t}\},(\texttt {n}\mapsto {}1),r=\texttt {find(n, t)})$, where n and t are variables of integer and tuple type, $(\texttt {n}\mapsto {}1)$ a symbolic store which maps $\texttt {n}$ to 1 and is undefined on all other variables, and find the linear search function from Listing 1. We write $\texttt {1}\in \texttt {t}$ to express that the value 1 is contained in t. For any $\sigma$ where $1$ is not contained in $\sigma (\texttt {t})$, we have $concr (s, \sigma )=\emptyset$. For all other states $\sigma '$, $concr _ store ((\texttt {n}\mapsto 1), \sigma ')=\sigma '[\texttt {n}\mapsto 1]$ (i.e., $\sigma '$, but with $\texttt {n}$ mapped to $\texttt {1}$). The concretization $concr (s, \sigma ')$ is then a state resulting from running find with arguments $1$ and $\sigma '(\texttt {t})$ (i.e., the values of n and t in $concr _ store ((\texttt {n}\mapsto 1), \sigma ')$) and assigning the result to $\texttt {r}$: $concr (s, \sigma ')(\texttt {r})$ is the index of the first $1$ in $\sigma '(\texttt {t})$.

By considering all possible concrete states as initial states for concretization, we obtain the semantics, i.e., the set of all represented states, of an SES.

Definition 4 (Semantics of SESs)

The semantics $\llbracket {s}\rrbracket$ of an SES $s\in SEStates$ is defined as the union of its concretizations: $\llbracket {s}\rrbracket {:}{=}\bigcup _{\sigma \in ConcrStates } concr (s, \sigma )$.

Usually, SE systems take one input SES to at least one output. Systems with state merging, however, also transition from several inputs states (the merged states) to one output state. The notion of SE transition relation defined in [82] goes one step further and permits $m$-to-$n$ transition relations for arbitrary $m$ and $n$. In principle, this allows for merging techniques producing more than one output state.

Definition 5 (SE Configuration and Transition Relation)

An SE Configuration is a set $Cnf \subseteq SEStates$. An SE Transition Relation is a relation $\delta \subseteq 2^{ SEStates }\times (2^{ SEStates }\times 2^{ SEStates })$ associating to a configuration $Cnf$ transitions $t=(I,O)$ of input states $I\subseteq Cnf$ and output states $O\subseteq {}2^{ SEStates }$. We call $Cnf \setminus {}I\cup {}O$ the successor configuration of the transition t for $Cnf$. The relation $\delta$ is called SE Transition Relation with (without) State Merging if there is a (there is no) transition with more than one input state, i.e., $\vert {I}\vert >1$. We write $Cnf {\xrightarrow {t}{}_{\delta }} Cnf '$ if $( Cnf ,t)\in \delta$ and $Cnf '$ is the successor configuration of t in $Cnf$.

The major contribution of the SE framework from [82] are the notions of exhaustiveness and precision defined subsequently.

Definition 6 (Exhaustive SE Transition Relations)

An SE transition relation $\delta \subseteq 2^{ SEStates }\times (2^{ SEStates }\times 2^{ SEStates })$ is called exhaustive iff for each transition $(I,O)$ in the range of $\delta$, $i\in {}I$ and concrete states $\sigma ,\sigma '\in ConcrStates$, it holds that $\sigma '\in concr (i, \sigma )$ implies that there is an SES $o\in {}O$ s.t. $\sigma '\in concr (o, \sigma )$.

Definition 7 (Precise SE Transition Relations)

An SE transition relation $\delta \subseteq 2^{ SEStates }\times (2^{ SEStates }\times 2^{ SEStates })$ is called precise iff for each transition $(I,O)$ in the range of $\delta$, $o\in {}O$ and concrete states $\sigma ,\sigma '\in ConcrStates$, it holds that $\sigma '\in concr (o, \sigma )$ implies that there is an SES $i\in {}I$ s.t. $\sigma '\in concr (i, \sigma )$.

The following lemmas (proved in [82]) connect exhaustiveness and precision with practice. Test generation requires precise SE to make sure that discovered failure states can be lifted to concrete, fault-inducing test inputs. Conversely, program proving requires exhaustive SE, s.t. a proof of the absence of assertion violations in the output SESs corresponds to a proof of the absence of errors in the inputs.

Lemma 1 (Bug Feasibility in Precise SE)

Let $\delta$ be a precise SE transition relation and $Cnf {\xrightarrow {(I,O)}{}_{\delta }} Cnf '$. If an assertion $\varphi \in Fml$ does not hold in some state $o\in Cnf '$, it follows that there is an $i\in Cnf$ s.t. $\varphi$ does not hold in $i$.

Lemma 2 (Validity of Assertions Proved in Exhaustive SE)

Let $\delta$ be an exhaustive SE transition relation and $Cnf {\xrightarrow {(I,O)}{}_{\delta }} Cnf '$. If an assertion $\varphi \in Fml$ holds in all states $o\in Cnf '$, it follows that $\varphi$ holds in all $i\in Cnf$.

The nice feature of these definitions is that they can be turned into a powerful automatic testing procedure for SE engines, as demonstrated subsequently.

3.3 An Oracle for Automatic Testing of SE Engines

From Definitions 6 and 7, we can derive an automated testing procedure for precision and exhaustiveness. Listing 2 shows the code of our testing routine for exhaustiveness; the version for precision works analogously. The algorithm specializes Definition 6: It only considers a finite number of initial states for concretization, does not account for state merging (i.e., only considers $1$-to-$n$ transitions), and is not robust against diverging programs (which could be mitigated by setting a timeout). We consider the most general input SES $i$ (Line 5) for a given program counter test_program, i.e., one with an empty path condition and simple assignments $\texttt {x}\mapsto \texttt {x}$ for each variable in the set variables, which typically are the “free” program variables in test_program. Then, we take num_runs concrete states $\sigma$ (Lines 12 to 16), compute $\{ concr (i, \sigma )\}$ (Lines 22 and 23) and $\{ concr (o, \sigma )\vert {}o\in {}O\}$ (Lines 18 to 20), where $O$ are all output states produced by the symbolic interpreter (computed in Lines 7 to 10). We verify that there is an output state $o$ satisfying the condition in Definition 6 by asserting that the former set is a subset of the latter one (Line 25). If this is not the case, we return the concrete input state used for concretization as a counterexample (Line 26). If no counterexample was found, we return None (Line 28).

Using the counterexample, we can examine the bug by comparing the outputs of the concrete and the symbolic interpreter (the symbolic interpreter produces only a single path since we start in a concrete state). Consider a simple while loop decrementing a variable idx by one as long as idx>= x. The exhaustiveness testing routine, for the baseline interpreter with a loop unrolling threshold of 2, produces an output like {x: -36, idx: 93}. Running the program in the concrete interpreter yields a final value of $-37\ne 93$ for $\texttt {idx}$: They are indeed different! This is because the symbolic interpreter unrolled the loop only two times, and not the necessary $\texttt {idx}-\texttt {x}=130$ times. Note that loop unrolling is precise, since there are always input states for which two times unrolling is sufficient. If the lack of exhaustiveness in the baseline interpreter was unexpected, a technique like [56] which only can detect precision problems would never have been able to find the problem.

Using the precision check, we discovered two real bugs in the interpreter. First, we did not consider negative array indices. In Python, t[-i] is equivalent to t[len(t)-i]. The second bug was more subtle. Integer division in Python is implemented as a “floor division,” such that 1 // -2 evaluates to -1, because results are always floored. In Z3 and languages like Java, the result of the division is 0. We thus had to encode floor division in our mapping to Z3 expressions.

This approach has certain advantages over the technique proposed by Kapus & Cadar [56], apart from also supporting exhaustiveness checking. They distinguish runs of the SE engine in single-path and multi-path modes. For single-path, they uniquely constrain symbolic inputs to chosen concrete inputs (such that only a single program path is followed). However, they obfuscate these bindings by encoding them in sufficiently complicated ways to prevent the solver from inferring those concrete values. This is to prevent the executor from falling back to concrete execution, such that the actual SE engine would not be tested. For the multi-path mode, they cannot use the test oracle comparing outputs, and resort to the crash and “function call chain” oracles only. Our approach does not require outwitting the solver, and naturally handles the multi-path mode. Kapus & Cadar automatically generate test programs (program counters) using the CSmith tool [92]. This should be integrated into our approach; otherwise, test quality still depends on human judgment.

To the best of our knowledge, the technique we presented is only the second approach to automatic testing of SE engines, and the first to test exhaustiveness and apply an output-based oracle to multi-path executions.

4 Techniques

Previously, we described the characteristics of a baseline symbolic interpreter without much fuzz, and introduced the central notions of exhaustiveness and precision by which one can judge whether an SE engine is suitable for test generation or program proving. Now, we shed some light on different design alternatives and advanced techniques listed in Table 1. We consider both exhaustive (loop invariants) and precise techniques (concolic and selective SE) as well as orthogonal techniques (compositional SE, state merging). More technical details are discussed in the SE surveys [8, 91] (which almost exclusively focus on such details). In particular, we omit areas such as the symbolic execution of concurrent programs and memory models for heap-manipulating programs. Concurrency adds to the path explosion problem, since different interleaving executions have to be considered [67]. The challenge is therefore to reduce the search space. This can be done, for instance, by restricting the class of checked properties (e.g., specifically to concurrency bugs [32, 89] or regressions [43]), or by excluding irrelevant interleavings in the absence of potential data races [54, 55]. Interesting topics related to symbolic memory modeling include the integration of Separation Logic [52, 73], and Dynamic Frames [57] and the Theory of Arrays [2, 34] into SE.

However, we think that the mentioned techniques are important design elements one should know and consider when analyzing and designing a symbolic executor.

In some cases, we extend the minipy language with new statement types to support a technique. Then, we also extend the concrete minipy interpreter to allow for an automatic cross-validation using the method described in Sect. 3.3.

4.1 Advanced Loop Treatment

Any symbolic executor has to ensure termination for programs with loops (and recursion). Our baseline interpreter implements bounded unrolling. This simple measure is precise, but not exhaustive; even when using SE for test generation and not program proving, that can be problematic if a bug hides beyond the set threshold.

Concolic Execution. Concolic execution (short for “concrete and symbolic execution,” coined in [77]) gracefully ensures termination. The idea is to let a concrete input steer the symbolic execution, collecting constraints along the way. Thus, the symbolic analysis terminates if, and only if, the concrete execution terminates for the given inputs. This can be implemented in an interpretation-based or execution-based way; for efficiency, most concolic engines are execution-based. To extract constraints from the program under test, those engines usually use runtime [93] or static instrumentation [21, 69, 77]. Another alternative is to run the tested program with proxy objects [10].

The baseline symbolic interpreter can be turned into an interpretation-based concolic executor in only eight lines of code (cf. [84]). We inherit from the baseline interpreter, and override the method constraint_unsatisfiable which is called, e.g., by the functions executing if statements and, in particular, loops, to check whether a path is feasible. Instead of directly calling Z3, we first instantiate the passed constraint to a variable-free formula, using a concrete state passed to the interpreter’s constructor. Consequently, the choice of which execution branch to follow is uniquely determined. It is also much faster to check concrete than symbolic constraints. This can be further optimized: The authors of [15], e.g., created an optimized Z3 fork for concrete constraints.

For the find function from Listing 1 and the concrete state setting needle to 2 and haystack to the tuple (1,), the concolic interpreter outputs an SET with a single, linear path. The constraints in the leaf node are (1) , (2) $\texttt {haystack[0]}\ne \texttt {needle}$, and (3) . Concolic execution, e.g., as implemented in SAGE [39], negates these constraints one by one, keeping the constraints occurring before the negated one as they are; the constraints occurring afterward are not considered. Negating the first constraint yields an empty haystack; negating the second one, and keeping the first, some tuple containing needle in its first element. If we negate the third constraint, we obtain a haystack with more than one element, the first of which is needle. With the initial input and the second new one, we already obtain full branch coverage in find.

Loop Invariants. A loop invariant [49] is a summary of a loop’s behavior that holds at the beginning of any loop iteration. Thus, we can replace a loop with its invariant, even if we do not know how many times a loop will be executed (for recursion, recursive contracts take a similar role). In principle, loop invariants can be fully precise, overapproximating, or underapproximating [82, Sect. 5.4.2]. In practice, however, the underapproximating variant is rarely used. Test case generation, which would be the use case for such a scenario, typically uses specification-free approaches (e.g., concolic testing) to deal with loops. Fully precise invariants are ideal, but frequently hard to come up with. Thus, loop invariants, as used in program proving, are usually sufficiently strong (w.r.t. the proof goal), but not necessarily precise, abstractions.

Loop invariants can be encoded using assertions, assumptions, and “havoc” statements. This approach is followed, e.g., by the Boogie verifier [9]. We implemented this by adding two new statement types to minipy: assume $expr$ adds an assumption $expr$ to the path condition, and havoc x assigns a fresh, symbolic value to variable x, effectively erasing all knowledge its previous value. Loop invariants are based on an inductive argument: If a loop invariant holds initially and is preserved by any loop iteration, is can be used to abstract the loop (use case).

We apply this idea to the find function (Listing 1). An invariant for the loop is that i stays positive and does never grow beyond len (haystack), and that at all previously visited positions, needle was not found (otherwise, we would have breaked from the loop). We extend the symbolic interpreter to take a list of predicate definitions that can be used similarly to Boolean-valued functions in minipy code. A predicate maps its arguments to a formula of type z3.BoolRef. The definition of $\texttt {Inv}(n, h, i)$ is .

We adapt the body of find to invariant-based SE in Boogie style. Listing 3 shows the result. In Line 2, we assert that the loop invariant Inv holds initially. Then, to enable reasoning about an arbitrary loop iteration, we havoc all variables (here only i) that are assigned in the loop body (Line 4). We assume the validity of the loop invariant (the induction hypothesis) in Line 5. The original while statement is transformed to an if (Line 8). In Line 13, we show that the loop invariant is preserved and still holds in the next iteration. If this check was successful, we assume falsity (Line 14), which renders the path condition unsatisfiable and causes SE to stop here.

Abrupt completion, such as the break statement in Line 10, complicates applying this method. Since we eliminated the loop, the break is syntactically illegal now. Addressing this requires a potentially non-trivial transformation of the loop body.

A solution to this problem is provided by Steinhöfel and Wasser in [86]. They propose so-called loop scope statements for invariant-based SE; in Listing 4 you find the loop scope version of find. One replaces the while loop with an if statement similarly to Listing 3. The if is put this inside a new loop-scope statement, which is passed the loop invariant Inv. Note that the original continue and break statements are preserved as is; indeed, the original loop body is not touched at all. Instead, a new continue statement is added as a last statement of the loop body, and a break statement is added as a last statement of the loop scope. The additional continue and break statements ensure that the body of the loop scope always completes abruptly. If it does so because of a continue, Inv is asserted; if it completes because of a break, the loop scope completes normally and execution is resumed. If the body completes for any other reason, the loop scope completes for the same reason.

Our symbolic interpreter does not transform the executed program into loop scope form on-the-fly as in [86] (which does not conform to our “interpreter style”). Instead, we implemented a program transformer which automatically turns loops into loop scope statements before they are symbolically interpreted. The complete implementation of the transformer spans only 18 lines of code.

4.2 Advanced Call Treatment

Function calls can cause two different kinds of problems in SE: First, there are too many feasible program paths in large, realistic programs. This leads to immense SETs in the case of interpretation-based SE, and many long, complicated path conditions to be processed in the case of concolic testing, both instances of path explosion. Second, the code of called functions might be unavailable, as in the case of library functions or system calls. There are two ways to address these problems. One is to use summaries of function behavior. Those can be manually specified, but also, in particular for test generation, automatically inferred. The other one is a non-exhaustive solution which, however, also works in the rare cases where summarization is not possible (e.g., for cryptographic hash functions): One concretizes function arguments to concrete values and simply executes the function non-symbolically. Existing constraints on variables not affected by the execution are retained, and SE can resume.

Compositional SE. Compositional SE works by analyzing functions individually, as opposed to complete systems. This is accomplished by annotating functions with summaries, which conjoin “constraints on the function inputs observed during the exploration of a path (...) with constraints observed on the outputs” [8]. Instead of symbolically executing a called function, we use its summary to obtain the resulting symbolic state, which can drastically reduce the overall search space.

Function summaries seem to have arisen independently in the areas of SE-based test generation and program verification. In the former area, Godefroid [36] introduces the idea, building on existing similar principles form interprocedural static analysis (e.g., [72]). As is common in automated test case generation, summaries are expected to be computed automatically; they are means for re-using previously discovered analysis results. Anand et al. [5] extend the original idea of function summaries to a demand-driven approach allowing lazy expansion of incomplete summaries, which further improves the performance of the analysis.

We did not find an explicit reference to the first original work using function summaries for modular, symbolic execution in the context of program verification. However, function summaries are already mentioned as a means for modularization in the first paper reporting on the KeY project [1], which appeared in 2000. Usually, function summaries are called “contract” in the verification context, inspired by the “design-by-contract” methodology [64]. Contracts are not only used for scalability, but additionally define the expected behavior of functions.

We integrated the latter variant of compositional SE, based on manually specified contracts, into our system by implementing a code transformer. The transformer replaces function calls by assertions of preconditions, havoc statements for assignment targets of function calls, and assumptions of postconditions. This resembles the “Boogie-style” loop invariant transformation described in Sect. 4.1, only that we do not verify that a function respects its contract when calling it. The verification can be done separately, for instance by assert statements in function bodies. Recall that since we support calls to externally specified predicates in assert statements, we can also assert properties that are outside the minipy language.

On-Demand Concretization. Selective SE interleaves concrete and symbolic execution on-demand. The authors of the S$^2$E tool [23] motivate this with the observation that there might be critical parts in a system one wants to analyze symbolically, while not caring so much about other parts. Two directions of context switches are supported: One can switch from concrete to symbolic (and back) by making function arguments symbolic and, after returning from the call, again concrete; and analogously switch from symbolic to concrete (and back). In our interpreter, one can switch from concrete to symbolic by adding a havoc statement, which makes a concrete assignment to a variable symbolic again. For the other direction, we add a concretize statement assigning to a variable a concrete value satisfying the current path condition by querying Z3.

To mitigate negative effects of concretization on exhaustiveness, S$^2$E marks concrete execution results as soft. Whenever a subsequent SE branch is made inactive due to a soft constraint, the system backtracks and chooses a different concretization. To increase the effect, constraints are also collected during concrete execution (as in concolic testing), allowing S$^2$E to infer concretizations triggering different paths. Note that these optimizations are not possible if the code of invoked functions is not available, or they cannot be symbolically executed for other reasons.

4.3 State Merging to Mitigate Path Explosion

Loop invariants, function summaries, and on-demand concretization are all instruments for mitigating the path explosion problem of SE. State merging is another instrument for that purpose. It can be used together with the aforementioned ones, and there are both exhaustive and precise variants. Furthermore, there are (even fully precise) state merging techniques that do not require additional specification and work fully automatically. The idea is to take multiple SESs arising from an SE step that caused a case distinction (e.g., guard evaluation, statements throwing exceptions, polymorphic method calls) to one summary state. Different merge techniques have been proposed in literature (e.g., [17, 46, 61, 78]); a framework for (exhaustive) state merging techniques is presented in [76] and subsumed by the more general SE theory proposed in [82] and discussed in Sect. 3.2.

A popular state merging technique uses If-Then-Else terms to summarize symbolic stores (e.g., [46, 61, 76]). Consider a simple program inverting a number i if it is negative. It consists of an if statement with guard and body i = i * -1. Two SESs arise from the execution of this statement: $(\{\texttt {i}<0\},(\texttt {i}\mapsto -\texttt {i}))$ and $(\{\texttt {i}\ge 0\},(\texttt {i}\mapsto {}\texttt {i}))$. Merging those two states with the If-Then-Else technique results in $(\emptyset ,(\texttt {i}\mapsto ITE (\texttt {i}<0,-\texttt {i},\texttt {i})))$. The right-hand side in the symbolic store evaluates to $-\texttt {i}$ if i was initially negative, and to the (nonnegative) initial value otherwise. Path constraints are merged by forming the disjunction of the inputs’ constraints, which in this case results in the empty (true) path condition.

To support state merging with the If-Then-Else technique in our symbolic interpreter, we add a merge statement to minipy. It is used like a try statement: One writes “ ” and puts the statements after which to merge inside the scope of that statement. Conveniently, Z3 offers If-Then-Else terms, reducing implementation effort. Otherwise, we could introduce a fresh constant for merged values instead and define its value(s) in the path condition.

A fact not usually discussed in literature is that If-Then-Else-based state merging can be imprecise if the path constraints in merged states are not mutually exclusive [83]. This can happen, e.g., if one tries to merge different states arising from unrolling a loop. An alternative are guarded value summaries as proposed by [78]. If we allow overlapping guards, fully precise loop state merging is possible.

Finally, one should consider that state merging generally increases the complexity of SESs and thus the solver load, which has to be weighed up against the benefits from saved symbolic branches. In our experience, state merging pays off if one merges locally (i.e., the programs inside the merge statements should be small) and early in SE. Kuznetsov et al. [61] systematically discuss this problem and devise a metric by which one can automatically decide whether or not to merge.

5 Applications

The strength of SE lies in its ability to deterministically explore many program paths with high precision. This is in contrast to fuzzing [65], including language-based [50, 51] and coverage-based fuzzing [14], where it always depends on chance and time whether a program path is reached. Only the integration of SE into whitebox fuzzing approaches [38, 39] enables fuzzers to enforce coverage of specific paths. On the other side of the spectrum are static analysis techniques such as Abstract Interpretation (AI) [25]. AI is fully automatic, but designed to operate on an abstract domain, which is why full precision is generally out of reach.

While one could, in principle, regard SE as a specialization of AI, there are striking differences. Amadini et al. [4] argue that SE is essentially a dynamic technique, as it executes programs in a forward manner and generally underapproximates the set of reachable states (unless supported by additional, costly specifications). Intrinsically static techniques, on the other hand, produce (possibly false) alarms and generally focus on smaller code regions. In their work, the authors provide a detailed discussion on the relation between the two techniques.

Consequently, SE is popular in the area of test generation, where high precision is vital. Yet, it has been successfully applied in program proving. Here, its precise, dynamic nature is a problem: When one needs abstraction, especially in the case of loops or recursive methods with symbolic guards or arguments, manual specifications are required. As pointed out in [2], specifications are the “new” bottleneck of SE-based program proving. On the other hand, SE-based proofs can address strong functional properties, while abstract interpreters like ASTRÉE [26] address coarser, general properties (e.g., division by zero or data races).

5.1 Test Generation

Precise SE is a strong tool for automatically generating high-coverage test cases. Frequently, the SE variant used to that end is referred to as Dynamic Symbolic Execution (DSE). Baldoni et al. [8] define this term as an interleaving of concrete and symbolic execution. Thus, DSE subsumes concolic and selective SE, which we discussed in Sects. 4.1 and 4.2. Although each concrete input used for concolic execution corresponds to exactly one symbolic path, concolic SE still suffers from path explosion. A symbolic path is associated to a set of atomic path constraints; one has to pick and negate one constraint, which may in turn result in a new path explored and new constraints to be negated. DART [38], e.g., chooses a depth-first strategy; SAGE [40], a tool which “has saved Microsoft millions of dollars” [40], uses coverage information to rank new inputs generated from constraint negation. As in the case of mutation-based graybox fuzzers like AFL³, the quality of the generated tests depends on the chosen initial input (which explains why concolic test generators are frequently referred to as whitebox fuzzers [8]). If this input, for example, is rejected as invalid by the program (e.g., by an input parser), it may take many rounds of negation and re-exploration before the actual program logic is reached. One way to address the problem of complex, structured input strings is to integrate language specifications with whitebox fuzzing [37].

SAGE’s use of coverage information to rank candidate inputs can already be seen as an integration of classic graybox fuzzing à la AFL. Driller [87] is a hybrid fuzzer using selective SE to identify different program compartments, while inexpensive mutation-based fuzzing explores paths within those compartments. In the QSYM [93] and FUZZOLIC [15] systems, the concolic component runs in parallel with a coverage-guided fuzzer. Both systems loosen the usual soundness requirements of SE: QSYM by “optimistic” solving (ignoring some path constraints), and FUZZOLIC by approximate solving using input mutations. For their benchmarks, the respective authors showed that QSYM outperforms Driller in terms of generated test cases per time and achieved code coverage, and FUZZOLIC outperforms QSYM (but less clearly). Both QSYM and FUZZOLIC scale to real-world programs, such as libpng and ffmpeg, and QSYM found 13 new bugs in programs that have been heavily fuzzed by Google’s OSS-Fuzz⁴.

Interpretation-based SE engines can also be used for (unit) test generation. The KeY TestGen [2, 29] tool, for example, executes programs with bounded loop unrolling, and obtains inputs satisfying the path conditions of the leaves in the resulting SET. With the right settings, the tool can achieve full MC/DC coverage [47] of the program under test [2]. As can be expected, however, this can lead to an explosion of the analysis costs and numbers of generated test cases.

5.2 Program Proving

The goal of program proving is not to demonstrate the presence, but the absence of bugs, for any possible input. In our impression, SE is less popular in program proving than in test generation. One possible reason might be that exhaustive SE, as required for program proofs (cf. Sect. 3.2), generally needs auxiliary specifications. Yet, program provers based on Weakest Precondition (WP) [28] reasoning, such as Boogie [9] and Frama-C [27], are closely related. A WP is a formula implied by any precondition strong enough to demonstrate that a program satisfies a given postcondition. Traditionally, WP-based systems compute WPs by executing a program starting from the leaves of its Control Flow Graph (CFG), specializing the postcondition in each step. SE, in turn, computes WPs by forward execution. Both approaches require specifications of loops and recursive functions.

To our knowledge, there are two actively maintained SE-based program provers. VeriFast [52] is a verifier for single- and multithreaded C and Java programs specified with separation logic assertions. The tool has been used in four industrial case studies [68] to verify the absence of general errors such as memory leaks. The authors discovered bugs in each case study. KeY  [2] is a program prover for single-threaded Java programs specified in the Java Modeling Language. Several sorting algorithms have been verified using KeY : Counting sort and Radix sort [42], the TimSort hybrid sorting algorithm [41], and Dual Pivot QuickSort [11]. For TimSort and Dual Pivot QuickSort, the actual implementations in the OpenJDK have been verified; TimSort (which is also used in Android and Python) is OpenJDK’s default sorting algorithm, and Dual Pivot QuickSort the default for primitive arrays.

The TimSort case study gained particular attention. During the verification, the authors of [41] discovered a bug present in the TimSort implementations from Android’s and Sun’s, and the OpenJDK, as well as in the original Python version. When one asks the (unfixed) algorithm to sort an array with sufficiently many segments of consecutive elements, it raises an ArrayOutOfBoundsException.

Dual Pivot QuickSort was successfully proven correct; however, a loop invariant specified in natural language was shown to be wrong.

Testing tools like QSYM and FUZZOLIC use “unsound” techniques to find more bugs faster. SE-based program proving can go the other way and integrate abstraction techniques inspired by Abstract Interpretation to increase automation. In [2, Chapter 6], several abstract domains for SE of Java programs, especially for heaps and arrays, are introduced. This approach retains full precision in the absence of loops or recursion. Should it be necessary, abstraction is applied automatically to find, e.g., the fixed point of a loop. However, only the changed portion of the state inside the loop is abstracted. Integrating SE with reasoning in abstract domains thus yields a program proving approach with the potential of full automation and increased precision compared to Abstract Interpretation. Unfortunately, to our knowledge, there exists no mature implementation of this approach.

5.3 Symbolic Debugging

Several works independently introducing SE [16, 19, 58] were motivated by debugging. Indeed, symbolic debugging has several advantages: (1) Dynamic debugging requires setting up a failure-inducing state, which can be nontrivial especially if one aims to debug individual functions deeply nested in the program. Using SE, one can take an over-approximating symbolic state. (2) The SE variant we call transparent, which maintains full SETs at the granularity of individual statements, has the potential to implement an omniscient debugger, which is hard to implement efficiently for dynamic debugging [71]. This enables programmers to arbitrarily step back and forth during debugging as needed.

To implement a symbolic debugger, one does not necessarily need an exhaustive SE engine. However, concolic approaches are unsuitable, since they do not construct SETs and might not have a notion of symbolic stores. Thus, in our opinion, an interpretation-based approach is required to implement symbolic debugging.

The first implementations of symbolic debuggers were independently developed in 2010, in the context of the VeriFast and KeY program verifiers [44, 53]. In [48], an improved implementation of KeY ’s Symbolic Execution Debugger (SED) was presented. Both tools allow forward and backward steps in execution paths and inspection of path constraints and symbolic memory. The VeriFast debugger supports the analysis of a single error path in the SET, while the SED shows full SETs. This is also motivated by different application scenarios: VeriFast offers debugging facilities for failed proof attempts, while the SED inventors explicitly address the scenario of debugging in absence of a proof attempt. The SED supports some extended features like visualization of different heap configurations or highlighting of subformulas in postconditions whose verification failed. In VeriFast, heaps are represented with separation logic assertions and not visualized.

Our minipy symbolic interpreter supports a limited degree of symbolic debugging. It visualizes SETs and explicitly represents path constraints and symbolic stores in nodes. Leaves are highlighted using the following color scheme: Red leaves represent raised exceptions (including failed assertions), green leaves represent nodes with unsatisfiable path conditions, and blue leaves all other cases.

5.4 Model Checking of Abstract Programs

Model checking usually abstracts the program under test into a graph-like structure and exhaustively searches this model to show the absence of (mostly generic) errors. Although the areas of model checking and formal software verification (including SE-based program proving) are slowly converging [79], one would usually not directly relate SE and model checking. Recently, however, a SE-based technique named Abstract Execution (AE) was proposed [82, 85], which allows for a rigorous analysis of abstract program models. An abstract program model is a program containing placeholder statements or expressions. These placeholders represent arbitrary statements or expressions conforming to the placeholder’s specifications. For example, one can restrict which locations a placeholder can read from or write to, define under which conditions instantiations complete abruptly, and impose postconditions for different (abrupt or normal completion) cases. AE is not intended to scale to big programs. Rather, it is used to model program verification problems that universally quantify over statements or expressions.

An example are program transformations, represented by pairs of abstract programs. In [82], we modeled nine Java refactoring techniques, and extracted preconditions for semantics-preserving transformations. Usually, the requirements for a behavior-preserving refactoring application are incompletely described in literature. A manual extraction of test cases from the models unveiled several bugs in the Extract Method refactoring implementations in IntelliJ IDEA and Eclipse. Our reports have been assigned “major” or “normal” priority and lead to bug fixes.⁵ Other applications of AE include cost analysis of program transformations [3], parallelization of sequential code [45], the delta-based verification of software product families [75], and “correct-by-construction” program development [90].

We implemented AE within the KeY system. One noteworthy feature of KeY is that it syntactically represents state changes within its program logic. This made it easy to add abstract updates representing the abstract state changes caused by placeholder statements or expressions. Indeed, we discovered that it is not so straightforward to implement AE, especially when using dynamic frames to represent underspecified memory regions, on top of our minipy symbolic interpreter.

AE is a noteworthy showcase of interpretation-based, exhaustive SE: It does not need to scale to large programs, since the goal is not program verification but, e.g., the verification of transformations. Thus, it covers a niche that cannot be adequately addressed by concolic testing or fuzzing, which can only ever consider pairs of concrete programs resulting from the application of a transformation.

6 Future Perspectives

The success of modern automated testing techniques (most prominently coverage-guided mutation-based fuzzers) cannot be denied. When writing this sentence, Google’s oss-fuzz had discovered 34,313 bugs in 500 open source projects. The 30 bugs in JavaScript engines discovered by the LangFuzz tool [51] translate to about 50,000 US$ in bug bounties. There are two key advantages of blackbox or graybox techniques over systematic testing approaches like SE: (1) They require no or only little code instrumentation and are applicable to any program for which a compiler or interpreter exists. (2) They are fast, with the only threshold being the execution time of the program under test. Considering Item (1), SE either crashes or outputs useless results if a program uses an unsupported statement or expression type. For that reason, many engines operate on Intermediate Languages (ILs) like LLVM, which commonly comprise a few dozen different instructions, while CPU instruction sets can easily reach hundreds to thousands [69]. For this paper, we substantially restricted the features of the minipy language to reduce the implementation effort. Not to mention that implementing a symbolic executor on source level for a language like Python with many high-level (e.g., functional and object-oriented) abstractions is highly nontrivial.

Let us assume that Item (1) has been adequately addressed (e.g., using a stable IL, or, as in the case of the SymQEMU system [70], a CPU emulation framework). Addressing the question of speed (Item (2)), it is tempting to say—if you are a supporter of SE—that analysis speed does not matter so much, since SE covers program paths systematically, while fuzzers rely mostly on chance. Instead of the effectiveness of a verification strategy, i.e., its ability to inspire a maximum degree of confidence in the correctness of a program, Böhme and Paul [13] suggest to put efficiency into the focus. In their words, an efficient verification technique (1) generates a sufficiently effective test suite in minimal time or (2) generates the most effective test suite in the given time budget. They address the efficient verification problem with a probabilistic analysis. Assume that the cost associated to the generation of one input by a random input generator $R$ is 1. We compare $R$ to a systematic input generator $S$ (e.g., a concolic tester) sampling an input with cost $c$. Böhme and Paul prove that, for a desired confidence $x$, the time taken by $S$ to sample an input must not exceed $(ex-ex^2)^{-1}$ times the time taken by $R$ to sample an input. Otherwise, $R$ is expected to achieve confidence $x$ earlier. If $R$, e.g., needs 10 ms to generate one test input, and we aim to establish that a program works correctly for 90% of its inputs, then $S$ must take less than 41 ms to come up with an input [13]. In the face of this observation, we must ask ourselves the question: Is it worth investing in SE techniques, or should we simply concentrate on improving randomized automated testing approaches?

Subsequently, we discuss scenarios where SE can assist or outperform randomized approaches, demonstrating that it has a place in future software verification.

Fast Sampling. As pointed out by Böhme and Paul, efficiency is key for a verification approach to be practically adopted. Recent work on compilation-based SE [69, 70] and “fuzzy” constraint solving [15, 93] address the execution and constraint solving components, which are the main bottlenecks of SE. Compromising soundness is justified if the analysis discovers bugs fast, and stays within the critical bound from [13].

Hybrid Fuzzing Tools like DRILLER [87], SAGE [40] and QSYM [93] combining SE with coverage-guided fuzzing showed promising results. In their paper [13], Böhme and Paul propose a hybrid approach switching from a random to a systematic tester when the expected time estimate of the random tester to detect the next partition exceeds a threshold. They proved, and demonstrated in simulations, that the hybrid tester is at least as efficient as the most efficient combination of the elementary testers. Finally, Bundt et al. [18] showed in a recent measurement study that “Hybrid fuzzers such as QSYM that integrate concolic execution to solve path constraints clearly outperform approaches that adopt a brute-force strategy.”

Verification of Critical Routines. Coverage alone would not have sufficed to unveil the TimSort bug [41]: How should a concolic (not to mention a random) tester come up with an array of 67,108,864 elements with sufficiently many short consecutive sections to trigger the “out of bounds” exception in a method that has been extensively used in practice for years? Interpretation-based, exhaustive SE is still one of the best techniques to ensure that there is really no algorithmic bug left even after heavy testing. Yet, we think that this will always require much person-power: Abstraction techniques can help exhaustive SE to get more automatic. This, however, comes at the cost of precision, such that ground is lost to competing, (more) automatic static analysis techniques. The golden bullet of fully precise (loop) summarization will probably be forever out of reach for realistic programs. Thus, we think that the program proving community should invest into better tooling for writing and fixing specifications, as well as into communicating idioms and best practices for verification-friendly program development, than to develop the next incomplete loop invariant inference approach.

SE for Model Checking. One way to remove the scalability issues of, in particular, interpretation-based SE, is to focus on small, yet meaningful, problems. The work on Abstract Execution is such an example. AE builds a modeling language on top of Java to express, e.g., program transformations. Using strong contracts with a variable degree of abstraction, practically relevant correctness properties of transformations are derived and proven correct. There are two ways of applying these results. One is to prove that the derived properties hold for actual transformations. This means that one has to show that an input to, e.g., a refactoring technique, satisfies a set of non-trivial preconditions, which can require coming up with strong loop invariants. Instead, we suggest to automatically derive test cases or assertions from the abstract model that are tailored to the transformed, concrete program. This brings together strong “once-and-for-all” results obtained from a heavyweight technique requiring annotations with targeted automatic testing of realistic programs: The best of two worlds.

7 Conclusion

Symbolic Execution is a popular, precise program exploration technique that can be lifted to an exhaustive approach to program proving. The SE community is split into two rarely interacting sub-communities: One dedicated to finding bugs, and one aiming to prove their absence. In this paper, we attempted an application-agnostic analysis of the foundations of SE. We provided a framework for classifying symbolic engines, and showed how to design and extend a symbolic interpreter. For illustrative purposes and to foster a deeper understanding, we implemented most aspects inside a new SE framework for a Python subset. We recapitulated a semantics for SE applying to both test generation and program proving, and derived from it a novel automated testing approach for SE engines. Finally, we elaborated on chosen applications of SE, ranging from test generation over symbolic debugging to model checking of abstract programs, and discussed the role of SE in future software verification.

The digital companion volume including our implementations is available at

https://rindphi.github.io/se-book-festschrift-rh