1 Introduction

Road vehicle dynamics analysis have greatly aided by the graphical methods developed over the previous decades. In particular the popular phase plane analysis method including contractility analysis [1], handling diagram [2], Milliken moment method (MMM) [3]. In summary these methods are used to analyse the planar motion of the vehicle. This author has previously published usage of these methods before [4, 5], as have many other authors [6], but this is an attempt to place all methods in a common framework and how the methods can be used in combination to analyze different aspects of the planar motion of road vehicles. The purpose of this methods paper is to present each method in detail and how they can be computed using a common vehicle dynamics model. Furthermore, the relationship between different points in the different representations are presented. The intended audience are students of vehicle dynamics and vehicle dynamics practitioners wishing to get a more holistic view of the planar yaw-sideslip dynamics.

This paper will focus on only the planar yaw/side-slip motion of passenger vehicles at a fixed longitudinal velocity. This may appear like an over simplistic approach to analysing something so complex as a road vehicle with advanced suspension and steering systems, but surprisingly many phenomena and characteristics are captured in these two interacting degrees of freedom. The control inputs that will be considered are front steering and yaw moment control, but the methods can easily be extended to include longitudinal force control, roll moment distribution, rear-wheel steering, etc.

This paper is organized such that first the simple non-linear single track vehicle dynamics model adopted from [7] that will be used throughout the analysis. Secondly each graphical method will be described in detail, including the methods used to create plot and how to interpret the results. These are the handling diagram, used for non-linear steady state analysis of the lateral acceleration versus a given steering input. Secondly the MMM diagram where the unbalanced yaw moment (non-steady state) is shown versus the lateral acceleration for a fixed steering input or side-slip angle. Thirdly, the phase portrait is presented that can be used to analyse the dynamic characteristics of a given fixed input solution in the vicinity of a fixed point (steady-state solution). Finally a summary of the different methods will be presented as well as what they have in common and which are the unique features of each method.

2 Vehicle Model

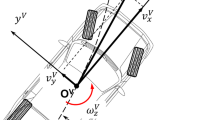
The vehicle model used throughout this paper is a standard 2-DOF non-linear bicycle model as shown in Fig. 1. Constant speed, small angles:

$$\begin{aligned} m v_x (\dot{\beta } + \dot{\psi }) = F_{yf}(\alpha _f) + F_{yr}(\alpha _r) \end{aligned}$$
(1)
$$\begin{aligned} I_{zz} \ddot{\psi } = l_f F_{yf}(\alpha _f) - l_r F_{yr}(\alpha _r) + M_z \end{aligned}$$
(2)
$$\begin{aligned} \alpha _f = \delta - \beta - l_f \frac{\dot{\psi }}{v_x} \end{aligned}$$
(3)
$$\begin{aligned} \alpha _r = -\beta + l_r \frac{\dot{\psi }}{v_x} \end{aligned}$$
(4)
Fig. 1.
figure 1

Single-track vehicle model

Full size image

The tire model in this paper is a simplified version of the Magic Tyre model:

$$\begin{aligned} F_y = D \sin (B \arctan (C \alpha )) \end{aligned}$$
(5)

where

$$\begin{aligned} D = \sqrt{\mu ^2 F_z^2 - F_x^2} \end{aligned}$$
(6)

and \(B = 3/2\) and \(C = 10\)

The other vehicle data used for the plots is shown in Table 1.

Table 1. Vehicle data used in this paper
Full size table

3 Handling Diagram

The handling diagram plots the steady-state lateral acceleration as function of the difference in front and rear slip angles. It can be used to analyse the steady-state characteristics of the vehicle, such as the understeer gradient, maximum lateral acceleration and steady-state fixed points for a given combination of vehicle speed, steering input and curve radius.

As an example, the handling diagram of the non-linear bicycle model can be found by assuming steady state (\(\dot{\beta }=0\) and \(\ddot{\psi }=0\)). We can now for any \(\alpha _f\) use (2) find for which \(\alpha _r\)

$$\begin{aligned} l_f F_{yf}(\alpha _f) - l_r F_{yr}(\alpha _r) + M_z = 0 \end{aligned}$$
(7)

From (1), we then have the steady-state lateral acceleration:

$$\begin{aligned} m a_y = m v_x \dot{\psi } = F_{yf}(\alpha _f) + F_{yr}(\alpha _r) \end{aligned}$$
(8)

Further, by combining (3) and (4) and that the curve radius \(R=v_x/\dot{\psi }\) we have that

$$\begin{aligned} \alpha _f-\alpha _r = \delta - L/R \end{aligned}$$
(9)

The understeer gradient is defined as

$$\begin{aligned} K_u = \frac{\partial \delta }{\partial a_y}-\frac{\partial L/R}{a_y} = \frac{\partial (\alpha _f-\alpha _r)}{\partial a_y} \end{aligned}$$
(10)

In Fig. 2 we can see the handling diagram for zero and positive yaw moment. There it can be seen that for a given positive yaw moment, the steering angle required for zero lateral acceleration is no longer zero (it is, in fact, negative). Also, the understeer gradient changes from negative (understeer) to positive (oversteer) for a certain lateral acceleration. This means that for a given steering input \(\delta \) and a given longitudinal speed \(v_x\), we have two fixed steady state conditions, one stable and one unstable. The neutral steer steering angle for a given lateral acceleration can be found by plotting \(a_y = v_x^2 /R\) vs L/R for a given longitudinal speed \(v_x\) with R as the independent variable. This is the red curve in Fig. 2. The distance between the handling curve and this curve is the steering angle required to achieve a certain lateral acceleration for a given speed. The lateral acceleration beyond which the vehicle becomes unstable is when

$$\begin{aligned} K_u \le L/v_x^2 \end{aligned}$$
(11)
Fig. 2.
figure 2

Handling diagram with zero (blue) and positive yaw moment \(M_z\) (green)

Full size image

4 MMM Diagram

In the Milliken Moment Method diagram shows the normalized unbalanced yaw moment \(C_N\) versus the normalized lateral acceleration \(A_Y\). These can be found from (1) and (2) such that

$$\begin{aligned} A_Y = \frac{F_{yf}+F_{yr}}{mg} \end{aligned}$$
(12)
$$\begin{aligned} C_N = \frac{l_f F_{yf} - l_r F_{yr}}{Lmg} \end{aligned}$$
(13)

and assuming \(\dot{\psi }=0\), we can for constant \(\delta \) or constant \(\beta \), draw the MMM diagram as can be seen in Fig. 3. This is done by plotting (13) as function of (12). In Fig. 3, the constant \(\delta \) and constant \(\beta \) curves are shown as well as the front and rear axle grip boundaries. The \({1}^\mathrm {st}\) and \({3}^\mathrm {rd}\) quadrant boundaries are front axle limits and the \({2}^\mathrm {nd}\) and \({4}^\mathrm {th}\) quadrant boundaries are rear axle limits. Along the dashed lines in the figure in the \({1}^\mathrm {st}\) and \({3}^\mathrm {rd}\) quadrants the rear axle force is zero. For steering from straight ahead, the yaw moment versus lateral acceleration will initially follow these lines until the rear axle force builds.

Fig. 3.
figure 3

MMM Diagram. Legend: green = constant \(\delta \), blue = constant \(\beta \), magenta = sine-with-dwell \(C_N\) vs \(A_Y\). The \({1}^\mathrm {st}\) and \({3}^\mathrm {rd}\) quadrant boundaries are front axle limits and the \({2}^\mathrm {nd}\) and \({4}^\mathrm {th}\) quadrant boundaries are rear axle limits.

Full size image

In Fig. 4 \(C_N\) and \(A_Y\) as function of time is shown for a sine with dwell maneuver [8]. The steering input maneuver is 0.7 Hz single period sinusoidal input with a 500 ms dwell after the second peak as shown with the green dashed lines in Fig. 4. The \(C_N\) vs \(A_Y\) is also shown in Fig. 3 (magenta curves). Here it can be seen that after reversal of the steering direction, the yaw moment is nearly double that which can be achieved by only steering from straight ahead running, as can be seen from the initial yaw moment period. This can be explained by the front and rear axle forces being opposite to each other and both contributing to the yaw moment. This in contrast to steering from straight ahead where only the front axle turns the vehicle. It can further be seen in the diagrams that when both axles are saturated (left vertex in the MMM diagram), the stabilizing yaw moment (after \(t>~2\)) is not enough to sufficiently fast reduce the yaw rate to zero after the steering input is zero. A very efficient way to overcome this slowly decaying skid is to apply a stabilizing yaw moment by differential braking, that is via yaw stability control by braking. This is now also standard equipment on all new passenger vehicles.

Fig. 4.
figure 4

Unbalanced normalized yaw moment \(C_N\) and the normalized lateral acceleration \(A_Y\) vs time including the steering input for a sine-with-dwell maneuver.

Full size image

5 Phase Portrait

Rewriting (1) and (2) as \(\dot{x}=f(x)\), with \(x_1=\beta \) and \(x_2=\dot{\psi }\):

$$\begin{aligned} \dot{x}_1=\frac{F_{yf}(\alpha _f(x)) + F_{yr}(\alpha _r(x))}{m v_x}-x_2 \end{aligned}$$
(14)
$$\begin{aligned} \dot{x}_2=\frac{l_f F_{yf}(\alpha _f(x)) - l_r F_{yr}(\alpha _r(x)) + M_z}{I_{zz}} \end{aligned}$$
(15)

In order to draw the phase portrait, record each gradient vector \(\dot{x}=f(x)\) for a number of combinations of points x. Connect each vector direction and magnitude in each point to create a phase portrait. The result can be seen in Fig. 5 and Fig. 6 where the Matlab function streamslice(X,Y,U,V) was used, with X,Y,U,V being 2-D matrices spanning vectors of \(x_1\), \(x_2\), \(\dot{x}_1\) and \(\dot{x}_2\), respectively. In each figure, the fixed points indicated for the same steering input shown in Fig. 2 are shown. As can be seen in Fig. 5, there is only one fixed point whereas Fig. 6 has two fixed points.

Fig. 5.
figure 5

Phase plane for an understeered vehicle (\(M_Z=0\))

Full size image

Each fixed point can be characterized using the Poincaré diagram using the trace-determinant plane for classifying phase portraits in 2D linear dynamical systems. This can be done by linearize \(\dot{x}=f(x)\) at each fixed point in the form

$$\begin{aligned} \dot{x} = A x \end{aligned}$$
(16)

For example, when \(\det (A)<0\), we have a saddle point, as can be seen in Fig. 6. The boundary between the stable (convergent) trajectories and unstable (divergent) trajectories is the so-called separatrix. This separatrix can be found through time integration of \(\dot{x} = - f(x)\) with initial conditions close to the saddle point. This boundary is the mangenta curve in Fig. 6. An approximation of the separatrix can be found from one of the eigenvectors of A when linearized at the saddle point. This eigenvector is the dashed black curve in the figure.

Fig. 6.
figure 6

Phase plane for a vehicle that changes from understeer to oversteer (\(M_Z>0\))

Full size image

6 Conclusions

This methods paper describes a few of the classical vehicle dynamics analysis methods in a common framework and how the methods can be used in combination to analyze different aspects of the planar motion of road vehicles. The methods described are the handling diagram for analysis of the non-linear steady-state characteristiscs, the phase plane analysis method to analyse the dynamic characteristics of a particular fixed point (or several) and the Milliken moment method diagram. In summary these methods are used to analyse the planar motion of the vehicle.

In summary, all three presented methods (handling diagram, moment method and phase portrait) are useful to analyse various aspects of the handling characteristics of a vehicle with a given steering and/or yaw moment input. In the handling diagram, the relationship between the steady-state lateral acceleration versus a range of steering inputs can be analysed. This is useful to analyse the steady-state stability and steering characteristics. With the moment method, in addition to all the steady-state solutions also all the non-steady state solutions for a range of steering inputs can be shown. This is useful to also understand the dynamic response to (sudden) changes in the steering input. In particular the effect of steering reversal on the yaw response was discussed. In the MMM diagram, it can clearly be seen that rapidly moving from one steering input to a negative steering input after the peak yaw moment was reached, can lead to about double the yaw moment for the changed steering input as was possible with only steering in one direction. This explains the usefulness of the sine-with-dwell maneuver used world-wide to evaluate the effectiveness of yaw stability control via differential braking (typically braking the outer front wheel) to avoid the skid motion induced by rapid steering reversals that can result from an emergency lane change.

This paper focuses on only the planar yaw/side-slip motion of passenger vehicles at a fixed longitudinal velocity. Even with this simplification surprisingly many phenomena and characteristics are captured in these two interacting degrees of freedom. The control inputs that are considered are front steering and yaw moment control, but the methods can easily be extended to include longitudinal force control, roll moment distribution, rear-wheel steering, etc.