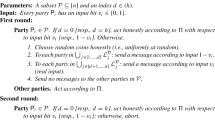Round-Optimal Byzantine Agreement

Abstract

Byzantine agreement is a fundamental primitive in cryptography and distributed computing, and minimizing its round complexity is of paramount importance. It is long known that any randomized r-round protocol must fail with probability at least $(c\cdot r)^{-r}$, for some constant c, when the number of corruptions is linear in the number of parties, $t = \theta (n)$. On the other hand, current protocols fail with probability at least $2^{-r}$. Whether we can match the lower bound agreement probability remains unknown.

In this work, we resolve this long-standing open question. We present a protocol that matches the lower bound up to constant factors. Our results hold under a (strongly rushing) adaptive adversary that can corrupt up to $t = (1-\epsilon )n/2$ parties, and our protocols use a public-key infrastructure and a trusted setup for unique threshold signatures. This is the first protocol that decreases the failure probability (overall) by a super-constant factor per round.

V. Goyal and C.-D. Liu-Zhang—Supported in part by the NSF award 1916939, DARPA SIEVE program, a gift from Ripple, a DoE NETL award, a JP Morgan Faculty Fellowship, a PNC center for financial services innovation award, and a Cylab seed funding award.

1 Introduction

Byzantine agreement (BA) is an essential building block and an extensively studied problem in distributed protocols: it allows a set of n parties to achieve agreement on a common value even when up to t of the parties may arbitrarily deviate from the protocol. BA was first formalized in the seminal work of Lamport et al. [LSP82], and since then, it has been the subject of a huge line of work (e.g. [DS83, PW96, FM97, CL99, KK06]).

A crucial efficiency metric for distributed protocols is their round complexity. That is, the number of synchronous communication rounds that are needed for a protocol to terminate. As shown by Dolev and Strong [DS83], any deterministic protocol for BA requires at least $t+1$ rounds. Fortunately, the seminal results of Ben-Or [Ben83] and Rabin [Rab83] show that such limitation can be circumvented by the use of randomization. In this regime, there are protocols that achieve expected constant number of rounds [FM97, KK06].

It is also known that any r-round randomized protocol must fail with probability at least $(c\cdot r)^{-r}$, for some constant c, when the number of corruptions, $t = \theta (n)$, is linear in the number of parties [KY84, CMS89, CPS19].

The seminal work of Feldman and Micali (FM) [FM97] introduced an unconditional protocol, secure up to $t<n/3$ corruptions, that achieves agreement in O(r) rounds except with probability $2^{-r}$. Assuming an initial trusted setup and for the case of binary input domain, the protocol requires 2r rounds to achieve the same agreement probability. Despite the extensive line of works [FG03, KK06, CM19, MV17, ADD+19] improving different parameters of the original FM protocol, the agreement probability was not improved until the very recent work of Fitzi, Liu-Zhang and Loss [FLL21], which showed a binary BA protocol that uses a trusted setup and requires $r+1$ rounds to achieve agreement except with probability $2^{-r}$.

To the best of our knowledge, up to date, there is no r-round protocol that fails with probability less than $2^{-r}$ after r rounds.

It is therefore natural to ask whether one can achieve a protocol that increases the agreement probability by more than a constant per round, hopefully matching the known lower bounds. Concretely, we ask whether one can achieve a round-optimal Byzantine agreement given a target probability of error; alternatively achieving the optimal probability within a fixed number of rounds r:

Is there an r -round BA protocol that achieves agreement except with probability $(c\cdot r)^{-r}$ , for some constant c , and secure up to some $t = \theta (n)$ corruptions?

We answer this question in the affirmative. We show an optimal protocol up to constants. Concretely, our protocol achieves the optimal agreement probability and simultaneous termination¹ within $3r + 1$ rounds and is secure against a strongly rushing adaptive adversary that can corrupt any $t = (1-\epsilon )n/2$ parties, for any constant $\epsilon >0$, assuming a public-key infrastructure (PKI) setup and a trusted setup for unique threshold signatures.

Note that, to the best of our knowledge, this is the first protocol that decreases the failure probability (overall) by a super-constant factor per round. No previous r-round protocol achieved less than $2^{-r}$ failure probability, even for any setup assumptions, and even against a static adversary corrupting up to any fraction $t = \theta (n)$ of parties.

1.1 Technical Overview

We give an overview of the main techniques used in our protocol.

Expand-and-Extract. Our starting point is the recent work by Fitzi, Liu-Zhang and Loss [FLL21], where the authors provide a new elegant way to design round-efficient BA protocols, called Expand-and-Extract.

The Expand-and-Extract iteration paradigm consists of three steps. The first step is an expansion step, where an input bit is expanded into a value with range $\ell$, via a so-called Proxcensus protocol. This protocol guarantees that the outputs of honest parties lie within two consecutive values (see Definition 2).

The second step is a multi-valued coin-flip, and the last step is an extraction technique, where the output bit is computed from the coin and the output of Proxcensus. The steps are designed such that parties are guaranteed to reach agreement except with probability $1/\ell$, assuming that the coin returns a common uniform $\ell$-range value. See Sect. 3 for a recap.

Our main technical contribution is a new Proxcensus protocol that expands the input bit into $\ell = (c \cdot r)^r$ values in 3r rounds, for any $t = (1-\epsilon )n/2$ corruptions, for some constant c that depends on $\epsilon$. Combining this with a 1-round coin-flip protocol [CKS05, LJY14], which can be instantiated using a trusted setup for unique threshold signatures, the desired result follows.

Round-Optimal Proxcensus. The protocol starts by positioning the honest parties into one of the extremes of a large interval [0, M] of natural values (for some large value M specified below). If the input of party $P_i$ is $x_i=0$, then $P_i$ positions himself in value 0, and if the input is $x_i=1$, then $P_i$ positions himself in the value $v = M$.

The protocol then proceeds in iterations of 3 rounds each. At each iteration, each party $P_i$ distributes its current value within the interval, and updates its value according to some deterministic function f. Importantly, each iteration guarantees that the values between any two honest parties get closer (overall) by a super-constant factor. Concretely, we achieve a protocol in which, after any sufficiently large number L of iterations, the distance between any two honest values is roughly at most L. By setting the initial range to $M \approx L^{L+1}$ values, we can group every L consecutive values into batches, to obtain a total of roughly $L^L$ batches, which will constitute the output values for the Proxcensus protocol.

To handle this high number of values, we will need to devise two ingredients: a mechanism that limits the adversary’s cheating capabilities, and a function f that allows the iteration-outputs of the honest parties to get closer, even when the function is evaluated on sets of values that are different (in a limited way).

Cheating-Limitation Mechanism. We specify a mechanism that, for each party $\widetilde{P}$, allows honest parties to decide at a specific iteration whether to take into account the value received from $\widetilde{P}$ or not. This mechanism provides two guarantees. First, if there is an honest party $P_i$ that takes into account the value received from $\widetilde{P}$, and another honest party $P_j$ that does not, then $\widetilde{P}$ is necessarily corrupted and all honest parties will ignore $\widetilde{P}$’s values in all future iterations. Second, if all honest parties consider the value received by $\widetilde{P}$, then $\widetilde{P}$ actually distributed the same consistent value to all honest parties.

These two guarantees have the effect that any corrupted party can cause differences between the values taken into consideration by honest parties at most once. That is, the amount of discrepancy between any two honest parties depends on the actual number of corrupted parties that actively cheated in that iteration.

In order to implement such a mechanism, we introduce a modification of the well-known graded broadcast [FM97] primitive, which we denote conditional graded broadcast. In this primitive, the sender has an input to be distributed, and every recipient holds an input bit $b_i$. The primitive then achieves the same properties as graded broadcast, but with a few differences. When all honest parties have as input $b_i = 0$, then the output of all honest parties has grade 0 (we call this property “no honest participation”). Moreover, even when a subset of honest parties have $b_i=0$, graded consistency is achieved. See Definition 3 for more details and Sect. 4 for a construction.

The mechanism can then be implemented as follows. Each party $P_i$ keeps track of a set of corrupted parties $\mathcal {C}$ that it identified as corrupted. At each iteration, $P_i$ distributes its current value $x_i$ via a conditional graded broadcast; $P_i$ only considers those values that have grade 1 or 2 to update its value via the function f, and ignores the values with grade 0. On top of that, $P_i$ updates its local set $\mathcal {C}$ with those parties that sent grade 0 or 1 (these parties are guaranteed to be corrupted by the graded broadcast primitive). Moreover, $P_i$ sets $b_i=0$ in any future conditional graded broadcast from any sender in $\mathcal {C}$.

Observe that if a dishonest sender $\widetilde{P}$ distributes values such that an honest party $P_i$ takes into account the value from $\widetilde{P}$ ($P_i$ receives grade at least 1), and another honest party $P_j$ does not consider $\widetilde{P}$’s value ($P_j$ gets grade 0), then necessarily $\widetilde{P}$ is corrupted, and all honest parties add $\widetilde{P}$ to their corrupted sets (this is because $P_j$ got grade 0, so graded broadcast guarantees that no honest party gets grade 2). It follows by “no honest participation” that all values from $\widetilde{P}$ will be ignored in future iterations. Moreover, if all honest parties take into account the value from $\widetilde{P}$, it means no honest party received grade 0, and therefore all parties obtain the same value (with grade 1 or 2). Note that in this case, $\widetilde{P}$ can still distribute values that are considered in further iterations; however it did not cause discrepancies in the current iteration.

Deterministic Function f. With the above mechanism, we reach a situation where at each iteration $\mathtt {it}$, the set of values considered by different honest parties $P_i$ and $P_j$ differ in at most $l_{\mathtt {it}}$ values, where $l_{\mathtt {it}}$ is the number of corrupted parties that distributed grade 1 to a party and grade 0 to the other party.

In order to compute the updated value, $P_i$ discards the lowest and the highest $t - c$ values from the set of considered values (those with grade at least 1), where c represents the number of values received with grade 0. Then, the new value is computed as the average of the remaining values.

Observe that because those c parties (that sent grade 0) are corrupted, then among the $n-c$ parties at most $t-c$ are corrupted. This implies that the updated value is always within the range of values from honest parties. Moreover, if the adversary doesn’t distribute different values at an iteration, the honest parties’ updated values will be the same, and will never diverge again.

With technical combinatorial lemmas (see Lemmas 6 and 7), we will show that with this deterministic update function, the distance between any two honest parties’ updated values decreases by a factor proportional to the number of corrupted parties $l_{\mathtt {it}}$. After L iterations, and bounding the sum of $l_{\mathtt {it}}$ terms by the corruption threshold t, we will show that the distance between honest values is bounded by $M\cdot (\frac{n-2t}{t} \cdot L)^{-L} + L$. Hence, by grouping every 2L consecutive values, we will be able to handle approximately $(\frac{n-2t}{t} \cdot L)^L = (\frac{2\epsilon }{1-\epsilon } \cdot L)^L$ values in Proxcensus within 3L rounds when $t = (1-\epsilon )n/2$. See more details in Sect. 5.

1.2 Related Work

The literature on round complexity of Byzantine agreement is huge, and different protocols achieve different levels of efficiency depending on many aspects, including the setup assumptions, the corruption threshold, input domain, etc.

In the following, we focus on the round-complexity of binary BA protocols, noting that these can be extended to multivalued BA using standard techniques [TC84], at the cost of an additional 2 rounds in the $t<n/3$ case, and 3 rounds in the $t<n/2$ case. Some of the constructions also use an ideal 1-round coin-flip protocol with no error nor bias, which can be instantiated using a trusted setup for unique threshold signatures [CKS05, LJY14].

Feldman and Micali [FM97] gave an unconditional protocol for $t<n/3$ with expected constant number of rounds. This protocol achieves agreement in O(r) rounds except with probability $2^{-r}$. Assuming an ideal coin, the protocol achieves the same agreement probability within (the smaller number of) 2r rounds for binary inputs.

Fitzi and Garay [FG03] gave the first expected constant-round protocol for $t<n/2$ assuming a PKI, under specific number-theoretic assumptions. This result was later improved by Katz and Koo [KK06], where they gave a protocol relying solely on a PKI. Assuming threshold signatures, Abraham et al. [ADD+19] extended the above results to achieve the first expected constant-round BA with expected $O(n^2)$ communication complexity, improving the communication complexity by a linear factor. These protocols can be adapted to achieve in O(r) rounds agreement except with probability $2^{-r}$. The concrete efficiency was improved by Micali and Vaikuntanathan [MV17], where the authors achieve agreement in 2r rounds except with probability $2^{-r}$, assuming an ideal coin for binary inputs.

Recently, Fitzi, Liu-Zhang and Loss [FLL21] generalized the Feldman and Micali iteration paradigm, and gave improvements in the concrete efficiency of fixed-round protocols, assuming an ideal coin. For binary inputs, the protocols incur a total of $r+1$ rounds for $t<n/3$, and $\frac{3}{2}r$ for $t<n/2$, to achieve agreement except with probability $2^{-r}$.

A line of work focused on achieving round-efficient solutions for broadcast, the single-sender version of BA, in the dishonest majority setting [GKKO07, FN09, CPS20, WXSD20, WXDS20].

Karlin and Yao [KY84], and also Chor, Merritt and Shmoys [CMS89] showed that any r-round randomized protocol must fail with probability at least $(c\cdot r)^{-r}$, for some constant c, when the number of corruptions, $t = \theta (n)$, is linear in the number of parties. This bound was extended to the asynchronous model by Attiya and Censor-Hillel [AC10].

Protocols with expected constant round complexity have probabilistic termination, where parties (possibly) terminate at different rounds. It is known that composing such protocols in a round-preserving fashion is non-trivial. Several works analyzed protocols with respect to parallel composition [Ben83, FG03], sequential composition [LLR06], and universal composition [CCGZ16, CCGZ17].

Cohen et al. [CHM+19] showed lower bounds for Byzantine agreement with probabilistic termination. The authors give bounds on the probability to terminate after one and two rounds. In particular, for a large class of protocols and a combinatorial conjecture, the halting probability after the second round is o(1) (resp. $1/2+o(1)$) for the case where there are up to $t<n/3$ (resp. $t<n/4$) corruptions.

2 Model and Definitions

We consider a setting with n parties $\mathcal {P}= \{P_1, P_2, \dots , P_n\}$.

2.1 Communication and Adversary Model

Parties have access to a complete network of point-to-point authenticated channels. The network is synchronous, meaning that any message sent by an honest party is delivered within a known amount of time. In this setting, protocols are typically described in rounds.

We consider an adaptive adversary that can corrupt up to t parties at any point in the protocol’s execution, causing them to deviate arbitrarily from the protocol. Moreover, the adversary is strongly rushing: it can observe the messages sent by honest parties in a round before choosing its own messages for that round, and, when an honest party sends a message during some round, it can immediately corrupt that party and replace the message with another of its choice.

2.2 Cryptographic Primitives

Public-Key Infrastructure. We assume that all the parties have access to a public key infrastructure (PKI). That is, parties hold the same vector of public keys $(pk_1, pk_2, \dots , pk_n)$, and each honest party $P _i$ holds the secret key $sk_i$ associated with $pk_i$.²

A signature on a value v using secret key sk is computed as $\sigma \leftarrow \mathsf {Sign}_{sk}(v)$; a signature is verified relative to public key pk by calling $\mathsf {Ver}_{pk}(v,\sigma )$. For simplicity, we assume in our proofs that the signatures are perfectly unforgeable. When replacing the signatures with real-world instantiations, the results hold except with a negligible failure probability.

Coin-Flip. Parties have access to an ideal coin-flip protocol $\mathsf {CoinFlip}$ that gives the parties a common uniform random value (in some range depending on the protocol of choice). This value remains uniform from the adversary’s view until the first honest party has queried $\mathsf {CoinFlip}$. Such a primitive can be achieved from a trusted setup of unique threshold signatures [CKS05, LJY14].

2.3 Agreement Primitives

Byzantine Agreement. We first recall the definition of Byzantine agreement.

Definition 1 (Byzantine Agreement)

A protocol $\varPi$ where initially each party $P _i$ holds an input value $x_i \in \{0,1\}$ and terminates upon generating an output $y_i$ is a Byzantine agreement protocol, resilient against t corruptions, if the following properties are satisfied whenever up to t parties are corrupted:

• Validity: If all honest parties have as input x, then every honest party outputs $y_i=x$.

• Consistency: Any two honest parties $P _i$ and $P _j$ output the same value $y_i = y_j$.

Proxcensus. Relaxations of Byzantine agreement have been proposed in the past, where the output value is typically augmented with a grade, indicating the level of agreement achieved in the protocol (see e.g. [FM97]). Proxcensus [CFF+05, FLL21] can be seen as a generalization of these primitives, where the grade is an arbitrary but finite domain. We consider a simplified version of the definition of Proxcensus [FLL21], to the case where the input is binary.

Definition 2 (Binary Proxcensus)

Let $\ell \ge 2$ be a natural number. A protocol $\varPi$ where initially each party $P _i$ holds an input bit $x_i \in \{0,1\}$ and terminates upon generating an output $y_i \in \{0, 1, \dots , \ell -1\}$ is a binary Proxcensus protocol with $\ell$ slots, resilient against t corruptions, if the following properties are satisfied whenever up to t parties are corrupted:

• Validity: If all honest parties input $x_i=0$ (resp. $x_i=1$), then every honest party outputs $y_i=0$ (resp. $y_i=\ell -1$).

• Consistency: The outputs of any two honest parties $P _i$ and $P _j$ lie within two consecutive slots. That is, there exists a value $v \in \{0,1,\dots ,\ell -2\}$ such that each honest party $P _i$ outputs $y_i \in \{v,v+1\}$.

Conditional Graded Broadcast. Graded broadcast [FM97, KK06, Fit03] is a relaxed version of broadcast. The primitive allows a sender to distribute a value to n recipients, each with a grade of confidence.

In our protocols, it will be convenient to have a slightly modified version of graded broadcast, where each party $P_i$ has an additional bit $b_{i}$, which intuitively indicates whether $P_i$ will send any message during the protocol. There are two main differences with respect to the usual graded broadcast definition. First, if all honest parties have $b_{i} = 0$ as input, then all honest parties output some value with grade 0. Second, we require the usual graded consistency property in the dishonest sender case even when any subset of honest parties have $b_{i} = 0$.

Definition 3

A protocol $\varPi$ where initially a designated party $P_s$ (called the sender) holds a value x, each party $P_i$ holds a bit $b_i$, and each party $P _i$ terminates upon generating an output pair $(y_i, g_i)$ with $g_i \in \{0, 1, 2\}$, is a conditional graded broadcast protocol resilient against t corruptions if the following properties hold whenever up to t parties are corrupted:

• 1. Conditional Validity: If $P_s$ is honest and each honest party has $b_i = 1$, then every honest party outputs (x, 2).

• 2. Conditional Graded Consistency: For any two honest parties $P _i$ and $P _j$:

  • $|{g_i - g_j}|\le 1$.

  • If $g_i > 0$ and $g_j > 0$, then $y_i=y_j$.

• 3. No Honest Participation: If all honest parties input $b_i = 0$, then every honest party outputs $(\bot ,0)$.

Assuming a public-key infrastructure, conditional gradecast can be achieved up to $t<n/2$ corruptions in 3 rounds (see Sect. 4).

3 Expand-and-Extract Paradigm

In this section we briefly recap the Expand-and-Extract paradigm, introduced by Fitzi, Liu-Zhang and Loss [FLL21].

The Expand-and-Extract paradigm consists of three steps. The first step is an expansion step, where parties jointly execute an $\ell$-slot binary Proxcensus protocol $\mathsf {Prox}_\ell$. That is, each party $P_i$ has as input bit $x_i$, and obtains an output $z_i = \mathsf {Prox}_\ell (x_i) \in \{0,1,\dots ,\ell -1\}$. At this point, the outputs of honest parties satisfy validity and consistency of Proxcensus.

The second step is a multi-valued coin-flip. Let $c_i \in \{0, 1, \dots , \ell -2\}$ denote the coin value that the parties obtain.

The last step is a cut, where the output bit is computed from the coin $c_i$ and the output $z_i$ of Proxcensus, simply as $y_i = 0$ if $z_i \le c_i$, and $y_i = 1$ otherwise (Fig. 1).

Fig. 1.

Party $P_i$ outputs a slot-value in $\{0,\dots ,\ell -1\}$, and the coin can “cut” the array of slots in any of the $\ell -2$ intermediate positions (indicated with dotted lines). If the obtained value lies on the left of the cut made by $c_i$ (indicated with a red line), the output is $y_i = 0$. Otherwise, the output is $y_i = 1$.

Assuming that the coin is ideal (no error and no bias), i.e. returns a common uniform value in the range $\{0,1,\dots ,\ell -2\}$, it is easy to see that parties reach agreement except with probability $1/(\ell -1)$:

• If all honest parties have input $x_i=0$, then after the first step the output of Proxcensus is $z_i = 0$, and the final output is $y_i=0$ no matter what the coin value is. Similarly, if the input is $x_i=1$, then $z_i = \ell -1$ and the output is $y_i=1$ because the largest coin value is $\ell -2$.

• Moreover, since honest parties lie in two adjacent slots after the invocation of $\mathsf {Prox}_\ell$, there is only one possible coin value (out of $\ell -1$) that lead to parties having different inputs.

We formally describe the protocol below.

Theorem 1

([FLL21]). Let $t<n$. Let $\mathsf {Prox_\ell }$ be an $\ell$-slot Proxcensus protocol, and $\mathsf {CoinFlip}$ be an $(\ell -1)$-valued ideal Coin-Flip protocol, secure up to t corruptions. Then, protocol $\varPi _{\mathtt {EE}}^{\ell }$ achieves binary Byzantine Agreement against an adaptive, strongly rushing adversary with probability $1 - \frac{1}{\ell -1}$.

4 Conditional Graded Broadcast

We describe our conditional graded broadcast protocol below, which is based on previous graded broadcast protocols [MV17, FLL21].

The protocol takes three rounds. The rounds are executed only if the input bit is $b_i = 1$. In the first round, the sender distributes its input signed. Then, when each party receives a value from the sender, it adds its own signature and echoes the pair of signatures along with the value to all parties. The third round consists of simply echoing all received pairs to every other party.

At the end of the third round, every party executes the output determination phase (this is executed irrespective of the value of $b_i$). A party outputs with grade 2 if it received from each of a total of $n-t$ parties a set of $n-t$ signatures on a value v, and no signature on any other value $v' \ne v$. Note that if an honest party outputs v with grade 2, then it is guaranteed that every honest party received at least one set of $n-t$ signatures on v, and no echo signature on any $v' \ne v$ in the second round. This constitutes exactly the condition to output grade 1. In any other case, the output is $(\bot ,0)$.

We show that $\mathsf {cGBC}(P_s)$ is a conditional gradecast protocol in a sequence of lemmas.

Theorem 2

Assuming a PKI infrastructure, $\mathsf {cGBC}(P_s)$ is a 3-round conditional graded broadcast protocol resilient against $t<n/2$ corruptions.

Lemma 1

$\mathsf {cGBC}(P_s)$ satisfies conditional validity.

Proof

Let x be the input of the sender. If the sender is honest and all honest parties have as input $b_i = 1$, then the sender sends its input to all parties, who then forward a signature on this value to everyone. Therefore, all parties collect a signature set on x of size at least $n-t$ and forward all these. At the end of round 3, they all collect at least $n-t$ consistent signature sets. Further note that since the sender is honest, no honest party can collect a tuple $(x',\sigma _s,\sigma )$ containing a valid signature from the sender for any other value $x' \ne x$.

Lemma 2

$\mathsf {cGBC}(P_s)$ satisfies conditional graded consistency.

Proof

We first show that if an honest party $P _i$ outputs $(y_i, g_i) = (v, 2)$, then every honest party $P _j$ outputs $(y_j, g_j)$ with $y_j = y_i$ and $g_j \ge 1$.

Since $g_i = 2$, $P _i$ received $n - t > t$ consistent signature sets $\varSigma _k$ for the same value $y_i$. As at least one of these sets is sent by an honest party, $P _j$ received at least one consistent $\varSigma _k$ on $y_i$. Moreover, $P _j$ does not receive any tuple $(y',\sigma _s,\sigma )$ with valid signatures for any value $y' \ne y_i$ at round 2. This is because $P _i$ did not receive any such tuple $(y',\sigma _s,\sigma )$ on $y' \ne y_i$ at round 3.

It remains to show that there cannot be two honest parties $P _i$ and $P _j$ that output $y_i$ and $y_j \ne y_i$, both with grade 1. In this case, $P _i$ received a set of $n-t$ signatures on $y_i$. This implies that there was at least one honest party that sent a tuple $(y_i,\sigma _s,\sigma )$ with valid signatures at round 2. Therefore, at the end of round 2, $P _j$ received this tuple and could not have output $y_j$ with grade 1.

Lemma 3

$\mathsf {cGBC}(P_s)$ satisfies no honest participation.

Proof

Assume that $b_i = 0$ for every honest party $P _i$. Since the honest parties do not send any messages at Round 1, and a consistent signature set $\varSigma$ requires at least $n - t > t$ signatures, no party receives any consistent signature set. Therefore, every honest party outputs $(\bot , 0)$.

5 Round-Optimal Proxcensus

In this section, we introduce a round-optimal Proxcensus protocol, for any $t<(1-\epsilon )n/2$, for constant $\epsilon >0$. The protocol achieves a super-exponential number of slots with respect to the number of rounds.

5.1 Protocol Description

The protocol is deterministic and runs for L iterations of 3 rounds each.

At the start of the protocol, parties position themselves into a large set [0, M] of integer values, which we denote as mini-slots. ($M = \left( \frac{n - 2t}{t} \right) ^L \cdot L^{L + 1}$ to be exact.)

If the input of party $P_i$ is $x_i=0$, then $P_i$ positions himself in the mini-slot $v = 0$, and if the input is $x_i=1$, then $P_i$ positions himself in the mini-slot $v = M$.

At each iteration, each party $P_i$ invokes an instance of conditional graded broadcast (see Definition 3 and Sect. 4 for a construction) to distribute the current mini-slot value. Given the outputs of these graded broadcasts, each party deterministically updates its mini-slot value (within [0, M]). Each iteration guarantees that the mini-slot values between any two honest parties get closer. Our process guarantees that after any number $L \ge \frac{1-\epsilon }{\epsilon }$ of iterations, the honest mini-slot values differ in at most 2L positions. To achieve that the honest parties lie within two consecutive final slots, each final slot will group every 2L consecutive mini-slots. The final number of slots will then be $\ell = \frac{M}{2L} = \frac{1}{2} \left( \frac{n - 2t}{t} \right) ^L \cdot L^{L}$.

Cheating Limitation Mechanism. At the core of our efficient Proxcensus protocol lies a mechanism to limit the adversary’s cheating capabilities.

Each party $P_i$ (locally) keeps track of a set of parties $\mathcal {C}$ that it identified as corrupted. The mechanism allows $P_i$ to select parties from whom $P_i$ should take into account their value, with two guarantees: For any corrupted party $\widetilde{P}$, it holds that 1) if there are honest parties $P_i$ and $P_j$ such that $P_i$ takes into account the value received from $\widetilde{P}$ but $P_j$ does not, then all honest parties identify $\widetilde{P}$ as corrupted and no honest party will further consider the values from $\widetilde{P}$ in the rest of the protocol. And 2) if all honest parties consider their respective received values from $\widetilde{P}$, then it is guaranteed that the received values are the same. These two properties heavily limit the adversary’s capabilities in influencing the output value.

We show how to implement this mechanism. At each iteration $\mathtt {it}$, parties distribute a value via conditional graded broadcast, and $P_i$ takes into account values with grade 1 or 2, but does not take into account values with grade 0. On top of that, $P_i$ updates its set $\mathcal {C}$ adding all parties from whom it received a value with grade 0 or 1 (these are clearly corrupted, since Conditional Graded Validity ensures that honest parties distribute grade 2). Moreover, $P_i$ does not participate in any conditional graded broadcast invocation where the sender is a party in $\mathcal {C}$.

The effect of this is as follows. Consider the case where a corrupted sender $\widetilde{P}$ distributes (possibly different values) to some honest parties $P_i$ and $P_j$, such that $P_i$ takes into account the value received from $\widetilde{P}$, but $P_j$ does not. In this case, $P_i$ received grade 1 and $P_j$ received grade 0, and both parties add $\widetilde{P}$ to their respective corrupted sets. This implies that no honest party will participate in any following conditional graded broadcast from $\widetilde{P}$ (this is because by Conditional Graded Consistency no honest party received grade 2), and therefore all parties obtain grade 0 by the No Honest Participation property of conditional graded broadcast in the following iterations. Moreover, if $\widetilde{P}$’s value is taken into account by all honest parties, this implies that all honest parties receive grade at least 1, and therefore Graded Consistency ensures that all honest parties receive the same value.

It follows that any corrupted party can cause differences between the values taken into consideration by honest parties at most once.

Mini-Slot Update Function. In order to compute the updated mini-slot value, $P_i$ discards the lowest and the highest $t - c$ values from the values received with grade at least 1, where c represents the number of values received with grade 0. Then, the new value is computed as the average of the remaining values. Note that all those c parties with grade 0 are actually corrupted, and among the $n-c$ parties there are at most $t-c$ corrupted. This implies that the updated value is always within the range of values from honest parties. In particular, if the adversary doesn’t send different values at an iteration, the honest parties’ updated values are exactly the same, and will never diverge again.

Let $l_{\mathtt {it}}$ be the number of corrupted parties that are identified for the first time by every honest party at iteration $\mathtt {it}$. We will show that the distance between any two honest parties’ updated values decreases essentially by a factor of $\frac{l_{\mathtt {it}}}{n - 2t + \sum _{i=1}^{\mathtt {it}} l_i}$. After L iterations, the values from honest parties will have distance at most $M\cdot \frac{t^L}{L^L} \cdot \frac{1}{(n - 2t)^L} + L= 2L$. See Lemmas 6 and 7.

We formally describe the protocol below.

We now prove that $\mathsf {OptimalProx}$ is an optimal Proxcensus for any $t = (1-\epsilon )\frac{n}{2}$ in a sequence of lemmas. The claim on the round complexity follows from the fact that the protocol runs for L iterations, and each iteration involves an instance of parallel graded conditional broadcast, which takes 3 rounds.

Theorem 3

Let $\epsilon >0$ be a constant, and let $L \ge \frac{1-\epsilon }{\epsilon }$ and $\ell = \lfloor \frac{1}{2} \left( \frac{2\epsilon }{1-\epsilon } \right) ^L L^L \rfloor$ be natural numbers. Assuming a PKI infrastructure, $\mathsf {OptimalProx}_L$ is a 3L-round Proxcensus protocol with $\ell + 1$ slots, resilient against $t = (1-\epsilon )\frac{n}{2}$ corruptions.

Let us denote by $\mathcal {C}_{\mathtt {it},P}$ the (local) set of parties that P identified as corrupted at iteration $\mathtt {it}$. We denote $C_\mathtt {it}^{\cap } = \bigcap _{P \textit{ honest}} \mathcal {C}_{\mathtt {it},P}$ to be the set of corrupted parties discovered by all honest parties up to iteration $\mathtt {it}$. Then, $l_\mathtt {it}= |{C_{\mathtt {it}}^{\cap } \setminus C_{\mathtt {it}-1}^{\cap }}|$ represents the number of corrupted parties that are newly discovered by every honest party exactly at iteration $\mathtt {it}$. These contain the parties that can cause differences in the updated mini-slot values obtained by honest parties.

Let us denote by $U_{\mathtt {it}}$ the set of updated mini-slot values $v_{\mathtt {it}}$ computed by honest parties at iteration $\mathtt {it}\ge 1$. Additionally, let $U_0 = \{0, M\}$.

Lemma 4

At every iteration $\mathtt {it}$, $T_{\mathtt {it}} \subseteq [\min U_{\mathtt {it}- 1}, \max U_{\mathtt {it}- 1}]$ for every honest party.

Proof

Let $P_i$ be an honest party. Note that its local set $\mathcal {C}^{0}_{\mathtt {it}}$ only contains parties from whom $P_i$ obtained grade 0. Conditional Graded Validity implies that these parties are corrupted (all instances with honest senders output grade 2 at all iterations, and no honest party stops participating in any of these instances).

Therefore, $c = |{\mathcal {C}^{0}_{\mathtt {it}}}| \le t$. The values in $V_{\mathtt {it}}$ are sent by the parties in $\mathcal {P} \setminus \mathcal {C}^{0}_{\mathtt {it}}$, and hence $|{V_{\mathtt {it}}}| = n - c$. These values contain all values in $U_{\mathtt {it}- 1}$ sent by the (at least) $n - t$ honest parties, and the values from at most $t - c$ corrupted parties.

Therefore, the multiset $T_{\mathtt {it}}$, obtained by discarding the highest and the lowest $t - c$ values within $V_{\mathtt {it}}$, contains only values within $[\min U_{\mathtt {it}- 1}, \max U_{\mathtt {it}- 1}]$.

Lemma 5

$\mathsf {OptimalProx}_{L}$ achieves Validity.

Proof

We assume that every honest party starts with input b. Then, $U_0 = \{b \cdot M\}$, and from Lemma 4 we obtain that $U_L \subseteq U_0$ and hence the set containing the value $v_L$ computed by every honest party is $U_L = \{b \cdot M\}$. Therefore, each honest party outputs $\frac{v_L\cdot \ell }{M} = \frac{b \cdot M \cdot \ell }{M} = b \cdot \ell$.

Lemma 6

Let $P$ and $P '$ denote two honest parties, and let $v_{\mathtt {it}}$ and $v'_{\mathtt {it}}$ be their respective updated mini-slot values (computed in line 7 of the protocol) at iteration $\mathtt {it}$. Then,

$$ |{v_{\mathtt {it}}- v'_{\mathtt {it}}}| \le \frac{l_{\mathtt {it}}}{n - 2t + \sum _{i=1}^{\mathtt {it}} l_i} \cdot (\max U_{\mathtt {it}-1} - \min U_{\mathtt {it}- 1}) + 1. $$

Proof

Since $v_{\mathtt {it}} = \lfloor \text {avg }T_{\mathtt {it}} \rfloor$ , where $\text {avg }T_{\mathtt {it}} = \frac{\sum _{v \in T_{\mathtt {it}} v}}{|{T_{\mathtt {it}}}|}$, it is enough to show:

$$ |{ \text {avg }T_{\mathtt {it}}- \text {avg }T'_{\mathtt {it}} }| \le \frac{l_{\mathtt {it}}}{n - 2t + \sum _{i=1}^{\mathtt {it}} l_i} \cdot (\max U_{\mathtt {it}-1} - \min U_{\mathtt {it}- 1}). $$

(The last additive term “$+1$” in the theorem statement accounts for the floor operation.)

Fix iteration $\mathtt {it}$. Consider the values that are received with grade at least 1 by P or $P'$. It will be convenient to arrange these values in an increasing order in an array A. The array contains exactly $k= n-c$ values, where $c = |{\mathcal {C}^0_{\mathtt {it}} \cap \mathcal {C}'^0_{\mathtt {it}} }|$ is the number of values that both P and $P'$ discard (they both receive grade 0).

Within this array of values, we denote by $I_1$ (resp. $I_2$) the set of indices containing the values that were received with grade 0 by P (resp. $P'$) and grade 1 by $P'$ (resp. P).

We then denote the resulting array $T^1$ (resp. $T^2$) created by 1) substituting the values at indices in $I_1$ (resp. $I_2$) in A by the special symbol $\bot$ and afterwards 2) further substituting the lowest and highest $(t - c) + |{I_1}|$ (resp. $(t - c) + |{I_2}|$) values also by $\bot$.

It is easy to see that $T^1$ (resp. $T^2$) was created using the exact same process as in the protocol and contains exactly the same values as the multiset $T_{\mathtt {it}}$ (resp. $T'_{\mathtt {it}}$), but conveniently arranged in an array.

Let $s= t - c$. Assuming that $|{I_1}| \ge |{I_2}|$ (the argument holds symmetrically when $|{I_2}| \ge |{I_1}|$), the technical combinatorial Lemma 8 and Lemma 4 imply that:

$$\begin{aligned} |{ \text {avg }T^1 - \text {avg }T^2}|&= |{ \text {avg }T_{\mathtt {it}}- \text {avg }T'_{\mathtt {it}} }| \\&\le \frac{ |{I_1}| }{ k- 2 s+ |{I_1}| } \cdot (\max U_{\mathtt {it}-1} - \min U_{\mathtt {it}- 1}) \\&\le \frac{ l_{\mathtt {it}} }{ k- 2 s+ l_{\mathtt {it}} } \cdot (\max U_{\mathtt {it}-1} - \min U_{\mathtt {it}- 1}) \\&\le \frac{l_{\mathtt {it}}}{n - 2t + \sum _{i=1}^{\mathtt {it}} l_i} \cdot (\max U_{\mathtt {it}-1} - \min U_{\mathtt {it}- 1}), \end{aligned}$$

where in the second inequality we used that $|I_1| \le l_{\mathtt {it}}$³, and in the last inequality we used that $k- 2 s+ l_{\mathtt {it}} = n - 2t + c + l_{\mathtt {it}}$, and the fact that $c \ge |{C_{\mathtt {it}-1}^{\cap }}| = \sum _{i = 1}^{\mathtt {it}-1} l_i$ (any corrupted party in $C_{\mathtt {it}-1}^{\cap }$ that is identified as corrupted by all honest parties distributes a grade 0 to all honest parties by the No Honest Participation property of conditional graded broadcast).

Lemma 7

$\mathsf {OptimalProx}_{L}$ achieves Consistency.

Proof

Lemma 4 implies that the honest parties’ outputs are within $\lfloor \frac{\ell }{M} \min U_{L} \rfloor$ and $\lfloor \frac{\ell }{M} \max U_{L} \rfloor$. Then, to prove that the honest parties’ outputs lie within two consecutive slots, it is enough to show that $\frac{\ell }{M} \left( \max U_{L} - \min U_{L} \right) \le 1$.

By iteratively applying Lemma 6, and using the fact that $U_0 = \{0,M\}$ and $\frac{l_{\mathtt {it}}}{n - 2t + \sum _{i = 1}^{\mathtt {it}} l_i} < 1$ for any $\mathtt {it}\le L$, we obtain:

$$\begin{aligned} \max U_{L} - \min U_{L}&\le M\cdot \prod _{\mathtt {it}= 1}^L \frac{l_{\mathtt {it}}}{n - 2t + \sum _{i = 1}^{\mathtt {it}} l_i} + L\\&\le M\cdot \prod _{\mathtt {it}= 1}^L l_{\mathtt {it}} \cdot \frac{1}{(n - 2t)^L} + L\\&\le M\cdot \frac{t^L}{L^L} \cdot \frac{1}{(n - 2t)^L} + L, \end{aligned}$$

where the last step follows from inequality of arithmetic and geometric means, and the fact that the sum of identified corrupted parties is at most t:

$$\begin{aligned} \left( \prod _{\mathtt {it}= 1}^L l_{\mathtt {it}} \right) ^{\frac{1}{L}} \le \frac{l_1 + l_2 + \dots + l_{L}}{L} \le \frac{t}{L} \implies \prod _{\mathtt {it}= 1}^L l_{\mathtt {it}} \le \frac{t^L}{L^L} \end{aligned}$$

Then, we bound $\frac{\ell }{M} \left( \max U_{L} - \min U_{L} \right)$ as follows:

$$\begin{aligned} \frac{\ell }{M} \left( \max U_{L} - \min U_{L} \right)&\le \ell \cdot \frac{1}{L^L} \left( \frac{t}{n - 2t} \right) ^L + \frac{\ell }{M} \cdot L \\&\le \ell \cdot \frac{1}{L^L} \left( \frac{t}{n - 2t} \right) ^L + \frac{\ell }{ \left( \frac{n - 2t}{t} \right) ^L \cdot L^{L + 1} } \cdot L \\&\le \ell \cdot \frac{1}{L^L} \left( \frac{t}{n - 2t} \right) ^L + \ell \cdot \frac{1}{L^L} \cdot \left( \frac{t}{n - 2t} \right) ^L \\&= 2 \ell \cdot \frac{1}{L^L} \left( \frac{t}{n - 2t} \right) ^L \le \ell \cdot \ell ^{-1} = 1, \end{aligned}$$

where in the last inequality we used that $\ell \ge 1$, which follows from the fact that $t = (1 - \epsilon ) \cdot \frac{n}{2}$ and $L\ge \frac{1 - \epsilon }{\epsilon }$.

6 Technical Combinatorial Lemma

In this section we prove the technical combinatorial lemma that allows to prove that the updated mini-slot values from honest parties get closer by the required amount, as stated in Lemma 6.

Consider an array A of k values sorted by increasing order and a number $s < k/2$. Further consider the array $T^1$ created as follows: $T^1$ has some of the values missing in indices from a fixed set $I_1$ and then the lowest and highest $s-|I_1|$ values are removed. Similarly, consider the array $T^2$ created in the same way, but with indices in $I_2$. See Fig. 2 for an example.

Let b be the maximum value among those remaining in array $T^1$ or $T^2$, and let a be the minimum value. Then, the following combinatorial lemma states that the averages of the remaining values in $T^1$ and $T^2$ differ in at most a fraction $\frac{ \max \left( |{I_1}|, |{I_2}|\right) }{ k- 2 s+ \max \left( |{I_1}|, |{I_2}| \right) }$ of $b-a$.

Fig. 2.

An example of A, $T^1$, and $T^2$, for $k= 10$, $s = 4$, $I^1 = \{2, 5, 7\}$, and $I^2 = \{6\}$.

Lemma 8

Let $A = [A_0, A_1, \dots , A_{k- 1}]$ denote an array where $A_0 \le A_1 \le \dots \le A_{k- 1}$. Let $s< k/2$ and let $I_1, I_2 \subseteq \{0, 1, \dots , k- 1\}$ denote two sets of indices such that $|{I_1 \cup I_2}| \le s$. Consider the arrays $T^1 = [T^1_0, T^1_1, \dots , T^1_{k- 1}]$ and $T^2 = [T^2_0, T^2_1, \dots , T^2_{k- 1}]$ constructed as follows: for $j \in \{1, 2\}$, we first set $T^j_i$ to $A_i$ if $i \notin I_j$ and otherwise to $\bot$, and afterwards we replace the lowest and the highest non-$\bot$ $\left( s- |I_j|\right)$ values in $T^j$ by $\bot$. Then,

$$\begin{aligned}&|{ \text {avg }\{T^1_i \ne \bot \}_ {i\in [0, k-1]} - \text {avg }\{T^2_i \ne \bot \}_ {i\in [0, k-1]} }|\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \le \frac{ \max \left( |{I_1}|, |{I_2}|\right) }{ k- 2 s+ \max \left( |{I_1}|, |{I_2}| \right) } (b - a), \end{aligned}$$

where $b = \max \{T^j_i \ne \bot \}_{j \in \{1,2\},i\in [0, k-1]}$ and $a = \min \{T^j_i \ne \bot \}_{j \in \{1,2\},i\in [0, k-1]}$.

Proof

Let $m_1 := |{I_1}|$ and $m_2 := |{I_2}|$. Without loss of generality, we assume that $m_1 \ge m_2$, meaning that $T^1$ contains at least as many non-$\bot$ values as $T^2$.

Let

$$\begin{aligned} v_1 := \text {avg }\{T^1_i \ne \bot \}_ {i\in [0, k-1]} = \frac{1}{|{ \{T^1_i \ne \bot \} }|} \sum _{ \{i: T^1_i \ne \bot \} } T^1_i,\\ v_2 := \text {avg }\{T^2_i \ne \bot \}_ {i\in [0, k-1]} = \frac{1}{|{ \{T^2_i \ne \bot \} }|} \sum _{ \{i: T^2_i \ne \bot \} } T^2_i. \end{aligned}$$

We first note that the number of non-$\bot$ values in $T^1$ is:

$$ |{ \{T^1_i \ne \bot \} }| = k- 2(s- m_1) - m_1 = k- 2s+ m_1. $$

Similarly, $|{ \{T^2_i \ne \bot \} }| = k- 2s+ m_2$.

We then obtain the following:

$$\begin{aligned} v_1 - v_2&= \frac{ \sum _{ \{i: T^1_i \ne \bot \} } T^1_i }{ k- 2s+ m_1 } - v_2 = \frac{ \sum _{ \{i: T^1_i \ne \bot \} } T^1_i - ( k- 2s+ m_1) \cdot v_2}{ k- 2s+ m_1 } \nonumber \\&= \frac{ \sum _{ \{i: T^1_i \ne \bot \} } T^1_i - ( k- 2s+ m_2) \cdot v_2 - (m_1 - m_2) \cdot v_2}{ k- 2s+ m_1 } \nonumber \\&= \frac{ \sum _{ \{i: T^1_i \ne \bot \} } T^1_i - \sum _{ \{i: T^2_i \ne \bot \} } T^2_i - (m_1 - m_2) \cdot v_2}{ k- 2s+ m_1 }. \end{aligned}$$

(1)

Analyzing the Term $\sum _{ \{i: T^1_i \ne \bot \} } T^1_i$. In order to analyze this sum, it will be convenient to look at the values in $T^1_i$ within three regions, separated by the indices $\texttt {start} = s- m_2$ and $\texttt {end} = k- (s- m_2) - 1$. Note that by construction, at least the lowest and the highest $s- m_2$ indices in $T^2$ contain $\bot$ as its value.

• Indices $i < \texttt {start}$. In this region, $T^2_i = \bot$. Moreover, since the values are ordered increasingly and $\{T^2_i \ne \bot \} \ne \varnothing$, we can bound any non-$\bot$ value $T^1_i = A_i \le A_{\texttt {start}} \le \min \{T^2_j \ne \bot \}$.

• Indices $i > \texttt {end}$. Similarly as above, $T^2_i = \bot$. Moreover, any non-$\bot$ value $T^1_i = A_i \ge A_{\texttt {end}} \ge \max \{T^2_j \ne \bot \}$.

• Indices $\texttt {start} \le i \le \texttt {end}$. Here non-$\bot$ values in $T^1$ and $T^2$ are within the values $A_{\texttt {start}}$ and $A_{\texttt {end}}$. In this region, we define the sets of subindices where exactly either $T^1$ or $T^2$ contain non-$\bot$ values. That is, $M^1 := \{\texttt {start} \le i \le \texttt {end} : T^1_i = \bot \text { and } T^2_i \ne \bot \}$ and $M^2 := \{ \texttt {start} \le i \le \texttt {end} : T^1_i \ne \bot \text { and } T^2_i = \bot \}$.

We can then express the sum of values in $T^1$ as:

$$\begin{aligned}&\sum _{\{i: T^1_i \ne \bot \}} T^1_i = \sum _{\{i< \texttt {start}: T^1_i \ne \bot \}} T^1_i + \sum _{\{\texttt {start} \le i \le \texttt {end}: T^1_i \ne \bot \}} T^1_i + \sum _{\{\texttt {end}< i : T^1_i \ne \bot \}} T^1_i \\&= \sum _{\{i< \texttt {start}: T^1_i \ne \bot \}} T^1_i + \sum _{\{\texttt {end} < i : T^1_i \ne \bot \}} T^1_i + \sum _{\{ i: T^2_i \ne \bot \}} T^2_i - \sum _{i \in M^1} T^2_i + \sum _{i \in M^2} T^1_i, \end{aligned}$$

since $\sum _{\{\texttt {start} \le i \le \texttt {end}: T^1_i \ne \bot \}} T^1_i = \sum _{\{ i: T^2_i \ne \bot \}} T^2_i - \sum _{i \in M^1} T^2_i + \sum _{i \in M^2} T^1_i$ (Fig. 3).

Fig. 3.

In the example from Fig. 2, $\texttt {start} = 3$ and $\texttt {end} = 6$. The brackets show how we split the indices of $T^1$ and $T^2$.

Using Eq. (1), we have:

$$ |{v_1 - v_2}| = \frac{1}{k- 2s+m_1} \cdot |{d}|, $$

where

$$\begin{aligned} d = \sum _{\{i< \texttt {start}: T^1_i \ne \bot \}} T^1_i - \sum _{i \in M^1} T^2_i + \sum _{\{\texttt {end} < i: T^1_i \ne \bot \}} T^1_i + \sum _{i \in M^2} T^1_i - (m_1 - m_2) \cdot v_2. \end{aligned}$$

(2)

In order to upper bound $|{d}|$, we find bounds for each of the summands.

Bounds for $\sum _{\{i < \texttt {start}: T^1_i \ne \bot \}} T^1_i$. In this region, any summand $T^1_i$ satisfies: $a = \min \{T^j_i \ne \bot \}_{j \in \{1,2\}} \le T^1_i \le A_{\texttt {start}}$.

Within this region of indices, the first $s-m_1$ indices have $\bot$ as their value (by construction of $T^1$). Therefore, the number of summands is

$$ |{ \{i < \texttt {start}: T^1_i \ne \bot \} }| = \texttt {start} - (s-m_1) - l= (m_1-m_2 - l), $$

where $l= |{ \{ s- m_1 \le i < \texttt {start}: T^1_i = \bot \} }|$.

Therefore, we have:

$$\begin{aligned} (m_1-m_2 - l) \cdot a \le \sum _{\{i < \texttt {start}: T^1_i \ne \bot \}} T^1_i \le (m_1-m_2 - l) \cdot A_{\texttt {start}}. \end{aligned}$$

(3)

Bounds for $\sum _{\{\texttt {end} < i: T^1_i \ne \bot \}} T^1_i$. Similarly, in this region, any summand $T^1_i$ satisfies $A_{\texttt {end}} \le T^1_i \le \max \{T^j_i \ne \bot \}_{j \in \{1,2\}} = b$.

Since the last $s-m_1$ indices have $\bot$ as their value:

$$ |{ \{ \texttt {end} < i: T^1_i \ne \bot \} }| = k- (s- m_1) - 1 - \texttt {end} - h= m_1 - m_2 - h, $$

where $h= |{ \{ \texttt {end} < i \le k- (s- m_1) - 1: T^1_i = \bot \} }|$.

Therefore, we have:

$$\begin{aligned} (m_1 - m_2 - h) \cdot A_{\texttt {end}} \le \sum _{\{\texttt {end} < i: T^1_i \ne \bot \}} T^1_i \le (m_1 - m_2 - h) \cdot b. \end{aligned}$$

(4)

Bounds for $\sum _{i \in M^1} T^2_i$. From the definition of $M^1$, any index $i \in M^1$ satisfies $\texttt {start} \le i \le \texttt {end}$. Moreover, any summand $T^2_i$, $i \in M^1$, satisfies that $A_{\texttt {start}} \le T^2_i \le A_{\texttt {end}}$.

By construction of $T^1_i$, we have that $|\{T^1_i = \bot : s- m_1 \le i \le k- (s- m_1) - 1 \}|= m_1$. This is because $T^1$ has $2(s-m_1)+m_1$ indices with $\bot$ in total, including the lowest and highest $s-m_1$ indices.

It follows that $|{ \{\texttt {start} \le i \le \texttt {end}: T^1_i = \bot \} }|= m_1 - l- h$.

Then, $|{M^1}| = |{ \{\texttt {start} \le i \le \texttt {end}: T^1_i = \bot \} }| - c = m_1 - l- h- c$, where c is the number of indices $\texttt {start} \le i \le \texttt {end}$ such that $T^1_i = T^2_i = \bot$. We obtain that

$$\begin{aligned} (m_1 - l- h- c) \cdot A_{\texttt {start}} \le \sum _{i \in M^1} T^2_i \le (m_1 - l- h- c) \cdot A_{\texttt {end}}. \end{aligned}$$

(5)

Bounds for $\sum _{i \in M^2} T^1_i$. The bounds are derived similarly as in the previous case. Any index $i \in M^2$ satisfies $\texttt {start} \le i \le \texttt {end}$, and any summand $T^1_i$, $i \in M^2$, satisfies that $A_{\texttt {start}} \le T^1_i \le A_{\texttt {end}}$.

By construction of $T^2_i$, we have that $|{ \{T^2_i = \bot : \texttt {start} \le i \le \texttt {end} \}}| = m_2$.

Then, $|{M^2}| = |{ \{\texttt {start} \le i \le \texttt {end}: T^2_i = \bot \} }| - c = m_2 - c$, where c is the number of indices $\texttt {start} \le i \le \texttt {end}$ such that $T^1_i = T^2_i = \bot$. We obtain that

$$\begin{aligned} (m_2 - c) \cdot A_{\texttt {start}} \le \sum _{i \in M^2} T^1_i \le (m_2 - c) \cdot A_{\texttt {end}}. \end{aligned}$$

(6)

Bounds for $(m_1-m_2) \cdot v_2$. Since $v_2$ is the average of the non-$\bot$ values in $T^2$, $A_{\texttt {start}} \le \min \{T^2_i \ne \bot \} \le v_2 \le \max \{T^2_i \ne \bot \} \le A_{\texttt {end}}$. Then, we have

$$\begin{aligned} (m_1-m_2) \cdot A_{\texttt {start}} \le (m_1-m_2) \cdot v_2 \le (m_1-m_2) \cdot A_{\texttt {end}}. \end{aligned}$$

(7)

Upper Bounding |d|. In order to upper bound $|{d}|$, we distinguish two cases.

• $v_1 \ge v_2$. Here, $|{d}| = d$. By using the inequalities (3) to (7) in Eq. (2) and simplifying the terms, we obtain that:

  $$\begin{aligned}&|{d}| \le c \cdot (A_{\texttt {start}} - A_{\texttt {end}}) + m_2 \cdot (A_{\texttt {end}} - b) \\&\qquad \qquad \qquad \qquad \quad +\, h\cdot (A_{\texttt {start}} - b) + m_1 \cdot (b - A_{\texttt {start}}) \le m_1 \cdot (b - a), \end{aligned}$$

  where in the last inequality we used that $c,h,m_1,m_2 \ge 0$ and $a \le A_{\texttt {start}} \le A_{\texttt {end}} \le b$.

• $v_1 \le v_2$. In this case, $|{d}| = -d$. By using the inequalities (3) to (7) in Eq. (2) and simplifying the terms, we obtain that:

  $$\begin{aligned}&|{d}| \le c \cdot (A_{\texttt {start}} - A_{\texttt {end}}) + l\cdot (a - A_{\texttt {end}}) + \\&\qquad \qquad \qquad \qquad \quad m_2 \cdot (a - A_{\texttt {start}}) + m_1 \cdot (A_{\texttt {end}} - a) \le m_1 \cdot (b - a), \end{aligned}$$

  where in the last inequality we used that $c,l,m_1,m_2 \ge 0$ and $a \le A_{\texttt {start}} \le A_{\texttt {end}} \le b$.

It follows that $|{d}| \le m_1 \cdot (b - a)$, and therefore $|{v_1 - v_2}| \le \frac{m_1}{k- 2s+ m_1} \cdot (b - a)$, which concludes the proof.

7 Putting It All Together

By instantiating the Proxcensus protocol from Theorem 3 in the Expand-and-Extract iteration paradigm from Theorem 1, we achieve the desired result.

Theorem 4

Let $\epsilon >0$ be a constant. Assuming a PKI infrastructure and an ideal 1-round Coin-Flip protocol, there is a $(3r+1)$-round Byzantine agreement protocol that achieves agreement except with probability at most $\left[ \lfloor \frac{1}{2} \left( \frac{2\epsilon }{1-\epsilon } r \right) ^{r} \rfloor \right] ^{-1}$ and is resilient against $t = (1-\epsilon )n/2$ corruptions, for any $r \ge \frac{1-\epsilon }{\epsilon }$.

Note that one can instantiate the 1-round ideal coin-flip from a trusted setup of unique threshold signatures (see [CKS05, LJY14]).

7.1 Comparison to Previous Protocols

We add a comparison to previous protocols in Fig. 4 for our setting with an ideal 1-round Coin-Flip. Our protocol achieves a lower failure probability when the number of honest parties is high. We therefore depict how the failure probability decreases with the number of rounds in three regimes: $t<n/10$, $t<n/3$ and $t = 0.49n$. In each of the regimes, we compare our protocol with the two more efficient known protocols.

Our figures show that in the regimes $t<n/10$ and $t<n/3$, our protocol achieves a lower failure probability than the previous protocols [FM97] and [FLL21] after a few tens of rounds. Concretely, after 6 (resp. 27) rounds compared to [FLL21], and 4 (resp. 13) rounds compared to [FM97]. On the other hand, when $t = 0.49n$, our protocol achieves a lower failure probability only after more than 200 rounds, compared to previous solutions [MV17, FLL21].

Fig. 4.

Comparison to previous protocols.

7.2 Open Problems

Our results leave a number of very exciting open problems.

Improving Constants. We leave open whether one can get similar results for the optimal threshold $t<n/2$. In a similar direction, our protocol is optimal up to constants, i.e. it achieves the optimal agreement probability for an r-round protocol within $c\cdot r$ rounds for some constant c. It would be interesting to see whether one can match the exact constants obtained from the known lower bounds.

Setup Assumptions. Another exciting direction would be to see whether similar results can be achieved from weaker setup assumptions. In particular, it would be interesting to see whether one can instantiate an ideal common-coin from plain PKI, or even with specific number-theoretic assumptions, within a constant (or even linear in r) number of rounds.

Early Termination. Finally, another interesting open question is to investigate whether one can leverage our protocols to achieve early termination. That is, a protocol that in expectation terminates in a constant number of rounds, but in the worst case it still achieves the optimal agreement probability.

Communication Complexity. Our protocol incurs a communication complexity of $O(n^4 (\kappa + r\log (r)))$ bits, where $\kappa$ is the size of a signature and r is the number of rounds. Using threshold signatures for the (conditional) graded broadcast primitive, we can save a linear factor n. It remains open to explore solutions with improved communication.