Abstract
It is widely accepted that every system should be robust in that “small” violations of environment assumptions should lead to “small” violations of system guarantees, but it is less clear how to make this intuition mathematically precise. While significant efforts have been devoted to providing notions of robustness for Linear Temporal Logic (LTL), branching-time logics, such as Computation Tree Logic (CTL) and CTL*, have received less attention in this regard. To address this shortcoming, we develop “robust” extensions of CTL and CTL*, which we name robust CTL (rCTL) and robust CTL* (rCTL*). Both extensions are syntactically similar to their parent logics but employ multi-valued semantics to distinguish between “large” and “small” violations of the specification. We show that the multi-valued semantics of rCTL make it more expressive than CTL, while rCTL* is as expressive as CTL*. Moreover, we devise efficient model checking algorithms for rCTL and rCTL*, which have the same asymptotic time complexity as the model checking algorithms for CTL and CTL*, respectively.
The work was partly funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) grant number 434592664, by Villum Investigator Grant S4OS held by Kim G. Larsen, and by the Danish National Research Center DIREC.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Specifications for reactive systems are typically written as an implication \(\varPhi \Rightarrow \varPsi \) where \(\varPhi \) is an environment assumption, and \(\varPsi \) is a system guarantee. However, the specification \(\varPhi \Rightarrow \varPsi \) is satisfied if the environment assumption \(\varPhi \) is violated, no matter how the system behaves. This is clearly inadequate since the environment assumptions will inevitably be violated in the real world: the true environment where the system will be deployed is often not entirely known at design time and, thus, can not be accurately and fully formalized by the formula \(\varPhi \).
To prevent systems from behaving arbitrarily when the environment assumption is violated, there have been concentrated efforts on improving the specifications for reactive systems by making them robust to the violations of the environment assumption. For instance, the works of Bloem et al. [2], Tarraf et al. [18], Doyen et al. [4], Ehlers et al. [5], and Tabuada et al. [15, 16] have provided different ways of introducing robustness for specifications in Linear Temporal Logic (LTL). All these approaches require some additional assumptions or additional quantitative information from the designer. This has motivated Tabuada and Neider [17] to introduce a new logic, called robust LTL (rLTL), which provides robustness without relying on any additional assumptions or input from a designer beyond an LTL formula. Inspired by this logic, the works of Neider et al. [13] introduced robust extensions for Prompt-LTL and Linear Dynamic Logic.
Most work on robustness has been directed at LTL. Branching-time logic, such as Computation Tree Logic (CTL) and CTL*, have received less attention in this regard, with a few exceptions. For instance, the work of French et al. [9] introduces a logic called RoCTL, but they use additional operators that require manual quantification of the violations.
To address this shortcoming, we develop robust extensions of CTL and CTL*, which we call robust CTL (rCTL) and robust CTL* (rCTL*). These logics are inspired by rLTL. Similar to rLTL, our new logics employ multi-valued semantics to track the degree of violations of a specification and are guided by two objectives: first, the syntax of rCTL and rCTL* is similar to the syntax of CTL and CTL*, respectively; second, the notion of robustness in these logics is intrinsic rather than extrinsic, i.e., robustness does not rely on the designers to provide quantitative information about the specification such as the number of violations permitted, ranks, cost, etc.
To demonstrate how our notion of robustness works, consider a specification \(\varPhi \Rightarrow \varPsi \) for a robot deployed in an office-like environment. The environment assumption \(\varPhi \) = \({\forall }{\Box }{\lnot }\) \(H\) states that humans never visit the initial location of the robot. On the other hand, the robot guarantee  states the following: “for all trajectories, regardless of the robot’s current position, the robot can return to its initial location in one time step” (Note that such a specification can not be expressed in LTL). Ideally, we would then want the following:
states the following: “for all trajectories, regardless of the robot’s current position, the robot can return to its initial location in one time step” (Note that such a specification can not be expressed in LTL). Ideally, we would then want the following:
-
if humans satisfy the assumption \(\varPhi \), then the robot should also satisfy the guarantee \(\varPsi \);
-
however, if humans violate the assumption by visiting the initial location a finite number of times before realizing their mistake and eventually not visiting it anymore, i.e., if they only satisfy \({\forall }{\Diamond }{\Box }{\lnot }H\), then rather than behaving arbitrarily, the robot should also satisfy
 , i.e., the robot eventually should be able to return to its initial location from any point;
, i.e., the robot eventually should be able to return to its initial location from any point; -
similarly, if humans violate the assumption by not visiting the initial location only infinitely often (or finitely often), i.e., if they satisfy \({\forall }{\Box }{\Diamond }{\lnot } H\) (or \({\forall }{\Diamond }{\lnot } H\)), then the robot should satisfy
 (or
(or  , respectively).
, respectively).
Later in this paper, we show that such a notion of robustness is indeed captured by the semantics of rCTL and rCTL*.
The first two contributions of the paper are robust variants of the logics CTL and CTL*, namely rCTL and rCTL*, respectively. Their semantics rely on a many-valued truth system that captures the various degrees of violation of a specification.
Second, we study the expressive power of rCTL and rCTL* and compare them to existing logics such as LTL, rLTL, CTL, and CTL*. The key results here are that rCTL is more expressive than CTL, while rCTL* has the same expressive power as CTL*.
Third, to demonstrate that rCTL and rCTL* specifications can be effectively used for verification, we provide efficient algorithms for model checking properties specified in these logics. We establish that the time complexity of rCTL and rCTL* model checking is linear and exponential, respectively, in the size of the formula, which is the same as the time complexity of CTL and CTL* model checking, respectively. Thus, robustness can be added to branching-time logics for free.
All proofs omitted due to space restrictions can be found in the full version [12].
2 Notation and Review of Computation Tree Logic
In this section, we review the syntax and semantics of CTL, which expresses properties of Kripke structures.
Throughout this paper, we fix a finite set \(\mathcal {P}\) of atomic propositions. A (finite) Kripke structure \(M = (S ,I,R,L)\) over \(\mathcal {P}\) consists of a finite set of states S, a set of initial states \(I\subseteq S\), a transition relation \(R\subseteq S\times S\) such that for all states s there exists a state \(s'\) satisfying \((s,s')\in R\), and a labeling function \(L:S\rightarrow 2^{\mathcal {P}}\). The set \(\mathrm {post}(s) = \{s'\in S \mid (s,s') \in R\}\) contains all successors of \(s \in S\). A path of the Kripke structure M is an infinite sequence of states \(\pi = s_0s_1\cdots \) such that \(s_{i+1} \in \mathrm {post}(s_i)\) for each \(i\ge 0\). For a state s, let \(\mathrm {paths}(s)\) denote the set of all paths starting from s. And for a path \(\pi \) and \(i\ge 0\), let \(\pi [i]\) denote the i-th state of \(\pi \), and \(\pi [i..]\) denotes the suffix of \(\pi \) from index i on.
Syntax. CTL formulas are classified into state and path formulas. Intuitively, state formulas express properties of states, whereas path formulas express temporal properties of paths. For ease of notation, we denote state formulas and path formulas by Greek capital letters and Greek lowercase letters, respectively. CTL state formulas over \(\mathcal {P}\) are given by the grammar
where \(p\in \mathcal {P}\) and \(\varphi \) is a path formula. CTL path formulas are given by the grammar

where  , and \(\mathbf {W}\) denote the operator next, eventually, always, until, and weak until, respectively.
, and \(\mathbf {W}\) denote the operator next, eventually, always, until, and weak until, respectively.
Semantics. Slightly deviating from the usual notation, we define the CTL semantics using a mapping \(V_{\text {CTL}}\) that maps a state/path and a CTL formula to a truth value in \(\mathbb {B} = \{0,1\}\). Given a state s and state formulas \(\varPhi ,\varPsi \), CTL semantics is defined as follows:
-
\(V_{\text {CTL}}(s,p) = {\left\{ \begin{array}{ll} 0 &{} \text {if }p\not \in L(s); \text { and} \\ 1 &{} \text {if }p\in L(s).\\ \end{array}\right. }\)
-
\(V_{\text {CTL}}(s,\varPhi \vee \varPsi ) = \max \{V_{\text {CTL}}(s,\varPhi ),V_{\text {CTL}}(s,\varPsi )\}.\)
-
\(V_{\text {CTL}}(s,\varPhi \wedge \varPsi ) = \min \{V_{\text {CTL}}(s,\varPhi ),V_{\text {CTL}}(s,\varPsi )\}.\)
-
\(V_{\text {CTL}}(s,\lnot \varPhi ) = 1-V_{\text {CTL}}(s,\varPhi )\).
-
\(V_{\text {CTL}}(s,\varPhi \Rightarrow \varPsi ) = \max \{1-V_{\text {CTL}}(s,\varPhi ),V_{\text {CTL}}(s,\varPsi )\}.\)
-
\(V_{\text {CTL}}(s,\exists \varphi ) = \max _{\pi \in \mathrm {paths}(s)} V_{\text {CTL}}(\pi ,\varphi ).\)
-
\(V_{\text {CTL}}(s,\forall \varphi ) = \min _{\pi \in \mathrm {paths}(s)} V_{\text {CTL}}(\pi ,\varphi ).\)
Similarly, for a path \(\pi \), the CTL semantics of path formulas is defined as given below:
-

-
\(V_{\text {CTL}}(\pi ,\Diamond \varPhi ) = \max _{i\ge 0} V_{\text {CTL}}(\pi [i],\varPhi ).\)
-
\(V_{\text {CTL}}(\pi ,{\Box }{\varPhi }) = \min _{i\ge 0} V_{\text {CTL}}(\pi [i],\varPhi ).\)
-
\(V_{\text {CTL}}(\pi ,\varPhi \mathbf {U} \varPsi ) = \max _{j\ge 0} \min \{V_{\text {CTL}}(\pi [j],\varPsi ), \min _{0\le i< j} V_{\text {CTL}}(\pi [i],\varPhi )\}.\)
-
\(V_{\text {CTL}}(\pi ,\varPhi \mathbf {W} \varPsi ) = \min _{j\ge 0} \max \{V_{\text {CTL}}(\pi [j],\varPhi ), \max _{0\le i\le j} V_{\text {CTL}}(\pi [i],\varPsi )\}.\)
Note that this definition is equivalent to the usual semantics of CTL [1].
3 Robust Computation Tree Logic
In this section, we robustify CTL by generalizing the ideas underlying robust LTL to CTL, obtaining the logic rCTL. We describe the syntax and semantics of rCTL and discuss the relation and differences between rCTL and other temporal logics.
As discussed in the robot example in the introduction, we want to capture the notion of robustness in CTL by ensuring that a small violation in environment assumptions leads to a small violation of system guarantees. To achieve that, we introduce robust semantics for CTL. Following arguments given by Tabuada and Neider [17], we first motivate the semantics of rCTL using an example. Consider the CTL path formula \({\Box }{p}\), where p is an atomic proposition. The formula can be satisfied in only one way, namely when p holds at every step (i.e., state) of the path. In contrast, the formula can be violated in several ways. Intuitively, \({\Box }{p}\) is violated in the worst manner when p fails to hold at every step. Then, we would prefer a case where p holds for finitely many steps. Even better would be the case when p holds at infinitely many steps. Finally, among all possible ways \({\Box }{p}\) can be violated, we would prefer the situation where p fails to hold for at most finitely many steps. Our robust semantics is designed to distinguish between satisfaction and these four different degrees of violation of \({\Box }{p}\). However, as convincing as this argument might be, a question persists: in which sense can we regard these five alternatives as canonical?
We answer this question by interpreting the satisfaction of \({\Box }{p}\) as a counting problem. Recall that the semantics of \({\Box }{p}\) for a path \(\pi \) is given by \(V_{\text {CTL}}((\pi ,\Box p) = \min _{i\ge 0} V_{\text {CTL}}(\pi [i],p)\). Now, observe that the truth value of the CTL formula \({\Box }{p}\) for a path \(\pi \) only depends on the number of occurrences of 0’s and 1’s in the infinite word \(\alpha = V_{\text {CTL}}(\pi [0],p)V_{\text {CTL}}(\pi [1],p)\cdots \in \mathbb {B}^{\omega }\) but not on their order. From this perspective, \({\Box }{p}\) is violated in the worst manner when p fails to hold at every step, which corresponds to the number of occurrences of 1 in \(\alpha \) being zero. The next degree of violation of \({\Box }{p}\) in which p holds at finitely many steps corresponds to having a finite number of 1’s. Similarly, the next degree of violation corresponds to having an infinite number of 1’s and an infinite number of 0’s. Among all the ways in which \({\Box }{p}\) is violated, the most preferred way corresponds to having finitely many 0’s. Finally, the satisfaction of \({\Box }{p}\) corresponds to having zero 0’s. Note that the position where 0’s and 1’s occur is irrelevant for our argument. Furthermore, note that by successively applying permutations that swap position i with position \(i + 1\) and leave all the remaining elements of \(\mathbb {N}\) unaltered, one can transform any \(\alpha \in \mathbb {B}^{\omega }\) into words of one of the following five forms: \(1^{\omega },0^k1^{\omega },(01)^{\omega },1^k0^{\omega },0^{\omega }\). It is not hard to verify that the five cases of violations of \({\Box }{p}\) that we discussed above amount to the words of the five forms given above. We thus conclude the need for five truth values to describe five different ways of counting 0’s and 1’s that correspond to five different canonical forms of violations of \({\Box }{p}\).
According to our motivating example \({\Box }{p}\), the desired semantics should have one truth value corresponding to true and four truth values corresponding to the different shades of false. It is instructive to think of truth values as elements of \(\mathbb {B}^4\). To ease notation, we denote such values by \(b = b_1b_2b_3b_4\) or \(b=(b_1,b_2,b_3,b_4)\) with \(b_i\in \mathbb {B}\). We denote the set of truth values as \(\mathbb {B}_4\), which consists of the five truth values \(\{0000,0001,0011,0111,1111\}\). The value 1111 corresponds to true, and the others correspond to different shades of false. The truth values are ordered naturally as \(0000< 0001< 0011< 0111< 1111\).
Syntax. Similar to the syntax of CTL, formulas of rCTL are also classified into state and path formulas. Furthermore, we equip every temporal operator with dots to distinguish the robust operators from the normal ones. rCTL state formulas over \(\mathcal {P}\) are formed according to the grammar
where \(p\in \mathcal {P}\) and \(\varphi \) is a path formula. rCTL path formulas are formed according to the grammar

Semantics. We now discuss the motivation behind our many-valued semantics for rCTL. The notion of a triangular-norm summarizes all the desirable properties of a many-valued conjunction (see P. Hájek [11] for details), and it is natural to model conjunction and disjunction in \(\mathbb {B}_4\) by min and max, respectively. Moreover, as in intuitionistic logic, we define the implication, denoted by \(a\rightarrow b\) on the level of truth values, such that \(c\le a \rightarrow b\) if and only if \(c \wedge a \le b\) for every \(c\in \mathbb {B}_4\). This leads to
However, the negation, denoted by \(\overline{a}\) on the level of truth values, defined by \(a\rightarrow 0000\) as in intuitionistic logic, is not compatible with our interpretation that all elements in \(\mathbb {B}_4\setminus \{1111\}\) represent different shades of false and, thus, their negation should be 1111. Therefore, we follow the ideas introduced by rLTL and use da Costa algebras to define the negation (see Priest and Graham [14] for details):
In other words, “true” (1111) gets mapped to “false” (0000), while “shades of false” get mapped to “true”.
It should be mentioned that working with a five-valued semantics has its price. As in intuitionistic logic, \(\overline{\overline{a}}\) may not be equal to a as evidenced by taking \(a=0111\). Although it is still true that \(\overline{\overline{a}} \rightarrow a\). Interestingly, we can think of double negation as quantization in the sense that true is mapped to true and all the shades of false are mapped to 0000 (false). Hence, double negation quantizes the five different truth values into two truth values (true and false) in a manner that is compatible with our interpretation of truth values.
Similar to the semantics of CTL, we define the semantics of rCTL by a mapping V, called valuation, that maps an rCTL formula and a state/path to an element of \(\mathbb {B}_4\). For an atomic proposition \(p\in \mathcal {P}\), it is defined classically:
-
\(V(s,p)= {\left\{ \begin{array}{ll} 0000 &{} \text {if }p\not \in L(s);\text { and} \\ 1111 &{} \text {if }p\in L(s). \\ \end{array}\right. }\)
Following the semantics of rLTL, we define the semantics for boolean connectives in rCTL using da Costa algebras, as follows:
-
\(V(s,\varPhi \vee \varPsi )=\max \Big \{V(s,\varPhi ),V(s,\varPsi )\Big \}.\)
-
\(V(s,\varPhi \wedge \varPsi )=\min \Big \{V(s,\varPhi ),V(s,\varPsi )\Big \}.\)
-
\(V(s,\lnot \varPhi )= \overline{V(s, \varPhi )}\)
-
\(V(s,\varPhi \Rightarrow \varPsi )= V(s,\varPhi )\rightarrow V(s,\varPsi )\)
For existential path quantification, we want \(V(s,\exists \varphi ) \ge b\) if there exists a path \(\pi \) from s such that \(V(\pi ,\varphi )\ge b\). Similarly, we want \(V(s,\forall \varphi ) \ge b\) if for all paths \(\pi \) from s holds that \(V(\pi ,\varphi )\ge b\). This leads to:
Now, for path formulas, we formalize the intuition above in the semantics of the temporal operators. Using the counting interpretation as discussed earlier, we define the semantics of  by
by

where \(V_{\ell }(\pi , \varphi )\) denotes the \(\ell \)-th entry of \(V(\pi , \varphi )\) for \(1\le \ell \le 4\).
The semantics of  mimics the classical semantics in that the truth value of
mimics the classical semantics in that the truth value of  on \(\pi \) is the maximal truth value of \(\varPhi \) that is assumed at any position of \(\pi \).
on \(\pi \) is the maximal truth value of \(\varPhi \) that is assumed at any position of \(\pi \).

Using a similar approach, the semantics for other temporal operators are defined as follows:
-

-

-
 where $$\begin{aligned} W_l = \max \left\{ V_l(\pi [j],\varPhi ), \max _{0\le i \le j} V_l(\pi [i],\varPsi )\right\} . \end{aligned}$$
where $$\begin{aligned} W_l = \max \left\{ V_l(\pi [j],\varPhi ), \max _{0\le i \le j} V_l(\pi [i],\varPsi )\right\} . \end{aligned}$$
Example 1
Having defined the rCTL semantics, let us recall the example of the specification for a robot given in Sect. 1: \(\varPhi \Rightarrow \varPsi \), where \(\varPhi = {\forall }{\Box }{\lnot }{H}\) is the environment assumption that humans never visit the initial location, and  is the robot guarantee that from any state in a path there exists a way for the robot to return to its initial location in one time step. The robust version of this formula is
is the robot guarantee that from any state in a path there exists a way for the robot to return to its initial location in one time step. The robust version of this formula is  . Let us see if this formula captures the robustness property as discussed in Sect. 1.
. Let us see if this formula captures the robustness property as discussed in Sect. 1.
Now, coming back to our example, suppose \(\varPhi _1 = \lnot H\) and  . Let us assume
. Let us assume  evaluates to 1111 for some Kripke structure. Then the following hold.
evaluates to 1111 for some Kripke structure. Then the following hold.
-
If humans never visit the initial location, then in any path, \(\varPhi _1\) holds at every state. Hence,
 evaluates to 1111. Then by the semantics of \(\Rightarrow \), the formula
evaluates to 1111. Then by the semantics of \(\Rightarrow \), the formula  also must evaluate to 1111. That means, in any path, \(\varPhi _2\) also holds at every state. Therefore, from any state of a path, the robot can return to its initial location in one time step. Hence, the desired behavior of the system is retained when the environment assumption holds with no violation.
also must evaluate to 1111. That means, in any path, \(\varPhi _2\) also holds at every state. Therefore, from any state of a path, the robot can return to its initial location in one time step. Hence, the desired behavior of the system is retained when the environment assumption holds with no violation. -
If humans violate the assumption by visiting the initial location finitely many times and eventually not visiting it anymore, then for any path, \(\varPhi _1\) holds eventually at every state. Hence,
 evaluates to 0111. Then, by the rCTL semantics,
evaluates to 0111. Then, by the rCTL semantics,  evaluates to 0111 or higher. Hence, in any path, \(\varPhi _2\) also needs to hold eventually at every state. That means, from any state in a path, the robot can return to its initial location eventually.
evaluates to 0111 or higher. Hence, in any path, \(\varPhi _2\) also needs to hold eventually at every state. That means, from any state in a path, the robot can return to its initial location eventually. -
Similarly, if \(\varPhi _1\) holds at infinitely (finitely) many states in every path, then \(\varPhi _2\) needs to hold at infinitely (finitely) many states in every path.
Hence, whenever the formula  evaluates to 1111, its semantics captures the intended robustness property by which a weakening of the assumption
evaluates to 1111, its semantics captures the intended robustness property by which a weakening of the assumption  leads to a weakening of the guarantee
leads to a weakening of the guarantee  .
.
Now, a natural question arises: does the formula still provide useful information when its value is lower than 1111. It follows from the semantics of implication that  evaluates to \(b<1111\) only when
evaluates to \(b<1111\) only when  evaluates to a higher value than b, whereas
evaluates to a higher value than b, whereas  evaluates to b. So, the desired system guarantee is not satisfied. However, the value of
evaluates to b. So, the desired system guarantee is not satisfied. However, the value of  still describes which weakened guarantee follows from the environment assumption. This can be seen as another measure of robustness: despite
still describes which weakened guarantee follows from the environment assumption. This can be seen as another measure of robustness: despite  not following from
not following from  , the system’s behavior is not arbitrary, a value of b is still guaranteed.
, the system’s behavior is not arbitrary, a value of b is still guaranteed.
3.1 Expressiveness of rCTL
In this section, we compare the expressiveness of rCTL with other temporal logics such as CTL, LTL, and rLTL. We show that the five truth values of rCTL make it more expressive than CTL. More precisely, there are properties that one can express in rCTL but not in CTL. However, the expressiveness of rCTL and LTL are incomparable; and the same also holds for rCTL and rLTL.
We compare the expressiveness of two classes of logics by comparing the expressiveness of their formulas. For logics A and B, we say A is as expressive as B if for every formula in B there is an equivalent formula in A. Moreover, we say A is more expressive than B if A is as expressive as B but the converse is not true. Furthermore, we say A and B have incomparable expressiveness if neither of A and B is as expressive as the other one. For branching time logics, we only consider the state formulas when comparing the expressiveness.
Now the question is what it means for two formulas to be equivalent. Intuitively speaking, equivalent means “express the same thing”. Formally, we define the equivalence of two formulas using their satisfaction sets. For a given Kripke structure, and a state formula \(\varPhi \), we define the satisfaction set \(\mathrm {Sat}(\varPhi ,b)\) of an rCTL formula \(\varPhi \) and with value \(b\in \mathbb {B}_4\) to be the set of states s such that \(V(s,\varPhi )\ge b\). Since the satisfaction sets of an rCTL (state) formula are always associated with a truth value in \(\mathbb {B}_4\), we always associate a truth value with an rCTL formula when comparing its expressiveness.
For two rCTL state formulas \(\varPhi _1, \varPhi _2\) and two truth values \(b_1,b_2\in \mathbb {B}_4\), we say \(\varPhi _1\) with truth value \(b_1\) is equivalent to \(\varPhi _2\) with truth value \(b_2\) if for every Kripke structure it holds that \(\mathrm {Sat}(\varPhi _1,b_1) = \mathrm {Sat}(\varPhi _2,b_2)\). Similarly, an rCTL formula \(\varPhi _1\) with truth value \(b_1\) is equivalent to a CTL formula \(\varPhi _2\) if for every Kripke structure it holds that \(\mathrm {Sat}(\varPhi _1,b_1) = \mathrm {Sat}_{\text {CTL}}(\varPhi _2)\), where \(\mathrm {Sat}_{\text {CTL}}(\cdot )\) denotes the satisfaction sets for CTL formulas. The equivalence between an rCTL formula and LTL formula is defined analogously.
Now, comparing the semantics of CTL and rCTL, an induction over the structure of formulas shows that the CTL semantics of a formula containing no implication can be recovered from the first bit of the rCTL semantics. Recall that \(V_{\text {CTL}}\) and \(V_1\) are the CTL valuation and the first bit of the rCTL valuation, respectively.
Lemma 1
For any CTL state formula \(\varPhi \) containing no implication, let \(\varPhi _r\) be the rCTL state formula obtained by dotting all temporal operators in \(\varPhi \). Then for any state s, it holds that \(V_{\text {CTL}}(s,\varPhi ) = V_1(s,\varPhi _r).\) Consequently, it holds that \(\mathrm {Sat}_{\text {CTL}}(\varPhi ) = \mathrm {Sat}(\varPhi _r,1111).\)
As we know that \(\varPhi \Rightarrow \varPsi \) is equivalent to \(\lnot \varPhi \vee \varPsi \) in CTL, hence, one can rewrite any CTL formula into a formula containing no implication. Therefore, by using Lemma 1, rCTL is at least as expressive as CTL.
However, the converse is not true, i.e., there exist rCTL formulas that have no equivalent CTL formula. For example, consider the rCTL formula  with truth value 0111. For a state s, we have \(s\in \mathrm {Sat}(\varPhi ,0111)\) if and only if for each \(\pi \in \mathrm {paths}(s)\), there exists j such that \(p\in L(\pi [i])\) for all \(i\ge j\), which is equivalent to each path \(\pi \in \mathrm {paths}(s)\) satisfying the LTL formula \({\Diamond }{\Box }{p}\). However, as we know, the formula \({\Diamond }{\Box }{p}\) can not be expressed in CTL (see Baier and Katoen [1] for details). Therefore, there is no CTL formula \(\varPsi \) such that \(\mathrm {Sat}(\varPhi ,0111) = \mathrm {Sat}_{\text {CTL}}(\varPsi )\). In total, we obtain the following result.
with truth value 0111. For a state s, we have \(s\in \mathrm {Sat}(\varPhi ,0111)\) if and only if for each \(\pi \in \mathrm {paths}(s)\), there exists j such that \(p\in L(\pi [i])\) for all \(i\ge j\), which is equivalent to each path \(\pi \in \mathrm {paths}(s)\) satisfying the LTL formula \({\Diamond }{\Box }{p}\). However, as we know, the formula \({\Diamond }{\Box }{p}\) can not be expressed in CTL (see Baier and Katoen [1] for details). Therefore, there is no CTL formula \(\varPsi \) such that \(\mathrm {Sat}(\varPhi ,0111) = \mathrm {Sat}_{\text {CTL}}(\varPsi )\). In total, we obtain the following result.
Theorem 1
rCTL is more expressive than CTL.
It is known that the expressiveness of LTL and CTL is incomparable, i.e., there exist CTL formulas (i.e., \({\forall }{\Diamond }{\forall }{\Box }{p}\)) for which there is no equivalent LTL formula, and there exist LTL formulas (i.e.,  ) for which there is no equivalent CTL formula (see Baier and Katoen [1] for details). The same holds for the expressiveness of LTL and rCTL. As we just saw that the first bit of the rCTL semantics captures the CTL semantics (for a formula with no implication), it follows that for the rCTL formula
) for which there is no equivalent CTL formula (see Baier and Katoen [1] for details). The same holds for the expressiveness of LTL and rCTL. As we just saw that the first bit of the rCTL semantics captures the CTL semantics (for a formula with no implication), it follows that for the rCTL formula  (with value 1111), there is no equivalent LTL formula. Furthermore, it is easy to see that the five-valued semantics does not help in expressing
(with value 1111), there is no equivalent LTL formula. Furthermore, it is easy to see that the five-valued semantics does not help in expressing  . Hence, using the proof of inexpressibility of \(\varphi \) in CTL, it can be shown that \(\varphi \) can not be expressed by any rCTL formula either. Intuitively, a Kripke structure satisfies the formula \(\varphi \) if all paths contain a pair of consecutive states where p holds. This property is inexpressible in rCTL as all path formulas are guarded with an existential or universal operator. One can express “all paths contain a state such that p holds at that state and at all (or some) of its successor” in rCTL, which is not the same as the property we want. Therefore, we obtain the following result.
. Hence, using the proof of inexpressibility of \(\varphi \) in CTL, it can be shown that \(\varphi \) can not be expressed by any rCTL formula either. Intuitively, a Kripke structure satisfies the formula \(\varphi \) if all paths contain a pair of consecutive states where p holds. This property is inexpressible in rCTL as all path formulas are guarded with an existential or universal operator. One can express “all paths contain a state such that p holds at that state and at all (or some) of its successor” in rCTL, which is not the same as the property we want. Therefore, we obtain the following result.
Theorem 2
rCTL and LTL have incomparable expressiveness.
In the paper on rLTL [17], Tabuada and Neider showed that LTL and rLTL are equally expressive. Hence, a direct corollary of Theorem 2 is the following:
Corollary 1
rCTL and rLTL have incomparable expressiveness.
3.2 rCTL Model Checking
The classical CTL model checking problem asks whether all executions of a system satisfy a given property. However, in the context of rCTL, this question is more involved due to rCTL’s many-valued semantics. A natural generalization is whether all executions satisfy a given property with at least a given value \(b_0\in \mathbb {B}_4\). Formally, the rCTL model checking problem is: for a given Kripke structure \(M = (S,I,R,L)\), an rCTL formula \(\varPhi \) and a truth value \(b_0\in \mathbb {B}_4\), does \(V(s,\varPhi ) \ge b_0\) hold for all initial states \(s\in I\)? Our rCTL model checking procedure is shown as pseudocode in Algorithm 1. It is similar to the standard CTL model checking algorithm in that it recursively computes the satisfaction sets \(\mathrm {Sat}(\varPsi ,b)\) for each subformulaFootnote 1 \(\varPsi \in \mathrm {Sub}(\varPhi )\) and each truth value \(b\in \mathbb {B}_4\). To check whether all paths of the Kripke structure starting in an initial state satisfy \(\varPhi \), it is then enough to check whether all initial states belong to \(\mathrm {Sat}(\varPhi ,b_0)\). Note that \(\mathrm {Sat}(\varPsi ,0000) = S\) since every state satisfies any rCTL formula \(\varPsi \) with truth value 0000.

The key idea of Algorithm 1 is to recursively compute the satisfaction sets using a dynamic programming technique. More precisely, we compute the satisfaction sets by induction over the construction of \(\varPhi \) as shown in Table 1. Since \(\mathrm {Sat}(\varPsi ,0000) = S\) for any rCTL formula \(\varPsi \), Table 1 only shows the case \(b>0000\). To simplify the following presentation of these cases, we split the discussion into three categories: atomic propositions, boolean connectives, and temporal operators.
Atomic Propositions. The valuation for atomic propositions is defined classically, as in the case of CTL. Hence, the satisfaction set \(\mathrm {Sat}(p,b)\) of an atomic proposition \(p\in \mathcal {P}\) with a value \(b>0000\) is the set of all states whose label contains p.
Boolean Connectives. The computation of the satisfaction sets for the boolean connectives closely follows the semantic definition based on the da Costa algebra. Conjunction and disjunction are implemented using the usual intersection and union of sets, respectively. The set \(\mathrm {Sat}(\lnot \varPhi ,b)\) is the complement of all states on which \(\varPhi \) evaluates to 1111 (recall that we assume \(b > 0000\)). Finally, the implementation of the implication is more involved. By definition, the set \(\mathrm {Sat}(\varPhi \Rightarrow \varPsi ,1111)\) is the set of states s for which \(V(s,\varPhi )\) is less than \(V(s,\varPsi )\); in set notation, this is expressed by the intersection of the sets \(\mathrm {Sat}(\varPsi ,b) \cup (S\setminus \mathrm {Sat}(\varPhi ,b))\) for each \(b\in \mathbb {B}_4\). For any other truth value \(b \le 0111\), \(\mathrm {Sat}(\varPhi \Rightarrow \varPsi ,b)\) consists of all states where the implication evaluates to 1111 or \(\varPsi \) evaluates to at least b.
Temporal Operators. For all temporal operators, we compute the satisfaction sets for existential and universal path formulas individually.
A state s satisfies the formula  with a value of at least b if one of its successors satisfies \(\varPhi \) with a value of at least b. Hence, the set
with a value of at least b if one of its successors satisfies \(\varPhi \) with a value of at least b. Hence, the set  is the set of states s such that one of its successors is in \(\mathrm {Sat}(\varPhi ,b)\). Similarly, the set
is the set of states s such that one of its successors is in \(\mathrm {Sat}(\varPhi ,b)\). Similarly, the set  is the set of states s such that all of its successors are in \(\mathrm {Sat}(\varPhi ,b)\).
is the set of states s such that all of its successors are in \(\mathrm {Sat}(\varPhi ,b)\).
Next, a state s satisfies the formula  with a value of at least b if there exists a path from s containing a state that satisfies \(\varPhi \) with a value of at least b. By applying expansion laws similar to those of CTL (see Baier and Katoen [1] for details), this statement is equivalent to s satisfying \(\varPhi \) with a value of at least b or one of its successors satisfying
with a value of at least b if there exists a path from s containing a state that satisfies \(\varPhi \) with a value of at least b. By applying expansion laws similar to those of CTL (see Baier and Katoen [1] for details), this statement is equivalent to s satisfying \(\varPhi \) with a value of at least b or one of its successors satisfying  with a value of at least b. Hence, as in CTL,
with a value of at least b. Hence, as in CTL,  is the smallest subset T of S satisfying \(\mathrm {Sat}(\varPhi ,b)\cup \{s\in S\mid \mathrm {post}(s)\cap T\not = \emptyset \}\subseteq T\). Equivalently, this set equals the least fixed point of the function
is the smallest subset T of S satisfying \(\mathrm {Sat}(\varPhi ,b)\cup \{s\in S\mid \mathrm {post}(s)\cap T\not = \emptyset \}\subseteq T\). Equivalently, this set equals the least fixed point of the function
where \(S_1=\mathrm {Sat}(\varPhi ,b)\), \(S_2=S\), and T is the fixed-point variable. To simplify our notation, we use standard notation for fixed points and write \(\mu T.F(T,\cdot )\), and \(\nu T.F(T,\cdot )\), respectively for the least and greatest fixed point of a function F(T,\(\cdot \)) with fixed-point variable T (which is unique for all functions we consider).
Similarly, a state s satisfies the formula  with a value of at least b if every path starting from s contains a state satisfying \(\varPhi \) with value at least b. Hence, the set
with a value of at least b if every path starting from s contains a state satisfying \(\varPhi \) with value at least b. Hence, the set  is the least fixed point \(\mu T. F_{\forall }(T,\mathrm {Sat}(\varPhi ,b),S)\) of the function
is the least fixed point \(\mu T. F_{\forall }(T,\mathrm {Sat}(\varPhi ,b),S)\) of the function
The characterization of the set  is more complex, and we discuss each truth value separately. Firstly, a state s satisfies
is more complex, and we discuss each truth value separately. Firstly, a state s satisfies  with value 1111 if there exists a path from s on which every state satisfies \(\varPhi \) with value 1111. By applying expansion laws similar to those of CTL, this statement is equivalent to s satisfying \(\varPhi \) with value 1111 and one of its successors satisfying
with value 1111 if there exists a path from s on which every state satisfies \(\varPhi \) with value 1111. By applying expansion laws similar to those of CTL, this statement is equivalent to s satisfying \(\varPhi \) with value 1111 and one of its successors satisfying  with value 1111. Hence, the set
with value 1111. Hence, the set  equals \(\nu T.F_{\exists }(T,\emptyset ,\mathrm {Sat}(\varPhi ,1111))\).
equals \(\nu T.F_{\exists }(T,\emptyset ,\mathrm {Sat}(\varPhi ,1111))\).
Next, a state s satisfies  with a value of at least 0111 if there exists a path from s on which eventually every state satisfies \(\varPhi \) with a value of at least 0111. It is not hard to verify that the set
with a value of at least 0111 if there exists a path from s on which eventually every state satisfies \(\varPhi \) with a value of at least 0111. It is not hard to verify that the set  is equal to the nested fixed point \(\mu T_1. \nu T_2. G_{\exists }(T_1,T_2,\emptyset ,\mathrm {Sat}(\varPhi ,0111))\) of the function
is equal to the nested fixed point \(\mu T_1. \nu T_2. G_{\exists }(T_1,T_2,\emptyset ,\mathrm {Sat}(\varPhi ,0111))\) of the function
The greatest fixed point of the function containing the last two terms (on the right side) of the above equation represents a property of a path that all states on that path satisfy \(\varPhi \) with a value of at least 0111 and then the least fixed point of the function ensures that there exists a path that has a suffix with that property.
Similarly, a state s satisfies  with a value of at least 0011 if there exists a path from s on which there exist infinitely many states satisfying \(\varPhi \) with a value of at least 0011. Note that the property that a path contains infinitely many states satisfying \(\varPhi \) (with a value b) is the dual of the property that a path contains finitely many states satisfying \(\varPhi \) (with a value b). Hence, similar to the last case, it is not hard to see that
with a value of at least 0011 if there exists a path from s on which there exist infinitely many states satisfying \(\varPhi \) with a value of at least 0011. Note that the property that a path contains infinitely many states satisfying \(\varPhi \) (with a value b) is the dual of the property that a path contains finitely many states satisfying \(\varPhi \) (with a value b). Hence, similar to the last case, it is not hard to see that

Finally, a state s satisfies  with a value of at least 0001 if there exists a path from s containing a state that satisfies \(\varPhi \) with a value of at least 0001, which is equivalent to satisfying
with a value of at least 0001 if there exists a path from s containing a state that satisfies \(\varPhi \) with a value of at least 0001, which is equivalent to satisfying  with a value of at least 0001. Hence,
with a value of at least 0001. Hence,  is the set \(\mu T.F_{\exists }(T,\mathrm {Sat}(\varPhi ,0001),S)\), as above.
is the set \(\mu T.F_{\exists }(T,\mathrm {Sat}(\varPhi ,0001),S)\), as above.
Analogously, one can characterize  using the fixed points of the functions \(F_{\forall }\) and \(G_{\forall }\), where
using the fixed points of the functions \(F_{\forall }\) and \(G_{\forall }\), where
Characterizations for  and
and  can be obtained similarly. In total, we obtain the result given below.
can be obtained similarly. In total, we obtain the result given below.
Theorem 3
Let \(M = (S,I,R,L)\) be a Kripke structure. Then for rCTL formulas \(\varPhi \) and truth values \(b\in \mathbb {B}_4 \setminus \{0000\}\), one can compute the sets \(\mathrm {Sat}(\varPhi ,b)\) recursively as specified in Table 1.
Algorithm 1 computes \(5\cdot |\mathrm {sub}(\varPhi )|\) satisfaction sets following the subformula ordering. Using the standard fixed-point iterations, which take linear time in the number of the states, each fixed point can be computed in linear time. Similarly, one can compute the nested fixed points in quadratic time in the number of states. Thus, we obtain the following.
Theorem 4
The rCTL model checking problem can be solved in time \(\mathcal {O}(N^2|\varPhi |)\), where N is the number of states of the given Kripke structure, and \(\varPhi \) is the given rCTL specification.
As we know, the CTL model checking algorithm also takes linear time in the size of the formula [1]. Hence, both model checking problems are in \(\mathrm {PTIME}\).
3.3 rCTL Satisfiability
This section considers the satisfiability problem for rCTL, which is: for a given rCTL formula \(\varPhi \) and truth value \(b_0\in \mathbb {B}_4\), does there exist a Kripke structure \(M = (S,I,R,L)\) such that \(I\subseteq \mathrm {Sat}(\varPhi ,b_0)\)? The rCTL satisfiability can be solved by translating the given rCTL formula and the given truth value into an equivalent \(\mu \)-calculus formula (see Bradfield and Walukiewicz [3] for definitions) of linear size and then checking the resulting formula for satisfiability. This is always possible relying on the fixed point characterizations described in Sect. 3.2 (see Table 1). Since the satisfiability problem for \(\mu \)-calculus is \(\mathrm {EXPTIME}\)-complete [3], rCTL satisfiability is in \(\mathrm {EXPTIME}\). A matching lower bound already holds for CTL [6].
Theorem 5
The satisfiability problem for rCTL is \(\mathrm {EXPTIME}\)-complete.
4 Robust CTL*
In this section, we present the robust version of CTL*, named robust CTL*, which combines the features of rCTL and rLTL. We show that rCTL* is more expressive than both and then present an algorithm for rCTL* model checking.
Syntax. Like CTL*, robust CTL* allows path quantifiers \(\exists \) and \(\forall \) to be arbitrarily nested with temporal operators. The syntax of rCTL* state formulas is the same as in rCTL. Moreover, rCTL* path formulas are similar to rLTL formulas, with the only difference being the use of arbitrary rCTL* state formulas as atoms. rCTL* state formulas over \(\mathcal {P}\) are formed according to the grammar
where \(p\in \mathcal {P}\) and \(\varphi \) is a path formula. rCTL* path formulas are formed according to the grammar

Semantics. As in CTL*, the semantics for rCTL* state and path formulas are analogous to rCTL and rLTL semantics, respectively. Let M be a Kripke structure and \(\varPhi \), \(\varPsi \) be rCTL* state formulas and \(\varphi \), \(\psi \) be rCTL* path formulas. Then for a state s, the rCTL* semantics \(V(s,\varPhi )\) is the same as the rCTL semantics. For a path \(\pi \), the semantics is analogous to rLTL semantics, as defined below.
-
\(V(\pi ,\varPhi ) = V(\pi [0],\varPhi \))
-
\(V(\pi ,\lnot \varphi )= \overline{V(\pi , \varphi )}\)
-

-
\(V(\pi ,\varphi \vee \psi )=\max \Big \{V(\pi ,\varphi ),V(\pi ,\psi )\Big \}\)
-
\(V(\pi ,\varphi \wedge \psi )=\min \Big \{V(\pi ,\varphi ),V(\pi ,\psi )\Big \}\)
-
\(V(\pi ,\varphi \Rightarrow \psi )= V(\pi ,\varphi )\rightarrow V(\pi ,\psi )\)
-

-

\(\min _{j\ge 0} \max _{i\ge j} V_3(\pi [i], \varPhi ), \max _{i\ge 0} V_4(\pi [i], \varPhi ))\)
-
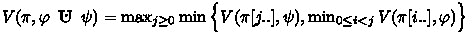
-
 where $$\begin{aligned} W_l = \max \left\{ V_l(\pi [j..],\varphi ), \max _{0\le i \le j} V_l(\pi [i..],\psi )\right\} \end{aligned}$$
where $$\begin{aligned} W_l = \max \left\{ V_l(\pi [j..],\varphi ), \max _{0\le i \le j} V_l(\pi [i..],\psi )\right\} \end{aligned}$$
Example 2
Having defined the rCTL* semantics, let us see how the rCTL* formula  is different from
is different from  , where \(\varPhi _1 = \lnot H\) states that humans are not at the robot’s initial location and
, where \(\varPhi _1 = \lnot H\) states that humans are not at the robot’s initial location and  states that the robot can return to its initial location in one time step, as described in Sect. 1. Assume
states that the robot can return to its initial location in one time step, as described in Sect. 1. Assume  evaluates to 1111. Then the formula
evaluates to 1111. Then the formula  must evaluate to 1111 for each path. Hence, the following holds:
must evaluate to 1111 for each path. Hence, the following holds:
-
If \(\varPhi _1\) holds at every state in a path \(\pi \), then
 evaluates to 1111. Hence, by the rCTL* semantics,
evaluates to 1111. Hence, by the rCTL* semantics,  must also evaluate to 1111. That means, \(\varPhi _2\) also holds at every state in \(\pi \). Hence, in any path, if humans never visit the initial location, then from every state, the robot can return to its initial location in one time step.
must also evaluate to 1111. That means, \(\varPhi _2\) also holds at every state in \(\pi \). Hence, in any path, if humans never visit the initial location, then from every state, the robot can return to its initial location in one time step. -
Similarly, if \(\varPhi _1\) holds eventually always for some path \(\pi \), then
 evaluates to 0111. Then, by the rCTL* semantics,
evaluates to 0111. Then, by the rCTL* semantics,  evaluates to 0111 or higher. Hence, \(\varPhi _2\) also needs to hold eventually always in \(\pi \). Therefore, if humans visit the initial location a few times and never visit it again in a path, then from any state in that path, the robot can return to its initial location eventually.
evaluates to 0111 or higher. Hence, \(\varPhi _2\) also needs to hold eventually always in \(\pi \). Therefore, if humans visit the initial location a few times and never visit it again in a path, then from any state in that path, the robot can return to its initial location eventually. -
Similarly, if \(\varPhi _1\) holds at infinitely (finitely) many states in some path \(\pi \), then \(\varPhi _2\) needs to hold at infinitely (finitely) many states in \(\pi \).
As we can see, the semantics of  captures the robustness property for every path separately, whereas the rCTL formula
captures the robustness property for every path separately, whereas the rCTL formula  captures the robustness property jointly for all paths starting from a state.
captures the robustness property jointly for all paths starting from a state.
To understand the difference, let us consider the Kripke structure M with initial state \(s_0\) as shown in Fig. 1 (where transitions are depicted by edges). Suppose the set of states that satisfy (with value 1111) the state formulas \(\varPhi _1\) and \(\varPhi _2\) are \(\{s_0,s_1\}\) and \(\{s_0,s_2\}\), respectively (as shown by the labels in the figure).
There are only two paths starting from \(s_0\), i.e., \(\pi _1 = s_0 s_1 s_1 \cdots \) and \(\pi _2 = s_0 s_2 s_2 \cdots \). Since \(\varPhi _1\) holds at every state in the path \(\pi _1\), we have  . Moreover, since \(\varPhi _1\) holds only at the first state in the path \(\pi _2\), we have
. Moreover, since \(\varPhi _1\) holds only at the first state in the path \(\pi _2\), we have  . Hence,
. Hence,  . Similarly, since \(\varPhi _2\) holds only at the first state of each path, we have
. Similarly, since \(\varPhi _2\) holds only at the first state of each path, we have  . Hence,
. Hence,  . Therefore, it holds that
. Therefore, it holds that  .
.
However, as we have  , it holds that
, it holds that  . Similarly, we have
. Similarly, we have  . Hence, we have
. Hence, we have

This is the case because both of the paths do not satisfy  with value 1111 individually, but collectively, the state \(s_0\) satisfies
with value 1111 individually, but collectively, the state \(s_0\) satisfies  .
.
4.1 Expressiveness of rCTL*
The satisfaction sets and the equivalence between two formulas in rCTL* are defined as for rCTL. Now, as we can see, rCTL* is an extension of both rCTL and rLTL. Therefore, it subsumes both rCTL and rLTL (and hence, it also subsumes LTL). Furthermore, using the discussion in Sect. 3.1, it is easy to see that the rCTL* formula  can not be expressed in rLTL or rCTL. In total, we obtain the following result:
can not be expressed in rLTL or rCTL. In total, we obtain the following result:
Theorem 6
rCTL* is more expressive than rLTL, rCTL, and LTL.
Now, using the same idea as in Lemma 1, one can recover the CTL* semantics of a formula with no implication from the first component of the rCTL* semantics. Conversely, using the same arguments as for the analogous result for rLTL [17, Proposition 5], one can translate each rCTL* formula into four CTL* formulas that captures the four components of the rCTL* semantics. Hence, we obtain the following result.
Theorem 7
CTL* and rCTL* are equally expressive.
4.2 rCTL* Model Checking
The model checking problem for rCTL* is analogous to that of rCTL, which is: for a given Kripke structure \(M = (S,I,R,L)\), an rCTL* formula \(\varPhi \) and a truth value \(b_0\in \mathbb {B}_4\), does \(V(s,\varPhi ) \ge b_0\) hold for all initial states \(s\in I\)? As we will see, to solve the rCTL* model checking problem, one can use a combination of rCTL and rLTL model checking. This is similar to CTL* model checking, which combines CTL and LTL model checking.
As in rCTL, for the rCTL* model checking, we use the characterization of the satisfaction sets. \(\mathrm {Sat}(\varPhi ,b)\) can be computed using Table 1 for every state formula \(\varPhi \) which is either an atomic proposition or can be expressed as a boolean combination (conjunction, negation, etc.) of two subformulas. Otherwise, we use an rLTL model checking algorithm to compute \(\mathrm {Sat}(\varPhi ,b)\) for a state formula starting with a path quantifier.
Let us first go through the basic concepts of rLTL and its model checking algorithm. As we have described earlier, rCTL* is an extension of rLTL. Both rCTL* path formulas and rLTL formulas are defined using the same grammar, with the only difference being the use of state formulas as atoms in rCTL*. Moreover, the valuation V for rLTL formulas is defined the same way as it is defined for rCTL* path formulas. Furthermore, given a Kripke structure M, an rLTL formula \(\varphi \), and a set of truth values \(B\subseteq \mathbb {B}_4\), the rLTL model checking problem is to determine whether for all paths \(\pi \) starting from an initial state in M, it holds that \(V(\pi ,\varphi )\in B\). To solve the rLTL model checking, Tabuada and Neider [17] have provided an algorithm to compute a generalized Büchi automaton (see Grädel et al. [10] for definition) recognizing all paths satisfying a given formula with a value \(b\in B\) for a given set \(B\subseteq \mathbb {B}_4\), as formalized below.
Lemma 2
(Tabuada and Neider [17]). Given an rLTL formula \(\varphi \), and a set of truth values \(B\subseteq \mathbb {B}_4\), one can construct a generalized Büchi automaton \(A_{\varphi ,B}\) with \(\mathcal {O}(5^{|\varphi |})\) states and \(\mathcal {O}(|\varphi |)\) accepting sets that recognizes all paths \(\pi \) such that \(V(\pi ,\varphi ) \in B\).
Then, one can solve the rLTL model checking problem by translating M into a Büchi automaton and determining the emptiness of \(L(M)\cap L(A_{\varphi ,\mathbb {B}_4\setminus B})\).
Coming back to computing \(\mathrm {Sat}(\varPhi ,b)\) for \(\varPhi \) starting with a path quantifier, let us consider \(\varPhi = \forall \varphi \). Observe that \(s\in \mathrm {Sat}(\forall \varphi ,b)\) if and only if \(V(s,\forall \varphi )\ge b\). Further, \(V(s,\forall \varphi )\ge b\) if and only if \(V(\pi ,\varphi )\ge b \text { for all }\pi \in \mathrm {paths}(s)\). The basic idea is now to replace all maximal proper state subformulas \(\varPsi \) of \(\varphi \) by fresh atomic propositions \(a_{\varPsi }\) and use the rLTL model checking algorithm to compute all the states from which all paths satisfy the rLTL formula \(\varphi \) with value at least b. However, we need to make a minor modification in the construction of the Büchi automaton of Lemma 2 such that for each \(a_{\varPsi }\), it holds that \(V(s,a_{\varPsi }) \ge b\) whenever \(s\in \mathrm {Sat}(\varPsi ,b)\) and \(V(s,a_{\varPsi }) < b\) whenever \(s\not \in \mathrm {Sat}(\varPsi ,b)\). This can be done by initializing these atomic propositions with the required truth value.
Similarly, we compute \(\mathrm {Sat}(\exists \varphi ,b)\) by the rLTL model checking algorithm using the observation that \(s\not \in \mathrm {Sat}(\exists \varphi ,b)\) if and only if \(V(\pi ,\varphi )< b \text { for all }\pi \in \mathrm {paths}(s)\).
Now, one can solve the rCTL* model checking problem using Algorithm 1. However, the time complexity of the algorithm is not the same as in rCTL since the computation of \(\mathrm {Sat}\) uses the rLTL model checking algorithm, which takes exponential time in the size of the formula (Tabuada and Neider [17]). Hence, the time complexity of the rCTL* model checking algorithm is dominated by the time complexity of the rLTL model checking algorithm.
Altogether, our algorithm runs in polynomial space (as rLTL model checking is in \(\mathrm {PSPACE}\) [17]). A matching lower bound already holds for CTL* [7].
Theorem 8
The rCTL* model checking problem is \(\mathrm {PSPACE}\)-complete.
As we know, CTL* model checking problem is also \(\mathrm {PSPACE}\)-complete [7]. Hence, both CTL* and rCTL* model checking problems have the same asymptotic complexity.
4.3 rCTL* Satisfiability
This section considers the satisfiability problem for rCTL*, which is: for a given rCTL* formula \(\varPhi \) and truth value \(b_0\in \mathbb {B}_4\), does there exist a Kripke structure \(M = (S,I,R,L)\) such that \(I\subseteq \mathrm {Sat}(\varPhi ,b_0)\)? One can solve rCTL* satisfiability by translating the given rCTL* formula and the truth value into an equivalent CTL* formula using Theorem 7 and then solving CTL* satisfiability. Since CTL* satisfiability is \(\mathrm {2EXPTIME}\)-complete, so is rCTL* satisfiability.
Theorem 9
The satisfiability problem for rCTL* is \(\mathrm {2EXPTIME}\)-complete.
5 Conclusion
Inspired by robust LTL, we first developed robust extensions of the logics CTL and CTL*, named rCTL and rCTL*, respectively. Second, we showed that rCTL is more expressive than CTL, while rCTL* is as expressive as CTL*. Third, we showed that the rCTL and rCTL* model checking problem lie in \(\mathrm {PTIME}\) and \(\mathrm {PSPACE}\), respectively, as do the CTL and CTL* model checking problem.
Tabuada and Neider [17] described quality as the dual of robustness. To illustrate this point, consider the CTL formula \(\Diamond \varPhi \Rightarrow \Diamond \varPsi \). According to the motto “more is better” we would prefer the system to guarantee the stronger property \(\Box \Diamond \varPsi \) whenever the environment satisfies the stronger property \(\Box \Diamond \varPsi \). And similarly, \(\Diamond \Box \varPhi \) should lead to \(\Diamond \Box \varPsi \) and \(\Box \varPhi \) should lead to \(\Box \varPsi \). Then, a natural question that arises for further research is whether there is an extension of CTL (and CTL*) that can be used to reason about both robustness and quality.
Another promising direction is to study the synthesis problem for rCTL and rCTL*. One approach would be to extend bounded synthesis (see Schewe and Finkbeiner [8] for details) to rCTL*.
Notes
- 1.
The set of subformulas is defined as for CTL. See Baier and Katoen [1] for details.
References
Baier, C., Katoen, J.: Principles of Model Checking. MIT Press (2008)
Bloem, R., Greimel, K., Henzinger, T.A., Jobstmann, B.: Synthesizing robust systems. In: Proceedings of 9th International Conference on Formal Methods in Computer-Aided Design, FMCAD 2009, 15–18 November 2009, Austin, Texas, USA, pp. 85–92. IEEE (2009). https://doi.org/10.1109/FMCAD.2009.5351139
Bradfield, J., Walukiewicz, I.: The mu-calculus and model checking. In: Clarke, E., Henzinger, T., Veith, H., Bloem, R. (eds.) Handbook of Model Checking, pp. 871–919. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-10575-8_26
Doyen, L., Henzinger, T.A., Legay, A., Nickovic, D.: Robustness of sequential circuits. In: Gomes, L., Khomenko, V., Fernandes, J.M. (eds.) 10th International Conference on Application of Concurrency to System Design, ACSD 2010, Braga, Portugal, 21–25 June 2010, pp. 77–84. IEEE Computer Society (2010). https://doi.org/10.1109/ACSD.2010.26
Ehlers, R., Topcu, U.: Resilience to intermittent assumption violations in reactive synthesis. In: Fränzle, M., Lygeros, J. (eds.) 17th International Conference on Hybrid Systems: Computation and Control (Part of CPS Week), HSCC 2014, Berlin, Germany, 15–17 April 2014, pp. 203–212. ACM (2014). https://doi.org/10.1145/2562059.2562128
Emerson, E.A., Halpern, J.Y.: Decision procedures and expressiveness in the temporal logic of branching time. J. Comput. Syst. Sci. 30(1), 1–24 (1985). https://doi.org/10.1016/0022-0000(85)90001-7
Emerson, E.A., Lei, C.: Modalities for model checking: branching time logic strikes back. Sci. Comput. Program. 8(3), 275–306 (1987). https://doi.org/10.1016/0167-6423(87)90036-0
Finkbeiner, B., Schewe, S.: Bounded synthesis. Int. J. Softw. Tools Technol. Transf. 15(5–6), 519–539 (2013). https://doi.org/10.1007/s10009-012-0228-z
French, T., McCabe-Dansted, J.C., Reynolds, M.: A temporal logic of robustness. In: Konev, B., Wolter, F. (eds.) Frontiers of Combining Systems, 6th International Symposium, FroCoS 2007, Liverpool, UK, 10–12 September 2007, Proceedings. Lecture Notes in Computer Science, vol. 4720, pp. 193–205. Springer (2007). https://doi.org/10.1007/978-3-540-74621-8_13
Grädel, E., Thomas, W., Wilke, T. (eds.): Automata, Logics, and Infinite Games: A Guide to Current Research [outcome of a Dagstuhl seminar, February 2001], Lecture Notes in Computer Science, vol. 2500. Springer (2002). https://doi.org/10.1007/3-540-36387-4
Hájek, P.: Metamathematics of Fuzzy Logic, Trends in Logic, vol. 4. Kluwer (1998). https://doi.org/10.1007/978-94-011-5300-3
Nayak, S.P., Neider, D., Roy, R., Zimmermann, M.: Robust computation tree logic. arXiv 2201.07116 (2022), https://arxiv.org/abs/2201.07116
Neider, D., Weinert, A., Zimmermann, M.: Robust, expressive, and quantitative linear temporal logics: pick any two for free. In: Leroux, J., Raskin, J. (eds.) Proceedings Tenth International Symposium on Games, Automata, Logics, and Formal Verification, GandALF 2019, Bordeaux, France, 2–3rd September 2019. EPTCS, vol. 305, pp. 1–16 (2019). https://doi.org/10.4204/EPTCS.305.1
Priest, G.: Dualising intuitionictic negation. Principia: Int. J. Epistemol. 13(2), 165–184 (2009). https://doi.org/10.5007/1808-1711.2009v13n2p165
Tabuada, P., Balkan, A., Caliskan, S.Y., Shoukry, Y., Majumdar, R.: Input-output robustness for discrete systems. In: Jerraya, A., Carloni, L.P., Maraninchi, F., Regehr, J. (eds.) Proceedings of the 12th International Conference on Embedded Software, EMSOFT 2012, part of the Eighth Embedded Systems Week, ESWeek 2012, Tampere, Finland, 7–12 October 2012, pp. 217–226. ACM (2012). https://doi.org/10.1145/2380356.2380396
Tabuada, P., Caliskan, S.Y., Rungger, M., Majumdar, R.: Towards robustness for cyber-physical systems. IEEE Trans. Autom. Control 59(12), 3151–3163 (2014). https://doi.org/10.1109/TAC.2014.2351632
Tabuada, P., Neider, D.: Robust linear temporal logic. In: Talbot, J., Regnier, L. (eds.) 25th EACSL Annual Conference on Computer Science Logic, CSL 2016, August 29 - September 1, 2016, Marseille, France. LIPIcs, vol. 62, pp. 10:1–10:21. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2016). https://doi.org/10.4230/LIPIcs.CSL.2016.10
Tarraf, D.C., Megretski, A., Dahleh, M.A.: A framework for robust stability of systems over finite alphabets. IEEE Trans. Autom. Control 53(5), 1133–1146 (2008). https://doi.org/10.1109/TAC.2008.923658
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this paper
Cite this paper
Nayak, S.P., Neider, D., Roy, R., Zimmermann, M. (2022). Robust Computation Tree Logic. In: Deshmukh, J.V., Havelund, K., Perez, I. (eds) NASA Formal Methods. NFM 2022. Lecture Notes in Computer Science, vol 13260. Springer, Cham. https://doi.org/10.1007/978-3-031-06773-0_29
Download citation
DOI: https://doi.org/10.1007/978-3-031-06773-0_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-06772-3
Online ISBN: 978-3-031-06773-0
eBook Packages: Computer ScienceComputer Science (R0)





 , i.e., the robot eventually should be able to return to its initial location from any point;
, i.e., the robot eventually should be able to return to its initial location from any point; (or
(or  , respectively).
, respectively).


 where
where  evaluates to 1111. Then by the semantics of
evaluates to 1111. Then by the semantics of  also must evaluate to 1111. That means, in any path,
also must evaluate to 1111. That means, in any path,  evaluates to 0111. Then, by the rCTL semantics,
evaluates to 0111. Then, by the rCTL semantics,  evaluates to 0111 or higher. Hence, in any path,
evaluates to 0111 or higher. Hence, in any path, 


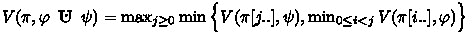
 where
where  evaluates to 1111. Hence, by the rCTL* semantics,
evaluates to 1111. Hence, by the rCTL* semantics,  must also evaluate to 1111. That means,
must also evaluate to 1111. That means,  evaluates to 0111. Then, by the rCTL* semantics,
evaluates to 0111. Then, by the rCTL* semantics,  evaluates to 0111 or higher. Hence,
evaluates to 0111 or higher. Hence, 