Abstract
In this paper, we examine the synthesis problem from a finite labeled transition system when the target is the class of weighted nets with (possibly) inhibitor and/or reset links, or some subclasses of them. We also discuss the intrinsic complexity of some cases; in particular we show that although some subclasses have a polynomial synthesis, most of the time it is NP-complete.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
In order to validate a system, instead of analyzing a model of the latter to check if it satisfies a set of desired properties, the synthesis approach tries to build a model “correct by construction” directly from those properties, and then to implement it. In particular, if the behavior of a system is specified by a finite labeled transition system (LTS for short), more or less efficient algorithms have been developed to build a bounded weighted Petri net with a reachability graph isomorphic to (or close to) the given LTS [3, 23]. It is also possible to target some subclasses of Petri nets [8], in particular choice-free nets and some of their specializations [7, 9, 10, 15] which present interesting features.
On the contrary, in order to extend a bit the power of the technique (it may happen that no net of the chosen subclass has an adequate behavior, even for the full class of weighted Petri nets), we may consider superclasses of the classic Petri net subclasses. For instance, in [16], one of us used (weighted) reset arcs. Here, we shall allow both weighted inhibitor and reset arcs, as well as some subcases. Since the analysis of such systems is a bit delicate (some properties even become undecidable [17]), this increases the interest to avoid analysis techniques in favor of synthesis ones.
Petri net synthesis has numerous practical applications, for example, in the field of process discovery to reconstruct a model from its execution traces [1], in supervisory control for discrete event systems [22], and in the design and synthesis of speed-independent circuits [13]. Usually, the synthesized system yields a structural model much smaller than the initial behavioral specification, and allows to build concrete implementations. Moreover, it allows to extract informations about concurrency and distributability features from the sequential behavior given by an LTS [5].
The paper is organized as follows. After recalling some basic notions on labeled transition systems and Petri nets, we present an extension of the latter, allowing general inhibitor and reset links. In the next section, we explain how to extend the classical regional approach to synthesize such a net, or a subclass of them, when possible, from a finite transition system. Then, we explain how to characterize the inherent complexity of a synthesis problem, and we delineate a new target class for which the synthesis is polynomial. In Sect. 4.4, we present two (pure) target classes for which the synthesis is NP-complete, and in the next section, we do the same with impure strict reset nets. The last section, as usual, concludes and presents some possible follow up.
2 Preliminaries
Definition 1
Transition System
A (deterministic) labeled transition system (LTS, for short) \(A=(S,E, \delta ,\iota )\) consists of two disjoint sets of states S and events E, a partial transition function \(\delta : S\times E \longrightarrow S\) and an initial state \(\iota \in S\). An event e occurs at state s, denoted by  , if \(\delta (s,e)\) is defined. By
, if \(\delta (s,e)\) is defined. By  we denote that \(\delta (s,e)\) is not defined. We abridge \(\delta (s,e)=s'\) by
we denote that \(\delta (s,e)\) is not defined. We abridge \(\delta (s,e)=s'\) by  and call the latter an edge with source s and target \(s'\). By
and call the latter an edge with source s and target \(s'\). By  , we denote that the edge
, we denote that the edge  is present in A.
is present in A.
A sequence  of edges is called a (directed labeled) path (from \(s_0\) to \(s_n\) in A). A is called reachable, if there is a path from \(\iota \) to s for every state \(s\in S\).
of edges is called a (directed labeled) path (from \(s_0\) to \(s_n\) in A). A is called reachable, if there is a path from \(\iota \) to s for every state \(s\in S\).
Two LTS \(A_1=(S_1,E,\delta _1,\iota _{1})\) and \(A_2=(S_2,E,\delta _2,\iota _{2})\) are isomorphic if there is a bijection \(\zeta :S_1\rightarrow S_2\) such that \(\zeta (\iota _1)=\iota _2\) and \(\delta _1(s,e)=s'\) if and only if \(\delta _2(\zeta (s), e)=\zeta (s')\) for all \(s, s'\in S_1\) and all \(e\in E\).
An LTS \(A=(S,E, \delta ,\iota )\) is finite if so are S and E. \(\square \) 1
If an LTS A is not explicitly defined, then we refer to its components by S(A) (states), E(A) (events), \(\delta _A\) (function), \(\iota _A\) (initial state). In this paper, we investigate whether a LTS corresponds to the reachability graph of a Petri net. There are various ways to present a Petri net or an extension thereof; here we chose a link oriented one, in order to make the definition of (weighted) arcs more uniform:
Definition 2
Inhibitor-Reset Petri Net: Specification and Semantics
An inhibitor-reset Petri net (IRPN, for short) \(N=(P,T,f,\mathfrak {m}_0)\) consists of finite and disjoint sets of places P and transitions T, a (total) flow function \(f: P \times T \rightarrow \mathbb {N}\times \mathbb {N}\times \{\textsf {classic},\textsf {inhibitor},\textsf {reset}\}\) and an initial marking \(\mathfrak {m}_0: P \rightarrow \mathbb {N}\). A link \((m,n,\textsf {type})\) will be said pure if \(m\cdot n=0\); it is k-limited (for some predefined \(k\in \mathbb {N}\)) if \(m,n\le k\); it is plain if it is 1-limited; it is strict if it is 0-limitedFootnote 1.
A transition \(t\in T\) can fire or occur in a marking \(\mathfrak {m}:P\rightarrow \mathbb {N}\), denoted by  , and this firing leads to the marking \(\mathfrak {m}'\), denoted by
, and this firing leads to the marking \(\mathfrak {m}'\), denoted by  , if, for all places \(p\in P\), \(f(p,t)=(m,n,\textsf {type})\) and
, if, for all places \(p\in P\), \(f(p,t)=(m,n,\textsf {type})\) and
-
1.
if \(\textsf {type}=\textsf {classic}\), then \(\mathfrak {m}(p)\ge m\) and \(\mathfrak {m}'(p)=\mathfrak {m}(p)-m+n\);
-
2.
if \(\textsf {type}=\textsf {inhibitor}\), then \(\mathfrak {m}(p)\le m\) and \(\mathfrak {m}'(p)=n\);
-
3.
if \(\textsf {type}=\textsf {reset}\), then \(\mathfrak {m}(p)\ge m\) and \(\mathfrak {m}'(p)=n\).
This notation extends to sequences \(w \in T^*\) and the reachability set  contains all the reachable markings of N. The reachability graph of N is the LTS \(A_N=(RS(N), T,\delta , \mathfrak {m}_0)\), where, for every reachable marking \(\mathfrak {m}\) of N and transition \(t \in T\) with
contains all the reachable markings of N. The reachability graph of N is the LTS \(A_N=(RS(N), T,\delta , \mathfrak {m}_0)\), where, for every reachable marking \(\mathfrak {m}\) of N and transition \(t \in T\) with  , the transition function \(\delta \) of \(A_N\) is defined by \(\delta (\mathfrak {m},t) = \mathfrak {m}'\). Two IRPNs are equivalent if their reachability graphs are isomorphic.
, the transition function \(\delta \) of \(A_N\) is defined by \(\delta (\mathfrak {m},t) = \mathfrak {m}'\). Two IRPNs are equivalent if their reachability graphs are isomorphic.
A place in N is said k-safe (for some predefined \(k\in \mathbb {N}\)) if, for each reachable marking \(\mathfrak {m}\), \(\mathfrak {m}(p)\le k\); it is safe if it is 1-safe; it is bounded if it is k-safe for some k not defined a priori. An IRPN N is k-safe\(\mid \)safe\(\mid \)bounded if so are all its places. \(\square \) 2
A classic (and easy) result for classic Petri nets immediately extends to IRPNs:
Corollary 1
Bounded system
An IRPN N is bounded if and only if its reachability graph \(A_N\) is finite.
\(\square \) 1
Many subclasses of nets may be defined from this definition. For instance,
Definition 3
Subclasses of Nets
An IRPN \(N=(P,T,f,\mathfrak {m}_0)\) is called
-
a strict inhibitor reset (Petri) net, denoted by SIRPN, if each link is either classic or strict reset or strict inhibitor;
-
a (strict) inhibitor (Petri) net, denoted by (S)IPN, if each link is either classic or (strict) inhibitor;
-
a (strict) reset (Petri) net, denoted by (S)RPN, if each link is either classic or (strict) reset;
-
a (Petri) net, denoted by PN, if all the links are classic;
-
pure if so are all the links (note that strict inhibitor and reset links are automatically pure);
-
plain if so are all the links (note that strict inhibitor and reset links are automatically plain).
\(\square \) 3
Graphically, the various kinds of links are represented as illustrated in Fig. 1, with the convention that arcs with zero weight are omitted.
3 Synthesis
Instead of analyzing a system and (try to) go from a system specification to its behavior (for instance given by the reachability graph), we may go the other way round:
Definition 4
Synthesis
Let \(A=(S,E,\delta , \iota )\) be an LTS. An IRPN N synthesizes A if its reachability graph is isomorphic to A. We then say that N solves A. \(\square \) 4
Synthesis is not exactly the symmetric of analysis, however. Indeed, while a system always has a unique behavior (given by its reachability graph), it may happen that a synthesis fails (then it is interesting to exhibit one or more sources of the failure), and if it is possible, there are infinitely many (behaviorally equivalent) solutions, sometimes with very different structures.
In the following, we shall always assume that the transition system A we start from is finite, so that it may be given explicitly and drawn easily (if not too large), and its synthesis solutions are bounded (see Corollary 1).
Classically [3], synthesis algorithms are related to the construction of regions, that we shall here adapt to our context:
Definition 5
IRPN-Region
Let \(A=(S,E,\delta , \iota )\) be a LTS. A pair of mappings \(R=(sup, sig)\) that consists of the support \(sup:S\rightarrow \mathbb {N}\) and the signature \(sig:E\rightarrow \mathbb {N}\times \mathbb {N}\times \{\textsf {classic},\textsf {inhibitor},\textsf {reset}\}\) is called a (IRPN-)region of A if, when \(\delta (s,e)=s'\), then the following conditions are satisfied:
-
1.
if \(sig(e)=(m,n,\textsf {classic})\), then \(sup(s)\ge m\) and \(sup(s')=sup(s)-m+n\);
-
2.
if \(sig(e)=(m,n,\textsf {inhibitor}\)), then \(sup(s)\le m\) and \(sup(s')=n\);
-
3.
if \(sig(e)=(m,n,\textsf {reset})\), then \(sup(s)\ge m\) and \(sup(s')=n\).
\(\square \) 5
Remark 1
Regions and Places
Intuitively, a region corresponds to a place in an IRPN solving A: sup yields the markings of that place corresponding to the various states of A (hence the initial marking is provided by \(sup(\iota )\)), and sig yields the links between that place and the various transitions (E(A) must be the same as the set T of transitions of any solution of A).
For convenience, for all \(e\in E(A)\), if \(sig(e)=(m,n,\textsf {type})\), then we define \(sig^-(e)=m\), \(sig^+(e)=n\) and \(sig^t=\textsf {type}\). \(\square \) 1
Remark 2
Construction of the Support
If \(R=(sup, sig)\) is a region of an LTS \(A=(S,E,\delta ,\iota )\), then we can reconstruct R already from \(sup(\iota )\) and sig, since every state s of A is reachable by a directed labeled path from \(\iota \): If  with \(s_0=\iota \) and \(s_n=s\), then, for all \(i\in \{0,\dots , n-1\}\), we get inductively \(sup(s_{i+1})\) from \(sup(s_i)\) and \(sig(e_{i+1})\). Hence, for the sake of simplicity, we shall often present a region \(R=(sup, sig)\) only by \(sup(\iota )\) and sig (it is necessary however to check that two different paths leading from \(\iota \) to the same state s yield the same support sup(s), and that the latter is always nonnegative). For an even more compact representation, we shall summarize events with the same signature as follows: \(\mathcal {E}_{m,n}^R=\{e\in E \mid sig(e)=(m,n,\textsf {classic})\}\), and \(\mathcal {E}_{\textsf {inhibitor}}^R=\{e\in E \mid sig(e)=(0,0,\textsf {inhibitor})\}\), and \(\mathcal {E}_{\textsf {reset}}^R=\{e\in E \mid sig(e)=(0,0,\textsf {reset})\}\). \(\square \) 2
with \(s_0=\iota \) and \(s_n=s\), then, for all \(i\in \{0,\dots , n-1\}\), we get inductively \(sup(s_{i+1})\) from \(sup(s_i)\) and \(sig(e_{i+1})\). Hence, for the sake of simplicity, we shall often present a region \(R=(sup, sig)\) only by \(sup(\iota )\) and sig (it is necessary however to check that two different paths leading from \(\iota \) to the same state s yield the same support sup(s), and that the latter is always nonnegative). For an even more compact representation, we shall summarize events with the same signature as follows: \(\mathcal {E}_{m,n}^R=\{e\in E \mid sig(e)=(m,n,\textsf {classic})\}\), and \(\mathcal {E}_{\textsf {inhibitor}}^R=\{e\in E \mid sig(e)=(0,0,\textsf {inhibitor})\}\), and \(\mathcal {E}_{\textsf {reset}}^R=\{e\in E \mid sig(e)=(0,0,\textsf {reset})\}\). \(\square \) 2
Definition 6
Synthesized Net
If \(A=(S,E,\delta ,\iota )\) is an LTS and \(\mathcal {R}\) a set of regions of A, then the synthesized net \(N_A^\mathcal {R}\) is defined by \(S_A^\mathcal {R}=(\mathcal {R}, E, f, \mathfrak {m}_0)\) such that \(f(e,R)=sig(e)\), and \(\mathfrak {m}_0(R)=sup(\iota )\) for all \(R=(sup, sig)\in \mathcal {R}\). \(\square \) 6
Definition 7
State Separation Property
Two distinct states \(s,s'\in S\) define the state separation atom, SSA for short, \((s,s')\) of an LTS \(A=(S,E,\delta ,\iota )\). A region \(R=(sup, sig)\) of A solves \((s,s')\) (equivalently: separates s and \(s'\)) if \(sup(s)\not =sup(s')\). A state \(s\in S\) is called solvable if, for every \(s'\in S\setminus \{s\}\), there is a region of A that solves the SSA \((s,s')\). If every state of A is solvable, then A has the state separation property, SSP for short. \(\square \) 7
Definition 8
Event State Separation Property
An event \(e\in E\) and a state \(s\in S\) of an LTS \(A=(S,E,\delta ,\iota )\) such that  define the event state separation atom, ESSA for short, (e, s) of A. A region \(R=(sup, sig)\) of A solves (e, s) (equivalently: separates e from s) if \(sig^-(e)>sup(s)\) when \(sig^t(e)=\textsf {classic} \text{ or } \textsf {reset}\) and \(sig^-(e)<sup(s)\) when \(sig^t(e)=\textsf {inhibitor}\). An event \(e\in E\) is called solvable if, for every state \(s\in S\) such that
define the event state separation atom, ESSA for short, (e, s) of A. A region \(R=(sup, sig)\) of A solves (e, s) (equivalently: separates e from s) if \(sig^-(e)>sup(s)\) when \(sig^t(e)=\textsf {classic} \text{ or } \textsf {reset}\) and \(sig^-(e)<sup(s)\) when \(sig^t(e)=\textsf {inhibitor}\). An event \(e\in E\) is called solvable if, for every state \(s\in S\) such that  , there is a region of A that solves the ESSA (e, s). If all events of A are solvable, then A has the event state separation property, ESSP for short. \(\square \) 8
, there is a region of A that solves the ESSA (e, s). If all events of A are solvable, then A has the event state separation property, ESSP for short. \(\square \) 8
Definition 9
Admissible Set
Let \(A=(S,E,\delta , \iota )\) be an LTS. A set \(\mathcal {R}\) of regions of A is called an admissible set if it witnesses the SSP and the ESSP of A, i. e., for every SSA, and for every ESSA of A, there is a region in \(\mathcal {R}\) that solves it. \(\square \) 9
The fundamental characterization [3, 14] of synthesizability for classic Petri nets extends immediately to IRPNs:
Theorem 1
Solvability of an LTS
Let \(A=(S,E,\delta , \iota )\) be an LTS. A is solvable by an IRPN if and only if there is an admissible set \(\mathcal {R}\) of (IRPN-)regions for A, and a possible solution is then \(N=N^\mathcal {R}_A\). \(\square \) 1
Above, we assumed that the target of a synthesis is the whole set of IRPNs, but it is easy to adapt the discussion to the case where the target is one of the subclasses mentioned in the previous section (or an intersection of them). One simply has to add some constraints to the definition of regions to be considered for the considered LTS:
Definition 10
Subclasses of Regions
A region \(R=(sup, sig)\) of an LTS \(A=(S,E, \delta , \iota )\) is called
-
an SIRPN-region if \(sig(e)=(m,n,\textsf {type})\) and \(\textsf {type}\in \{\textsf {inhibitor}, \textsf {reset}\}\) imply \(m=n=0\) for all \(e\in E\);
-
an (S)IPN-region if \(sig^t(e)\in \{\textsf {classic}, \textsf {inhibitor}\}\) for all \(e\in E\) (and \(sig(e)=(m,n,\textsf {inhibitor})\) implies \(m=n=0\) for all \(e\in E\));
-
an (S)RPN-region if \(sig^t(e)\in \{\textsf {classic}, \textsf {reset}\}\) for all \(e\in E\) (and \(sig(e)=(m,n,\textsf {reset})\) implies \(m=n=0\) for all \(e\in E\));
-
a PN-region if \(sig^t(e)=\textsf {classic}\) for all \(e\in E\);
-
a k-safe region, if \(sup(s)\le k\) for each \(s\in S\) (with \(k=1\) for safeness);
-
a pure region, if \(sig^-(e)=0\) or \(sig^+(e)=0\) for each \(e\in E\);
-
a k-limited region if \(sig^-(e),sig^+(e)\le k\) for each \(e\in E\) (with \(k=1\) for plainness),
where the meaning of the acronyms correspond to Definition 3. \(\square \) 10
Then, if we want to restrict our attention to the synthesis of, for example, plain (S)RPNs, we have to look for an admissible set of plain (S)RPN-regions, according to Theorem 1. In the obvious way, we use the corresponding restricted regions for the other net classes (and combinations thereof).
All those separation problems (with possibly additional constraints) may be solved by existing (integer) linear programming tools or SMT-based model checking, but it is necessary to first choose adequately the type of each link. Note however that it is not necessary to solve each separation problem from scratch: we may first check if one of the regions computed previously does not already solve the new separation problem we consider. The result will of course rely on the order in which the various separation problems are considered (besides the fact that each separation problem may sometimes have many possible solutions).
It is possible to also search for solutions with a minimal number of places/regions.
4 Complexity
4.1 Membership in NP
Concerning the inherent complexity of the IRPN synthesis, we may first observe that it is in NP:
Theorem 2
NP-synthesis
Let \(A=(S,E,\delta , \iota )\) be an LTS. Its IRPN solvability is in NP.
Proof: The number of ESSAs and SSAs to be solved is (quadratic, hence) polynomial in the size of A. For each of them, a Turing machine can guess non-deterministically the type of the signature of the events, for instance: \(e_{i_1},\dots , e_{i_p}\) are of type \(\textsf {classic}\), \(e_{j_1},\dots , e_{j_q}\) are of type \(\textsf {inhibitor}\), and \(e_{\ell _1},\dots , e_{\ell _r}\) are of type \(\textsf {reset}\). Then, finding an adequate region amounts to solve a system (of polynomial size) of linear constraints in the integer domain, as follows:
There are \(\vert S \vert +2\cdot \vert E\vert \) variables \(x_i\), where \(sup(s_i)=x_i\) for all \(i\in \{1,\dots , \vert S\vert \}\), while \(sig^-(e_i)=x_{\vert S\vert +i}\), and \(sig^+(e_i)=x_{\vert S\vert +\vert E\vert + i}\) for all \(i\in \{1,\dots , \vert E\vert \}\); the constraints are then
-
1.
For all \(i\in \{1,\dots , \vert S\vert +2\cdot \vert E\vert \}\): add \(x_i\ge 0\) (all variables are in \(\mathbb {N}\))
-
2.
For all \(n\in \{1,\dots , p\}\), and all \(i,j\in \{1,\dots , \vert S\vert \}\), if
 , then add
, then add -
(a)
\(x_i - x_{\vert S\vert +i_n}\ge 0\), which ensures \(sup(s_i)\ge sig^-(e_{i_n})\), and
-
(b)
\(x_j - x_i + x_{\vert S\vert +i_n} - x_{\vert S\vert + \vert E\vert + i_n} =0\), which ensures \(sup(s_j)=sup(s_i)-sig^-(e_{i_n})+sig^+(e_{i_n})\).
-
(a)
-
3.
For all \(n\in \{1,\dots , q\}\), and all \(i,j\in \{1,\dots , \vert S\vert \}\), if
 , then add
, then add -
(a)
\(x_i - x_{\vert S\vert +j_n} \le 0\), which this ensures \(sup(s_i)\le sig^-(e_{j_n})\), and
-
(b)
\(x_j - x_{\vert S\vert + \vert E\vert + j_n} =0\), this ensures \(sup(s_j)=sig^+(e_{j_n})\).
-
(a)
-
4.
For all \(n\in \{1,\dots , r\}\), and all \(i,j\in \{1,\dots , \vert S\vert \}\), if
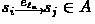 , then add
, then add -
(a)
\(x_i - x_{\vert S\vert +\ell _n} \ge 0\), which ensures \(sup(s_i)\ge sig^-(e_{\ell _n})\), and
-
(b)
\(x_j - x_{\vert S\vert + \vert E\vert + \ell _n} =0\), this ensures \(sup(s_j)=sig^+(e_{\ell _n})\).
-
(a)
-
5.
In order to solve \(\alpha =(s_f,e_g)\), add \(x_f - x_{\vert S\vert + g}\le -1\), which ensures \(sup(s_f) < sig^{-}(e_g)\), if \(e_g\) corresponds to the types \(\textsf {classic}\) or \(\textsf {reset}\), and \(x_{\vert S\vert + g} - x_f \le -1\), which ensures \(sup(s_f) > sig^{-}(e_g)\), if \(e_g\) corresponds to \(\textsf {inhibitor}\).
-
6.
In order to solve \(\alpha =(s_i,s_j)\), create two systems, one where we add \(x_i-x_j\le -1\) and one where we add \(x_j-x_i\le -1\), which ensures \(sup(s_i)\ne sup(s_j)\).
-
7.
Other constraints may be added to restrict the target class; for instance, for all \(i\in \{1,\dots , \vert S\vert \}\): add \(x_i\le k\) if we aim at synthesizing a k-safe net; for all \(i\in \{1,\dots , \vert E\vert \}\): add \(x_{|S|+i}\le k\) and \(x_{|S|+|E|+i}\le k\) if we aim at synthesizing a k-limited net.
Solving such a system may be assimilated to an integer linear programming problem (without an economic function to optimize, or with a null economic function) (ILP for short), and it is known that ILP belongs to NP [20]. \(\square \) 2
4.2 Polynomial Cases
In the procedure described in the previous section to solve a separation property, we first have to fix the type of link for each transition: this is generally exponential, hence we may suspect that (in most cases) the synthesis problem is NP-complete [19]. There are cases however where it is polynomial in the size of the transition system to be solved. For instance, this was shown [3] when the target is the class of classic Petri nets without additional constraints (essentially, in that case, there is no choice to make for the link types and one has to solve a system of homogeneous linear constraints of linear size; one can solve it polynomially in the rational range and then multiply all the found variables by some common factor to get an integer solution, if there is one). The same is true when the target is the class of pure classic Petri nets without additional constraints [4], using slightly different regions.
But there are other interesting cases; for instance we shall now show that the synthesis remains polynomial when the target is the class of strict inhibitor nets (without additional constraints). To do that, we shall first introduce complementary places.
Lemma 1
Complementary Place
Let \(N=(P,T,f,\mathfrak {m}_0)\) be an IRPN and \(p\in P\) a place in it bounded by some value \(k\in \mathbb {N}\) (i.e., for any reachable marking \(\mathfrak {m}\), \(\mathfrak {m}(p)\le k\)). Let also \(l=max_{t\in T}\{n\mid f(p,t))=(m,n,\textsf {classic})\}\), \(h=max_{t\in T}\{m,n\mid f(p,t))=(m,n,\textsf {type}) \text{ and } \textsf {type}\ne \textsf {classic}\}\) and \(\mu =\max \{k+l,h\}\). Let \(\widehat{N}\) be the net obtained from N by introducing a fresh place \(\widehat{p}\) (the complementary of p) with initial marking \(\mu -\mathfrak {m}_0(p)\) and such that, for each \(t\in T\), the link between \(\widehat{p}\) and t is built as illustrated in Fig. 2. Then \(\widehat{N}\) and N are behaviorally equivalent and, for each marking \(\widehat{\mathfrak {m}}\) reached in \(\widehat{N}\), \(\widehat{\mathfrak {m}}(p)+\widehat{\mathfrak {m}}(\widehat{p})=\mu \) (and is thus constant).
Proof: Since \(\widehat{N}\) has one place more than N, and the initial marking of \(\widehat{N}\) is the same as N when restricted to P, any evolution of \(\widehat{N}\) is also one of N, and the restriction to P of the reached marking in \(\widehat{N}\) is the marking reached with the same evolution in N.
If \(\mathfrak {m}\) is a marking reachable in N, from the choice of \(\mu \) we have \(\mu -\mathfrak {m}(p)\ge 0\), and if \(\widehat{\mathfrak {m}}\) is the marking in \(\widehat{N}\) obtained by adding to \(\mathfrak {m}\) that \(\widehat{\mathfrak {m}}(\widehat{p})=\mu -\mathfrak {m}(p)\), it may be observed that for any transition \(t\in T\), if t is enabled by \(\mathfrak {m}\) in N, then it is also enabled by \(\widehat{\mathfrak {m}}\) in \(\widehat{N}\). Indeed, if \(\mathfrak {m}(p)\ge m\), then \(\mu -\mathfrak {m}(p)\le \mu -m\) (reset case), if \(\mathfrak {m}(p)\le m\), then \(\mu -\mathfrak {m}(p)\ge \mu -m\) (inhibitor case), and from the choice of \(\mu \) again \(\mu -\mathfrak {m}(p)\ge n\) (classic case). In any case, from the choice of \(\mu \) again, \(\mu -m\ge 0\) and \(\mu -n\ge 0\) when they are used. Moreover, if  in N, and
in N, and  in \(\widehat{N}\), it is easy to see that the restriction of \(\widehat{\mathfrak {m}}'\) to P is \(\mathfrak {m}'\), and \(\widehat{\mathfrak {m}}'(\widehat{p})=\mu -\mathfrak {m}'(p)\). Since initially (by construction), \(\widehat{\mathfrak {m}}_0(\widehat{p})=\mu -\mathfrak {m}_0(p)\), by induction we get that the evolutions are the same in N and \(\widehat{N}\). Moreover, if \(\mathfrak {m}\) is reached after some evolution in N, the marking \(\widehat{\mathfrak {m}}\) reached in \(\widehat{N}\) after the same evolution only differs from \(\mathfrak {m}\) by \(\widehat{\mathfrak {m}}(\widehat{p})=\mu -\mathfrak {m}(p)\).
in \(\widehat{N}\), it is easy to see that the restriction of \(\widehat{\mathfrak {m}}'\) to P is \(\mathfrak {m}'\), and \(\widehat{\mathfrak {m}}'(\widehat{p})=\mu -\mathfrak {m}'(p)\). Since initially (by construction), \(\widehat{\mathfrak {m}}_0(\widehat{p})=\mu -\mathfrak {m}_0(p)\), by induction we get that the evolutions are the same in N and \(\widehat{N}\). Moreover, if \(\mathfrak {m}\) is reached after some evolution in N, the marking \(\widehat{\mathfrak {m}}\) reached in \(\widehat{N}\) after the same evolution only differs from \(\mathfrak {m}\) by \(\widehat{\mathfrak {m}}(\widehat{p})=\mu -\mathfrak {m}(p)\).
Finally, from this property, if two evolutions lead to \(\mathfrak {m}_1\) and \(\mathfrak {m}_2\) in N, and the same evolutions lead to \(\widehat{\mathfrak {m}}_1\) and \(\widehat{\mathfrak {m}}_2\) in \(\widehat{N}\), then \(\mathfrak {m}_1=\mathfrak {m}_2\) if and only if \(\widehat{\mathfrak {m}}_1=\widehat{\mathfrak {m}}_2\). Consequently, we do not only have the same evolutions, but also the same reachability graph (up to isomorphism). \(\square \) 1
This exhibits an interesting relationship between inhibitor links and reset ones, but there is also a case where we have an even more interesting relationship between inhibitor links and classic ones.
Lemma 2
Complementary Place and Special Inhibitor Links
In the construction of Lemma 1, if the link between p and t in N is in \(\{0\}\times \mathbb {N}\times \{\textsf {inhibitor}\}\), then in \(\widehat{N}\) we may replace the links between t and \(\{p,\widehat{p}\}\) by classic ones, as illustrated in Fig. 3.
Proof: From the construction (and the analysis in the proof of Lemma 1), if \(\widehat{\mathfrak {m}}\) is reachable in \(\widehat{N}\) and  , since \(\widehat{\mathfrak {m}}(p)+\widehat{\mathfrak {m}}(\widehat{p})=\mu \), we must have \(\widehat{\mathfrak {m}}(\widehat{p})=\mu \) and \(\widehat{\mathfrak {m}}(p)=\mathfrak {m}(p)=0\), which indeed allows to fire t from \(\mathfrak {m}\) in N. The relationship between the resulting markings in both N and \(\widehat{N}\) is as before. \(\square \) 2
, since \(\widehat{\mathfrak {m}}(p)+\widehat{\mathfrak {m}}(\widehat{p})=\mu \), we must have \(\widehat{\mathfrak {m}}(\widehat{p})=\mu \) and \(\widehat{\mathfrak {m}}(p)=\mathfrak {m}(p)=0\), which indeed allows to fire t from \(\mathfrak {m}\) in N. The relationship between the resulting markings in both N and \(\widehat{N}\) is as before. \(\square \) 2
Corollary 2
Bounded IRPNs With Only Classic and Strongly Guarded Inhibitor Links are Behaviorally Equivalent to Classic Nets
If a bounded IRPN only has links in \(\mathbb {N}\times \mathbb {N}\times \{\textsf {classic}\}\cup \{0\}\times \mathbb {N}\times \{\textsf {inhibitor}\}\) (i.e., classic or strongly guarded inhibitor links, since m determines how the transition is guarded), then it is behaviorally equivalent to a (bounded) net with only classic links, i.e., a classic Petri net.
Proof: One simply has to apply Lemmata 1 and 2 to each place (or only to the ones having a non-classic link). \(\square \) 2
Corollary 3
Bounded SIPNs
Any bounded SIPN is behaviorally equivalent to a bounded net with only classic links, i.e., a classic Petri net.
\(\square \) 3
Theorem 3
Synthesis of SIPNs
The synthesis problem with the class of SIPNs as target is polynomial.
Proof: Since we only consider finite transition systems, when they have solutions, they are bounded. From Lemma 2, introducing strict inhibitor links does not extend the expressive power of classical links and we only have to search for solutions in the class of (bounded) weighted Petri nets, for which we mentioned before that the problem is polynomial. \(\square \) 3
Of course, this result relies on the fact that we consider general weighted Petri nets as target. It may be observed that Lemma 1 and its corollaries are not valid if we require that nets are pure or plain or k-safe. This certainly does not mean that there are no other efficient solvable cases. However, there are important subclasses of IRPNs for which we know they do not have efficient synthesis procedures (unless P = NP), such as (pure) safe SIPN, (pure) safe SRPN, safe SIRPN [24], and (pure) k-safe PN, for any fixed \(k\in \mathbb {N}\) [25]. In the following sections, we shall exhibit other NP-complete subclasses.
4.3 General Approach of the NP-completeness Proofs
In Sects. 4.4, and 4.5, we shall show that the synthesis problem for several subclasses of IRPNs is NP-complete. Our proofs for NP-completeness follow a common approach based on (polynomial) reductions of the problem 3Sat, which has been shown to be NP-complete in [19]:

It is based on the notion of clause, i.e., a set of literals, where a literal is either a Boolean variable or its negation; a clause is interpreted as a disjunction of its items; and a set of clauses is interpreted as their conjunction. A 3-clause is a clause of size 3 and, if \(X\in \mathfrak {U}\) is a variable, then we denote its negation by \(\overline{X}\).
Example 1
The instance \( (\mathfrak {U},M) \) with variables \( \mathfrak {U} =\{X_0,X_1,X_2,X_3\} \), and clauses \( M =\{M_0,M_1, M_2\}\) such that \(M_0=\{X_0,X_1,\overline{X_2}\}\), \(M_1=\{\overline{X_0},\overline{X_1},\overline{X_3}\}\), and \(M_2=\{\overline{X_1},X_2,X_3\}\) allows a positive decision, since \(b(X_0)=b(X_2)=0\), and \(b(X_1)=b(X_3)=1\) defines a truth assignment for M.
In the following, unless explicitly stated otherwise, \((\mathfrak {U}, M)\) is an arbitrary but fixed input of 3Sat, where \(\mathfrak {U}=\{X_0,\dots , X_{n-1}\}\), \(M=\{M_0,\dots , M_{m-1}\}\) and \(M_i=\{L_{i_0}, L_{i_1}, L_{i_2}\}\) for all \(i\in \{0,\dots , m-1\}\). By \(\mathcal {L}=\bigcup _{i=0}^{m-1}\{L_{i_0}, L_{i_1}, L_{i_2}\}\), we refer to the set of all literals of M. Moreover, by a little abuse of notation, for every assignment b for \((\mathfrak {U}, M)\), we let \(b(\overline{X_i})=1-b(X_i)\) for all \(i\in \{0,\dots , n-1\}\). Finally, we assume without loss of generality that each variable and its negation occur at least once, but not in the same clause.
The common principle of the proofs for the NP-hardness can be summarized as follows: We reduce \((\mathfrak {U}, M)\) to an LTS A, of size polynomial in n and m, which is the composition of several gadgets, and represents, for every \(i\in \{0,\dots , m-1\}\), the clause \(M_i\) by a directed path on which the literals of \(M_i\) are events. The LTS A has an ESSA \(\alpha \) such that if \(R=(sup, sig)\) is a region that solves \(\alpha \), and goes along with the addressed net class, then we can extract a truth assignment for \((\mathfrak {U},M)\) from the signature sig of the literal events of A. Hence, if there is an admissible set \(\mathcal {R}\) for A, implying that \(\mathcal {R}\) contains a region that solves \(\alpha \), then there is an assignment for \(\mathfrak {U}\) that satisfies all clauses of M. Conversely, if there is a truth assignment for \((\mathfrak {U},M)\), then there is an admissible set of regions for A; in general, we shall construct adequate regions \(R_i\) from the construction of \(sup_i\) and \(sig_i\). Hence, A is a yes-instance if and only if \((\mathfrak {U},M)\) is a yes-instance.
4.4 The Synthesis Complexity of Several Plain Subclasses of SIRPN
In this section, we shall prove the following theorem:
Theorem 4
Plain Subclasses of IRPN: NP-complete Cases
Deciding, for a given LTS A, whether there is
-
1.
a pure and plain PN, or a pure and plain SRPN, or
-
2.
a pure and plain SIPN, or a pure and plain SIRPN, or
-
3.
a plain PN, or a plain SIPN, or a plain SRPN, or a plain SIRPN
whose reachability graph is isomorphic to A is NP-complete.
\(\square \) 4
Theorem 2 showed that all these synthesis problems are in NP. Hence, it remains to prove the hardness part. For that, we follow our general approach. However, the nets of Item 1, and the ones from Item 2, and 3 need a slightly (but crucially) different construction, which result in LTS \(A_1\), and \(A_2\), respectively. These LTS are defined as follows:
First of all, the LTS \(A_1\) has the edges  and
and  , where \(h_0\) is the initial state of \(A_1\). On the other hand, the LTS \(A_2\) has the edge
, where \(h_0\) is the initial state of \(A_1\). On the other hand, the LTS \(A_2\) has the edge  , and again \(h_0\) is the initial state. Moreover, for every \(i\in \{0,\dots , m-1\}\), \(A_1\), and \(A_2\) have the following directed path that represents the clause \(M_i=\{L_{i_0}, L_{i_1}, L_{i_2}\}\) by using its literals as events:
, and again \(h_0\) is the initial state. Moreover, for every \(i\in \{0,\dots , m-1\}\), \(A_1\), and \(A_2\) have the following directed path that represents the clause \(M_i=\{L_{i_0}, L_{i_1}, L_{i_2}\}\) by using its literals as events:

Finally, for every \(i\in \{0,\dots , n-1\}\), the LTSs \(A_1\), and \(A_2\) implement the following gadget \(G_{i}\) that uses the variable \(X_i\) and its negation \(\overline{X_i}\) as events:

In the following, as long as not explicitly stated otherwise, by \(S_1\) and \(E_1\) (\(S_2\) and \(E_2\)), we refer to the set of states and the set of events of \(A_1\) (of \(A_2\)), respectively. If we apply the reduction to the input of Example 1, then we obtain the LTSs \(A_1\), and \(A_2\) of Fig. 4.
The reductions based on Example 1: the solid and dashed lines define \(A_1\), and the solid lines and the dotted line define \(A_2\).
Lemma 3
Plain Solvability of ESSA \((k, h_1)\) Implies Truth Assignment
If the ESSA \(\alpha =(k, h_1)\) is solvable (1) by a pure and plain SRPN-region of \(A_1\), respectively (2) by a plain SIRPN-region of \(A_2\), then there is a truth assignment for \((\mathfrak {U},M)\).
Proof: Let \(R=(sup, sig)\) be a region of \(A_1\) that solves \(\alpha \) and such that, for all \(e\in E_1\), \(sig^t(e)\in \{\textsf {classic}, \textsf {reset}\}\) and
-
if \(sig(e)=(x,y,\textsf {classic})\), then \(x=0\) or \(y=0\), and \(x,y\in \{0,1\}\),
-
if \(sig(e)=(x,y,\textsf {reset})\), then \(x=0=y\),
Since R solves \(\alpha \), we must have \(sig(k)=(1,0,\textsf {classic})\) and \(sup(h_1)=0\).
Similarly, if \(R=(sup, sig)\) is a plain SIRPN-region of \(A_2\) that solves \(\alpha \), then \(sig(k)\not \in \{(0,0,\textsf {reset}),(0,0,\textsf {classic}),(0,1,\textsf {classic})\}\); moreover, since  , \(sig(k)\not \in \{(0,0,\textsf {inhibitor}),(1,1,\textsf {classic})\}\) so that again \(sig(k)=(1,0,\textsf {classic})\) and \(sup(h_1)=0\).
, \(sig(k)\not \in \{(0,0,\textsf {inhibitor}),(1,1,\textsf {classic})\}\) so that again \(sig(k)=(1,0,\textsf {classic})\) and \(sup(h_1)=0\).
Let \(i\in \{0,\dots , m-1\}\). Since k occurs at \(t_{i,0}\) and at \(t_{i,4}\), and \(sig(k)=(1,0,\textsf {classic})\), we have that \(sup(t_{i,0})\ge 1\le sup(t_{i,4})\). Moreover, since \(sup(h_1)=0\), we get that \(sig(a_i)=(0,1,\textsf {classic})\), \(sup(t_{i,0})=1\) and \(sup(t_{i,1})=0\). Hence, there is a \(j\in \{0,1,2\}\) such that the event \(L_{i_j}\) of \(\{L_{i_0}, L_{i_1}, L_{i_2}\}\) satisfies \(sig(L_{i_j})=(0,1,\textsf {classic})\). We argue that this impliesFootnote 2 \(sig(\overline{L_{i_j}})\not =(0,1,\textsf {classic})\). Indeed, let \(\ell \in \{0,\dots ,m-1\}\) be such that \(L_{i_j}\in \{X_\ell ,\overline{X_\ell }\}\). If \(sig(X_\ell )=sig(\overline{X_\ell })=(0,1,\textsf {classic})\), then we have \(sup(g_{\ell ,2})=sup(g_{\ell ,0})+2\). This implies \(sig(c_{\ell })=(x,y,\textsf {classic})\) with \(y\ge 2\), which contradicts the plainness of R. Hence, \(sig(\overline{L_{i_j}})\not =(0,1,\textsf {classic})\).
Since i was arbitrary, we obtain the following observation: For every \(i\in \{0,\dots , m-1\}\), there is an event \(e\in M_i\) such that \(sig(e)=(0,1,\textsf {classic})\); and for each event \(e\in M_i\), if \(sig(e)=(0,1,\textsf {classic})\), then \(sig(\overline{e})\not =(0,1,\textsf {classic})\).
Let \(b:\mathfrak {U}\rightarrow \{0,1\}\) be the (well-defined) assignment for \(\mathfrak {U}\), which, for all \(X\in \mathfrak {U}\), is defined as follows: \(b(X)=1\text { if } sig(X)=(0,1,\textsf {classic})\), and 0 otherwise.
Needless to say that b is a well-defined assignment, that is, if \(b(X)=x\) and \(b(X)=y\), then \(x=y\). Similarly, if \(b(X)=x\), then \(b(\overline{X})=1-x\), since both cases are mutually exclusive.
We argue that b satisfies every clause: Let \(i\in \{0,\dots , m-1\}\). As argued above, there is \(j\in \{0,1,2\}\) such that the literal \(L_{i_j}\in M_i\) has signature \(sig(L_{i_j})=(0,1,\textsf {classic})\). If \(L_{i_j}=X\) for some variable \(X\in \mathfrak {U}\), then \(b(X)=1\) and thus \(M_i\) is satisfied. Otherwise, \(L_{i_j}=\overline{X}\) for some variable \(X\in \mathfrak {U}\), which implies \(sig(X)\not =(0,1,\textsf {classic})\) and thus \(b(X)=0\) according to the definition of b. This, however, implies \(b(\overline{X})=1\) so that \(M_i\) is satisfied. By the arbitrariness of i, we have that b is a truth assignment for \((\mathfrak {U}, M)\). \(\square \) 3
By Lemma 3, the existence of an admissible set implies a truth assignment for \((\mathfrak {U}, M)\), since such a set implies the solvability of \((k,h_1)\). Conversely, we have to prove that, if there is a truth assignment for \((\mathfrak {U}, M )\), \(A_1\) and \(A_2\) both allow admissible sets of regions, with signatures corresponding to the wanted target net class. In order to simplify the presentation, we shall only give the support of the initial state and the signatures which are not \((0,0,\textsf {classic})\), where we collect events by sets \(\mathcal {E}_{m,n}^R\), \(\mathcal {E}_{\textsf {inhibitor}}^R\) and \(\mathcal {E}_{\textsf {reset}}^R\) following Remark 2. This will allow to construct the full region and to check that the construction is sound. Illustrations of our constructions may be found in the appendices.
Fact 1
All SSAs of \(A_1\) are solvable by pure and plain PN-regions.
Proof:
-
If \(sup_0(h_0)=0\) and
 , then \(R_0\) solves \(h_0\).
, then \(R_0\) solves \(h_0\). -
If \(sup_1(h_0)=0\), \(\mathcal {E}_{0,1}^{R_1}=\{u\}\) and \(\mathcal {E}_{1,0}^{R_1}=\{a_0,\dots , a_{m-1}\}\), then \(R_1\) solves \(h_1\).
Let \(i\in \{0,\dots , n-1\}\).
-
If \(sup_2(h_0)=0\) and \(\mathcal {E}_{0,1}^{R_2}=\{b_i\}\), then \(R_2\) solves \(g_{i,0}, g_{i,1}\) and \(g_{i,2}\).
-
If \(sup_3(h_0)=0\) and \(\mathcal {E}_{0,1}^{R_3}=\{c_i, X_i\}\), then \(R_3\) solves \((g_{i,0}, g_{i,1})\) and \((g_{i,0},g_{i,2})\).
-
If \(sup_4(h_0)=0\) and \(\mathcal {E}_{0,1}^{R_4}=\{c_i, \overline{X_i}\}\) then \(R_4\) solves \((g_{i,1}, g_{i,2})\).
As a consequence, since i was arbitrary, all the \(g_{i,j}\)’s are solvable.
Let \(i\in \{0,\dots , m-1\}\).
-
If \(sup_5(h_0)=0\) and \(\mathcal {E}_{0,1}^{R_5}=\{a_i\}\), then \(R_5\) solves (t, s) for all \(t\in S(T_i)\) and all \(s\in S\setminus S(T_i)\).
-
Let \(G_{\ell _0}, G_{\ell _1}\) and \(G_{\ell _2}\) be the gadgets containing the events \(L_{i_0}\), \(L_{i_1}\) and \(L_{i_2}\), respectively. If \(sup_6(h_0)=0\) and \(\mathcal {E}_{0,1}^{R_6}=\{k\}\cup \{L_{i_0},L_{i_1}, L_{i_2}\}\cup \{c_{\ell _0},c_{\ell _1}, c_{\ell _2}\}\), then \(R_6\) solves \((s,s')\) for all \(s\not =s'\in \{t_{i,0},\dots , t_{i,5}\}\) (recall that no clause contains both a literal and its negation). As a consequence, since i was arbitrary, all the \(t_{i,j}\)’s are solvable.
Finally, since, for all \(s\in S\setminus \{h_2\}\), we have argued that s is solvable, it follows that \(h_2\) is solvable as well. Altogether, we have witnessed the SSP of \(A_1\). \(\square \) 1
Fact 2
If there is a truth assignment for \((\mathfrak {U},M)\), then all ESSAs of \(A_1\) are solvable by pure and plain PN-regions.
Proof: We start with the \(a_i\)’s: If \(sup_0(h_0)=0\), \(\mathcal {E}_{0,1}^{R_0}=\{u\}\) and \(\mathcal {E}_{1,0}^{R_0}=\{a_0,\dots , a_{m-1}\}\), then \(R_0\) solves all the \(a_i\)’s.
We proceed with the \(c_i\)’s: Let \(i\in \{0,\dots , n-1\}\) be arbitrary but fixed and let \(i_0,\dots , i_\ell \in \{0,\dots , m-1\}\) be the indices such that \(X_i\in M_{i_j}\) for all \(j\in \{0,\dots ,\ell \}\).
-
If \(sup_1(h_0)=0\), \(\mathcal {E}_{0,1}^{R_1}=\{b_i,a_{i_0},\dots ,a_{i_\ell }\}\) and \(\mathcal {E}_{1,0}^{R_1}=\{X_i, c_i\}\), then \(R_1\) solves \((c_i,s)\) for all necessary states \(s\in S\setminus \bigcup _{j=0}^{\ell } S(T_{i_j})\).
-
If \(sup_2(h_0)=0\), \(\mathcal {E}_{0,1}^{R_2}=\{b_i\}\cup \{a_j\mid j\in \{0,\dots , m-1\}\setminus \{i_0,\dots , i_\ell \} \}\) and \(\mathcal {E}_{1,0}^{R_2}=\{\overline{X_i}, c_i\}\), then \(R_2\) solves \((c_i, s)\) for the remaining states s. Since i was arbitrary, all the \(c_i\)’s are solvable.
We proceed with k and u: Let b be a valid truth assignment for \((\mathfrak {U},M)\) and let \(i\in \{0,\dots , m-1\}\).
-
If \(sup_3(h_0)=1\), \(\mathcal {E}_{1,0}^{R_3}=\{u,k\}\) and \(\mathcal {E}_{0,1}^{R_3}=\{a_0,\dots , a_{m-1}\}\cup \{c_0,\dots , c_{n-1}\}\cup \{X_i,\overline{X_j}\mid b(X_i)=1,b(X_j)=0,i,j\in \{0,\dots , n-1\}\}\), then \(R_3\) solves (k, s) and (u, s) for all \(s\in \{h_2,h_1\}\).
-
If \(sup_4(h_0)=1\), \(\mathcal {E}_{1,0}^{R_4}=\{k\}\cup \{b_0,\dots , b_{n-1}\}\) and \(\mathcal {E}_{0,1}^{R_4}=\{u\}\), then \(R_4\) solves (k, s) for all \(s\in \bigcup _{j=0}^{n-1}\{g_{j,0},g_{j,1},g_{j,2}\}\).
-
If \(sup_5(h_0)=1\), \(\mathcal {E}_{1,0}^{R_5}=\{k\}\) and \(\mathcal {E}_{0,1}^{R_5}=\{c_{i_2}, L_{i_2}\}\cup (\{a_0,\dots , a_{m-1}\}\setminus \{a_i\})\), then \(R_5\) solves (k, s) for all \(s\in \{t_{i,1},t_{i,2}, t_{i,3}, t_{i,5}\}\).
-
If \(sup_6(h_0)=1\) and \(\mathcal {E}_{1,0}^{R_6}=\{u\}\cup \{b_0,\dots , b_{n-1}\}\), then \(R_6\) solves (u, s) for all \(s\in S\setminus \{h_2,h_1\}\).
Since i was arbitrary, this completes the separability of k and u.
We proceed with the variable events: Let \(i\in \{0,\dots , n-1\}\) be arbitrary but fixed and let \(i_0,\dots , i_\ell \in \{0,\dots , m-1\}\) be the indices such that \(X_i\in M_{i_j}\) for all \(j\in \{0,\dots , \ell \}\).
-
If \(sup_7(h_0)=0\), \(\mathcal {E}_{1,0}^{R_7}=\{X_i,c_i\}\) and \(\mathcal {E}_{0,1}^{R_7}=\{b_i\}\cup \{ a_{i_0},\dots ,a_{i_\ell }\}\), then \(R_7\) solves \((X_i,s)\) for all necessary states \(s\in S\setminus \bigcup _{j=0}^\ell \{t_{i_j,0},\dots , t_{i_j,4}\}\). (Note that \((X_i,t_{j,5})\) is solved for all \(j\in \{0,\dots , m-1\}\)).
-
If we exchange \(X_i\) with \(\overline{X_i}\) (according to \(R_7\)) and consider \(i_0,\dots , i_\ell \in \{0,\dots , m-1\}\) to be the indices such that \(\overline{X_i}\in M_{i_j}\) for all \(j\in \{0,\dots , \ell \}\), then the resulting region solves \((\overline{X_i},s)\) for all necessary states \(s\in S\setminus \bigcup _{j=0}^\ell \{t_{i_j,0},\dots , t_{i_j,4}\}\) except \(s=g_{i,0}\).
-
If \(sup_8(h_0)=0\), \(\mathcal {E}_{1,0}^{R_8}=\{\overline{X_i}\}\) and \(\mathcal {E}_{0,1}^{R_8}=\{X_i\}\cup \{a_0,\dots , a_{m-1}\}\), then \(R_8\) solves \((\overline{X_i},g_{i,0})\).
It remains to argue that the literals are separable from the \(t_{i,j}\)’s, when \(j\not =5\). Let \(i\in \{0,\dots , m-1\}\).
-
If \(sup_9(h_0)=0\), \(\mathcal {E}_{1,0}^{R_9}=\{L_{i_0}, c_{i_0}\}\) and \(\mathcal {E}_{0,1}^{R_9}=\{b_{i_0}, k\}\), then \(R_9\) solves \((L_{i_0},s)\) for all \(s\in \{t_{i,0},t_{i,2},t_{i,3}, t_{i,4}\}\).
-
If \(sup_{10}(h_0)=0\), \(\mathcal {E}_{1,0}^{R_{10}}=\{L_{i_1}, c_{i_1}\}\) and \(\mathcal {E}_{0,1}^{R_{10}}=\{c_{i_0}\}\cup \{ b_{i_1}\}\cup \{a_0,\dots , a_{m-1}\}\setminus \{a_i\}\), then \(R_{10}\) solves \((L_{i_1},s)\) for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,3}, t_{i,4}\}\). Similarly, one shows that \((L_{i_2}, s)\) can be solved for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,2},t_{i,4}\}\).
Since i was arbitrary, all the literal events are solvable. \(\square \) 2
Altogether, we get the following lemma:
Lemma 4
Truth Assignment Implies Suitable Admissible Set for \(A_1\)
If there is a truth assignment for \((\mathfrak {U},M)\), then \(A_1\) has an admissible set of pure and plain PN-regions.
Let us now consider the synthesizability of \(A_2\). Similarly to the arguments for \(A_1\), there is a set of pure and plain PN-regions that solve all the SSAs of \(A_2\). Hence, we restrict ourselves to the solvability of the ESSAs.
The following fact deals with ESSAs, whose solvability needs possibly impure or inhibitor links:
Fact 3
There is a pure and plain SIPN-region, as well as an impure and plain PN-region, of \(A_2\) that solves (k, s) for all \(s\in \bigcup _{i=0}^{n-1}S(G_i)\).
Proof: If \(sup_0(h_0)=0\), \(\mathcal {E}_{\textsf {inhibitor}}^{R_0}=\{k\}\) and \(\mathcal {E}_{0,1}^{R_0}=\{b_0,\dots , b_{m-1}\}\), then \(R_0\) is a suitable pure and plain SIPN-region.
If \(sup_1(h_0)=1\), \(\mathcal {E}_{1,1}^{R_1}=\{k\}\) and \(\mathcal {E}_{1,0}^{R_1}=\{b_0,\dots , b_{m-1}\}\), then \(R_1\) is a suitable impure and plain PN-region. \(\square \) 3
Fact 4
If there is a truth assignment b for \((\mathfrak {U}, M)\), then there is an admissible set of pure and plain PN-regions solving the ESSAs of \(A_2\) not addressed by Fact 3.
Proof: Recall that \(\mathcal {L}\) is the set of the literals of M and b is extended to \(\mathcal {L}\), i. e., \(b(\overline{X})=1-b(X)\) for all \(X\in \mathfrak {U}\).
We start with k:
-
If \(sup_0(h_0)=1\), \(\mathcal {E}_{1,0}^{R_0}=\{k\}\cup \{b_0,\dots , b_{n-1}\}\) and \(\mathcal {E}_{0,1}^{R_0}=\{L\in \mathcal {L}\mid b(L)=1\}\cup \{a_0,\dots , a_{m-1}\}\cup \{c_0,\dots , c_{n-1}\}\), then \(R_0\) solves \((k,h_1)\).
Let \(i\in \{0,\dots , m-1\}\).
-
If \(sup_1(h_0)=2\), \(\mathcal {E}_{1,0}^{R_1}=\{k\}\) and \(\mathcal {E}_{0,1}^{R_1}=\{L_{i_2}, c_{i_2}\}\cup (\{a_0,\dots , a_{m-1}\}\setminus \{a_i\})\), then \(R_1\) solves (k, s) for all \(s\in \{t_{i,1}, t_{i,2}, t_{i,3}, t_{i,5}\}\).
Since i was arbitrary, the claim follows for k.
We proceed with the \(a_i\)’s and \(b_i\)’s: Let \(i\in \{0,\dots , m-1\}\) and \(j\in \{0,\dots , n-1\}\).
-
If \(sup_2(h_0)=1\) and \(\mathcal {E}_{1,0}^{R_2}=\{a_0,\dots , a_{m-1}\}\cup \{b_0,\dots , b_{n-1}\}\), then \(R_2\) solves \((a_i,s)\) and \((b_j,s)\) for all \(s\in S\setminus \{h_0, h_1\}\).
-
If \(sup_3(h_0)=0\), \(\mathcal {E}_{1,0}^{R_3}=\{a_0,\dots , a_{m-1}\}\) and \(\mathcal {E}_{0,1}^{R_3}=\{k\}\), then \(R_3\) solves \((a_i,h_0)\).
-
The region \(R_0\) of this proof also solves \((b_i,h_1)\) for all \(i\in \{0,\dots , n-1\}\). Since i and j were arbitrary, this proves the claim for the \(a_i\)’s and \(b_i\)’s.
We proceed with the \(c_i\)’s: Let \(i\in \{0,\dots , n-1\}\).
-
If \(sup_4(h_0)=0\), \(\mathcal {E}_{1,0}^{R_4}=\{c_i, X_i\}\) and \(\mathcal {E}_{0,1}^{R_4}=\{b_i\}\cup \{a_j\mid j\in \{0,\dots , m-1\}: X_i\in M_j\}\), then \(R_4\) solves \((c_i, s)\) for all \(s\in S\setminus (\{t_{j,0},\dots ,t_{j,5}\mid j\in \{0,\dots , m-1\}:X_i\in M_j \}\cup \{g_{i,0}\})\).
-
If \(sup_5(h_0)=0\), \(\mathcal {E}_{1,0}^{R_5}=\{c_i, \overline{X_i}\}\) and \(\mathcal {E}_{0,1}^{R_5}=\{b_i\}\cup \{a_j\mid j\in \{0,\dots , m-1\}: \overline{X_i}\in M_j\}\), then, for all \(j\in \{0,\dots , m-1\}\), \(R_5\) solves \((c_i, s)\) for all \(s\in S(T_j)\) if \(X_i\in M_j\). Since i was arbitrary, this proves the claim for the \(c_i\)’s.
It remains to consider the literal events: Let \(i\in \{0,\dots , n-1\}\) be arbitrary but fixed and let \(i_0,\dots , i_\ell \) be the indices such that \(X_i\in M_{i_j}\) for all \(j\in \{0,\dots , \ell \}\).
-
If \(sup_6(h_0)=0\), \(\mathcal {E}_{1,0}^{R_6}=\{c_i, X_i\}\) and \(\mathcal {E}_{0,1}^{R_6}=\{a_{i_0},\dots , a_{i_\ell }\}\), then \(R_6\) solves \((X_i, s)\) for all \(s\in S\setminus (\bigcup _{j=0}^{\ell }\{t_{j,0}, \dots , t_{j,3}\}\). (We stress that \((X_i, t_{j,4})\) and \((X_i, t_{j,5})\) are solved for every \(j\in \{0,\dots , m-1\}\).)
Similarly, if we interchange \(X_i\) with \(\overline{X_i}\) and let \(i_0,\dots , i_\ell \) select the clauses that contain \(\overline{X_i}\), then the resulting region solves \((\overline{X_i}, s)\) for all \(s\in S\setminus (\{g_{i,0}\}\cup \bigcup _{j=0}^{\ell }\{t_{j,0}, \dots , t_{j,3}\}\).
-
If \(sup_7(h_0)=0\), \(\mathcal {E}_{1,0}^{R_7}=\{\overline{X_i}\}\) and \(\mathcal {E}_{0,1}^{R_7}=\{X_i\}\cup \{a_j\mid j\in \{0,\dots , m-1\}: \overline{X_i}\in M_j\}\), then \(R_7\) solves \((\overline{X_i}, g_{i,0})\).
It remains to solve the literal events within their gadgets:
-
If \(sup_8(h_0)=0\), \(\mathcal {E}_{1,0}^{R_8}=\{L_{i_0}, a_i, c_{i_0}\}\) and \(\mathcal {E}_{0,1}^{R_8}=\{k,b_{i_0}\}\), then \(R_8\) solves \((L_{i_0}, s)\) for all \(s\in \{t_{i,0}, t_{i,2}, t_{i,3}\}\).
-
If \(sup_9(h_0)=1\), \(\mathcal {E}_{1,0}^{R_9}=\{L_{i_1}, a_i, c_{i_1}\}\) and \(\mathcal {E}_{0,1}^{R_9}=\{L_{i_0}, c_{i_0}\}\), then \(R_9\) solves \((L_{i_1}, s)\) for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,3}\}\).
Similarly, one shows that \((L_{i_2}, s)\) is solvable for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,2}\}\).
Since i was arbitrary, this completes the proof. \(\square \) 4
Altogether, we get the following lemma:
Lemma 5
Truth Assignment Implies Suitable Admissible Set for \(A_2\)
If there is a truth assignment for \((\mathfrak {U},M)\), then \(A_2\) has an admissible set of pure and plain SIPN-regions, and also of impure and plain PN-regions.
Moreover, gathering Lemmata 3, 4 and 5, we get Theorem 4.
4.5 The Synthesis Complexity of Impure SRPN and SIRPN
The following theorem states the main result of this section:
Theorem 5
Synthesis of SRPN and SIRPN is NP-complete
Deciding whether there is a SRPN or a SIRPN whose reachability graph is isomorphic to a given LTS is NP-complete. \(\square \) 5
By Theorem 2 the addressed synthesis problems belong to NP. In order to prove the hardness part, we follow again the announced general approach: First of all, the LTS A has the following gadget \(H_0\) that provides the ESSA \(\alpha =(k,h_{1})\):

Moreover, for every \(i\in \{0,\dots , m-1\}\), the LTS A has the following gadgets \(T_i\) at which the literals of the clause \(M_i=\{L_{i_0}, L_{i_1}, L_{i_2}\}\) occur as events:

Finally, for every \(i\in \{0,\dots , n-1\}\), the LTS has the following three gadgets \(G_{i,0}, G_{i,1}\) and \(G_{i,2}\), that use the i-th variable and its negation as events:

Let \(S_I= \{h_0\}\cup \{t_{0,0}, \dots , t_{m-1,0}\}\cup \bigcup _{i=0}^{n-1}\{g_{i,0}, g_{i,1}, g_{i,2}\}\) be the set of the initial states of A’s gadget. Finally, to complete the construction, we use the initial state \(\iota \) and, for every state \(s\in S_I\), a fresh and unambiguous event \(u_s\) to connect the gadgets with \(\iota \) by  .
.
Recall that we here assume all non-classic regions \(R=(sup, sig)\) to be strict, that is, if \(sig(e)=(m,n,\texttt {type})\) with \(\texttt {type}\in \{\textsf {inhibitor}, \textsf {reset}\}\), then \(m=n=0\). We first observe the following simple facts:
Fact 5
Let \(i\in \{0,\dots , n-1\}\) and \(L_i\in \{X_i,\overline{X_i}\}\), and let \(R=(sup, sig)\) be a region of A. If \(sig(L_i)=(m,n,\textsf {classic})\) with \(n>m\), then \(sig^-(\overline{L_i})\ge sig^+(\overline{L_i})\).
Proof: Let \(R=(sup, sig)\) be a region of A, such that \(sig(X_i)=(m,n,\textsf {classic})\) with \(n>m\). This implies \(sup(g_{i,0,1}) > sup(g_{i,0,0})\ge 0\) and thus \(sig(a_i)=(x,y,\textsf {classic})\) with \(y-x=n-m\). By  , this implies \(sup(g_{i,2,1})>sup(g_{i,2,0})\ge 0\), and thus \(sig^t(b_i)=\textsf {reset}\) or \(sig(b_i)=(x',y',\textsf {classic})\) with \(x' > y'\). Hence, by the signature of \(b_i\), we have that \(sup(g_{i,1,1})=0\) or \(sup(g_{i,1,0}) > sup(g_{i,1,1})\), which implies that if \(sig(\overline{X_i})=(m',n',\textsf {classic})\), then \(m'>n'\) or \(m'=n'=0\), hence the claim. Analogously, one argues for the other case. \(\square \) 5
, this implies \(sup(g_{i,2,1})>sup(g_{i,2,0})\ge 0\), and thus \(sig^t(b_i)=\textsf {reset}\) or \(sig(b_i)=(x',y',\textsf {classic})\) with \(x' > y'\). Hence, by the signature of \(b_i\), we have that \(sup(g_{i,1,1})=0\) or \(sup(g_{i,1,0}) > sup(g_{i,1,1})\), which implies that if \(sig(\overline{X_i})=(m',n',\textsf {classic})\), then \(m'>n'\) or \(m'=n'=0\), hence the claim. Analogously, one argues for the other case. \(\square \) 5
Fact 6
Let \(s\not =s'\in S\) be states and \(e\in E\) an event such that  and
and  are edges of A. If \(R=(sup, sig)\) is a region of A such that \(sup(s)\not =sup(s')\), then \(sig^t(e)=\textsf {reset}\) and \(sup(s')=0\).
are edges of A. If \(R=(sup, sig)\) is a region of A such that \(sup(s)\not =sup(s')\), then \(sig^t(e)=\textsf {reset}\) and \(sup(s')=0\).
Proof: If \(sig(e)=(0,0,\textsf {inhibitor})\), then we get \(sup(s)=sup(s')=0\), which contradicts \(sup(s)\not =sup(s')\). If \(sig(e)=(m,n,\textsf {classic})\), then, by  , we have \(sup(s')=sup(s')-m+n\) and thus \(m=n\). Moreover, by
, we have \(sup(s')=sup(s')-m+n\) and thus \(m=n\). Moreover, by  and \(sup(s')\not =sup(s)\), we get \(\vert -m+n\vert >0\) and thus \(m\not =n\), which is again a contradiction. Hence, \(sig^t(e)=\textsf {reset}\) and \(sup(s')=0\). \(\square \) 6
and \(sup(s')\not =sup(s)\), we get \(\vert -m+n\vert >0\) and thus \(m\not =n\), which is again a contradiction. Hence, \(sig^t(e)=\textsf {reset}\) and \(sup(s')=0\). \(\square \) 6
Lemma 6
Strict synthesis implies truth assignment
If there is an admissible set of SIRPN-regions for A, then there is a truth assignment for \((\mathfrak {U}, M)\).
Proof: Since \(\mathcal {R}\) is an admissible set, it contains a region \(R=(sup, sig)\) that solves \(\alpha =(k,h_1)\). If \(sig(k)=(0,0,\textsf {inhibitor})\), then \(0=sup(h_0) \not =sup(h_1)\). By Fact 6 and \(sup(h_0) \not =sup(h_1)\), we get \(sig(y)=\textsf {reset}\) and thus \(sup(h_1)=0\), which is a contradiction. Moreover, if \(sig(k)=(0,0,\textsf {reset})\), then R does not solve \(\alpha \). Hence, we have \(sig(k)\in \mathbb {N}\times \mathbb {N}\times \{\textsf {classic}\}\) and \(sig^-(k)>sup(h_1)\ge 0\).
Since R is a region, by  , we get \(sup(h_0)\ge sig^-(k)\) and thus \(sup(h_0)> sup(h_1)\). By Fact 6, this implies \(sig^t(y)=\textsf {reset}\).
, we get \(sup(h_0)\ge sig^-(k)\) and thus \(sup(h_0)> sup(h_1)\). By Fact 6, this implies \(sig^t(y)=\textsf {reset}\).
Let \(i\in \{0,\dots , n-1\}\). By \(sig^t(y)\!\!=\!\!\textsf {reset}\) and  , we get \(sup(t_{i,0})=0\). On the other hand, by
, we get \(sup(t_{i,0})=0\). On the other hand, by  , we get \(sup(t_{i,3})\ge sig^-(k)>0\) and thus \(sup(t_{i,3})>sup(t_{i,0})\). This implies that there is a literal \(L\in \{L_{i_0}, L_{i_1}, L_{i_2}\}\) such that \(sig^+(L) > sig^-(L)\).
, we get \(sup(t_{i,3})\ge sig^-(k)>0\) and thus \(sup(t_{i,3})>sup(t_{i,0})\). This implies that there is a literal \(L\in \{L_{i_0}, L_{i_1}, L_{i_2}\}\) such that \(sig^+(L) > sig^-(L)\).
Since i was arbitrary, we obtain the following observation: For every \(i\in \{0,\dots , m-1\}\), there is an event \(e\in M_i\) such that such that \(sig^+(e) > sig^-(e)\), which implies \(sig^-(\overline{e}) \ge sig^+(\overline{e})\), by Fact 5.
Let \(b:\mathfrak {U}\rightarrow \{0,1\}\) be the assignment for \(\mathfrak {U}\), which, for all \(X\in \mathfrak {U}\), is defined as follows: \(b(X)=1\) if \(sig^+(X) > sig^-(X)\) and 0 otherwise.
The assignment is well-defined, since both cases are mutually exclusive. We argue that b satisfies every clause. Let \(i\in \{0,\dots , n-1\}\) be arbitrary but fixed: As argued above, there is \(j\in \{0,1,2\}\) such that the literal \(L_{i_j}\in M_i\) has signature \(sig^+(L_{i_j}) > sig^-(L_{i_j})\). If \(L_{i_j}=X\) for some variable \(X\in \mathfrak {U}\), then \(b(X)=1\) and thus \(M_i\) is satisfied. Otherwise, \(L_{i_j}=\overline{X}\) for some variable \(X\in \mathfrak {U}\), which implies \(sig^-(X) \ge sig^+(X)\) (by Fact 5) and thus \(b(X)=0\) according to the definition of b. This, however, implies \(b(\overline{X})=1\) so that \(M_i\) is satisfied. By the arbitrariness of i, we have that b is a truth assignment for \((\mathfrak {U}, M)\). \(\square \) 6
For the converse direction, we argue that the existence of a model implies an admissible set of plain SRPN-regions of A. For the presentation of these regions, we shall use the same conventions as for Lemma 4. Moreover, for the sake of simplicity, we often only define (sup, sig) when restricted to \(S\setminus \{\iota \}\) and \(E \setminus U_s\), which is justified as follows: If \(sup: S\setminus \{\iota \}\) and \(sig: E \setminus U_s \rightarrow \mathbb {N}\times \mathbb {N}\times \{\textsf {classic}, \textsf {inhibitor}\}\), such that, for all \(s,s'\in S\setminus \{\iota \}\) and for all \(e\in E \setminus U_s\), the presence of  implies that (sup, sig) behaves like a region according to Definition 5 and, moreover, for every state \(s\in \{h_0\}\cup \{t_{0,0}, \dots , t_{m-1,0}\}\cup \bigcup _{i=0}^{n-1}\{g_{i,0}, g_{i,1}, g_{i,2}\}\) holds \(sup(s)\in \{0,1\}\), then it is easy to see that (sup, sig) can be extended to a region of A, where \(sup(\iota )\in \{0,1\}\) and \(sig(u)\in \{(m,n,\textsf {classic}) \mid m,n\in \{0,1\}\}\) for all events \(u\in U_s\), since the latter occur only once in A. Hence, for an even more compact representation we restrict the representation of sup to \(s\in \{h_0\}\cup \{t_{0,0}, \dots , t_{m-1,0}\}\cup \bigcup _{i=0}^{n-1}\{g_{i,0}, g_{i,1}, g_{i,2}\}\), since we can then compute sup for all states \(S\setminus \{\iota \}\) by Remark 2 (and check its coherence).
implies that (sup, sig) behaves like a region according to Definition 5 and, moreover, for every state \(s\in \{h_0\}\cup \{t_{0,0}, \dots , t_{m-1,0}\}\cup \bigcup _{i=0}^{n-1}\{g_{i,0}, g_{i,1}, g_{i,2}\}\) holds \(sup(s)\in \{0,1\}\), then it is easy to see that (sup, sig) can be extended to a region of A, where \(sup(\iota )\in \{0,1\}\) and \(sig(u)\in \{(m,n,\textsf {classic}) \mid m,n\in \{0,1\}\}\) for all events \(u\in U_s\), since the latter occur only once in A. Hence, for an even more compact representation we restrict the representation of sup to \(s\in \{h_0\}\cup \{t_{0,0}, \dots , t_{m-1,0}\}\cup \bigcup _{i=0}^{n-1}\{g_{i,0}, g_{i,1}, g_{i,2}\}\), since we can then compute sup for all states \(S\setminus \{\iota \}\) by Remark 2 (and check its coherence).
Fact 7
There is a set of plain SRPN-regions of A that solve all SSAs of A.
Proof: If \(sup_0(\iota )=0\) and  , then \(R_0\) solves \(\iota \).
, then \(R_0\) solves \(\iota \).
Let \(i\in \{0,\dots , m-1\}\). If \(sup_1(\iota )=1\) and \(\mathcal {E}_{1,0}^{R_1}=\{u_{t_{i,0}}\}\), then \(R_1\) solves \((s, s')\) for all states \(s\in S(T_i)\) and all states \(s'\in S\setminus S(T_i)\). Similarly, one shows, for any fixed \(i\in \{0,\dots , n-1\}\) and \(j\in \{0,1,2\}\), that the states \(g_{i,j,0}\) and \(g_{i,j,1}\) are solvable.
Since i was arbitrary, it only remains to show that different states of the same gadget are separable.
If \(sup_2(\iota )=1\) and \(\mathcal {E}_{\textsf {reset}}^{R_2}=\{y\}\), then \(R_2\) solves \((h_0,h_1)\).
The following implicitly defined regions complete the proof of this fact:
Let \(i\in \{0,\dots , m-1\}\). Let \(sup(h_0)=sup_3(t_{0,0})=\dots =sup(t_{m-1,0})=0\) and, for every \(j\in \{0,1,2\}\), let \(sup_3(g_{i_j,2,0})=1\) if \(L_{i_j}\not \in \mathfrak {U}\) (i.e. \(L_{i_j}\) is a negated variable); let \(\mathcal {E}_{0,1}^{R_3}=\{L_{i_0}, L_{i_1}, L_{i_2}\} \cup \{a_{i_j}\mid j\in \{0,1,2\}\text { and } L_{i_j}\in \mathfrak {U}\} \cup \{b_{i_j}\mid j\in \{0,1,2\}\text { and } L_{i_j}\not \in \mathfrak {U}\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_3}=\{a_{i_j}\mid j\in \{0,1,2\}\text { and } L_{i_j}\not \in \mathfrak {U}\} \cup \{b_{i_j}\mid j\in \{0,1,2\}\text { and } L_{i_j}\in \mathfrak {U}\}\). Then \(R_3\) solves \((s,s')\) for all \(s\not =s'\in \{t_{i,0},\dots , t_{i,4}\}\). Since i was arbitrary, this shows the solvability of the \(t_{i,j}\)’s.
Let \(i\in \{0,\dots , n-1\}\).
-
If, for all \(s\in S_I\), \(sup(s)=1\) if \(s\in \{g_{i,0,0}, g_{i,1,0}\}\) and otherwise \(sup(s)=0\), and \(\mathcal {E}_{\textsf {reset}}^{R_4}=\{X_i,\overline{X_i}, a_i, b_i\}\), then \(R_4\) solves \((g_{i,j,0},g_{i,j,1})\) for all \(j\in \{0,1\}\).
-
If, for all \(s\in S_I\), \(sup(s)=1\) if \(s=g_{i,2,0}\) and \(sup(s)=0\) otherwise, \(\mathcal {E}_{0,1}^{R_5}=\{\overline{X_i}, b_1\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_5}=\{a_i\}\), then \(R_5\) solves \((g_{i,2,0}, g_{i,2,1})\). Since i was arbitrary, the \(g_{i,j,\ell }\)’s are solvable. \(\square \) 7
Fact 8
If there is truth assignment for \((\mathfrak {U},M)\), then there is a set of plain SRPN-regions of A that solves all ESSAs of A.
Proof: First of all, if \(a\in E\) is an event and \(q\in S\) a state of a gadget that does not contain a, then (a, q) is solvable by a plain classic region \(R=(sup, sig)\): define \(sup(s)=1\) for the states of the gadgets containing a, \(sup(s)=0\) for the other states, \(sig(a)=(1,1,\textsf {classic})\) and \(sig(e)=(0,1,\textsf {classic})\) if e goes from \(\iota \) to any gadget that contains a (and \((0,0,\textsf {classic})\) otherwise). Hence, in the following, for every \(e\in E\), we only deal explicitly with the gadgets that contain e.
We start with k: Let b be a valid truth assignment for \((\mathfrak {U},M)\);
let \(sup_0(h_0)=1\) and \(sup_0(t_{i,0})=0\) for all \(i\in \{0,\dots , m-1\}\); for all \(i\in \{0,\dots , n-1\}\), let \(sup_0(g_{i,0,0})=sup_0(g_{i,1,0})=sup_0(g_{i,2,0})=0\) if \(b(X_i)=1\) and let \(sup_0(g_{i,2,0})=1\) and \(sup_0(g_{i,0,0})=sup_0(g_{i,1,0})=0\) if \(b(X_i)=0\); let \(\mathcal {E}_{1,1}^{R_0}=\{k\}\), \(\mathcal {E}_{\textsf {reset}}^{R_0}=\{y\}\cup \{a_i\mid i\in \{0,\dots , n-1\}: b(X_i)=0\}\cup \{b_i \mid i\in \{0,\dots , n-1\}: b(X_i)=1\}\) and \(\mathcal {E}_{0,1}^{R_0}=\{X_i, a_i\mid i\in \{0,\dots , n-1\}: b(X_i)=1\}\cup \{\overline{X_i}, b_i\mid i\in \{0,\dots , n-1\}: b(X_i)=0\}\). Then \(R_0\) solves \((k,h_1)\).
Let \(i\in \{0,\dots , m-1\}\).
Let \(sup_1(h_0)=sup_1(t_{0,0})=\dots =sup(t_{m-1,0})=1\) and \(sup_1(g_{i_2,2,0})=1\) if \(\overline{L_{i_2}}\in \mathfrak {U}\) (i.e. \(L_{i_2}\) is the negation of a variable) and \(sup(s)=0\) for the other states \(s\in S_I\); let \(\mathcal {E}_{1,1}^{R_1}=\{k\}\), \(\mathcal {E}_{0,1}^{R_1}=\{L_{i_2}\} \cup \{b_{i_2} \mid \overline{L_{i_2}}\in \mathfrak {U}\} \cup \{a_{i_2}\mid L_{i_2}\in \mathfrak {U}\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_1}=\cup \{a_{i_2} \mid \overline{L_{i_2}}\in \mathfrak {U}\} \cup \{b_{i_2}\mid L_{i_2}\in \mathfrak {U}\}\). Then \(R_1\) solves (k, s) for all \(s\in \{t_{i,0},t_{i,1}, t_{i,2}\}\). Since i was arbitrary, that completes the solvability of k.
We proceed with y: If, for all \(s\in S_I\), \(sup_2(s)=1\) if \(s\in \{h_0,t_{0,0},\dots ,t_{m-1,0}\}\) and 0 otherwise, \(\mathcal {E}_{1,1}^{R_2}=\{y\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_1}=\bigcup _{i=0}^{m-1}M_i\), then \(R_2\) solves (y, s) for all \(s\in \bigcup _{i=0}^{m-1}\{t_{i,1}, t_{i,2}, t_{i,3}\}\). This proves the solvability of y.
We proceed with the \(a_i\)’s and the \(b_i\)’s: Let \(i\in \{0,\dots ,n-1\}\). If, for all \(s\in S_I\), \(sup(s)=1\) if \(s\in \{g_{i,0,0}, g_{i,2,0}\}\) and 0 otherwise, \(\mathcal {E}_{1,0}^{R_3}= \{a_i\}\), \(\mathcal {E}_{0,1}^{R_3}= \{b_i, \overline{X_i}\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_3}= \{X_i\}\), then \(R_3\) solves \((a_i, g_{i,0,1})\) and \((a_i, g_{i,2,1})\).
Similarly, one shows the solvability of \((b_i, g_{i,1,1})\) and \((b_i,g_{i,2,0})\). Since i was arbitrary, this shows the solvability of the \(a_i\)’s and \(b_i\)’s.
Finally, we argue that the literal events are separable:
Let \(i\in \{0,\dots , m-1\}\). If, for all \(s\in S_I\), if \(s\in \{t_{0,0},\dots , t_{m-1,0}\}\cup \{g_{i_0,0,0}\mid L_{i_0}\in \mathfrak {U}\}\cup \{g_{i_0,1,0}\mid L_{i_0}\not \in \mathfrak {U}\} \), then \(sup_4(s)=1\), and \(sup_4(s)=0\) otherwise, \(\mathcal {E}_{1,0}^{R_4}=\{L_{i_0}\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_4}=\{a_{i_0}\mid L_{i_0}\in \mathfrak {U}\}\cup \{b_{i_0}\mid L_{i_0}\not \in \mathfrak {U}\}\), then \(R_4\) solves \((L_{i_0}, s)\) for all \(s\in \{t_{i,1}, t_{i,2}, t_{i,3}\}\). Moreover, \(R_4\) solves \((L_{i_0}, g_{i_0,0,1})\) if \(L_{i_0}\in \mathfrak {U}\), and \((L_{i_0}, g_{i_0,1,1})\) otherwise.
We now argue that \((L_{i_1}, s)\) can be solved for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,2}\}\) and \(s=g_{i_0,0,1}\) if \(L_{i_0}\in \mathfrak {U}\), respectively \(s=g_{i_0,1,1}\) if \(L_{i_0}\not \in \mathfrak {U}\). For space reasons, we consider only the case where \(L_{i_1}\in \mathfrak {U}\) and \(L_{i_0}\not \in \mathfrak {U}\) (i.e. \(L_{i_0}\) is a negated variable). The other cases for \(L_{i_0}\) and \(L_{i_1}\) being a variable or its negation are similar.
If, for all \(s\in S_I\), if \(s\in \{g_{i_1,0,0}, g_{i_0,2,0}\}\cup \{t_{i,j}\mid j\in \{0,\dots , m-1\}\setminus \{i\}\}\), then \(sup_5(s)=1\), and \(sup_5(s)=0\) otherwise, \(\mathcal {E}_{1,0}^{R_5}=\{L_{i_1}\}\), \(\mathcal {E}_{0,1}^{R_5}=\{L_{i_0}, b_{i_0}\}\) and \(\mathcal {E}_{\textsf {reset}}^{R_5}=\{a_{i_0}, a_{i_1}\}\), then \(R_5\) solves \((L_{i_1}, s)\) for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,2}, g_{i_1,0,1}\}\).
Similarly, one shows that \((L_{i_2}, s)\) is solvable for all \(s\in \{t_{i,0}, t_{i,1}, t_{i,3}\}\) (and \(g_{i_2,0,1}\) or \(g_{i_2,1,1}\), depending on whether \(L_{i_2}\in \mathfrak {U}\) or not). Since i was arbitrary, the literal events are solvable. This completes the proof. \(\square \) 8
Altogether, we get the following lemma:
Lemma 7
Truth Assignment Implies Suitable Admissible Set for A
If there is a truth assignment for \((\mathfrak {U},M)\), then there is an admissible set of (plain) SRPN-regions for A.
Since every SRPN-region is a SIRPN-region, gathering Lemmata 6 and 7, we get Theorem 5.
5 Conclusion
We have introduced a rather general class of Petri nets with inhibitor and reset links and showed how to synthesize them. While all the introduced net classes belong to the complexity class NP (Theorem 2), we exhibited some interesting subclasses for which the synthesis is polynomial (Theorem 3), and some for which it is NP-complete (Theorems 4 and 5). Figure 5 provides an overview of our findings, but also shows that there are still some open cases, even if reset and inhibitor links are assumed to be strict.
As future works, we plan to characterize the synthesis complexity for these open cases pictured by Fig. 5. After that, the next natural step is to characterize the complexity of synthesis of (pure) Petri nets with reset or inhibitor links or both, where these links do not necessarily have to be strict. Moreover, it remains to incorporate the corresponding algorithms into existing synthesis tools like SYNET [3], APT [11], GENET [12], or others.
Notes
- 1.
I.e., \(m=n=0\): strict inhibitor links correspond to usual inhibitor arcs found in the literature [18, 21]; strict reset links correspond to the kind of reset arcs sometimes found in the literature [2]; strict classic links correspond to the fact that some transitions are not connected to some places.
- 2.
As usual, if \(L_{i_j}=\overline{X_\ell }\), we state that \(\overline{L_{i_j}}=X_\ell \).
References
van der Aalst, W.M.P.: Process Mining - Discovery, Conformance and Enhancement of Business Processes. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19345-3
Akshay, S., Chakraborty, S., Das, A., Jagannath, V., Sandeep, S.: On petri nets with hierarchical special arcs. In: Meyer, R., Nestmann, U. (eds.) 28th International Conference on Concurrency Theory, CONCUR 2017, September 5–8, 2017, Berlin, Germany. LIPIcs, vol. 85, pp. 40:1–40:17. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2017). https://doi.org/10.4230/LIPIcs.CONCUR.2017.40
Badouel, E., Bernardinello, L., Darondeau, P.: Polynomial algorithms for the synthesis of bounded nets. In: Mosses, P.D., Nielsen, M., Schwartzbach, M.I. (eds.) CAAP 1995. LNCS, vol. 915, pp. 364–378. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-59293-8_207
Badouel, E., Bernardinello, L., Darondeau, P.: Petri Net Synthesis. TTCSAES, Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47967-4
Badouel, E., Caillaud, B., Darondeau, P.: Distributing finite automata through Petri net synthesis. Formal Asp. Comput. 13(6), 447–470 (2002). https://doi.org/10.1007/s001650200022
Badouel, E., Darondeau, P.: On the Synthesis of General Petri Nets. Research Report RR-3025, INRIA (1996). https://hal.inria.fr/inria-00073668
Best, E., Devillers, R.: Characterisation of the state spaces of live and bounded marked graph petri nets. In: Dediu, A.-H., Martín-Vide, C., Sierra-Rodríguez, J.-L., Truthe, B. (eds.) LATA 2014. LNCS, vol. 8370, pp. 161–172. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04921-2_13
Best, E., Devillers, R., Erofeev, E., Wimmel, H.: Target-oriented Petri net synthesis. Fundamenta Informaticae 175, 97–122 (2020). https://doi.org/10.3233/FI-2020-1949
Best, E., Devillers, R., Schlachter, U.: Bounded choice-free Petri net synthesis: algorithmic issues. Acta Informatica 55(7), 575–611 (2017). https://doi.org/10.1007/s00236-017-0310-9
Best, E., Devillers, R.R., Erofeev, E.: A new property of choice-free Petri net systems. In: Application and Theory of Petri Nets and Concurrency - 41st International Conference, PETRI NETS 2020, Paris, France, 24–25 June 2020, Proceedings, pp. 89–108 (2020). https://doi.org/10.1007/978-3-030-51831-8_5
Best, E., Schlachter, U.: Analysis of petri nets and transition systems. In: Proceedings 8th Interaction and Concurrency Experience, ICE 2015, Grenoble, France, 4–5 June 2015, pp. 53–67 (2015). https://doi.org/10.4204/EPTCS.189.6
Carmona, J., Cortadella, J., Kishinevsky, M.: Genet: a tool for the synthesis and mining of petri nets. In: Ninth International Conference on Application of Concurrency to System Design, ACSD 2009, Augsburg, Germany, 1–3 July 2009, pp. 181–185 (2009). https://doi.org/10.1109/ACSD.2009.6
Cortadella, J., Kishinevsky, M., Kondratyev, A., Lavagno, L., Yakovlev, A.: A region-based theory for state assignment in speed-independent circuits. IEEE Trans. CAD Integr. Circ. Syst. 16(8), 793–812 (1997). https://doi.org/10.1109/43.644602
Desel, J., Reisig, W.: The synthesis problem of Petri nets. Acta Inf. 33(4), 297–315 (1996). https://doi.org/10.1007/s002360050046
Devillers, R., Hujsa, T.: Analysis and synthesis of weighted marked graph Petri nets. In: Application and Theory of Petri Nets and Concurrency - 39th International Conference, PETRI NETS 2018, Bratislava, Slovakia, 24–29 June 2018, Proceedings, pp. 19–39 (2018). https://doi.org/10.1007/978-3-319-91268-4_2
Devillers, R.R.: Synthesis of (choice-free) reset nets. In: Application and Theory of Petri Nets and Concurrency - 42nd International Conference, PETRI NETS 2021, Virtual Event, 23–25 June 2021, Proceedings, pp. 274–291 (2021). https://doi.org/10.1007/978-3-030-76983-3_14
Dufourd, C., Finkel, A., Schnoebelen, P.: Reset nets between decidability and undecidability. In: Automata, Languages and Programming, 25th International Colloquium, ICALP 1998, Aalborg, Denmark, 13–17 July 1998, Proceedings, pp. 103–115 (1998). https://doi.org/10.1007/BFb0055044, https://doi.org/10.1007/BFb0055044
Flynn, M.J., Agerwala, T.: Comments on capabilities, limitations and correctness of petri nets. In: Lipovski, G.J., Szygenda, S.A. (eds.) Proceedings of the 1st Annual Symposium on Computer Architecture, Gainesville, FL, USA, December 1973, pp. 81–86. ACM (1973). https://doi.org/10.1145/800123.803973
Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. Freeman, W. H, New York City (1979)
Gathen, J., Sieveking, M.: A bound on solutions of linear integer equalities and inequalities. Proc. Am. Math. Soc. 72, 155–155 (1978). https://doi.org/10.2307/2042554
Hack, M.: Petri net language. In: MIT Technical Report 159 (1976)
Holloway, L.E., Krogh, B.H., Giua, A.: A survey of Petri net methods for controlled discrete event systems. Disc. Event Dyn. Syst. 7(2), 151–190 (1997). https://doi.org/10.1023/A:1008271916548
Schlachter, U.: Over-approximative Petri net synthesis for restricted subclasses of nets. In: Language and Automata Theory and Applications - 12th International Conference, LATA 2018, Ramat Gan, Israel, 9–11 April 2018, Proceedings, pp. 296–307 (2018). https://doi.org/10.1007/978-3-319-77313-1_23
Tredup, R.: The complexity of synthesizing sf nop-equipped boolean Petri nets from g-bounded inputs. Trans. Petri Nets Other Model. Concurr. 15, 101–125 (2021)
Tredup, R.: The complexity of synthesis of \(b\)-bounded petri nets. Fundamenta Informaticae 183(1–2), 2019 (2021). https://fi.episciences.org/8821
Acknowledgements
We would like to thank the anonymous reviewers for their detailed comments and helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this paper
Cite this paper
Devillers, R., Tredup, R. (2022). Synthesis of Inhibitor-Reset Petri Nets: Algorithmic and Complexity Issues. In: Bernardinello, L., Petrucci, L. (eds) Application and Theory of Petri Nets and Concurrency. PETRI NETS 2022. Lecture Notes in Computer Science, vol 13288. Springer, Cham. https://doi.org/10.1007/978-3-031-06653-5_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-06653-5_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-06652-8
Online ISBN: 978-3-031-06653-5
eBook Packages: Computer ScienceComputer Science (R0)





 , then add
, then add  , then add
, then add 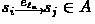 , then add
, then add 


 , then
, then 