Keywords

1 Introduction

Link prediction, as a task of predicting the relationship between entities, plays a vital role in many graph mining applications, such as social networks [21] and biology network [18]. It can be divided into two categories. One is to predict missing links on static graph, and the other predicts new links that may appear in the future on dynamic graph. Since many real-world networks are dynamic, whose nodes and edges appear or disappear over time, dynamic link prediction [4] can keenly capture the variation trend and achieve better prediction effect, therefore attracts wide attention. For instance, in social networks, we predict future interactions between users for friend recommendation; In academic networks, we study the cooperation of scholars to predict their future co-workers.

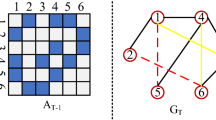
Dynamic link prediction aims to learn the evolution of the graph from historical information and predict future links. Existing methods mainly extract features (structure and attribute information) at different time from the entire graph and use those time-stamped features to model graph dynamic, such as GCRN [16], EvolveGCN [14], DynamicTriad [22]. However, all these methods ignore the fact that the entire graph usually contains diverse structures, and the evolution of different structures over time is different. This may lead to suboptimal performence of link prediction. For example, Fig. 1 shows the evolve of subgraphs with varying structures from time t to time \(\text {t+1}\). In blue and yellow dense subgraphs, more links will appear at next time. In green sparse subgraph, it is unlikely to have more future node interactions. Simply learning the evolution of the entire graph without distinguishing structures will affect the accuracy of link prediction. Therefore, it is necessary to use a multi-granularity graph instead. The graphs of different granularities contain different structures, which facilitates better learning graph structural characteristics and dynamics. However, existing dynamic link prediction methods can’t well divide graph to multi-granularity subgraphs to learn the evolution of graphs under different granularities. Although in static link prediction there are some methods learn graph structural characteristics on multiple granularities such as mlink [1] and PME [2], this kind of method only build multi-granularity graphs on the local subgraph composed of nodes and their neighbors, without dividing global similar structures to same granularity. Thus, it can hardly be applied to dynamic link prediction to learn the co-evolution pattern of the global similar structures. A recent method CTGCN [11] uses multi-granularity graphs to capture richer hierarchical structure features for dynamic link prediction. However, it does not distinguish the structure evolution under different granularities.

Fig. 1.
figure 1

It shows the changes of the subgraphs from time t to t+1. The red line represents the new link, and the circle represents the local multi-granularity subgraph divided by the one-hop and two-hop neighbors of the middle node (best see in color).

Full size image

Multi-granularity graphs can mine richer structure characteristics. Still, when applied to dynamic link prediction tasks, the inherent difficulty mainly originates from two aspects: 1) How to divide multi-granularity graphs? 2) How to learn structural features and evolution patterns on multi-granularity graphs? To better explain the first problem, the circle in Fig. 1 shows a partition way to get the multi-granularity subgraphs by node multi-order neighbors. Still, this method only focuses on the local multi-level structure, ignoring that, on the entire graph, the structures in the blue and yellow subgraphs are similar and have similar evolution patterns. Thus we attempt to seek a graph partition method that can retain both local and global information. For the second problem, the diversity of the structural characteristic and dynamics of multi-granularity dynamic graphs forces us to design a unified framework to aggregate them.

To materialize our idea, we present a novel Temporal K-truss based Recurrent Graph Convolutional Network (TKRGCN) for dynamic link prediction, which learns structural characteristics and dynamics from different granularity. Specifically, we employ k-truss decomposition to extract multi-granularity subgraphs which preserve both local and global structure information. To better extract features to capture diverse structural information, we modify GCN to alleviate the problem of over-smoothing as the number of layers deepens, enabling GCN to propagate high-order features effectively. Then we design a framework to learn the evolution process of subgraphs of different granularities. Subgraphs of different granularities make different contributions to the evolution of the entire graph. Discriminatively treating different subgraphs helps to model the complete evolution process. We conduct extensive experiments on six real-world datasets and the result shows that our model performs better than current state-of-the-art methods. The main contributions of this paper are as follows:

  • We propose TKRGCN for dynamic link prediction, which learns structural characteristics and dynamic evolution from different granularity subgraphs while preserving both local and global similar subgraph features.

  • We decouple GCN and deepen the propagation depth of GCN to alleviate the performance degradation so that GCN can effectively extract high-order features from the subgraph.

  • The experiment results demonstrate that TKRGCN outperforms the state-of-the-art benchmark in link prediction.

2 Related Work

The dynamic link prediction method needs to capture both structural properties and time evolution patterns. It mainly falls into two broad categories: discrete methods and continuous methods. Discrete methods pay more attention to changes in structural characteristics of dynamic graphs. Many methods use the architecture of combining GNNs [15] and RNNs [13] such as GCRN [16], RgCNN [17] and GGNN [10]. EvolveGCN [14] adapts to GCN in the time dimension by using RNNs to encode the parameters of GCN. DynGEM [6] employs autoencoder to generate highly non-linear node embeddings and makes some improvements on computation. In addition, continuous methods more consider the graph evolving process. DynamicTriad [22] models dynamic network evolution through modeling the triadic closure process. Dyrep [19] defines topological evolution and node interaction to simulate the evolution of dynamic graphs. However, these methods do not consider the multi-granularity dynamic graph evolution. Although CTGCN [11] divides out the multi-granularity graph to better capture the structural information, it does not distinguish the different evolution modes under the multi-granularity.

In static link prediction, there are some methods to learn graph structural characteristics on multiple granularities. For instance, mlink [1] proposes a node aggregation method that can transform the enclosing subgraph into different scales to learn scale-invariant features. PME [2] integrates first-order and second-order proximities and projects feature to different spaces to model nodes and links. But, they only build multi-granularity graphs on the local subgraphs and can hardly be applied to dynamic link prediction to learn the co-evolution pattern of the global similar structures.

3 Preliminaries

Consider a static undirected graph as \(G=(V,E)\), where \(V=\{v_1,\dots ,v_N\}\) denotes the node set with N nodes and E is the link set. We denote the dynamic graph G as an ordered set of snapshots \(\{G^1,G^2,\dots ,G^{T}\}\) from time step 1 to T. \(G_t=(V,E^t)\) is the state of the graph at time step t with a shared node set V and \(E^t\) contains the links that appear at time step t. The adjacency matrix \(A^t\in \mathbb {R}^{n\times n}\) can be either weighted or unweighted.

Given a series of snapshots represented by \(A=\{A^1,A^2,\dots ,A^t\}\) and node features \(X=\{X^1,X^2,\dots ,X^t\}\), the goal is to predict \(A^{t+1}\) at time \(t+1\). In our method, we learn the mapping series \(F=\{f_1,f_2,\dots ,f_t\}\) that \(f_t\) encodes each node in \(G^t\) into an embedding space with \(d (d\ll N)\) dimension. The node embeddings at time step \(t+1\) will be utilized to predict links.

4 The Proposed Method

We propose Temporal K-truss based Recurrent Graph Convolutional Network (TKRGCN) shown in Fig. 2, our method consists the following two parts: 1) Multi-granularity graph partition and feature extraction: To mine richer graph information, we apply the k-truss decomposition algorithm to divide multi-granularity subgraphs. This algorithm retains the local similar structure and reflects the global structural similarity, which is conducive to better learning the evolution of dynamic graphs later. Besides, to capture diverse structural information, we decouple GCN and deepen the depth of feature propagation, thus alleviating the problem of deep GCN performance degradation and enabling GCN to extract high-order features. 2) Spatio-temporal evolution embedding: To learn the structural characteristics and temporal evolution process from multi-granularity subgraphs, we design a novel architecture composed of RNNs and Attention, which learn structural information and temporal evolution of different granularities. Discriminatively treating different subgraphs helps to model the entire graph embedding.

4.1 Multi-granularity Graph Partition and Feature Extraction

Multi-granularity Graph Partition. To mine rich multi-granularity structures, we utilize k-truss decomposition [8] to obtain subgraphs. The definition is defined as follows:

Fig. 2.
figure 2

Schematic illustration of TKRGCN.

Full size image

Theorem. k-truss decomposition: Given a graph G and \(k \in \mathbb {N}\), a k-truss subgraph \(\widehat{G}_k\) of G is the largest subgraph such that \(\forall e \in E(\widehat{G}_k)\), \(sup_{\widehat{G}_k}(e) \ge k-2\).

\(sup_{\widehat{G}_k}(e)\) is the support of edge e, defined as the number of triangles containing e. G is divide to a series of nested hierarchical subgraphs \(\{\widehat{G}_2,\widehat{G}_3,\dots ,\widehat{G}_{k_{max}}\}\) by k-truss decomposition, where \(k_{max}\) is the max subgraph truss number. According to the definition, \(\widehat{G}_1 = \widehat{G}_2\), so the index of subgraphs start from 2.

From the definition, we know that a subgraph with a high value of k has a denser structure and fewer nodes. Thus the probability of links between nodes in \(\widehat{G}_k\) is greater. Intuitively, the more friends two people have in common, the stronger their relationship will be. In social networks, many groups are interconnected with dense structures, such as peer groups. People usually have close connections with members of the same group and have little contact with other groups. Meanwhile, the evolution of structurally similar groups, such as peer groups from different companies, is similar. K-truss decomposition can divide these similar structures into subgraphs under the same granularity, which is convenient for learning the common evolution process of these global similar structures.

In summary, the multi-granularity subgraphs based on k-truss decomposition retain both local and global similar structures, helping to capture rich hierarchical structure information and learn the evolution process of structures under different granularities, respectively.

Modified GCN Architecture. To extract sufficient features from each subgraph to reflect the diversity of structures, we need to propagate features in large fields. An effective and stable method for feature extraction is GCN [9], which learns high-order node features by iteratively aggregating the features from its neighbors. GCN mainly includes two operations: feature propagation and feature transformation. The former is the propagate operation that propagates features about a node’s neighbors to this node, and the latter represents the transform operation that maps the aggregated node features to a required embedding space. There are many variants of GCN. For instance, a general GCN [9] is formulated as

$$\begin{aligned} X^{\left( l\right) }=\sigma \left( {\widetilde{D}}^{-\frac{1}{2}}\widetilde{A}{\widetilde{D}}^{-\frac{1}{2}}X^{\left( l-1\right) }W^{\left( l\right) }\right) , \end{aligned}$$
(1)

where \(\widetilde{A}=A+I\) is the adjacency matrix with self-connections and I is the identity matrix. \(\widetilde{D}=diag(\sum _{j}{{\widetilde{A}}_{ij})}\) denotes a diagonal matrix where each diagonal entry is the same as corresponding position entry in \(\widetilde{A}_{ij}\). \(\sigma ()\) is a nonlinear activation function. The propagation of (1) is \(P^{(l)}=\widetilde{D}^{-\frac{1}{2}}\widetilde{A}{\widetilde{D}}^{-\frac{1}{2}}X^{\left( l-1\right) }\) while the transform operation is \(\sigma \left( P^{\left( l-1\right) }W^{\left( l\right) }\right) \).

High-order features are necessary to model multi-granularity graph structures. A one-layer GCN only considers the direct neighbors of nodes, while the multi-layer stacking GCN can learn high-order structural features, but the problem of over-smoothing may occur. Over-Smoothing refers to the fact that as the layer deepens, the features of all nodes in the same connected component tend to be the same. Thus GCN performs worse as it goes deeper. Some works [7, 12] point out that the excessive entanglement of transformation and propagation in current GCN is the key factor that affects the performance of the model. Decoupling these two operations can effectively alleviate the over-smoothing problem. Inspired by this, We design a mGCN with disentangling propagation and transformation operation as follows:

$$\begin{aligned} X^0=MLP\left( X_{init}\right) , \end{aligned}$$
(2)
$$\begin{aligned} X^j={\widetilde{D}}^{-\frac{1}{2}}\widetilde{A}^j{{\widetilde{D}}^{-\frac{1}{2}}}X^0, \ \ \ j=1,2,\cdots ,J, \end{aligned}$$
(3)
$$\begin{aligned} att^{j}=\sigma (MLP(X^j)), \ \ \ j=0,1,2,\cdots ,J, \end{aligned}$$
(4)
$$\begin{aligned} X_{out}=softmax(sum(att^0\circ X^0, \cdots , att^J\circ X^J)), \end{aligned}$$
(5)

where J is the depth of the propagation, \(X^0 \in \mathbb {R}^{N \times d} \) maps the initial node feature \(X_{init}\). \(att^j \in \mathbb {R}^{N \times 1}\) is trained to adaptively adjust the information that each node should retain in each propagation depth. \(\circ \) means the element of att is multiplied by the corresponding d-dimensional node vector. \(X_{out}\) is calculated by combining each propagation layer \(X^j\). We apply our mGCN on k-truss subgraphs at each time t and get

$$\begin{aligned} X^t_{k}=mGCN({A}^t_k,X_{init,k}^t). \end{aligned}$$
(6)

In our mGCN, we decouple the feature propagation and transformation and deepen the propagation depth separately. By learning parameters att, we can adjust the information that the node should retain in different propagation layers so that mGCN can be applied to larger receptive fields without affecting performance.

4.2 Spatio-temporal Evolution Embedding

To learn spatial and temporal embedding in multi-granularity graphs, we design the following architecture shown in Fig. 2.

Spatial Embedding. In spatial dimension, we intend to capture structure embedding from multi-granularity subgraphs. It can be seen from the previous section that there is a strong connection between the multi-granularity subgraphs \(\{X^t_{2}, X^t_{3}, \cdots , X^t_{K}\}\) obtained by k-truss decomposition. RNN is exactly suitable for processing highly correlated sequences. On snapshot \(G^t\), we reverse the sequence as \(\{X^t_{K},X^t_{K-1}, \cdots ,X^t_{2}\}\) and feed it into RNNs to learn structure information in spatial dimension. We have a mathematical representation as:

$$\begin{aligned} \begin{aligned} S^t_2 =&RNN(X^t_{K}\ \ \ ,\ S^t_{1}),\\ S^t_3 =&RNN(X^t_{K-1},\ S^t_{2}),\\&\cdots \\ S^t_K =&RNN(X^t_{2}\ \ \ \ ,\ S^t_{K-1}),\\ \end{aligned} \end{aligned}$$
(7)

where \(S^1=0\) is the initial matrix. \(S^t_k\) represents the hidden state and \(X^t_k\) denotes the input feature. In the input sequence, the subgraph with a high value of k has a denser structure and fewer nodes. Therefore, the reverse order sequence input into RNN is to learn the structural development pattern from the dense small graph to the large sparse graph. In this process, the structure information under different granularities is merged. The final hidden state output \(S^t_K\) contains the structural properties of the entire snapshot. We do this on each snapshot and ultimately obtain spatial node embeddings at each time \(\{S^1_{K}, S^2_{K}, \cdots , S^T_{K}\}\). Besides, RNN has many variants, we use the Gated Recurrent Unit (GRU) [3].

Temporal Embedding. The k-truss based multi-granularity subgraph extracts the similar structure on the whole graph into the same granularity subgraph, which retains the local and global similar structure. In temporal dimension, subgraphs of different granularities make different contributions to the evolution of the entire graph. Discriminatively treating different subgraphs helps to model the complete evolution process. We use RNN to learn how the subgraphs evolve over time of different granularities. Under each granularity k, we input \(\{X^1_{k},X^2_{k}, \cdots ,X^T_{k}\}\) into RNN as follows:

$$\begin{aligned} \begin{aligned} H^1_k =&RNN(X_{k}^{1}, H_k^{0}),\\ H^2_k =&RNN(X_{k}^{2}, H_k^{1}),\\&\cdots \\ H^T_k =&RNN(X_{k}^{T}, H_k^{T-1}),\\ \end{aligned} \end{aligned}$$
(8)

where T is the length of the time sequence. The temporal module is similar to the spatial module, and the difference is their input. Note that the structure embedding sequence \(\{S^1_{K}, S^2_{K}, \cdots , S^T_{K}\}\) is also fed into the temporal module with the same formula as (8) and output \(S^T\).

To obtain the final node representation for link prediction, we use the multi-head attention mechanism to learn the importance of the temporal embedding and spatial embedding and get the final node embedding \(H_{out}\). The formula is defined as follows:

$$\begin{aligned} H_{out} = MultiHeadAtten(S^T,H_2^T,\cdots ,H_K^T). \end{aligned}$$
(9)

4.3 Optimization

To estimate the parameters of our model, we need to specify an objective function to optimize. We design an unsupervised loss function described as:

$$\begin{aligned} \mathcal {L} = \sum _{t=1}^{T}\sum _{u\in V} ( \mathcal {L}_{u^+}^t- \mathcal {L}_{u^-}^t), \end{aligned}$$
(10)
$$\begin{aligned} \mathcal {L}_{u^+}^t =\sum _{v^+\in \mathcal {N}^+(u)}{\sigma (<h_u,h_{v^+}>)}, \end{aligned}$$
(11)
$$\begin{aligned} \mathcal {L}_{u^-}^t =\sum _{v^-\in \mathcal {N}^-(u)}{\sigma (<h_u,h_{v^-}>)}. \end{aligned}$$
(12)

The “positive” node set \(\mathcal {N}^+(u)\) includes the nodes that sampled in fixed-length random walks where node u has appeared and the “negative” nodes in \(\mathcal {N}^-(u)\) are randomly sampled from the entire graph. \(<,>\) denotes the Hadamard product. Such a design guarantees the representations of closely related nodes are close while the irrelevant nodes are far away from each other.

5 Experiments

5.1 Datasets and Baselines

We experiment on six dynamic datasets in KONECTFootnote 1 and SNAPFootnote 2. Details are summarized in Table 1. All the datasets are split by month.

Table 1. Datasets.
Full size table

We compare our model with two static methods and five dynamic methods.

  • GCN [9]: It can simultaneously perform end-to-end learning of node features and structures.

  • GAT [20]: As an optimization method of GCN, GAT introduces an attention mechanism to calculate the attention coefficient of the current node and its neighbors to reduce the impact of noise.

  • GCRN [16]: A direct dynamic embedding method that lets GCN process each snapshot and provides the output of GCN to the time series component RNN to learn the temporal patterns.

  • DynGEM [6]: It uses a deep autoencoder to get non-linear graph embedding and proposes PropSize to increase the scale of the neural network dynamically.

  • Dyngraph2vec [5]: A continuation of DynGEM which consider the historical information of the past l snapshots. It has three variants: dyngraph2vecAE, dyngraph2vecRNN, and dyngraph2vecAERNN.

  • EvolveGCN [14]: EvolveGCN uses RNNs to evolve GCN parameters. It has better results in extreme situations where nodes change frequently.

  • CTGCN [11]: It uses k-core and GCN to capture the hierarchical nature of graphs and extends it to dynamic graphs.

Settings. We use the previous \(l=5\) snapshots \(G^{t-l+1}-G^t\) to predict the link in \(G^{t+1}\). The k-truss decomposition is used to extract 3 subgraphs from each snapshot, namely, 2-truss to 4-truss subgraphs. For fair comparisons, we set the embedding dimension \(d=128\) and uniformly utilize 2 layers in GCN, GAT, GCRN, EvolveGCN.

5.2 Performance Comparison

We conduct several experiments on link prediction. Each link feature vector is calculated by the Hadamard product of the node-pair vectors. We train a logistic regression classifier with L2 regularization to classify the positive and negative links. In addition, the static version of our method KRGCN(remove the temporal module) can also perform static link prediction, which predicts the missing links using only the known information at time t. The area under the curve(AUC) is employed as the evaluation metric. We take the average of AUC as the final result.

Table 2 demonstrates the link prediction results on six datasets in static and dynamic models. The best results are shown in bold. Due to memory limitations, the AUC of DynAE and DynAERNN are not available on some datasets indicated by ‘-’. Our method TKRGCN outperforms other methods on each dataset, which strongly proves the effectiveness of our approach in using multi-granularity subgraphs to capture structural and temporal information. Moreover, our static method KRGCN surpasses some dynamic methods, showing that our multi-granularity strategy can capture more effective structural properties.

Table 2. Average AUC scores for link prediction.
Full size table

An essential hyper-parameter is K. It determines the granularity level of the graph. To analyze the influence of K on TKRGCN, we design a small-scale experiment, take the last 20 snapshots of four datasets for training and shorten the embedding dimensions to 32. The results are shown in Fig. 3. In the beginning, with the increase of K, link prediction performance has a specific improvement, especially in UCI.

Fig. 3.
figure 3

The AUC performance of various k numbers on four datasets.

Full size image

5.3 Ablation Study

To further investigate the impact of k-truss decomposition and modified GCN module for TKRGCN, we reconstruct the architecture as a)TKRGCN-sGCN: replace the modified GCN with a simple GCN [9] in TKRGCN; b)TKRGCN-single: TKRGCN without multi-granularity subgraphs. As shown in Table 3, TKRGCN performs better than the other two methods on all datasets, illustrating that both the modified GCN and the k-truss decomposition have a positive effect on TKRGCN. Additionally, compared with TKRGCN-sGCN, the performance of TKRGCN-single drops more, which indicates that k-truss based multi-granularity subgraph partition strategy is essential to dynamic link prediction.

Table 3. AUC for ablation study.
Full size table

6 Conclusion

In this paper, we propose a novel framework named TKRGCN for dynamic link prediction, which learns structural characteristics and dynamic evolution from multi-granularity subgraphs while preserving both local and global similar subgraph features. To better extract features in different subgraphs, we deepen the propagation depth of GCN to alleviate the over-smoothing problem so that GCN can be applied to larger receptive fields. The experimental results validate our method’s effectiveness. Our future work will focus on studying large-scale dynamic graphs.