Keywords

10.1 Introduction

Bridge infrastructure is imperative to economic development; however, it is subjected to continuous deterioration due to aging, traffic, and environmental conditions. The extent of deterioration needs to be monitored regularly to ensure the structural integrity of bridges. According to ASCE 2021 Report Card, nearly 231,000 bridges in the USA still need repair and preservation work. The majority of the bridges are assessed periodically using visual inspections, which can be subjective, expensive, and susceptible to errors. Bridge health monitoring (BHM) provides an effective solution to address these challenges of assessing the severity of the aging state of bridge infrastructure. Vibration-based BHM usually involves direct instrumentation with sensors such as accelerometers to extract the modal parameters from the ambient or forced vibrations [1, 2]. However, it involves traffic interruptions, bridge closures, high labor and equipment costs, and a high risk to the equipment being used on site.

As an alternative to direct BHM, researchers [3,4,5] have focused on indirect BHM (iBHM) in recent years. iBHM leverages the vehicle traveling over the bridge as a data acquisition device as well as a source of excitation. While traversing over the bridge, an instrumented vehicle can excite the bridge and collect the vibration response of the bridge. The majority of iBHM studies have focused on moving mass, moving load, and moving sprung-mass model to capture the dynamic effects of bridges in vehicle measurements. Out of these studies, the moving sprung mass model best represents the moving vehicle over the bridge by considering the inertia effects of the vehicle. However, the vehicle measurements passing over a bridge always contain bridge frequencies along with driving frequency and vehicle frequency. Therefore, it is always a challenge to delineate the effects of the latter two parameters from the measured data. Moreover, many factors such as road profile, vehicle systems, and vehicle-bridge interactions affect the performance of iBHM [5].

The idea of using a test vehicle to extract the bridge frequencies was initially proposed by [6] and was validated numerically by [7] using a simply supported beam. It was concluded that vehicle response was largely dominated by driving frequency, vehicle frequency, and the associated pairs of shifted frequencies of bridges. It was also observed that the displacement response of the vehicle was influenced by the vehicle speed, while the vehicle acceleration response was affected by the bridge frequencies. In this study, it was assumed the mass of the vehicle was small compared to the bridge. Later, empirical mode decomposition (EMD) was used by [8] to extract the higher modes of the bridge using experimental studies [9], and the importance of the selection of the most appropriate vehicle properties in a bridge was discussed. Unlike identification of bridge frequencies using previous iBHM methods, [10] conducted a study to identify the absolute damping of a bridge from the vehicle response and detect the damage. Theoretical simulations, including a simplified 2 degree-of-freedom (DOF) half-car vehicle-bridge interaction model, were used to validate the method for a range of bridge spans and vehicle speeds.

The relationship between driving velocity, vehicle frequency, and bridge frequency was examined analytically and experimentally by [11]. In their study, the effects of surface roughness, vehicle damping, and expansion joints were ignored. From the results, it was clear that higher vehicle velocities, in this case, larger than 30 km/h, created technical and practical difficulties due to vehicle bouncing impact on expansion joint and shorter response duration. [12] used the vehicle response to identify the vehicle bridge interaction (VBI) forces. The identification process was completed using a coupled 4-DOF half-car model in theoretical simulations. Based on moving force identification (MFI) theory, the proposed method identified the global bending stiffness of a bridge and predicted the pavement roughness, which was insensitive to noise. This was the first-ever approach that used the MFI theory to solve the VBI model and identify unknown vehicle forces. In a recent study, the finer frequency resolution capability of wavelet transform was leveraged by [13] to visualize the bridge damage using the response from a passing vehicle. The study also investigated the use of a subtracted signal from two consecutive axles to remove the effect of road roughness and showed good agreement between the extracted and theoretical bridge frequencies. In another study, [14] introduced the wavelet entropy theory in which the optimal wavelet scale is selected by minimizing wavelet entropy. This approach was a step forward in enhancing the existing wavelet-based damage detection methods.

[15] examined the practical viability of drive-by bridge inspection using numerical and experimental investigations. The authors proposed an index based on vehicle and bridge frequencies to quantify the performance of transmission between the bridge and the vehicle. The results indicated that more information related to bridge dynamics could be collected using a vehicle with a higher sensitivity index. The first few bridge vibration modes were identified using the test vehicle moving at constant and low speed. The study provided a benchmark that can be used to design a bridge inspection system capable of practical drive-by monitoring. [16] proposed an instantaneous frequency identification technique based on modified S-transform reassignment. The resolution was enhanced by introducing a frequency function in the Gaussian window with two parameters determined by the time-frequency (TF) concentration criterion. Numerical studies validated the effect of road profile roughness and vehicle parameters such as weight and speed on the time-varying characteristic identification. However, throughout the literature, little attention has been made to the investigation of VBI using time-frequency domain analysis. The time-varying nature of VBI due to the movement of the vehicle along the bridge gives rise to frequency variations. A powerful TF analysis method can track the frequencies of the VBI system in which vehicle and bridge are coupled at the contact point, and instantaneous frequencies vary in time.

This paper aims at exploring the difference in types of frequencies found in the vehicle response from iBHM using a robust time-frequency method, namely, Wavelet Packet Transform (WPT). In the numerical investigation, a vehicle travels over a bridge model at varying speeds, and its response is collected to be analyzed using the proposed methodology. In the laboratory experiment, a moving vehicle model travels over a scaled bridge model. WPT is used to decompose the signal collected from the vehicle into its individual components, namely, bridge frequencies, vehicle frequencies, and driving frequencies. Direct and indirect monitoring data are compared using the proposed methodology. The arrangement of this paper is provided as follows: the next section is used to provide a background about the VBI and WPT and their respective governing equations, followed by the proposed methodology of this paper. In the next two sections, the numerical and experimental investigations are presented, and lastly, a conclusion is provided for the highlights and contributions of this study.

10.2 Background

10.2.1 VBI in iBHM

The concept of iBHM uses a vehicle passing over a bridge as an excitation source and as a sensor. Figure 10.1 shows an example of a simplified VBI model that is used for the theoretical formulation. The vehicle is modeled as a quarter car with lumped mass m v and spring of stiffness k v. The bridge is modeled as a simply supported Euler-Bernoulli beam with length L and a constant cross-section and smooth profile. The beam is assumed to have a constant flexural rigidity EI and a constant mass density \( \overline{m} \) throughout the length. The vertical displacements of the vehicle and the beam are denoted by q v and u b, respectively. From the equation of motion of coupled VBI system, the solution in the form of vertical displacement of the beam can be expressed as [7]:

$$ {u}_b\left(x,t\right)=\sum_n\frac{\Delta _{stn}}{1-{S}_n^2}\left\{\sin \frac{n\pi x}{L}\left[\sin \frac{n\pi vt}{L}-{S}_n\sin {\omega}_{bn}t\right]\right\} $$
(10.1)
Fig. 10.1
figure 1

Vehicle model moving across the bridge [8]

Full size image

Using Duhamel’s integral, the vertical displacement of the vehicle can be obtained as [8]:

$${\fontsize{8.5}{10.5}\selectfont\begin{array}{l} {q}_v(t)=\sum_n\left\{{H}_{dl,n}\cos \frac{\left(n-1\right)\pi v}{L}t-{H}_{dr,n}\cos \frac{\left(n+1\right)\pi v}{L}t+{H}_{v,n}\cos {\omega}_vt-{H}_{bl,n}\cos \left({\omega}_{b,n}-\frac{n\pi v}{L}\right)t+{H}_{br,n}\cos \left({\omega}_{b,n}+\frac{n\pi v}{L}\right)t\right\} \end{array}}$$
(10.2)

The vertical acceleration response of a vehicle can be obtained by differentiating Eq. 10.2 [8]:

$${\fontsize{8.5}{10.5}\selectfont\begin{array}{l} {\ddot{q}}_v(t)=\sum_n\left\{-{\overset{\sim }{H}}_{dl,n}\cos \frac{\left(n-1\right)\pi v}{L}t+{\overset{\sim }{H}}_{dr,n}\cos \frac{\left(n+1\right)\pi v}{L}t-{\overset{\sim }{H}}_{v,n}\cos {\omega}_vt+{\overset{\sim }{H}}_{bl,n}\cos \left({\omega}_{b,n}-\frac{n\pi v}{L}\right)t-{\overset{\sim }{H}}_{br,n}\cos \left({\omega}_{b,n}+\frac{n\pi v}{L}\right)t\right\} \end{array}}\vspace*{-12pt}$$
(10.3)
$$ {H}_{dl,n}=\frac{\Delta_{st,n}}{2\left(1-{S}_n^2\right)\left(1-{\mu}_{n-1}^2{S}_{n-1}^2\right)}\vspace*{-12pt} $$
(10.4)
$$ {H}_{dr,n}=\frac{\Delta_{st,n}}{2\left(1-{S}_n^2\right)\left(1-{\mu}_{n+1}^2{S}_{n+1}^2\right)}\vspace*{-12pt} $$
(10.5)
$$ \kern7.75em {H}_{v,n}=\frac{2{\Delta}_{st,n}{\upmu}_n^2{S}_n^2}{\left(1-{S}_n^2\right)}\left[\frac{1}{\left(1-{\mu}_{n-1}^2{S}_{n-1}^2\right)\left(1-{\mu}_{n+1}^2{S}_{n+1}^2\right)}-\frac{1}{\left\{1-{\mu}_n^2\left(1-{S}_n^2\right)\right\}{\left\{1-{\mu}_n^2\left(1+{S}_n\right)\right\}}^2}\right]\vspace*{-12pt} $$
(10.6)
$$ {H}_{bl,n}=\frac{\Delta_{st,n}{S}_n}{2\left(1-{S}_n^2\right)\left\{1-{\mu}_n^2{\left(1-{S}_n\right)}^2\right\}}\vspace*{-12pt} $$
(10.7)
$$ {H}_{br,n}=\frac{\Delta_{st,n}{S}_n}{2\left(1-{S}_n^2\right)\left\{1-{\mu}_n^2{\left(1+{S}_n\right)}^2\right\}}\vspace*{-12pt} $$
(10.8)
$$ {\overset{\sim }{H}}_{dl,n}={H}_{dl,n}{\omega}_{b,n-1}^2{S}_{n-1}^2\vspace*{-12pt}$$
(10.9)
$$\vspace*{-12pt} {\overset{\sim }{H}}_{dr,n}={H}_{dr,n}{\omega}_{b,n+1}^2{S}_{n+1}^2\vspace*{-12pt} $$
(10.10)
$$ {\overset{\sim }{H}}_{v,n}={H}_{v,n}{\omega}_v^2\vspace*{-12pt} $$
(10.11)
$$ {\overset{\sim }{H}}_{bl,n}={H}_{bl,n}{\omega}_{b,n}^2{\left(1-{S}_n\right)}^2\vspace*{-12pt} $$
(10.12)
$$ {\overset{\sim }{H}}_{br,n}={H}_{br,n}{\omega}_{b,n}^2{\left(1-{S}_n\right)}^2 $$
(10.13)

The acceleration response of the vehicle traveling over the bridge can be generated using Eq. 10.3. Five terms involved in vehicle response in Eq. 10.3 can be labeled into three groups as driving frequencies, including \( \Big(\frac{\left(n-1\right)\pi v}{L}\ \mathrm{and}\ \frac{\left(n+1\right)\pi v}{L}\Big) \); vehicle frequency ω v; and bridge frequencies, including \( \Big({\omega}_{bn}-\frac{n\pi v}{L} \)and \( {\omega}_{bn}+\frac{n\pi v}{L}\Big) \). n indicates the index of the vibration modes of the bridge. It may be observed that the bridge frequencies ω bn are shifted by an equal amount to the vehicle speed \( \pm \frac{n\pi v}{L} \). The importance of bridge frequency terms \(\Big( {\omega}_{bn}-\frac{n\pi v}{L} \) and \( {\omega}_{bn}+\frac{n\pi v}{L}\Big) \) is crucial, and it will be verified whether these terms are practically visible in the vehicle response.

10.2.2 WPT

Wavelet packet transform (WPT) is a powerful time-frequency decomposition technique that can be used to decompose a particular signal into its low- and high-frequency components. This method results in both approximated and detailed coefficients [17]. Recently, [18] used a scaled bridge model for the damage detection in the shear connectors. The damage was characterized using changes in wavelet packet energy. Over the recent years, WPT has also been explored for structural damage identification [19,20,21]. The decomposition process using WPT is a recursive filter-decimation operation. After j levels of decomposition, a signal f(t) can be represented as [18]:

$$ f(t)=\sum_{i=1}^{2j}{f}_j^i(t) $$
(10.14)

A linear combination of wavelet packet functions \( {\psi}_{j,k}^i(t) \) can be used to represent the wavelet packet component signal \( {f}_j^i(t) \) [18]:

$$ {f}_j^i(t)=\sum_{k=-\infty}^{\infty }{c}_{j,k}^i(t){\psi}_{j,k}^i(t) $$
(10.15)

where a wavelet packet is a function with three indices, i, j, and k, which correspond to modulation, scale, and translation, respectively. Furthermore, wavelet packet coefficients, \( {c}_{j,k}^i(t) \), can be calculated as:

$$ {c}_{j,k}^i(t)={\int}_{-\infty}^{\infty }f(t){\psi}_{j,k}^i(t) dt $$
(10.16)

In another study, wavelet packet energy spectrum was used to create a real-time and early damage alarming system for an operational metro subway line. [22] utilized the signal denoising and wavelet packet energy spectrum to estimate and construct the damage indicators, namely, energy ratio deviation and energy ratio variance. Computational issues and accurate sensor placement were the shortcomings of this study. The application of WPT in the detection of micro-damage initiation was experimentally verified by [23]. To identify the beginning and growth of micro-damage in concrete, the energy change rate of the wavelet packet was calculated and defined as a criterion for micro-damage initiation. The results revealed that a larger wavelet packet energy change rate corresponded to a larger distribution area of micro-damage.

10.3 Methodology

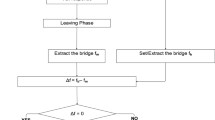
In this section, the proposed methodology and the steps involved in analyzing the data are discussed. The proposed method includes indirect monitoring, acquisition of vehicle measurement, and post-processing of the measured data. In Fig. 10.2, the data is collected from the vehicle containing the contributions of the vehicle and the bridge. After the data acquisition step, WPT is used for signal processing and to decompose the signal into its simpler components. The output of this step includes driving frequencies, bridge frequencies, and vehicle frequencies. In the next two sections, the proposed approach is verified using experimental data.

Fig. 10.2
figure 2

Proposed methodology

Full size image

10.4 Numerical Investigation

A coupled VBI system is simulated using Eq. 10.2 and the model shown in Fig. 10.1. Consider a simply supported beam subjected to a vehicle moving at speed υ. The mass and stiffness of the vehicle are 1200 kg and 500 kN/m, respectively. The simply supported beam has a length of 25 m and a mass density of 4800 kg/m. Young’s modulus of elasticity, E, for the beam is 2.75 × 1010 N/m2, and moment of inertia, I, for the beam is 0.12 m4.

Figure 10.3 shows the Fast Fourier Transform (FFT) of the vehicle acceleration response traveling at a speed of 40 km/h. The first frequency peak in this figure corresponds to the driving frequency, and the second and third frequency peaks represent the bridge frequency terms. The fourth frequency peak in Fig. 10.3 represents vehicle frequency, and the last two frequency peaks represent the second pair of bridge frequencies. As the dynamic response of the bridge is measured through the vehicle, the resultant is a pair of bridge frequencies, and the bridge frequency can be calculated by averaging the two values. The signal is processed through the WPT, which decomposes it into wavelet coefficients, shown in Fig. 10.4. It can be seen that the WPT algorithm can efficiently decompose the signal into its components. Driving frequencies, bridge frequencies, and vehicle frequencies are well separated using WPT. Figures 10.5 and 10.6 show the FFT and WPT results, respectively, for a vehicle traveling at a speed of 60 km/h over the bridge. It can be noted that WPT can decompose the frequency peaks from Fig. 10.5 into distinct individual peaks, which can be further classified into bridge frequencies, vehicle frequencies, and driving frequencies.

Fig. 10.3
figure 3

FFT of vehicle acceleration response at a speed of 40 km/h

Full size image
Fig. 10.4
figure 4

WPT coefficients of vehicle acceleration response at a speed of 40 km/h

Full size image
Fig. 10.5
figure 5

FFT of vehicle acceleration response at a speed of 60 km/h

Full size image
Fig. 10.6
figure 6

WPT coefficients of vehicle acceleration response at a speed of 60 km/h

Full size image

10.5 Laboratory Experiment

A scaled vehicle bridge interaction model is built to investigate the viability of the indirect bridge monitoring approach. The bridge model used in the experiment is a 2.4 m simply supported wooden beam shown in Fig. 10.7. The bridge is instrumented with accelerometer sensors at the mid-span to collect the bridge response during the vehicle crossings shown in Fig. 10.8. The parameters for the bridge are shown in Table 10.1. A two-axle vehicle, shown in Figs. 10.7 and 10.8, is selected to travel across the bridge at a speed of 2 m/s. The vehicle is remotely controlled using a smartphone during its multiple passages over the bridge. An accelerometer sensor is mounted under the vehicle between the two axles to collect the vibration response of the vehicle shown in Fig. 10.8. A sampling frequency of 200 Hz is used for both sensors used in this experiment. The bridge is subjected to forced vibrations using a shaker table from underneath, shown in Fig. 10.8. Forced vibrations are used to mimic the ambient vibrations of a bridge that may be caused due to wind excitations.

Fig. 10.7
figure 7

Experimental vehicle model

Full size image
Fig. 10.8
figure 8

Vehicle and beam instrumented with accelerometer sensors

Full size image
Table 10.1 Properties of the bridge model
Full size table

Figure 10.9 shows the FFT results for the bridge and vehicle acceleration response. Two bridge frequencies directly measured from the bridge deck, which can be seen in Fig. 10.9a, are mentioned in the first column (f direct) of Table 10.2. Using the analytical formula to calculate the bridge frequency pair, the frequency pair values are calculated and are shown in the second column (f analytical pair) of Table 10.2. The measured values of the frequency pair are shown in Fig. 10.9b and are tabulated in the third column (f measured pair) of Table 10.2. By averaging the frequency pair values from column 3 of Table 10.2, the bridge frequencies are calculated for the indirect method and are shown in column 4 (f indirect) of Table 10.2. It can be seen that the values from column 1 and column 4 of Table 10.2 are close to each other and indirect monitoring can be used as a reliable way of measuring the natural frequencies of a bridge. Figure 10.10 shows the WPT coefficients for the vehicle acceleration response from Fig. 10.9b. It shows that the various frequency components from Fig. 10.9b can be well separated by the WPT algorithm and can be classified using a TF method. Further studies are undergoing to differentiate between these frequencies separated by the WPT algorithm.

Fig. 10.9
figure 9

FFT of (a) bridge acceleration response and (b) vehicle acceleration response

Full size image
Table 10.2 Frequency values of bridge and vehicle responses
Full size table
Fig. 10.10
figure 10

WPT coefficients of vehicle acceleration response

Full size image

10.6 Conclusion

Bridge infrastructure is an important element of economic development and needs to be maintained regularly. Mobile sensor networks can be leveraged to monitor the bridges at a fractional cost of current monitoring methods. Using the passing vehicles traveling over a bridge as an actuator and a sensor is an active research area. This study investigates the feasibility of drive-by bridge monitoring with numerical and experimental investigations. Responses from the passing vehicle, containing the bridge dynamics data filtered through the suspension of the vehicle itself, are collected and fed into the WPT algorithm. WPT is used to delineate the various frequency contributions from the bridge, vehicle, and vibrations due to the movement of the vehicle. The output of WPT contains bridge frequencies, vehicle frequencies, and driving frequencies, which cannot be differentiated without a TF method. A TF-based modulation can be used as a quantification method to classify the individual components resulting from WPT. Future studies are underway to differentiate between the frequency components using the feature extraction tools.