Smart Active Vibration Control System of a Wind Turbine Blade Using Piezoelectric Material

Abstract

Vibration suppression has become one of the major issues in sensitive structures. The active vibration control (AVC) has been widely used in the field of vibration damping in rotary structures. In this article, deriving analytical solution of lateral vibration and active vibration control of a wind turbine (WT) blade are investigated. First, a new semi-analytical solution is developed to obtain the lateral deflection of a wind turbine blade under external loadings. We propose a method to map a wind turbine blade to an Euler-Bernoulli beam with the same conditions, in order to find vibration and dynamic responses of the blade by solving analytical vibration solutions of the Euler-Bernoulli beam. Piezoelectric (PZT) material is used in this research as an actuator-sensor to excite the structures and sense the responses. The governing equations of the beam with piezoelectric patches are derived based on the integration of the piezoelectric transducer vibration equations into the vibration equations of the Euler-Bernoulli beam structure. Finite element model of the wind turbine blade with piezoelectric patches is developed. A unique transfer function matrix is derived. The beam structure is projected to the blade by using a unique transfer function matrix which is derived by exciting the structures and achieving responses. The results obtained from the mapping method are compared with the results achieved from the FE model of the blade. A satisfying agreement has been observed between the results. Next, in order to suppress the transverse vibration of the wind turbine blade, piezoelectric ceramic patches are used as an actuator in combination with linear quadratic regulator (LQR) control system. The obtained results show that the proposed smart control system contains PZT patches and LQR control system is able to efficiently suppress lateral vibration.

1.1 Introduction

The control of unwanted vibration of wind turbine blades plays a key role in ensuring wind turbines’ (WT) high efficiency and cost-effectiveness and also, increasing the structure’s lifetime. Blade vibrations cause extreme operation instability of wind turbines and even catastrophic failure of the whole turbine which must be prevented from. Many investigations have been conducted to control vibration of sensitive rotary structures by utilizing passive, active, and semi-active control systems. In order to damp the undesired vibration of structures, proper actuators are needed to apply controlling forces. Due to the changing blade dynamics and excitation conditions, passive control methods have been less utilized for rotating structures. Active control typically provides large vibration reduction which can be tremendously helpful in damping unwanted vibration of sensitive structures. This control process needs to employ smart materials. Among different smart materials, piezoelectrics have three unique advantages, being lightweight, low cost, and convenient usage, as well as provide sensing and actuating features which can make them an appropriate material for vibration control. Piezoelectric (PZT) transducers have been widely used in active vibration control systems owing to their special properties as sensor and actuator. PZT transducers have been utilized in various shapes and forms such as perfect layer along surfaces of structures or patches in different sizes. Piezoelectric-based vibration alleviation can reduce the unwanted vibration levels of rotating structures consequently abating the risk of high cycle fatigue while lowering blade weight and drag. In this research, we propose an active vibration control system with PZT patches as sensor and actuator. To simulate the implementation of active control rules on structures, we propose an innovative semi-analytical method to project an actual shape of a wind turbine blade to the same scale of an Euler-Bernoulli beam in order to derive an analytical solution for the wind turbine blade’s dynamic response and then use the method to apply controlling rules to a wind turbine blade. Implementation of controlling rule on the wind turbine blade is not feasible by using finite element commercial software like ANSYS due to high computational cost. Hence, the proposed transfer function method is used as a surrogate to obtain the controlled deflections of a wind turbine blade in this research. Therefore, in the first step, we focus on developing a new semi-analytical solution to obtain lateral deflection of a wind turbine blade under different external loadings, and next, a suitable control system is designed in order to suppress unwanted transverse deflection of a wind turbine blade.

Derivation of analytical solutions for vibration and elasticity analysis of structures has always been noticed as an important field of research in structure analysis and design. Due to the low computational cost especially for large-scale structures, analytical solutions of dynamic responses have attracted considerable attention. However, deriving analytical solution for many structures could be very challenging due to their complicated geometry. Moreover, during recent years, a considerable increase of global warming caused sustainable energies, such as wind energy, to have absorbed wide attention as great alternative energy resources. Various types of wind turbines, such as off-shore and on-shore wind turbines with different sizes and power outputs, have been investigated in recent years as a result of this fact. Normally, large and complex wind turbines have been more concentrated due to their efficient power generation capacity. Large-scale wind turbines can suffer from significant vibrational deflection, particularly on the edges of their blades. These unwanted vibrations can cause severe structural damage and failure of the power generation systems. Due to their complex shapes and continuous interaction between wind flows and their blades, analyzing dynamical and vibrational responses of wind turbine blades is tremendously complicated. A new understanding of analytical solutions for analyzing dynamic behaviors of these kinds of structures, can contribute to the analytical analyzing of different mechanical and structural systems including twisters and heavy solid structures. In comparison to analytical methods, the vibration of these twister structures has primarily been investigated using finite element (FM) simulation and other numeric methods such as finite difference (FD) and differential quadrate (DQ). To control vibration of structures, three controlling systems including passive, active, and semi-active have been considered. These systems use various controlling rules such as proportional pulse derivative (PD), fuzzy logic control, and sliding mode control. Active control outperforms other methods for wind turbine blades due to various environmental excitation conditions and itprovides large vibration reduction.

At the first step, this research aims to propose a unique semi-analytical solution for a wind turbine blade, which can describe lateral blade movements under specific external forces. In general, a semi-analytical solution technique is proposed to solve linear partial differential equations. The semi-analytical method depends on analytically solving the equations derived by discretizing the spatial coordinates of partial differential equations. Semi-analytical approaches have a substantial advantage over numerical methods in terms of solution time. This study demonstrates how to project the real form of a wind turbine blade to the same size as an Euler-Bernoulli beam to derive an analytical solution for the wind turbine blade’s dynamic and vibration response. The blade of the GE 1.5 megawatt model, which has 45 meter blades on a 9 meter tower, is considered in this work. The blade’s material is assumed steel in order to simplify deriving equations. Plumbum-titania-zirconia is considered as piezoelectric sensor-actuator patches to sense and actuate structures. At the second step, for the purpose of alleviation of vibrations and transverse deflection of the wind turbine blade with piezoelectric patches, a linear quadratic regulator (LQR) control method is designed in this research. Due to decreasing computational cost, the proposed semi-analytical method is used to project controlled transverse vibration of the actual shape of the wind turbine blade to the Euler-Bernoulli beam instead of utilizing finite element model of the blade in order to implement control rules.

1.1.1 Background

Rotating structures, which have significance in many practical applications such as turbine blade, airplane propellers, and robot manipulators, have been investigated for a long time. The vibrations of twister beams have been widely studied with different types of beam models, e.g., Euler-Bernoulli and Timoshenko, using analytical or semi-analytical solutions and numerical or finite element methods (FEMs). The majority of previous research considered Euler-Bernoulli and Timoshenko models to describe twister and under-loading beams without considering shear deformations. The normal frequencies, mode shapes, and maximum vertical displacements of rotary beams have all been studied in order to better understand their dynamic behaviors. However, it is challenging to obtain dynamic behaviors of rotary beams due to various environmental elements including different wind flows and gravity loads. Huang et al. [1] obtained the natural frequencies of an Euler-Bernoulli beam during high-speed rotation using an exponential series solution. Arvin [2] investigates the nonlinear free vibrations of a rotating beam. He utilizes the von Kármán-strain displacement relations and derived nonlinear motion equations by Hamilton’s principle. Da Silva [3] presents a systematic and versatile research of a helicopter rotor blade’s responses. At the first step, he developed full nonlinear partial differential equations governing the motion of the blade, which take into account geometric nonlinearities caused by deformation, and then the system’s equilibrium solution was described by the system. Yigit et al. [4] studied the flexural movement of a radially rotating beam connected to a rigid body. Fully connected nonlinear motion equations were derived utilizing the extended Hamilton’s principle. Hanagud [5], Baruh [6], and Choura et al. [7] studied dynamical models of rotating Euler-Bernoulli beams without considering centripetal forces on beams. Most of previous studies about dynamical models of structures did not investigate the interaction between fluids and structures [8]. Song et al. [8] established an elaborate model in understanding the fluid-structure interaction between a structure and air flow. The arbitrary mesh interface (AMI) framework was used in conjunction with the open-source OpenFOAM tools. Wang et al. [9] provided numerical simulations of wind turbine blade-tower interaction. The vibration analysis of wind turbine blades or other rotating beam form structures may be broken down into two sections. The first is edge-wise vibration that occurs outside of the rotating circle of the beam, and the second is flap-wise vibration that occurs in the rotation plate. Lee et al. [10] studied flap-wise vibration of a composite rotational Euler-Bernoulli beam and the relationship between rotational speed and natural frequencies. Asr et al. [11] suggested prestressing in the blade structure of the H-Darrieus wind turbine in the context of axial compression stress that their research presented a structural comparison in terms of their dynamic vibrational response among reference and prestressed turbine rotor configurations. Jokar et al. [12] obtained the dynamic modeling and free vibration analysis of horizontal axis wind turbine blades in the flap-wise direction by evaluating blade kinetic and potential energies and using Hamilton’s principle. Farsadi et al. [13] perform a semi-analytical solution for the free vibration analysis of uniform and symmetric pre-twisted rotating TW which adopts the Green-Lagrange strain tensor to derive the strain field of the system and Hamilton’s principle to derive the governing equations of the dynamic system. Afzali et al. [14] derive a vibration model for a H-rotor/Giromill blade that the authors assume the blade under transverse bending and twisting deformation was treated as a uniform straight elastic Euler-Bernoulli beam. Derivation of the energy equations and simplified aerodynamic models for bending and twisting blades have been distributed, and the equations of Lagrange have been extended to assumed modal coordinates to derive nonlinear motion equations for bending and twisting blades [15,16,17,18,19]. Meksi et al. [20] derived the equations of motion of functionally graded sandwich plates from Hamilton’s principle based on a new shear deformation plate theory. Alsabagh et al. [21] implemented the Rayleigh-Ritz method for a typical 5-MW wind turbine blade and developed MATLAB codes and then obtained natural frequencies for both flap-wise and edge-wise vibrational behavior. Chen et al. [22] derive a dynamic model of curved beams by using the absolute nodal coordinate formulation based on the radial point interpolation method (RPIM). Chen et al. [23] examined the free vibration of rotating tapered Timoshenko beams by using the technique of variational iteration. Mokhtar et al. [24] investigate the rotor-stator interaction phenomenon in the finite element (FE) framework by using Lagrange multiplier based on contact mechanics. Tang et al. [25] present a developed approach that is used to identify the operational blade vibration modes by measuring the vibrational displacements with a non-contact single point laser sensor during the wear process. Liu et al. [26] study structural vibrations by establishing a dynamic equilibrium equation of a coupled system. They develop a blade’s excitation force model consisting of transverse and vertical excitation forces using a quasi-steady method. Hamilton’s principle and the finite element (FE) method with a rotating pre-twisted and leaned cantilever beam model (RPICBM) with the flap-wise-chordwise-axial-torsional coupling are set up by Zheng et al. [27] who validate the efficacy of the model through comparisons with the literature and the FE models in ANSYS. Warminski et al. [28] study dynamics of a rotor composed of a flexible beam linked to a slewing rigid hub based on extended Euler-Bernoulli theory for a slender beam model, which considers a nonlinear curvature, synchronized transverse and longitudinal oscillations, and the hub’s non-constant angular velocity. In different engineering structures, rotating composite beams and blades have a wide variety of applications [29]. Rafiee et al. [29] present a comprehensive analysis of scientific papers on rotating composite beams as presented in the past decades that for the flexural study of a sandwich beam combined with a piezoelectric layer. Wang [30] proposes a fundamental mechanics model uses the Maxwell equation in the formulation in order to extract the distribution of the piezoelectric potential. Chen et al. [31] develop a semi-analytical solution of the dynamic features of the AG-WEC by the frequency and time domain analysis based on the potential flow principle. Huang et al. [32] present a high-order finite element model and sliding model control method for a rotating flexible structure with the piezoelectric layers in order to effectively reduce the vibration. Lin [33] uses proportional and derivative controls to damp the vibration of a rotating beam by using a pair of PZT sensor and actuator layers. Bendine et al. [34] investigate on the active vibration control of a composite plate using discrete piezoelectric patches. A finite element model with PZT patches was derived based on first-order shear deformation theory, and a damping effect on composite plate was provided by using PZT actuators and applying linear quadratic regulator (LQR) control algorithm. Larbi and Deu [35] presented an efficient electromechanical finite element formulation to analyze the dynamic analysis of a cantilever beam with piezoelectric patches. Ma et al. [36] investigated on an active vibration control of a moving cantilever beam with piezoelectric ceramics as actuator by using pulse derivative closed-loop feedback system. Sivrioglu et al. [37] successfully tried to attenuate the vibration of a blade with a piezoelectric actuator patch implementing robust multi-objective control. The controlled response of a fuzzy logic controller was measured for various piezoelectric materials in active vibration control by Sharma et al. [37] and then compared them with each other. A smart active vibration control system was proposed with a new robust controlled by Cui et al. [38]. In their investigation, the system comprised PZT materials, signal conditioning, and the embedded sensor system. Pu et al. [39] applied an adaptive vibration control system contains a filtered-U least mean square algorithm and a surface bonded piezoelectric actuator to a smart structure. An active control system was designed by Brahem et al. [40] based on a full-state linear quadratic regulator controller which was applied to a rotary beam in order to alleviate the vibration. Shakir and Saber [41] developed a linear coupled finite element model by ANSYS for the piezoelectric actuation of a cantilever beam to study smart beam behavior in open- and closed-loop cases. Qiu et al. [42] developed a sliding mode control strategy to damp the vibration of a piezoelectric flexible cantilever plate. The finite element modeling was utilized to simulate the controller on bending and torsional vibration in their research. Ghaderi and Ghatei [43] presented an integrated virtual synchronization/linear quadratic regulator method to identify the system’s unknown physical parameter and vibration control of structures based on estimated parameters.

1.2 Theory and Modeling

To obtain analytical solutions for dynamic and vibration responses to any external forces and excitations and applying control rules, unlike complex structures such as wind turbine blades, the Euler-Bernoulli beam has been widely investigated. Since the Euler-Bernoulli beam theory is based on a few key assumptions and the beam has a simple geometric form, analytical study of the Euler-Bernoulli beam is achievable. The Euler-Bernoulli beam theory assumes that “plane sections remain plane” and that deformed beam angles (slopes) are small; thus, shear deformations may be ignored. The novelty of this research work includes the projection of a wind turbine blade’s deformations and lateral deflections to the same scale of Euler-Bernoulli beam and then using this mapping system for applying controlling rules on the wind turbine blade and obtained controlled vibration movements of the blade. We proposed a unique transfer function matrix to undertake the projection of a wind turbine blade to an Euler-Bernoulli beam. Lateral deflections of the Euler-Bernoulli beam are transferred to the wind turbine blade by utilizing the proposed transfer function matrix. This projection will permit us to simply obtain the dynamic and vibration responses of a wind turbine using the Euler-Bernoulli beam. Next, to damp the unwanted lateral deflection of the wind turbine blade, linear quadratic regulator (LQR) is considered in this study. An active vibration control is proposed in this study combining piezoelectric material as actuator and a designed linear quadratic regulator control method. The transfer function method is used to implement the control system on the structure in order to decrease computational costs.

To develop the transfer function matrix, both the wind turbine blade and the Euler-Bernoulli beam need to be excited with the same external excitation. At the next step, the lateral movements of selective specific nodes on their surfaces are obtained. Furthermore, in the proposed method, the Euler-Bernoulli beam should have the same length with the wind turbine blade which is 45 meters in this study. We obtain the lateral deflection of the Euler-Bernoulli analytically in this research. FE models are used to calculate the counterpart of the wind turbine blade. Piezoelectric patches are utilized to apply external excitations and sense the dynamic responses of both the wind turbine blade and the Euler-Bernoulli beam. Due to the electromechanical properties, piezoelectric materials are effective sensors and actuators. The piezoelectric sensors/actuators are patched on the surfaces of both structures. The external excitations and the dynamic responses of the structures are measured by the piezoelectric patches. To derive two initial function matrices related to the Euler-Bernoulli beam with PZT patches and the wind turbine blade with PZT patches, same external loadings are applied to the structures, and corresponding responses are obtained. Next, two initial function matrices are used to achieve a total transfer function for the whole system. At the final step, to damp unwanted lateral vibration of the blade, an active vibration control system is designed. To obtain controlled transverse movements of the blade, first, the controlling rules are applied to the to the governing dynamic equations of the beam with PZT patches under an external loading. Then, controlled lateral movements of the blade are obtained using the proposed mapping system. ion of the wind turbine blade.

1.2.1 The Euler-Bernoulli Beam Includes Piezoelectric Patches

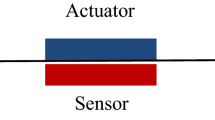
An anticipated shape of the beam with patches is depicted in Fig. 1.1.

Fig. 1.1

Anticipated figure of the beam with piezoelectric patches

The beam under discussion here is considered as an Euler-Bernoulli beam with length (L), width (b), and height (h) which are divided into n equal sections. The boundary conditions of the beam are considered to be a cantilever beam, similar to a blade in a wind turbine, attached at one end to a support, in order to achieve the best results. Edgewise vibrations are discarded in this research. Moreover, the piezoelectric patches are assumed to be set along the transversal direction of the structure. The length of each piezoelectric patch L _p became the following:

$$ {L}_p={x}_{2 bj}-{x}_{1 bj} $$

(1.1)

where j shows the number of sensors, b indicates the beam, and 2 and 1 are the beginning and the end of the patch, respectively. x _2bj and x _1bj show the distance of the end tip and the beginning of the n ^th sensor-actuator from the base, respectively. In this research, L _p is considered as 10 cm for each sensor. Furthermore, the width of each piezoelectric patch is the same as the width of the beam b, and it is located at the end of each section on the beam.

1.2.2 Analytical Modeling of the Euler-Bernoulli Beam Includes PZT Patches

Shearing deformations are neglected in the Euler-Bernoulli theory; therefore, shearing tension and strain are not included. In this theory, the shear force is derived by this equation:

$$ V=\frac{dM}{dx} $$

(1.2)

The energy method and Lagrange equations are used to obtain the governing equation for the Euler-Bernoulli beam with PZT patches. Then the assumed mode method is employed to solve acquired obtained equation. The total strain energy of the Euler-Bernoulli beam is provided as the following:

$$ U=\kern0.5em \frac{1}{2}{\int}_0^L\kern0.5em \underset{A}{\int}\left({\sigma}_{xx}{\varepsilon}_x\right) dAdx $$

(1.3)

By inserting the associated equations for stress and strain of the Euler-Bernoulli beam, Eq. 1.3 can be represented as:

$$ U=\frac{1}{2}{\int}_0^L\kern0.75em {D}_{xx}{\left(\frac{\partial {u}_z\left(x,t\right)}{\partial x}\right)}^2 dx\kern3.25em $$

(1.4)

where D _xx is defined as:

$$ {D}_{xx}= EI(x) $$

(1.5)

σ _xx and ε _x are the normal stress and normal strain in x direction, respectively. E is the Young modulus, and I(x) is the second moment of area in x direction. To derive the related strain energy equation for the beam, Eq. 1.5 needs to be substituted into Eq. 1.4, as the following:

$$ \kern0.75em U=\kern0.5em \frac{1}{2}{\int}_0^L\kern0.5em \left( EI(x){\left(\frac{\partial {u}_z(x.t)}{\partial x}\right)}^2\right) dx $$

(1.6)

where u _z(x) describes the transverse deflection of the beam at some position x.

The total formulation of the Euler-Bernoulli beam’s kinetic energy is provided as:

$$ T=\frac{1}{2}{\int}_0^L\kern0.5em \underset{A}{\int}\left(\rho {\nu}_z^2\right) dAdxdx $$

(1.7)

where ν _z is velocity and it can be presented as:

$$ {\nu}_z=\frac{\partial {u}_z(x.t)}{\partial t} $$

(1.8)

To formulate the Euler-Bernoulli beam’s cumulative kinetic energy and simplify it, Eq. 1.8 could be replaced into Eq. 1.7, as:

$$ T=\frac{1}{2}{\int}_0^L\kern0.5em \left(\rho A(x){\left(\frac{\partial {u}_z(x.t)}{\partial t}\right)}^2\right) dx $$

(1.9)

By assuming the linear PZT constitutive relations and obtaining the governing equation of the vibration of the PZT patches, the stress and strain of these patches can be derived as:

$$ {\sigma}_{xx}^p={c}_{11}^E{S}_1-{e}_{31}{E}_3\vspace*{-18pt} $$

(1.10)

$$ {\varepsilon}_{xx}^p={S}_1=-y\frac{\partial^2{u}_z\left(x,t\right)}{\partial {x}^2} $$

(1.11)

where 1, 2, and 3 show the X, Y, and Z directions, respectively. ${c}_{11}^E$, e ₃₁, and E ₃ are modules of elasticity of the PZT in constant electric field, piezoelectric stress constant, and the electric field across the electrodes of the PZT, respectively. The following is the relation between the electrical field and the voltage applied to the piezoelectric patch electrodes:

$$ {E}_3=\frac{V(t)}{h_a} $$

(1.12)

V(t) is applied harmonic voltage. The correlation between the piezoelectric stress constant and the associated strain constant, d ₃₁, is provided as:

$$ {e}_{31}={c}_{11}^E{d}_{31} $$

(1.13)

Thus, the equations of the strain energy and kinetic energy of a piezoelectric patch are formulated as:

$$ {U}_j^p=\frac{1}{2}{\int}_{x_{1a}}^{x_{2a}}\kern0.5em \left({c}_{11}^E{I}_p{\left(\frac{\partial^2{u}_z(x.t)}{\partial {x}^2}\right)}^2+{J}_pV(t){\left(\frac{\partial^2{u}_z(x.t)}{\partial {x}^2}\right)}^2\right) dx \vspace*{-18pt}$$

(1.14)

$$ {T}_j^p=\frac{1}{2}{\int}_{x_{1a}}^{x_{2a}}\kern0.5em {\rho}_a{h}_ab{\left(\frac{1}{2}\frac{\partial {u}_z(x.t)}{\partial x}\right)}^2 dx $$

(1.15)

To obtain the overall strain of the Euler-Bernoulli beam with the piezoelectric sensor and actuator, the strain energy of the piezoelectric patches must be contributed to the strain energy of the Euler-Bernoulli beam. The above process must be applied for the kinetic energy of the piezoelectric patches and the Euler-Bernoulli beam, respectively. As a result, the cumulative strain energy and kinetic energy of the beam including PZT patches are obtained as follows:

$$ U=\frac{1}{2}{\int}_0^L\kern0.75em \left( EI(x){\left(\frac{\partial {u}_z(x.t)}{\partial x}\right)}^2\right) dx+\frac{1}{2}{\int}_{x_{1a}.j}^{x_{2a.j}}\kern0.5em \left({c}_{11}^E{I}_p{\left(\frac{\partial^2{u}_z(x.t)}{\partial {x}^2}\right)}^2+{J}_pV(t){\left(\frac{\partial^2{u}_z(x.t)}{\partial {x}^2}\right)}^2\right){dx}_{j=1:n,} \vspace*{-18pt}$$

(1.16)

$$ T=\frac{1}{2}{\int}_0^L{\displaystyle \begin{array}{c}\kern0.5em \left(\rho A(x){\left(\frac{\partial {u}_z(x.t)}{\partial t}\right)}^2\right) dx+{\int}_{x_{1a.j}}^{x_{2a.j}}\kern0.5em {\rho}_a{h}_ab{\left(\frac{1}{2}\frac{\partial {u}_z(x.t)}{\partial x}\right)}^2{dx}_{j=1:n}\\ {}\ \end{array}} $$

(1.17)

where j indicates the number of piezoelectric patches.

1.2.3 Assumed Mode Method

To solve the governing equations of the beam and the piezoelectric patch, the assumed mode approximation is used. The transverse deflection under actuation of a surface-bonded PZT patch may be represented as:

$$529580\dot{}1\mathrm{\dot{}En\dot{}}1\mathrm{\dot{}Equ}18\mathrm{\dot{}Print}$$

(1.18)

where п _k shows the admissible function which satisfies geometrical boundaries and q _k describes the corresponding unknown. By replacing Eq. 1.18, into Eqs. 1.16 and 1.17, these equations can be represented as:

$$U=\frac{1}{2}{\int }_0^L\mathit{EI}\sum _{k=1}^b\sum _{l=1}^b\left(q_k{\mathrm{п}}_k^{\prime }\right)\left(q_l{\mathrm{п}}_l^{\prime }\right)\mathit{dx}+{\left(\frac{1}{2}{\int }_{x_{1a.j}}^{x_{2a.j}}{c}_{11}^E{I}_p\sum _{k=1}^b\sum _{l=1}^b{q}_k{q}_l{{\mathrm{п}}_k}^{\prime \prime }{{\mathrm{п}}_l}^{\prime \prime }\mathit{dx}+\frac{1}{2}{\int }_{x_{1a}.j}^{x_{2a.j}}{J}_{p}V\left(t\right)\sum _{k=1}^b{q}_k{{\mathrm{п}}_k}^{\prime \prime }\mathit{dx}\right)}_{j=1:n}$$

(1.19)

$$T=\frac{1}{2}{\int }_0^L\mathit{\rho A}\sum _{k=1}^b\sum _{l=1}^b\dot{q_k}\dot{q_l}{\mathrm{п}}_k{\mathrm{п}}_l\mathit{dx}+{\left(\frac{1}{2}{\int }_{x_{1a.j}}^{x_{2a.j}}{\rho }_a{h}_{a}b\sum _{k=1}^b\sum _{l=1}^b\dot{q_k}\dot{q_l}{\mathrm{п}}_k{\mathrm{п}}_l\mathit{dx}\right)}_{j=1:n}$$

(1.20)

The Lagrange equation is presented as:

$$ \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial T}{\partial \dot{q_j}}\right)-\frac{\partial T}{\partial {q}_j}+\frac{\partial U}{\partial {q}_j}=0 $$

(1.21)

The simple matrix form of the governing equation of the Euler-Bernoulli beam with the PZT patch is derived by substituting Eqs. 1.19 and 1.20 into the Lagrange Eq. 1.21 as:

$$ M\left\{\ddot{q}\right\}+K\left\{q\right\}=-V(t)\eta $$

(1.22)

where M, K, and η are presented as:

$$M=\left[\frac{1}{2}{\int }_0^L\mathit{\rho A}{\mathrm{п}}_k{\mathrm{п}}_l\mathit{dx}+{\left(\frac{1}{2}{\int }_{x_{1a.j}}^{x_{2a.j}}{\rho }_a{h}_{a}b{\mathrm{п}}_k{\mathrm{п}}_l\mathit{dx}\right)}_{j=1:n}\right]$$

(1.23)

$$K=\left[\frac{1}{2}{\int }_{-\frac{L}{2}}^{\frac{L}{2}}\mathit{\rho A}{\mathrm{п}}_k^{\prime }{\mathrm{п}}_l^{\prime }\mathit{dx}+{\left(\frac{1}{2}{\int }_{x_{1a.j}}^{x_{2a.j}}{c}_{11}^E{I}_p{\mathrm{п}}_k^{\prime \prime }{\mathrm{п}}_l^{\prime \prime }\mathit{dx}\right)}_{j=1:n}\right]$$

(1.24)

$$529580\dot{}1\mathrm{\dot{}En\dot{}}1\mathrm{\dot{}Equ}25\mathrm{\dot{}Print}$$

(1.25)

1.2.4 Finite Element Modeling

The FE modeling of the GE 1.5 MW wind turbine’s blade including PZT patches is constructed in ANSYS code. The length of the blade is 45 meters. The piezoelectric patches are attached to the blade in the same way as the Euler-Bernoulli beam is, as shown in Fig. 1.2. The connection between the PZT patches and the beam is considered to be perfect. The blade is modeled using the same beam geometry as in the analytical modeling, and the simulation is carried out three-dimensionally. In the combined field of transient structural dynamics and the electric field, the simulation of the model is performed. Defining the blade’s structural damping in FEM has a high influence on obtaining a precise approximation of the real blade’s behavior. The Rayleigh damping is considered as the structural damping model of the blade. The coefficients are obtained as α = 0.0027 and β = 0.0000017 which are the mass corresponding coefficient and stiffness corresponding coefficient, respectively.

Fig. 1.2

Section’s estimated diagram from the blade to the beam

1.2.5 The Wind Turbine Blade Projection on the Euler-Bernoulli Beam

Due to the fact that the velocity of wave propagation in solid media is only related to the frequency ranges of actuation, not the time when excitations are applied to a structure, both systems (the wind turbine blade and the Euler-Bernoulli beam) could be considered as time-invariant. The linear properties may be utilized to determine vibrational features applied to any external force since both systems are linear time-invariant (LTI). As a result of developing a semi-analytical solution for the wind turbine blade to derive the blade’s lateral deflections under various external forces, the linear time-invariant feature of the system is employed to depict an efficient, feasible, and accurate model. The proposed method leverages the linear time-invariant characteristics. As a result, only LTI systems may employ the proposed transfer projection function. The transmitted pulse signal is considered as an impulse function to obtain the frequency responses of both the FE model of the blade and the analytical model of the Euler-Bernoulli beam. A pulse signal is applied to every actuator’s location of the Euler-Bernoulli beam with piezoelectric patches. Then, the n outcomes of pulse signals are reached using the analytical equations of the beam by each applying the pulse signal to an actuator. Instead of sending the transmitted pulse signal, the unit step function can be utilized in LTI systems to identify structural frequency responses. Herein, in order to solve the equations in the time domain, the unit step function is used. To obtain the system’s responses to the transmitted pulse signal, the achieved amplitude responses from n points are differentiated for each actuation. The frequency domain is considered to extract exact responses since many noises were present among the reached responses. Noises show small frequencies and are recognizable in the frequency domain. Furthermore, in the frequency domain, high frequencies generated by the resonance phenomena can be removed. To increase the ratio of signals to noises, overvoltage is required. A step function output is defined as y _u(t). The outcomes need to be differentiated with respect to time in order to obtain the impulse function responses. The response of the impact function y _δ(t) equaled as the following:

$$ {y}_{\delta }(t)=\frac{d{y}_u(t)}{dt} $$

(1.26)

Then, the frequency response is as the following:

$$ {Y}_{\delta}\left(\omega \right)= FFT\left({y}_{\delta }(t)\right) $$

(1.27)

By applying the unit step function to each PZT actuator, n outputs from each n sensors are obtained in every actuation (n is 45 in this research). Each element of the function matrix of the beam and the blade is achieved as the following:

$$ {g}_{ij}= FFT\ \left(j\mathrm{th}\ \mathrm{output}\right)/ FFT\ \left(i\mathrm{th}\ \mathrm{input}\right) $$

(1.28)

where j indicates the number of sensor (output) and i shows the number of actuator (input). Finally, the [N × N] matrix of function G is derived by repeating this procedure for every section:

$$ G\left(i,j\right)={g}_{ij}\kern0.5em i,j=1,2,\dots .,n $$

(1.29)

Using these external excitations and associated responses, the n × n initial function matrix is derived for the Euler-Bernoulli beam with piezoelectric patches. A n × n initial function matrix is derived for the wind turbine blade with patches by applying the same external excitations and deriving lateral movements in the same way. In order to obtain amplitude responses of the blade, the FE model of the wind turbine blade with patches is constructed in ANSYS code.

By performing the mentioned method on the beam and the blade, two initial function matrices are achieved, G _b and G _w for the beam with PZT patches and the blade with PZT patches, respectively. At this step, the total transfer function matrix is derived by applying any same external dynamic load (U _s) to both systems and concerning the linear feature of the whole system as:

$$ {Y}_b={G}_b.{U}_s \vspace*{-18pt}$$

(1.30)

$$ {Y}_w={G}_w.{U}_s $$

(1.31)

By utilizing linear feature of the whole system,

$$ {Y}_w=\left(\raisebox{1ex}{${G}_w$}\!\left/ \!\raisebox{-1ex}{${G}_b$}\right.\right).{Y}_b $$

(1.32)

Finally, the total transfer function matrix is obtained using two initial matrices that were achieved in the previous step as:

$$ {G}_T=\left(\raisebox{1ex}{${G}_w$}\!\left/ \!\raisebox{-1ex}{${G}_b$}\right.\right) $$

(1.33)

Under the same external loading, the total transfer function G _T can project vibrational and tensional outcomes of the analytical solution of the Euler-Bernoulli beam with PZT patches to the wind turbine blade with PZT patches (Eqs. 1.31, 1.32, and 1.33). As shown in Fig. 1.3, the suggested approach may be organized as a semi-analytical solution to determine lateral deflection of the blade to external forces. The steps for determining lateral movements of the wind turbine blade using a semi-analytical method are as follows:

• Step 1. Obtain governing equations of the Euler-Bernoulli beam with the attached piezoelectric actuator and sensor using energy method.

• Step 2. Solve derived governing equations using the assumed mode method.

• Step 3. Develop finite element model of the wind turbine blade with PZT patched.

• Step 4. Obtain frequency responses of both systems, the FE model of the blade and the analytical model of the Euler-Bernoulli beam, by applying the transmitted pulse signal.

• Step 5. Derive initial function matrices for the Euler-Bernoulli beam and the wind turbine blade.

• Step 6. Obtain the total transfer function using two achieved initial function matrices with respect to linear properties of the systems.

Fig. 1.3

Flowchart of the total transfer function deriving process

1.2.6 The Implementation of Control System

As one of the aims of this study is to implement a control rule on the wind turbine blade in order to damp the unwanted lateral vibration, linear quadratic regulator (LQR) is considered. The controlling rules of the control system are applied on the wind turbine blade by using piezoelectric patches and the transfer function method. The 45 PZT patches are used to apply the designed linear quadratic regulator rules on the Euler-Bernoulli beam. The linear quadratic regulator is a common design technique which provides practical feedback gains. The purpose of linear quadratic regulator controlling method is trying to determine a state-feedback optimal control force which can minimize the definite quadratic cost function Eq. 1.35. The weighted matrices of the control performance index which are used to design optimal state-feedback gains are usually determined by trial and error via simulation. Authors mainly randomly select Q and R to determine whether they meet simulation requirements. In this research, we continue to adjust Q and R until they meet the requirements which include damping flap-wise deflection and using minimum energy as needed voltage for PZT patches as much as possible. The purpose of this section is to obtain two weighted matrices in LQR controller in order to design an optimal active vibration control system. To derive LQR, the generic form of the system can be written in a state-space form

$$ \dot{X}= Ax(t)+ Bu(t) $$

(1.34)

And which all of the n states x are available for the controller. The optimal state-feedback controller or LQR minimizes the infinite quadratic cost function Eq. 1.35, including the state variables (x) and control action (u). Here, {Q, R} are the symmetric positive semi-defined weighting matrix and the positive weighting factor, respectively, that tune the penalty on the excursion of state variables and control action. To minimize the integral performance index Eq. 1.35, the continuous time algebraic Riccati equation Eq. 1.36 can be used.

$$ J={\int}_0^{\infty}\left[{x}^T(t) Qx(t)+{u}^T Ru(t)\right] dt \vspace*{-18pt}$$

(1.35)

$$ {A}^TP+ PA- PB{R}^{-1}{B}^TP+Q=0 $$

(1.36)

The state-feedback optimal control force u(t) is [44]:

$$ u(t)= Kx(t) $$

(1.37)

where:

$$ K=-{R}^{-1}{B}^TP $$

(1.38)

K is unknown as an optimal controller gain and P is the unique, symmetric, positive semi-definite solution to the algebraic Riccati equation (ARE) Eq. 1.36.

The term x ^T(t)Qx(t) is a measure of control precision, and the term u ^T Ru(t) is a measure of control effort. Here, X = {q ₁, q ₂, …, q _n}^T is the lateral displacement vector obtained from n sensors on the structural system. u(t) is the control input, i.e., controlling force. The state-space representation of Eq. 1.22 is provided as Eq. 1.34; then:

$$ x=\left(\genfrac{}{}{0pt}{}{x_1}{x_2}\right)=\left(\genfrac{}{}{0pt}{}{q}{\dot{q}}\right)\vspace*{-18pt} $$

(1.39)

$$ A=\left[\begin{array}{cc}0& I\\ {}{M}^{-1}K& {M}^{-1}C\end{array}\right];B=\left[\begin{array}{c}0\\ {}{M}^{-1}U\end{array}\right] $$

(1.40)

where M, K, and C are the system mass, the system stiffness, and the damping matrices, respectively, and U is the control force vector. Figure 1.4 shows the block diagram for the control loop simulation.

Fig. 1.4

Block diagram for control

1.3 Results and Discussion

The Euler-Bernoulli beam and the FEM model of the wind turbine blade are loaded separately with three external different loadings to validate the proposed semi-analytical solution. A sine distributed load with an amplitude of 20 kg/m³ and attack angles of 15, 30, and 45 degrees are applied, respectively. The Reilly-Ritz method is employed to discretize a continuous force generated by applied external loadings to the number of divided pieces (number of actuators-sensors) on the Euler-Bernoulli beam. The comparison of analytical and FEM outcomes of the 35th sensors is shown in Fig. 1.5.

Fig. 1.5

The outcomes of the analytical results and FEM results for the 35th sensor under loading number 2 (30-degree attack angle)

Figure 1.5 shows an acceptable compliance between analytical and FEM results. Furthermore, the error between the outcomes of the analytical solution and FEM for each sensor by applying the loading number 2 (30-degree attack angle) are shown in Fig. 1.6. Based on the achieved results, there are no clear and precise patterns in the error rates dependent on sensor locations, as seen in Fig. 1.6. The results demonstrate that as the sensors’ distance from the base of the wind turbine increases, the method’s accuracy diminishes; nevertheless, there are certain outliers to the patterns, as shown in Fig. 1.6. The vibration domain of the structure naturally grows with augmentation of the distance from support, which is one cause for obtaining escalating rate of errors by raising the sensors’ interval from the base. Therefore, the span from the base can be considered as a determining factor for the method’s precision.

Fig. 1.6

Error percentage for each sensor under loading number 2 (30-degree attack angle)

The control system is implemented on the blade using the transfer function method and the Euler-Bernoulli beam in this research as using the finite element modeling directly to apply controlling rules on structures is tremendously time-consuming. A linear quadratic regulator was designed which is a proper control system as the considered structural system in this study is time-invariant. The 45 piezoelectric patches are used to apply the designed linear quadratic regulator rules on the Euler-Bernoulli beam, and then the controlled lateral deflections of the beam are mapped to the wind turbine blade with the proposed transfer function method to obtain the suppressed transverse vibration of the blade. In the design process of the linear quadratic regulator control method, the R and Q matrices are assumed unity matrix and γI, respectively, in which Gamma is a scalar. The calculation for transient response is performed with a time step of 0.01 sec. Figure 1.7 shows the results of applying controlling rule on the tip of the blade, sensor number 45, which has the maximum lateral deflection. The outcomes of damping vibration of the 45th sensor on the blade under loading number 2 (30-degree attack angel) are provided as below:

Fig. 1.7

The outcomes of applying controlling rule for the 45th sensor under loading number 2 (30-degree attack angle)

The task of the proposed active vibration control system is to suppress the vibration magnitude of the nodes. According to the achieved results, satisfactory performance of the LQR control system with PZT patches, is demonstrated for the wind turbine blade. The results indicate that the performance of the control system outperforms by decreasing the amount of Gamma as it can be seen in Fig. 1.7.

1.4 Conclusion

In this paper, a smart active vibration control system including LQR control method and piezoelectric actuator is proposed to damp the transverse deflection of a wind turbine blade. In the first part, an effective semi-analytical solution based on a unique transfer function matrix for a wind turbine blade is presented. The energy technique was used to drive the governing equations of the Euler-Bernoulli beam with the attached piezoelectric actuator and sensor. The impact of changing mass, stiffness, and electromechanical coupling between the beam and the piezoelectric actuator and sensor is considered by integrating the characteristic vibration equations of the piezoelectric patches into the characteristic equations of the Euler-Bernoulli beam. The obtained governing equations are then solved using the assumed mode method. Rayleigh damping factors are used to develop the FE model of the wind turbine blade and piezoelectric patches. A pulse signal is applied to every actuator’s location in both systems to derive initial transfer function matrices and obtain the responses for the Euler-Bernoulli beam with PZT patches and the wind turbine blade with PZT patches. Concerning the linear feature of the whole system, the final transfer function matrix is derived by applying same external dynamic force to both systems. The Euler-Bernoulli beam and the FE model of a wind turbine blade are loaded independently with three distinct loads to verify the mapping performance of the final transfer function matrix. The results demonstrate that the deflections derived directly from the FE model of the wind turbine blade and the movements obtained using the proposed method have a good correlation. Furthermore, the accuracy of the method diminished by increasing the distance of the sensors from the base of the wind turbine blade due to the natural expansion of the structure’s vibration domain in longer distance from the support. To damp the lateral vibration of the wind turbine blade, an active vibration control system was proposed including the designed LQR control system and PZT patches as actuator. Since using finite element modeling commercial software could not be feasible due to the heavy cost of computation, the semi-analytical solution is used for the implementation of controlling rules. Achieved results demonstrate satisfying performance of the proposed active vibration control of the wind turbine blade under external loadings.