Keywords

1 Introduction

Device-to-Device (D2D) communication is a promising technique for allowing two proximity user equipment to communicate directly [1]. And it can be classified into two categories according to the frequency band which can work, one is licensed-band D2D and the other is unlicensed-band D2D [2]. For the reason that the interference produced by the licensed-band D2D is easily controlled by the BS, hence the most existing works commonly focus on the licensed-band D2D [3]. But meanwhile, there are existing problem on the resource scheduling of the whole system. Hence designing an efficient resource scheduling scheme is very important.

There are three aspects that the scheduling scheme needs to concern, i.e., mode selection, resource allocation and power coordination. Especially, the earlier scheduling schemes mainly focus on the resource allocation or power coordination for the reuse direct D2D mode, and particularly, scheduling schemes on resource allocation are more based on graph theory [4,5,6,7]. For the scheduling scheme on mode selection and channel allocation, [8, 9] complete the channel allocation during the mode selection under the fully loaded cellular network and relatively lightly loaded cellular network based on the three D2D mode, i.e., cellular mode, direct D2D mode and relay D2D mode, especially when the cellular network is fully loaded, i.e., the cellular network only considers the reuse D2D mode, the thought that letting the integer programming transform linear programming is proposed under the condition that the relay is considered or not. In addition, there are existing mode selection and resource allocation which apply the D2D communication to the vehicular communication based on the cellular mode, dedicated mode and reused mode [10], and more special in the paper, the mode selection among the cellular mode and dedicated mode is selected based on the distance between the vehicular to vehicular. And the scheduling schemes based on the reinforcement learning and graph theory on mode selection and resource allocation also exist [11, 12]. For the resource allocation and power coordination, in [13], the paper transforms the constraint into feasible region, and derive the optimal power allocation that the D2D users reuse the cellular users and then using the Hungarian algorithm to solve the final problem. In [14], the paper also first delimits the feasible region, and then deduces the optimal power allocation that single D2D users reuse the cellular user, and then using the KM algorithm to solve the multi-pair D2D users to reuse the spectrum resources of the cellular users. For the jointly considering the mode selection, resource allocation and power coordination, in [15], the optimal power allocation of the reuse direct D2D mode and reuse relay D2D mode is derived first, and then the paper compares the transmission rate of the above two modes under the optimal power allocation, and then based on the results, the optimal working mode is determined and the Hungarian algorithm is finally adopted to derive the final results. Integrating the above papers, the core work is power allocation, and when finish the power allocation, the final results can be derived by adopting some casual algorithm.

But the above algorithms possess two limitations. One is that the scheduling algorithms mainly assume that the BS can acquire the perfect channel state information (CSI) of the channel that the BS needs, but lacking the consideration of the partly-known CSI of the channel and the other is that the most algorithms only consider the criteria on the physical layer and lacking the consideration of the criteria on the link layer. Thus it is important to propose a joint scheduling scheme which jointly considers the criteria on physical layer and link layer under the condition that the CSI is partly-known. Accordingly, in this paper, scheduling algorithms that can jointly perform power coordination, channel allocation for the D2D users which can only work on the reuse direct D2D mode by taking into account both the transmission rate criteria of the physical layer and the transmission delay criteria of the link layer are proposed, and the end-to-end transmission delay estimation schemes for the reuse direct D2D mode are also presented when only the statistical characteristics for the interference channel are known.

The rest of the paper is organized as followed. In Sect. 2, the considered system model is displayed. Section 3 is the problem formulation, and delay estimation, optimization objective solving are also introduced in the Sect. 3. Section 4 is the performance evaluation, Sect. 5 concludes the paper.

2 System Model

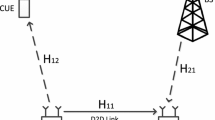
As illustrated in Fig. 1. The considered system model is a single-cell system scenario, and M cellular user equipments (CUEs), K pairs of D2D user equipments (DUEs) coexist in the cell. \(\{ C_1 ,C_2 ,...,C_m ,...,C_M \}\) denote the M CUEs, \(\{ S_1 ,S_2 ,...,S_k ,...,S_K \}\) and \(\{ D_1 ,D_2 ,...,D_k ,...,D_K \}\) denote the source and destination DUE of the K pairs of DUEs. For emphasizing the effect on introducing D2D communications, the system model is assumed as a fully loaded system model where DUEs can only access the system via the channel reuse, moreover, the DUEs can only work on the reuse direct D2D mode and each CUE’s channel can only be reused by one D2D pair. DUE must reuse the uplink channel of the selected CUE.

Owing to the CSI of the channel between CUE-DUE which needs much signal overhead to acquire, thus BS can’t acquire the perfect CSI of the channel between CUE-DUE and only masters the pass loss based on the distance, thus the channel gain in the system is build by two situations. The channel gain between transmit a and receive b except for the CUE-DUE is expressed as followed:

$$ g_{a,b} = k_0 \zeta_{a,b}^f \zeta_{a,b}^s l_{a,b}^{ - \alpha } $$
(1)

where \(k_0\) and \(\alpha\) denote the path loss constant and path loss exponent, \(\zeta_{a,b}^f\) and \(\zeta_{a,b}^s\) denote the fast and slow fading components. And the channel gain of the CUE-DUE is expressed as:

$$ h_{C_m ,D_k } = k_0 \beta_{C_m ,D_k } l_{C_m ,D_k }^{ - \alpha } $$
(2)

where \(\beta_{C_m ,D_k }\) denotes channel fading component and \(l_{C_m ,D_k }\) denotes the distance between CUE-DUE.

Fig. 1.
figure 1

System model

Full size image

3 Problem Formulation

The purpose of the paper is to maximize the transmission rate of the system while guaranteeing the delay constraint of the DUEs and QoS of the DUEs and CUEs under the condition that the CSI are partly known by the BS. For the reason that the BS can not master the perfect CSI of the interference channel CUE-DUE, thus the minimum SINR requirement of the DUE can’t be guaranteed, hence in this paper, we refer related literature to use the statistical characteristics for the interference channels to guarantee the QoS of the interference channel CUE-DUE, i.e., the probability of the actual SINR of DUE which lower than SINR requirement lower than a given threshold:

$$ \Pr \left\{ {\frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + p_{k,m}^{(C1)} h_{C_m ,D_k } }} < \xi_{\min } } \right\} \le \psi $$
(3)

where \(p_{k,m}^{(D)}\) and \(p_{k,m}^{(C1)}\) denotes the transmit power of DUE and reused CUE, \(g_{S_k ,D_k }\) denotes the channel gain of DUE, \(\sigma^2\) and \(\xi_{\min }\) denote the noise power and minimum requirement of SINR, and \(\psi\) denotes the maximal outage overflow probability of the system.

For the reason that BS can’t master the perfect CSI of the interference channel CUE-DUE, hence the transmit outage is inevitable, so we also refer the related literature to use the indicator function \(\Phi\) to denote the outage event of the DUE. When \(\Phi\) equals to 1, which denotes the received SINR lower than the given SINR requirement and the receiver of the DUE can’t demodulate the signal from the transmit, otherwise, the receiver of the DUE can modulate the signal from the transmit, thus the transmit rate can be denoted as:

$$ r_{k,m}^D = {\mathbb{E}}\left\{ {\left[ {B_0 \log_2 \left( {1 + \frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + p_{k,m}^{(C1)} h_{C_m ,D_k } }}} \right)} \right]|\Phi = 0} \right\} $$
(4)

where \(B_0\) denotes the bandwidth of the channel.

According to the related literature, above equitation can also denoted as followed:

$$ r_{k,m}^D = \int_0^l {B_0 \log_2 \left( {1 + \frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + \beta_{C_m ,D_k } p_{k,m}^{(C1)} H_{C_m ,D_k } }}} \right)} \frac{{f(\beta_{C_m ,D_k } )}}{F(l)}d\beta_{C_m ,D_k } $$
(5)

where \(l\) denotes the critical value of \(\beta_{C_m ,D_k }\) and equals to \(\frac{{p_{k,m}^{(D)} g_{S_k ,D_k } - \xi_{\min } \sigma^2 }}{{p_{k,m}^{(C1)} \xi_{\min } H_{C_m ,D_k } }}\), \(H_{C_m ,D_k }\) equals to \(k_0 l_{C_m ,D_k }^{ - \alpha }\), \(f( \cdot )\) and \(F( \cdot )\) denote the probability density function and cumulative distribution function when the channel obey Rayleigh fading, and the value can be denoted as:

$$ f(\beta_{C_m ,D_k } ) = \left\{ {\begin{array}{*{20}l} {\lambda e^{ - \lambda \beta_{C_m ,D_k } } } \hfill & { \, \beta_{C_m ,D_k } > 0} \hfill \\ 0 \hfill & { \, \beta_{C_m ,D_k } \le 0} \hfill \\ \end{array} } \right. $$
(6)
$$ F(\beta_{C_m ,D_k } ) = \left\{ {\begin{array}{*{20}l} {1 - \lambda e^{ - \lambda \beta_{C_m ,D_k } } } \hfill & {\beta_{C_m ,D_k } \rm{ \ge }0} \hfill \\ 0 \hfill & {\beta_{C_m ,D_k } \rm{ < }0} \hfill \\ \end{array} } \right. $$
(7)

where \(\lambda\) denotes the mean value of \(\beta_{C_m ,D_k }\), and assumed that it equates to 1.

When CUE is not reused by DUE, the rate of the CUE can be denoted as:

$$ r_m^{(C)} = B_0 \log_2 \left( {1 + \frac{{p_m^{(C)} g_{C_m ,B} }}{\sigma^2 }} \right) $$
(8)

where \(p_m^{(C)}\) and \(g_{C_m ,B}\) denote the transmit power of CUE when the CUE is not reused by the DUE and the channel gain between CUE and BS.

When the CUE is reused by the DUE, the rate of the CUE can be denoted as:

$$ r_{k,m}^{(C1)} = B_0 \log_2 \left( {1 + \frac{{p_{k,m}^{(C1)} g_{C_m ,B} }}{{p_{k,m}^{(D)} g_{S_k ,B} + \sigma^2 }}} \right) $$
(9)

where \(g_{S_k ,B}\) denotes the channel gain between DUE and BS.

Hence the joint scheduling algorithm can be mathematically modelled as:

$$ \left( {{{\mathbf{p}}}^* ,{{\mathbf{x}}}^* } \right) = \mathop {\arg \max }\limits_{{{\mathbf{p}}},{{\mathbf{x}}}} \left\{ {\sum_{k = 1}^K {\sum_{m = 1}^M {x_{k,m}^{(1)} } } \left( {r_{k,m}^{(C1)} + r_{k,m}^{(D)} } \right)} \right.\left. { + \sum_{m = 1}^M {\left( {1 - \sum_{k = 1}^K {x_{k,m}^{(1)} } } \right)} r_m^{(C)} } \right\} $$
(10)
$$ subject\,to:x_{k,m}^{(1)} \in \{ 0,1\} ,\forall k,m $$
(11)
$$ \sum_{k = 1}^K {x_{k,m}^{(1)} \le 1,\forall m} $$
(12)
$$ \sum_{m = 1}^M {x_{k,m}^{(1)} } \le 1,\forall k $$
(13)
$$ \sum_{m = 1}^M {x_{k,m}^{(1)} u_{k,m} } \le u_{\max } ,\forall k $$
(14)
$$ \sum_{m = 1}^M {x_{k,m}^{(1)} p_{k,m}^{(D)} } \le P_{max}^D ,\forall k $$
(15)
$$ \sum_{k = 1}^K {x_{k,m}^{(1)} } p_{k,m}^{(C1)} + \left( {1 - \sum_{k = 1}^K {x_{k,m}^{(1)} } } \right)p_m^{(C)} \le P_{\max }^C ,\forall m $$
(16)
$$ \sum_{m = 1}^M {x_{k,m}^{(1)} } \Pr \left\{ {\frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + p_{k,m}^{(C1)} h_{C_m ,D_k } }} < \xi_{\min } } \right\} \le \sum_{m = 1}^M {x_{k,m}^{(1)} } \psi ,\forall k $$
(17)
$$ \sum_{k = 1}^K {x_{k,m}^{(1)} } \frac{{p_{k,m}^{(C1)} g_{C_m ,B} }}{{p_{k,m}^{(D)} g_{S_k ,B} + \sigma^2 }} + \left( {1 - \sum_{k = 1}^K {x_{k,m}^{(1)} } } \right) \times \frac{{p_m^{(C)} g_{C_m ,B} }}{\sigma^2 } \ge \xi_{\min } ,\forall m $$
(18)

where \(x_{k,m}^{(1)}\) denotes the channel select factor, and when the k-th DUE reuse the channel of the m-th CUE, \(x_{k,m}^{(1)} = 1\), otherwise, \(x_{k,m}^{(1)} = 0\). \(u_{k,m}\) and \(u_{\max }\) denotes the delay of the channel of DUE and delay requirement. \(P_{max}^D\) and \(P_{\max }^C\) denote the maximal transmit power of the DUE and CUE. (12) and (13) restrict that a DUE can most be reused by one DUE. (14) is the delay requirement constraint. (15) and (16) are the transmit power constraint. (17) and (18) are the QoS constraint of DUE and CUE.

In order to solve the above optimization problem, the first thing is to derive the delay of the reuse direct D2D communications based on the channel probability and statistical characteristics for the interference channels.

3.1 Delay Estimation

D2D link can be treated as a queue server, and it can be denoted by a queuing model, as illustrated in Fig. 2. DUE \(S_k\) and \(D_k\) denote the source and destination DUE. \(A_{k,t}\) and \(Q_{k,t}\) denote the number of new arrival packet and queue packets at source DUE at t-th time slot, \(U_{k,t}\) denotes the number of the transmitted packets.

Fig. 2.
figure 2

Queuing model of D2D link

Full size image

For better depicting the model, the time axis is divided into time slots with length of \(\Delta T\). Assuming that packet arrival process is stationary and follows passion distribution, and the arrive rate is \(\lambda_k\), then the probability of j packets arriving at the source DUE at t-th time slot is depicted as:

$$ p\left( {A_{k,t} = j} \right) = \frac{{\left( {\lambda_k \Delta T} \right)^j }}{j!}e^{ - \lambda_k \Delta T} ,j \in (0,1,2, \cdots ) $$
(19)

Assuming that the transmitted packets always happen before the new arrival packets at every slot, then the relationship between \(Q_{k,t}\) and \(Q_{k,t - 1}\) can be described as followed:

$$ Q_{k,t} = \min \left[ {B,\max \left( {0,Q_{k,t - 1} - U_{k,t} } \right) + A_{k,t} } \right] $$
(20)

where \(B\) denotes the buffer size, i.e., the number that the source DUE can store at most.

For the reason that the BS can not master the perfect CSI of the interference link CUE-DUE, hence the transmitted rate \(U_{k,t}\) is uncertain. Under the condition, the probability of transmitting n packets at t-th time slot can be obtained based on the statistical characteristics of the interference channels, and the process of the solving is presented as followed:

$$ \begin{array}{*{20}l} {\Pr \left\{ {U_{k,t} = n} \right\}} \hfill & {\ = \Pr \left\{ {\left. {\left[ {\frac{{\Delta Tr_{k,m}^{(D)} }}{L}} \right] = n} \right\}} \right.} \hfill \\ \, \hfill & { = \Pr \left\{ {\frac{nL}{{\Delta T}} \le B_0 \log_2 \left( {1 + \frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + p_{k,m}^{(C1)} k_0 \beta_{C_m ,D_k } l_{C_m ,D_k }^{ - \alpha } }}} \right)} \right.\left. { < \frac{(n + 1)L}{{\Delta T}}} \right\}} \hfill \\ \, \hfill & { = \Pr \left\{ {\left. {2^{nL(\Delta TB0)^{ - 1} } - 1 \le \frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + p_{k,m}^{(C1)} k_0 \beta_{C_m ,D_k } l_{C_m ,D_k }^{ - \alpha } }} < 2^{(n + 1)L(\Delta TB0)^{ - 1} } - 1} \right\}} \right.} \hfill \\ \end{array} \, $$
(21)

where L denotes the number of data bits in a packet.

Further simplify (21), the above equitation can be depicted as:

$$ \begin{array}{*{20}l} {\Pr \left\{ {U_{k,t} = n} \right\}} \hfill & {{ = }\Pr \left\{ {\beta_{C_m ,D_k } \le \frac{a - (c - 1)\sigma^2 }{{(c - 1)b}}} \right\} - \Pr \left\{ {\beta_{C_m ,D_k } < \frac{a - (d - 1)\sigma^2 }{{(d - 1)b}}} \right\}} \hfill \\ \, \hfill & { = \Pr \left\{ {\beta_{C_m ,D_k } \le e_1 } \right\} - \Pr \left\{ {\beta_{C_m ,D_k } < f_1 } \right\}} \hfill \\ \end{array} $$
(22)

where \(a = p_{k,m}^{(D)} g_{S_k ,D_k }\), \(b = p_{k,m}^{(C1)} k_0 l_{C_m ,D_k }^{ - \alpha }\), \(c = 2^{nL(\Delta TB_0 )^{ - 1} }\) and \(d = 2^{(n + 1)L(\Delta TB_0 )^{ - 1} }\), \(e_1 = \frac{a - (c - 1)\sigma^2 }{{(c - 1)b}}\), \(f_1 = \frac{a - (d - 1)\sigma^2 }{{(d - 1)b}}\).

and then (22) can be further depicted as:

$$ \Pr \left\{ {U_{k,t} = n} \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {e_1 \le 0,f_1 < 0} \hfill \\ {1 - e^{ - e_1 } } \hfill & {e_1 > 0,f_1 \le 0} \hfill \\ {\ e^{ - f_1 } - e^{ - e_1 } } \hfill & {e_1 > 0,f_1 > 0} \hfill \\ \end{array} } \right. $$
(23)

According to the expression of \(A_{k,t}\) and \(U_{k,t}\), the value are not related to the time, hence the following will let the \(A_k\) and \(U_k\) express the number of new arrival packets and transmitted packets at arbitrarily slot.

Based on the relationship between the number of buffers at two slots, the queue state transition probability matrix can be depicted as:

$$ \begin{gathered} P\left( {Q_{k,t} = \theta_k |Q_{k,t - 1} = \varphi_k } \right) \hfill \\ = \left\{ {\begin{array}{*{20}l} {\Pr \left\{ {A_k = \rm{\theta }_k } \right\} \, } \hfill & {\varphi_k = 0,0 \le \rm{\theta }_k \le B - 1} \hfill \\ {\sum\limits_{j = B}^\infty {\Pr } \left\{ {A_k = j} \right\} \, } \hfill & {\varphi_k = 0,\rm{\theta }_k = B} \hfill \\ {\sum\limits_{n = \varphi_k }^\infty {\Pr } \left\{ {A_k = 0} \right\}\Pr \left\{ {U_k = n} \right\} \, } \hfill & {1 \le \varphi_k \le B,\rm{\theta }_k = 0} \hfill \\ {\sum\limits_{n = \varphi_k }^\infty {\Pr } \left\{ {A_k = \rm{\theta }_k } \right\}\Pr \left\{ {U_k = n} \right\}} \hfill & \, \hfill \\ { + \sum\limits_{n = \varphi_k - \rm{\theta }_k }^{\varphi_k - 1} {\Pr } \left\{ {A_k = \rm{\theta }_k + n - \varphi_k } \right\}\Pr \left\{ {U_k = n} \right\} \, } \hfill & {1 \le \varphi_k \le B,1 \le \rm{\theta }_k \le \varphi_k ,\rm{\theta }_k \ne B} \hfill \\ {\sum\limits_{n = \varphi_k }^\infty {\Pr } \left\{ {A_k = \rm{\theta }_k } \right\}\Pr \left\{ {U_k = n} \right\}} \hfill & \, \hfill \\ { + \sum\limits_{n = 0}^{\varphi_k - 1} {\Pr } \left\{ {A_k = \rm{\theta }_k + n - \varphi_k } \right\}\Pr \left\{ {U_k = n} \right\} \, } \hfill & {1 \le \varphi_k \le B - 1,\varphi_k < \rm{\theta }_k \le B - 1} \hfill \\ {\sum\limits_{j = B}^\infty {\sum\limits_{n = \varphi_k }^\infty {\Pr } \left\{ {A_k = j} \right\}\Pr \left\{ {U_k = n} \right\}} } \hfill & \, \hfill \\ { + \sum\limits_{n = 0}^{\varphi_k - 1} {\left( {\Pr \left\{ {U_k = n} \right\}\sum\limits_{j = B + n - \varphi_k }^\infty {\Pr } \left\{ {A_k = j} \right\}} \right)} \, } \hfill & {1 \le \varphi_k \le B,\rm{\theta }_k = B} \hfill \\ \end{array} } \right. \hfill \\ \end{gathered} $$
(24)

And the packet queuing state transition can be depicted by a Finite state Markov Chain (FSMC), then the stationary probability vector \(\Omega_{k,m}\) can be denoted by:

$$ \left\{ \begin{gathered} \Omega_{k,m} = \Omega_{k,m} P \hfill \\ \sum_{i = 0}^B {\Omega_{k,m}^i } = 1 \hfill \\ \end{gathered} \right. $$
(25)

where \(\Omega_{k,m}^i\) denotes the stationary probability of the \(i\) packets stored in the source of the DUE. The average packet queue length \(\overline{{Q_{k,m} }}\) can be obtained by:

$$ \overline{{Q_{k,m} }} = \sum_{i = 0}^B {\left( {i \times \Omega_{k,m}^i } \right)} $$
(26)

Let \(u_{k,m}\) denote the delay of the D2D link, and it can be denoted as followed based on the Littles law:

$$ u_{k,m} = \overline{{Q_{k,m} }}/\left( {\left( {1 - \phi_{k,m} } \right) \times E[A_{k,t} ]} \right) $$
(27)

where \(E[A_{k,t} ] = \lambda_k \Delta T\) denotes average number of the packets arriving at the source DUE at a slot and \(\phi_{k,m}\) denotes the packet loss rate. And \(\phi_{k,m}\) can be obtained by:

$$ \phi_{k,m} = {{D_{k,m} } / {\left( {E[A_k ]} \right)}} $$
(28)

where \(D_{k,m}\) denotes the loss number caused by the limited length of the buffer at source DUE, and \(A_k\) denotes the stationary distribution of \(A_{k,t}\). The calculation of the \(D_{k,m}\) can be obtained by:

$$ \begin{array}{*{20}l} {D_{k,m} } \hfill & { = \sum\limits_{m = 1}^B {\Omega_{k,m}^m } \sum\limits_{n = 0}^{m - 1} {\Pr } \left\{ {U_k = n} \right\}\sum\limits_{j = B + n - m}^\infty {(m + j - n - B)} \Pr \left\{ {A_k = j} \right\}} \hfill \\ \, \hfill & { + \sum\limits_{m = 1}^B {\Omega_{k,m}^m } \sum\limits_{n = m}^\infty {\Pr } \left\{ {U_k = n} \right\}\sum\limits_{j = B}^\infty {(j - B)} \Pr \left\{ {A_k = j} \right\}} \hfill \\ \, \hfill & { + \Omega_{k,m}^0 \sum\limits_{j = B}^\infty {(j - B)} \Pr \left\{ {A_k = j} \right\}} \hfill \\ \end{array} $$
(29)

Based on the derivation process, the end-to-end delay can be obtained.

3.2 Optimization Objective Solving

From (10), we can know that the optimization objective is not the linear function and the optimization problem contains the integer variable, hence the optimization problem belongs to the MINLP. For the MINLP, it is difficult to derive the final resolution. Hence we will divide the original problem into two problem to solve, that are power allocation and channel allocation, but the first thing to do first is to control the DUEs to access the network, i.e., access control.

Access Control

The accessing control based on the delay requirement, power constraint requirement and QoS requirement will be presented as followed. Only when the DUE satisfy the above three requirements, the DUE can access the network, otherwise, the DUE can’t access the network.

When the k-th DUE can reuse the m-th CUE to access the network, the DUE must satisfies the following equations:

$$ u_{k,m} \le u_{\max } $$
(30)
$$ p_{k,m}^{(D)} \le P_{max}^D ,p_{k,m}^{(C1)} \le P_{\max }^C $$
(31)
$$ \frac{{p_{k,m}^{(C1)} g_{C_m ,B} }}{{p_{k,m}^{(D)} g_{S_k ,B} + \sigma^2 }} \ge \xi_{\min } $$
(32)
$$ \Pr \left\{ {\frac{{p_{k,m}^{(D)} g_{S_k ,D_k } }}{{\sigma^2 + p_{k,m}^{(C1)} h_{C_m ,D_k } }} < \xi_{\min } } \right\} \le \psi $$
(33)

when the constraints don’t consider the delay constraint, i.e., don’t consider the (30), whether the k-th DUE can reuse the channel of m-th CUE to work on the reuse direct D2D communications can judge by the distance of CUE-DUE. And only when the real distance of CUE-DUE exceeds the shortest distance, DUE can reuse the channel of the CUE to work on the reuse direct D2D communications. Moreover when the distance satisfy the distance requirements, there are multiple transmit power pairs \((p_{k,m}^{(D)} ,p_{k,m}^{(C1)} )\) which can satisfy the (31)-(33) and they can construct three kinds of the feasible access areas, as illustrated in Fig. 3. Three kinds of feasible access regions which don’t consider delay constraint where \(lc\) denotes that the (32) takes the equation, and \(l^{\prime}_d\) denotes that the (33) takes the equation.

Fig. 3.
figure 3

Three kinds of feasible access regions which don’t consider delay constraint

Full size image

Assuming that the set of the CUE which satisfies the requirement of distance is CS, if the CS is null, the DUE can’t work on the reuse direct D2D communications, otherwise, the delay requirement of the DUE which reuses the CUE in the set need to verify in addition. According to the literature [13, 14], we verified the minimum delay in the feasible access region are D and F. Hence if the D or F satisfy the delay requirement, the DUE can reuse the channel of the CUE to work on the reuse direct D2D communications, otherwise, delete the CUE from the CS, and then justify the CS whether is null, if the CS is null, the DUE can’t work on the reuse direct D2D communications, otherwise, D2D can work on the reuse direct D2D communications.

Power Allocation and Channel Allocation

The following will allocate the power for the DUEs which can access the network and reused CUEs to maximize the sum rate of them, i.e., \(y = r_{k,m}^{(C1)} + r_{k,m}^{(D)}\) and the optimization problem can be described as:

$$ \left( {p_{{k,m}}^{{(C1)^{*} }} ,p_{{k,m}}^{{(D)^{*} }} } \right) = \mathop {\arg \max }\limits_{{(p_{{k,m}}^{{(C1)}} ,p_{{k,m}}^{{(D)}} )}} y $$
(34)

subject to: (30)–(33).

When the optimization problem doesn’t consider the delay requirement, the heuristic solution of the optimization is:

  1. (1)

    In Fig. 3 (a), the optimal allocation point is D and E;

  2. (2)

    In Fig. 3 (b), the optimal allocation point is F and G;

  3. (3)

    In Fig. 3 (c), the optimal allocation point is F, H and E.

D and F must satisfy the delay requirement, but the E, G and H may not satisfy delay requirement, hence in this paper, we let the D and F to be the power allocation point, but it is also a heuristic solution and may not an optimal solution. The power of D and F are \((P_{\max }^C ,\frac{{P_{\max }^C g_{Cm,B} - \xi_{\min } \sigma^2 }}{{\xi_{\min } g_{S_k ,B} }})\) and \((\frac{{(P_{max}^D g_{Sk,B} + \sigma^2 )\xi_{\min } }}{{g_{Cm,B} }},P_{max}^D )\).

When finishing the power allocation, the original optimization problem can be denoted as followed:

$$ \left( {{{\varvec{x}}}^* } \right) = \mathop {\arg \max }\limits_{{\varvec{x}}} \left\{ {\sum_{k = 1}^K {\sum_{m = 1}^M {x_{k,m}^{(1)} } } \left( {r_{k,m}^{(C1)} + r_{k,m}^{(D)} - r_m^{(C)} } \right)} \right. $$
(35)

subject to: (11)-(13).

And the resolution can be solved by related software.

4 Performance Evaluation

The simulation scenario is a single cell with radius 500m. CUE and DUE randomly distribute with the center of BS, and the destination D2D randomly distributes with the center of source DUE. The major parameters are listed in Table 1.

Table 1. Major parameters used in performance evaluation
Full size table

The following will validate the effective of the algorithm, the promotion of the system performance and the influence on the performance of methods by some major parameters in the system.

Based on the proposed algorithm, the first step is the evaluation of system transmit performance promotion of introducing the reuse direct D2D mode, as illustrated in Fig. 4. In the simulation, the parameter set as: \(M = 10\), \(\psi = 0.2\), \(\lambda = 7000\), \(B = 30\) and \(u_{\max } = 4\). From Fig. 4, we can see that comparing to the situations without considering the reuse direct D2D mode, considering the reuse direct D2D mode can better promote the system performance, moreover the promotion of the performance increases with the D2D pairs. The results also validate the effective of the algorithm and the importance of considering the reuse direct D2D mode.

Fig. 4.
figure 4

System sum transmission rate versus number of D2D pairs

Full size image

The major characteristic of the paper is considering the transmission delay, thus the influence on the delay by the major parameters is evaluated as followed. Randomly generating a pair of DUE and CUE, observing the influence on the delay by the major parameters. The parameters of the channel generate randomly with fixed distribution and the position of the CUE and DUE generate randomly, hence the change of the delay is wide. In order to observe the influence by the parameters better and provide the reference for the latter, we only retain the relatively small delay results, as illustrated in Fig. 5. The parameters set as: \(p_{k,m}^{(D)} = 21{\text{ dBm}}\) and \(p_{k,m}^{(C1)} = 24{\text{ dBm}}\). From the figure, we can see that when the buffer fixes, the delay will increase with the packets arrival rate, because the increasing of the packets arrival rates will lead to the increasing of average packet queue length and loss rate, hence the delay will increase. In addition, the delay will also increase with the buffer size, that is because increasing of the buffer size will lead to the increasing of the average packet queue length.

Fig. 5.
figure 5

Transmission delay versus packets arrival rate and buffer size

Full size image

Above simulation evaluates the delay performance, the following will evaluate the influence by major parameters in the system on the performance of the system, as illustrated in Fig. 6. The parameters in the simulations set as: \(M = 10\), \(K = 5\), \(\psi = 0.2\) and \(u_{\max } = 4\). From the results we can see that when the buffer is 30 and 50, the rate of the system is more easily influenced by the packets arrival rate and decreasing with the packets arrival rate. The reason is that the delay will change more obvious with the larger buffer, and the number of the DUE satisfied the delay constraint will decrease, hence the sum rate of the system will decrease.

Fig. 6.
figure 6

System sum transmission rate versus packets arrival rate and buffer size

Full size image

The following will evaluate the influence by maximal outage overflow probability and delay requirement on the system sum transmission rate. The simulation results illustrate in Fig. 7. And the parameters set as: \(M = 15\), \(K = 10\), \(\lambda = 7000\) and \(B = 30\). From the figure, we can see that the system sum transmission rate will increase with the maximal outage overflow probability and delay requirement. The reason is that the number satisfied the access constraint will increase no matter the increasing of the maximal outage overflow probability and delay requirement.

Fig. 7.
figure 7

System sum transmission rate versus maximal outage overflow probability and delay requirement

Full size image

5 Conclusions

In this paper, we consider the CSI are partly known at the BS and propose a cross-layer joint scheduling scheme that can jointly perform power coordination, channel allocation for D2D capable users by taking into account both the transmission rate criteria of physical layer and the transmission delay criteria of link layer, and meanwhile, the delay estimation method of the reuse direct D2D mode is given. At last, the effectiveness of the joint scheduling scheme and the increase of the system performance brought in the reuse direct D2D mode are validated, in addition, the simulations also analyze the influence of the major system parameters on the performance on the joint scheduling scheme.