1 Introduction

Recently, the wireless industry has experienced a substantial leap in the development of proximity-based applications, especially for social networking services. This is the motivation to standardize the device-to-device (D2D) discovery and communication of the third generation partnership project (3GPP) long-term evolution (LTE) [1]. By enabling mobile users to discover the presence of other users in their proximity and to communicate directly with each other, instead of through a base station (BS) and core network, the D2D technique can open up a host of new applications for social networking, local advertising [2, 3], and public safety [4]. Moreover, the use of D2D communications in an underlay mode can improve the overall performance of cellular systems in terms of the spectral efficiency, energy efficiency, cell coverage, traffic offloading, and so on [5,6,7,8].

However, spectrum sharing between the D2D and cellular links during underlay D2D transmissions may result in severe mutual interference, so it is necessary to devise an effective means to deal with this interference in order to ensure the quality of service (QoS) for both the D2D link and the cellular link. Recently, various attempts have been carried out to tackle the interference problem. The authors in [9] presented a power control method for D2D users in order to suppress the interference from a D2D link to a cellular link. The power optimization problem was addressed in [10, 11] to maximize the sum rate of cellular and D2D links by taking the interference of both directions into account. Another approach is to coordinate the resource allocation of the D2D and cellular links such that a cellular link and a D2D link under potentially high interference conditions are not allocated the same resources [12]. Although their approaches are different, all of these methods intend to lower the power of the interference received at the cellular link to less than a certain limit in order to protect the cellular users from the D2D transmissions. Resources can thus be allocated based on either the channel state information or the location information of the users. However, the methods proposed in these works were built upon a centralized model where the BS is responsible for managing resource allocation and power control for both the cellular and D2D communication links. It is important to note that such a centralized approach usually incurs high overhead, especially when the number of users in the cell is large.

In this paper, we propose interference-aware D2D transmission schemes to reduce the interference from D2D links to cellular links, assuming that the D2D transmitter is equipped with multiple antennas. Multiple antennas can be exploited to improve data rates through spatial multiplexing, to achieve spatial diversity, and to suppress various kinds of interference [13]. The use of multiple antennas in D2D communications for various purposes was investigated in a few previous studies. In [14], a codebook-based precoding scheme was proposed to maximize the signal-to-interference-plus-noise ratio (SINR) of the D2D link; sequential joint transceiver optimization is an optimization framework proposed in [15] that maximizes the sum rate of both the D2D and cellular links. In [16], a multi-antenna transmission scheme was developed for the cellular link in order to not generate interference for the D2D link so that the SINR of the D2D link improves. In [17], interference cancellation precoding strategies were proposed at the BS to improve the throughput achievable for the overall system. However, [17] considered only the case where the BS is equipped with multiple antennas while D2D users and cellular users have a single antenna. Similar work was performed in [18] for the case where the number of antennas for the users is larger than that for the BS. Most of these schemes require a high level of cooperation among the BS, cellular users, and D2D users, and they also mainly deal with interference from a cellular link to a D2D link. However, it will be more important to control the interference from a D2D link to a cellular link in the sense that the cellular users should be treated as primary users to D2D users. Motivated by these observations, we propose interference-aware D2D transmission schemes to maximize the achievable rate of D2D link while ensuring a good performance for the cellular link.

Specifically, we consider a scenario where cellular downlink resources are shared between the cellular links and D2D links. As a result, the performance of the cellular user is degraded due to the interference from the D2D transmitter (D2D-TX). We thus aim to maximize the achievable rate for D2D communications under two constraints: D2D-TX power constraint and interference constraint. Assuming that the D2D-TX is equipped with multiple antennas, we propose two strategies to handle the interference from the D2D link to the cellular link. Interference nulling (IN), the first strategy, constrains the transmit signal from D2D-TX to lie on the null space of the interference channel so that the cellular link is free of the interference. Interference constraining (IC), the second strategy, intends to limit the interference generated so as to keep the interference for the cellular user below a certain threshold. We thus provide efficient numerical algorithms to attain optimal D2D transmit signals based on convex optimization. The transmit beamforming and receive beamforming matrices for the D2D link are then computed through cooperation between the D2D-TX and D2D-RX. Hence, the proposed scheme works in a distributed manner in that each D2D link can be established and managed by itself with minimal involvement of the BS.

The rest of this paper is organized as follows. Section 2 presents the system model and formulates the optimization problem. The IN and IC strategies are proposed in Sect. 3. The numerical results are presented in Sect. 4, and the conclusions are drawn in Sect. 5.

Notations Bold lowercase letters and bold uppercase letters are used to represent vectors and matrices, respectively. For any square matrix \({\mathbf {M}}\), \(\left| {\mathbf {M}}\right|\) and rank\(({\mathbf {M}})\) denote its determinant and rank, respectively, tr\(({\mathbf {M}})\) denotes the trace, and \({\mathbf {M}}^{H}\) denotes the conjugate transpose. \({\mathbf {M}} \succeq 0\) indicates that \({\mathbf {M}}\) is a positive semi-definite matrix. \({\mathbf {I}}_{n}\) represents an \(n \times n\) identity matrix, and \({\mathbb {E}}\left[ \cdot \right]\) stands for the expectation operator.

2 System Model and Problem Formulation

In this section, we describe the underlay D2D communication system in a cellular network, and then establish an optimization problem for transmit/receive beamforming matrices and transmit power allocation of the D2D link.

Fig. 1
figure 1

Underlay D2D system reusing the downlink resources of a cellular link

Full size image

2.1 System Model

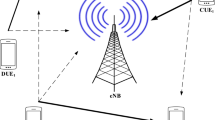
As illustrated in Fig. 1, we consider a single cell scenario where the cellular user equipment (CUE) shares its downlink resource with a D2D link comprised of a D2D transmitter (D2D-Tx) and a D2D receiver (D2D-Rx). The numbers of antennas at the D2D-Tx, D2D-Rx, BS and CUE are respectively denoted as \(M_1\), \(N_1\), \(M_2\) and \(N_2\), and it is assumed that \(M_1 > 1\), \(N_1 > 1\), \(M_2 > 1\) and \(N_2 \ge 1\). For convenience, the D2D link between the D2D-Tx and D2D-Rx and the cellular downlink from the BS to CUE are designated as links 1 and 2, respectively, as shown in Fig. 1. Accordingly, the channel matrix \({\mathbf {H}}_{ij}\, \triangleq\, \sqrt{\alpha _{ij}}\mathbf {G}_{ij}\) is associated with the transmitter of the link i and the receiver of the link j for \(i,j \in \left\{ 1,2\right\}\), in which \(\alpha _{ij}\) corresponds to long-term channel gain due to path loss and shadowing and \(\mathbf {G}_{ij}\) corresponds to the short-term fading. It is assumed that each entity of \(\mathbf {G}_{ij}\) follows an independent and identically distributed (i.i.d.) Gaussian distribution with zero mean and unit variance. The D2D-Tx is assumed to have perfect knowledge for \({\mathbf {H}}_{11}\) and \({\mathbf {H}}_{12}\) but not to have any knowledge for \({\mathbf {H}}_{21}\) and \({\mathbf {H}}_{22}\).

Let \({\mathbf {x}}_1\) and \({\mathbf {x}}_2\) denote the transmit symbol vectors at the D2D-Tx and at the BS, respectively, and let \({\mathbf {V}}\) and \({\mathbf {U}}\) denote the transmit beamforming vector at the D2D-Tx and receive beamforming vector at the D2D-Rx, respectively. Then, the received symbol vectors \({\mathbf {y}}_1\) at the D2D-Rx and \({\mathbf {y}}_2\) at the CUE can be expressed as

$$\begin{array}{ll} {\mathbf {y}}_1 = {\mathbf {U}}^H{\mathbf {H}}_{11}{\mathbf {V}}{\mathbf {x}}_1 + {\mathbf {U}}^H{\mathbf {H}}_{21}{\mathbf {x}}_2 + {\mathbf {U}}^{H}\mathbf {n}_{1}, \\ {\mathbf {y}}_2 = {\mathbf {H}}_{22} {\mathbf {x}}_2 + {\mathbf {H}}_{12}{\mathbf {V}}{\mathbf {x}}_1 + \mathbf {n}_{2}, \end{array}$$
(1)

where \(\mathbf {n}_{1}\) and \(\mathbf {n}_{2}\) denote the additive white Gaussian noise (AWGN) vector at the D2D-Rx and at the CUE, respectively. Each entry of \(\mathbf {n}_{1}\) and \(\mathbf {n}_{2}\) is assumed to be i.i.d. complex Gaussian random variables with zero mean and variance of \(\sigma _n^2\). Without considering the interference from the BS to D2D-RX, the achievable rate R of the D2D link is computed as [19]

$$\begin{aligned} R = \log _2 \left| {\mathbf {I}}_{N_{1}}+\frac{{\mathbf {U}}^H{\mathbf {H}}_{11}{\mathbf {V}} {\mathbf {S}}{\mathbf {V}}^H{\mathbf {H}}_{11}^{H}{\mathbf {U}}}{\sigma _n^2}\right| . \end{aligned}$$
(2)

where \({\mathbf {S}}\) represents the D2D transmit covariance matrix, i.e., \({\mathbf {S}}\,\triangleq\, {\mathbb {E}}\left[ {\mathbf {x}}_1{\mathbf {x}}_1^H\right]\).

2.2 Problem Formulation

When the downlink resources for a CUE are shared with the D2D link, the D2D-TX may produce interference to the CUE. Obviously, a higher D2D transmit power will improve the performance of the D2D link while causing higher interference to the cellular link. In other words, there is a tradeoff between the performance of the D2D link and that of the cellular link according to the transmit signal at the D2D-Tx. Considering that the cellular link should be protected against the D2D interference to a certain extent, a fundamental issue is to determine the optimal transmit signal to attain the maximum throughput of D2D link while guaranteeing the performance of the cellular link. To solve this question, we first note that \({\mathbf {S}}\) in (2) is positive semi-definite, and \(P\,\triangleq\, \text {tr}({\mathbf {S}})\) denotes the total transmit power of the D2D-TX.

We also note that the real achievable throughput of the D2D link should be lower than that in (2) due to the effect of the BS on D2D-RX, and the level of this effect will be mentioned in the next section. Due to the limited knowledge of the channel between the BS and D2D-RX at the D2D-TX side, it only attempts to maximize its own throughput without considering the interference from the BS. To ensure the performance of the cellular link, the SINR at the CUE must be higher than a predefined SINR threshold \(\theta\). Suppose that the BS distributes its power \(P_2\) equally to each antenna, then we have a constraint given as

$$\begin{aligned} \frac{\text {tr}({\mathbf {H}}_{22}{\mathbf {H}}_{22}^H P_2/M_2)}{\text {tr}({\mathbf {H}}_{12}{\mathbf {V}}{\mathbf {S}}{\mathbf {V}}^H{\mathbf {H}}_{12}^H) + \sigma _n^2} \ge \theta , \end{aligned}$$
(3)

which can be rewritten as

$$\begin{aligned} \text {tr}({\mathbf {H}}_{12}{\mathbf {V}}{\mathbf {S}}{\mathbf {V}}^H{\mathbf {H}}_{12}^H) \le \frac{\alpha _{22}^2 P_2 \text {tr}({\mathbf {H}}_{22}{\mathbf {H}}_{22}^H)}{\theta M_2 } - \sigma _n^2 \,\triangleq\, y_0. \end{aligned}$$
(4)

\(y_0\) in (4) represents the maximum level of interference allowed for the cellular link. We assume that the CUE perfectly knows the channel between the BS and itself. Under this assumption, the CUE can compute \(y_0\) on its own and then sends this information to D2D-TX. D2D-TX can use it in turn to decide the adequate transmit power.

Finally, the optimization problem can be formulated as

$$\begin{array}{ll} \underset{{\mathbf {S}}}{\max }\quad \log _2 \left| {\mathbf {I}}_{N_{1}}+\frac{{\mathbf {U}}^H{\mathbf {H}}_{11}{\mathbf {V}} {\mathbf {S}}{\mathbf {V}}^H{\mathbf {H}}_{11}^{H}{\mathbf {U}}}{\sigma _n^2}\right| , \\ \text {subject\ to}\nonumber \end{array}$$
(5a)
$$\begin{aligned}&\text {tr}({\mathbf {V}}{\mathbf {S}}{\mathbf {V}}^H) \le \bar{P}, \end{aligned}$$
(5b)
$$\begin{aligned}&\text {tr}({\mathbf {H}}_{12}{\mathbf {V}}{\mathbf {S}}{\mathbf {V}}^H{\mathbf {H}}_{12}^H) \le y_0, \end{aligned}$$
(5c)
$$\begin{aligned}&{\mathbf {S}} \succeq 0. \end{aligned}$$
(5d)

The problem attempts to maximize the achievable rate of D2D the link in the case that the D2D-TX perfectly knows the D2D channel. The constraint in (5b) corresponds to the transmit power constraint (\(\bar{P}\) denotes the maximum transmit power of D2D-TX) while (5c) corresponds to the interference constraint to ensure the performance of the cellular link. The constraint in (5d) indicates that the transmit covariance matrix \({\mathbf {S}}\) is positive semi-definite. Note that the problem falls into a convex optimization problem, and thus it can be efficiently solved using standard convex optimization methods [20].

3 Optimization of Beamforming and Power Allocation

We present two approaches to the optimization problem in (5) corresponding to two different designs for beamforming vectors \({\mathbf {U}}\) and \({\mathbf {V}}\). Section 3.1 presents interference nulling (IN) as the first strategy. We design the transmit beamforming vector such that it is orthogonal to the channel between D2D-TX and CUE. In other words, the D2D signal will lie on the null space of the interference channel, leading to no interference received at the CUE. In this case, the left-hand side of (5c) becomes equal to zero, and thus the constraint is always met. In Sect. 3.2, we present the interference constraint (IC), which constitutes the other strategy. In this case, the transmit beamforming vector is designed so that the interference caused to CUE is just below \(y_0\). Hence, IN can be regarded as a special case of IC with \(y_0\) set to 0.

3.1 Interference Nulling Strategy

It is necessary to assume that the number of antennas at D2D-TX is more than that at CUE to realize IN, i.e., \(M_1 > N_2\). Under such condition, the singular value decomposition (SVD) of the channel matrix \({\mathbf {H}}_{12}\) can be represented as [19]

$$\begin{aligned} {\mathbf {H}}_{12}^H = {\mathbf {U}}_0 {\mathbf {\Sigma }}_0 {\mathbf {V}}_0. \end{aligned}$$
(6)

Let \(\mathbf {A}\in { \mathbf {C}}^{M_1\times N_2}\) be a matrix constructed from the first \(N_2\) columns of \({\mathbf {U}}_0\) and let \({\mathbf {H}}_{\perp }\) be the projection of \({\mathbf {H}}_{11}\) onto the null space of \(\mathbf {A}\), then we have [21]

$$\begin{aligned} {\mathbf {H}}_{\perp } = {\mathbf {H}}_{11}({\mathbf {I}}_{M_{1}} - \mathbf {A}\mathbf {A}^H). \end{aligned}$$
(7)

Note that the rank of the orthogonal projection \({\mathbf {H}}_{\perp }\) is determined as \(M_{\perp } \,\triangleq\, \text {rank}({\mathbf {H}}_{\perp }) = \text {min} (M_1 - N_2 , N_1)\), and the SVD of the matrix \({\mathbf {H}}_{\perp }\) can be expressed as

$$\begin{aligned} {\mathbf {H}}_{\perp } = {\mathbf {U}}_{\perp } {\mathbf {\Sigma }}_{\perp } {\mathbf {V}}_{\perp }^{H}. \end{aligned}$$
(8)

From (7), it is easy to have

$$\begin{aligned} \begin{aligned}&{\mathbf {H}}_{\perp } \mathbf {A} = \mathbf {0} \\ \Rightarrow \quad&{\mathbf {U}}_{\perp } {\mathbf {\Sigma }}_{\perp } {\mathbf {V}}_{\perp }^H \mathbf {A} \mathbf {B} = \mathbf {0} \\ \Rightarrow \quad&{\mathbf {\Sigma }}_{\perp } {\mathbf {V}}_{\perp }^H {\mathbf {H}}_{12}^H = \mathbf {0}, \end{aligned} \end{aligned}$$
(9)

where \(\mathbf {B} \,\triangleq\, \mathbf {A}^H {\mathbf {H}}_{12}^H\), which implies that \({\mathbf {H}}_{12}^H = \mathbf {A}\mathbf {B}\). Note that \({\mathbf {\Sigma }}_{\perp }\) is a diagonal matrix with the last \(N_2\) components being zero on its diagonal. Therefore, the first \(M_1-N_2\) columns of \({\mathbf {H}}_{12} {\mathbf {V}}_{\perp }\) are zero vectors. If we construct the matrix \({\mathbf {V}}\) by selecting the first \(M_1 - N_2\) columns of \({\mathbf {V}}_{\perp }\), we have \({\mathbf {H}}_{12}{\mathbf {V}}=0\). Furthermore, if we let \({\mathbf {U}} = {\mathbf {U}}_{\perp }\), we have

$$\begin{aligned} \begin{aligned} {\mathbf {U}}^H{\mathbf {H}}_{11}{\mathbf {V}}&= {\mathbf {U}}^H ({\mathbf {H}}_{\perp } +{\mathbf {H}}_{11} \mathbf {A} \mathbf {A}^H) {\mathbf {V}} \\&= {\mathbf {U}}^H {\mathbf {H}}_{\perp } {\mathbf {V}} = {\mathbf {\Sigma }}, \end{aligned} \end{aligned}$$
(10)

where the second equality is a result of \(\mathbf {A}^H{\mathbf {V}}=\mathbf {0}\). \({\mathbf {\Sigma }}\) in (10) is seen to be a diagonal matrix with its diagonal components composed of those of \({\mathbf {\Sigma }}_{\perp }\) and zeros. This suggests that if we adopt \({\mathbf {V}}\) as the transmit beamforming vector at D2D-TX and \({\mathbf {U}}\) as the receive beamforming vector at D2D-RX, no interference will be generated to CUE. Let \(\bar{{\mathbf {y}}}_1 \,\triangleq\, {\mathbf {U}}^H {\mathbf {y}}_1\) be the signal after receive beamforming, and let \({\mathbf {x}}_1 = {\mathbf {V}} \bar{{\mathbf {x}}}_1\). Then the signal vector at D2D-RX after transmit and receive beamforming can be expressed as

$$\begin{aligned} \begin{aligned} \bar{{\mathbf {y}}}_1&=\alpha _{11} {\mathbf {U}}^H {\mathbf {H}}_{11} {\mathbf {V}} \bar{{\mathbf {x}}}_1 + \alpha _{21} {\mathbf {U}} ^H {\mathbf {H}}_{21}{\mathbf {x}}_2 + {\mathbf {U}}^H \mathbf {n} \\&= \alpha _{11} {\mathbf {\Sigma }} \bar{{\mathbf {x}}}_1 + \alpha _{21} {\mathbf {U}}^H {\mathbf {H}}_{21}{\mathbf {x}}_2 + \bar{\mathbf {n}}, \end{aligned} \end{aligned}$$
(11)

where \(\bar{\mathbf {n}}\) is the post-beamforming noise vector, and it follows a distribution identical to \(\mathbf {n}\). The matrix \({\mathbf {\Sigma }}\) will have \(\sqrt{\lambda _i}\) on the ith diagonal and zeros elsewhere. This means that the D2D channel is decomposed into \(M_{\perp }\) parallel independent channels where the ith channel is associated with input \(\bar{x}_{1i}\), output \(\bar{y}_{1i}\), transmit power \(p_i\) and channel gain \(\sqrt{\lambda _i}\). As a result, the optimization problem in (5) with IN beamforming is reduced to an optimal power allocation problem as

$$\begin{aligned} \begin{aligned} \underset{{\mathbf {P}}}{\max }&\quad \sum _{i=1}^{M_{\perp }}{\text {log}_2 \left( 1 +\frac{\lambda _i P_i}{\sigma _n^2} \right) }, \\ \text {subject\ to}&\quad \\&\quad \sum _{i=1}^{M_{\perp }}{P_i} \le \bar{P}, \\&\quad P_i \ge 0, \quad i=1,2,\ldots ,M_{\perp }, \end{aligned} \end{aligned}$$
(12)

where \({\mathbf {P}} \,\triangleq\, \{P_1, P_2, \ldots , P_{M_{\perp }}\}\) is a vector of optimization variables. The optimal power allocation to provide the maximum sum rate can be found using the conventional water-filling algorithm [22]. The optimal solution takes the following form:

$$\begin{aligned} P_i = \left( \omega - \frac{\sigma _n^2}{\lambda _i}\right) ^+ , \quad i=1,2,\ldots ,M_{\perp }, \end{aligned}$$
(13)

where \(\left[ x\right] ^+ \,\triangleq\, \text {max}(x,0)\), and \(\omega\) stands for the water level that satisfies \(\sum _{i=1}^{M_{\perp }}{P_i}= \bar{P}.\)

3.2 Interference Constraining Strategy

Although the IN strategy completely eliminates the interference to CUE, it has a critical drawback in that it can be used only when D2D-TX is equipped with more antennas than CUE. The IC strategy proposed in this subsection restricts the interference to CUE to just lower than a threshold instead of nullifying the interference. Note that this strategy works irrespective of the number of antennas at D2D-TX. Nevertheless, the optimization problem becomes more complicated since the constraint (5c) cannot be removed. As a result, it is not easy to derive a closed-form solution. We propose an efficient algorithm to find the optimal solution.

The SVD of channel \({\mathbf {H}}_{11}\) for the D2D link can be written as

$$\begin{aligned} {\mathbf {H}}_{11} = {\mathbf {U}}_{11}{\mathbf {\Sigma }}_{11} {\mathbf {V}}_{11}^{H}, \end{aligned}$$
(14)

of which the rank is defined as \(M \,\triangleq\, \text {min}\left( M_1, N_1\right)\). Accordingly, \({\mathbf {\Sigma }} \in { \mathbf {C}} ^{M \times M}\) can be expressed as \({\mathbf {\Sigma }} = \text {diag}\left( \sqrt{\lambda _1}, \sqrt{\lambda _2}, \ldots , \sqrt{\lambda _M}\right)\), where \(\lambda _{i}\)’s denote the eigenvalues of \({\mathbf {H}}_{11}\). We set \({\mathbf {V}}\) as the transmit beamforming vector at D2D-TX and \({\mathbf {U}}^H\) as the receive beamforming vector at D2D-RX. Let \(\bar{{\mathbf {x}}}_1 \,\triangleq\, {\mathbf {V}}{\mathbf {x}}_1\) and \(\bar{{\mathbf {y}}}_1 \,\triangleq\, {\mathbf {U}}^H {\mathbf {y}}_1\), then the signal received at D2D-RX is given as

$$\begin{aligned} \bar{{\mathbf {y}}}_1=\alpha _{11}{\mathbf {\Sigma }} \bar{{\mathbf {x}}}_1 + \alpha _{21} {\mathbf {U}}^H {\mathbf {H}}_{21}{\mathbf {x}}_2 + \bar{\mathbf {n}}. \end{aligned}$$
(15)

Note that the D2D channel is decomposed into M parallel independent channels where the ith channel is associated with input \(\bar{x}_{1i}\), output \(\bar{y}_{1i}\), and channel gain \(\lambda _i\). Consequently, the achievable rate for the D2D link can be expressed as

$$\begin{aligned} R = \sum _{i=1}^{M}{\log _2 \left( 1 +\frac{\lambda _i P_i}{\sigma _n^2} \right) }. \end{aligned}$$
(16)

Moreover, the interference that D2D-TX generates to CUE can be computed from \(\alpha _{12} {\mathbf {H}}_{12} {\mathbf {V}} \bar{{\mathbf {x}}}_1\). Let \(\mathbf {v}_i\) be the ith column vector of \({\mathbf {V}}\), then the interference associated to the ith antenna of D2D-TX is equal to \(a_i P_i\), where \(a_i \,\triangleq\, \left\| \alpha _{12} {\mathbf {H}}_{12} \mathbf {v}_i\right\| ^2\). Therefore, the total amount of interference that D2D-TX generates to CUE equals \(\sum _{i=1}^{M}a_i P_i\). As a result, the optimization problem in (5) can be rewritten as

$$\begin{aligned} \begin{aligned} \underset{{\mathbf {P}}}{\max }&\quad \sum _{i=1}^{M}{\log _2 \left( 1 +\frac{\lambda _i P_i}{\sigma _n^2} \right) }, \\ \text {subject\ to}&\quad \sum _{i=1}^{M}{P_i} \le \bar{P}, \\&\quad \sum _{i=1}^{M}{a_i P_i} \le y_0, \\&\quad P_i \ge 0, \quad i=1,2,\ldots ,M. \end{aligned} \end{aligned}$$
(17)

The solution for (17) can be found by partitioning the problem into two sub-problems, as given in Lemma 1.

Lemma 1

Consider the following two sub-problems of the original problem (17).

Sub-problem (a)

$$\begin{aligned} \begin{aligned} \underset{{\mathbf {P}}}{\max }&\quad \sum _{i=1}^{M}{\log _2 \left( 1 +\frac{\lambda _i P_i}{\sigma _n^2} \right) } \\ \text {subject\ to}&\quad \sum _{i=1}^{M}{P_i} \le \bar{P}, \\&\quad P_i \ge 0, \quad i=1,2,\ldots ,M, \end{aligned} \end{aligned}$$
(18)

Sub-problem (b)

$$\begin{aligned} \underset{{\mathbf {P}}}{\max }&\quad \sum _{i=1}^{M}{\log _2 \left( 1 +\frac{\lambda _i P_i}{\sigma _n^2} \right) }\nonumber \\ \text {subject\ to}&\quad \sum _{i=1}^{M}{a_i P_i} \le y_{0}, \nonumber \\&\quad P_i \ge 0, \quad i=1,2,\ldots ,M. \end{aligned}$$
(19)

Then, the optimal solution of the original problem (17) can be either the solution of sub-problem (a) or that of sub-problem (b). Otherwise, the optimal solution is obtained when equality holds in both of the inequality constraints in (17). In the latter case, the solution can be found from

$$\begin{aligned} \sum _{i=1}^{M}\left( \frac{\ln 2}{u + v a_i} - \frac{1}{\lambda _i}\right) ^{+} = \bar{P}, \end{aligned}$$
(20)
$$\begin{aligned} \sum _{i=1}^{M}\left( \frac{a_i \ln 2}{a_i v + u} - \frac{a_i}{\lambda _i}\right) ^{+} = \bar{y}_{0}, \end{aligned}$$
(21)

where the water-levels u and v can be determined using an iterative method.

Proof

The Lagrangian function for (17) can be defined as

$$\begin{aligned} \mathcal {L}({\mathbf {P}},u,v) = \sum _{i=1}^{M}{\log _2 \left( 1 + \frac{\lambda _i P_i}{\sigma _n^2} \right) } + u \left( \bar{P} - \sum _{i=1}^{M}{P_i}\right) + v \left( y_0 - \sum _{i=1}^{M}{a_i P_i}\right) , \end{aligned}$$
(22)

where u and v are Lagrange multipliers. The corresponding Karush–Kuhn–Tucker (KKT) conditions are given as

$$\begin{aligned}&\frac{\partial {\mathcal {L}}}{\partial {P_i}} = 0 , \end{aligned}$$
(23)
$$\begin{aligned}&u \left( \bar{P} - \sum _{i=1}^{M}{P_i}\right) = 0,\quad v \left( \bar{y}_0 - \sum _{i=1}^{M}{a_i P_i}\right) = 0, \end{aligned}$$
(24)
$$\begin{aligned}&\sum _{i=1}^{M}{P_i} \le \bar{P},\quad \sum _{i=1}^{M}{a_i P_i} \le \bar{y}_0, u \ge 0, v \ge 0, \end{aligned}$$
(25)
$$\begin{aligned}&P_i \ge 0. \end{aligned}$$
(26)

Similarly, we can obtain the Lagrangian functions and KKT conditions for the two sub-problems (18) and (19), which are omitted here. Note that the sub-problems fall into a conventional water-filling problem, and therefore they have a unique solution. Let \({\mathbf {P}}^{*}_a\) and \({\mathbf {P}}^{*}_b\) be the optimal solutions for sub-problems (a) and (b), respectively.

Apparently, there are four possible cases to satisfy the conditions in (24):

$$\begin{aligned}&\text {Case\,1 }\,\, u = 0, v = 0 , \end{aligned}$$
(27)
$$\begin{aligned}&{\text{Case}}\,2\,\, u \ne 0, v = 0,\quad {\bar{P}} = \sum _{i=1}^{M}{P_i}, \end{aligned}$$
(28)
$$\begin{aligned}&{\text{Case}}\,3\,\, v \ne 0, u = 0,\quad {\bar{y}}_0 = \sum _{i=1}^{M}{a_i P_i}, \end{aligned}$$
(29)
$$\begin{aligned}&{\text{Case}}\,4\,\, u \ne 0, v \ne 0,\quad {\bar{P}} = \sum _{i=1}^{M}{P_i}, \quad{\bar{y}}_0 = \sum _{i=1}^{M}{a_i P_i}. \end{aligned}$$
(30)

We do not need to consider Case 1 in (27), since it conflicts with (34). Now, assume that Case 2 in (28) happens, then the Lagrangian function and the KKT conditions in (22)–(26) are reduced to

$$\begin{aligned}&\mathcal {L}({\mathbf {P}},u) = \sum _{i=1}^{M}{\log _{2} \left( 1 +\frac{\lambda _i P_i}{\sigma _n^2} \right) } + u \left( \bar{P} - \sum _{i=1}^{M}{P_i}\right) \end{aligned}$$
(31)
$$\begin{aligned}&\frac{\partial {\mathcal {L}}}{\partial {P_i}} = 0,\quad u \left( \bar{P} - \sum _{i=1}^{M}{P_i}\right) = 0,\quad \sum _{i=1}^{M}{P_i} \le \bar{P}, u \ge 0, P_i \ge 0\quad \end{aligned}$$
(32)
$$\begin{aligned}&\sum _{i=1}^{M}{a_i P_i} \le \bar{y}_0. \end{aligned}$$
(33)

(31)–(32) correspond to the Lagrangian function and KKT conditions of sub-problem (a). Therefore, it has the unique solution \({\mathbf {P}}_a\). The remaining work is to examine whether \({\mathbf {P}}^{*}_{a}\) satisfies (33). If it does, \({\mathbf {P}}_a\) becomes the solution of the primal optimization problem. Otherwise, we continue to consider Case 3 in (29). Similar to Case 2, \({\mathbf {P}}^{*}_{b}\) becomes the solution of the primal optimization problem once it satisfies \(\sum _{i=1}^{M}{a_i P^{*}_{bi}} \le \bar{y}_0\), where \(P^{*}_{bi}\) denotes the ith entry of \({\mathbf {P}}^{*}_{b}\). If neither \({\mathbf {P}}^{*}_{a}\) nor \({\mathbf {P}}^{*}_{b}\) can be the solution, we only need to consider Case 4 in (30). From (23), it is not difficult to derive

$$\begin{aligned} P_i = \frac{\ln 2}{u + va_i} - \frac{\sigma _n^2}{\lambda _i}, \end{aligned}$$
(34)

which we substitute into (30) to obtain (20) and (21), considering (26). \(\square\)

figure d

According to Lemma 1, Algorithm 1 finds the solution for (5). After initialization, the algorithm first computes the solution of the sub-problem (a) and check whether it satisfies a remaining constraint of the original problem. If it does satisfy the remaining constraint, it becomes the final solution. Otherwise, the same procedure begins with the sub-problem (b). If neither sub-problem (a) nor (b) yields the final solution, a water-filling solution obtained from (20) and (21) becomes the final solution.

4 Numerical Results

In this section, we evaluate the performance of the proposed D2D transmission schemes in a cellular system. We consider a system in which D2D-TX and D2D-RX are equipped with \(M_1 = N_1 = 4\) antennas while the BS and CUE have \(M_2 = 8\) and \(N_2 = 2\) antennas, respectively.Footnote 1 Other parameters used for the simulations are tabulated in Table 1. Note that the parameters are chosen referring to 3GPP TR 36.942 [23]. In particular, a 5 MHz bandwidth is divided into 25 resource blocks (RBs) with 12 subcarriers in each RB. Each CUE is assumed to be allocated one RB and a D2D link shares resources with one specific CUE.

Table 1 Simulation parameters
Full size table
Fig. 2
figure 2

Performance comparison of IN and IC strategies without considering interference from the BS

Full size image
Fig. 3
figure 3

Performance comparison of IN and IC strategies considering interference from the BS

Full size image
Fig. 4
figure 4

Performance of the IC strategy for various values of the SINR threshold at CUE

Full size image

Figure 2 shows the achievable rate for a D2D link versus a transmit power of D2D-TX (\(P_{1}\)) when the interference from the BS is ignored. The IN strategy exhibits better performance than the IC strategy for a high transmit power, i.e., \(P_1 \ge 18\) dBm, since the IN strategy can fully exploit the power available at the BS. Meanwhile, the achievable rate for the IC strategy tends to saturate as the D2D transmit power increases because D2D-TX cannot use up all the power it has due to the interference constraint at CUE. The achievable rate for the IN strategy continues to increase with the D2D transmit power since no interference is generated to CUE no matter how large the D2D transmit power is. However, the IC strategy at a low transmit power slightly outperforms the IN strategy because the IC strategy can create more spatial channels. This implies that the performance in the low-power regime is dominated by the number of spatial channels rather than by the interference since the effect of the interference on the IC strategy is less significant for lower transmit power.

In Fig. 3, we present the achievable rate for a D2D link versus a transmit power of D2D-TX when the interference from the BS is accounted for. When compared to the results in Fig. 2, the achievable rate for the D2D link is reduced by 0 to 1 bps depending on the transmit power. Nevertheless, the performance trends are quite similar to those of Fig. 2.

Figure 4 shows the achievable rate for a D2D link for various values of SINR required at the CUE. As expected, the performance of the IC strategy is shown to degrade as the required SINR at CUE increases, especially for high D2D transmit power. Obviously, the performance of the IN strategy will be affected by the SINR required at the CUE.

5 Conclusions

In this paper, we have proposed D2D transmission schemes to efficiently share downlink resources in a cellular system when D2D users are equipped with multiple antennas. We formulated an optimization problem that maximizes the achievable rate for the D2D link while satisfying the transmit power constraint at D2D-Tx and an interference constraint at the CUE. Interference nulling (IN) and interference constraining (IC) were proposed as two transmission strategies, and the optimal transmit power allocations are determined for both strategies. The IN strategy completely eliminates the interference to CUE whereas the IC strategy limits the interference just below a certain threshold. Numerical results were presented to evaluate and compare the performance of the two strategies. The IN strategy was shown to outperform the IC strategy in a high D2D transmit power regime while the IC strategy is better in a low D2D transmit power regime. With known channel state information, both strategies can be implemented at the D2D transmitter with minimal involvement of the base station, without causing overhead to the base station. Future work will extend the transmission schemes and algorithms developed in this paper to the case where a CUE shares its resources with multiple D2D links.