Keywords

1 Introduction

Within the framework of the classical theory, piezoelectricity and piezomagneticity describe the linear coupling effects arising in elastic solids under the action of external electromagnetic field and/or mechanical loading. Then, the electro/magneto-mechanical coupling between the electric/magnetic polarization and the uniform strain occurs only in noncentrosymmetric crystals. On the other hand, it is known that the nonuniform strain field (finite value of strain gradients) can induce an electric polarization in crystalline dielectrics (even in centrosymmetric ones). The electric polarization induced by the strain gradient is referred to as flexoelectricity [30, 34]. The dependence between strain gradient and magnetic polarization is known as flexomagneticity [8, 9, 20]. Nowadays, due to the useful properties, the flexoelectric and flexomagnetic materials are widely used in sensors, actuators, filters, delay line resonators and other acoustic devices where the high-frequency surface waves may occur. In the recent decade, researches have paid special attention to the Love-type wave propagation in layered structures. The Love wave is a transverse surface wave having one component of mechanical displacement, which is parallel to the guiding layer surface and perpendicular to the direction of the wave propagation. Such kind of a surface wave in an isotropic layer deposited on isotropic substrate was originally studied by Love in 1911 [19]. The Love-wave problems in electro-magneto-elastic layered structures are widely investigated in recent studies, but the literature is mostly focused on the piezoelectric crystals [4, 7, 18, 35] and piezomagnetic or piezoelectromagnetic materials [1, 3, 5, 6, 10, 31]. The mentioned investigations were based on the postulates of the classical theory. However, to consider the effect of flexoelectricity/flexomagneticity on the surface wave propagation, the non-classical theories should be used.

To take into account the microscopic aspects of material structure and interatomic interactions, the generalized mathematical model with polarization gradient was used to investigate the Love wave propagation in centrosymmetric, isotropic, dielectric layer attached to an isotropic half-space [21]. Making use of non-classical theory with surface effects, the behavior of Love waves in an electrically-shorted piezoelectric nanofilm on an elastic substrate was studied by Zhang with co-workers [37]. Recently, the strain gradient theory of electroelastic media with flexoelectricity has been used to study the existence of Love wave in structure consisting of a flexoelectric layer rigidly linked to an elastic substrate [33]. In the above paper, in addition to the strain gradient, the effect of the high-order electric quadrupoles was considered as well. The results showed that the dispersion curves of Love waves are strongly dependent on the guiding layer thickness if its thickness reduces to nanometers. It was also derived that if the flexoelectricity is taken into account, the real part of the phase velocity can exceed the shear bulk wave velocity in the substrate and thus the ‘cut-off wave numbers’ can emerge [13, 33]. Using the governing equations of the strain gradient piezoelectricity, Singhal et al. [26, 27] analytically investigated the Love-type wave vibrations in a piezoelectric thin film overlying the pre-stressed elastic plate and studied the flexoelectricity effect in distinct piezoelectric materials (PZT-2, PZT-4, PZT-5H, LiNbO3, BaTiO3). These investigations proved that the flexoelectric effect is pronounced for sufficiently large wave numbers. On the other hand, series of studies [11, 12, 14, 15, 24, 25, 32] revealed that for high-frequency waves, it is very important to consider the micro-inertia effect. Using the strain gradient theory, a combined influence of the flexoelectric coefficients and micro-inertia characteristic length on electromechanical behavior of Love wave has been considered in [13]. It was found that flexoelectricity increases the phase velocity of Love wave while the micro-inertia effect decreases its value. The authors concluded that both the flexoelectricity and micro-inertia effect signifficantly influence the phase velocity of short-length waves and could not be omitted in layered structures with nano-scale dimensions.

Although the Love wave propagation with consideration of the flexoelectric effect has been investigated in several papers [13, 26, 27, 33], there are no studies using the mathematical models for Love waves in piezo-/flexo-magnetic structures. It should be noted that up to now, some results regarding the flexomagnetic effect in solids have been published (see for example, [8, 9, 20, 22, 36]). However, studies on the flexomagnetic effect are very seldom in literature. Since Love waves in magneto-electro-elastic materials have a practical importance, in this paper we study the influence of piezo-/flexo-magnetic effect combined with micro-inertia effect on Love wave propagation in a nano-sized wave-guiding piezomagnetic layer rigidly bonded to a piezoelectric substance. In order to separate the influence of the electric and magnetic effects on the Love waves, the piezo- and flexo-electric properties are omitted in the layer.

The paper structure is as follows. The linear equations of magneto-electro-elastic anisotropic media with flexomagneticity and micro-inertia effect are summarized in Sect. 2.1. Equations that describe the Love wave propagation (anti-plane motion) in piezoelectric and flexomagnetic ceramics are presented in Sects. 2.2 and 2.3, respectively. Section 2.4 contains the equations and general solution to the boundary problem in vacuum. Boundary conditions and dispersion relation are obtained in Sect. 2.5. Numerical results for the following material combination ‘flexomagnetic ceramic CoFe2O4 and piezoelectric ceramic BaTiO3’ are presented in Sect. 3. The conclusions are drawn in final Sect. 4.

2 Formulation and Theoretical Treatment of the Problem

2.1 Basic Relations

Based on the results presented in works [5, 8, 17, 28], the free energy density function F of a magneto-electro-elastic continuum with piezo-/flexo-magnetic and piezo-electric effects can be generalized as:

$$\begin{aligned} F = & \frac{1}{2}c_{ijkl} \varepsilon_{ij} \varepsilon_{kl} - \frac{1}{2}\mu_{ij} H_{i} H_{j} - \frac{1}{2}a_{ij} E_{i} E_{j} + \frac{1}{2}g_{jklmni} \eta_{jkl} \eta_{mni} \\ & - d_{kji} \varepsilon_{ij} H_{k} - e_{kji} \varepsilon_{ij} E_{k} - q_{ij} E_{i} H_{j} - \xi_{ijkl} H_{i} \eta_{jkl} . \\ \end{aligned}$$

Here, \(\varepsilon_{ij}\), \(E_{i}\), and \(H_{i}\) are the strain, electric field, and magnetic field components, respectively; \(\eta_{mni}\) is the component of strain-gradient tensor; \(c_{ijkl}\), \(e_{ijk}\), \(d_{ijk}\), \(a_{ij}\), \(\mu_{ij}\) and \(q_{ij}\) represent the elastic, piezoelectric, piezomagnetic, electric permittivity, magnetic permeability and magneto-electric constants, respectively; \(g_{jklmni}\) is the higher order elastic coefficient representing the strain-gradient elasticity, and \(\xi_{ijkl}\) is the flexomagnetic coefficient.

For an anisotropic piezoelectric/piezomagnetic media with flexomagneticity, the linear coupled constitutive equations can be expressed as follows:

$$\sigma_{ij} = \frac{\partial F}{{\partial \varepsilon_{ij} }} = c_{ijkl} \varepsilon_{kl} - e_{kij} E_{k} - d_{kij} H_{k} ,$$
(1)
$$\tau_{jkl} = \frac{\partial F}{{\partial \eta_{jkl} }} = - \xi_{ijkl} H_{i} + g_{jklmni} \eta_{mni} ,$$
(2)
$$D_{i} = - \frac{\partial F}{{\partial E_{i} }} = e_{ijk} \varepsilon_{jk} + a_{ij} E_{j} + q_{ij} H_{j} ,$$
(3)
$$B_{i} = - \frac{\partial F}{{\partial H_{i} }} = d_{ijk} \varepsilon_{jk} + q_{ij} E_{j} + \mu_{ij} H_{j} + \xi_{ijkl} \eta_{jkl} .$$
(4)

Here, symbols \(\sigma_{ij}\), \(\tau_{ijk}\), \(D_{i}\) and \(B_{i}\) are used to denote the stress tensor, higher-order stress, electric displacement and magnetic induction tensors, respectively. Note that the last terms in Eqs. (2) and (4) are the contribution from the strain gradients.

The linear strain–displacement relations and expressions for the strain-gradient tensor are defined as:

$$\,\varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)\,,\,\,\,\eta_{ijk} = \varepsilon_{ij,k} = \frac{1}{2}\left( {u_{i,jk} + u_{j,ik} } \right),$$
(5)

where \(u_{i}\) is the component of the displacement vector, and comma stands for partial differentiation with respect to the indicated space coordinate.

Within the quasi-static approximation, the equations, which relate the electric field and magnetic field vectors to electric potential \(\varphi_{e}\) and magnetic potential \(\psi_{m}\), are:

$$E_{j} = - \varphi_{e,j} \,,\,\,H_{j} = - \psi_{m,j} .$$
(6)

When the micro-inertia effect is taken into account, the motion equation can be written as follows [2, 29]:

$$\sigma_{ij,j} - \tau_{ijk,jk} = \rho \left( {1 - l_{1}^{2} \nabla^{2} } \right)\ddot{u}_{i} ,$$
(7)

where ρ is the mass density, \(l_{1}\) is used to denote the micro-inertia characteristic length, ∇ is nabla operator and the dot over the vector component \(u_{i}\) refers to the time derivative. Note that the micro-inertia characteristic length \(l_{1}\) is linked to the microstructure of the material [2].

For the electrostatics, in media without free electric charges, the electric and magnetic fields are governed by the Gauss-Coulomb and the Gauss–Faraday laws and are given by [16]:

$$D_{k,k} = 0,\,\,B_{k,k} = 0.$$
(8)

Field equations (7), (8), constitutive and kinematic relations (1)–(6) are needed for a unique set of equations of linear strain gradient theory of piezo-flexomagnetic continua with micro-inertia effect.

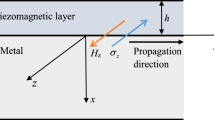
Let us obtain the differential equations describing the Love wave propagation in a layered structure formed by a piezoelectric transversely isotropic semi-infinite substrate and a thin piezo/-flexo-magnetic guiding layer. The medium above the layer is air. A Cartesian coordinate system (x, y, z) is chosen in such a way that the x-axis is vertical to the substrate surface (see Fig. 1). Assume that the surface wave propagates in the y-direction and its amplitude decays with depth along the x-axis. We suppose that the upper surface of the piezo/-flexo-magnetic layer (\(x = - h\)) is traction free with open-circuit conditions for the electric and magnetic fields. Note that constitutive relations (1)–(4) take on a different form in the guiding layer and in the substrate because of the different material properties.

Fig. 1
figure 1

Schema of the layered structure and choice of the coordinate system

Full size image

2.2 Piezoelectric Substrate (Domain \(x > 0\))

The substrate is considered as a piezoelectric material. Because of huge dimensions of the substrate, the flexo-electric/magnetic and micro-inertia effects are supposed to be negligible. In this case, constitutive relations (1)–(4) can be written as:

$$\sigma_{ij}^{h} = c_{ijkl}^{h} \varepsilon_{kl}^{h} - e_{kij}^{h} E_{k}^{h} ,$$
(9)
$$D_{i}^{h} = e_{ijk}^{h} \varepsilon_{jk}^{h} + a_{ij}^{h} E_{j}^{h} + q_{ij}^{h} H_{j}^{h} ,$$
(10)
$$B_{i}^{h} = q_{ij}^{h} E_{j}^{h} + \mu_{ij}^{h} H_{j}^{h} .$$
(11)

Note that here and in what follows, all quantities related to the half-space are indicated by superscript ‘h’.

In the current work, the tetragonal crystal of the point group 4 mm is considered. Hence, by using Voigt notation, the fourth-rank tensor \({\mathbf{c}}^{h} = \left\{ {c_{ijkl}^{h} } \right\}\), the third-rank tensor \({\varvec{e}}^{h} = \left\{ {e_{kij}^{h} } \right\}\), the second-rank tensors \({\mathbf{a}}^{h} = \left\{ {a_{ij}^{h} } \right\}\), \({{\varvec{\upmu}}}^{h} = \left\{ {\mu_{ij}^{h} } \right\}\) and \({\mathbf{q}}^{h} = \left\{ {q_{ij}^{h} } \right\}\) can be represented in the matrix form as follows [23]:

$$\left[ {\begin{array}{*{20}c} {c_{11}^{h} } & {c_{12}^{h} } & {c_{13}^{h} } & 0 & 0 & 0 \\ {c_{12}^{h} } & {c_{11}^{h} } & {c_{13}^{h} } & 0 & 0 & 0 \\ {c_{13}^{h} } & {c_{13}^{h} } & {c_{33}^{h} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {c_{44}^{h} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{44}^{h} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {c_{66}^{h} } \\ \end{array} } \right],\,\left[ {\,\begin{array}{*{20}c} 0 & 0 & {e_{31}^{h} } \\ 0 & 0 & {e_{31}^{h} } \\ 0 & 0 & {e_{33}^{h} } \\ 0 & {e_{15}^{h} } & 0 \\ {e_{15}^{h} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],\,\,\left[ {\begin{array}{*{20}c} {b_{11}^{h} } & 0 & 0 \\ 0 & {b_{11}^{h} } & 0 \\ 0 & 0 & {b_{33}^{h} } \\ \end{array} } \right],$$

where the notation \(b_{ij}^{h} \in \left\{ {a_{ij}^{h} ,\mu_{ij}^{h} ,\,q_{ij}^{h} } \right\}\) is used.

The quantities that characterize the wave propagation within the substrate are:

$$\begin{gathered} {\mathbf{u}}^{h} = \left( {0,0,u_{3}^{h} (x,y,t} \right),\,\,{\mathbf{E}}^{h} = \left( {E_{1}^{h} (x,y,t),E_{2}^{h} (x,y,t),0} \right) \hfill \\ {\mathbf{B}}^{h} = \left( {B_{1}^{h} (x,y,t),B_{2}^{h} (x,y,t),0} \right), \hfill \\ \end{gathered}$$
$$\varphi_{e}^{h} = \varphi_{e}^{h} \left( {x,y,t} \right),\,\,\psi_{m}^{h} = \psi_{m}^{h} \left( {x,y,t} \right).$$

The non-vanishing strain and stress tensors components and electromagnetic field vectors can be given as:

$$\varepsilon_{13}^{h} = \frac{1}{2}\frac{{\partial u_{3}^{h} }}{\partial x},\,\,\varepsilon_{32}^{h} = \frac{1}{2}\frac{{\partial u_{3}^{h} }}{\partial y},$$
(12)
$$E_{1}^{h} = - \frac{{\partial \varphi_{e}^{h} }}{\partial x},\,E_{2}^{h} = - \frac{{\partial \varphi_{e}^{h} }}{\partial y},\,B_{1}^{h} = - \frac{{\partial \psi_{m}^{h} }}{\partial x},\,B_{2}^{h} = - \frac{{\partial \psi_{m}^{h} }}{\partial y},$$
(13)
$$\sigma_{31}^{h} = 2c_{44}^{h} \varepsilon_{31}^{h} - e_{15}^{h} E_{1}^{h} ,\,\sigma_{32}^{h} = 2c_{44}^{h} \varepsilon_{32}^{h} - e_{15}^{h} E_{2}^{h} ,$$
(14)
$$D_{1}^{h} = a_{11}^{h} E_{1}^{h} + q_{11}^{h} H_{1}^{h} + 2e_{15}^{h} \varepsilon_{13}^{h} ,\,D_{2}^{h} = a_{11}^{h} E_{2}^{h} + q_{11}^{h} H_{2}^{h} + 2e_{15}^{h} \varepsilon_{32}^{h} ,$$
(15)
$$B_{1}^{h} = q_{11}^{h} E_{1}^{h} + \mu_{11}^{h} H_{1}^{h} ,\,B_{2}^{h} = q_{11}^{h} E_{2}^{h} + \mu_{11}^{h} H_{2}^{h} .$$
(16)

The general solution for waves spreading in y-direction of the infinite half-space can be obtained by the method of separation of variables as follows:

\(u_{3}^{h} \left( {x,y,t} \right) = u^{h} (x)e^{ik(y - ct)} ,\,\varphi_{e}^{h} \left( {x,y,t} \right) = \varphi^{h} (x)e^{ik(y - ct)} ,\,\psi_{m}^{h} \left( {x,y,t} \right) = \psi^{h} (x)e^{ik(y - ct)} .\)

Here, \(u^{h} (x)\), \(\varphi^{h} (x)\) and \(\psi^{h} (x)\) are unknown functions which represent the amplitudes of the mechanical displacement, electric potential and magnetic potential in half-space; k denotes the wave number, c is the phase velocity, and i is the imaginary unit defined by formula \(i = \sqrt { - 1}\).

Hence, for deformable half-space without micro-inertia effect, the governing set of differential equations reduces to:

$$c_{44}^{h} \frac{{d^{2} u^{h} }}{{dx^{2} }} - \left( {c_{44}^{h} - \rho^{h} c^{2} } \right)k^{2} u^{h} + e_{15}^{h} \left( {\frac{{d^{2} \varphi^{h} }}{{dx^{2} }} - k^{2} \varphi^{h} } \right) = 0,$$
(17)
$$\frac{{d^{2} \varphi^{h} }}{{dx^{2} }} - k^{2} \varphi^{h} = \frac{{e_{15}^{h} }}{{\overline{a}_{11}^{h} }}\left( {\frac{{d^{2} u^{h} }}{{dx^{2} }} - k^{2} u^{h} } \right),$$
(18)
$$\frac{{d^{2} \psi^{h} }}{{dx^{2} }} - k^{2} \psi^{h} = - \frac{{q_{11}^{h} e_{15}^{h} }}{{\mu_{11}^{h} \overline{a}_{11}^{h} }}\left( {\frac{{d^{2} u^{h} }}{{dx^{2} }} - k^{2} u^{h} } \right).$$
(19)

Here, \(\rho^{h}\) denotes the mass density of substrate, and \(\overline{a}_{11}^{h} = a_{11}^{h} \left[ {1 - {{\left( {q_{11}^{h} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {q_{11}^{h} } \right)^{2} } {a_{11}^{h} \mu_{11}^{h} }}} \right. \kern-\nulldelimiterspace} {a_{11}^{h} \mu_{11}^{h} }}} \right]\).

Since the displacement, electric and magnetic potentials in the substrate should tend to zero far away from the interface (that is, \(u_{3}^{h} \to 0,\,\,\,\varphi_{e}^{h} \to 0\), \(\psi_{m}^{h} \to 0\) as \(x \to + \infty\)), a general solution to Eqs. (17)–(19) can be found as:

$$u_{3}^{h} \left( {x,y,t} \right) = C_{1} e^{ - \beta kx} e^{ik(y - ct)} ,$$
(20)
$$\varphi_{e}^{h} \left( {x,y,t} \right) = \left( {\frac{{e_{15}^{h} }}{{\overline{a}_{11}^{h} }}C_{1} e^{ - \beta kx} + C_{2} e^{ - kx} } \right)e^{ik(y - ct)} ,$$
(21)
$$\psi_{m}^{h} \left( {x,y,t} \right) = \left( { - \frac{{q_{11}^{h} e_{15}^{h} }}{{\mu_{11}^{h} \overline{a}_{11}^{h} }}C_{1} e^{ - \beta kx} + C_{3} e^{ - kx} } \right)e^{ik(y - ct)} .$$
(22)

Here, \(C_{1}\), \(C_{2}\), and \(C_{3}\) are unknown constants, \(\beta = \sqrt {1 - c^{2} /(c_{pe}^{h})^2} \), and \(c_{pe}^h = \sqrt {\bar{c}_{44}^h/{\rho ^h}}\) is the velocity of the shear wave in piezoelectric substrate where \(\overline{c}_{44}^{h}\) is given by \(\overline{c}_{44}^{h} = c_{44}^{h} + {{\left( {e_{15}^{h} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {e_{15}^{h} } \right)^{2} } {\overline{a}_{11}^{h} }}} \right. \kern-\nulldelimiterspace} {\overline{a}_{11}^{h} }}\).

2.3 Flexomagnetic Wave-Guide Layer (Domain \(- h < x < 0\))

Studying the Love waves in a guiding layer, the displacement vector has an axial component \(u_{3}\) only, that is \({\mathbf{u}} = \left( {0,0,u_{3} (x,y,t} \right)\). The electric field vector, magnetic field vector, electric potential and magnetic potential are assumed to be as follows: \({\mathbf{E}} = \left( {E_{1} (x,y,t),E_{2} (x,y,t),0} \right)\), \({\mathbf{B}} = \left( {B_{1} (x,y,t),B_{2} (x,y,t),0} \right)\), \(\varphi_{e} = \varphi_{e} \left( {x,y,t} \right)\), \(\psi_{m} = \psi_{m} \left( {x,y,t} \right)\). The kinematic relations are:

$$\varepsilon_{31} = \frac{1}{2}\frac{{\partial u_{3} }}{\partial x},\,\varepsilon_{32} = \frac{1}{2}\frac{{\partial u_{3} }}{\partial y},$$
(23)
$$\begin{gathered} \,\eta_{131} = \eta_{311} = \frac{1}{2}\frac{{\partial^{2} u_{3} }}{{\partial x^{2} }}\,,\,\,\eta_{232} = \eta_{322} = \frac{1}{2}\frac{{\partial^{2} u_{3} }}{{\partial y^{2} }}\,, \hfill \\ \eta_{231} = \eta_{321} = \eta_{132} = \eta_{312} = \frac{1}{2}\frac{{\partial^{2} u_{3} }}{\partial x\partial y}\,, \hfill \\ \end{gathered}$$
(24)
$$E_{1} = - \frac{{\partial \varphi_{e} }}{\partial x},\,E_{2} = - \frac{{\partial \varphi_{e} }}{\partial y},$$
(25)
$$H_{1} = - \frac{{\partial \psi_{m} }}{\partial x},\,H_{2} = - \frac{{\partial \psi_{m} }}{\partial y}.$$
(26)

For flexomagnetic ceramic, constitutive equations (1)–(4) can be rewritten as:

$$\sigma_{31} = 2c_{44} \varepsilon_{31} - d_{15} H_{1} ,\,\sigma_{32} = 2c_{44} \varepsilon_{32} - d_{15} H_{2} ,$$
(27)
$$\tau_{311} = \xi_{52} H_{2} ,\,\tau_{321} = - \xi_{41} H_{1} ,\,\tau_{321} = - \xi_{41} H_{1} ,\,\tau_{322} = \xi_{41} H_{2} ,$$
(28)
$$D_{1} = a_{11} E_{1} + q_{11} H_{1} ,\,D_{2} = a_{11} E_{2} + q_{11} H_{2} ,$$
(29)
$$B_{1} = 2d_{15} \varepsilon_{31} + q_{11} E_{1} + \mu_{11} H_{1} + 2\left( {\xi_{41} + \xi_{52} } \right)\eta_{321} ,$$
(30)
$$B_{2} = 2d_{15} \varepsilon_{32} + q_{11} E_{2} + \mu_{11} H_{2} - 2\xi_{52} \eta_{311} - 2\xi_{41} \eta_{322} .$$
(31)

The following notation is adopted here for the flexomagnetic coefficients \(\xi_{2311} = \xi_{2131} = - \xi_{52} ,\,\xi_{1312} = \xi_{1132} = \xi_{52} ,\,\xi_{1231} = \xi_{1321} = \xi_{41} ,\,\xi_{2232} = \xi_{2322} = - \xi_{41}\) Following Yang et al. [33], the effect of strain gradient terms is neglected in the formulae (28), i.e. \(g_{jklmni} = 0\).

Substitution of constitutive equations (27)–(31) and kinematic relations (23)–(26) into balance equations (7) and (8) yields:

$$\begin{gathered} c_{44} \left( {\frac{{\partial^{2} u_{3} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{3} }}{{\partial y^{2} }}} \right) + d_{15} \left( {\frac{{\partial^{2} \psi_{m} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{m} }}{{\partial y^{2} }}} \right) + \xi_{41} \left( {\frac{{\partial^{3} \psi_{m} }}{{\partial y^{3} }} - \frac{{\partial^{3} \psi_{m} }}{{\partial x^{2} \partial y}}} \right) \hfill \\ = \rho \left[ {\frac{{\partial u_{3} }}{{\partial t^{2} }} - l_{1}^{2} \left( {\frac{{\partial^{4} u_{3} }}{{\partial t^{2} \partial x^{2} }} + \frac{{\partial^{4} u_{3} }}{{\partial t^{2} \partial y^{2} }}} \right)} \right], \hfill \\ \end{gathered}$$
(32)
$$\left( {\frac{{\partial^{2} \varphi_{e} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi_{e} }}{{\partial y^{2} }}} \right) = - \frac{{q_{11} }}{{a_{11} }}\left( {\frac{{\partial^{2} \psi_{m} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{m} }}{{\partial y^{2} }}} \right)$$
(33)
$$- q_{11} \left( {\frac{{\partial^{2} \varphi_{e} }}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi_{e} }}{{\partial y^{2} }}} \right) - \mu_{11} \left( {\frac{{\partial^{2} \psi_{m} }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi_{m} }}{{\partial y^{2} }}} \right)$$
$$+ d_{15} \left( {\frac{{\partial^{2} u_{3} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{3} }}{{\partial y^{2} }}} \right) + \xi_{41} \left( {\frac{{\partial^{3} u_{3} }}{{\partial x^{2} \partial y}} - \frac{{\partial^{3} u_{3} }}{{\partial y^{3} }}} \right) = 0.$$
(34)

Governing set of equations (32)–(34) describes the propagation of the surface acoustic wave and its associated electromagnetic field in the piezo-/flexo-magnetic wave-guide layer. Comparing to the classical theory for piezo-magneticity, additional terms proportional to the flexomagnetic coefficient \(\xi_{41}\) and micro-inertia characteristic length \(l_{1}\) appeared in governing equations (32) and (34).

The displacement component, electric and magnetic potentials are assumed as:

$$u_{3} \left( {x,y,t} \right) = u(x)e^{ik(y - ct)} ,$$
(35)
$$\varphi_{e} \left( {x,y,t} \right) = \varphi (x)e^{ik(y - ct)} ,$$
(36)
$$\psi_{m} \left( {x,y,t} \right) = \psi (x)e^{ik(y - ct)} .$$
(37)

where \(u(x)\), \(\varphi (x)\) and \(\psi (x)\) are the amplitudes of the mechanical displacement, electric and magnetic potentials in a wave-guide layer.

Substitution of expressions (35)–(37) into governing equations (32)–(34) yields system of ordinary differential equations:

$$\left( {c_{44} - \rho l_{1}^{2} k^{2} c^{2} } \right)\frac{{d^{2} u}}{{dx^{2} }} + \left[ {\rho c^{2} \left( {1 + l_{1}^{2} k^{2} } \right) - c_{44} } \right]k^{2} u$$
$$+ \left( {d_{15} - ik\xi_{41} } \right)\frac{{d^{2} \psi }}{{dx^{2} }} - \left( {d_{15} + ik\xi_{41} } \right)k^{2} \psi = 0,$$
(38)
$$\left( {\frac{{d^{2} \varphi }}{{dx^{2} }} - k^{2} \varphi } \right) = - \frac{{q_{11} }}{{a_{11} }}\left( {\frac{{d^{2} \psi }}{{dx^{2} }} - k^{2} \psi } \right),$$
(39)
$$\begin{gathered} q_{11} \left( {\frac{{d^{2} \varphi }}{{dx^{2} }} - k^{2} \varphi } \right) + \mu_{11} \left( {\frac{{d^{2} \psi }}{{dx^{2} }} - k^{2} \psi } \right) - \left( {d_{15} + ik\xi_{41} } \right)\frac{{d^{2} u}}{{dx^{2} }} \hfill \\ + \left( {d_{15} - ik\xi_{41} } \right)k^{2} u = 0. \hfill \\ \end{gathered}$$
(40)

The general solution to equations (38)–(40) can be written as follows:

$$u\left( x \right) = S_{1} \left( {N_{1} e^{{k\Lambda_{1} x}} + N_{2} e^{{ - k\Lambda_{1} x}} } \right) + S_{2} \left( {N_{3} e^{{k\Lambda_{2} x}} + N_{4} e^{{ - k\Lambda_{2} x}} } \right),$$
(41)
$$\begin{aligned} \varphi (x) = & N_{5} e^{kx} + N_{6} e^{ - kx} \\ & - \frac{{q_{11} }}{{a_{11} }}\left( {N_{1} e^{{k\Lambda_{1} x}} + N_{2} e^{{ - k\Lambda_{1} x}} + N_{3} e^{{k\Lambda_{2} x}} + N_{4} e^{{ - k\Lambda_{2} x}} } \right), \\ \end{aligned}$$
(42)
$$\psi \left( x \right) = N_{1} e^{{k\Lambda_{1} x}} + N_{2} e^{{ - k\Lambda_{1} x}} + N_{3} e^{{k\Lambda_{2} x}} + N_{4} e^{{ - k\Lambda_{2} x}} .$$
(43)

Here, \(N_{j} \,\,(j = 1,...,6)\) are unknown constants to be determined and the following notations are used:

$$\begin{gathered} \Lambda_{1}^{2} = \frac{{2c_{m}^{2} - c^{2} \, - 2l_{1}^{2} c^{2} k^{2} - 2k^{2} d_{\xi }^{2} + \sqrt D }}{{2\left( {c_{m}^{2} - l_{1}^{2} k^{2} c^{2} + k^{2} d_{\xi }^{2} } \right)}},\, \hfill \\ \Lambda_{2}^{2} = \frac{{2c_{m}^{2} - c^{2} \, - 2l_{1}^{2} c^{2} k^{2} - 2k^{2} d_{\xi }^{2} - \sqrt D }}{{2\left( {c_{m}^{2} - l_{1}^{2} k^{2} c^{2} + k^{2} d_{\xi }^{2} } \right)}}, \hfill \\ \end{gathered}$$
$$\begin{gathered} S_{1} = - \frac{{d_{15} \left( {\Lambda_{1}^{2} - 1} \right) - i\xi_{41} k\left( {\Lambda_{1}^{2} + 1} \right)}}{{\left( {c_{44} - l_{1}^{2} \rho c^{2} k^{2} } \right)\left( {\Lambda_{1}^{2} - 1} \right) + \rho c^{2} }}, \hfill \\ S_{2} = - \frac{{d_{15} \left( {\Lambda_{2}^{2} - 1} \right) - i\xi_{41} k\left( {\Lambda_{2}^{2} + 1} \right)}}{{\left( {c_{44} - l_{1}^{2} \rho k^{2} c^{2} } \right)\left( {\Lambda_{2}^{2} - 1} \right) + \rho c^{2} }}, \hfill \\ \end{gathered}$$
$$D = c^{4} + 8d_{\xi }^{2} c^{2} k^{2} \left( {1 + 2l_{1}^{2} k^{2} } \right) - 16c_{m}^{2} d_{\xi }^{2} k^{2} ,$$
$$d_{\xi }^{2} = \frac{{\xi_{41}^{2} }}{{\rho \overline{\mu }_{11} }},\,c_{m}^{2} = \frac{{\overline{c}_{44} }}{\rho },\,\overline{c}_{44} = c_{44} + \frac{{d_{15}^{2} }}{{\overline{\mu }_{11} }},\,\overline{\mu }_{11} = \mu_{11} \left( {1 - \frac{{q_{11}^{2} }}{{a_{11} \mu_{11} }}} \right).$$

2.4 The Air (Domain \(x < - h\))

Since the layer is made of the piezomagnetic ceramic, we take the electromagnetic field in the air (domain \(x < - h\)) into account. We consider the air as a vacuum. Both the electric and magnetic potentials in the vacuum satisfy the Laplace equations, i.e., \(\nabla^{2} \varphi_{e}^{v} = 0\) and \(\nabla^{2} \psi_{m}^{v} = 0\). Here, \(\nabla^{2}\) is the two-dimensional Laplac operator, and superscript ‘v’ indicates the electric and magnetic potentials in the vacuum. The potentials tend to zero far away from the surface \(x = - h\) along the negative x-direction, i.e., \(\,\varphi_{e}^{v} \to 0\) and \(\,\psi_{e}^{v} \to 0\) as \(x \to - \infty\). Therefore, the electromagnetic field above the layer is given by the expressions:

$$\varphi_{e}^{v} \left( {x,y,t} \right) = C_{4} e^{kx} e^{ik(y - ct)} ,\,\psi_{m}^{v} \left( {x,y,t} \right) = C_{5} e^{kx} e^{ik(y - ct)} ,$$
(44)

where \(C_{4}\) and \(C_{5}\) are the unknown constants. The electric displacement \(D_{i}^{v} = a_{0} E_{i}^{v}\) and magnetic induction \(B_{i}^{v} = \mu_{0} H_{i}^{v}\) in the air (\(x < - h\)) are as follows:

$$D_{1}^{v} = - a_{0} \frac{{\partial \varphi_{e}^{v} }}{\partial x} = - kC_{4} a_{0} e^{kx} e^{ik(y - ct)} ,\,D_{2}^{v} = - a_{0} \frac{{\partial \varphi_{e}^{v} }}{\partial y} = - ikC_{4} a_{0} e^{kx} e^{ik(y - ct)} ,$$
(45)
$$B_{1}^{v} = - \mu_{0} \frac{{\partial \psi_{m}^{v} }}{\partial x} = - kC_{5} \mu_{0} e^{kx} e^{ik(y - ct)} ,\,B_{2}^{v} = - \mu_{0} \frac{{\partial \psi_{m}^{v} }}{\partial y} = - ikC_{5} \mu_{0} e^{kx} e^{ik(y - ct)} .$$
(46)

Here, \(a_{0}\) and \(\mu_{0}\) are the electric permittivity and magnetic permeability of vacuum, respectively.

2.5 Boundary Conditions and Dispersion Equation

The eleven unknown constants \(N_{j} \,\,(j = 1 - 6)\) and \(C_{l} \,\,(l = 1 - 5)\) are determined by the boundary conditions at surfaces \(x = - h\) and \(x = 0\).

In case of the electrical and magnetic open-circuit conditions, we require the flux of electric displacements, magnetic inductions, as well as the electric and magnetic potentials to be continuous across the surface \(x = - h\). Thus, for traction-free interfaces and continuity of displacements, we consider the complete boundary conditions as:

On the surface \(x = - h\):

$$\left. {\left( {\left( {\sigma_{31} - \tau_{311,1} - \tau_{312,2} } \right) - \tau_{321,2} + \rho l_{1}^{2} \frac{{\partial \ddot{u}_{3} }}{\partial x}} \right)} \right|_{x = - h} = 0,$$
(47)
$$\begin{gathered} \left. {\varphi_{e} } \right|_{x = - h} = \left. {\varphi_{e}^{v} } \right|_{x = - h} ,\,\left. {D_{1} } \right|_{x = - h} = \left. {D_{1}^{v} } \right|_{x = - h} , \hfill \\ \left. {\psi_{m} } \right|_{x = - h} = \left. {\psi_{m}^{v} } \right|_{x = - h} ,\left. {B_{1} } \right|_{x = - h} = \left. {B_{1}^{v} } \right|_{x = - h} . \hfill \\ \end{gathered}$$
(48)

On the interface between the layer and half-space \(x = 0\):

$$\left. {u_{3} } \right|_{x = 0} = \left. {u_{3}^{h} } \right|_{x = 0} ,\,\left. {\left( {\left( {\sigma_{31} - \tau_{311,1} - \tau_{312,2} } \right) - \tau_{321,2} + \rho l_{1}^{2} \frac{{\partial \ddot{u}_{3} }}{\partial x}} \right)} \right|_{x = 0} = \left. {\sigma_{31}^{h} } \right|_{x = 0} ,$$
(49)
$$\left. {\varphi_{e} } \right|_{x = 0} = \left. {\varphi_{e}^{h} } \right|_{x = 0} ,\,\left. {D_{1} } \right|_{x = 0} = \left. {D_{1}^{h} } \right|_{x = 0} ,\,\left. {\psi_{m} } \right|_{x = 0} = \left. {\psi_{m}^{h} } \right|_{x = 0} ,\,\left. {B_{1} } \right|_{x = 0} = \left. {B_{1}^{h} } \right|_{x = 0} .$$
(50)

Here, \(\tau_{31} = \left( {\sigma_{31} - \tau_{311,1} - \tau_{312,2} } \right) - \tau_{321,2} + \rho l_{1}^{2} \frac{{\partial \ddot{u}_{3} }}{\partial x}\) is the z-component of generalized tractions on the surface x = const, \(y,\,z \in \left( { - \infty ,\,\infty } \right)\).

Thus, the propagation problem of the Love wave in the layered structure turns into the solution of (20)–(22), (35)–(37), (41)–(43) and (44)–(46) under boundary conditions (47)–(50).

Substitution of the general solutions into boundary conditions (47)–(50) produces eleven homogeneous algebraic linear equations to find unknown constants \(N_{j} \,\,(j = 1 - 6)\) and \(C_{l} \,\,(l = 1 - 5)\). Eliminating \(C_{l} \,\,(l = 1 - 5)\), \(N_{5}\) and \(N_{6}\) from the obtained set of equations we get four equations with respect to \(N_{j} \,\,(j = 1 - 4)\) which can be written in a matrix form as follows: \({\mathbf{MN}} = 0\), where \({\mathbf{N}}^{T} = \left[ {\begin{array}{*{20}c} {N_{1} } & {N_{2} } & {N_{3} } & {N_{4} } \\ \end{array} } \right]\), and M is a 4 × 4 coefficient matrix. The elements of matrix M are given by formulae:

\(m_{11} = b_{1} e^{{ - kh\Lambda_{1} }} ,\,m_{12} = - b_{1} e^{{kh\Lambda_{1} }} ,\,m_{13} = b_{2} e^{{ - kh\Lambda_{2} }} ,\,m_{14} = - b_{2} e^{{kh\Lambda_{2} }} ,\)

\(m_{21} = \left( {n_{1} + \mu_{0} } \right)e^{{ - kh\Lambda_{1} }} ,\,m_{22} = - \left( {n_{1} - \mu_{0} } \right)e^{{kh\Lambda_{1} }} ,\)

\(m_{23} = \left( {n_{2} + \mu_{0} } \right)e^{{ - kh\Lambda_{2} }} ,\,m_{24} = - \left( {n_{2} - \mu_{0} } \right)e^{{kh\Lambda_{2} }} ,\)

\(m_{31} = \left[ {b_{1} + \left( {c_{pe}^{h} } \right)^{2} \beta \rho^{h} S_{1} } \right] - \frac{{\left( {n - 1} \right)}}{{\left( {n + 1} \right)}}\frac{{a_{11} }}{{a_{11}^{h} }}\left( {b_{1} - b\rho^{h} S_{1} } \right),\)

\(m_{32} = - \left[ {b_{1} - \left( {c_{pe}^{h} } \right)^{2} \beta \rho^{h} S_{1} } \right] + \frac{{\left( {n - 1} \right)}}{{\left( {n + 1} \right)}}\frac{{a_{11} }}{{a_{11}^{h} }}\left( {b_{1} + b\rho^{h} S_{1} } \right),\)

\(m_{33} = \left[ {b_{2} + \left( {c_{pe}^{h} } \right)^{2} \beta \rho^{h} S_{2} } \right] - \frac{{\left( {n - 1} \right)}}{{\left( {n + 1} \right)}}\frac{{a_{11} }}{{a_{11}^{h} }}\left( {b_{2} - b\rho^{h} S_{2} } \right),\)

\(m_{34} = - \left[ {b_{2} - \left( {c_{pe}^{h} } \right)^{2} \beta \rho^{h} S_{2} } \right] + \frac{{\left( {n - 1} \right)}}{{\left( {n + 1} \right)}}\frac{{a_{11} }}{{a_{11}^{h} }}\left( {b_{2} + b\rho^{h} S_{2} } \right),\)

\(m_{41} = n_{1} - \mu_{11}^{h} ,\,m_{42} = - \left( {n_{1} + \mu_{11}^{h} } \right),\,m_{43} = n_{2} - \mu_{11}^{h} ,\,m_{44} = - \left( {n_{2} + \mu_{11}^{h} } \right).\)

Note that in the above formulae, for simplicity the terms with magneto-electric constants \(q_{11}^{h}\) and \(q_{11}\) are neglected and the following notations are adopted:

\(\begin{aligned}&b_{1} = \left[ \left( c_{44} - \rho l_{1}^{2} k^{2} c^{2} \right)S_{1} + d_{15} - ik\xi_{41} \right]\Lambda_{1} ,\\ &b_{2} = \left[ {\left( {c_{44} - \rho l_{1}^{2} k^{2} c^{2} } \right)S_{2} + d_{15} - ik\xi_{41} } \right]\Lambda_{2} ,\end{aligned}\)

\(\begin{aligned}& n_{1} = \left[ {d_{15} S_{1} - \mu_{11} + ik\left( {\xi_{41} + \xi_{52} } \right)S_{1} } \right]\Lambda_{1} ,\\&n_{2} = \left[ {d_{15} S_{2} - \mu_{11} + ik\left( {\xi_{41} + \xi_{52} } \right)S_{2} } \right]\Lambda_{2} ,\end{aligned}\)

\(b = \left( {\frac{{e_{15}^{h} e_{15}^{h} }}{{\rho^{h} a_{11}^{h} }} - \left( {c_{pe}^{h} } \right)^{2} \beta } \right),\,n = \frac{{\left( {a_{11} - a_{0} } \right)}}{{\left( {a_{11} + a_{0} } \right)}}e^{ - 2kh} .\)

From the above equations one can observe that the flexomagneticity-related terms are dependent on the wave number k, while the micro-inertia-related terms are dependent on \(k^{2}\).

Non-trivial solution to the boundary-value problem can be obtained if the determinant of matrix M is equal to zero. This condition leads to the transcendental dispersion equation \(\det \left[ {{\mathbf{M}}(c,k)} \right] = 0\), which determines the dependence of the Love-wave phase velocity c on the wave numbers k, i.e., c = c(k). Since for the guiding layer, the influence of flexo-/piezo-magnetic and micro-inertia effects is taken into account and due to the consideration of piezoelectric properties of the substrate, the dispersion relation becomes very complicated and numerical methods should be used to solve it.

3 Numerical Results

Note that the Love wave exhibits a multimode character. Since the first mode is characterized by the largest amplitude, in current work, the attention has been focused on the electro-magneto-mechanical properties of this mode only. Following [33], we assume the wave number to be positive real quantity while the phase velocity of Love wave is considered as a complex one, \(c = c_{1} + ic_{2}\). The imaginary part of velocity \(c_{2}\) characterizes the wave attenuation. The negative value of \(c_{2}\) means that the modified wave amplitude (wave amplitude \(\times e^{{ - ic_{2} t}}\)) drops, whereas the positive value of \(c_{2}\) implies that the modified wave amplitude grows with increasing time.

In this section, the numerical results regarding the dispersion relation of Love wave are provided for a layered structure with the following material properties ‘flexomagnetic ceramic CoFe2O4 and piezoelectric ceramic BaTiO3’. The material coefficients for barium titanate and cobalt ferrite are chosen as follows [5, 6, 28]:

\(\rho^{h} = 5.8\,\, \times 10^{3} \,\,{\text{kg}}/{\text{m}}^{3} ,\,c_{44}^{h} = 4.3 \times 10^{10} \,\,{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{2} }},\,e_{15}^{h} = 11.6\,\,{{\text{C}} \mathord{\left/ {\vphantom {{\text{C}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}}\)

\(a_{11}^{h} = 1.12 \times 10^{ - 8} \,\,{{\text{F}} \mathord{\left/ {\vphantom {{\text{F}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}},\,\mu_{11}^{h} = 0.5 \times 10^{ - 5} \,\,{{{\text{Ns}}^{2} } \mathord{\left/ {\vphantom {{{\text{Ns}}^{2} } {{\text{C}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{C}}^{2} }}\)

\(\rho = 5.3\,\, \times 10^{3} \,\,{\text{kg}}/{\text{m}}^{3} ,\,c_{44} = 4.53 \times 10^{10} \,\,{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{m}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{m}}^{2} }}\)

\(d_{15} = 550\,\,{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{Am}}}}} \right. \kern-\nulldelimiterspace} {{\text{Am}}}},\,a_{11} = 0.8 \times 10^{ - 10} \,\,{{\text{F}} \mathord{\left/ {\vphantom {{\text{F}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}},\mu_{11} = 5.9 \times 10^{ - 4} \,\,{{{\text{Ns}}^{2} } \mathord{\left/ {\vphantom {{{\text{Ns}}^{2} } {{\text{C}}^{2} }}} \right. \kern-\nulldelimiterspace} {{\text{C}}^{2} }}.\)

For air, the electric permittivity and magnetic permeability coefficients are \(a_{0} = 8.85 \times 10^{ - 12} \,{{\text{F}} \mathord{\left/ {\vphantom {{\text{F}} {\text{m}}}} \right. \kern-\nulldelimiterspace} {\text{m}}}\) and \(\mu_{0} = 4\pi \times 10^{-7} \,{{\text{H/m} }}\). In numerical calculations, it is assumed that flexomagnetic coefficients \(\xi_{41}\) and \(\xi_{52}\) are equal to each other, i.e., \(\xi_{41} = \xi_{52} \equiv \xi\), and their order increases from 10–6 to 10–5 [8, 28]. Usually, the dynamic characteristic length \(l_{1}\) is set to be proportional to the material lattice parameter [32]. In this study, we assume \(l_{1}\) to range from 0.4 Å to 6 Å. In calculations, it is also assumed that the thickness of the guiding layer is equal to 40 nm.

Figure 2 illustrate the influence of micro-inertia characteristic length on Love wave phase velocity when the flexomagneticity is neglected, i.e., \(\xi_{41} = \xi_{52} = 0\). To study the influence of micro-inertia characteristic length on the dispersion curve, we assume that the above parameter ranges from 0.4 Å to 1.2 Å (Fig. 2a) or 1 Å to 3 Å (Fig. 2b). In this case, the imaginary part of phase velocity is equal to zero. In Fig. 2, the classical electro-magneto-elasticity solution (\(l_{1}\) = 0) is also shown for comparison (see the solid line). It can be seen that for sufficiently large wave numbers, the micro-inertia characteristic length parameter has an effect on the phase velocity of the wave. Increasing the micro-inertia length parameter from 0.4 Å to 3 Å, the wave velocity decreases. The effect becomes more pronounced for larger values of micro-inertia characteristic length (Fig. 2b). The numerical investigations also showed that when the dynamic characteristic length \(l_{1}\) does not exceed 0.1 ÷ 0.2 Å, the dispersion curve coincides with the results obtained from the classical theory. In that case, the influence of micro-inertia effect can be neglected.

Fig. 2
figure 2

The phase velocity of Love wave versus wave number k for the guiding layer thickness 40 nm and various micro-inertia characteristic lengths. The influence of flexomagneticity is neglected (i.e., \(\xi_{41} = \xi_{52} = 0\))

Full size image

The effect of flexomagnetic properties of the guiding layer on the wave velocity is illustrated in Fig. 3, where the influence of micro-inertia effect is not considered, i.e., it is assumed that \(l_{1}\) = 0. Grey solid lines present the corresponding classical solution for piezomagnetic layer on a piezoelectric substrate. Within the classical theory, the phase velocity of Love wave is a monotonously decreasing function with the wave number. The presence of flexomagneticity leads to a complex function of phase velocity with negative imaginary part. In this case, from Fig. 3 it is observed that the real part of phase velocity first decreases for lower values of the wave number, reaches the minimum and then begins to rise. For a sufficiently large wave number, the phase velocity is higher than the one predicted by the classical theory. The imaginary part of the wave velocity, imag(c), displays the same trends, that is, it first declines and then begins to increase. The minimum of imaginary part of phase wave velocity decreases if the flexomagnetic coefficients \(\xi_{41}\) and \(\xi_{52}\) grow. This means that better wave attenuation is for larger values of the flexomagnetic coefficients. When flexomagnetic constant \(\xi\) is equal to \(2.1 \times 10^{ - 6} {\text{Tm}}\), \(4.6 \times 10^{ - 6} {\text{Tm}}\) and \(10^{ - 5} {\text{Tm}}\), the real part of the phase velocity can exceed the shear wave velocity in the substrate and, therefore, the so-called ‘cut-off regions’ can appear in the considered layered structure (see dashed, dotted and dash-dotted lines). In these regions, the Love wave is not capable of propagating.

Fig. 3
figure 3

Real and imaginary parts of phase velocity of Love wave versus wave number k for the guiding layer thickness 40 nm and various values of the flexomagnetic coefficients. The influence of micro-inertia terms is neglected (i.e., \(l_{1}\) = 0)

Full size image

Next, the micro-inertial effect is considered. Figures 4, 5 and 6 illustrate the coupled effect of the flexomagneticity and micro-inertia characteristic length on the profile of the dispersion curves. In Fig. 4, the solid, dashed, dotted and dash-dotted lines are plotted for the values of flexomagnetic coefficients \(10^{ - 6}\) Tm, \(2.1 \times 10^{ - 6}\) Tm, \(4.6 \times 10^{ - 6}\) Tm and \(10^{ - 5} \,\,{\text{Tm}}\), respectively. In the calculations, the micro-inertia characteristic length is assumed to be 4 Å. A solid grey line presents the result obtained from the classical theory of elastic electromagnetic media without flexomagneticity and micro-inertia effect. We found that the profile of the dispersion curves changes significantly if flexomagnetic and micro-inertia effects are considered. As can be seen from Fig. 4, due to combining influence of flexomagneticity and micro-inertia effect, for large wave numbers, the real part of phase velocity increases with the increase of the flexomagnetic coefficient \(\xi\) if \(\xi\) = \(2.1 \times 10^{ - 6} \,{\text{Tm}}\), \(4.6 \times 10^{ - 6} \,{\text{Tm}}\) and \(10^{ - 5}\) Tm. However, if \(\xi = 10^{ - 6} \,{\text{Tm}}\), the influence of micro-inertia terms becomes dominant and the real part of the phase velocity is smaller than the ones predicted by the classical theory. We also found that if the micro-inertia effect is taken into account, the cut-off regions do not occur when the \(\xi\) = \(2.1 \times 10^{ - 6}\) Tm. This means that the profile of dispersion curve significantly depends on the ratio of the flexomagnetic coefficients and micro-inertia characteristic length.

Fig. 4
figure 4

Real and imaginary parts of phase velocity of Love wave versus wave number k for the guiding layer thickness 40 nm, \(l_{1}\) = 0.4 nm and various values of the flexomagnetic coefficients

Full size image
Fig. 5
figure 5

Real and imaginary parts of phase velocity of Love wave versus wave number k for the guiding layer thickness 40 nm, \(\xi_{41} = \xi_{52} = 10^{ - 6} {\text{Tm}}\) and various values of the micro-inertia characteristic length

Full size image
Fig. 6
figure 6

The effect of the guiding layer thickness on the real and imaginary parts of phase velocity for flexomagnetic coefficients \(\xi_{41} = \xi_{52} = 10^{ - 6} \,{\text{Tm}}\), \(l_{1}\) = 0 (figure a) and \(l_{1}\) = 0.2 nm (figure b)

Full size image

Figure 5 gives profiles of dispersion curves for flexomagnetic coefficient 10–6 Tm and values of the micro-inertia characteristic length 2 Å, 4 Å and 6 Å. From Fig. 5 it is observed that micro-inertia terms have a significant influence on the real part of phase velocity c. This effect is stronger for high wave number (short wavelengths). When the wave number k is small, the imaginary parts of phase velocity calculated from various values of the micro-inertia characteristic length are close to each other. Decreasing distinctions in dispersion curves for imag(c) can be observed only at large wave numbers.

Figure 6 shows the dispersion curves for the values of the guiding layer thickness 20 nm, 30 nm, 40 nm and 50 nm. The result obtained from the generalized theory of flexomagnetic media without micro-inertia effect is presented in Fig. 6a. The dispersion curves in Fig. 6b are plotted with the assumption that characteristic length is equal to 2 Å. As can be seen from the curves, the effect of the layer thickness is more pronounced for narrower layers. The minimum of real(c) decreases whereas the minimum of imag(c) increases if the guiding layer thickness increases. Reducing the layer thickness, the wave attenuation reaches its maximum at higher wave numbers k. From Fig. 6a, b one can also observe that the influence of micro-inertia terms becomes important for sufficiently high wave numbers.

4 Conclusions

The classical theories are not capable of appropriately describe the magneto-electro-mechanical behavior of Love waves in a nano-scale flexo-piezomagnetic layer overlying the piezoelectric half-space. The influence of flexomagneticity and micro-inertia effect should be considered in this case. In this study, the behavior of magneto-electro-elastic surface Love waves in a structure consisting of piezoelectric substrate of crystal class 4 mm and flexo-piezomagnetic elastic layer is studied. Mathematical model of a substrate takes the piezoelectric properties of the material into account while the relations for a nano-thin layer accommodate the influence of flexomagneticity and micro-inertia effect. A solution to dispersion relation is found for magneto-electrically open boundary conditions. The dependence of phase wave velocity on the wave number is numerically studied in detail for piezomagnetic ceramics CoFe2O4 and piezoelectric ceramics BaTiO3 for various values of flexomagnetic coefficients and micro-inertia characteristic length.

The study proved that both flexomagnetic and micro-inertia effects play an important role in layered structures at the micro-/nano-scales and can significantly affect the profiles of dispersion curves. Numerical investigations showed that growing flexomagnetic coefficient increases the Love wave phase velocity, while its value decreases with increasing the micro-inertia length parameter. The influence of flexomagnetic and micro-inertia effects is remarkable for sufficiently high wave numbers. This influence is more pronounced for a smaller thickness of wave-guide layer as well as for larger values of micro-inertia characteristic lengths and flexomagnetic coefficients. Contrary to the prediction of the classical theories, if the flexomagnetic properties of a layer are taken into account, the cut-off regions can occur in the considered layered structure in case of large values of flexomagnetic coefficients and a small micro-inertia characteristic length. The profile of dispersion curves and the presence or absence of cut-off regions in these curves, depend on the guiding layer thickness, and on the ratio between the values of flexomagnetic coefficients and the micro-inertia characteristic length.

The obtained results can be helpful in mathematical modelling and engineering applications of new small-scale acoustic devices made of smart piezoelectric and piezomagnetic materials.