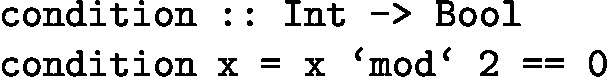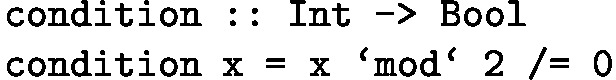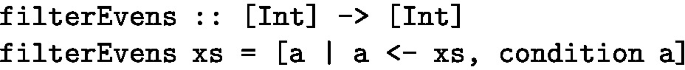1 Introduction

Program synthesis, the automatic construction of a computer program from a user specification, is a challenging and central problem in the field of artificial intelligence (AI) [7]. Programming has been classified as “AI-hard” [35] since all problems in AI can reduce to programming, and thus our progress in program synthesis serves as a good benchmark for how close we are to achieving general artificial intelligence [21]. In addition, program synthesis has broad applications in software engineering. For example, software development often entails refactoring old code to improve structure or readability without affecting behavior, which program synthesis can help automate. In addition, program synthesis can allow non-programmers to efficiently perform computational tasks [3].

Two of the main approaches to program synthesis are stochastic search through genetic programming [14], and formal verification methods such as symbolic solving [7]. However, solver-based methods do not scale beyond small programs such as introductory programming problems [9], and many current approaches are constrained in scope [21]. In this paper, we propose a new program synthesis model which leverages pre-existing code, in the form of functions that we call “program pieces”, and synthesizes the high-level program structure. This model allows for an approach that incorporates refinement type checking [32], a formal verification method, into genetic programming search.

Genetic programming (GP) is a search technique that begins with an initial population of programs from the search space, and evolves and combines the most “fit” programs through non-deterministic processes similar to biological evolution to move towards an optimal solution [25]. In particular, GP proceeds in generations, where in each generation the search selects the most fit programs and varies them to get a new generation of more evolved and more fit programs. In GP systems, the performance of the search depends heavily on the fitness function, since incorrect programs need a good heuristic to optimize [7, 22]. A common fitness function is the program’s accuracy on a set of example inputs and outputs. However, having a large set of examples is computationally expensive [6], while a small set of examples leads to under-specification and often the wrong generalizations [7]. NetSyn [17] showed that using neural networks to learn a fitness function can improve GP performance. This suggests that there is still room for improvement in the design of the fitness function.

On the other hand, formal verification methods can be used to synthesize programs through symbolic proofs of satisfiability and correctness. One example of a formal verification method is refinement type checking [32], which is a stronger form of type checking that can enforce predicates on types. Specifically, a user can define stricter input and output types for a function using refinement types, so that the refinement type check enforces expected preconditions and postconditions. The liquid type system [28] allows for efficient static checking of refinement type safety, without requiring every expression to be manually annotated. However, as mentioned above, formal methods alone do not scale well beyond small programs.

Our key idea in this paper is to improve scalability by decomposing programs into program pieces, which are functions provided by the user or imported from a library. We form candidate programs by composing program pieces. By abstracting away logical units of code into these program pieces, we reduce the search space for the synthesis, thus enabling us to solve larger synthesis problems. Furthermore, this allows users of our system to make use of built-in functions or external libraries, which can provide complex logic for free.

An additional benefit of this decomposition is that we can use refinement types to specify the input and output types of program pieces, which specifies the overall intended behavior of the program we want to synthesize. In our proposed system, we use refinement type checking as a fitness function within our GP algorithm. In particular, we define a novel fitness function based on the number of errors that result from the refinement type check, so that programs with fewer errors have better fitness. Using this fitness function, we observe that the GP search converges towards a program that has no type errors, which we consider to be correct since the refinement types specify the intended behavior. In addition, unlike fitness functions based on input-output examples which are under-specified as mentioned above, refinement types provide a formal specification of the entire input and output spaces.

We present the following contributions in this paper:

  • A general-purpose program synthesis model that synthesizes programs by composing preexisting program pieces

  • A fitness function on programs composed of pieces that enables GP to find good programs, derived from the number and type of errors that result from refinement type checking

  • An evaluation of the new fitness function in this model

We evaluate the performance of our proposed fitness function against a fitness function that uses accuracy on input-output examples. We find that on average, with our refinement type-based fitness function, the GP search finds solutions in about 20% fewer generations than when we use input-output examples.

The remainder of the paper is structured as follows: first, we outline our methods, including how we translate the refinement type check into a fitness function (Sect. 2). Next, we describe our experiments and results (Sect. 3). Finally, we discuss related work (Sect. 4) and conclusions (Sect. 5).

2 Method

We will present our method in 4 sections. First, we describe our program synthesis model, defining program pieces and introducing a running example (Sect. 2.1). Next, we outline our base genetic programming (GP) algorithm and how it synthesizes programs (Sect. 2.2). Next, we briefly introduce refinement types and LiquidHaskell (Sect. 2.3). Then, we present our new fitness function, describing how we integrate information from LiquidHaskell into the base GP algorithm (Sect. 2.4).

2.1 Program Synthesis Model

In our program synthesis model, programs are composed of program pieces, which are functions provided by the user or imported from built-in and external libraries. As a running example, we consider a list filtering problem that we call FilterEvens: given a list of integers, return a list containing only the even integers from the input. The example below, and subsequent examples, will use Haskell syntax [11]. A user might provide the following 3 program pieces:

Example 1

Program pieces for FilterEvens

  1. 1.

    condition takes in integer x and returns true if x is even, false otherwise.

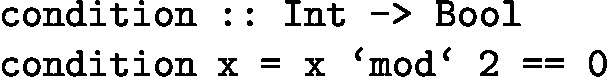
    figure a
  2. 2.

    condition takes in integer x and returns true if x is odd, false otherwise.

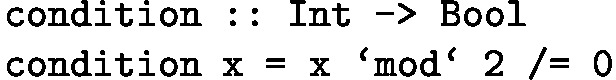
    figure b
  3. 3.

    filterEvens takes in an array of integers xs and returns the array containing all members from xs for which condition is true.

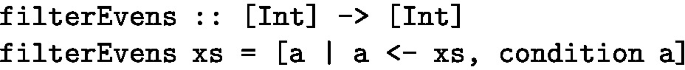
    figure c

A correct program would consist of pieces 1 and 3. Note that piece 2 is not ultimately needed; a user will not have complete knowledge of the implementation, so they may include pieces that the synthesis algorithm chooses not to use.

2.2 Genetic Programming Algorithm

In the context of program synthesis, genetic programming evolves a population of candidate programs over time to find an optimal program [14]. Candidate programs are defined by their chromosome, a sequence of integers representing the indexes of the program pieces that compose that program. For example, using our FilterEvens problem defined in Example 1, the chromosome \(c=[1,3]\) corresponds to this program consisting of piece numbers 1 and 3:

Example 2

Program defined by chromosome [1, 3], which uses the correct condition to filter a list to only contain even integers

figure d

A sketch of our base genetic programming algorithm is shown in Algorithm 1. We provide a set of parameters \(\varTheta \) which includes the population size, chromosome length, mutation and crossover rate for variation, tournament size, and elite size, and parameter G, the number of generations to run for. We also provide a fitness function f, which computes a heuristic representing how “good” each candidate solution is, along with a set of input/output examples X which we use to test candidate programs to compute fitness (described in more detail below).

The algorithm proceeds in the following steps, labeled with the corresponding line numbers in Algorithm 1:

  • Generate individuals (1): Let |c| be the chromosome length and |P| the number of program pieces; both are provided in the parameters. We generate a random individual by generating |c| random numbers, each in the range [0, |P|). This list represents the chromosome for that individual. We repeat the process \(\texttt {pop\_size}\) times to generate an initial population.

  • Compute fitness (2, 6): We use the provided fitness function f to compute fitness for each individual in the population.

  • Selection (4): To select individuals for variation, we use tournament selection [4]. The tournament size t is provided in the parameters \(\varTheta \). We will run \(\texttt {pop\_size}\) tournaments, where each tournament selects t individuals at random from the population and selects the individual with best fitness. Thus, individuals with higher fitness are more likely to be selected for variation.

  • Variation (5): We use two variation operators to create new individuals.

    • Mutation [23]: With probability equal to the mutation rate, we mutate an individual as follows. Given a chromosome c, we choose an index uniformly at random from [0, |c|), and change it to a new value, also chosen uniformly at random from the range of possible values [0, |P|), to get new chromosome \(c'\).

    • Single-Point Crossover [24]: With probability equal to the crossover rate we create two new individuals as follows. Given two chromosomes \(c_1\) and \(c_2\), we choose an index uniformly at random to be the crossover point p. We create new individuals \(c_1'\) and \(c_2'\) such that \(c_1'\) contains the left part of \(c_1\), up to index p, and the right part of \(c_2\), from index \(p+1\) to the end, and vice versa for \(c_2'\).

  • Replacement (7): We use an elitism strategy [26] to update the population. Let e be the elite size provided in the parameters \(\varTheta \). We choose our new population to consist of the e individuals from the current generation before variation with the best fitness, plus the \((\texttt {pop\_size} - e)\) individuals after variation with the best fitness.

figure e

Fitness Function. In our base algorithm, we use a standard fitness function: the candidate program’s accuracy on the example test cases X [14]. In particular, given some chromosome c, fitness is given by

$$\begin{aligned} f_{IO}(X, c) = \frac{\text {number of correct examples}}{\text {total number of examples}} \end{aligned}$$

Under this fitness function, programs which perform better on the example cases will have higher fitness. However, there are potential problems with using input-output examples, as mentioned in Sect. 1. This fitness function only specifies a program’s intended behavior for a small set of examples, and a solution that succeeds on these examples may not necessarily generalize to others [13]. This leads us to explore refinement types as an alternate way to compute fitness.

2.3 Refinement Types and LiquidHaskell

Refinement types are types that further restrict the space of possible values by specifying a predicate. For example, we can express the filterEvens function from our running example using refinement types as follows, indicating that it takes a list of integers as input and outputs a list of even integers:

Example 3

LiquidHaskell Refinement Type Specification for filterEvens

figure f

LiquidHaskell [34] is a plugin for Haskell which supports refinement types, including static checking of refinement type safety using a symbolic solver such as Z3 [20]. We can express a function like filterEvens in Example 3, and LiquidHaskell will verify at compile time that filterEvens satisfies the refined type. In this case LiquidHaskell checks that the output of filterEvens is always a list of even integers. If the check fails, LiquidHaskell outputs errors showing which refinement type specifications were not satisfied. This static checking is able to not only restrict integer values, but also enforce properties of lists and other complex types, so it is applicable to a broad range of functions.

2.4 Refinement Types Fitness Function

For certain types of problems, such as the FilterEvens example we have defined, refinement types are able to express the intended behavior of the program. Because this is a symbolic check, it verifies that behavior over all valid inputs without relying on example test cases.

To make use of this property, we leverage LiquidHaskell’s refinement type checking to define a new fitness function for the GP. To do so, we require that the user provide a refinement for each program piece. Since refinements are based only on the intended behavior of a function, and do not depend on the implementation, we assume that users will be able to provide refinements even for library functions that will be used in the synthesized code.

A naive fitness function that simply runs the LiquidHaskell type check would return a binary value (0 if it fails, 1 if it passes), which does not work well as a heuristic. Instead, we can look more closely at LiquidHaskell’s output, which includes syntax errors and refinement type errors, to construct a more fine-grained function.

Syntax Errors. We assume that individual program pieces, which are often built-in functions or library functions, are free of syntax errors. Under this assumption, the only syntax errors that can be produced by combining program pieces are multiple definition errors (for pieces that have the same name and function signature), and missing definition errors (for pieces that were declared in other pieces but don’t appear in the solution). The maximum number of syntax errors that can result is equal to the length of the chromosome.

Refinement Type Errors. Refinement type checking is only performed after regular syntax checking, so no refinement type errors are reported if a program has incorrect syntax. Otherwise, if the program has no syntax errors, LiquidHaskell will report one error per refinement (i.e. per function signature) that is not satisfied. Thus, the maximum possible number of refinement type errors is also equal to the length of the chromosome.

Fitness Function. We construct our fitness function using a linear scale based on the number and type of errors reported. In addition, we follow the principle that syntax errors are generally “worse” than refinement type errors; syntax errors indicate structural issues like duplicated or missing program pieces, while refinement type errors mean that the program has the right structure.

Therefore, for a given chromosome c (with length |c|) where LiquidHaskell produces s syntax errors and t refinement type errors, we calculate the following fitness function:

$$\begin{aligned} f_{RT}(c) = {\left\{ \begin{array}{ll} 0.5 - \frac{s}{2 |c |} &{} {\text {if }} s>0 {\text { (syntax checking fails)}} \\ 1 - \frac{t}{2 |c |} &{} {\text {if }} s=0 {\text { (syntax checking succeeds)}} \end{array}\right. } \end{aligned}$$
(1)

From Eq. 1, programs that have syntax errors always have fitness \({<} 0.5\) while programs that have no syntax errors will have fitness \({\ge } 0.5\). A program that has no syntax or refinement type errors, such as the program given in Example 2, has a fitness value of 1 and is considered to be correct.

As another example, consider the program in our FilterEvens specification with the chromosome [2, 3]. We include the LiquidHaskell refinement type specifications as well:

Example 4

Program defined by chromosome [2, 3], which uses the incorrect condition, filtering the list to contain odd integers

figure g

This program compiles without syntax errors, but the filterEvens refinement type specification is not satisfied as the given condition yields odd instead of even integers. Thus, this program produces 0 syntax errors and 1 refinement type error, resulting in a fitness value of \(1 - \frac{1}{2 \cdot 2} = 0.75\). This program is given a higher fitness than, for example, one that is missing a condition function, which would cause syntax errors.

We will use this fitness function with our original GP algorithm as described in Algorithm 1.

3 Experiments and Results

In this section we present an evaluation of our new fitness function based on refinement type checking. Our goal is to assess whether it can provide a performance and scalability improvement over two baselines: a standard fitness function based on input-output examples, and random search. In Sect. 3.1 we specify our benchmark problems and what program pieces we use in the synthesis. In Sect. 3.2 we describe our experimental setup. Next, in Sect. 3.3 we outline the results of our evaluation. Lastly, in Sect. 3.4 we discuss limitations of our technique and possible threats to its validity.

3.1 Program Synthesis Problems

We use a set of 3 program synthesis problems for evaluation. Some are adapted from a general program synthesis benchmark suite [9] and expanded for our program synthesis model as described below. All of them have the property that their behavior can be expressed using refinement types. For program pieces, we chose building blocks that are likely to be part of the standard library for any language, such as checking if an integer is even or filtering a list, as well as domain-specific functions that the user would provide, such as a function that joins two sorted partitions used in sorting algorithms. Below are the problem specifications and a high level description of what program pieces are included.

  1. 1.

    List Filtering (adapted from Count Odds in [9]): Given a list of integers, filter the list and return 3 new lists containing just the even integers, just the odd integers, and just the integers greater than 2. We provide several possible filtering conditions as program pieces, including the correct ones as well as others that are not needed for the correct solution.

  2. 2.

    Insertion Sort: Given a list of integers, sort them in ascending order using insertion sort. We provide several possible conditions for determining when to insert, as well as a skeleton for the sort. The skeleton provides the control flow, so our search needs to find the correct conditions and operations to fit into the skeleton.

  3. 3.

    QuickSort: Given a list of integers, sort them in ascending order using quicksort. We provide a skeleton for the sort function, as in Insertion Sort, as well as different possible ways of partitioning the list for quicksort.

3.2 Experimental Setup

For each selected program synthesis problem, we run 60 trials and report performance as the number of generations taken to find a solution. We compare the following 3 variants of GP search:

  1. 1.

    RefinementTypes (RT): GP search using our new fitness function based on counting errors from refinement type checking (Eq. 1).

  2. 2.

    IOExamples (IO): GP search using a baseline fitness function using accuracy on a set of input-output example cases, as described in Sect. 2.2. For each problem, we choose a small (\({<} 10\)) but diverse set of examples. Specifically, we ensure that the example sets cover all execution paths in a correct solution.

  3. 3.

    RandomSearch (RS): Random generation of individuals. To make this comparable with GP search, we proceed in generations, where pop_size individuals are randomly generated and evaluated per generation. As with GP search we can report the number of generations taken to find a solution. Thus, the total number of fitness evaluations is the same (pop_size * generations), so the running time is approximately equal as well. We include this as a baseline to verify that GP is well suited to our program synthesis model and provides an improvement over naive random search.

We also run each problem on 3 different search space sizes to evaluate scalability; we vary the size of the search space by including or excluding different optional program pieces which are not needed in a correct solution.

The common parameters that we used for all experiments is shown in Table 1. Note that for ease of implementation, we terminate searches after 20 generations and report a run as having taken 20 generations if it does not find a solution.

Table 1. Experiment parameters
Full size table

We tuned the max generations and population size to find a setting in which most trials find a solution before reaching the max generation limit. We did not tune the other parameters.

Our implementation, including problem specifications and program piece specifications for each problem, is available on GitHubFootnote 1.

3.3 Results

Table 2 shows the results of our experiments. For each problem and set of program pieces, the search space size is calculated as \(|P|^{|c|}\), where |P| is the number of program pieces and |c| is the length of the chromosome. We present the sample mean \(\bar{x}\) and standard deviation s of the number of generations taken to find a solution for each fitness function.

The p-values shown in the table come from comparing the two specified variants using the Mann-Whitney U nonparametric test [18], which tests the null hypothesis that two sets of samples have the same population distribution (in particular, the probability that a random member from population 1 is greater than a random member from population 2 is 1/2). The p-values have also been adjusted for multiple hypothesis testing using the Bonferroni correction to decrease the likelihood of Type I error [1]; specifically, we multiply p-values by 2, the number of simultaneous hypotheses we are testing.

Table 2. Experiment Results. We run 60 trials per problem, search space size, and variant and record the number of generations taken to find a solution. We report the sample mean \(\bar{x}\) and standard deviation s. The p-values come from the Mann-Whitney U nonparametric test and have been adjusted using the Bonferroni correction for multiple hypothesis testing. p-values less than 0.05 are in bold.
Full size table

We can see from the table that in general, RefinementTypes finds a solution in fewer generations than the two baselines. Across all the experiments, RefinementTypes achieves an average improvement of 20% over IOExamples and 32% over RandomSearch. The p-values show that the improvement is significant (\(p < 0.05\)) in most cases.

We hypothesize that a key reason for the performance improvement is the difference in fitness values for programs that have syntax errors. For IOExamples, all programs that have syntax errors have a fitness value of 0 since the fitness evaluation is not able to run at all (the program cannot be interpreted). We can see in Fig. 1a that for IOExamples, many candidate programs (all those with syntax errors) have fitness values of 0, and there are not many distinct fitness values. On the other hand, the RefinementTypes fitness function provides a heuristic even if there are syntax errors, as seen in Fig. 1b, where there are four distinct fitness values for programs with syntax errors (fitness \({<} 0.5\)). This is helpful because among programs that have syntax errors, some are still closer to correct (e.g. less errors) and the RefinementTypes fitness function can capture that. Therefore, in areas of the search space corresponding to programs that have syntax errors, the new fitness function can still guide the GP search whereas those programs are all evaluated to be equally “unfit” by the IOExamples fitness function. In the trial shown in Fig. 1, the search using IOExamples is unable to find a solution after 20 generations, whereas the additional heuristic information provided by RefinementTypes allows the GP search to find a solution after 10 generations.

Fig. 1.
figure 1

Scatter plots of population’s fitness values over time (generations) for (a) IOExamples and (b) RefinementTypes fitness functions. Each plots was generated from one trial run on the QuickSort problem with the same search space size and population size. Each point (g, f) represents an individual in generation g with a fitness value of f, and the opacity increases with the number of individuals with fitness value f.

Full size image

We also see from the table that the p-value generally remains below 0.05 as the search space size increases, which shows that the performance improvements that we observe can potentially scale to larger problems as well.

3.4 Threats to Validity

We note that refinement types are not applicable to every problem; for example, some string manipulations, such as the Double Letters problem from [9], would be difficult to express using refinement types since they involve complex dependencies between indices of the string. In addition, we observed that the GP search overall runs an order of magnitude slower in terms of wall-clock time when using the refinement type check rather than example cases as a fitness function. We did not optimize our implementations; in particular, there are many I/O operations that may be unnecessary in a better implementation, so this difference may change after optimization.

4 Related Work

Since the fitness function is so integral in GP search, many researchers have studied different ways of defining the fitness function. NetSyn [17], mentioned in Sect. 1, uses a neural network to learn a better fitness function based on input-output examples. CrowdBoost [2] explores evolving the fitness function along with candidate programs during GP. Hemberg et al. [10] show that it is possible to improve search performance by using domain knowledge extracted from the problem description to construct the fitness function. Implicit fitness sharing [19], in which multiple individuals that solve the same example case must “share” the reward, can also improve search performance by preserving population diversity. Another related approach is behavioral programming [15, 16], which introduces the use of the full execution trace of a candidate program in the evaluation stage rather than relying solely on a scalar objective fitness function.

Others have investigated using formal methods like model checking and Hoare logic for program verification as the basis for the fitness function in GP [8, 12]. Our approach similarly uses formal methods for the GP’s fitness function, but we use refinement types, which are often less verbose and require less manual annotation than Hoare logic; with LiquidHaskell, it is very easy to define and verify refinement types for program pieces [33].

Prior works have also explored refinement types and their applicability to program synthesis. Synquid [27] uses refinement types for program synthesis without GP by decomposing the type specifications and solving local type constraints. Fonseca et al. [5] suggest an approach for combining GP with refinement types, including a possible fitness function for refinements expressed in their programming language; however, they do not present any experimental data or results.

A similar approach for improving practicality of program synthesis is program sketching, where a user provides a partially-complete template of a program, and the synthesis algorithm fills in the missing low-level details [29]. This has been implemented successfully for certain problem domains in systems like Sketch [31] and Psketch [30], which achieve better efficiency because the search space is restricted. Our approach is analogous but inverted: the user provides building blocks and the synthesis algorithm finds a correct composition of those building blocks. This has the same benefit of restricting the search space and can be useful in situations where a user does not have enough knowledge of the program structure to build a sketch.

5 Conclusions

Our results show that it is possible to express complex programs such as sorting using our program piece-based model. Using this model for program synthesis, we can make use of refinement type checking to express correctness properties of the program. We show that in this model, using refinement type checking to evaluate fitness within GP search can provide an improvement over using an example-based fitness evaluation. These results merit further investigation into different approaches to achieving scalability in program synthesis as well as different ways of incorporating symbolic solving within GP search. In future work, we hope to evaluate a wider set of benchmarks, including more complex problems with larger search spaces. We also hope to further explore ways to formalize and potentially automate the construction of program pieces, for example by searching the standard library, or using GP to “fill in” missing pieces.