Abstract
We propose a novel approach to stream definition and manipulation. Our solution is based on two key ideas. Regular corecursion, which avoids non termination by detecting cyclic calls, is enhanced, by allowing in equations defining streams other operators besides the stream constructor. In this way, some non-regular streams are definable. Furthermore, execution includes a runtime check to ensure that the stream generated by a function call is well-defined, in the sense that access to an arbitrary index always succeeds. We extend the technique beyond the simple stream operators considered in previous work, notably by adding an interleaving combinator which has a non-trivial recursion scheme.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Applications often deal with data structures which are conceptually infinite; among those data streams (unbounded sequences of data) are a paradigmatic example, important in several application domains as the Internet of Things. Lazy evaluation is a well-established and widely-used solution to data stream generation and processing, supported, e.g., in Haskell, and in most stream libraries offered by mainstream languages, as
 . In this approach, data streams can be defined as the result of an arbitrary function. For instance, in Haskell we can write
. In this approach, data streams can be defined as the result of an arbitrary function. For instance, in Haskell we can write

Functions which only need to inspect a finite portion of the structure, e.g., getting the i-th element, can be correctly implemented, thanks to the lazy evaluation strategy as exemplified below.

More recently, another approach has been proposed [2, 11, 14, 19], called regular corecursion, which exploits the fact that streams as
 above are periodic, a.k.a. regular following the terminology in [8], meaning that the term 1:2:1:2:1: ... is infinite but has a finite number of subterms. Regular streams can be actually represented at runtime by a finite set of equations involving only the stream constructor, in the example \(\textit{x}= 1 : 2 : \textit{x}\). Furthermore, function definitions are corecursive, meaning that they do not have the standard inductive semantics; indeed, even though the evaluation strategy is call-by-value, thanks to the fact that pending function calls are tracked, cyclic calls are detected, avoiding in this case non-termination.
above are periodic, a.k.a. regular following the terminology in [8], meaning that the term 1:2:1:2:1: ... is infinite but has a finite number of subterms. Regular streams can be actually represented at runtime by a finite set of equations involving only the stream constructor, in the example \(\textit{x}= 1 : 2 : \textit{x}\). Furthermore, function definitions are corecursive, meaning that they do not have the standard inductive semantics; indeed, even though the evaluation strategy is call-by-value, thanks to the fact that pending function calls are tracked, cyclic calls are detected, avoiding in this case non-termination.
For instance, with regular corecursionFootnote 1 we have:

Despite their differences, in both approaches programmers are allowed to write intuitively ill-formed definitions such as
 ; any access to indexes of the stream returned by this function leads to non-termination both with lazy evaluation and regular corecursion. However, while in the regular case it is simple to reject the result of calling
; any access to indexes of the stream returned by this function leads to non-termination both with lazy evaluation and regular corecursion. However, while in the regular case it is simple to reject the result of calling
 by checking a guardedness syntactic condition, the Haskell compiler does not complain if one calls such a function. In this paper, we propose a novel approach to stream generation and manipulation, providing, in a sense, a middle way between those described above. Our solution is based on two key ideas:
by checking a guardedness syntactic condition, the Haskell compiler does not complain if one calls such a function. In this paper, we propose a novel approach to stream generation and manipulation, providing, in a sense, a middle way between those described above. Our solution is based on two key ideas:
-
Corecursion is enhanced, by allowing in stream equations other typical operators besides the stream constructor; in this way, some non-regular streams are supported. For instance, we can define
 , with
, with
 the pointwise addition and
the pointwise addition and
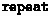 defined by
defined by
 .
. -
Execution includes a runtime check which rejects the stream generated by a function call if it is ill-formed, in the sense that access to an index could possibly diverge. For instance, the call
 raises a runtime error.
raises a runtime error.
In this way we achieve a convenient trade-off between expressive power and reliability; indeed, we do not have the full expressive power of Haskell, where we can manipulate streams generated as results of arbitrary functions, but, clearly, the well-definedness check described above would be not decidable. On the other hand, we significantly augment the expressive power of regular corecursion, allowing several significant non-regular streams, at the price of making the well-definedness check non-trivial, but still decidable.
The main formal results are (1) Theorem 1 stating the soundness of the runtime check; (2) Theorem 2 stating that the optimized definition of the runtime check in Sect. 5 is equivalent to the simpler one given in Sect. 4. In particular, for contribution (1) the interleaving operator requires a more involved proof in comparison with [3] (see Sect. 6), while for (2) we show that the optimized definition improves the time complexity from \(O(N^2)\) to \(O(N \log N)\).
In Sect. 2 we formally define the calculus, in Sect. 3 we show examples, in Sect. 4 we define the well-formedness check, and in Sect. 5 its optimized version. Finally, in Sect. 6 we discuss related and further work. More examples of derivations and omitted proofs can be found in the extended version [4].
2 Stream Calculus
Figure 1 shows the syntax of the calculus.
A program is a sequence of (mutually recursive) function declarations, for simplicity assumed to only return streams. Stream expressions are variables, conditionals, expressions built by stream operators, and function calls. We consider the following stream operators: constructor (prepending a numeric element), tail, pointwise arithmetic operators, and interleaving. Numeric expressions include the access to the i-thFootnote 2 element of a stream. We use \(\overline{\textit{fd}}\) to denote a sequence \(\textit{fd}_1, \dots , \textit{fd}_n\) of function declarations, and analogously for other sequences.
The operational semantics, given in Fig. 2, is based on two key ideas:
-
1.
some infinite streams can be represented in a finite way
-
2.
evaluation keeps trace of already considered function calls
To obtain (1), our approach is inspired by capsules [13], which are expressions supporting cyclic references. That is, the result of a stream expression is a pair \(({{\textit{s}},{\rho }})\), where \(\textit{s}\) is an (open) stream value, built on top of stream variables, numeric values, the stream constructor, the tail destructor, the pointwise arithmetic and the interleaving operators, and \(\rho \) is an environment mapping variables into stream values. In this way, cyclic streams can be obtained: for instance, \(({{\textit{x}},{\textit{x}\mapsto {\textit{n}}\mathbin {\texttt {:}}{\textit{x}}}})\) denotes the stream constantly equal to \(\textit{n}\).
We denote by \( dom (\rho )\) the domain of \(\rho \), by \(\textit{vars}(\rho )\) the set of variables occurring in \(\rho \), by \(\textit{fv}(\rho )\) the set of its free variables, that is, \(\textit{vars}(\rho )\setminus dom (\rho )\), and say that \(\rho \) is closed if \(\textit{fv}(\rho )=\emptyset \), open otherwise, and analogously for a result \(({{\textit{v}},{\rho }})\).
To obtain point (2) above, evaluation has an additional parameter which is a call trace, a map from function calls where arguments are values (dubbed calls for short in the following) into variables.
Altogether, the semantic judgment has shape \({\textit{e},\rho ,\tau }\!\Downarrow \!({{\textit{v}},{{\rho '}}})\), where \(\textit{e}\) is the expression to be evaluated, \(\rho \) the current environment defining possibly cyclic stream values that can occur in \(\textit{e}\), \(\tau \) the call trace, and \(({{\textit{v}},{{\rho '}}})\) the result. The semantic judgments should be indexed by an underlying (fixed) program, omitted for sake of simplicity. Rules use the following auxiliary definitions:
-
\(\rho \sqcup \rho '\) is the union of two environments, which is well-defined if they have disjoint domains; \(\rho \{\textit{x}\mapsto \textit{s}\}\) is the environment which gives \(\textit{s}\) on \(\textit{x}\), coincides with \(\rho \) elsewhere; we use analogous notations for call traces.
-
\(\textit{se} [\overline{\textit{v}}/\overline{\textit{x}}]\) is obtained by parallel substitution of variables \(\overline{\textit{x}}\) with values \(\overline{\textit{v}}\).
-
\( fbody (\textit{f})\) returns the pair of the parameters and the body of the declaration of \(\textit{f}\), if any, in the assumed program.
Intuitively, a closed result \(({{\textit{s}},{\rho }})\) is well-defined if it denotes a unique stream, and a closed environment \(\rho \) is well-defined if, for each \(\textit{x}\in dom (\rho )\), \(({{\textit{x}},{\rho }})\) is well-defined. In other words, the corresponding set of equations admits a unique solution. For instance, the environment \({\{\textit{x}\mapsto \textit{x}\}}\) is not well-defined, since it is undetermined (any stream satisfies the equation \(\textit{x}=\textit{x}\)); the environment \(\{\textit{x}\mapsto \textit{x}[+]\textit{y},\textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}}\}\) is not well-defined as well, since it is undefined (the two equations \(\textit{x}=\textit{x}\mapsto \textit{x}[+]\textit{y},\textit{y}={1}\mathbin {\texttt {:}}{\textit{y}}\) admit no solutions for x). This notion can be generalized to open results and environments, assuming that free variables denote unique streams, as will be formalized in Sect. 4.
Rules for values and conditional are straightforward. In rules (cons), (tail) and (op), arguments are evaluated and the stream operator is applied without any further evaluation. That is, we treat all these operators as constructors.
The rules for function call are based on a mechanism of cycle detection [2]. Evaluation of arguments is handled by a separate rule (args), whereas the following two rules handle (evaluated) calls.
Rule (invk) is applied when a call is considered for the first time, as expressed by the first side condition. The body is retrieved by using the auxiliary function fbody, and evaluated in a call trace where the call has been mapped into a fresh variable. Then, it is checked that adding the association of such variable with the result of the evaluation of the body keeps the environment well-defined, as expressed by the judgment \( wd (\rho ,\textit{x},\textit{s})\), which will be defined in Sect. 4. If the check succeeds, then the final result consists of the variable associated with the call and the updated environment. For simplicity, here execution is stuck if the check fails; an implementation should raise a runtime error instead. An example of stuck derivation is shown in [4].
Rule (corec) is applied when a call is considered for the second time, as expressed by the first side condition. The variable \(\textit{x}\) is returned as result. However, there is no associated value in the environment yet; in other words, the result \(({{\textit{x}},{\rho }})\) is open at this point. This means that \(\textit{x}\) is undefined until the environment is updated with the corresponding value in rule (invk). However, \(\textit{x}\) can be safely used as long as the evaluation does not require \(\textit{x}\) to be inspected; for instance, \(\textit{x}\) can be safely passed as an argument to a function call.
For instance, if we consider the program
 , then the judgment
, then the judgment  , with \(\rho =\{\textit{x}\mapsto \textit{y},\textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{x}}\}\), is derivable; however, while the final result \(({{\textit{x}},{\rho }})\) is closed, the derivation contains also judgments with open results, as happens for
, with \(\rho =\{\textit{x}\mapsto \textit{y},\textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{x}}\}\), is derivable; however, while the final result \(({{\textit{x}},{\rho }})\) is closed, the derivation contains also judgments with open results, as happens for  and
and  . The full derivation can be found in [4].
. The full derivation can be found in [4].
Finally, rule (at) computes the \(i\)-th element of a stream expression. After evaluating the arguments, the result is obtained by the auxiliary judgment \( at _\rho (\textit{s},i)=\textit{n}\), whose straightforward definition is at the bottom of the figure. Rules (at-)\(\Vert \) (-even) and (at-)\(\Vert \) (-odd) define the behaviour of the interleaving operator, which merges two streams together by alternating their elements.
When evaluating \( at _\rho (\textit{s},i)\), if \(\textit{s}\) is a variable free in the environment, then execution is stuck; again, an implementation should raise a runtime error instead.
3 Examples
First we show some simple examples, to explain how corecursive definitions work. Then we provide some more significant examples.
Consider the following function declarations:

With the standard semantics of recursion, the calls, e.g.,
 and
and
 lead to non-termination. Thanks to corecursion, instead, these calls terminate, producing as result \(\mathtt {({{\textit{x}},{\{\textit{x}\mapsto {0}\mathbin {\texttt {:}}{\textit{x}}\}}})}\), and \(\mathtt {({{\textit{x}},{{\{}\textit{x}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}},\textit{y}\mapsto {2}\mathbin {\texttt {:}}{\textit{x}}{\}}}})}\), respectively. Indeed, when initially invoked, the call
lead to non-termination. Thanks to corecursion, instead, these calls terminate, producing as result \(\mathtt {({{\textit{x}},{\{\textit{x}\mapsto {0}\mathbin {\texttt {:}}{\textit{x}}\}}})}\), and \(\mathtt {({{\textit{x}},{{\{}\textit{x}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}},\textit{y}\mapsto {2}\mathbin {\texttt {:}}{\textit{x}}{\}}}})}\), respectively. Indeed, when initially invoked, the call
 is added in the call trace with an associated fresh variable, say \(\textit{x}\). In this way, when evaluating the body of the function, the recursive call is detected as cyclic, the variable \(\textit{x}\) is returned as its result, and, finally, the stream value \(\mathtt {{0}\mathbin {\texttt {:}}{\textit{x}}}\) is associated in the environment with the result \(\textit{x}\) of the initial call. In the sequel, we will use
is added in the call trace with an associated fresh variable, say \(\textit{x}\). In this way, when evaluating the body of the function, the recursive call is detected as cyclic, the variable \(\textit{x}\) is returned as its result, and, finally, the stream value \(\mathtt {{0}\mathbin {\texttt {:}}{\textit{x}}}\) is associated in the environment with the result \(\textit{x}\) of the initial call. In the sequel, we will use
 as a shorthand for
as a shorthand for
 . The evaluation of
. The evaluation of
 is analogous, except that another fresh variable \(\textit{y}\) is generated for the intermediate call
is analogous, except that another fresh variable \(\textit{y}\) is generated for the intermediate call
 . The formal derivations are given below.
. The formal derivations are given below.

For space reasons, we did not report the application of rule (value). In both derivations, note that rule (corec) is applied, without evaluating the body of
 once more, when the cyclic call is detected.
once more, when the cyclic call is detected.
The following examples show function definitions whose calls return non-regular streams, notably, the natural numbers, the natural numbers raised to the power of a number, the factorials, the powers of a number, the Fibonacci numbers, and the stream obtained by pointwise increment by one.

The definition of
 uses corecursion, since the recursive call
uses corecursion, since the recursive call
 is cyclic. Hence the call
is cyclic. Hence the call
 returns \(({{\textit{x}},{{\{}\textit{x}\mapsto {0}\mathbin {\texttt {:}}{(\textit{x}[+]\textit{y})}, \textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}}{\}}}})\). The definition of
returns \(({{\textit{x}},{{\{}\textit{x}\mapsto {0}\mathbin {\texttt {:}}{(\textit{x}[+]\textit{y})}, \textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}}{\}}}})\). The definition of
 is a standard inductive one where the argument strictly decreases in the recursive call. Hence, the call, e.g.,
is a standard inductive one where the argument strictly decreases in the recursive call. Hence, the call, e.g.,
 , returns
, returns
\(({{\textit{x}_2},{{\{\textit{x}_2\mapsto \textit{x}_1[*]\textit{x},\textit{x}_1\mapsto \textit{x}_0[*]\textit{x}, \textit{x}_0\mapsto \textit{y}, \textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}}, \textit{x}\mapsto {0}\mathbin {\texttt {:}}{(\textit{x}[+]\textit{y}')}, \textit{y}'\mapsto {1}\mathbin {\texttt {:}}{\textit{y}'}\}}}}).\) The definitions of
 , and
, and
 are corecursive. For instance, the call
are corecursive. For instance, the call
 returns \({({{\textit{z}},{\textit{z}\mapsto {{1}\mathbin {\texttt {:}}{((\textit{x}[+]\textit{y})[*]z)}}, \textit{x}\mapsto {0}\mathbin {\texttt {:}}{(\textit{x}[+]\textit{y}'}), \textit{y}\mapsto 1:\textit{y}, \textit{y}'\mapsto 1:\textit{y}'}})}\). The definition of
returns \({({{\textit{z}},{\textit{z}\mapsto {{1}\mathbin {\texttt {:}}{((\textit{x}[+]\textit{y})[*]z)}}, \textit{x}\mapsto {0}\mathbin {\texttt {:}}{(\textit{x}[+]\textit{y}'}), \textit{y}\mapsto 1:\textit{y}, \textit{y}'\mapsto 1:\textit{y}'}})}\). The definition of
 is non-recursive, hence always converges, and the call
is non-recursive, hence always converges, and the call
 \(\textit{s}\)
\(\textit{s}\)
 returns \(({{\textit{x}},{{\{}\textit{x}\mapsto \textit{s}[+]\textit{y}, \textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}}{\}}}})\).
returns \(({{\textit{x}},{{\{}\textit{x}\mapsto \textit{s}[+]\textit{y}, \textit{y}\mapsto {1}\mathbin {\texttt {:}}{\textit{y}}{\}}}})\).
The next few examples show applications of the interleaving operator.

Function
 generates the stream which alternates sequences of occurrences of
generates the stream which alternates sequences of occurrences of
 and
and
 , with the number of repetitions of the same number duplicated at each step, that is,
, with the number of repetitions of the same number duplicated at each step, that is,
 .
.
A more involved example shows a different way to generate the stream of all powers of
 starting from \(2^1\):
starting from \(2^1\):

The following definition is an instance of a schema generating the infinite sequence of labels obtained by a breadth-first visit of an infinite complete binary tree where the labels of children are defined in terms of that of their parent.

In particular, the root is labelled by
 , and the left and right child of a node with label
, and the left and right child of a node with label
 are labelled by
are labelled by
 and
and
 , respectively. Hence, the generated stream is the sequence of natural numbers starting from
, respectively. Hence, the generated stream is the sequence of natural numbers starting from
 , as it happens in the array implementation of a binary heap.
, as it happens in the array implementation of a binary heap.
In the other instance below, the root is labelled by
 , and children are labelled with
, and children are labelled with
 if their parent has label
if their parent has label
 . That is, nodes are labelled by their level.
. That is, nodes are labelled by their level.

In this case, the generated stream is more interesting; indeed,
 .
.
The following function computes the stream of partial sums of the first \(i+1\) elements of a stream s, that is,
 :
:

Such a function is useful for computing streams whose elements approximate a series with increasing precision; for instance, the following function returns the stream of partial sums of the first \(i+1\) elements of the Taylor series of the exponential function:

Function
 calls
calls
 with the argument
with the argument
 corresponding to the stream of terms of the Taylor series of the exponential; hence, by accessing the \(i\)-th element of the stream, we have the following approximation of the series:
corresponding to the stream of terms of the Taylor series of the exponential; hence, by accessing the \(i\)-th element of the stream, we have the following approximation of the series:

Lastly, we present a couple of examples showing how it is possible to define primitive operations provided by IoT platforms for real time analysis of data streams; we start with
 , which allows aggregation by addition of data in windows of length
, which allows aggregation by addition of data in windows of length
 :
:

For instance,
 returns the stream \(\textit{s}'\) s.t. \(\textit{s}'(i)=\textit{s}(i)+\textit{s}(i+1)+\textit{s}(i+2)\). On top of
returns the stream \(\textit{s}'\) s.t. \(\textit{s}'(i)=\textit{s}(i)+\textit{s}(i+1)+\textit{s}(i+2)\). On top of
 , we can easily define
, we can easily define
 to compute the stream of average values of
to compute the stream of average values of
 in windows of length
in windows of length
 :
:

4 Well-Definedness Check
A key feature of our approach is the runtime check ensuring that the stream generated by a function call is well-defined, see the side condition \( wd ({\rho '},\textit{x},\textit{s})\) in (invk); in this section we formally define the corresponding judgment and prove its soundness. Before doing this, we provide, for reference, a formal abstract definition of well-definedness.
Intuitively, an environment is well-defined if each variable in its domain denotes a unique stream. Semantically, a stream \(\sigma \) is an infinite sequence of numeric values, that is, a function which returns, for each index \(i\ge 0\), the i-th element \(\sigma (i)\). Given a result \(({{\textit{s}},{\rho }})\), we get a stream by instantiating variables in \(\textit{s}\) with streams, in a way consistent with \(\rho \), and evaluating operators. To make this formal, we need some preliminary definitions.
A substitution \(\theta \) is a function from a finite set of variables to streams. We denote by \({\llbracket \textit{s}\rrbracket }\theta \) the stream obtained by applying \(\theta \) to \(\textit{s}\), and evaluating operators, as formally defined below.
Given an environment \(\rho \) and a substitution \(\theta \) with domain \(\textit{vars}(\rho )\), the substitution \( \rho [\theta ] \) is defined by:
Then, a solution of \(\rho \) is a substitution \(\theta \) such that \( \rho [\theta ] = \theta \).
A closed environment \(\rho \) is well-defined if it has exactly one solution. For instance, \({\{\textit{x}\mapsto {1}\mathbin {\texttt {:}}{\textit{x}}\}}\) and \({\{\textit{y}\mapsto {0}\mathbin {\texttt {:}}{(\textit{y}[+] \textit{x})},\ \textit{x}\mapsto 1:\textit{x}\}}\) are well-defined, since their unique solutions map \(\textit{x}\) to the infinite stream of ones, and \(\textit{y}\) to the stream of natural numbers, respectively. Instead, for \({\{\textit{x}\mapsto 1[+]\textit{x}\}}\) there are no solutions. Lastly, an environment can be undetermined: for instance, a substitution mapping \(\textit{x}\) into an arbitrary stream is a solution of \({\{\textit{x}\mapsto \textit{x}\}}\).
An open environment \(\rho \) is well-defined if, for each \(\theta \) with domain \(\textit{fv}(\rho )\), it has exactly one solution \(\theta '\) such that \(\theta \subseteq \theta '\). For instance, the open environment \(\{\textit{y}\mapsto {0}\mathbin {\texttt {:}}{(\textit{y}[+] \textit{x})}\}\) is well-defined.
In Fig. 3 we provide the operational characterization of well-definedness. The judgment \( wd (\rho ,\textit{x},\textit{s})\) used in the side condition of rule (invk) holds if \(\mathsf {wd}_{\rho '}(\textit{x},\emptyset )\) holds, with \({\rho '}\,{=}\,{\rho \{\textit{x}\mapsto \textit{v}\}}\). The judgment \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) means well-definedness of a result. That is, restricting the domain of \(\rho \) to the variables reachable from \(\textit{s}\) (that is, either occurring in \(\textit{s}\), or, transitively, in values associated with reachable variables) we get a well-defined environment; thus, \( wd (\rho ,\textit{x},\textit{s})\) holds if adding the association of \(\textit{s}\) with \(\textit{x}\) preserves well-definedness of \(\rho \).
The additional argument \( m \) in the judgment \(\mathsf {wd}_\rho (\textit{s}, m )\) is a map from variables to integer numbers. We write \( m ^{+1}\) and \( m ^{-1}\) for the maps \(\{(\textit{x}, m (\textit{x})+1) \mid {\textit{x}\in dom ( m )}\}\), and \(\{(\textit{x}, m (\textit{x})-1) \mid \textit{x}\in dom ( m )\}\), respectively.
In rule (main), this map is initially empty. In rule (wd-var), when a variable \(\textit{x}\) defined in the environment is found the first time, it is added in the map with initial value 0 before propagating the check to the associated value. In rule (wd-corec), when it is found the second time, it is checked that constructors and right operands of interleave are traversed more times than tail operators, and if it is the case the variable is considered well-defined. Rule (wd-delay), which is only added for the purpose of the soundness proof and should be not part of an implementationFootnote 3, performs the same check but then considers the variable occurrence as it is was the first, so that success of well-definedness is delayed. Note that rules (wd-var), (wd-corec), and (wd-delay) can only be applied if \(\textit{x}\in dom (\rho )\); in rule (wd-corec), this explicit side condition could be omitted since satisfied by construction of the proof tree.
In rule (wd-fv), a free variable is considered well-defined.Footnote 4 In rules (wd-cons) and (wd-tail) the value associated with a variable is incremented/decremented by one, respectively, before propagating the check to the subterm. In rule (wd-nop) the check is simply propagated to the subterms. In rule (wd-)\(\Vert \), the check is also propagated to the subterms, but on the right-hand side the value associated with a variable is incremented by one before propagation; this reflects the fact that, in the worst case, \( at _\rho (\textit{s}_1\Vert \textit{s}_2,i)= at _\rho (\textit{s}_1,i)\), and this happens only for \(i=0\), while for odd indexes \(i\) we have that \( at _\rho (\textit{s}_1\Vert \textit{s}_2,i)= at _\rho (\textit{s}_2,i-k)\), with \(k\ge 1\); more precisely, \(k=1\) only when \(i=1\); for all indexes \(i>1\) (both even and odd), \(k>1\). For instance, the example
 , which has the same semantics as
, which has the same semantics as
 , would be considered not well-defined if we treated the interleaving as the pointwise arithmetic operators.
, would be considered not well-defined if we treated the interleaving as the pointwise arithmetic operators.
Note that the rules in Fig. 3 can be immediately turned into an algorithm which, given a stream value \(\textit{s}\), always terminates either successfully (finite proof tree), or with failure (no proof tree can be constructed). On the other hand, the rules in Fig. 2 defining the \( at _\rho (\textit{s},i)=\textit{n}\) judgment can be turned into an algorithm which can possibly diverge (infinite proof tree).
Two examples of derivation of well-definedness and access to the \(i\)-th element can be found in [4] for the results obtained by evaluating the calls
 and
and
 , respectively, with
, respectively, with
 and
and
 defined as in Sect. 3. Below we show an example of failing derivation:
defined as in Sect. 3. Below we show an example of failing derivation:
As depicted in Fig. 4, the check succeeds for the left-hand component of the interleaving operator, while the proof tree cannot be completed for the other side. Indeed, the double application of the tail operator makes undefined access to stream elements with index greater than 1, since the evaluation of \( at _\rho (\textit{x},2)\) infinitely triggers the evaluation of itself.
To formally express and prove that well-definedness of a result implies termination of access to an arbitrary index, we introduce some definitions and notations. First of all, since the result is not relevant for the following technical treatment, for simplicity we will write \( at _\rho (\textit{s},i)\) rather than \( at _\rho (\textit{s},i)=\textit{n}\). We call derivation an either finite or infinite proof tree. We write \(\mathsf {wd}_\rho (\textit{s}', m ')\vdash \mathsf {wd}_\rho (\textit{s}, m )\) to mean that \(\mathsf {wd}_\rho (\textit{s}', m ')\) is a premise of a (meta-)rule where \(\mathsf {wd}_\rho (\textit{s}, m )\) is the conclusion, and \(\vdash ^\star \) for the reflexive and transitive closure of this relation.
Lemma 1
-
1.
A judgment \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) has no derivation iff the following condition holds:

-
2.
If the derivation of \( at _\rho (\textit{s},j)\) is infinite, then the following condition holds:

Lemma 2
If \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s}',i)\), and \(\mathsf {wd}_\rho (\textit{s}', m )\vdash ^\star \mathsf {wd}_\rho (\textit{s},\emptyset )\) with \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) derivable, and \(\textit{x}\in dom ( m )\), then
\({\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}', m )}\) for some \( m '\) such that \( m '(\textit{x})- m (\textit{x}) \le i-i'\).
Proof
The proof is by induction on the length of the path in \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s}',i)\).
-
Base. The length of the path is 0, hence we have \( at _\rho (\textit{x},i)\vdash ^\star at _\rho (\textit{x},i)\). We also have \(\mathsf {wd}_\rho (\textit{x}, m )\vdash ^\star \mathsf {wd}_\rho (\textit{x}, m )\), and we get the thesis since \( m (\textit{x})= m (\textit{x})+i-i\).
-
Inductive step. By cases on the rule applied to derive \( at _\rho (\textit{s}',i)\).
-
(at-var) We have \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\rho (\textit{y}),i)\vdash at _\rho (\textit{y},i)\). There are two cases:
-
If \(\textit{y}\not \in dom ( m )\) (hence \(\textit{y}\ne \textit{x}\)), we have \(\mathsf {wd}_\rho (\rho (\textit{y}), m \{\textit{y}\mapsto 0\})\vdash \mathsf {wd}_\rho (\textit{y}, m )\) by rule (wd-var), the premise is derivable, hence by inductive hypothesis we have \({\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\rho (\textit{y}), m \{\textit{y}\mapsto 0\})}\), and \({ m '(\textit{x})\le m \{\textit{y}\mapsto 0\}(\textit{x})+i-i'}= m (\textit{x})+i-i'\), hence we get the thesis.
-
If \(\textit{y}\in dom ( m )\), then it is necessarily \( m (\textit{y})>0\), otherwise, by Lemma 1-(1), \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) would not be derivable. Hence, we have \({\mathsf {wd}_\rho (\rho (\textit{y}), m \{\textit{y}\mapsto 0\})\vdash \mathsf {wd}_\rho (\textit{y}, m )}\) by rule (wd-delay), hence by inductive hypothesis we have \({\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\rho (\textit{y}), m \{\textit{y}\mapsto 0\})}\), and \({ m '(\textit{x})\le m \{\textit{y}\mapsto 0\}(\textit{x})+i-i'}\). There are two subcases:
-
If \(\textit{y}\ne \textit{x}\), then \( m \{\textit{y}\mapsto 0\}(\textit{x})= m (\textit{x})\), and we get the thesis as in the previous case.
-
If \(\textit{y}=\textit{x}\), then \( m \{\textit{x}\mapsto 0\}(\textit{x})=0\), hence \( m '(\textit{x})\le i-i'\le m (\textit{x})+i-i'\), since \( m (\textit{x})>0\).
-
-
-
(at-cons-0) Empty case, since the derivation for \( at _\rho ({\textit{n}}\mathbin {\texttt {:}}{\textit{s}},0)\) does not contain a node \( at _\rho (\textit{x},i')\).
-
(at-cons-succ) We have \( at _\rho ({\textit{n}}\mathbin {\texttt {:}}{\textit{s}},i)\), and \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s},i-1)\). Moreover, we can derive \(\mathsf {wd}_\rho ({\textit{n}}\mathbin {\texttt {:}}{\textit{s}}, m )\) by rule (wd-cons), and by inductive hypothesis we also have \(\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}, m ^{+1})\), with \( m '(\textit{x})\le m ^{+1}(\textit{x})+(i-1)-i'\), hence we get the thesis.
-
(at-tail) This case is symmetric to the previous one.
-
(at-nop) We have \( at _\rho (\textit{s}_1{[{\textit{op}}]}\textit{s}_2,i)\), and either \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s}_1,i)\), or \({ at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s}_2,i)}\). Assume the first case holds, the other is analogous. Moreover, we can derive \(\mathsf {wd}_\rho (\textit{s}_1{[{\textit{op}}]}\textit{s}_2, m )\) by rule (wd-nop), and by inductive hypothesis we also have \(\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}_1, m )\), with \( m '(\textit{x})\le m (\textit{x})+i-i'\), hence we get the thesis.
-
(at-\(\Vert \)-even) We have \( at _\rho (\textit{s}_1\Vert \textit{s}_2,2i)\) and \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s}_1,i)\). By inductive hypothesis, we have \(\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}_1, m )\), with \( m '(\textit{x})\le m (\textit{x})+i-i'\). Moreover, \(\mathsf {wd}_\rho (\textit{s}_1, m )\vdash {}\mathsf {wd}_\rho (\textit{s}_1{\Vert }\textit{s}_2, m )\) holds by rule (wd-)\(\Vert \), hence we have \(\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}_1{\Vert }\textit{s}_2, m )\) with \({ m '(\textit{x})\le m (\textit{x})+2i-i'}\) and, thus, the thesis.
-
(at-\(\Vert \)-odd) We have \( at _\rho (\textit{s}_1\Vert \textit{s}_2,2i+1)\) and \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s}_2,i)\). By inductive hypothesis, we have \(\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}_2, m ^{+1})\), with \( m '(\textit{x})\le m ^{+1}(\textit{x})+i-i'\). Moreover, \(\mathsf {wd}_\rho (\textit{s}_2, m )\vdash {}\mathsf {wd}_\rho (\textit{s}_1{\Vert }\textit{s}_2, m )\) holds by rule (wd-)\(\Vert \), hence we have \(\mathsf {wd}_\rho (\textit{x}, m ')\vdash ^\star \mathsf {wd}_\rho (\textit{s}_1{\Vert }\textit{s}_2, m )\) with \( m '(\textit{x})\le m (\textit{x})+2i+1-i'\) and, thus, the thesis.
-
Lemma 3
If \( at _\rho (\textit{x},i')\vdash ^\star at _\rho (\textit{s},i)\), and \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) derivable, then
\({\mathsf {wd}_\rho (\textit{x}, m )\vdash ^\star \mathsf {wd}_\rho (\textit{s},\emptyset )}\) for some \( m \) such that \(\textit{x}\not \in dom ( m )\).
Proof
Easy variant of the proof of Lemma 2.
Theorem 1
If \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) has a derivation then, for all \(j\), \( at _\rho (\textit{s},j)\) either has no derivation or a finite derivation.
Proof
Assume by contradiction that \( at _\rho (\textit{s},j)\) has an infinite derivation for some \(j\), and \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) is derivable. By Lemma 1–(2), the following condition holds:
Then, starting from the right, by Lemma 3 we have \({\mathsf {wd}_\rho (\textit{x}, m )\vdash ^\star \mathsf {wd}_\rho (\textit{s},\emptyset )}\) for some \( m \) such that \(\textit{x}\not \in dom ( m )\); by rule (wd-var) \(\mathsf {wd}_\rho (\rho (\textit{x}), m \{\textit{x}\mapsto 0\})\vdash \mathsf {wd}_\rho (\textit{x}, m )\), and finally by Lemma 2 we have:
5 An Optimized Algorithm for Well-Definedness
The definition of well-definedness in Fig. 3 can be easily turned into an algorithm, since, omitting rule (wd-delay), at each point in the derivation there is at most one applicable rule. Now we will discuss its time complexity, assuming that insertion, update and lookup are performed in constant time. It is easy to see that when we find a stream constructor we need to perform an update of the map \(\rho \) for every variable in its domain. If we consider the following environment:
\(\rho =(x_0,\{x_0\mapsto 0:x_1,x_1\mapsto 0:x_2, x_2\mapsto 0:x_3, x_3\mapsto 0:x_4,\ \ldots \ , x_n\mapsto 0:x_0\})\)
we get the derivation presented in Fig. 5. Here, the number of constructor occurrences for which we have to perform an update of all variables in the domain of the map is linearly proportional to the number N of nodes in the derivation tree; since the domain is increased by one for each new variable, and the total number of variables is again linearly proportional to N, it is easy to see that we have a time complexity quadratic in N.
We propose now an optimized version of the well-definedness check, having a time complexity of \(O(N \log N)\). On the other hand, the version we provided in Fig. 3 is more abstract, hence more convenient for the proof of Theorem 1.
In the optimized version, given in Fig. 6, the judgment has shape \(\mathsf {owd}_\rho (\textit{s},\mathsf {m},\pi )\), where \(\pi \) represents a path in the proof tree where each element corresponds to a visit of either the constructor or the right operand of interleave (value 1 for both) or the tail operator (value −1), and \(\mathsf {m}\) associates with each variable an index (starting from 0) corresponding to the point in the path \(\pi \) where the variable was found the first time. The only operation performed on a path \(\pi \) is the addition \(\pi \mathbin {\cdot }b\) of an element b at the end.
In rule (main), both the map and the path are initially empty. In rule (owd-var), a variable \(\textit{x}\) defined in the environment, found for the first time, is added in the map with as index the length of the current path. In rule (owd-corec), when the same variable is found the second time, the auxiliary function \( sum \) checks that more constructors and right operands of interleave have been traversed than tail operators (see below). In rule (owd-fv), a free variable is considered well-defined as in the corresponding rule in Fig. 3. In rules (owd-cons), (owd-tail) and (op-wd), the value corresponding to the traversed operator is added at the end of the path (1 for the constructor and the right operand of interleave, −1 for the tail operator). Lastly, rules (owd-nop) behaves in a similar way as in Fig. 3. The semantics of the auxiliary function \( sum \) is straightforward: starting from the point in the path where the variable was found the first time, the sum of all the elements is returned.
Let us now consider again the example above:
\(\rho =(x_0,\{x_0\mapsto 0:x_1,x_1\mapsto 0:x_2, x_2\mapsto 0:x_3, x_3\mapsto 0:x_4,\ \ldots \ , x_n\mapsto 0:x_0\})\)
By the new predicate \(\mathsf {owd}\), we get a derivation tree of the same shape as in Fig. 5. However, \( sum \) is applied to the path \(\pi \) only at the leaves, and the length of \(\pi \) is linearly proportional to the depth of the derivation tree, which coincides with the number N of nodes in this specific case; hence, the time complexity to compute \( sum (0,\pi )\) (that is, \( sum (\mathsf {m}(x_0),\pi )\)) is linear in N. Finally, since for inner nodes only constant time operations are performedFootnote 5 (addition at the end of the path, and map insertion and lookup), the overall time complexity is linear in N.
As worst case in terms of time complexity for the predicate \(\mathsf {owd}\), consider
\( {\rho _i=(\textit{x}_0,\{\textit{x}_0\mapsto 0:\textit{x}_1[+]\textit{x}_1,\textit{x}_1\mapsto 0:\textit{x}_2[+]\textit{x}_2, \textit{x}_2\mapsto 0:\textit{x}_3[+]\textit{x}_3, \ldots \ , x_i\mapsto 0:x_0\})} \)
The derivation tree for this environment is shown in Fig. 7, where \(\mathsf {m}_i\) abbreviates the map \(\{\textit{x}_0\mapsto 0, \textit{x}_1\mapsto 1, \ldots , \textit{x}_i\mapsto i\}\).
As already noticed, for inner nodes only constant time operations are performed, and the length of the paths in the leaves is linearly proportional to the depth D of the derivation tree; however, in this worst case the number of leaves is not just one, but is linearly proportional to the total number N of nodes in the derivation tree, hence the depth D is linearly proportional to \(\log N\). Therefore the overall time complexity is \(O(N \cdot D)\), that is, \(O(N \cdot \log N)\).
We now show that the optimized version of the judgment has the same semantics as its counterpart presented in Sect. 4. First of all we formally state that, in Fig. 3, rule (wd-delay) does not affect derivability.
Lemma 4
A judgment \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) has a derivation iff it has a derivation which does not use rule (wd-delay).
Proof
The right-to-left implication is obvious. If \(\mathsf {wd}_\rho (\textit{s},\emptyset )\) uses rule (wd-delay), all the (first in their path) occurrences of the rule can be replaced by rule (wd-corec), still getting a derivation.
Then, we define a relation between the auxiliary structures used in the two judgments:
For all \( m \) and \(({{\mathsf {m}},{\pi }})\), \( m \bowtie (\mathsf {m},\pi )\) holds iff
\( dom ( m )= dom (\mathsf {m})\) and, for all \(\textit{x}\in dom ( m )\), \( m (\textit{x})= sum (\mathsf {m}(x),\pi )\).
In this way, we have the following generalization, whose straightforward proof can be found in [4].
Theorem 2
If \(\mathsf {m}\bowtie (\mathsf {m},\pi )\), then, for all \(\textit{s}\), \(\mathsf {wd}_\rho (\textit{s}, m )\) is derivable iff \(\mathsf {owd}_\rho (\textit{s},\mathsf {m},\pi )\) is derivable.
Corollary 1
\(\mathsf {wd}_\rho (\textit{s},\emptyset )\) is derivable iff \(\mathsf {owd}_\rho (\textit{s},\emptyset ,\epsilon )\) is derivable.
6 Related and Future Work
As mentioned in Sect. 1, our approach extends regular corecursion, which originated from co-SLD resolution [1, 6, 18, 19], where already considered goals (up to unification), called coinductive hypotheses, are successfully solved. Language constructs that support this programming style have also been proposed in the functional [14] and object-oriented [2, 7] paradigm.
There have been a few attempts of extending the expressive power of regular corecursion. Notably, structural resolution [15, 16] is an operational semantics for logic programming where infinite derivations that cannot be built in finite time are generated lazily, and only partial answers are shown. Another approach is the work in [8], introducing algebraic trees and equations as generalizations of regular ones. Such proposals share, even though with different techniques and in a different context, our aim of extending regular corecursion; on the other hand, the fact that corecursion is checked is, at our knowledge, a novelty of our work.
For the operators considered in the calculus and some examples, our main sources of inspiration have been the works of Rutten [17], where a coinductive calculus of streams of real numbers is defined, and Hinze [12], where a calculus of generic streams is defined in a constructive way and implemented in Haskell.
In this paper, as in all the above mentioned approaches derived from co-SLD resolution, the aim is to provide an operational semantics, designed to directly lead to an implementation. That is, even though streams are infinite objects (terms where the constructor is the only operator, defined coinductively), evaluation handles finite representations, and is defined by an inductive inference system. Coinductive approaches can be adopted to obtain more abstract semantics of calculi with infinite terms. For instance, [9] defines a coinductive semantics of the infinitary lambda-calculus where, roughly, the semantics of terms with an infinite reduction sequence is the infinite term obtained as limit. In coinductive logic programming, co-SLD resolution is the operational counterpart of a coinductive semantics where a program denotes a set of infinite terms. In [2], analogously, regular corecursion is shown to be sound with respect to an abstract coinductive semantics using flexible coinduction [5, 10], see below.
Our calculus is an enhancement of that presented in [3], with two main significant contributions: (1) the interleaving operator, challenging since it is based on a non-trivial recursion schema; (2) an optimized definition of the runtime well-definedness check, as a useful basis for an implementation. Our main technical results are Theorem 1, stating that passing the runtime well-definedness check performed for a function call prevents non-termination in accessing elements in the resulting stream, and Theorem 2, stating that the optimized version is equivalent.
Whereas in [3] the well-definedness check was also a necessary condition to guarantee termination, this is not the case here, due to the interleaving operator. Consider, for instance, the following example:  . The judgment \(\mathsf {wd}_\rho (s,\emptyset )\) is not derivable, in particular because of
. The judgment \(\mathsf {wd}_\rho (s,\emptyset )\) is not derivable, in particular because of  , since \({\mathsf {wd}_\rho (s,\{s\mapsto -1\})}\) is not derivable and, hence,
, since \({\mathsf {wd}_\rho (s,\{s\mapsto -1\})}\) is not derivable and, hence,  ,
,  , and
, and  . However, \( at _\rho (s,i)\) is well-defined for all indexes i; indeed, \( at _\rho (s,1)=0\) is derivable, \( at _\rho (s,0)=k\) is derivable iff \( at _\rho (s,1)=k\) is derivable, and, for all \(i>1\), \( at _\rho (s,i)=k\) is derivable iff \( at _\rho (s,j)=k\) is derivable for some \(j<i\), hence \( at _\rho (s,i)=0\) is derivable for all i. We leave for future work the investigation of a complete check.
. However, \( at _\rho (s,i)\) is well-defined for all indexes i; indeed, \( at _\rho (s,1)=0\) is derivable, \( at _\rho (s,0)=k\) is derivable iff \( at _\rho (s,1)=k\) is derivable, and, for all \(i>1\), \( at _\rho (s,i)=k\) is derivable iff \( at _\rho (s,j)=k\) is derivable for some \(j<i\), hence \( at _\rho (s,i)=0\) is derivable for all i. We leave for future work the investigation of a complete check.
In future work, we plan to also prove soundness of the operational well-definedness with respect to its abstract definition. Completeness does not hold, as shown by the example
 which is not well-formed operationally, but admits as unique solution the stream of all zeros.
which is not well-formed operationally, but admits as unique solution the stream of all zeros.
Finally, in the presented calculus a cyclic call is detected by rule (corec) if it is syntactically the same of some in the call trace. Although such a rule allows cycle detection for all the examples presented in this paper, it is not complete with respect to the abstract notion where expressions denoting the same stream are equivalent, as illustrated by the following alternative definition of function
 as presented in Sect. 3:
as presented in Sect. 3:

If syntactic equivalence is used to detect cycles, then the call
 diverges, since the terms passed as argument to the recursive calls are all syntactically different; as an example, consider the arguments \(\textit{x}\) and
diverges, since the terms passed as argument to the recursive calls are all syntactically different; as an example, consider the arguments \(\textit{x}\) and  passed to the initial call and to the first recursive call, respectively, in the environment
passed to the initial call and to the first recursive call, respectively, in the environment  ; they are syntactically different, but denote the same stream.
; they are syntactically different, but denote the same stream.
In future work we plan to investigate more expressive operational characterizations of equivalence.
Other interesting directions for future work are the following.
-
Investigate additional operators and the expressive power of the calculus.
-
Design a static type system to prevent runtime errors such as the non-well-definedness of a stream.
-
Extend corecursive definition to flexible corecursive definitions [10, 11] where programmers can define specific behaviour when a cycle is detected. In this way we could get termination in cases where lazy evaluation diverges. For instance, assuming to allow also booleans results for functions, we could define the predicate
 , checking that all the elements of a stream are positive, specifying as result
, checking that all the elements of a stream are positive, specifying as result
 when a cycle is detected; in this way, e.g.,
when a cycle is detected; in this way, e.g.,
 would return the correct result.
would return the correct result.
Notes
- 1.
Here we use the syntax of our calculus, where, differently from Haskell, functions are uncurried, that is, take as arguments possibly empty tuples delimited by parentheses.
- 2.
For simplicity, here indexing and numeric expressions coincide.
- 3.
Indeed, it does not affect derivability, see Lemma 4 in the following.
- 4.
Non-well-definedness can only be detected on closed results.
- 5.
This holds for any valid derivation tree and not for this specific case.
References
Ancona, D.: Regular corecursion in Prolog. Comput. Lang. Syst. Struct. 39(4), 142–162 (2013)
Ancona, D., Barbieri, P., Dagnino, F., Zucca, E.: Sound regular corecursion in coFJ. In: Hirschfeld, R., Pape, T. (eds.) ECOOP’20 - Object-Oriented Programming. LIPIcs, vol. 166, pp. 1:1–1:28. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020)
Ancona, D., Barbieri, P., Zucca, E.: Enhanced regular corecursion for data streams. In: ICTCS’21 - Italian Conference on Theoretical Computer Science (2021)
Ancona, D., Barbieri, P., Zucca, E.: Enhancing expressivity of checked corecursive streams (extended version) (2022). https://arxiv.org/abs/2202.06868
Ancona, D., Dagnino, F., Zucca, E.: Generalizing inference systems by coaxioms. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 29–55. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_2
Ancona, D., Dovier, A.: A theoretical perspective of coinductive logic programming. Fund. Inform. 140(3–4), 221–246 (2015)
Ancona, D., Zucca, E.: Corecursive featherweight Java. In: FTfJP’12 - Formal Techniques for Java-like Programs, pp. 3–10. ACM Press (2012)
Courcelle, B.: Fundamental properties of infinite trees. Theoret. Comput. Sci. 25, 95–169 (1983)
Czajka, L.: A new coinductive confluence proof for infinitary lambda calculus. Log. Methods Comput. Sci. 16(1) (2020)
Dagnino, F.: Flexible coinduction. Ph.D. thesis, DIBRIS, University of Genova (2021)
Dagnino, F., Ancona, D., Zucca, E.: Flexible coinductive logic programming. Theory Pract. Logic Program. 20(6), 818–833 (2020). Issue for ICLP 2020
Hinze, R.: Concrete stream calculus: an extended study. J. Funct. Program. 20(5–6), 463–535 (2010)
Jeannin, J.-B., Kozen, D.: Computing with capsules. J. Autom. Lang. Comb. 17(2–4), 185–204 (2012)
Jeannin, J.-B., Kozen, D., Silva, A.: CoCaml: functional programming with regular coinductive types. Fund. Inform. 150, 347–377 (2017)
Komendantskaya, E., Johann, P., Schmidt, M.: A productivity checker for logic programming. In: Hermenegildo, M.V., Lopez-Garcia, P. (eds.) LOPSTR 2016. LNCS, vol. 10184, pp. 168–186. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63139-4_10
Komendantskaya, E., Power, J., Schmidt, M.: Coalgebraic logic programming: from semantics to implementation. J. Log. Comput. 26(2), 745–783 (2016)
Rutten, J.J.M.M.: A coinductive calculus of streams. Math. Struct. Comput. Sci. 15(1), 93–147 (2005)
Simon, L.: Extending logic programming with coinduction. Ph.D. thesis, University of Texas at Dallas (2006)
Simon, L., Bansal, A., Mallya, A., Gupta, G.: Co-logic programming: extending logic programming with coinduction. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 472–483. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73420-8_42
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this paper
Cite this paper
Ancona, D., Barbieri, P., Zucca, E. (2022). Enhancing Expressivity of Checked Corecursive Streams. In: Hanus, M., Igarashi, A. (eds) Functional and Logic Programming. FLOPS 2022. Lecture Notes in Computer Science, vol 13215. Springer, Cham. https://doi.org/10.1007/978-3-030-99461-7_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-99461-7_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-99460-0
Online ISBN: 978-3-030-99461-7
eBook Packages: Computer ScienceComputer Science (R0)





 , with
, with
 the pointwise addition and
the pointwise addition and
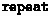 defined by
defined by
 .
. raises a runtime error.
raises a runtime error.


















 , checking that all the elements of a stream are positive, specifying as result
, checking that all the elements of a stream are positive, specifying as result
 when a cycle is detected; in this way, e.g.,
when a cycle is detected; in this way, e.g.,
 would return the correct result.
would return the correct result.