Dissipative Rogue Waves

Abstract

In this chapter, the history and main characteristics of rogue waves in the oceans are introduced. Due to phenomenological and physical analogies between extreme events in optics and hydrodynamics, the concept of optical rogue waves is extended into optics, associated with a long-tailed intensity histogram in the long-wavelength range of fiber optical supercontinuum spectra. Then, we discuss the real-time techniques for observing optical rogue waves. Namely, the well-known dispersive-Fourier-transform-based ultrafast spectroscopy and the time magnifier based on space-time duality. Further, the optical rogue waves in dissipative systems that often referred as open systems far away from the thermodynamic equilibrium, are reviewed briefly, including ultrafast lasers, microresonators, extended systems, and optical polarization rogue waves. These dissipative optical systems can be described by the Ginzburg-Landau equations, and various dynamical processes of fluctuation, pulsing, bifurcation, turbulence, and chaos are expected to be observed. Finally, two possible interpretations, and the predictabilities of dissipative rogue waves are also discussed.

16.1 Introduction

16.1.1 Rogue Waves in the Oceans

Rogue waves (RWs) are known as extremely large amplitude waves, which propagate in open oceans. Such rare events emerge with unexpectedly large probabilities, deviating from the power law wave-amplitude statistics which are typical for random processes, and leave without a trace [1,2,3,4,5,6,7]. As depicted in Fig. 16.1, these events constitute water walls as high as 20–30 m, which impose a threat for ships and ocean liners. From both the matters of physics and industrial applications, huge efforts have been devoted to explore the rogue waves.

Fig. 16.1

Huge wave on the Bay of Biscay. (Reproduced from NOAA Photo Library) [8]

RWs can be experimentally identified by the presence of heavy-tailed statistics, typically L-shaped, describing the appearance of rare events [9]. Several models have been developed based on the weak nonlinear interactions between thousands of waves, through the nonlinear Schrödinger equations (NLSEs), where both numerical simulation and analytical solutions such as breathers or turbulence have been carried out. Different RWs mechanisms have been proposed so far: from the simple linear random superposition of independent weak waves, to nonlinear effects such as modulation instability (MI) and the subsequent formation of localized breathers. When the coherence of a physical system is deteriorated, RWs with diverse parameters may occur in different dimensions [10,11,12]. However, the steep profile during the extreme events seems to be too freak to be captured. Other efforts have been devoted to the experimental observations on the directional oceans or laboratory. The debate about the origin of rogue waves continues, and, in my opinion, it will be long as far as concerning the great gulf between the theory and experiments.

16.1.2 Introduction of Optical Rogue Waves

Given the harsh conditions, studying RWs in their natural environment is problematic. The term of RWs has been expanded to other domains. Examples include: the fluence profiles of multi-filaments, liquid helium, and high intensity pulses in supercontinuum generation in optical fibers [13,14,15,16,17,18]. In 2007, due to phenomenological and physical analogies between extreme events in optics and hydrodynamics, D. R. Solli et al. introduced the concept of optical RWs, associated with a long-tailed intensity histogram in the long-wavelength range of fiber optical supercontinuum spectra [14]. As shown in Fig. 16.2, using a real-time detection based on dispersive Fourier transformation (DFT), they observe optical RWs in soliton-fission supercontinuum based on a micro-structured optical fiber. Their results high light the energy coupling between the solitons and other wave packets, and the characteristic lifetime during the formation of optical RWs.

Fig. 16.2

(a) Schematic of experimental setup. (b) Histograms of filtered intensities for average power of 0.8μW (red), 3.2μW(blue), and 12.8μW(green) [14]

Since then, much effort has been dedicated to finding RW solutions of the nonlinear Schrödinger equation in different physical systems: various kinds of breathers have been proposed as examples of optical RWs [15, 19,20,21]. Recently, real-time detection techniques, such as the DFT and time-lens, have been utilized to identify the presence of coherent pulses with extremely high intensities. An abrupt phase change across the pulse profile was found to be associated with optical RWs [22, 23]. The presence of a RWs is identified by a trough-to-crest height larger than 2 times the significant wave height (SWH). Moreover, the occurrence of RWs in optics can be identified in different domains: for example, in the pulse intensity for the time domain [14], in the spectral width for the frequency domain [24], in the spatial intensity in a two-dimensional camera image [13, 25], the depth of dark pulses [26], and the presence of spectrally narrowband pulses with a right-skewed distribution [27]. One example is given in Fig. 16.3, where the concept of rogue rather than the intensities is taken seriously. For a comprehensive investigation of optical RWs, additional dimensions can be introduced.

Fig. 16.3

The dark RWs in the depth of dark pulses [27]

16.1.3 Real-Time Techniques for Observing Optical Rogue Waves

For capturing the ultrafast and transient rogue waves, there are two fundamental challenges within any real-time techniques. One is the trade-off between the speed and the detection sensitivity of the optoelectronic detectors because fewer photons are collected during the short integration time [28]. The other is the trade-off between the measured dynamic range and the speed of the real-time analog-to-digital converter. The two shortcomings restrict the direct characterization of optical ultrafast pulses with durations in picosecond and sub-picosecond order. Specially, for these non-repetitive and transient RWs events, the insufficient sampling rate and detecting bandwidth distort the measured optical signals. Until now, two kinds of real-time characterization of ultrafast pulse have been well developed, namely, the dispersive-Fourier-transform-based ultrafast spectroscopy [29], and the time-lens-based time magnifier [30].

16.1.3.1 Dispersive-Fourier-Transform-Based Ultrafast Spectroscopy

The DFT technology stems from the spatiotemporal duality [31]: the transmission of a temporal pulse in a dispersive element with a sufficiently large dispersion is analogous to the diffraction of a beam passing through a lens in the far-field approximation. The frequency-domain spectral information of the pulse is thus mapped into the temporal pulse waveform, and the stretched light pulse has the same shape as the spectral intensity envelope, as shown in Fig. 16.4. According to NLSE, the amplitude envelope evolution of output pulse from the dispersion component without the consideration of gain and loss can be expressed by [32]:

$$ {\left|u\left(z,T\right)\right|}^2=\frac{1}{4{\pi}^2}{\left|{\int}_{-\infty}^{+\infty}\overset{\sim }{u_s}\left(0,\omega -{\omega}_0\right){e}^{i\frac{\beta_2{z}_0}{2}{\left(\omega -{\omega}_0-\frac{T}{\beta_2{z}_0}\right)}^2} d\omega \right|}^2, $$

(16.1)

where ${\tilde{u}}_s$ represent the amplitude envelope of the tested device and pulse source, respectively. ω is the light frequency, ω₀ is the center frequency, β₂ is the second-order dispersion coefficient, z is the propagation distance, and T is the time in the reference frame of the pulse propagating with the group velocity given by T(ω) = β₂z(ω − ω₀) the intensity profile of the temporally dispersed pulse then becomes proportional to:

$$ {\left|u\left(z,T\right)\right|}^2=\frac{2}{\pi {\beta}_2z}{\left|\overset{\sim }{u_s}\left(0,\frac{T}{\beta_2z}\right)\right|}^2, $$

(16.2)

Therefore, the wavelengths and stretched time relation, Δτ = |D|zΔλ, where D denotes the total amount of temporal dispersion, Δτ is the stretched time duration into which the optical spectrum is mapped. Via this technique the sub-picosecond pulses are stretched into nanoseconds. However, such real-time ultrafast spectroscopy technology can only obtain the spectrum information of a single pulse. It is impossible to clearly and accurately measure the time when the RWs appear.

Fig. 16.4

Principle of dispersive Fourier transform

16.1.3.2 Time Magnifier

Inspired by space-time duality and temporal imaging [33], the narrow-band dispersion (time domain) of a plane-wave light in a dielectric medium exhibits a behavior similar to the paraxial diffraction (space) of a monochromatic beam in free space. Mathematically, the propagation distance in the space domain is a direct analog of group delay dispersion (GDD) in the time domain. The ideal time imaging system requires GDD to be independent of frequency. The following Fig. 16.5 shows the principle of time magnifier.

Fig. 16.5

Principle of time magnifier. (a) Spatial analog of time magnifier. (b) Schematic diagram of a time magnifier

Analogous to the space-lens magnification system, in time-lens based time magnifier system, the temporal imaging condition satisfy the following formula [30]:

$$ \frac{-1}{\varphi_1^{\prime \prime }}+\frac{1}{\varphi_2^{\prime \prime }}=\frac{1}{\varphi_f^{\prime \prime }}, $$

(16.3)

Where the ${\varphi}_1^{\prime \prime }$, ${\varphi}_2^{\prime \prime }$ and ${\varphi}_{\textrm{f}}^{\prime \prime }$ are the GDD of input output and time lens. Herein, the function of time-lens part of Fig. 16.6a is to induce quadratic spatial phase modulation to input pulse. Such the temporal phase modulation can be expressed as [30]:

$$ \varnothing \left(\textrm{t}\right)=\frac{t^2}{2{\varphi}_f^{\prime \prime }}, $$

(16.4)

Where the focal GDD ${\varphi}_{\textrm{f}}^{\prime \prime }$ can be induced by phase modulator [34] or nonlinear parametric process [35]. Therefore, a magnifier ultrafast pulse replica will be generated from the input waveform with a magnification ratio:

$$ \textrm{M}=\left|\frac{\varphi_2^{\prime \prime }}{\varphi_1^{\prime \prime }}\right|, $$

(16.5)

Eventually, combining a real-time oscilloscope and high-speed photodetector, the round-trip evolution of ultrafast temporal structures will be experimentally resolved at sub-ps resolution, and RWs can be identified [36], directly.

Fig. 16.6

(a) The single-shot spectra of 100 consecutive pulses with the laser operating in the transition regime. (b) Example spectra for a particular explosion event [40]. (Reprinted with permission from Ref. [40] © The Optical Society)

16.2 Dissipative Rogue Waves

16.2.1 Rogue Waves in Dissipative Systems

Considering both the fundamental and possible industrial applications, the RWs in optical systems have been under huge investigations. Examples include the MI, supercontinuum. All those freak events appear in the conservative and integrable systems, which can be described by the nonlinear Schrödinger equations.

In fact, all the real physical systems tend to be dissipative. A dissipative system is often referred as an open system that far away from the thermodynamic equilibrium, while its balance can be sustained via exchanges of energy, matter, or entropy. Ultrafast laser system is a typical dissipative optical system, where sustained energy supply and dissipation factors, such as loss, are continuously undergo within the resonator. Together with the nonlinearity, dispersion, et al., such a kind of dissipative optical system can be described by the Ginzburg-Landau equations.

$$ \frac{\partial A}{\partial z}=\left(\frac{g}{\omega_{\textrm{g}}^2}-j\frac{\upbeta_2}{2}\right)\frac{\partial^2A}{{\partial t}^2}+\left(g+ j\gamma {A}^2\right)A $$

(16.6)

Where A is the field envelope, z is the propagating distance, t is the frame time moving at the signal velocity, 𝛽₂ is the GVD parameter, 𝛾 is the self phase modulation coefficient, g is the saturated gain coefficient, and ω_g is the gain bandwidth. Depending on the specific parameters of the optical dissipative systems, one would expect to observe the dynamical processes of fluctuation, pulsing, bifurcation, turbulence, and chaos. RWs, which are extremely sensitive to initial conditions and perturbations, are always anticipated in those dynamics. They are identified in ultrafast laser systems, microresonator, or other extended systems, utilizing the single-shot techniques based on DFT and Time-lens effects.

16.2.2 Dissipative Rogue Waves in Ultrafast Lasers

The coherent structures and patterns are generally arising from the composite balance between conservative and dissipative effects in various areas of physics, ranging from quantum mechanics to astrophysics. Therein, the dissipative solitons are highly coherent solutions of nonlinear wave equations, and provide an ideal platform for study of nonlinear optical dynamics. So far, numerous striking soliton dynamics have been investigated in dissipative soliton fiber lasers, including dissipative soliton molecules [37], dissipative soliton rain [38], noise-like pulses (NLPs) [39], dissipative soliton explosions [40], buildup of dissipative solitons [41] and so on. All of these nonlinear processes are frequently accompanied by energy oscillation in laser cavity, as well as the generation of high amplitude waves.

Thanks to the development of real-time measurement, which offers a powerful tool to characterization the transient nonlinear dynamics in ultrafast laser. In 2015, researchers from university of Auckland identify clear explosion signatures of a Yb-doped mode-locked fiber laser that is operating in a transition regime between stable and noise-like emission [40]. This transition between these two regimes can be achieved by increasing the pump power. Meanwhile, in the noise-like regime the Raman scattering is stimulated by the huge energy oscillations during soliton explosions process. The single-shot experimental results are shown in following figure. Where after, two groups have identified the optical rogue waves during soliton explosions in coherent and incoherent dissipative ultrafast laser cavity [42, 43].

One more interesting found is that the researchers have discovered that akin to solitons, breathing dissipative solitons can also exhibit explosions. And such breathing dissipative solitons and breathing dissipative solitons explosions also induce optical rogue waves, as shown in following Fig. 16.7 [44].

Fig. 16.7

Intensity histograms of the three mode-locking regimes. (a) Stable dissipative solitons. (b) Breathing dissipative solitons. (c) Breathing dissipative soliton explosions. The black line denotes the SWH [44]

The soliton molecules may also excite RWs. In 2019, a group in China have experimentally investigated the dynamics of soliton molecules in the normal-dispersion regime [45]. They show that the separation between two bound dissipative solitons (DSs) evolves aperiodically. An additional modulation on the spectra is observed suggesting that the DSs split aperiodically. Such a splitting occurs when the DSs exchange energy. Moreover, rogue waves are present in the soliton molecule (Fig. 16.8).

Fig. 16.8

(a) Real-time spectra of soliton molecules. (b) The field autocorrelation trace calculated from the spectra. (c) The corresponding temporal intensity evolutions measured by a photodetector. (d) Spectral intensity histogram of the soliton molecule [45]. (Reprinted with permission from Ref. [45] © The Optical Society)

For characterizing the rogue waves among the noise-like pulses or soliton rain, the dispersive Fourier transform based single-shot measurement is not accurate enough. As the rogue waves appear among the pulses cluster more randomly, the DFT based real-time spectroscopy to hardly capture the intensity peaks of pulse waveform. The time magnifier based on time-lens effect has been utilized to capture the temporal waveform for NLPs or soliton rain [36]. To enable self-triggering, a pump signal is produced from the signal under test. As can be seen in Fig. 16.9, the NLPs output from laser cavity is broaden spectrally and amplified. The reproduced the synchronous pump laser undergoes parametric process with signal, thereby achieving a self-triggered time magnifier with sub-picosecond resolution. Using this powerful technique, real-time observation of NLPs structures has been realized, and RWs were also observed under a sub-ps timescale. The ORWs in NLPs might have been resulted from the interaction of noise-like temporal structures and the energy convergence toward a single coherent pulse [36].

Fig. 16.9

(a) Schematic diagram of synchronized time magnifier for NLPs. (b) Detailed temporal structure of the NLPs. (c) Pulse intensity histogram of the NLPs waveforms. (d) A Typical example of a rogue event. (e) Pulse evolution over 100 consecutive round trips [36]. (Reprinted with permission from Ref. [36] © The Optical Society)

16.2.3 Dissipative Rogue Waves in Microresonators

In addition to the ultrafast laser systems, in recent years, RWs in microresonators have been also extensively reported [46,47,48,49,50]. The whispering-gallery-mode (WGM) resonator can be made from a glass microsphere, a crystal disk, or an integrated resonator. Dissipative RWs appear in WGM resonators, due to the chaotic interplay between Kerr nonlinearity and anomalous group-velocity dispersion. Researchers have observed freak events associated with non-Gaussian statistics, and theoretical evidence of RWs in WGM resonators by investigating the nonlinear dynamics in the resonator with the Lugiato-Lefever equation (LLE), resulting from the collision of soliton breathers in the process of hyperchaotic Kerr comb generation.

Figure 16.10 depicts the evolution of the optical field in the WGM resonator pumped by a continuous-wave laser via the evanescent field of a tapered fiber [46]. This figure displays a snapshot of the numerical simulations that shows a rogue wave, which is characterized by extreme amplitude and very rare occurrence. For the color-coded map of the evolution of the field intensity with time, for F² = 6 and 8, stable solitons and soliton breathers emerge. As the pump is increased to F² = 10 and 20, rare, and extremely high amplitude waves are encountered.

Fig. 16.10

The evolution of the optical field in the WGM resonator. F² denotes the square of the dimensionless pump term F in the LLE, which is proportional to the laser power [46]

The corresponding spatial distribution of the optical field along the azimuthal direction of the cavity is in the left column of Fig. 16.11. In the right column, the statistical distribution of the wave heights is shown with a logarithmic scale. For higher pump powers (F² = 10), the soliton breathers start to interact with one another. And the statistical distribution of the peak heights becomes continuous. The feature of an exponential decay of the distribution characterizes the threshold value, the SWH. When wave height is at least twice the SWH, a rogue wave occurs.

Fig. 16.11

Left column: Spatial distribution of the optical intensity in the cavity when the highest wave occurs for different pump powers. Right column: The intensity histograms of the optical pulses for different F² [46]

16.2.4 Dissipative Rogue Waves in Extended Systems

Apart from the systems mentioned above, rogue waves can be observed in other extended systems, including nonlinear optical cavity [47, 51,52,53] or even linear regime [25, 54], where RWs with non-Gaussian probability distribution occur. Take the multimode optical fiber for example, RWs result from interference between multiple transverse modes.

Figure 16.12 also depicts a ring cavity consists of three high-reflectivity dielectric mirrors, together with a liquid crystal light valve (LCLV) composed of a liquid crystal cell with one of the walls made of a slice of the photorefractive crystal. The LCLV is pumped by a plane-wave optical beam provided by a solid-state laser at 532 nm. The light amplification in the cavity is based on wave mixing with the pump beam. The PDFs of the cavity field intensity are obtained from large number of images and thereafter the histograms of the intensity value are performed. It is known that an exponential trend corresponds to a Gaussian statistics for the field amplitude. In other words, an exponential intensity PDF is characteristic of a speckles pattern, where many uncoupled modes independently contributed to each point. At low pump, the behavior is Gaussian. However, when the pump increases, the increasing nonlinear coupling results in a complex space-time dynamic. When PDF exhibits a large deviation from Gaussian distribution, rogue events occur.

Fig. 16.12

(a) schematic of the experimental setup. (b) PDF of the cavity field intensity with different pump intensities [53].

16.2.5 Optical Polarization Rogue Waves

Until now, all the RWs are identified based on the probability distributions of the temporal intensities within specific filtered wavelength range, or the integrated intensities of the obtained single-shot spectra. Namely, the RWs are identified in the temporal and in the spatial domains based on the SWH method. Yet another inherently fundamental parameter of the laser emission, its state of polarization (SOP), has received relatively less attention [43, 55, 56]. In particular, the dynamics of the laser SOP has not been fully demonstrated. Yet, the corresponding SOPs would behavior rather complex trajectories, especially in the dissipative laser systems.

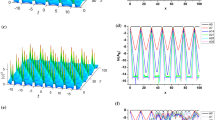
Figure 16.13 depicts the evolving SOP distributions for a filtered wavelength in the laminar-turbulent transition of the PMLs at different pump powers [57]. It is clear that the corresponding SOPs for wavelengths far away from the laser center line bifurcate into a cross-like shape on the Poincaré sphere. The multiple wave mixing processes generate new frequencies with separately evolving output SOP azimuth and ellipticity angles, resulting in perpendicular lines aligning with either a meridian or a parallel curve on the Poincaré sphere, respectively. The onset of SOP turbulence is accompanied by the loss of system coherence. Irregular polarization states locating outside of the main polarization directions emerge when the pump power exceeds 250 mW. This scattering of SOPs aggravates when the intracavity power is further increased. This result seems natural when we consider the usual road map for chaos, resulting from a cascade of successive period-doubling bifurcations. Whenever the pump power is larger than 600 mW, the cascaded four wave mixing (FWM) leads to a fully developed turbulent evolution, and the SOPs of filtered wavelengths appears as totally random.

Fig. 16.13

Experimentally measured polarization states for filtered wavelengths under various pump powers for PMLs [57]

The irregular polarization state of laser emission is associated with the emergence of a new kind of optical rogue waves in randomly-driven mode-locking systems, namely optical rogue waves in polarization domain. Different from the temporal or spatial rogue waves, RWs in polarization domain are vector, and a new method is introduced for their characterization. The SOPs can be expressed as Ŝ = (s₁, s₂, s₃). Therefore, the relative distance, r, between two SOPs is defined by

$$ r=\left|{S}_m-{S}_n\right|=2{\sin}^{-1}\left(\sqrt{{\left({S}_{m1}-{S}_{n1}\right)}^2+{\left({S}_{m2}-{S}_{n2}\right)}^2+{\left({S}_{m3}-{S}_{n3}\right)}^2}/2\right) $$

(16.7)

The probabilities of the distance between various SOPs under different pump powers for filtered wavelengths are depicted in Fig. 16.14 [58]. A mere cross-like bifurcation of the SOP results in a distorted Gaussian function, while that for the total turbulence trends to be Gaussian shaped. During the laminar-turbulence transition of the SOP, L-shaped probability density function (PDF) distributions deviating from the Gaussian statistics prove that photons with large excursions of their SOP obey their own PDF, which is a characteristic property of extreme events in the polarization domain rather than the temporal or spectral domains. Considering the similarities, we referred it as polarization rogue waves (PRWs).

Fig. 16.14

Optical polarization rogue waves in the polarization laminar-turbulent transition for NLPs [58]. (Reprinted with permission from Ref. [58] © The Optical Society)

The PRWs is a phenomenon that is universal in any nonlinear dissipative optical systems undergo coherence deterioration. It is attributed to the stochastic mixing of its longitudinal modes, where vector FWM cascades with nonlinear chaotic phase-matching conditions. In fact, even for a high coherent ultrafast laser system, when perturbated by excessive energy or phase, new frequencies with freak SOPs can be excited by the possible FWMs. Figure 16.15 schematically shows a normal-dispersioned fiber ring cavity mode-locked by a saturable absorbing film made by single-wall-carbon-nanotubes, where dissipative solitons (DSs) are produced. DSs are high coherent solutions of nonlinear wave equations, and arise from a balance between nonlinearity, dispersion, and loss/gain. At variance with NLSE solitons in integrable fiber systems operating in the anomalous dispersion regime, DSs in dissipative fiber laser systems operating in the normal dispersion regime exhibit extremely complex and striking dynamics.

Fig. 16.15

Schematic of the fiber laser cavity and measurement methods [59]

For such a laser cavity, stable DS can be observed with a pump power threshold of 55 mW, where the rectangle-shaped optical spectrum with a FWHM of 13.6 nm is shown. For pump powers between 55 mW and 65 mW, the laser operates in a stable DS regime. For a pump power of 70 mW, regular DSs with neatly rectangle-shaped optical spectra are frequently detected. Yet, much broader optical spectra persisting near the square spectrum may also be occasionally encountered, exhibiting two extremely high peaks. This DS explosion. For soliton explosions, the balance of nonlinearity, dispersion, and loss/gain for the DS is perturbed by the surplus cavity gain at large pump powers. Part of the DS energy dissipates into CWs via the explosion, and the DS maintains its property of a highly coherent pulse.

The PRWs are identified during the DS explosion. Figure 16.16 illustrates the corresponding SOP distributions. It is clear from the distribution of points on the Poincaré sphere that the corresponding SOPs for each wavelength are evolving from a random cloud into a fixed narrow domain as the pump power grows larger. When a stable DS is formed, a well-defined SOP trajectory vs. frequency is observed on the Poincaré sphere. Whereas for pump powers above 66 mW, the SOPs of unstable DSs exhibit fluctuations (Fig. 16.16d). For even stronger pump powers (Fig. 16.16e), these intense fluctuations trend to be spreading more on the Poincaré sphere, especially for frequencies locating on the two spectral edges. The instability and fluctuations of SOPs on the two edges of the spectrum reveal a new aspect of the complex dynamics in DS formation, which so far has been largely unnoticed.

Fig. 16.16

Evolution of SOPs for various filtered wavelengths and different pump powers [59]

Figure 16.17 depicts the PDF of r when the DS is deteriorated at high pump powers. As can be seen, the PDF has a quasi-Gaussian shape at the 1568 nm wavelength (in the center region of the DS spectrum). Howbeit, for wavelengths far away from the DS spectral center, a trend develops towards the generation of L-shaped PDFs, which characterize the emergence of extreme events in the polarization domain, rather than in time or frequency domains. In other words, the irregular SOP of a deteriorated DS is associated with the emergence of a new type of optical rogue waves in the polarization dimension, namely PRWs. Such rogue events appear with both unexpected SOP values and relatively large probabilities of occurrence. From a statistical point of view, the occurrence of polarization rogue waves can be testified by the emergence of a heavy tail in the measured histogram. As shown for the 1568 nm wavelength, 1.8% of the events have a value that is larger than the twice of the SWH. Whereas rogue events represent about 3.8% of the events at the 1564 nm wavelength.

Fig. 16.17

Histograms of the relative distance between points on the Poincaré sphere for 70 mW pump power [59]

Similarly, the PRWs can be identified by any supercontinuum generation under nonlinear optical processes. The DS from Fig. 16.15 is compressed and amplified by a commercial high gain erbium-doped fiber amplifier, and injected into 20 m of highly nonlinear fiber with zero dispersion at 1550 nm. The commercially available ZDF has an effective diameter of 3.86μm and a nonlinear coefficient of 10 W⁻¹ km⁻¹. Such a fiber facilitates phase matching of FWM over an ultra-broad frequency range, and octave-spanning spectrum can be easily obtained. In our experiment, primary sidebands are generated by MI. Next, new frequencies are generated by cascaded FWM among those sidebands and the DS spectrum. Namely, all FWM procedures are possible. Primarily, we observe the MI with a degenerate FWM process. During supercontinuum generation (SCG), a transition from high to low spectral coherence may be controlled by varying the pump pulse peak power. Consequently, RWs in temporal, spectral, and polarization domains emerge in the SCG process.

To characterize the emergence of PRWs in SCG, we calculate the PDFs of SOP for wavelengths ranging from 1541 nm to 1557 nm. Figure 16.18a illustrates their SOPs values, for a fixed pump power of 100 mW. As can be seen, SOPs emerging at 1557 nm are scattered within a single domain. Whereas, as the wavelength is blue-shifted, the SOPs evolve into two separate domains. For wavelengths situated even farther away from the DS pump, the corresponding SOPs scatter within three different domains, which are continuously interchanging their energy. Those wavelengths are generated by vector FWM processes, which occur among all possible polarization interactions in a nonpolarization maintaining fiber. For wavelengths between 1543 nm and 1547 nm, the corresponding histograms in Fig. 16.18b–f clearly denote the existence of optical PRWs. The histograms are highly sensitive to the specific filtered wavelength. For example, at 1543 nm and 1547 nm, SOPs with rogue positions are observed on the Poincaré sphere, as denoted by the heavy tails at large r values. However, double PDFs, and even triple PDFs may appear, depending on the wavelength selected.

Fig. 16.18

SOPs and histograms at the pump power of 100 mW [60]. (Reprinted with permission from Ref. [60] © The Optical Society)

Polarization rogue waves are quite different from the intensity distributions for conventional RWs. Quantitatively, PRWs are identified based on the PDF of relative distance, r, between any two points on the Poincaré sphere for the single frequency, while conventional RWs denote the emergence of ultrahigh intensities within wide frequencies. The corresponding temporal intensities for PRWs may not be large enough, even may be ultrasmall when we consider the forming procedure. The PRWs are more than the polarization aspect of the conventional RWs. However, we also believe that there is a connection between the PRWs and conventional RWs, as they are both formed only under high nonlinear process. A more convincing and reliable investigation between them requires single-shot measurement of the intensity and polarizations simultaneously, together with more rigorous theoretical analysis.

16.3 Generating Mechanisms of Dissipative Rogue Waves

16.3.1 Two Interpretations

The recent years have witnessed a growing interest for RWs in optics. While great debates on the classification of different kinds of RWs are clear in this community. In the pioneer works, the optical filtering has been taken seriously by the following researchers [14, 17, 24]. Based on different experimental systems, there are mainly two possible interpretations have been, not completely, partially accepted. While the two groups both admit the two main phenomenological features. The first one is the deviations of wave amplitude statistics from the Gaussian behavior. The other is the coherent build up in an extended spatio-temporal system. For optical fibers, the parameter is mainly limited to the dispersion, where time-frequency structures are formed. While for spatially extended optical systems, the two-dimensional structures are formed on the transverse wave front. Therefore, a reliable model should be described by partially differential equations, where either dispersion or nonlinearity leads to a coherent build-up of giant waves [9]. While, we have to admit that the chaotic behaviors or noise-induced intermittency, which described by ordinary equations, have to be considered for the RWs classification [61]. The later care about the probability of the RWs, which arise a fundamental question: the predictability of RWs. The researchers found that the RWs do not necessarily appear without a warning, but often preceded by a short phase of relative order [62,63,64]. The predictability can only be understood by the turbulence language.

The well-known theoretical model is the breathers for high nonlinear optical system. In fact, it lies on the ocean-optics analogy. Both the dynamics of ocean waves and pulse propagation in optical fibers can be modeled by the NLSE. For a more complex system, an extended version for the Ginzburg-Landau equation. For optics, the NLSE describes the pulse envelope modulating an electric field, while for water it represents the envelope modulating surface waves. Certain analogy does exist. Yet, such an analogy shall not be extended for the different higher order perturbations.

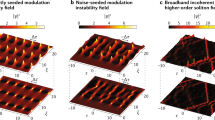
The most interesting phenomenon associated with the RWs in optical fibers are the formation of breathers [65,66,67,68,69,70]. These high coherent structures can be regards as a kind of solitons on finite background. They have certain analytical solutions. This is easy to understand: the optical system always tends to be loss, and the pure soliton is out-of-balanced by the mismatch of nonlinearity and dispersion. There are several kinds of breathers: the Akhmediev breathers, the Kuznetsov-Ma solitons, the Peregrine soliton. More higher orders of solutions are possible with even stronger localization and higher intensities. Figure 16.19 shows the properties of the breathers with spatial and temporal localization structures. These different breathers are frequently be used as the interpretation of RWs, both in the MI, the fiber resonator, or supercontinuum generation.

Fig. 16.19

Various kinds of solitons and breathers [15]

Despite of the success in interpreting RWs as a coherent structure, either in the soliton or breather, controversy still exists. This originate the experiment observation of incoherent soliton, which firstly found in photorefractive crystals [71]. It results from the spatial self-trapping of incoherent light in a highly noninstantaneous response nonlinear medium. The noninstantaneous photorefractive nonlinearity averages field fluctuations when its response time is much longer than the correlation time of the beam. More achievements have been made, such as, the existence of incoherent dark solitons [72], the modulation instability of incoherent waves [73, 74], the incoherent solitons in resonant interactions [75], or spectral incoherent solitons in optical fibers [76]. For all the statistical nonlinear optics, the kinetic waves theory provides a nonequilibrium thermodynamic description of turbulence. Recent experiments provide general physical insights of the RWs in the optical turbulence [77]. Depending on the amount of incoherence, different regimes are identified. Figure 16.20 depicts the probabilities for three regimes: the coherent rogue quasi-solitons, the intermittent-like rogue quasi-solitons that appear and disappear erratically, and the sporadic RWs that emerge from the turbulent fluctuations.

Fig. 16.20

Average of the maximum intensity peak as a function of the Hamiltonian density [77]

16.3.2 Are the Dissipative Rogue Waves Predictable?

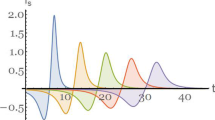
As soon as the discovery of RWs, a fundamental question arises: Are the RWs predictable? The answers are just controversial as the interpretations of the RWs. When we follow the first explanation: RWs are rare extreme localized waves, which can be modeled by high order solitons, breathers, or their continuously coupling superpositions, and exact analytical solutions of NLSE with perturbations can be founded at prescribed conditions [62]. In this sense, predictable RWs are rational. One example is the second-order breathers based on NLSEs with a quadratic potential modulated spatially [78]. By controlling the modal parameter or spatial frequencies, the giant waves can be manipulated by overlapping the Kuznetsov-Ma breathers and Peregrine soliton, as depicted by Fig. 16.21. For this case, the simulations hold true, although partially, as both the boundary conditions and simulation accuracy will deteriorate their predictabilities.

Fig. 16.21

RWs as second-order breathers, which are superpositions of Kuznetsov-Ma breathers and Peregrine solitons [78]. (Reprinted with permission from Ref. [78] © The Optical Society)

While another question occurs: are the RWs formed in dissipative systems predictable? After all, the basic nature of dissipative system is the spontaneous formation of symmetry breaking and complex, even chaotic structures. The dissipative factors make the NLSE unsuitable for describing unintegrable systems, but only Ginzburg-Landau equations. And in most cases, there are only numerical simulations, and analytical solutions are hard to find as the dissipative dynamics are extremely sensitive to the initial perturbations. This behavior resembles to the very beginning of “disappearing without the slightest trace” of RWs [14], thus challenging the prediction of dissipative RWs. This is especially true in highly nonlinear optical systems, such as the PRWs in PML, or supercontinuum generation: the probabilities of finding freak SOP is decreasing when the coherence is deteriorated. In this sense, the prediction of RWs in dissipative systems is similar to the prediction of trajectory of system undergoing from laminar to turbulence, you can find the difference when the fluctuations and even bifurcations occur, yet it is far away to figure it out when the system is fully chaotic.