A Fast Heuristic Approach for the Assignment and Sequencing Storage Location Problem Under a Two Level Storage Policy

Abstract

We consider a storage allocation problem which combines storage location assignment with sequencing decisions about the assigned storage locations, and which originates from a real-world application context. We propose a very efficient successive constrained shortest path method, which outperforms a matheuristic approach recently proposed in the literature in terms of both the computational time required and regarding the quality of the solutions found.

1 Introduction

Storage Location Assignment Problems (SLAPs) are operational problems aiming at defining the exact physical location of a set of items in a storage area, which broadly could be a warehouse, a yard, the bunt of a container ship or even a tram/bus depot. Such decisions are made by considering some long-term storage assignment policies (random, dedicated and class-based are the most popular [1, 2]), that broadly prescribe the rules to follow when stocking is needed, by respecting additional requirements related to the specific application context and, generally, by optimizing criteria such as material handling cost or storage space utilization [3,4,5].

The problem addressed in this paper has been motivated by a real application involving a production site of an Italian company, in Tuscany, whose large warehouse (more than 10,000 m²) is the subject of a big modernization project requesting the resolution of a SLAP with operations research techniques. Specifically, a set of storage locations (SLs) has to be assigned to a set of different product types, each with its own storage demand expressed in number of items to store in a given time horizon. Each SL has a fixed capacity and can be assigned to at most one product type, i.e., different types of products cannot share the same SL. The majority of the product types can be stored in any available SL, i.e., a random storage policy is considered. However, special product types do exist, which have to be preferably managed according to a dedicated storage policy.

In addition, a suitable sequencing of the assigned SLs must be devised for each product type, i.e., it has to be decided the ordering with which the assigned SLs will be filled up during the storing operations. A motivation is that a FIFO (First-In First-Out) order picking policy based on the time of permanence of the items in the warehouse has to be pursued, separately per product type, when items must be retrieved to fulfill customers’ orders. The sequencing established for the assigned SLs will thus allow to easily implement the FIFO policy in the successive order picking steps. Moreover, the selected sequencing also determines the availability of additional extra storage per product type. Specifically, an additional amount of storage can be made available on the top of pairs of consecutive SLs along the sequence, provided that they are fully replenished and physically contiguous, thus allowing a two level stocking policy. The objective is to maximize the storage capacity which remains available after the assignment of the SLs.

The recent paper [6] describes the problem more formally, providing two Mixed Integer Linear Programming (MILP) formulations and the proof of its NP-hardness. Additionally, since the state-of-the-art commercial solver CPLEX is not able to address real-size instances, such those faced daily by our industrial partner, a simple yet effective matheuristic approach to tackle such instances is proposed in [6]. Further models to SLAP have been proposed in [7].

In this paper, we propose a heuristic solution method based on successive constrained shortest paths. The heuristic is able to find solutions to real-size instances in a few seconds, also improving the quality of those found in [6] in terms of both available storage capacity and other crucial features that our industrial partner is interested in.

The paper is organized as follows. We briefly describe the problem statement in Sect. 2. The heuristic method designed to tackle the problem is presented in Sect. 3. Section 4 describes the experimental plan and reports the results of the preliminary computational experiments we performed. Finally, Sect. 5 concludes the paper and identifies some future directions of research.

2 Problem Statement

Let $\mathcal K$ be the set of the different product types requiring storage in a given time horizon, and q ^k be the number of items of product type k that needs storage, for each $k \in \mathcal K$. Let $\mathcal S$ be the set of available SLs in the warehouse where the products in $\mathcal K$ have to be stocked, each SL $s \in \mathcal S$ having a capacity u _s. Two subsets of $\mathcal K$ of special product types are given: $\mathcal K_P \subseteq \mathcal K$ denoting perishable products and $\mathcal K_{HR} \subseteq \mathcal K$ denoting high rotational products. Products in $\mathcal K_P$ and $\mathcal K_{HR}$ should be preferably stocked in specific SLs, denoted as $\mathcal S_P \subseteq \mathcal S$ and $\mathcal S_{HR} \subseteq \mathcal S$, respectively.

The addressed problem consists in assigning a sequence of available SLs to each $k \in \mathcal K$, by satisfying the following constraints:

• each SL in $\mathcal S$ can be assigned to a unique product type in $\mathcal K$;

• the sum of the capacities of the SLs assigned to a product type plus the extra storage made available for it on the top level (in case of pairs of fully replenished and physically contiguous SLs) must be greater than or equal to the storage demand of the product type;

• the special product types in $\mathcal K_{P}$ and $\mathcal K_{HR}$ should be preferably assigned to SLs in $\mathcal S_{P}$ and $\mathcal S_{HR}$, respectively;

with the aim of maximizing the residual storage capacity, i.e., the one which remains available after the assignment of the SLs.

Figure 1 depicts a storage area where three SLs are occupied by some items in the first level (two are consecutive and one is isolated) and four SLs are available for stocking (three are consecutive and one is isolated), depicted as full black rectangles and as white rectangles, respectively. An example of the two level storage policy is shown for the first two occupied SLs. The residual storage capacity, in this case, is defined as the sum of the capacities of the 4 available SLs at the ground level, plus the capacities exploitable on top of SLs 1 and 2, as well as on top of 2 and 3.

Fig. 1

Available SLs in a storage area

3 A Successive Constrained Shortest Path Method

For each product type $k \in \mathcal {K}$, the proposed heuristic finds a constrained shortest path on a suitable auxiliary graph, whose set of nodes describes the current availability of SLs in the warehouse. This path specifies the SLs assigned to k and the order in which they must be filled up, in such a way as to guarantee that the total capacity of the assigned SLs is enough to store the q ^k items required by k, taking into account the possibility of exploiting extra storage on the top of the assigned SLs. After the assignment to k, the auxiliary graph is suitably pruned by removing the assigned nodes and the corresponding incident arcs, to avoid that the corresponding SLs can be assigned to product types other than k.

In the following subsections, we introduce the auxiliary graph, we present the constrained shortest path problem to be solved for each product type and we describe the overall heuristic method.

3.1 The Auxiliary Graph

In the auxiliary graph $\mathcal G=(\mathcal N, \mathcal A)$, the set of nodes $\mathcal N$ consists of:

• a fictitious source node Σ,

• a fictitious target node Θ,

• a set $\mathcal {L}$ containing one node for each currently available SL in the warehouse.

The set $\mathcal {L}$ is partitioned into two subsets, $\mathcal {L}^I$ and $\mathcal {L} \setminus \mathcal {L}^I$: $\mathcal {L}^I$ is composed of all those nodes of $\mathcal L$ corresponding to isolated SLs in the warehouse (that is, no contiguous SL is available for storage, like SL 4 in Fig. 1), while $\mathcal {L} \setminus \mathcal {L}^I$ is in turn partitioned into $\cup _{h=1,\dots ,H} \mathcal {F}_h$ subsets, each of them defining a group of nodes associated with physically contiguous SLs. For example, SLs 1, 2 and 3 in Fig. 1 define one of these groups. A generic subset $\mathcal {F}_h$ contains nodes of type $\{j^h_1, j^h_2,\dots , j^h_{\vert \mathcal {F}_h \vert } \}$, where $j^h_1$ and $j^h_{\vert \mathcal {F}_h \vert }$ respectively denote the nodes associated with the first and the last SL of the physically contiguous group $\mathcal {F}_h$ (like SLs 1 and 3 in Fig. 1), while the remaining nodes $j^h_m$, with $1 < m < \vert \mathcal {F}_h\vert$, are associated with intermediate SLs (like SL 2 in Fig. 1). In particular, the SL associated with node $j^h_m$ is in between the SLs associated with nodes $j^h_{m-1}$ (being the previous one) and $j^h_{m+1}$ (being the next one).

A capacity u _j is associated with each node $j \in \mathcal {L}$. It coincides with the capacity of the SL the node j is associated with, if the SL is isolated or it is the first SL in a group of physically contiguous SLs; otherwise, it coincides with its double, so as to model the two level storage policy. Moreover, a profit $\delta _j^k$ is defined for each product type $k \in \mathcal K$ and each node $j \in \mathcal {L}$. This profit aims to favour the assignment of k to the preferable subsets $\mathcal S_P$ or $\mathcal S_{HR}$, if $k \in \mathcal K_P$ or $k \in \mathcal K_{HR}$. Otherwise, it tends to favour the assignment of k to SLs in $\mathcal {S} \setminus (\mathcal {S}_P \cup \mathcal {S}_{HR})$.

The set of arcs $\mathcal A$ is defined in order to model the assignment of a sequence of SLs to each product type in $\mathcal {K}$. The set $\mathcal A$ contains:

• arcs ( Σ, j), with $j \in \mathcal {L}^I$, and arcs $(\Sigma , j^h_1)$, with h = 1, …, H, to model the assignment of the first SL to a product type;

• arcs (j,  Θ), with $j \in \mathcal {L}$, to model the assignment of the last SL to a product type;

• arcs $(j^h_m,j^h_{m+1})$, with h = 1, …, H and $m=1,\dots , \vert \mathcal {F}_h \vert -1$, to model the assignment of the available SL $j^h_{m+1}$ immediately after the available and contiguous SL $j^h_m$;

• arcs $(j^h_{\vert \mathcal {F}_h \vert },j^{h'}_1)$, with h, h′ = 1, …, H, and h ≠ h′, to model the assignment of the SL $j^{h'}_1$ of group $\mathcal {F}_{h'}$ immediately after the SL $j^h_{\vert \mathcal {F}_h \vert }$ of group $\mathcal {F}_h$;

• arcs $(j^h_{\vert \mathcal {F}_h \vert },i)$, with h = 1, …, H, and $i \in \mathcal {L}^I$, to model the assignment of the isolated SL i immediately after the SL $j^h_{\vert \mathcal {F}_h \vert }$ of group $\mathcal {F}_h$;

• arcs $(i, j^h_1)$, with $i \in \mathcal {L}^I$ and h = 1, …, H, to model the assignment of the SL $j^h_1$ of group $\mathcal {F}_h$ immediately after the isolated SL i;

• arcs (i, j), $i,j \in \mathcal {L}^I$, and i ≠ j, to model the assignment of the isolated SL j immediately after the isolated SL i.

Finally, a weight c _ij is associated with each arc $(i,j) \in \mathcal A$, which indicates the amount of space which becomes unavailable for future assignments due to the joint assignment of i and j to k:

$$\displaystyle \begin{aligned}c_{ij} = \begin{cases} u_j & \text{if }j \neq \Theta, \\ u_i & \text{if }j = \Theta\text{ and }\exists\ h\text{ such that }i = j^h_1, \\ u_i/2 & \text{if }j = \Theta\text{ and }\exists\ h\text{ such that }i = j^h_m,\text{ with }1 < m < |\mathcal{F}_h| , \\ 0 & \text{if }j = \Theta\text{ and }\exists\ h\text{ such that }i = j^h_{\vert \mathcal{F}_h \vert}\text{ or }i \in \mathcal{L}^I. \end{cases} \end{aligned}$$

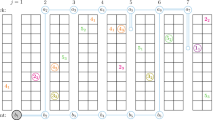
Figure 2 reports the auxiliary graph associated with the available SLs depicted in Fig. 1. In this example, the capacity of each SL is 10 items. Thus, according to the definition above, the capacity of nodes 1 and 4 is equal to 10, while the capacity of nodes 2 and 3 is equal to 20 to model the two level storage policy. Nodes 1 and 4 are linked with Σ through an entering arc and each node is linked to Θ through an exiting arc. The weight associated with each arc ( Σ, j), j = 1, 4, is equal to the capacity of node j, i.e., 10. The weight associated with the arcs (j,  Θ) is 0 for j = 3 and j = 4 (since 3 is the last SL of a group of contiguous SLs, and 4 is an isolated SL), while it is 10 for j = 1 and j = 2 (since 1 represents the first SL and 2 an intermediate SL of a group of contiguous SLs). Finally, the weight of an arc entering node j, with j ≠  Θ, is equal to the capacity of j.

Fig. 2

Graph representation of the available SLs depicted in Fig. 1

3.2 The Constrained Shortest Path Problem

Given the current product type $k \in {\mathcal K}$, the problem of determining a directed path from Σ to Θ in the auxiliary graph $\mathcal G$, which represents the sequence of SLs assigned to k, is formulated using the following two families of variables:

• x _ij ∈{0, 1}, for any $(i,j) \in \mathcal A$, to model the sequence of SLs assigned to k in terms of a directed path in $\mathcal G$ from node Σ to node Θ;

• $y_i \in \mathbb {Z}_+$, for any $i \in \mathcal N$, to model Miller-Tucker-Zemlin-like constraints, aimed at avoiding subtours.

For each $i \in \mathcal N$, we also define $\mathcal N^+(i)$ and $\mathcal N^-(i)$ as the sets of nodes linked to $i \in \mathcal {N}$ via an exiting and an entering arc, respectively:

$$\displaystyle \begin{aligned} \mathcal N^+(i) = \left\{ j \in \mathcal N:\ \exists\ (i,j) \in \mathcal A\right\}, \qquad \mathcal N^-(i) = \left\{ j \in \mathcal N:\ \exists\ (j,i) \in \mathcal A\right\}. \end{aligned} $$

(1)

The constrained shortest path problem related to k can be formulated as follows:

$$\displaystyle \begin{aligned} & \min\ \sum_{(i,j) \in \mathcal A} c_{ij} x_{ij} - \sum_{j \in \mathcal N} \delta^k_{j} \sum_{i \in \mathcal N^{-}(j)} x_{ij} & \end{aligned} $$

(2)

$$\displaystyle \begin{aligned} & \sum_{j \in \mathcal N^{-}(i)} x_{ji} - \sum_{j \in \mathcal N^{+}(i)} x_{ij} = \begin{cases} -1 & \text{if } i=\Sigma \\ 0 & \text{if }i \in \mathcal{L} \\ 1 & \text{if } i=\Theta \end{cases} & \forall\ i \in \mathcal N, \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} & \sum_{j \in \mathcal N}\sum_{i \in \mathcal N^{-}(j)} u_{j} x_{ij} \geq q^k, & \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} & y_j - y_i -1 + (1-x_{ij})|\mathcal N| \geq 0 & \forall\ (i,j) \in \mathcal{A}. \end{aligned} $$

(5)

The objective function (2) consists of two parts: the first summation defines the primary optimization goal to be minimized, i.e., the space no longer available in the warehouse after storing items of type k along the nodes of the path; the second sum is related to the secondary optimization goal, i.e., the request that special product types should be preferably stored in specific SLs. It involves parameters $\delta ^k_{j}$ which are set in such a way that it is convenient to assign SL j to the product type k, if j is one of the preferable SLs for k. Constraints (3) define a directed path for k, by means of the binary variables x _ij, in terms of a unitary flow sent from the source node Σ to the target node Θ, with the aim of modeling the assignment of a sequence of SLs to k. Constraint (4) imposes that the sum of the capacities of the nodes along the path be greater than or equal to the storage demand of the product type k. Finally, constraints (5) are Miller-Tucker-Zemlin-like constraints, which avoid subtours in the returned solution [8].

Figure 3 shows two feasible solutions referring to the auxiliary graph in Fig. 2, assuming q ^k = 25. The solution on the left assigns to k the sequence of SLs 4, 1, and 2, whose total capacity, given by the sum of the node capacities, is 40, enough to stock all the items of k. The selected SLs will be filled starting from 4 (10 items), passing then to 1 (other 10 items), and finally considering 2 (the remaining 5 items). The space no longer available in the warehouse for future assignments, i.e., the first sum of (2), is 50. Notice that the assignment of the SL 2 will make unavailable the extra storage on top of 2 and 3 in the future: this is why a weight 10 is associated with the arc (2,  Θ). The solution on the right, instead, which is optimal, assigns the SLs 1 and 2 to k, with total capacity 30. The selected SLs will be filled starting from 1 (10 items) and then passing to 2, thus exploiting the capacity made available on top of 1 and 2 (10 items at the ground level and the remaining 5 on top of 1 and 2). The space no longer available for future assignments is 40, better than in the previously considered solution.

Fig. 3

Two feasible solutions representations

3.3 The Overall Heuristic Method

As outlined before, the idea underlying the heuristic approach is to address the product types in cascade, each time solving the constrained shortest path problem described in Sect. 3.2 over an auxiliary graph which is progressively pruned. The steps of the heuristic method are summarized in Algorithm 1.

Algorithm 1: Successive constrained shortest path method

At the beginning, the product types in $\mathcal K$ are sorted in a nonincreasing order with respect to the number of items to stock. In the first iteration, the first product type in the resulting ordered set is considered. The constrained shortest path problem in Sect. 3.2 is solved on the graph defined in Sect. 3.1, where the set of nodes $\mathcal {L}$ corresponds to all the available SLs in the warehouse. In any successive iteration, say t, the t-th product type in the considered order is analysed and the corresponding constrained shortest path problem is solved over a graph obtained from the initial one by removing all the nodes corresponding to the SLs assigned till iteration t and their incident arcs. The complete solution is finally given by the set of the paths which have been separately determined for all the product types in $\mathcal K$.

4 Numerical Experiments

Two types of experiments have been performed. The first one aims at analysing the performance of the heuristic for different values of the parameters $\delta ^k_{j}$, while in the latter we compare the results of the heuristic here proposed with the ones returned by the matheuristic in [6]. The heuristic has been implemented by using the language OPL and solved via CPLEX 12.6 (IBM ILOG, 2016). All the experiments have been conducted on an Intel Xeon 5120 computer with 2.20 GHz and 32 GB of RAM.

4.1 The Instances

We considered the same set of real instances solved in [6], corresponding to 20 randomly selected days. The instances are divided into two classes, called ClassHA and ClassLA, each referring to 10 days where the number of items to stock is higher (ClassHA) or lower (ClassLA) than the average number of items to stock over the 20 selected days. Two kinds of special product types exist, i.e., perishable (P) and high rotational (HR), which should be preferably assigned to specific SLs. More in detail, the instances in ClassHA have to assign 1150 items of 14 different product types on average: 1.2% are items of type P, whereas 21.2% are items of type HR. The instances in ClassLA have to assign 787 items of 11 different product types on average: 1.5% are items of type P, whereas 40.7% are items of type HR.

4.2 Efficacy and Efficiency of the Heuristic Approach

As specified, parameters $\delta ^k_{j}$ are used to favour the assignment of specific SLs to special product types. In particular, if product k is of type P, then its preferable SLs are those specified in subset $\mathcal {S}_P \subset \mathcal {S}$. In this case, $\delta ^k_{j} > 0$ if $j \in \mathcal {S}_P$, and $\delta ^k_{j} = 0$ otherwise. The same logic applies to a product k of type HR, for which $\delta ^k_{j}$ are set in such a way to favour the assignment of SLs belonging to subset $\mathcal {S}_{HR} \subset \mathcal {S}$. On the other hand, for a product k neither of type P nor HR, $\delta ^k_{j}$ tend to favour the assignment of SLs in $\mathcal {S} \setminus (\mathcal {S}_P \cup \mathcal {S}_{HR})$. Three settings for positive values of $\delta ^k_{j}$ have been investigated, of form $\delta ^k_{j}=p \cdot u_{j}$, where p = 0.2, 0.5 and 0.8.

Table 1, for both the instances in ClassLA and ClassHA, shows the features of the solutions our industrial partner is interested in for the different settings of $\delta ^k_{j}$. Specifically, we report the average solving time (in seconds), the average space available after the assignment (given by the total capacity of the empty SLs at the ground level plus, whenever two empty SLs are contiguous, the capacity of the SL that can be created on top of them), the percentage of items of type P assigned to SLs in $\mathcal {S}_P$, and the percentage of items of type HR assigned to SLs in $\mathcal {S}_{HR}$.

Table 1 Performance of the heuristic for ClassLA and ClassHA

As expected, by increasing p, i.e., the value of $\delta ^k_j$, the percentage of items of types in P and HR assigned to their preferable SLs increases, at the expenses of the space available after the assignment. In fact, as already observed in [6], the two objectives are often conflicting, since forcing the assignment of items to specific locations may be in contrast with the maximization of the total space available after the assignment. Interestingly, the higher is value p, the lower is the average solving time.

ClassHA was identified in [6] as the hardest group of instances to solve with the matheuristic, mainly due to the higher number of items to stock. As opposed, the heuristic seems to address such instances more easily. The higher number of items to stock per product type in ClassHA requires longer paths. This implies a wide pruning of the associated graphs at each iteration of the heuristic, and smaller and easier constrained shortest path problems to address during the resolution process.

4.3 Comparison with a Matheuristic Approach

The SLAP here addressed has been formulated in [6] as a multicommodity flow model, where the assignment of SLs is simultaneously addressed for all the product types in ${\mathcal K}$. Specifically, given an auxiliary graph whose set of nodes correspond to the SLs available in the warehouse, $\vert {\mathcal K}\vert$ directed paths are sought along which the quantity q ^k is sent for each k, by taking into account the two level storage policy. The objective function aims at maximizing the available storage capacity after the assignment and the number of items of types $\mathcal K_P$ and $\mathcal K_{HR}$ assigned to $\mathcal S_P$ and $\mathcal S_{HR}$, respectively. A two-phase matheuristic has been proposed in [6], which is based on decomposition. In the first phase, ${\mathcal K}$ is partitioned into Λ subsets, in such a way that each group contains about the same number of items to store. Thus, Λ subproblems are generated and sequentially solved by CPLEX, each time removing those SLs already assigned in the previous solved subproblems. Finally, the Λ solutions obtained are merged into a unique solution, which is provided as initial feasible solution to the Branch and Bound algorithm of CPLEX. The matheuristic relies on several parameters, whose impact on the performance of the resolution process has been deeply investigated, by identifying a suitable parameter setting.

Table 2 compares the results obtained by the heuristic here proposed with the ones achieved by the matheuristic in [6], on the set of instances described in Sect. 4.1. For the matheuristic, the most suitable parameter setting devised in [6] has been used. For the heuristic, we selected p = 0.5 as a good compromise between efficiency and efficacy of results. Table 2 reports, separately for ClassLA and CLassHA, the average solving time (in seconds), the average space available in the warehouse after the assignment, the percentage of items of type P assigned to their preferable SLs, and the percentage of items of type HR assigned to their preferable storage locations.

Table 2 Comparison between the proposed heuristic and the matheuristic in [6]

For ClassLA, the successive constrained shortest path heuristic outperforms the matheuristic for the preferable SLs assigned to the special product types. The available space after the assignment is almost the same, just decreasing of a few units on average. For ClassHA, the results are similar for both the approaches, with the successive constrained shortest path heuristic outperforming the matheuristic regarding the available space after the assignment. The strength of the heuristic is the time required to obtain solutions. In fact, it is of about 3 seconds on average, i.e., about one thousandth of the time required by the matheuristic. The proposed heuristic thus appears to be a very promising tool to solve the addressed SLAP problem, rapidly determining solutions which, for the majority of the tested instances, also improve the quality of the solutions found by the matheuristic approach.

5 Conclusions

A very fast successive constrained shortest path heuristic has been proposed to address the assignment of items to SLs jointly with sequencing decisions about the assigned SLs, as required in a real application context. The heuristic ouperforms the matheuristic in [6] on real-size instances, in terms of both solving time and solution quality. Future research will address a more general problem where storage allocation decisions are considered jointly with the routing of the vehicles in charge of moving items towards the selected locations.