Keywords

1 Introduction

Examination timetabling, course timetabling and school timetabling constitute educational timetabling [1] which is a fundamental task of schools and universities. According to Wren [2], “Timetabling is the allocation, subject to constraints, of given resources to objects being placed in space time, in such a way as to satisfy as nearly as possible a set of desirable objectives”. A well-organised educational timetable ensures a sound operation of an educational institute. Educational Timetabling Problems (ETP) are considered the constraint satisfaction problems which involve multiple factors, such as educators, students, classrooms and teaching equipment, as a whole. ETPs have been widely studied with multiple artificial intelligence algorithms developed, mainly including heuristics algorithms, novel approaches and multi-agent systems [3]. Heuristics algorithms consist of meta-heuristics and hyper heuristics [4]. Novel approaches can be classified as hybrid approaches and fuzzy logic approaches [3]. However, there is a lack of general solution solving a wide range of ETPs, resulted from the definition differences of hard and soft constraints in different universities [5]. Besides, each method has its applicability and strengths.

Currently, COVID-19 crisis challenges the traditional teaching format. Traditionally, ETP should consider teaching staff availabilities and infrastructure capability. However, as social distancing practices, schools and universities have to transfer face-to-face classes and assessments online, which causes the hard and soft constraints of ETP changed. Especially for examination timetabling problems, multiple new conditions emerge, such as non-invigilator, unlimited room capacity, technical issues and diverse exam durations. Those features, to the best knowledge of the authors, have not been studied in conventional ETP research, which inspires this research to investigate the Online Examination Timetabling (OET) problem and to develop a model for solving the problem.

The contributions of this research include a conceptual model for the OET problem, a conflict table for constraint handling and a modified Artificial Bee Colony (ABC) algorithm for solving the OET problem.

The organisation of this article is as follows: In Sect. 2, the existing approaches and algorithms for solving ETPs are reviewed. Section 3 proposes a conceptual model of the OET based on the discussion of the general features of the OET problems. A conflict table aiming to shrink the search space is introduced to handle the main hard constraint. In Sect. 4, a modified ABC algorithm is applied to solve the problem. The experiment based on the data from a local university for the proposed model is presented in Sect. 5. In order to further verify the effectiveness, the proposed approach is compared with the Constraint Programming (CP) method in Sect. 6. Section 7 concludes the article.

2 Literature Review

The approaches for solving ETPs have been studied over 50 years since Appleby, Blake and Newman [6] initiated a study in school timetabling. Around 3000 computational timetabling articles are published every year, within which university timetabling problems occupy over 85% proportion [5]. Educational Timetabling is to allocate a number of educational activities, such as exams, lectures, tutorials and meetings, into finite timeslots and/or room-slots [7]. Each activity has its unique conditions needed to be satisfied. The conditions are different from instance to instance depending on the priorities given by different educational institutes. Generally, those conditions could be categorised into hard constraints and soft constraints. Hard constraints decide the feasibility of a timetabling problem solution. Soft constraints impact the solution quality [8]. Schaerf [1] classified ETPs as course timetabling, school timetabling and examination timetabling problems. Course timetabling is to allocate lectures and tutorials to timeslots, classrooms or other teaching facilities avoiding an individual student taking more than one class at the same time. School timetabling, based on curriculum, assigns lecturers and tutors to a scheduled course timetable, taking their availabilities and specialisations as hard constraints [9]. Examination timetabling is to ensure no student taking two or more exams simultaneously and to optimise resource usage within an examination period [10]. Unlike course timetabling or school timetabling, in an examination, rooms or examiners could be assigned to different courses at the same time [8, 9]. For each type of the ETPs, the hard constraints are commonly defined as below.

Hard constraints for course timetabling problems [3, 11, 12]:

  • No student can take more than one class at the same time.

  • Only one course can be taught in one classroom at a time.

  • Timeslots for assigning courses in are limited to one day.

  • The number of students in a class cannot exceed the capacity of a classroom.

  • All courses must be allocated in a regular basis as required.

Hard constraints for school timetabling problems [13,14,15]:

  • No teacher can deliver more than one class at the same time.

  • Teachers cannot be scheduled to timeslots when they are unavailable.

  • Teachers must be allocated to the courses they are capable to deliver.

  • For co-teaching classes, the teachers must be allocated in the same timeslots.

Hard constraints for examination timetabling problems [8, 16,17,18,19]:

  • Every exam must be assigned in consecutive timeslots and cannot be split.

  • Exams must be invigilated, meaning examiner(s) will be allocated.

  • No student can sit more than one exam simultaneously.

  • The number of examinees cannot exceed the capacity of the exam hall in a timeslot.

  • Every exam must be scheduled.

Educational timetabling problems are NP-complete problems [20], meaning that it may be impossible to find a polynomial-time algorithm to solve the problem. In addition to the traditional constraint programming method, more and more researchers are interested in seeking stochastic methods in recent years [21]. Mainly, those methods are heuristic approaches and novel methods [3, 5, 21]. Heuristic approaches are problem-independent [22], including meta-heuristics and hyper-heuristics. Meta-heuristic approaches are known as approximate methods which aim at finding better solutions in a reasonable computational time rather than the best solution [23]. Meta-heuristics approaches are inspired by the nature mechanisms, such as biological systems, physical and chemical processes, for their success in solving multi-objective and combinational optimisation problems [24]. Hyper-heuristics is to heuristically choose a heuristic [25]. Instead of using a technique derived from specific scenarios, hyper-heuristics solve problems with more generalised solutions [26]. Novel methods include hybrid approaches, fuzzy logic approaches and Multi-Agent Systems (MAS). Hybrid approaches combine different approaches with the purpose to mitigate the weakness of a single approach. Fuzzy logic approaches focus on solving those problems which do not have a precisive classification [27, 28] resulting in the difficulty of quantitating and modelling. Multi-agent systems engage several artificial intelligence techniques, as agents, to collaboratively accomplish a common goal [29]. Every agent is independent, able to communicate with each other and to do tasks incompletely.

Based on the algorithms abovementioned, many applications have been evolved and developed. In heuristics scope, Soria-Alcaraz et al. [30] applied iterated local search, and Soria-Alcaraz, Özcan, Swan, Kendall and Carpio [31] adopted perturbative hyper-heuristics to solve course timetabling problems. Odeniyi, Omidiora, Olabiyisi and Aluko modified Simulated Annealing (SA) approach, while Kheiri and Keedwell [32] introduced a sequence-based selection hyper-heuristic framework to find solutions for school timetabling problems. Kasm, Mohandes, Diabat and El Khatib combined constructive heuristics with colour graphing [33], and Bykov and Petrovic developed Step Counting Hill Climbing to tackled examination timetabling problems. Hybrid approaches are approach combinations. Those combinations for solving ETPs include but are not limited to Artificial Bee Colony (ABC) with Hill Climbing (HC) [34], HC with SA [35], Cat Swarm Optimisation (CSO) with swap operator [13], tabu with genetic algorithm [36], ABC with Simple Local Search (SLS) and Harmony Search (HS) [37], and ABC with Great Deluge (GD) [38]. To deal with ill-defined problems [39], many fuzzy logic applications were developed to solve ETPs for universities, such as the University of Malaysia Sabah Labuan [40], Islamic Azad University [41], University of Eswatini and Uludag University [42]. Since, universities’ resources, such as rooms, teaching facilities and teaching staff, are shared with different faculties, faculties need to negotiate with each other for different resources and bring discussion results to their administrations to come up with a solution. To mimic the negotiation processes, many universities have adopted MAS and let the agents play the roles of negotiators, administrators and planers [29]. For example, the University of Gdansk [43] utilised MAS to simulate administration, database, room and teacher agent and scheduler.

Due to the idiosyncrasy of ETPs, there is a lack of universal solutions for general ETPs. The key components of ETPs, such as rooms, teachers, courses, students and timeslots, are different from university to university. Universities prioritise and weigh those components differently. In addition, the university structures, educational policies and procedures diversify the differences dramatically. Therefore, a number of ETP approaches reviewed in this article were based on particular business scenarios.

This research will apply ABC algorithm to solve the online examination timetabling problem driven by a local university’s practice. The reasons for adopting ABC algorithm are: 1) ABC was proved to be an efficient algorithm for solving multivariable, multimodal optimisation problems [44]. 2) ABC algorithm is simple, efficient and effective in solving many optimisation problems compared to traditional algorithms, such as Differential Evolution, Genetic Algorithm, Particle Swarm Optimisation (PSO) [37]. 3) ABC algorithm is easy to be implemented with a few parameters [44].

3 A Conceptual Model of the Online Examination Timetabling

This section presents the features of the OET problem, conducts mathematically modelling and proposes a conceptual model for the OET problem including a novel approach for hard constraint handling.

To model and simulate the application, the word “unit” is used to represent a learning subject in the rest of the article, while other literature mentioned in Sect. 2 may use “course” for the subject.

3.1 OET Problems Features

Originated from the local university’s conduct of online examination, the new features of OET problems are derived as below:

  • Students participate in exams remotely. But students still cannot take two exams simultaneously. It is expected that students are not overloaded.

  • Every exam only can be allocated once in the exam period.

  • Exams are non-invigilated and open book. Similar to an assessment, but the timeframe is shorter. Through teaching and learning management systems, students can download the exam questions, and upload the answers within the designated exam durations. It is realised that the non-invigilated examination may cause academic integrity issues, however, this is not in the scope of this research.

  • Although exams move online, an exam duration cannot be fragmented. That is, the exam duration should be continuous from the scheduling point of view.

  • An exam duration could be extended up to 12 h. This is to consider the technical issues such as Internet connection failure and/or ICT system faults.

  • Physical room capacity is not taken into account.

  • Without the limitation of room capacity, the number of examinations to share the same timeslots is unlimited.

  • Since the number of exams put in a day could be many, the administrative load would be increased. The examination downloading and uploading could intensify the traffic of the IT system. Therefore, to balance the ICT network traffic should be taken into consideration.

3.2 Symbols and Terms Definition

Parameters

P:

Number of days of the whole exam period

N:

Number of exam units to be allocated

Variables

t:

Duration (in hours) of each exam, \(t \in \left\{ {1, \ldots , 12} \right\}\)

w:

Number of days a timetabling solution uses, \(w \to P\)

a:

set of exams allocated in one day, \(a \in \left\{ {1, \ldots N} \right\}\)

v:

Average number of units distributed in w, \(v = \frac{N}{w}\)

x:

Number of exam units that cannot be allocated in P, \(x = N - \mathop \sum \nolimits_{i = 1}^{w} a_{i} \).

3.3 Hard Constraints and Fitness Function

Eight hard constraints have been identified, as follows.

  1. 1.

    Each student cannot take more than one exam simultaneously.

  2. 2.

    Each unit only can be allocated once in the whole exam period.

  3. 3.

    All units must be allocated.

  4. 4.

    An exam whose duration is less than eight hours must be allocated in business hours.

  5. 5.

    An exam whose duration is less than or equal to twelve hours must be allocated in one day.

  6. 6.

    An exam cannot be allocated on a timeslot that is blocked by administration (e.g., a scheduled maintenance time).

  7. 7.

    The duration of an exam must be consecutive.

  8. 8.

    The whole period of the examination must not be greater than the designated days.

A feasible solution has to satisfy all the hard constraints. During the solution-seeking process, a formulation as in Eq. 1 is introduced to evaluate the fitness \(f\left( w \right)\) of the current search node and then lead the algorithm to a feasible solution.

$$ min\;\;f\left( w \right) = \left\{ {\begin{array}{*{20}l} {\frac{{\mathop \sum \nolimits_{i = 1}^{x} t_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} t_{i} }} \times \frac{w - P}{P},} \hfill & {if\;\;\;\;w > P} \hfill \\ {0,} \hfill & {if\;\;\;\;w\,\le\,P} \hfill \\ \end{array} } \right. $$
(1)

The major goal of this project is to let the number of days (w) that a solution uses is no more than the number of days (P) that the examination administration designates. Therefore, w should be less than or equal to P, in other words, \(f\left( w \right) \) is required to be zero. When w is greater than P, the proportions, that total hours of excessive exams to all exams and the number of excessive days to designated days, will jointly affect the fitness value. Seeking a feasible solution without hard constraint violation is the aim of this research. The purpose to establish Eq. (1) is to set up an intermediate value for bees to detect better food sources. The algorithm will chase the lesser \(f\left( w \right)\) in the search space unit w equals to or smaller than P, then f(w) will be set to zero directly. After that, all the solutions that have \(f\left( w \right)\) equal to zero will be outputted as feasible solutions.

3.4 Soft Constraint

When multiple feasible solutions are found, the soft constraint will be applied to filter the most preferred one. In order to avoid exam data traffic congestion and reduce administrative workload, exams need to be levelly distributed to the whole designated exam period. To evaluate the evenness, Standard Deviation formulation (2) is adopted. The less the \(\sigma\) is, the more balanced solution will be. Thus, among feasible solutions, the solution with the least \(\sigma\) will be chosen as the best solution.

$$ \sigma = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{w} \left( {a_{i} - v} \right)^{2} }}{w}} \;\;\;\;{\text{where}}\;\;\;\;w \le P $$
(2)

3.5 The Proposed Conceptual Model

The proposed conceptual model is illustrated in Fig. 1. Preliminarily, course data are retrieved from the student enrolment database, which includes student unique identifications and the courses they have enrolled in. Based on the retrieved course data, a conflict table can be constructed. The conflict table is introduced to shrink search space, which will be detailed in Sect. 3.6. After consulting the conflict circumstances, the exam profiles, such as exam duration, will be required. To seek solutions from the shrunk search space for OET problems, a modified ABC algorithm is applied. After that, all the solutions found will be filtered to output the best solution with a minimum soft constraint violation.

Fig. 1.
figure 1

The conceptual model of OET

Full size image

The fundamental hard constraint of examination timetabling is that no one student can take more than one examination simultaneously. Consequently, every conflict between units should be known at the very beginning. For an individual student, all the units enrolled are conflicted with each other in the examination period. Therefore, the conflict unit table can be formed from all the students’ unit enrolment data. A feasible examination timetable is to arrange, within a day, non-conflict exam units to share timeslots, and to avoid the timeslot overlap between conflict exam units. But the conflict exam units could be allocated consecutively. In other words, a solution is a combination of overlapping non-conflict and/or consecutive conflict units. As the number of possible combinations is vast, a Computational Intelligence algorithm is needed to get a better solution efficiently and effectively. Before the algorithm runs, parameters, such as the period of a whole examination and the duration of each unit exam, will be required.

3.6 Constraint Handling Approach

As mentioned earlier, the major hard constraint is to prevent any student from taking more than one examination at the same time. Based on this principle, a conflict table is established to restrain the search space. When seeking a solution, every two examination units conflicting in the conflict table will be kept from sharing timeslots. As the conflict table is an aggregation from the student enrolment database, the solution search space is largely shrunk.

The data structure of the conflict table is illustrated in Fig. 2 with Java language expression, which collects every exam unit as a unique data item and records all the conflict exam units to be its subset.

Fig. 2.
figure 2

Data structure of conflict table

Full size image

The conflict unit table is generated by consulting students’ enrolment database. The flowchart of the conflict table construction is presented in Fig. 3.

Fig. 3.
figure 3

Conflict table construction flowchart

Full size image

The method will consult every student’s data to get their unit enrolment situation. When a student’s data is retrieved, each enrolled unit is compared with the existing conflict table. If the unit is not in the conflict table, this unit will be inserted into the table as a new item and the other units will be put into the conflict unit field. If the unit is found in the conflict table, then the other units will be added to this unit’s conflict unit field but a deduplicating method will be implemented to ensure every unit in the conflict unit field is unique. When every student has been consulted, the complete conflict table is constructed.

A simplified example of constructing a conflict table is shown in Table 1 and Table 2. For instance, in Table 1, student S1 enrolled units A, B and C, and student S3 enrolled units A, C and E. Hence, it is known that unit A conflicts with units B, C and E. As result, units B, C and E have been placed into the conflict unit field of A in Table 2. After consulted students S1, S2 and S3, the conflict table for units A, B, C, D and E can be established.

Table 1. Example of unit enrolment
Full size table
Table 2. Example of conflict table
Full size table

4 A Modified ABC Algorithm for the Proposed OET Model

The ABC algorithm is adopted in the research for seeking better solutions from the search space shrunk by the conflict table. This section firstly introduces the original ABC algorithm. A modified ABC algorithm for the proposed OET model is presented afterward.

4.1 Description of Original ABC Algorithm

ABC is introduced by Karaboga [44] inspired by the behaviours of social insects. Self-organisation and labour division is its basic mechanism. This algorithm simulates the way that honeybees self-arrange to forage with four major traits, including positive feedback, negative feedback, fluctuations and multiple interactions. Positive feedback reinforces a foraging process, encouraging bees to create convenient paths. Negative feedback prevents positive feedback from saturation, such as food source exhaustion and over-population to a destination. Fluctuations help to discover new paths by randomly walking. Although fluctuations may cause errors, it is significant for creativity. Multiple interaction mechanisms ensure the information can be delivered to each node of the network. In the labour division, honeybees are categorised to be employed foragers and unemployed foragers. With the food sources, these two bee characters can form a minimal model of forage selection. Food sources stand for the possible solutions for the problems to be solved. Food sources are valued with many factors, such as the distances to the nest and the lavishness. Employed bees take the responsibility to investigate the food sources and then bring the information about the sources back to the nest. Unemployed bees consist of two groups: scouts and onlookers. Scouts search the surroundings of the nest to exploit new food sources while onlookers set in the nest to build up food sources from the information shared by employed bees. Onlookers determine the profitability of the food sources.

ABC algorithm includes four stages: 1) in the initialisation stage, several solutions (food resources) will be initialised; 2) in the employed bee stage, bees will be sent to the initialised solutions to implement search tasks; 3) in the onlooker bee stage, bees will select a better solution according to the solution fitness; 4) in scout bee stage, bees will explore new solutions. The equations of each stage are detailed below.

Solution Population

The number of solutions SN will be randomly generated with different dimension D. The solution generating rule as follows:

$$ s_{i}^{d} = s_{min}^{d} + random\left( {0,1} \right)\left( {s_{max}^{d} - s_{min}^{d} } \right), $$
(3)

Where \(i \in \left\{ {1, \ldots ,SN} \right\}, d \in \left\{ {1, \ldots D} \right\}\). \(s_{max}^{d}\) and \(s_{min}^{d}\) is the upper bound and low bound for the dimension d.

After the population, solutions will be evaluated and randomly allocated with employed bees to be exploited. The exploitation process will be enforced repeatedly in R times. During the exploitation, scout bee(s) will explore new solution(s).

Employed Bee Stage

Based on the assigned solutions, employed bee es will generate a neighbour solution with the below equation.

$$ es_{i}^{d} = s_{i}^{d} + \varphi_{i}^{d} \left( {s_{i}^{d} - s_{k}^{d} } \right) $$
(4)

Where \(k \in \left\{ {1, \ldots ,SN} \right\}\) is randomly chosen and \(k \ne i\). \(\varphi_{i}^{d}\) is randomly generated in the range of [−1, 1]. \(s_{k}^{d}\) is a neighbour of \(s_{i}^{d}\).

The \(es_{i}^{d}\) will be evaluated and compared to \(s_{i}^{d}\). If the fitness of \(es_{i}^{d}\) is better than or equals to \(s_{i}^{d}\), then \(es_{i}^{d}\) will be chosen. Otherwise, \(s_{i}^{d}\) will be remained.

Onlooker Bee Stage

Onlookers will evaluate the possibility value (p) of each solution provided by employed bees. After the evaluation, onlooker bees will exploit the high possibility solution. The possibility equation is represented as below.

$$ p_{i} = \frac{{fit\left( {es_{i} } \right)}}{{\mathop \sum \nolimits_{n = 1}^{SN} fit\left( {es_{n} } \right)}} $$
(5)

Where \(fit\left( {es_{i} } \right)\) is the fitness of \(es_{i}\) generated in employed bee stage.

Scout Bee Stage

$$ s_{i} = s_{min} + random\left( {0,1} \right)\left( {s_{max} - s_{min} } \right) $$
(6)

If any solution found by an employed bee has been abandoned in the onlooker stage because of its p, the owner of the abandoned solution will become a scout bee. This scout bee will look for a new solution in a way similar to the solution population, which is shown in Eq. 6.

Key parameters of the original ABC algorithm are:

  • SN: number of populated solutions which equals to employed and onlooker bees.

  • MAX-ITERATION: max number of exploitation cycle.

4.2 A Modified ABC Algorithm for OET

Fig. 4.
figure 4

Modified ABC algorithm for OET

Full size image

ABC is adopted for OET problem in this research. The exam combination pool is the search space. As each exam can and only can be assigned once in the whole examination period, the allocated units have to be bypassed. Therefore, this research will modify Eq. 4 into Eq. 7, where \(\vartheta \in \left\{ {1, \ldots ,UN} \right\}\), UN is the number of unvisited exams \(UN \subset N\).

$$ es_{i}^{d} = s_{i}^{d} + random\left( {0,1} \right)\left( {\vartheta_{Max}^{d} - \vartheta_{min}^{d} } \right) $$
(7)

Unlike employed bees choosing a better solution with fitness Eq. 1, the key role of onlooker bees is to exploit the neighbourhood for a better solution by probability value with Eq. 5. In order to avoid overexploitation, a parameter called exploitation_counter is introduced. If a solution is exhaustedly exploited (exploitation_counter reaches maximum number which is defined as MAX_EXPOITATION in Fig. 4) without probability value improvement or the solution has the biggest local exploitation_counter, a scout bee would replace the onlooker bee to discover a new food source. Since the goal of this research is to obtain feasible solutions, when one of them is found, it will be outputted, and the related bee will be converted to a scout bee immediately. The modified algorithm pseudocode is represented in Fig. 4.

The major modifications are summarised as below:

  • Preprocess original data to generate the conflict table to limit search space.

  • Use modified Eq. 7 for neighbour search to avoid duplicated exploration.

  • Use the exploitation-counter to abandon exhausted sources in order to avoid over-exploitation.

Output solutions anytime if a feasible solution is found, and the bee will be converted to be a scout bee immediately.

5 Experiment

5.1 Experimental Settings

This research obtained a large dataset from a local university, detailed as follows.

  • Number of data items: 16,246

  • Number of students: 9,399

  • Number of examinations: 209

  • Range of examinations that a student takes: 1 to 4

  • The whole period of examination: 7 days (resulted from manual arrangement)

With the purpose to test the flexibility of the proposed algorithm, the experiment has been configured with extra conditions presented below.

  • Range of examination duration: 3 to 12 h (detailed in Table 3)

  • Timeslot limitation: examinations whose duration is less than or equals to 8 h must be allocated in the daytime. (Daytime: 8 am to 5 pm)

Table 3. Number of exam distribution in duration
Full size table
Table 4. ABC algorithm parameter settings
Full size table

The proposed approach was experimented with the below environment.

  • Operation system: Windows 10 Education Edition

  • Integrated development environment: IntelliJ IDEA Ultimate 2019.3

  • Programming language: Java

  • Computer hardware system: Intel® Core™ i5-9500 3.00 GHz; 16.0 GB memory; integrated graphics card

The algorithm has been experimented with ten samples as presented in Table 4. Each sample is set with different parameters in the number of bees, the number of iterations and the MAX_EXPOITATION. The number of bees represents the coverage of solution population in the search space; The number of iterations is expected to test whether the increase of searching rounds will improve the result; the MAX_EXPOITATION is to decide the deep of exploitation. Each sample will be fed in the proposed algorithm ten times. To choose reasonable initial parameters, this research referenced the first ABC algorithm experiment conducted in [44] and configures the number of bees to be 20 and the number of iterations to be 500.

To evaluate the experiment result, three values have been recorded, including time-spent, days and soft constraint violations. The time-spent indicates how much time the algorithm used to seek a solution under a particular parameter setting; the days shows how many days the best solution needs to allocate all the examinations; The soft constraint violations refer to the fitness value of the best solution calculated with Eq. 2.

5.2 Experimental Results

The experiment results for each sample are shown in Table 5 with average value, the best value, standard deviation and Coefficient of Variation (CV), from which the following conclusions could be drawn.

Table 5. Experiment results (ten times runs)
Full size table

  • The algorithm can obtain a feasible solution in a short time for a big dataset. In Sample A, the proposed algorithm reaches the best solution within 75 s.

  • Increasing the number of iterations can minimise the soft constraint violation. Compared to Sample A who runs 500 iterations, Sample E executes two times of iteration (1000), which improves the soft constraint violation by 3.57% (from Sample A 38.02756 to Sample E 36.71591). However, significantly increasing number of iterations does not linearly improve the soft constraints. The number of iteration that Sample J operates is ten times greater than Sample A. But the improvement is merely 7.96% (from Sample A 38.02756 to Sample J 34.99916).

  • Increasing the number of bees improves the result. Comparing to Sample E, Sample G and Sample I deploy three times and four times of bees respectively. The soft constraint violations improved 5.68% (from Sample E 38.35568 to Sample G 36.1736 on average) and 9.05% (from Sample E 38.35568 to Sample I 34.88421 on average).

  • Deepening exploitation was not cost-effective. Compared to Sample E, Sample H inputs five times MAX_EXPOITATION, but the soft constraint violation only minimized by 5.3% (from 38.3556 to 36.3180)

  • The proposed approach can stably output solutions with given parameters as the all the coefficient of variation (CV) is less than 10%.

  • Overall, Sample A consumed the smallest population and achieved satisfactory results with the least iteration. Therefore, the settings are reasonable for the proposed OET model.

6 Comparison Study

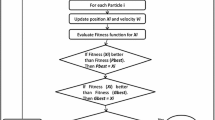
The examination timetabling problem of this research is posed by the COVID-19 pandemic crisis, which makes it difficult to find a similar study to compare the experimental result. In order to verify the performance of the proposed approach in solving OET problem, a Constraint Programming (CP) [17] method is implemented for the comparison study as ETPs are considered constraint satisfaction problems. CP has been proved successful in solving various problems, such as vehicle routing and timetabling [45]. The flowchart of the CP for the proposed model is illustrated in Fig. 5.

Firstly, the exam and enrolment data are retrieved to construct the conflict table, which is the same as the processes described in Fig. 1 and Fig. 3. The program then creates a day and then selects an exam from the exam list in turn. If the selected exam does not conflict with other exams in that day slot, the exam will be allocated on the day. Otherwise, a consecutive exam in the exam list will be consulted. If all the unallocated exams have been visited and none of them can be assigned in the current day, a new day will be created for them. When a new day is created, if the number of days violates the hard constraint, the program will backtrack the exam list. When all the exams have been allocated without hard constraint violation, a feasible solution will be recorded. In order to find out all the feasible solutions that the proposed CP can come out with, this research will fully backtrack each exam in the exam list even a feasible solution is found. All the feasible solutions will be filtered by the soft constraint. Also, after an exam list is completely backtracked, the list will be arranged to form a new array by the way of moving the first element of the list to the end with the purpose to evenly expose each element in each variable selection phase. When every rearrangement is finished, in other words, the last element of the original list has reached the first position of the array, the program terminates.

To compare with CP, the proposed ABC approach uses Sample A in Table 4, which has the smallest population and iterations. The same university dataset in Sect. 5.1 is used in the experiment. The comparative items include the number of feasible solutions found, the elapsed time for seeking the first feasible solution, the number of days the solution uses to allocate all the exams, the time of the program execution, and the soft constraint violations. The comparison results are presented in Table 6. As CP selects exam units sequentially, its experimental results are almost the same in each execution, Table 6 lists only one set of CP results. On the contrary, ABC generates solutions randomly and outputs results differently in each execution. Therefore, this comparison study tests ABC ten times and lists the best and the average results respectively. Since in this comparison, the ABC is re-run, its results are slightly different from Table 5.

Fig. 5.
figure 5

Constraint programming flowchart

Full size image

From Table 6 the following findings are observed.

  • ABC can find out much more solutions than CP does. The number of solutions ABC found is 5.68 times more than the number of solutions CP did (340.9 compares to 60).

  • ABC is 27.3 times faster than CP in finding the first feasible solutions (4.1 ms compares to 112 ms)

  • ABC and CP are competitive in getting the best solution in the number of days used.

  • ABC consumes a longer time than CP to complete the program execution. (74054 ms compares to 4117 ms).

  • ABC approach has achieved a less soft constraint violation than the CP approach 2.35 times (37.84188 compares to 87.202). This indicates the applied ABC approach can even the examination density in the whole exam period.

Overall, the modified ABC algorithm can provide better results than CP method in this research. It can quickly find out a better solution. Although the whole running time ABC uses is longer than CP, the minute level discrepancy in computational time could be ignored compared to the importance of soft constraint violation for the proposed problem.

Table 6. Comparison results of ABC approach and CP approach
Full size table

7 Conclusions

This research aims at providing an approach for solving OET problem under the COVID-19 pandemic crisis. Examination timetabling problem is one of the ETPs, which has been widely studied for decades and therein multiple algorithms and approaches have been created and introduced. However, the scarcity of universal solutions for ETPs results in the need that every practical scenario requires a specific analysis and method selection. Moreover, with social distancing practice due to the pandemic, many universities and schools around the world move their educational activities online, which makes ETPs more challenging. In order to cope with the challenge, this research proposed a conceptual model to solve the online examination timetabling problems along with a conflict table constructed to handle the hard constraint. A modified Artificial Bee Colony algorithm was proposed to solve the OET problems. The proposed approach possesses multiple merits: 1) the conflict table proposed converts big volume raw data to be a shrunk search space; 2) the modified ABC algorithm changes neighbour search process to avoid over-exploration; 3) introducing MAX_EXPOITATION parameter lest overexploitation. The experimental result shows the proposed algorithm can effectively solve OET problems with several advantages: 1) quickness, the algorithm can reach a feasible solution in 4.1 ms on average, which is 27.3 times faster than CP does. 2) effectiveness, the algorithm provides feasible solutions 7.7 times larger than CP in solution volume. 3) reasonableness, the algorithm is able to gain more reasonable solutions in soft constraint violations, 2.3 times over CP.

The research can be applied to post-pandemic education as long as the examination is conducted online. The future works include more algorithm evaluation comparing with other evolutionary algorithms and extending the model to other educational timetabling problems such as school timetabling.