Keywords

1 Introduction

The most applications of Wireless Sensor Networks (WSNs) have the common requirement of continuous monitoring [1], which poses challenges to the battery-powered sensors and brings the energy efficiency problems in virtual backbone construction [2, 3] and broadcast and multicast routing [4]. To solve the energy problems of the WSNs, most researchers proposed two kinds of strategies, i.e., one is the wake-sleep batch scheduling of sensors, and another one is collecting energy from external environment based on energy transformation module of sensors. However, the former strategy may cause the reduction of data reliability and the latter one has low efficiency of energy transformation. To this end, Wireless Rechargeable Sensor Networks (WRSNs) has emerged with the advantages of high charging efficiency via static charging stations or mobile charging vehicles, which can guarantee the timeliness of charging and the service quality of network coverage.

The most important problem of the WRSN with mobile chargers is to design the charging plans which mainly focuses on the charging pattern, charging order arrangement and charging amount assignment. This paper studies the charging planning problem of a mobile charger for charging sensors from the perspectives of charging amount assignment and charging path planning, which is to maximize the charging efficiency of the charger for guaranteeing the continuously works of the WRSN.

The existing research on the charing planning of mobile chargers focused on two aspects, demand-driven charging strategies and periodic charging ones. For the demand-driven charging strategies [5] proposed a path planning algorithm to choose the sensors in low-power status and satisfy their charging requirement based on a threshold value \(\beta \) on the remaining energy. The authors in [6] predicted the energy consumption of sensors and transformed the charging cost as a monotone submodular function, then introduced a \((1-\frac{1}{e})/4\)-ratio algorithm for the problem. The authors in [7] proposed a spatial-and-temporal optimization algorithm for real-time charging for eliminating the exhausted sensors and adding the powered new ones. The studies in [8, 9] aimed at designing the algorithm of path planning and charging assignment to maximize the network lifetime and minimize the charging consumption.

For periodic charging strategies, the authors in [10] designed a constant-ratio approximation algorithm for charging path planning problem under the powering limitation model. And the authors in [11] applied the region-separation and charging-discretion into the charing solution and proposed a \(\frac{1-\xi }{4(1-1/e)}\)-ratio algorithm. The authors in [12] considered the one-to-many charging model and designed a constant-ratio algorithm. Recently, the new charging technology has drawn attentions of researchers like the \((1-\xi )(1-e)/e\)-ratio algorithm based on the energy transferring depending on the obstacles in [13], the \((3+\xi )\)-ratio algorithm for multiple-chargers in one-vehicle model in [14] and the periodic charging algorithm with the optimal movement speed in [15].

However, the existing literature mentioned above did not consider the energy efficiency. In this paper, we consider the demand-driven charging planning for a single mobile charger in WRSNs, which includes the charging path planning and the charging energy assignment to maximize the energy efficiency of the charger. The contributions of this paper are shown as below.

  1. (1)

    We propose a single-charger charging planning problem for WRSNs, called the Charging Scheduling problem with Maximized Energy Efficiency in WRSNs (CS-MEE Problem) based on the energy consumption model. The goal of the problem is to maximize the charging energy efficiency of the charging process in a period. The mathematical model and NP-hardness proof of problem are both given.

  2. (2)

    To solve the CS-MEE problem, we propose an heterogeneous-weighted-graph algorithm, CS-HWG Algorithm, which is composed of Charging Energy Assignment and Charging Path Planning. And we analyze the time complexity of the algorithm.

  3. (3)

    The extensive simulations are performed to verify the effectiveness of the proposed algorithm for the CS-MEE problem.

This paper is organized as follows. Section 2 introduces the network model, energy consumption model and problem formulation. In Sect. 3, we propose a heuristic algorithm to solve the problem and analyze the approximation ratio of the algorithm. Simulations are shown in Sect. 4. Section 5 concludes this paper.

2 System Model and Problem Formulation

2.1 Network Model

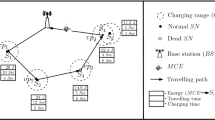
We consider a WRSN composed of n stationary rechargeable sensors deployed in a two-dimensional plane, which are denoted by set \(S=\{s_1,s_2,...,s_n\}\). Each sensor \(s_i\) is deployed at the position \((x[s_i],y[s_i])\) and powered by a rechargeable battery with the maximum energy capacity \(E^0_i\). These sensors perform the area coverage task collaboratively and the current battery energy of \(s_i\) is denoted as \(E^{cur}_i\). We assume that the coverage strategy is determined or periodically adjusted depending on their initial energies. There are three kinds of status of sensors depending on the charging requirements based on two thresholds, \(E^{low}\) and \(E^{min}\): (1) Working Status. \(E^{low}<E^{cur}_i\le E^0_i\); (2) Low-power Status. \(E^{min}<E^{cur}_i\le E^{low}\); (3) Charging Status. \(0<E^{cur}_i\le E^{min}\).

There is one mobile charger to charge sensor nodes with low remaining energy, which is denoted as node c. Charger c starts the charging task from its service station located at \(c_0=(x[c],y[c])\) and ends the task back to its station. And the charger has the initial energy \(E_{max}\) in the assumption that \(E_{max}\) can satisfy the charging requirement of all the sensors or the charging amount for sensors cannot be less than \(\theta \cdot E_{max}\), where \(\theta \) is a parameter closed to 1. Since the sensors with lower remaining energy may cause exhaustion and monitoring failure, the charging task firstly guarantee the impletion of the sensors in Charging Status. If there is the remaining energy for the charger, the charging for sensors in Low-power Status will be considered and the charging for sensors in Working Status is in a similar way.

2.2 Energy Consumption Model

In the cooperative coverage task, the static sensors are in charge of covering the target area and the mobile charger is responsible for charging the sensors into Working Status. The energy consumption of chargers includes two aspects:

  • (1) Charging Energy Consumption. Due to the determined coverage strategy, the maximum charging energy for sensor \(s_i\) with the energy capacity \(E^0_i\) and the remaining energy \(E^{cur}_i\) in the current coverage mission. Since the coverage scheduling is assumed to be determined in advance, \(E^{cur}_i\) has been known before charging scheduling. We denote the scheduled charging energy for \(s_i\) as \(C(s_i)\). Furthermore, we consider the inevitable energy loss in the process of charging and the charging energy consumption is regarded as \(\alpha \) time of the required amount, i.e. \(E_i^{charging}=\alpha \cdot C(s_i)\cdot g_i\), where \(g_i\) are defined as follows:

    (1)

  • (2) Moving Energy Consumption. Considering the charging model in close range, the mobile charger should move to the position of the sensor with low power for charging. Thus the moving distance is the Euclidean distance and calculated based on the locations of the charger and sensor, which is denoted as \(dist(c, s_i)\). Here we denote the energy consumption rate as \(\beta \), thus the moving energy consumption is \(E_i^{moving}=\beta \cdot dist(c, s_i)\cdot g_i\).

Based on the two kinds of energy consumption of chargers, we define the energy efficiency of the charging process as follows.

Definition 1

(Charging Energy Efficiency). Based on a charging scheduling, the energy efficiency is the proportion of the energy consumption on charging in the overall energy cost, which is denoted as \(EE=\frac{\sum _{s_i\in S}E_i^{charging}}{\sum _{s_i\in S}(E_i^{charging}+E_i^{moving})}\).

2.3 Problem Formulation

We study the charging planning problem to realize the goal of maximizing the charging energy efficiency. The charging scheduling is composed of two parts, the charging energy assignment denoted as \(EA=\{C(s_i)|1\le i\le n\}\) (where \(C(s_i)\) is the scheduled charging energy on \(s_i\)) and the charging path \(path_c\) denoted as a sequence of locations passing by c. Based on the above preliminaries, we refer to the problem as the Charging Scheduling problem with Maximized Energy Efficiency in WRSNs (CS-MEE Problem), whose detailed definition is shown as follows.

Definition 2

(CS-MEE Problem)

Given a set \(S=\{s_1, s_2, \cdots , s_n\}\) of n rechargeable sensors where each sensor \(s_i\) has the battery capacity \(E^0_i\) and the initial energy \(E^{cur}_i\), one mobile charger c with its starting service station \(c_0\) and the initial energy \(E_{max}\), Charging Scheduling problem with Maximized Energy Efficiency in WRSNs (CS-MEE Problem) is to find a charging scheduling strategy denoted as two-tuples (EA ,  path), such that

  1. (1)

    the \(path_c\) starts from \(c_0\) and ends at \(c_0\),

  2. (2)

    for each sensor \(s_i\in S\), \(E_i^{charging}+E^{cur}_i\le E^0_i\),

  3. (3)

    the Charging Priorities(CP) for the sensors are increased according to their status: CP(Working Status)<CP(Low-power Status)<CP(Charging Status);

  4. (4)

    \(\theta \cdot E_{max} \le \sum _{s_i\in S}(E_i^{charging}+E_i^{moving})\le E_{max}\), or all sensors can be charged by c, where \(\theta \) is a parameter closed to 1,

  5. (5)

    the charging energy efficiency \(EE=\frac{\sum _{s_i\in S}E_i^{charging}}{\sum _{s_i\in S}(E_i^{charging}+E_i^{moving})}\) is maximized.

In the following, we will introduce the mathematical formulation of the CS-MEE Problem.

$$\begin{aligned} \begin{aligned} Maximize ~~\frac{\sum _{s_i\in S}\big (\alpha \cdot C(s_i)\cdot g_i\big )}{\sum _{s_i\in S}\big (\alpha \cdot C(s_i)\cdot g_i+\beta \cdot dist(c, s_i)\cdot g_i\big )} \end{aligned} \end{aligned}$$
(2)

s.t.

$$\begin{aligned} E^{cur}_i+\alpha \cdot C(s_i)\cdot g_i \le E^0_i ~~~~~~~~~~~~~i=1, 2, \cdots , n \end{aligned}$$
(3)
$$\begin{aligned} \theta \cdot E_{max}\le \sum _{s_i\in S}\big (C(s_i)\cdot g_i+\beta \cdot dist(c, s_i)\cdot g_i\big ) \le E_{max}~~~~~~~~~~~~~ \end{aligned}$$
(4)
$$\begin{aligned} g_i\in \{0, 1\}~~~~~~~~~~~i=1, 2, \cdots , n \end{aligned}$$
(5)

The function (2) is to maximize the charging energy efficiency. Constraint (3) express that the charged energy amount of each sensor cannot beyond the sensor’s battery capacity. Constraint (4) is the charging energy consumption constraint which ensures that the charging energy amount of the charger will not exceed the initial energy of the charger. Constraints (5) defines the domain of the variable \(g_i\).

In the following theorem, we will give the NP-hardness proof of the problem.

Theorem 1

CS-MEE Problem is NP-hard.

Proof

To prove the NP-hardness of CS-MEE Problem, we consider a special case of it: all the sensors are in Charging Status (\(g_i=1\) for \(1\le i\le n\)) and they have the same current energies \(E^{cur}_i\)s. In this case, the charging energy for sensor \(s_i\), \(C(s_i)\) is the maximum amount \(E^0_i-E^{cur}_i\), which is unified represented as C.

Thus the objective of the problem is driven to be maximizing \(\frac{\sum _{s_i\in S}\big (\alpha \cdot C(s_i)\big )}{\sum _{s_i\in S}\big (\alpha \cdot C(s_i)+\beta \cdot dist(c, s_i)\big )}\). Based on equivalent conversion, the objective can be rewritten into maximizing \(\frac{1}{1+\frac{\beta }{\alpha \cdot C}\sum _{s_i\in S} dist(c, s_i)}\). Note that \(\alpha \), \(\beta \) and C are predefined or can be calculated. By denoting \(\frac{\beta }{\alpha \cdot C}\) as a constant const the objective becomes from maximizing \(\frac{1}{1+const\cdot \sum _{s_i\in S} dist(c, s_i)}\) to minimizing \(\sum _{s_i\in S} dist(c, s_i)\).

It can be easily found that the problem in this special case is equivalent to the Travelling Salesman Problem (TSP), which has been proved NP-hard [16]. Since a special case of CS-MEE problem is NP-hard, CS-MEE problem is also NP-hard, which completes the proof.    \(\square \)

3 Algorithms for CS-MEE Problem

In this section, we propose an heterogeneous-weighted-graph algorithm, CS-HWG Algorithm, which is composed of two phases, Charging Energy Assignment and Charging Path Planning. And we will analyze the time complexity of CS-HWG Algorithm.

We firstly give the preliminaries in Lines 1–7 of Algorithm 1: since the sensors with the higher charging requirements have larger priorities, we give a baseline value according to the divergence indicator among the sensors’ battery capacities, i.e., \(DI=\lceil \max _{1\le i,j\le n} \frac{E^0_i}{E^0_j}\rceil \). We assign the priorities for the three kinds of sensors’ status respectively: (1) For the ones in Charging Status, its priority \(pri(s_i)= DI^2\); (2) For the sensors in Low-Power Status, \(pri(s_i)= DI\); (3) For the sensors in Working Status, the charging priority is assigned as \(pri(s_i)=\frac{1}{DI}\). This priority assignment measure can guarantee that the gap between the pairs of the priorities belonged to different requirements can be widen. Furthermore, it also consider the charging demands and the energy capacity of sensors: for the sensors in Charging Status, the charging requirement is greatest and the maximum charging energy \((E^0_i-E^{cur}_i)\) could be satisfied. Thus \(pri(s_i)= DI^2\) which is larger than those in other two statuses.

Phase 1: Charging Energy Assignment

Phase 1.1: Heterogeneous-weighted Graph Construction

Constructing the auxiliary graph is a classic method to model the practical problem, and the auxiliary graph is either a node-weighted graph or an edge-weighted graph. In CS-MEE Problem, we construct a particular auxiliary graph with node-weights and edge-weights, heterogeneous-weighted graph, as shown in Lines 10–19 of Algorithm 1. The node set is composed of the positions of sensors and a charger, \(V = S\bigcup C\). With the consideration of the sensor deployment density, we give the assumptions for spares graphs and dense ones. For spares graphs, we introduce a limitation value \(l_0\) of the moving distance between twice of charging, which can avoid excess consumption of the chargers’ energy for some single charging. Thus \(E=\{(s_i,s_j)|\forall s_i, s_j\in V\) and \(dist(s_i, s_j)\le l_0\}\). For dense graphs, \(l_0\) can be regarded as infinity.

The weight assignment is with the consideration of charging cost and moving cost: When considering the charging cost, it is decided by each sensor’s maximum charging requirement or the charged energy amount. Thus the node weight is denoted as \(weight(s_i)=\alpha \cdot (E^0_i-E^{cur}_i)\) and the node weight set \(VW = \{weight(s_i)|\forall s_i\in S\}\). When considering the moving cost, it is determined by the Euclidean distances between the pairs of nodes in the network, i.e., the edge weight is calculated by \(weight(s_i, s_j)=\beta \cdot dist(s_i, s_j)\). And the edge weight set \(EW = \{weight(s_i, s_j)|\forall (s_i, s_j)\in E\}\). Then we complete the construction of the heterogeneous-weighted graph, \(G=(V, E, VW, EW)\).

Phase 1.2: Charged Node Filtering

Considering high charging efficiency and limitation of the charger’s initial energy \(E_{max}\), we filter the nodes with necessary charging requirements like those in Charging Status. Since \(E_{max}\) is limited to satisfy the charging requirements for part of sensors, we firstly reserve the consumption on charging movement \(E_{moving}^{res}\), which is calculated in Step 21. And the calculation is based on the length of the Minimum Hamilton Cycle which can guarantee to pass across all the sensors in Charging Status. Then the remaining energy \(E_{max}-E_{moving}^{res}\) can be assign for charging sensors.

Based on the new \(E_{max}\), we assign the charging amount according to the sensors’ charging priorities and filter the sensors with necessary charging requirements. The assignment is realized in three loops as shown in Lines 24–28: firstly the charging requirement of the sensors in Charging Status can be satisfied and the assigned charging amount is \(C(s_i) = \frac{pri(s_i)}{DI^2} \cdot (E^0_i-E^{cur}_i)\). If the charger has the remaining energy, the sensors in Low-Power Status can be charged. The charging for sensors in Working Status is in the similar way.

The filtering is based on the assigned charging energy \(C(s_i)\) as shown in Lines 29–31: if \(C(s_i)=0\), \(s_i\) will be out of the consideration later and eliminated from V and E. The we obtain the filtered node set \(V'\) and node set \(E'\).

Phase 1.3: Edge-weighted Graph Transformation

To solve the problem on the constructed heterogeneous-weighted graph, the weights’ distribution on both nodes and edges is not beneficial to global optimization. In other words, the energy consumption of chargers is composed of charging cost and moving cost, which cannot exceed the maximum limitation \(E_{max}\). Thus the two kinds of energy cost should be measured by uniform standard, and we adopt the edge weight as the measurement. Here we introduce an equivalent transformation method of blending node weights into edge weights, as shown in Lines 34–40 of Algorithm 1:

For each node in the filtered set \(V'\), we revalue the node weight with the consideration of the charging priority and the uniform magnitude of node weights and edge weights, i.e., \(weight'(s_i)=\frac{1}{pri(s_i)}\cdot \beta \cdot avrdist\cdot \frac{weight(s_i)}{E^0_i}\), where \(avrdist=\frac{\sum _{1\le i,j\le n}dist(s_i, s_j)}{|E'|}\) is the average distance among all the pairs of sensors. Note that avrdist is a normalization factor for modifying the node weight into the similar magnitude with those of the edge weight. And \(\frac{1}{pri(s_i)}\) indicates that the node with higher charging priority has smaller node weight, which is consistent with that the node pair with low moving cost has smaller edge weight.

Since the sensor’s charging can be finished by the charger’s only one pass, we equally divide the node weight into two parts, e.g. \(\frac{1}{2}weight'(s_i)\). And then we distribute the divided node weight to the weight of the node’s associated edges, i.e., \(weight'(s_i, s_j) = weight(s_i, s_j) + \frac{1}{2}weight'(s_i) + \frac{1}{2}weight'(s_j)\), which updates the edge weight set. Then we will perform charging planning based on the transformed edge-weighted graph \(G' =(V', E', EW')\).

Phase 2: Charging Path Planning

Based on the auxiliary graph \(G' =(V', E', EW')\), we perform the algorithm for TSP Problem and the charging path \(path_c\) of the charger c can be obtained. The detailed description is shown in Algorithm 1.

Theorem 1

The time complexity of CS-HWG Algorithm is \(O(n^3)\), where n is the number of sensors.

Proof

According to the description of Algorithm 1, there are three parts as shown in Algorithm 1, the preliminaries, Phase 1 and Phase 2. We analyze the time complexities for these parts as follows: For the preliminaries in Lines 1–7, the charging priority assignment has the time complexity of O(n). For Phase 1, Phase 1.1 (Heterogeneous-weighted Graph Construction) and Phase 1.3 (Edge-weighted Graph Transformation) both perform for all the nodes and edges, whose time consumptions are directly related to the number of nodes and that of edges. Thus their time complexities are both \(O(n^2)\). For the node filtering (Lines 23–32) in Phase 1.2 (Charged Node Filtering), its time complexity is O(n). Furthermore, TSP Algorithm is applied in Phase 1.2 and Phase 2, which has a larger time complexity of \(O(n^3)\) [17].

To sum up, the time complexity of CS-HWG Algorithm is \(O(n^3)\), which completes the proof.    \(\square \)

figure a

4 Simulation Results

The simulation experiments are performed in a two-dimension planar with the size of \(M*M\). On the plane, there are n sensors randomly deployed; for each sensor \(s_i\), there is a uniform parameter \(E^0\) denoting the maximum battery capacity. And \(s_i\)’s current battery energy \(E^{cur}_i\) is valued in the range of \([0,\frac{4}{5}\cdot E^0]\) and it battery capacity \(E^0_i\) is set in \([E^{cur}_i,E^0]\). The two indictors for the sensors’ status, \(E^{low}\) and \(E^{min}\) are assigned \(\frac{3}{5}\cdot E^0\) and \(\frac{3}{10}\cdot E^0\). The moving distance limitation between any pair sensors \(l_0\) is set as 50.

For the optimization goal of MVB-GRC Problem, we evaluate the proposed algorithm in terms of the energy efficiency, which is denoted as Energy Efficiency. The four parameters, the side length of the region M, the number of sensors n, the initial energy of the charger \(E_{max}\), and the maximum energy capacity of sensors \(E^0\) are considered as the potential factors on performance of charing scheduling. And we consider the following four groups of parameter settings and we repeat the experiment 100 times and adopt the average values for each setting: (1) M varies from 40 to 160 by the step of 20 with fixed n, \(E^0\) and \(E_{max}\); (2) n varies from 60 to 160 by the step of 20 with fixed M, \(E^0\) and \(E_{max}\); (3) \(E_{max}\) varies from 2500 to 5500 by the step of 500 with fixed M, \(E^0\) and n; (4) \(E^0\) varies from 40 to 100 by the step of 20 with fixed M, n and \(E_{max}\).

Fig. 1.
figure 1

Energy efficiency by comparing two TSP algorithms

Full size image

Firstly we apply two TSP Algorithms with approximation ratios of 2 and 1.5 [17] (denoted as 2-ratio TSP and 1.5-ratio TSP) in Charging Path Planning Phase and evaluate their performance measure. As shown in Fig. 1, with the changes of the four parameters, 1.5-ratio TSP outperforms 2-ratio TSP on energy efficiency. The reason is that the former algorithm can construct a better Hamilton Cycle which is closer to the optimal one, i.e., 1.5-ratio TSP constructs a charging path with less length than that generated from 2-ratio TSP. Then the scheme with less charging path length can enhance the whole charging efficiency. Moreover with the growth of M as shown in (a), the energy efficiency fluctuates in the range [0.65, 0.87] and gets stable when \(M>120\); with the increasing of n, \(E_{max}\) or \(E^0\) in (b)-(d), two algorithms both enter a smooth status with little fluctuations on the energy efficiency. It is because that the region scale directly influences the maximum length of charging paths, which determines the results obtained by TSP algorithms.

Fig. 2.
figure 2

Energy efficiency by varing M

Full size image
Fig. 3.
figure 3

Energy efficiency by varing n

Full size image

Secondly, with the advantages of 1.5-ratio TSP Algorithm, we continue to perform the simulations via applying it and evaluate the algorithm’s performance with the change of four parameters.

As shown in Fig. 2, with the growth of M, the energy efficiency presents upward tendency and moderate fluctuation when \(E_{max}=1000,2000,3000,4000\). Compared with \(E_{max}=1000\), the influence of M on the energy efficiency becomes smaller with a larger \(E_{max}=4000\), which shows that the region scale has little impact on the algorithm with a larger initial energy of the charger. It can be explained by that when the initial energy of the charger is sufficient, the charging requirements of all the sensors can be satisfied which can keep the energy efficiency on a high level.

As shown in Fig. 3, the energy efficiency obtained by CS-HWG Algorithm remains upward trend with the increasing of n at the fixed \(E_{max}=1000,2000,3000,4000\). Especially when \(n>100\), the results among different \(E_{max}\) enter a relative steady state [0.80, 0.95] with little fluctuations. It shows the algorithm can satisfy the charging requirements of the majority of the sensors. The reason is that with the increasing of network scale with a fixed region scale, the deployment density becomes higher which is helpful to reduce the moving energy consumption; at the same time, the increased initial energy of the charger can meet more charing requirements for the sensors.

Fig. 4.
figure 4

Energy efficiency by varing \(E_{max}\)

Full size image
Fig. 5.
figure 5

Energy efficiency by varing \(E^0\)

Full size image

As shown in Fig. 4, the energy efficiency fluctuates up and down with the increasing of \(E_{max}\), which is especially apparent when \(E_{max}\in [3500,5500]\) with a fixed \(n=100\). The amplitude of fluctuation becomes unapparent with the growth of n, i.e., the results when \(n=200\) remain in [0.87, 0.93]. It can be explained by that when the network scale gets larger, the different between each pair of sensors’ charing requirement becomes relative smaller, which is benefit for improve the charger’s charging efficiency. Thus with the increased initial energy of the charger, the change of energy efficiency can enter a smooth status.

As shown in Fig. 5, comparing the results when \(E_{max}=1000,2000,3000,4000\), the changing of \(E^0\) has a steady impact on increasing the energy efficiency with different \(E_{max}\), i.e. the results remain [0.85, 0.95] when \(E^0>80\). It shows that the maximum battery capacity of sensors \(E^0\) has limited influence on the performance of our algorithm. It is because that \(E^0\) determines the maximum charging requirements for sensors, which cannot decide the actual charging amount. The algorithm is designed to meet the most necessary charging requirements first and perform selective fully-charged-mode charging to sensors in different status, which is for enhancing the whole energy efficiency.

Finally, we can draw the conclusion that the network scale n and the initial energy of the charger \(E_{max}\) has more influence than the region scale M and the energy capacity of the sensors \(E^0\) in terms of the energy efficiency of the whole charging process.

5 Conclusion

In this paper, we investigate the maximum energy efficiency charing planning problem for one mobile charger in WRSNs. We formally define the problem and propose a heuristic algorithm composed of charing energy assignment and path planning, which is based on heterogeneous-weighted graph construction and edge-weighted graph transformation. Furthermore, we apply two approximation algorithms in the charging path phase and perform the simulation experiments to evaluate the algorithm’s performance. In the future, we have great interest on investigating the maximum energy efficiency charging planning problem for multiple chargers in WRSNs.