Stoneley Waves in Media with Microstructure

Abstract

The role of microstructure in affecting propagation of antiplane Stoneley waves, that are waves localized at the discontinuity surface between two perfectly-bonded half-spaces, is considered. Microstructure is described within the linear theory of isotropic couple stress elastic materials with micro-inertia. The dispersion relation is a symmetric tri-term combination of the Rayleigh functions in the relevant half-space with a coupling term. In contrast to classical elasticity, where antiplane Stoneley waves are never supported and in-plane waves exist only inasmuch as shear velocities for the half-spaces are close enough, it is found that propagation is largely possible, although it occurs beyond a cuton frequency. For the latter, an explicit expression is given alongside dispersion curves. These results may adopted in next-generation non-destructive testing (NDT) appliances to account for the material microstructure.

1 Introduction

Stoneley waves are localised waves propagating at the interface between two perfectly bonded half-spaces. They owe their name to Robert Stoneley, who first investigated them in the context of seismic waves and the layered structure of the Earth [18, 19, 19]. The special feature about Stoneley waves is that, in classical elasticity, they occur under restrictive conditions, which make them appear rather exceptional. Explicit statement of those conditions has been given much later by Schölte [17]. Stoneley waves have been extensively investigated [2], especially in the context of anisotropic material [4, 11, 16], ocean acoustics [5] and borehole dynamics [20]. This interest, which carries over to the recent contributions [1, 3, 8, 9], is especially driven by the desire to circumvent such limitations and explore new settings which support Stoneley wave propagation under general conditions, whereby they may serve as novel probing tools for the inspection of the discontinuity surfaces inside materials. In this pursue, researchers are inspired by the great success of Rayleigh waves, which, by virtue of their capacity to propagate in a large array of situations, have been put to advantage in many technical and scientific applications: ranging from non-destructive testing (NDT) to seismology, from ocean acoustics to ground-moving high-speed vehicles. Indeed, recent studies show that, in contrast to classical materials, microstructured media allow propagation of antiplane Rayleigh waves [12, 13, 15]. In this work, we discuss the role that material microstructure may have in supporting existence of antiplane Stoneley waves. By considering microstructure through the linear theory of couple stress isotropic materials with micro-inertia, it is shown that antiplane Stoneley waves propagate under general conditions, beyond a cuton frequency. This stands in contrast to classical media, where antiplane Stoneley waves are not supported. In fact, it appears that antiplane Stoneley waves, just like antiplane Rayleigh waves, are perturbations of bulk shear waves and emerge from mode conversion of these with an evanescent mode (that is absent in classical media) [12, 14].

2 Mechanical Framework for Antiplane Stoneley Waves

In a couple-stress (CS) material, the stress state depends on the classical force stress tensor $\boldsymbol{s}$, as well as on the couple stress tensor $\boldsymbol{\mu }$. Just like the first determines the traction vector, the latter determines the internal reduced couple vector $\boldsymbol{q}$, acting across the surface of normal $\boldsymbol{n}$

$$\begin{aligned} \boldsymbol{q} = \boldsymbol{\mu }^\mathrm{T} \boldsymbol{n}, \end{aligned}$$

where the superscript $\mathrm{T}$ denotes transposition, i.e. row-column inversion. The force stress tensor $\boldsymbol{s}$ is decomposed into its symmetric and skew-symmetric parts, respectively $\boldsymbol{\sigma }$ and $\boldsymbol{\tau }$,

$$\begin{aligned} \boldsymbol{s}=\boldsymbol{\sigma }+\boldsymbol{\tau }. \end{aligned}$$

Conversely, $\boldsymbol{\mu }$ is decomposed into its deviatoric and spherical parts

$$\begin{aligned} \boldsymbol{\mu } = \boldsymbol{\mu }_\mathrm{\scriptscriptstyle D} + \boldsymbol{\mu }_\mathrm{\scriptscriptstyle S}, \end{aligned}$$

where, for the latter, it is $\boldsymbol{\mu }_\mathrm{\scriptscriptstyle S} = \tfrac{1}{3} \left( \boldsymbol{\mu } \cdot \boldsymbol{1}\right) \boldsymbol{1}$, assuming that a dot denotes the scalar product and $\boldsymbol{1}$ is the rank-2 identity tensor.

For the body $\mathcal {B}$, the internal virtual work may be expressed as follows (see, e.g., [10, 15]):

$$\begin{aligned} \int _{\mathcal {B}} \left( \boldsymbol{\sigma } \cdot {\text {grad}}\ \boldsymbol{u} + \boldsymbol{\mu } \cdot {\text {grad}}^\mathrm{T} \boldsymbol{\varphi } \right) \mathrm {d}V, \end{aligned}$$

(1)

where ${\text {grad}}$ denotes the gradient operator and a superscript T indicates transposition. Here, $\boldsymbol{u}$ and $\boldsymbol{\varphi }$ are the (virtual) displacement and the micro-rotation vector fields. For CS materials, the displacement field $\boldsymbol{u}$ determines the micro-rotation field $\boldsymbol{\varphi }$ through

$$\begin{aligned} \boldsymbol{\varphi }=\frac{1}{2}{\text {curl}}\ \boldsymbol{u}, \quad \Leftrightarrow \quad \varphi _i = \frac{1}{2}\mathbb {E}_{ijs} u_{s,j}, \end{aligned}$$

(2)

where it is understood that a subscript comma denotes partial differentiation, i.e. $u_{i,j}=({\text {grad}}\ \boldsymbol{u})_{ij} = \partial u_i/\partial x_j$, and $\mathbb {E}$ is the rank-3 permutation tensor.

The displacement field is related to the linear strain tensor $\boldsymbol{\varepsilon }$ through

$$\begin{aligned} \boldsymbol{\varepsilon }={\text {Sym}}{\ }{{\text {grad}}\ \boldsymbol{u}}. \end{aligned}$$

(3)

Similarly, the torsion-flexure (or wryness, or curvature) tensor is introduced

$$\begin{aligned} \boldsymbol{\chi }={\text {grad}}\ \boldsymbol{\varphi }. \end{aligned}$$

(4)

From Eqs. (1, 2) and (4), it is deduced that the torsion-flexure tensor is purely deviatoric, $\boldsymbol{\chi }=\boldsymbol{\chi }_\mathrm{\scriptscriptstyle D}$, and so is the couple stress tensor. To light notation, hereinafter $\boldsymbol{\mu }$ is written with the understanding that $\boldsymbol{\mu }_\mathrm{\scriptscriptstyle D}$ is meant.

2.1 Constitutive Equations

For isotropic materials, two extra material parameters are introduced alongside the classical Lamé moduli, $\varLambda$ and $G>0$, namely $\ell >0$ and $-1<\eta <1$, that characterise the microstructure. With these and following [10], a free-energy density $U(\boldsymbol{\varepsilon },\boldsymbol{\chi })$ is constructed such that

$$\begin{aligned} \boldsymbol{\sigma }&= \frac{\partial U}{\partial \boldsymbol{\varepsilon }}, \quad \Rightarrow \quad \boldsymbol{\sigma } = 2 G\boldsymbol{\varepsilon } + \varLambda ({\text {tr}}\,\boldsymbol{\varepsilon }) \boldsymbol{1}, \end{aligned}$$

(5a)

$$\begin{aligned} \boldsymbol{\mu }&= \frac{\partial U}{\partial \boldsymbol{\chi }}, \quad \Rightarrow \quad \boldsymbol{\mu } = 2 G \ell ^2 \left( \boldsymbol{\chi }^\mathrm{T} + \eta \boldsymbol{\chi } \right) . \end{aligned}$$

(5b)

2.2 Equations of Motion

The equations of motion, in the absence of body forces, read

$$\begin{aligned} {\text {div}}\ \boldsymbol{s}&= \rho \ddot{\boldsymbol{u}}, \end{aligned}$$

(6a)

$$\begin{aligned} 2{\text {axial}}\ \boldsymbol{\tau }+{\text {div}}\ \boldsymbol{\mu }&= J \ddot{\boldsymbol{\varphi }}, \end{aligned}$$

(6b)

having indicated time differentiation with a superposed dot. Here, $\rho$ and $J\ge 0$ are the mass density and the rotational inertia per unit volume, respectively. Besides, $({\text {axial}}\ \boldsymbol{\tau })_{i}=\tfrac{1}{2}\mathbb {E}_{ijk} \tau _{jk}$ denotes the axial vector attached to the skew-symmetric tensor $\boldsymbol{\tau }$. Equation (6b) may be solved for $\boldsymbol{\tau }$ to yield

$$\begin{aligned} \boldsymbol{\tau } = -\tfrac{1}{2}\boldsymbol{\mathbb {E}} \left( {\text {div}}\ \boldsymbol{\mu } - J \ddot{\boldsymbol{\varphi }}\right) . \end{aligned}$$

(7)

2.3 Antiplane Shear Deformations

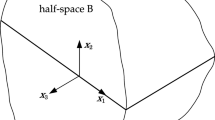
Two half-spaces, named A and B, are considered, in perfect contact along a plane surface, see Fig. 1. A right-handed Cartesian coordinate system $(O,x_1,x_2,x_3)$ is introduced whose axes are directed along the relevant unit vectors $(\boldsymbol{e_1},\boldsymbol{e_2},\boldsymbol{e_3})$. The co-ordinate system is located in such a way that the plane $x_2=0$ corresponds to the contact surface between A and B. Both half-spaces possess a microstructure, which is described within the theory of linear couple stress (CS) elasticity.

Fig. 1.

Two half-spaces, named A and B, in perfect contact along the joining surface $x_2=0$

Antiplane shear deformations are considered, such that, in each half-space, the displacement field $\boldsymbol{u}$ reduces to the out-of-plane component only

$$ u_3(x_1,x_2,t), $$

and there is no dependence on the $x_3$ co-ordinate. As a result, the only non-vanishing components of the strain and of the curvature tensors are

$$\begin{aligned} \varepsilon _{13}&= \tfrac{1}{2}u_{3,1},&\varepsilon _{23}&= \tfrac{1}{2}u_{3,2}, \end{aligned}$$

(8a)

$$\begin{aligned} \varphi _{1}&= \tfrac{1}{2}u_{3,2},&\varphi _{2}&= -\tfrac{1}{2}u_{3,1}, \end{aligned}$$

(8b)

$$\begin{aligned} \chi _{11}&=-\chi _{22}= \tfrac{1}{2}u_{3,12},&\chi _{21}&=-\tfrac{1}{2}u_{3,11},&\chi _{12}&=\tfrac{1}{2}u_{3,22}. \end{aligned}$$

(8c)

Also, accounting for the constitutive relations (5) and in light of (8), it is

$$\begin{aligned} \sigma _{13}&= G u_{3,1},&\sigma _{23}&= G u_{3,2}, \end{aligned}$$

(9a)

$$\begin{aligned} \mu _{11}&=-\mu _{22}= G (\ell )^2 (1+\eta ) u_{3,12},&\mu _{21}&= G (\ell )^2 (u_{3,22}-\eta u_{3,11}), \end{aligned}$$

(9b)

$$\begin{aligned} \mu _{12}&= -G (\ell )^2 (u_{3,11}-\eta u_{3,22}), \end{aligned}$$

(9c)

regardless of $\varLambda$.

The equilibrium equations (6) lend

$$\begin{aligned} \sigma _{13,1}+\sigma _{23,2}+\tau _{13,1} +\tau _{23,2}&= \rho \ddot{u}_3, \end{aligned}$$

(10a)

$$\begin{aligned} \mu _{11,1}+\mu _{21,2}+2\tau _{23}&= J \ddot{\varphi }_1, \end{aligned}$$

(10b)

$$\begin{aligned} \mu _{12,1}+\mu _{22,2}-2\tau _{13}&= J \ddot{\varphi }_2. \end{aligned}$$

(10c)

Substituting Eqs. (8b) and (9) into (7), the skew-symmetric part of the stress tensor is obtained

$$\begin{aligned} \tau _{13} =-\tfrac{1}{2}G \ell ^2 \hat{\triangle }u_{3,1} + \tfrac{J}{4} \ddot{u}_{3,1}, \quad \tau _{23} =-\tfrac{1}{2}G \ell ^2 \hat{\triangle }u_{3,2} + \tfrac{J}{4} \ddot{u}_{3,2}, \end{aligned}$$

(11)

wherein $\hat{\triangle }$ indicates the two-dimensional Laplace operator in the dimensional co-ordinates $x_1$ and $x_2$. For homogeneous media, Eqs. (9a, 10a) and (11) provide a single governing equation in terms of displacement

$$\begin{aligned} G \left( \tfrac{1}{2}\ell ^2 \hat{\triangle }\hat{\triangle } u_3 - \hat{\triangle } u_3 \right) - \frac{J}{4} \hat{\triangle } \ddot{u}_3 + \rho \ddot{u}_3 = 0. \end{aligned}$$

(12)

2.4 Reduced Force and Couple Stress Traction Vectors

The reduced force and couple stress traction vectors, respectively $\boldsymbol{p}$ and $\bar{\boldsymbol{q}}$, acting across a surface with unit normal $\boldsymbol{n}$, are given by

$$\begin{aligned} \boldsymbol{p} = \boldsymbol{s}^\mathrm{T} \boldsymbol{n} + \tfrac{1}{2}{\text {grad}}\ \mu _{nn} \times \boldsymbol{n}, \qquad \bar{\boldsymbol{q}} = \boldsymbol{\mu }^\mathrm{T} \boldsymbol{n} - \mu _{nn} \boldsymbol{n}, \end{aligned}$$

(13)

where $\mu _{nn} = \boldsymbol{n} \cdot \boldsymbol{\mu } \boldsymbol{n} = \boldsymbol{q} \cdot \boldsymbol{n}$ and $\times$ denotes the cross product between vectors. For the boundary surface $x_2=0$ separating the two half-spaces, it is

$$ \boldsymbol{n}^\mathrm{\scriptscriptstyle A}=\boldsymbol{e_2}=-\boldsymbol{n}^\mathrm{\scriptscriptstyle B}, $$

and consequently

$$\begin{aligned} p_3^\mathrm{\scriptscriptstyle A}= s_{23}^\mathrm{\scriptscriptstyle A}+ \tfrac{1}{2}\mu _{22,1}^\mathrm{\scriptscriptstyle A}, \quad \bar{q}_1^\mathrm{\scriptscriptstyle A}= \mu _{21}^\mathrm{\scriptscriptstyle A}, \quad \text{ with }\quad \bar{q}_2^\mathrm{\scriptscriptstyle A}=0, \end{aligned}$$

(14a)

for A, and

$$\begin{aligned} p_3^\mathrm{\scriptscriptstyle B}= -\left( s_{23}^\mathrm{\scriptscriptstyle B}+ \tfrac{1}{2}\mu _{22,1}^\mathrm{\scriptscriptstyle B}\right) , \quad \bar{q}_1^\mathrm{\scriptscriptstyle B}= -\mu _{21}^\mathrm{\scriptscriptstyle B}, \quad \text{ with }\quad \bar{q}_2^\mathrm{\scriptscriptstyle B}=0, \end{aligned}$$

(14b)

for B.

2.5 Nondimensional Form of the Governing Equations

For the sake of definiteness, quantities are normalized against the half-space A. Accordingly, the dimensionless coordinate

$$ \boldsymbol{\xi }=\frac{\boldsymbol{x}}{\varTheta \ell ^\mathrm{\scriptscriptstyle A}}, \quad \boldsymbol{x}=[x_1, x_2], $$

is let together with the reference time $T^\mathrm{\scriptscriptstyle A}=\ell ^\mathrm{\scriptscriptstyle A}/c_\mathrm{\scriptstyle s}^\mathrm{\scriptscriptstyle A}$, whereby the dimensionless time is introduced as

$$ \tau =\frac{t}{T^\mathrm{\scriptscriptstyle A}}. $$

$c_\mathrm{\scriptstyle s}^\mathrm{\scriptscriptstyle A}=\sqrt{G^\mathrm{\scriptscriptstyle A}/\rho ^\mathrm{\scriptscriptstyle A}}$ is the shear wave speed of classical elasticity (CE) for material A and $c_s^\mathrm{\scriptscriptstyle B}=\sqrt{G^\mathrm{\scriptscriptstyle B}/\rho ^\mathrm{\scriptscriptstyle B}}$ the corresponding wave speed for material B. Further, let

$$\begin{aligned} \beta = \frac{\ell ^\mathrm{\scriptscriptstyle B}}{\ell ^\mathrm{\scriptscriptstyle A}}, \qquad \upsilon =\frac{T^\mathrm{\scriptscriptstyle A}}{T^\mathrm{\scriptscriptstyle B}}, \end{aligned}$$

(15)

whereby $\upsilon \beta ={c_\mathrm{\scriptstyle s}}^\mathrm{\scriptscriptstyle B}/{c_\mathrm{\scriptstyle s}}^\mathrm{\scriptscriptstyle A}$ is the bulk shear wave ratio in CE. Substituting these nondimensional variables in Eq. (12), provides the governing equations, holding in A and B, in nondimensional form

$$\begin{aligned} \triangle \triangle u_3^\mathrm{\scriptscriptstyle A}- 2 \varTheta ^2 \triangle u_3^\mathrm{\scriptscriptstyle A}-2 \varTheta ^4 \left[ \frac{(\ell _0^\mathrm{\scriptscriptstyle A})^2}{\varTheta ^2} \triangle u^\mathrm{\scriptscriptstyle A}_{3,\tau \tau } - u^\mathrm{\scriptscriptstyle A}_{3,\tau \tau } \right]&=0, \end{aligned}$$

(16a)

$$\begin{aligned} \triangle \triangle u_3^\mathrm{\scriptscriptstyle B}- 2 \frac{\varTheta ^2}{\beta ^2} \triangle u_3^\mathrm{\scriptscriptstyle B}-2 \varTheta ^4 \left[ \frac{(\ell _0^\mathrm{\scriptscriptstyle B})^2}{\varTheta ^2\upsilon ^2\beta ^2} \triangle u^\mathrm{\scriptscriptstyle B}_{3,\tau \tau } - \frac{1}{\upsilon ^2\beta ^4}u^\mathrm{\scriptscriptstyle B}_{3,\tau \tau } \right]&=0, \end{aligned}$$

(16b)

where $\triangle$ indicates the two-dimensional Laplace operator in the dimensionless coordinates $\xi _1$ and $\xi _2$ and

$$ \ell _0^{A,B} = \frac{\ell _d^{A,B}}{\ell ^{A,B}} \quad \text{ with } \quad \ell _d^{A,B} = \frac{1}{2} \sqrt{\frac{J^{A,B}}{\rho ^{A,B}}}. $$

3 Analysis in the Frequency Domain

For time-harmonic straight-crested antiplane wave solutions moving in the sagittal plane $(\xi _1,\xi _2)$, it is

$$\begin{aligned} u_3^{A,B}(\xi _1,\xi _2,\tau ) = W^{A,B}(\xi _1,\xi _2) \exp (-\imath \varOmega \tau ), \end{aligned}$$

(17)

being $\imath =\sqrt{-1}$ is the imaginary unit and $\varOmega = \omega T^\mathrm{\scriptscriptstyle A}>0$ the nondimensional frequency. Substituting the solution form (17) into Eqs. (), a pair of meta-biharmonic partial differential equations (PDEs) is arrived at

$$\begin{aligned} \left[ \triangle \triangle - 2 \left( 1-(\ell _0^\mathrm{\scriptscriptstyle A})^2 \varOmega ^2 \right) \varTheta ^2 \triangle -2 \varOmega ^2 \varTheta ^4 \right] W^\mathrm{\scriptscriptstyle A}&= 0, \end{aligned}$$

(18a)

$$\begin{aligned} \left[ \triangle \triangle - 2 \left( 1-\frac{(\ell _0^\mathrm{\scriptscriptstyle B})^2}{\upsilon ^2} \varOmega ^2 \right) \frac{\varTheta ^2}{\beta ^2} \triangle -2 \varOmega ^2 \frac{\varTheta ^4}{\upsilon ^2\beta ^4} \right] W^\mathrm{\scriptscriptstyle B}&= 0. \end{aligned}$$

(18b)

Equation (18a) is easily factored out [13]

$$\begin{aligned} \left( \triangle + {\delta ^2} \right) \left( \triangle - 1 \right) W^\mathrm{\scriptscriptstyle A}= 0, \end{aligned}$$

(19)

having let

$$\begin{aligned} \varTheta ^2 = \frac{\sqrt{\left( 1-(\ell _0^\mathrm{\scriptscriptstyle A})^2 \varOmega ^2\right) ^2+2 \varOmega ^2}-1+(\ell _0^\mathrm{\scriptscriptstyle A})^2 \varOmega ^2}{2 \varOmega ^2}. \end{aligned}$$

(20)

By Vieta’s theorem for polynomials, it is $\delta = 2 \delta _\mathrm{cr}\varTheta ^2$, it being

$$ {\ell _0^\mathrm{\scriptscriptstyle A}}_\mathrm{cr}=\frac{1}{\sqrt{2}}, \quad \text {and} \quad \delta _\mathrm{cr}= {\ell _0^\mathrm{\scriptscriptstyle A}}_\mathrm{cr}\varOmega =\frac{\varOmega }{\sqrt{2}}. $$

Similarly, Eq. (18b) factors as

$$\begin{aligned} \left( \triangle + \delta _1^2 \right) \left( \triangle - \delta _2^2 \right) W^\mathrm{\scriptscriptstyle B}= 0, \end{aligned}$$

(21)

where the dimensionless wavenumbers for bulk travelling and bulk evanescent waves in medium B have been let

$$\begin{aligned} \delta _1^2 = \frac{\delta \psi }{\beta ^2 \upsilon ^2}, \quad \delta _2^2 = \frac{\delta }{\beta ^2 \psi }. \end{aligned}$$

Turning to the boundary conditions, Eqs. (14a) are rewritten in the new symbols

$$\begin{aligned} p_3^\mathrm{\scriptscriptstyle A}&= -\frac{G^\mathrm{\scriptscriptstyle A}}{2 \varTheta ^3} \left[ \left( \delta ^2-1\right) W^\mathrm{\scriptscriptstyle A}_{,2} +(\eta ^\mathrm{\scriptscriptstyle A}+2) W^\mathrm{\scriptscriptstyle A}_{,112}+W^\mathrm{\scriptscriptstyle A}_{,222}\right] , \end{aligned}$$

(22a)

$$\begin{aligned} \bar{q}_1^\mathrm{\scriptscriptstyle A}&=\frac{G^\mathrm{\scriptscriptstyle A}\ell _0^\mathrm{\scriptscriptstyle A}}{\varTheta ^2} \left( W^\mathrm{\scriptscriptstyle A}_{,22}-\eta W^\mathrm{\scriptscriptstyle A}_{,11}\right) , \end{aligned}$$

(22b)

and the same goes with Eqs. (14b)

$$\begin{aligned} p_{3}^\mathrm{\scriptscriptstyle B}&= -\frac{G^\mathrm{\scriptscriptstyle B}}{2 \varTheta ^3} \left\{ \beta ^2 \left[ \left( \eta ^\mathrm{\scriptscriptstyle B}+2\right) W^\mathrm{\scriptscriptstyle B}_{,112}+{W}^\mathrm{\scriptscriptstyle B}_{,222}\right] +\frac{\kappa _2^2}{\upsilon ^2} \left( \frac{\psi ^2}{\upsilon ^2 }-1 \right) {W}^\mathrm{\scriptscriptstyle B}_{,2} \right\} , \end{aligned}$$

(23a)

$$\begin{aligned} \bar{q}_{1}^\mathrm{\scriptscriptstyle B}&=\frac{G^\mathrm{\scriptscriptstyle B}\ell _0^\mathrm{\scriptscriptstyle B}}{\varTheta ^2} \beta ^2 \left( {W}^\mathrm{\scriptscriptstyle B}_{,22}-\eta ^\mathrm{\scriptscriptstyle B}{W}^\mathrm{\scriptscriptstyle B}_{,11} \right) . \end{aligned}$$

(23b)

3.1 Waves Localized at the Half-Spaces’ Interface

Waves propagating at the interface $\xi _2=0$ have the form

$$W^{A,B}(\xi _1,\xi _2) = \ell ^{A,B} w^{A,B}(\xi _2) \exp \left( \imath \kappa \xi _1 \right) ,$$

with $K=k \ell ^\mathrm{\scriptscriptstyle A}$ denoting the dimensionless (spatial) wavenumber in the propagation direction $\xi _1$ and $\kappa =\varTheta K$. The dimensional phase speed in the propagation direction easily follows

$$\begin{aligned} c = \frac{\omega }{k} = \frac{\varOmega }{\kappa }\,\varTheta c_\mathrm{\scriptstyle s}^\mathrm{\scriptscriptstyle A}. \end{aligned}$$

(24)

Providing for decay, waves become localized at the interface

$$\begin{aligned} w^\mathrm{\scriptscriptstyle A}(\xi _2)&= a_1 \exp \left( A_1 \xi _2 \right) + a_2 \exp \left( A_2 \xi _2 \right) , \\ w^\mathrm{\scriptscriptstyle B}(\xi _2)&= b_1 \exp \left( -B_1 \xi _2 \right) + b_2 \exp \left( -B_2 \xi _2 \right) , \end{aligned}$$

with

$$\begin{aligned} A_1&= \sqrt{\kappa ^2-\delta ^2},&A_2&= \sqrt{\kappa ^2+1}, \\ B_1&= \sqrt{\kappa ^2-{\delta _1^2}},&B_2&= \sqrt{\kappa ^2+{\delta _2^2}}. \end{aligned}$$

Branch cuts for the square roots are taken parallel to the imaginary axis in anti-symmetric fashion and the square root is made definite by taking the branch which warrants

$$ \sqrt{s} \rightarrow \sqrt{x}, \quad \text {as} \quad s \rightarrow x \in \mathbb {R}^+. $$

Hereinafter, a superscript asterisk denotes complex conjugation, i.e. given $s=\Re (s)+\imath \Im (s)$, it is $s^*=\Re (s)-\imath \Im (s)$. Let’s define the antiplane Rayleigh function [14]

$$\begin{aligned} R_0(\kappa , \lambda _1,\lambda _2,\eta ) = (\eta \kappa ^2-\lambda _1 \lambda _2)^2 -\lambda _1\lambda _2 \left( \lambda _1 + \lambda _2 \right) ^2, \end{aligned}$$

(25)

that is valid for either half-space. Indeed, for the half-space A, it is $\lambda _{1,2} = A_{1,2}$, $\eta =\eta ^A$, and one may define $R_0^\mathrm{\scriptscriptstyle A}(\kappa ) =R_0(\kappa , A_1,A_2,\eta ^\mathrm{\scriptscriptstyle A})$, to be compared with the corresponding expression in [12, 13]. In similar fashion, for the half-space B, it is $R_0^\mathrm{\scriptscriptstyle B}(\kappa ) =R_0(\kappa , B_1,B_2,\eta ^\mathrm{\scriptscriptstyle B})$.

3.2 Dispersion Relation for Stoneley Waves

It is now possible to deduce the dispersion relation for antiplane Stoneley waves in couple-stress elasticity. To this aim, perfect contact conditions are imposed and a linear system in the amplitudes $a_1, a_2, b_1, b_2$ is arrived at

$$\begin{aligned} w^\mathrm{\scriptscriptstyle A}(0)&=w^\mathrm{\scriptscriptstyle B}(0), \\ \frac{\mathrm {d}w^\mathrm{\scriptscriptstyle A}}{\mathrm {d}\xi _2}(0)&=\frac{\mathrm {d}w^\mathrm{\scriptscriptstyle B}}{\mathrm {d}\xi _2}(0), \\ \bar{q}^\mathrm{\scriptscriptstyle A}_{1}(0)&=\bar{q}^\mathrm{\scriptscriptstyle B}_{1}(0), \\ p^\mathrm{\scriptscriptstyle A}_{3}(0)&=p^\mathrm{\scriptscriptstyle B}_{3}(0). \end{aligned}$$

This homogeneous system system admits non-trivial solutions when the determinant of the linear system vanishes

$$\begin{aligned} \Delta (\kappa ) = 0. \end{aligned}$$

(26)

Equation (26) is the secular (or frequency) equation for Stoneley waves and, letting $\varGamma =G^\mathrm{\scriptscriptstyle B}/G^\mathrm{\scriptscriptstyle A}$, it reads

$$\begin{aligned} \Delta (\kappa ) = \varGamma \beta ^2 \left( A_1-A_2\right) \left( B_1-B_2\right) D_0(\kappa ), \end{aligned}$$

having let

$$\begin{aligned} D_0(\kappa ) = \frac{1}{\varGamma \beta ^2} R_0^\mathrm{\scriptscriptstyle A}(\kappa ) -2 D_1(\kappa ) + \varGamma \beta ^2 R_0^\mathrm{\scriptscriptstyle B}(\kappa ). \end{aligned}$$

(27)

Here, $R_0^\mathrm{\scriptscriptstyle A}(\kappa )$ and $R_0^\mathrm{\scriptscriptstyle B}(\kappa )$ are the Rayleigh functions derived from (25), while $D_1(\kappa )$ is a coupling term

$$\begin{aligned}&D_1(\kappa ) = \left( \eta ^\mathrm{\scriptscriptstyle A}\kappa ^2 -A_1 A_2 \right) \left( \eta ^\mathrm{\scriptscriptstyle B}\kappa ^2 - B_1 B_2 \right) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \quad +\tfrac{1}{2}\left( A_1 A_2+B_1 B_2 \right) \left( A_1+A_2\right) \left( B_1+B_2\right) . \end{aligned}$$

(28)

Equation (27) is the “Rayleigh function” for the antiplane Stoneley problem in CS media, whence it is named the Stoneley function. Its counterpart, within CE elasticity, is given in [6]. When $A=B$, whence

$$\begin{aligned} (\varGamma ,\beta ,\upsilon ,\psi ,\eta ^\mathrm{\scriptscriptstyle k}) = (1,1,1,\delta ,\eta ^\mathrm{\scriptscriptstyle A}=\eta ^\mathrm{\scriptscriptstyle B}), \end{aligned}$$

one simply gets

$$ D_{0,\mathrm \scriptscriptstyle A=B}(\kappa ) = -4 A_1 A_2 (A_1+A_2)^2, $$

which only allows antiplane bulk waves.

Fig. 2.

Cuton frequency as a function of the ratio $\varGamma$ between the shear moduli of media A and B, with the parameter set $\upsilon =\beta =1.1$, $\ell _0^\mathrm{\scriptscriptstyle B}=0.5$, $\eta ^\mathrm{\scriptscriptstyle B}=0.5$ and $\ell _0^\mathrm{\scriptscriptstyle A}=0.3$ (solid, black), $\ell _0^\mathrm{\scriptscriptstyle A}=0.4$ (dotted, blue), $\ell _0^\mathrm{\scriptscriptstyle A}=0.5$ (dashed, red). Transition from an horizontal to a vertical asymptote occurs. The missing part of each curve, as well as the region beyond either asymptote, is due to the breakdown of the condition $\delta >\delta _1$, which is assumed in this plot, see [14] for further details.

3.3 Cuton Frequency for Antiplane Stoneley Waves

The frequency equation (26) admits a cuton frequency, beyond which Stoneley waves may propagate. To see this, it is enough to show that a real root is possible only inasmuch as

$$\begin{aligned} D_0(\delta _M) \ge 0, \end{aligned}$$

(29)

with $\delta _M=\max (\delta ,\delta _1)$. Indeed, for large wavenumbers $\kappa$, one deduces the asymptotics

$$\begin{aligned} D_0(\kappa ) = -\left( 3-\eta ^\mathrm{\scriptscriptstyle B}+ \frac{\eta ^\mathrm{\scriptscriptstyle A}+1}{\beta ^2 \varGamma }\right) \left[ 3-\eta ^\mathrm{\scriptscriptstyle A}+\beta ^2 \varGamma \left( \eta ^\mathrm{\scriptscriptstyle B}+1\right) \right] \kappa ^4 + \dots < 0, \\ \text {as} \quad \kappa \rightarrow \infty . \end{aligned}$$

(30)

Besides, it is observed that, for a given triple $\delta , \delta _1$ and $\delta _2$, $D_0(\kappa )$ is monotonic decreasing (for a proof of this see [14] and the argument principle therein). It is concluded that a single real zero for $D_0$ is possible if condition (29) holds. This condition has a double purpose:

• 1. on the one hand, it may be employed as a propagation condition, which provide the minimum frequency $\varOmega$ beyond which propagation is possible, namely the cuton frequency $\varOmega _{cuton}$;

• 2. on the other hand, given an admissible propagation frequency $\varOmega \ge \varOmega _{cuton}$, it provides the range of stiffness ratios $\varGamma$ for which propagation is possible.

Figure 2 shows the cuton frequency as a function of $\varGamma$, in the assumption $\delta _M=\delta >\delta _1$. Vertical or horizontal asymptotes appear, beyond which the opposite inequality holds, see Fig. 3. For a deeper investigation of the possible propagation scenarios, also concerning existence and uniqueness, see [14].

Fig. 3.

Cuton frequency as a function of the ratio $\varGamma$ for $\upsilon =\beta =1.1$, $\ell _0^\mathrm{\scriptscriptstyle B}=0.5$, $\eta ^\mathrm{\scriptscriptstyle B}=0.5$ and $\ell _0^\mathrm{\scriptscriptstyle A}=0.3$. The solid curve is obtained from (29), assuming $\delta >\delta _1$, while the converse gives the dashed curve

4 Dispersion Curves

Real zeros of Eq. (27) provide travelling wave solutions. Since these sit in the open interval $\kappa > \delta _M$, Stoneley waves are slower than the slowest bulk wave. For instance, assuming $\delta >\delta _1$, then bulk waves in the half-space B are fastest (with wavenumber $\delta _1$) and, as described in [12], they originate the fastest Rayleigh waves (wavenumber $\kappa _{1R}$). Moving down speed-wise, Stoneley waves are met, that are faster than the slowest Rayleigh wave, whose wavenumber is located in close proximity of $\delta$, that is the wavenumber of the slowest bulk waves, the latter taking place in the half-space A. This result has been pointed out in [7] and in [11], without providing a formal proof.

Fig. 4.

Frequency spectrum for antiplane Stoneley waves for $\upsilon =\beta =1.1$, $\ell _0^\mathrm{\scriptscriptstyle A}=0.3 < \ell _0^\mathrm{\scriptscriptstyle B}=0.5$, $\eta ^\mathrm{\scriptscriptstyle B}=0.5$, $\varGamma =0.1$ (solid, black) and $\varGamma =0.3$ (red, dashed). Curves almost overlap but start at widely different cuton frequencies, namely $\varOmega _{cuton}=0.89$ and $\varOmega _{cuton}=2.1$, respectively for $\varGamma =0.1$ and $\varGamma =0.3$

Fig. 5.

Dispersion curves for antiplane Stoneley waves for $\upsilon =\beta =1.1$, $\ell _0^\mathrm{\scriptscriptstyle A}=0.3 < \ell _0^\mathrm{\scriptscriptstyle B}=0.5$, $\eta ^\mathrm{\scriptscriptstyle B}=0.5$, $\varGamma =0.1$ (solid, black) and $\varGamma =0.3$ (red, dashed)

Figure 4 plots the frequency spectrum of antiplane Stoneley waves having taken $\upsilon =\beta =1.1$, $\ell _0^\mathrm{\scriptscriptstyle A}=0.3 < \ell _0^\mathrm{\scriptscriptstyle B}=0.5$ and $\eta ^\mathrm{\scriptscriptstyle B}=0.5$, and $\varGamma =0.1$ and $\varGamma =0.3$. It appears that curves almost overlap, although they start from widely different cuton frequencies. Since curves are clearly non-linear, dispersion occurs. Indeed, the corresponding dispersion curves are plotted in Fig. 5.

5 Conclusions

In this paper, Stoneley waves are investigated within the context of couple stress theory with micro-inertia, in an attempt to incorporate the role of material microstructure into the wave pattern. This consideration brings substantial modification in the propagation pathways, for antiplane Stoneley waves appear to be sustained under broad conditions. This stands in sheer contrast with the state of the matter in classical elasticity, according to which antiplane Stoneley waves are not supported altogether, while in-plane Stoneley waves may propagate under rather restrictive conditions on the material constants of the media in contact, cf. [17]. Indeed, lack of propagation for antiplane waves, that is found in classical elasticity, is relaxed, by consideration of the material microstructure, into propagation beyond a cuton frequency. An explicit expression for the latter is given which may serve either as a propagation condition, that provides the cuton frequency for a given setup, or as an admissibility condition, which restricts the permitted range of material parameters. The dispersion relations is also discussed and reveals a complex wave pattern. The appearance of antiplane Stoneley waves propagating under general conditions possesses important downfalls in many areas. In seismology, it suggests that seismic energy may escape at the boundary between the Earth’s layers. In micro-device design, it provides new pathways for long-range interaction. Finally, in non-destructive testing of materials, it paves the way for novel approaches which rely on non-surface waves that, as such, are capable of capturing defects inside the material.

5.1 Funding

This research was supported under the grant POR FESR 2014-2020 ASSE 1 AZIONE 1.2.2 awarded to the project “IMPReSA” CUP E81F18000310009.