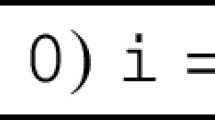Lightweight Nontermination Inference with CHCs

Abstract

Non-termination is an unwanted program property (considered a bug) for some software systems, and a safety property for other systems. In either case, automated discovery of preconditions for non-termination is of interest. We introduce NtHorn, a fast lightweight non-termination analyser, able to deduce non-trivial sufficient conditions for non-termination. Using Constrained Horn Clauses (CHCs) as a vehicle, we show how established techniques for CHC program transformation and abstract interpretation can be exploited for the purpose of non-termination analysis. NtHorn is comparable in power to the state-of-the-art non-termination analysis tools, as measured on standard competition benchmark suites (consisting of integer manipulating programs), while typically solving problems an order of magnitude faster.

1 Introduction

Inference of preconditions for Non-Termination (NT) is of interest in program analysis, debugging and verification. For some systems, the possibility of non-termination is a bug. For other systems, premature termination is unwanted, so that non-termination becomes a safety property.

Non-termination is an archetypal undecidable problem. Assume P ranges over the set of programs expressible in some Turing complete language, and S ranges over (non-empty) sets of inputs to P. Then the problem of whether P fails to terminate on every $s \in S$ is undecidable, and not semi-decidable. This is true even when S is restricted to being a finite non-empty set. Moreover, a proof that P terminates on every element of some set S tells us nothing about P’s behaviour on (subsets of) S’s complement, and in particular it tells us nothing about non-termination. Obviously, absence of a proof of termination is no proof of the absence of termination.

Inferring sufficient conditions for NT is not always possible even for non-terminating programs. For instance, if the variable i ranges over $\mathbb {Z}$, the program can be shown non-terminating by choosing always a non-negative value for i (demonic non-determinism), but no condition on the input i (apart from the trivial false) is sufficient to ensure non-termination. Namely, the loop iteration does not depend on the initial value of i, only on non-deterministic assignments within the loop.

A central tool for proving non-termination is the notion of recurrence set [24], a set of runtime states from which flow of control cannot escape. The non-termination problem is complementary to proving termination; but while a safety violation can be witnessed by a finite trace, a failure to terminate has no such witness. Instead, a witness to non-termination is a path from an initial state to a recurrence set. So we are interested in finding some conditions on the initial state that ensure that such a path occurs.

Although finding preconditions for non-termination is a fundamental problem, it has received far less attention than other termination and non-termination problems (the work of Le et al. [32] is a notable exception). Our approach to the problem is inspired by Chen et al. [10] who reduce the problem to proving safety using a sequence of reachability queries. Let bad states be those that exit the program (or loop) under consideration, and good states those that get stuck in it. Then the problem is to infer preconditions that ensure all executions stay within good states. We achieve this in two steps: (i) compute a necessary precondition from the bad states, whose complement is a potential candidate for non-termination and (ii) refine the candidate with a sufficient precondition from the states that enter the program (loop). Our method is potentially applicable to large code bases, as it rests on relatively cheap program analysis and transformation. To our knowledge, the combination of necessary and sufficient precondition reasoning has not previously been applied to the task.

Fig. 1.

Original program (left) and CHC encoding of its reachable states (right)

Before we present the approach formally, let us consider the example in Fig. 1 (left), a modified version of a program studied by Le et al. [32]. Assume the variables range over the full set $\mathbb {Z}$ of integers. Then the program fails to terminate if the input satisfies $\mathtt {(b > 100 \wedge a \ge 1) \vee (b < 100 \wedge a \ge 1)}$ (equivalently $\mathtt {b \ne 100 \wedge a \ge 1}$). This is because $\mathtt {a}$ and $\mathtt {b}$ are always positive when entering the loop, and the loop condition $\mathtt {a}\ge 1$ is always maintained, as $\mathtt {a}$ increases at a higher rate than $\mathtt {b}$ decreases. Automatic derivation of these preconditions is challenging for at least three reasons:

• (i) The desired result is a disjunction of linear constraints—so we need the ability to express disjunctive information.

• (ii) Abstract interpretation working forward or backward from the goal such as ($\mathtt {a \le 0}$) derives top as invariant for the loop. That is, without a more sophisticated approach, we lose critical information about $\mathtt {a}$ and $\mathtt {b}$.

• (iii) We use over- and under-approximations to obtain sound and precise results, since the precondition must ensure that all traces enter the loop but none exit. While the first part (all traces enter the loop) requires under-approximation, the second part (none exit) can be achieved by negating an over-approximation that exits the loop.

We address Challenge (i) via partial evaluation or control flow refinement, creating a finite number of versions of each predicate—this is essential for deriving disjunctive invariants.

Challenge (ii) is addressed via forward and backward abstract interpretation, together with constraint specialisation. Challenge (iii) is addressed by refining over-approximations with under-approximations (Sect. 4).

While our approach is inspired by the ideas behind HipTNT+ [32], it rests entirely on simpler methods from transformation-based program analysis of Constrained Horn Clauses: control flow refinement via partial evaluation [17], constraint specialisation [27], and clause splitting [19]. We make these contributions:

• We reduce the problem of precondition inference for non-termination to precondition inference for safety using a sequence of reachability queries inspired by the work of Chen et al. [10], which reduces proving non-termination to proving safety.

• We present an enhanced modular algorithm that combines under- and over-approximation techniques based on abstract interpretation and program transformation to derive sound and precise preconditions. It includes a novel mechanism of deriving a more general precondition through iterative refinement, which comes with refined termination criteria (Sect. 4).

• Our method uniformly handles non-linear clauses (arising from modelling function calls, recursion, and nested loops) over linear integer arithmetic.

• A proof of concept is implemented in the tool NtHorn, and we present experiments which show that our prototype implementation is competitive with state-of-the-art tools for automated proof of non-termination (Sect. 5).

2 CHCs, Recurrence Sets and Preconditions

We represent a program as a set of Constrained Horn clauses (CHCs). This is convenient for representing imperative programs and properties such as reachability queries in a uniform way. Analysis of the program and its properties is then done by analysing the corresponding CHCs. The translation of imperative programs to CHCs is standard [16, 23, 25, 36] so we omit the details. From here on, by ‘program’ we mean a program’s CHC encoding, unless otherwise stated.

Constrained Horn Clauses (CHCs). An atom is a formula $p(\mathbf {x})$ with p a predicate symbol and $\mathbf {x}$ a tuple of arguments. A CHC is a first-order formula written $p_0(\mathbf {x}_0) \leftarrow \varphi , p_1(\mathbf {x}_1), \ldots , p_k(\mathbf {x}_k)$, with $\varphi$ a finite conjunction of quantifier-free constraints on variables $\mathbf {x}_i$ wrt. some constraint theory $\mathbb {T}$, and $p_i(\mathbf {x}_i)$ are atoms. A clause $p_0(\mathbf {x}_0) \leftarrow \varphi _1 \vee \varphi _2, \beta$ with a disjunctive constraint is rewritten as $p_0(\mathbf {x}_0) \leftarrow \varphi _1, \beta$ and $p_0(\mathbf {x}_0) \leftarrow \varphi _2, \beta$. A constrained fact is a clause of the form $p_0(\mathbf {x}_0) \leftarrow \varphi$, where $\varphi$ is a constraint. A clause is linear if $k \le 1$, otherwise non-linear. A program is linear if all of its clauses are linear.

Given a clause set P, we assign a unique identifier to each clause in P. Further, we assume the theory $\mathbb {T}$ is equipped with a decision procedure and a projection operator, and that it is closed under negation. The notation $\varphi |_{V}$ represents the constraint formula $\varphi$ projected onto variable set V. $\varphi \models _{\mathbb {T}} \psi$ (or equivalently $\models _{\mathbb {T}}\varphi \Rightarrow \psi$) says that $\varphi$ entails $\psi$ over $\mathbb {T}$. We write $P \vdash _{\mathbb {T}}A$ when an atom A is derivable from program P wrt. an axiomatisation of $\mathbb {T}$. We omit the subscript $\mathbb {T}$ when it is clear from the context.

CHC Encoding. Figure 1 (right) shows the CHC representation of the example, encoding the reachable states. The clause $c_1$ specifies the initial states of the program via the predicate init which is always reachable. Similarly, $c_2$ and $c_3$ encode the reachability of the second if condition via the predicate if. Clauses $c_4$ and $c_5$ encode the reachability of the while loop via the predicate wh. Clause $c_4$ states that the loop is reachable if if is reachable, while $c_5$ states that the loop is (re-)reachable from the end of its own body (recursive case). Clauses $c_6$ and $c_7$ encode the return from the program. Clause $c_6$ states that the program terminates if $\mathtt {a<0}$ upon loop exit, while clause $c_7$ states that the program terminates when $\mathtt {b=0}$ and the control does not satisfy the condition of the second if. The coloured clauses are not part of the program, but are added to aid the analysis. We employ two special predicates en and ex which respectively encode the states entering the loop and exiting the loop or the program. Note that multiple clauses for these predicates are possible given multiple loop entries/exits.

Definition 1

(Initial clauses and nodes). Let P be a program with a distinguished predicate $p^{I}$ which we call the initial predicate. The constrained facts of the form $p^I(\mathbf {x}) \leftarrow \theta$ are the initial clauses of P. We extend the term “initial predicate” and use the symbol $p^I$ to refer also to renamed versions of the initial predicate that arise during clause transformations.

For the program in Fig. 1, $\mathtt {init}$ is the initial predicate and $\mathtt {init(a,b) \leftarrow true }$ is the initial clause. We shall assume integer programs, that is, all variables take integer values. Let $\mathtt {val}: V \rightarrow \mathbb {Z}$ map variables to their values. We overload $\mathtt {val}$ to also map a tuple of variables to the tuple of their values.

A set of CHCs defines a transition system, defined as follows (in the following we shall freely interchange these concepts):

Definition 2

(Transition system). A transition system of a linear program P is a tuple $\mathcal {T}=(S,R,I)$, where

• $S=Pd\times 2^{\mathbb {Z}^{|V|}}$ is the set of states where Pd is the set of predicates of P (including $false$) and V is a finite set of program variables.

• $R \subseteq S \times S$ is a transition relation. There is a transition from $(p,\mathtt {val}(\mathbf {x}))$ to $(p',\mathtt {val}(\mathbf {x'}))$ labelled by c if there is a clause $p'(\mathbf {x'}) \leftarrow \varphi \wedge p(\mathbf {x}) \in P$ with identifier c and if $\mathtt {val}(\mathbf {x}) \models \varphi$ then $\mathtt {val}(\mathbf {x'}) \models \varphi$.

• $I \subseteq S$ is a set of initial states.

Non-termination and Recurrence Set. A transition system $\mathcal {T}=(S,R,I)$ is non-terminating iff there is an infinite sequence $s_0,s_1, s_2\ldots ,$ of states, with $s_0 \in I$ and $(s_i,s_{i+1}) \in R$. Non-termination of a relation R is witnessed by the existence of an (open) recurrence set [24]: a non-empty set $\mathcal {G}$ of states such that (i) $\mathcal {G}$ contains an initial state and (ii) each $s \in \mathcal {G}$ has a successor in $\mathcal {G}$. A program is non-terminating iff its transition system contains a recurrence set [24].

Chen et al. [10] extend the notion to closed recurrence set which facilitates automation using established techniques like abstract interpretation or model checking. A closed recurrence set is an open recurrence set $\mathcal {G}$ with the additional property that, for each $s \in \mathcal {G}$, all of its successors are in $\mathcal {G}$. Our method relies on closed recurrence sets to automate the reasoning.

Preconditions. Given a transition system $\mathcal {T}=(S,R,I)$, we define functions $\mathsf{pre}: 2^S \rightarrow 2^S$, $\mathsf{post}: 2^S \rightarrow 2^S$ and $\widetilde{\mathsf{pre}}: 2^S \rightarrow 2^S$ as follows.

• $\mathsf{post}(S') = \{ s' \in S\mid \exists s \in S': (s, s') \in R \}$ returns the set of states having at least one of their predecessors in the set $S' \subseteq S$;

• $\mathsf{pre}(S') = \{ s \in S \mid \exists s' \in S': (s, s') \in R \}$ returns the set of states having at least one of their successors in the set $S' \subseteq S$;

• $\widetilde{\mathsf{pre}}(S') = \{ s \in S \mid \forall s' \in S: (s, s') \in R \Rightarrow s' \in S' \}$ returns the set of states having all of their successors in the set $S' \subseteq S$.

With these functions, we can now state precondition inference problems.

Invariants. Given a transition system $\mathcal {T}=(S,R,I)$ and a set of initial states $S' \subseteq S$, the invariant inference problem consists of inferring the set of reachable states from $S'$ as $\mathsf{inv}(\mathcal {T},S')=\mathsf{lfp}~\lambda X.\ S' \cup \mathsf{post}(X).$

Necessary Preconditions. Given a transition system $\mathcal {T}=(S,R,I)$ and a goal set $S' \subseteq S$ of states, the necessary precondition inference problem consists of inferring the set of initial states as $\mathsf{nec\_pre}(\mathcal {T},S')=\mathsf{lfp}~\lambda X.\ S' \cup \mathsf{pre}(X)$, which guarantees that some of its executions will stay in $S'$.

Sufficient Preconditions. Given a transition system $\mathcal {T}=(S,R,I)$ and a goal set $S' \subseteq S$ of states, the sufficient precondition inference problem consists of inferring the set of initial states as $\mathsf{suf\_pre}(\mathcal {T},S')= \mathsf{gfp}~\lambda X.\ S' \cap \widetilde{\mathsf{pre}}(X)$, which guarantees that all of its executions will stay in $S'$.

Note that the functions $\mathsf{inv}, \mathsf{nec\_pre}~\text {and}~\mathsf{suf\_pre}$ are not computable in general. Therefore, approximations of these functions are computed instead, which provide “one-sided” guarantees. The state-of-the-art techniques for computing $\mathsf{nec\_pre}$ use over-approximations based on abstract interpretation [12] and are given in [2, 3, 13, 30, 37], while that for computing $\mathsf{suf\_pre}$ use backward under-approximation or negation of some necessary preconditions [28, 34, 35, 37]. In addition, these techniques can profitably be combined with CHC transformations such as [15, 17, 21, 27] to enhance the precision of these analyses.

Example 1

Our approach derives preconditions as follows. First $\lambda _{\texttt {en}}=b\ne 100$ and $\lambda _{\texttt {ex}}=\mathtt {(b \ge 101 \wedge a \le 0) \vee (b \le 99 \wedge a \le 0)}\equiv a\le 0 \wedge b \ne 100$ are found as necessary preconditions for the reachability of en and ex, resp. Now $\lambda =\lambda _{\texttt {en}} ~\wedge ~ \lnot \lambda _{\texttt {ex}} \equiv \mathtt {a\ge 1 \wedge b \ne 100}$ represents the initial states that might reach the loop entry but not the loop exit. We consider $\lambda$ a candidate for sufficient precondition, using that to strengthen the initial clause to $\mathtt {init(a,b) \leftarrow a\ge 1 \wedge b \ne 100}$. Then using backward under-approximation [34] from the goal en, we derive $\mathtt {a\ge 1 \wedge b \ne 100}$ as a sufficient precondition for the reachability of en—which happens to be the optimal precondition for non-termination in this case. If we just used under-approximations without strengthening the initial clauses, we would obtained only $\mathtt {a\ge 1 \wedge b > 100}$ or $\mathtt {a\ge 1 \wedge b < 100}$, and not both.    $\square$

3 CHC Transformations and Their Roles in Non-termination Analysis

We now summarise common CHC transformations that we use, such as partial evaluation, constraint specialisation and clauses splitting. We highlight their role in non-termination analysis. They are goal preserving transformations (or specialisations): given a program P and a goal A, the transformation of P wrt. to the goal A yields another program $P'$ such that $P \vdash _{\mathbb {T}} A$ iff $P' \vdash _{\mathbb {T}} A$. In our setting, the goals are en and ex. Informally, we produce a specialised version of P that preserves the derivations of en and ex, but not necessarily other goals.

1. Partial Evaluation (PE). PE of a set P of CHCs wrt. goal A produces a specialised version of P preserving only those derivations that are relevant for deriving A. It produces a polyvariant specialisation, which is essential for deriving disjunctive information. The partial evaluation algorithm utilised here is an instantiation of the algorithm given in [20], which is parameterised by an “unfolding rule” $\mathsf{unfold}_P$ and an abstraction operation $\mathsf {abstract}_{\varPsi }$.

The unfolding rule $\mathsf{unfold}_P$ takes a set S of constrained facts and “partially evaluates” each element of S, using the following unfolding rule. For each $(p(\mathbf {x}) \leftarrow \theta ) \in S$, first construct the set of clauses $p(\mathbf {x}) \leftarrow \psi ', \beta '$ where $p(\mathbf {x}) \leftarrow \psi ,\beta$ is a clause in P, and $\psi ',\beta '$ is obtained by unfolding $\psi \wedge \theta ,\beta$ by selecting atoms so long as they are deterministic (atoms defined by a single clause) and is not a call to a recursive predicate, and $\psi '$ is satisfiable in $\mathbb {T}$. $\mathsf{unfold}_P$ returns the set of constrained facts $q(\mathbf {y}) \leftarrow \psi '\vert _{\mathbf {y}}$ where $q(\mathbf {y})$ is an atom in $\beta '$.

Given an initial set $S_0$, the closure of the $\mathsf{unfold}_P$ operation can be obtained as $\mathsf{lfp}\ \lambda S.\ S_0\cup \mathsf{unfold}_P(S)$. It is not computable in general; so instead we compute a set $\mathsf {cfacts}(S_0) = \mathsf{lfp}\ \lambda S.\ S_0\cup \mathsf {abstract}_{\varPsi }(\mathsf{unfold}_P(S))$, where the abstraction operation $\mathsf {abstract}_{\varPsi }$ performs property-based abstraction [23] wrt. a finite set of properties $\varPsi$. A set of clauses is then generated by applying $\mathsf{unfold}_P$ to each $\mathsf {cfacts}(S_0)$ and renaming the predicates in the resulting clauses according to the different versions produced by $\mathsf {abstract}_{\varPsi }$. We refer to [21] for more details.

2. Constraint Specialisation (CS). A CS of P wrt. goal A and set $\varPsi$ of properties [27] is a transformation in which each clause $(p(\mathbf {x}) \leftarrow \varphi , \beta ) \in P$ is replaced by $p(\mathbf {x}) \leftarrow \varphi , \underline{\psi }, \beta$ (the difference from the original underlined), where $(p(\mathbf {x}) \leftarrow \psi ) \in \varPsi$, such that the resulting set of clauses preserves the derivation of A. As a result, all paths that are irrelevant for deriving A can be eliminated.

Fig. 2.

PE of Fig. 1 wrt. ex (left) and its CS version (right) with inferred constraints underlined. The last clause on LHS is eliminated since its body is strengthened to $false$.

Example 2

(Continued from Example 1). The program in Fig. 2 (left) is obtained by PE of Fig. 1 wrt. ex. Observe that the recursive clause $\texttt {wh}$ is effectively eliminated, as it cannot contribute to a derivation of ex. The constraint in the initial clauses $\mathtt {b\ge 101 \vee b\le 99 \equiv b\ne 100}$ is a necessary precondition for the reachability of ex. This is further strengthened to $\mathtt {(a \le 0 \wedge b\ge 101) \vee (a \le 0 \wedge b\le 99)}$ $\mathtt {\equiv a \le 0 \wedge b\ne 100}$ with constraint specialisation wrt. ex to Fig. 2 (left), which propagates $\mathtt {a\le 0}$ from the goal ex and $\mathtt {b\ge 101 \vee b\le 99}$ from the constrained facts to other clauses, resulting in the program on the right. Similarly, we obtain $\mathtt {b\ne 100}$ as a necessary precondition for the reachability of en.    $\square$

3. Clause Splitting. Given a clause $(p(\mathbf {x}) \leftarrow \varphi , \beta ) \in P$ and a set $\varPsi$ of properties, clause splitting replaces the clause by $p(\mathbf {x}) \leftarrow \varphi , \underline{\psi }, \beta$ and $p(\mathbf {x}) \leftarrow \varphi ,\underline{\lnot \psi }, \beta$, producing $P'$ (new constraints are underlined), where $(p(\mathbf {x}) \leftarrow \psi ) \in \varPsi$. This embodies case splits, allowing case-based reasoning. Fioravanti et al. [19] use a related technique for splitting clauses to achieve deterministic programs. Unlike the previous transformations, it is goal independent, that is, for all atoms A of P, $P \vdash _{\mathbb {T}} A$ iff $P' \vdash _{\mathbb {T}} A$.

Common to these transformations is the set $\varPsi$ of properties, which determine the quality of the resulting clauses. Soundness of CS also depends on the choice of $\varPsi$. Though the above program transformation techniques are generic for CHCs and are taken from the literature, application or program specific choices of $\varPsi$ that we describe next make them surprisingly effective in practice. In addition to this, our contribution is to put these transformation together and apply them for inferring preconditions for NT, which has not been considered before.

Fig. 3.

Synthetic example

We now discuss the specific choices we make for each of the transformations and illustrate the differences with other choices using the synthetic but representative example shown in Fig. 3.

For PE. The set $\varPsi$ contains the following constrained facts, generated from each clause $p(\mathbf {x}) \leftarrow \varphi ,p_1(\mathbf {x_1}),\ldots ,p_n(\mathbf {x_n}) \in P$.

• $p(\mathbf {x}) \leftarrow \varphi \vert _\mathbf {x}$ and for each $z \in \mathbf {x}$, $p(\mathbf {x}) \leftarrow \varphi \vert _{\{z\}}$

• for $1 \le i \le n$, $p_i(\mathbf {x_i}) \leftarrow \varphi \vert _{\mathbf {x_i}}$ and for each $z \in \mathbf {x_i}$, $p_i(\mathbf {x_i}) \leftarrow \varphi \vert _{\{z\}}$.

The effect of property-based abstraction using this choice for $\varPsi$ is to create a finite number (at most $2^{\vert \varPsi \vert }$) of versions of a predicate for different call contexts and answer constraints. This choice of $\varPsi$, obtained syntactically from the program, has been found to provide a good balance of speed and precision.

Fig. 4.

PE of Fig. 3 wrt. ex; respective $\varPsi$s are shown in upper part

Example 3

Figure 4 shows PE programs for the program P in Fig. 3 wrt. ex with two different choices of the set of properties $\varPsi$. $\varPsi$ in Fig. 4 (left) are computed as described above, while on the right are computed as follows: $\varPsi = \bigcup _{(p(\mathbf {x}) \leftarrow \varphi ,B) \in P} \{p(\mathbf {x}) \leftarrow \varphi \vert _\mathbf {x} \}$. The purpose here is to show that the choice of $\varPsi$ is important in getting a right specialisation. The program on the left is an empty program since there is a vacuous base case ($\mathtt {p_1(a,b) \leftarrow false }$), while the program on the right is identical to the original (no specialisation was performed).    $\square$

For CS. The properties $\varPsi$ have to be invariants for the program to produce sound transformation. They can be obtained e.g., via forward (from the constrained facts) or backward (from the goal) abstract interpretation or their combination [3]. In our case, they are obtained from forward abstract interpretation of the query-answer transformed program [27]. $\varPsi$ thus obtained analysing the program produces sound transformation, which is also found to be precise.

Example 4

Forward analysis of the program in Fig. 3 yields $\mathtt {p(a,b) \leftarrow a \ge b}$ as invariant for $\mathtt {p(a,b)}$. This is because (i) if $c_2$ is not taken then we have $\mathtt {a=b}$ from $c_1$ and obviously $\mathtt {a \ge b}$ holds, (ii) if $c_2$ is taken then $\mathtt {a>0}$ is maintained since $\mathtt {a}$ is incremented by b in each iteration and we initially had $\mathtt {a=b}$. Since $\mathtt {b}$ is not modified in $c_2$, $\mathtt {a \ge b}$ holds. We now use $\varPsi =\{ \mathtt {p(a,b) \leftarrow a \ge b} \}$ to specialise the program in Fig. 3 wrt. ex, obtaining the clauses $c_1$, $\mathtt {p(b+c,b) \leftarrow a>0, \underline{a\ge b}, p(c,b)}$ and $\mathtt {\texttt {ex}\leftarrow a<b,\underline{a\ge b}, p(a,b)}$. Note that the last clause is trivially satisfied. Instead of applying forward or backward analysis in isolation, applying forward-backward analysis will immediately detect that $\mathtt {p(a,b) \leftarrow false }$, and the subsequent specialisation using the result yields an empty program.    $\square$

For Clause Splitting. We describe some heuristics specific to (non-)termination analysis, requiring separation of terminating and non-terminating computations. The targets are recursive clauses (loops) $p(\mathbf {x'}) \leftarrow \varphi , p(\mathbf {x})$. (i) Given a loop, a potential ranking function for the loop is an expression $e(\mathbf {x})$ over variables $\mathbf {x}$ which is non-negative (bounded from below) but not necessarily decreasing from $p(\mathbf {x})$ to $p(\mathbf {x'})$. In this case, we choose the property $\{p(\mathbf {x}) \leftarrow e(\mathbf {x}) > e(\mathbf {x'}) \}$ (see Example 5). (ii) The property $\{p(\mathbf {x}) \leftarrow x \ge 0 \mid x \in \mathbf {x}, \models _{\mathbb {T}} \varphi \wedge x\ge 0\}$ is useful when we have non-deterministic branches or assignments; but care needs to be taken to control the blow-up of clauses.

Example 5

Taking $\mathtt {p(a,b) \leftarrow a=b}$ to be the initial clause of the program in Fig. 3, the program does not terminate; e.g., for input $\mathtt {a=1,b=1}$. Below we apply clause splitting which reveals which clause causes non-termination. The expression a is a potential ranking function for the loop, as it is non-negative and not necessarily decreasing. We derive $\varPsi =\{\mathtt {p(a,b) \leftarrow a+b <a} \}$. Now splitting $\mathtt {c_2}$ with $\varPsi$ yields $\mathtt {c_{2a}}$: $\mathtt {p(a+b,b) \leftarrow a>0, \underline{b<0}, p(a,b)}$ and $\mathtt {c_{2b}}$: $\mathtt {p(a+b,b) \leftarrow a>0, \underline{b \ge 0}, p(a,b)}$ (the new constraints are underlined). Such a splitting guarantees that every infinite run of the program must use $\mathtt {c_{2b}}$ as suffix. This information can be exploited by (non-)termination analysers.    $\square$

4 An Algorithm for Conditional Non-termination

We now present an algorithm for inferring sufficient preconditions for non-termination. The main method is Algorithm 1. As a program can only get stuck in loops or recursive code, and the translation to CHCs replaces loops with recursion, the analysis focuses on the recursive strongly connected components (SCCs) in the CHC dependency graph. As the first step, we compute the SCCs of the input set P of CHCs. Each component is a set of (non-constraint) predicates, which is either non-recursive or a set of (possibly mutually) recursive predicates. The algorithm for computing SCCs returns the components in topologically sorted order $S_1, \ldots ,S_n$, such that for each $S_i$, no predicate in $S_i$ depends on any predicate in $S_j$ where $j > i$. Then it annotates the program with appropriate reachability queries and computes a sufficient precondition for each annotated program using Algorithm 2 in a modular way. These preconditions are combined disjunctively to yield the overall result. The function $\mathsf{annotate\_program}(P,C)$ inserts two sets of clauses to P given an SCC C as follows.

$$ \begin{array}{l} \{ \texttt {en}\leftarrow \varphi _{\mid _{\mathsf {vars}(\beta )}}, \beta \mid (H \leftarrow \varphi , \beta ) \in P, \mathsf {pred}(H) \in C, \forall a\ (a \in \mathsf {pred}(\beta ) \Rightarrow a \not \in C)\} \\ \cup ~\{ \texttt {ex}\leftarrow \varphi _{\mid _{\mathsf {vars}(\beta )}}, \beta \mid (H \leftarrow \varphi , \beta ) \in P, \mathsf {pred}(H) \not \in C, \forall a\ (a \in \mathsf {pred}(\beta ) \Rightarrow a \in C)\} \end{array} $$

where $\mathsf {pred}(H)$ is the predicate symbols of H and $\mathsf {pred}(\beta )$ is the set of predicate symbols in $\beta$. The special clauses for $\texttt {en}$ encode the reachability of C in P while the clauses for $\texttt {ex}$ encode the exit condition of C in P. We explore all SCCs with the aim of obtaining a more general precondition but for proving non-termination it suffices to find a non-trivial precondition for an SCC.

Example 6

For the program in Fig. 1, there is a single SCC, namely the one containing the predicate $\{ \mathtt {wh} \}$. The clauses $\mathtt {c_8}~\mathrm {and}~\mathtt {c_9}$ respectively encode the reachability of the entry and exit of this SCC.    $\square$

Algorithm 2 takes as input and annotated program P (with clauses for $\texttt {en}$ and $\texttt {ex}$); it returns a sufficient precondition for non-termination (a linear constraint over $\mathbb {T}$ in DNF). Recall that we derive preconditions in two steps: (i) compute a necessary precondition from the bad states, encoded by the predicate ex, whose complement is a potential candidate for non-termination and (ii) refine the candidate with a sufficient precondition from the states that enter the loop, encoded by the predicate en. Let us first focus on step (i), the generation of necessary preconditions, using backward over-approximating analysis. Since these conditions need to be negated to derive candidates, their precision is important. It is well known that program specialisations, possibly applied iteratively [28] can enhance (refine) precision of such analysis. A disadvantage of this is the blind refinement of states possibly exiting the loop without knowing its frontier with the states entering it. This misses opportunities to avoid redundant computation as well as to guide the refinement process at an early stage. We therefore choose to maintain two over-approximations, namely of the states entering the loop ($\lambda _{\texttt {en}}$) and of the states exiting it ($\lambda _{\texttt {ex}}$). We iteratively refine these (See Algorithm 2). This enables the use of over-approximating analyses which are more developed than their under-approximating counterparts. Further, step (ii) is only applied to strengthen the candidate $\lambda =\lambda _{\texttt {en}} \wedge \lnot \lambda _{\texttt {ex}}$ to a sufficient condition. This is achieved by applying under-approximating analysis to $\mathsf{replace\_init}(P,\lambda )$ instead of the original P, so as to retain refined initial condition $\lambda$ derived from the analysis of step (i).

Definition 3

($\mathsf{replace\_init}(P,\lambda )$)). Let P be a program and $\lambda$ a constraint over $\mathbb {T}$. The function replace_init returns clauses of P by replacing the initial clauses $\{(p^I(\mathbf {x}) \leftarrow \theta _i) \mid 1 \le i \le k\}$ by $\{(p^I(\mathbf {x}) \leftarrow \lambda )\}$.

Algorithm 2. The variable $\sigma _{nt}$ accumulates the result and is initialised to $false$. $\varphi _{old}$ keeps track of the initial states that could reach both en and ex; it is initialised to $true$ (line 3). The following operations are carried out within the while loop. The formulae $\lambda _{en}$ and $\lambda _{ex}$ (line 5 and 6) represent the set of initial states that can reach en and ex, resp., and are computed using the method nec_pre. The algorithm returns when (i) no initial state can reach en ($\lambda _{en} \equiv false$) (line 8), or (ii) the initial states satisfying $\varphi _{new}=\lambda _{en} \wedge \lambda _{ex}$ that can reach both en and ex amount to $false$, or the set of initial states does not shrink further from its previous value $\varphi _{old}$ (line 14). The set of states captured by $\varphi _{new}$ is an over-approximation. The algorithm aims to reduce the slack as much as possible, to be able to separate terminating traces from non-terminating ones. To this end it (i) constructs a revised program from P focusing only on the shared region and (ii) shrinks either of the regions ($\lambda _{en}, \lambda _{ex}$) via iterative specialisations. We construct the revised program as follows.

Definition 4

($\mathsf{constrain\_init}(P,\varphi )$). Let P be a program and $\varphi$ a constraint over $\mathbb {T}$. constrain_init returns the clauses of P by replacing the initial clause set $\{(p^I(\mathbf {x}) \leftarrow \theta _i) \mid 1 \le i \le k\}$ by the set $\{(p^I(\mathbf {x}) \leftarrow \varphi \wedge \theta _i) \mid 1 \le i \le k\}$.

Proposition 1

$\mathsf{constrain\_init}(P,\varphi )$ is an under-approximation of P.

Proof

(Sketch). $P_1 = \mathsf{constrain\_init}(P,\varphi )$ contains exactly the same clauses as P, except for the initial clauses, which are possibly constrained. Hence for all atoms A, if $P_1 \vdash _{\mathbb {T}} A$ then $P \vdash _{\mathbb {T}} A$. That is, $P_1$ is an under-approximation of P.

Since non-termination is preserved by under-approximation [10], we need to ensure that the precondition does as well. This is in fact the case given that these program only differ in their initial clauses. Thus, any initial state that definitely reaches en and stays in the loop of $P_1$ also does the same in P. Before formally stating this property, let us first define (in terms of CHCs) what it means for a program P to have $\varphi$ as a sufficient precondition for NT.

Definition 5

(Sufficient precondition for CHCs). Let P be a program annotated with appropriate reachability queries (for en and ex) as described above and $\varphi$ a constraint over $\mathbb {T}$. Let $P_1=\mathsf{replace\_init}(P, \varphi )$. Then we say $\varphi$ is a sufficient precondition for NT of P if $\varphi \rightarrow (P_1 \vdash _{\mathbb {T}} \texttt {en}\wedge P_1 \not \vdash _{\mathbb {T}} \texttt {ex})$.

Proposition 2

(Lifting sufficient conditions). If $\varphi$ is a sufficient precondition for non-termination of $\mathsf{constrain\_init}(P,\sigma )$ (for some $\sigma$) then it is also a sufficient precondition of P.

Proof

(Sketch). Let $P_1=\mathsf{constrain\_init}(P, \sigma )$. Since $P_1$ and P have identical clauses except for the initial clauses, $\mathsf{replace\_init}(P_1, \varphi )$ and $\mathsf{replace\_init}(P, \varphi )$ yield identical clauses. So $\varphi$ is also a sufficient precondition of P (Definition 5).    $\square$

Note the initial states satisfying the formula $(\lambda _{en} \wedge \lnot \lambda _{ex})$ may reach en but definitely not ex, so they are seen as potential candidates for non-termination. The candidates are then strengthened to sufficient preconditions ($\sigma _{en}$) using the method suf_pre (line 12). If $\sigma _{en} \equiv false$, then either all traces of $P_1$ (line 11) are terminating or suf_pre loses precision. Observe that we use $\mathsf{replace\_init}(P,\lambda )$ (computed from P and $\lambda$ using Definition 3) where $\lambda =\lambda _{en} \wedge \lnot \lambda _{ex}$ instead of P to limit our attention to those initial states that can reach en. If no termination criterion is satisfied, the algorithm repeats (line 18) with $\mathsf{constrain\_init}(P,{\varphi _{new}})$ (Definition 4) since the states that satisfy $\varphi _{new}$ are the ones whose termination status is unknown so far. Note that the construction of $\mathsf{constrain\_init}(P,{\varphi _{new}})$ requires $\varphi _{new}$ to be converted to DNF, which may blow up the number of resulting initial clauses, but in our experiments we have not observed that.

Soundness and Termination of the Algorithms. We now study some properties, including soundness and termination of the Algorithms 1 and 2.

All the components used in Algorithm 2 terminate, but the algorithm itself may not, owing to the fact that $\varphi _{new}$ can be decreased indefinitely (the algorithm keeps refining). This is typical of algorithms for undecidable problems such as non-termination. So we want to ensure a weaker property, that is, of progress. Progress is made, in the sense that each iteration explores a strictly smaller set of initial states whose termination status are not yet known. We state this formally:

Proposition 3

(Progress and Termination of Algorithm 2). Algorithm 2 either terminates or progresses.

Proof

(Sketch). By induction on the number of iteration of the while loop.

Progress. Let $\varphi _{old}$ and $\varphi _{new}$ be formulas characterising the set of initial states yet to be proven non-terminating at each successive iteration respectively. Note that the algorithm iterates only if $\varphi _{new} \models \varphi _{old}$ and $\varphi _{old} \not \models \varphi _{new}$, that is, if $\varphi _{new}$ is strictly smaller than $\varphi _{old}$, in the set view.

Termination. Note that each individual operation in the loop, including nec_pre, which is computed using abstract interpretation and program transformations, terminate. The only condition under which the algorithm diverges is when $\varphi _{new}$ is strictly smaller than $\varphi _{old}$; in this case the algorithm progresses.    $\square$

Observe that each iteration of Algorithm 2 computes a valid precondition for non-termination of P even when under-approximations are used (Proposition 2). The disjunctive combination of such preconditions is also a valid precondition for non-termination of P. Again, we state this as a proposition.

Proposition 4

(Composing Preconditions). Let $\varPhi$ be a set of formulas such that each $\varphi \in \varPhi$ is a sufficient precondition for non-termination of P. Then so is $\bigvee \varPhi$.

Proof

(Sketch). $\bigvee \varPhi$ satisfies the condition of Definition 5.    $\square$

Proposition 5

(Soundness of Algorithm 2). Let P be a program. If Algorithm 2 returns $\sigma$ for P, then $\sigma$ is a sufficient precondition for non-termination of P.

Proof

(sketch). This follows from Proposition 2 and 4, with Definition 5: At each iteration the algorithm computes a formula that satisfies the condition of Definition 5 (the formula is a sufficient precondition). Proposition 2 allows us to lift any such formula computed for $\mathsf{constrain\_init}(P,\varphi )$ (for some $\varphi$) to P itself, and Proposition 4 allows us to disjunctively combine such formulas to a valid precondition for P.    $\square$

The program shown here does not terminate when $\mathtt {x\ne 0}$. On input $\mathtt {x>0}$ it gets stuck in the first loop, on $\mathtt {x<0}$ in the second. Generally, a program P with n loops may get stuck in loops $l_1, \ldots , l_n$, resp., on input satisfying formulas $\varphi _1, \ldots , \varphi _n$. If each such $\varphi _i$ is a sufficient precondition for non-termination of P, then so is $\bigvee _{i=1}^{n} \varphi _i$. Taken together, Proposition 4 and 5 ensure the correctness of Algorithm 1:

Theorem 1

(Soundness of Algorithm 1). Let P be a program. If Algorithm 1 returns $\sigma$ for P, then $\sigma$ is a sufficient precondition for non-termination of P.

Corollary 1

If $\varphi \not \equiv false$ is a precondition for non-termination of a program P, then P is non-terminating.

Proof

(Sketch). $\varphi \not \equiv false$ implies there is at least an input (satisfying $\varphi$) to P on which it does not terminate.    $\square$

If Algorithm 1 returns $false$ for P, then P’s non-termination status is unknown.

5 Implementation and Experiments

Implementation. We implemented Algorithm 1 as a prototype tool, NtHorn, available from https://github.com/bishoksan/NtHorn.git. It is written in Ciao Prolog [8] and uses PPL [1] and Yices 2.2 [18] for constraint manipulation. While refinement of candidate preconditions to the sufficient ones can be done with a tool such as [34], currently the implementation uses a simpler approach, namely, the reachability of the respective loop entry from each candidate—using the safety prover Rahft [29]. This gives a proof of non-termination as well as some conditions on the initial states and is used in the experiments. NtHorn handles integer programs only (the classical setting for (non-)termination work [10]), but our techniques apply beyond integer arithmetic.

We rely on abstract interpretation and CHC transformations for inferring sound and precise necessary preconditions. In particular, our implementation performs forward and backward constraint propagation using the constraints derived from polyhedral abstraction [14] obtaining a specialised version of the program [27]. To enhance the precision of the analysis further, we apply a sequence of program transformations including control-flow refinement using partial evaluation [21], clause splitting, strengthening of initial clauses, and we iteratively refine necessary preconditions for entering and exiting a loop.

Experimental Setting. We evaluated the approach on benchmarks from the C_Integer category of TermComp’20 [38]. The benchmark suite consists of 335 programs with nondeterminism: 111 non-terminating, 223 terminating, and one (Collatz) for which termination is unknown. Evaluation was done on 111 non-terminating programs, ignoring the terminating ones, as NtHorn can only prove non-termination. These are typical loop programs (simple or nested) with branches. Some of these loops have non-deterministic conditions while others contain non-deterministic assignments. We used small-step encoding to translate them to CHCs, obtaining only linear clauses. We run several configurations of NtHorn, namely NtHorn(X) where X can be partial evaluation pe, constraint specialisation cs, clause splitting csp, or some combination. Then we compare against state-of-the-art (non)-termination tools that participated in this category: AProVE [22], iRankFinder [5], UltimateAutomizer [26] and VeryMax [31]. We used TermComp’20 versions of these tools. We add HipTNT+ [32] (http://loris-7.ddns.comp.nus.edu.sg/~project/hiptnt/plus/), as it shares with NtHorn’s the ability to infer preconditions. We run several configurations of NtHorn to study the impact of different CHC transformations. Since we could not run iRankFinder due to some front-end issues, we took the evaluation results from StarExec [38].

Experiments were performed on a MacBook Pro, 2.7 GHz Intel Core i5 processor, 16 GB memory, running OS X 10.11.6. Timeout was 300 s (the competition standard) per instance. The results are shown in Table 1. The three last columns show, in order, the number of programs proved non-terminating, the number given up within 300 s or timeout, and the average time taken by all instances including the “gave up” instances. Among the tools, NtHorn and HipTNT+ are the only tools capable of deriving a precondition. It would be interesting to compare the generality of the preconditions inferred by our tools. But we could not do so due to the difference in our (non-standard) output formats. So with these experiments, we seek to answer the following questions:

• Q1. Will the proposed method allow us to derive non-termination preconditions (or prove non-termination) in practice?

• Q2. How does it compare to state-of-the-art tools for proving non-termination?

• Q3. What role do the CHC transformations play?

Table 1. Experimental results on the TermComp’20 (C_Integer) suite.

Results. The results show different profiles wrt. to solved instances and performance for the tools. AProVE (resp. VeryMax), the category winner in 2020 (resp. 2019), solves two (resp. four) instances more than NtHorn, while the rest solve less. This shows a remarkable effectiveness of our particular combination of mostly off-the-shelf techniques. The configuration NtHorn(cs) solves only 58 instances, while NtHorn(cs $\cdot$ pe) solves 94. The best result is achieved with NtHorn(cs $\cdot$ pe $\cdot$ csp). We find that each component transformation has a positive impact. Not only can we solve more problems (at the cost of solving time), we also generate more general preconditions. The combination cs $\cdot$ pe $\cdot$ csp has been chosen based on experiments, but its effectiveness aligns with our intuition. Namely, csp derives new domain specific constraints that pe can take advantage of during polyvariant specialisation, and cs, which is based on abstract interpretation, greatly benefits from the resulting specialised form.

As for speed, NtHorn(cs $\cdot$ pe $\cdot$ csp) (from here on “NtHorn”) is an order of magnitude faster than the alternatives, solving each case in less than a second, while giving up on 13 cases. The median time was 1 s, while the instance such as NO_04 with 5-level of nesting and Lcm resp. took 135 and 58 s and a few other took slightly more than a second. We believe the speed is due to abstract interpretation (which in this context is relatively efficient), together with the lightweight program transformation. Also, unlike other tools, NtHorn focuses on proving just non-termination. Among the 13 cases, NtHorn fails to handle LogMult and DoubleNeg because they involve non-linear operations. They are proved non-terminating only by iRankFinder. The cases Narrowing and NarrowKonv are shown non-terminating only by NtHorn, VeryMax and HipTNT+, while ChenFlurMukhopadhyay-SAS2012-Ex2.11 only by NtHorn and HipTNT+. NtHorn could not generate preconditions for 4 programs. These programs contain non-deterministic assignments that affect loop conditions; it might be possible that sufficient preconditions do not exist for them, though they can be shown terminating, as discussed in Sect. 1.

In summary, the results answer Q1–Q3 positively. NtHorn can be used to derive preconditions for NT and is comparable in power to the leading non-termination analysis tools, when applied to integer programs. Notably, NtHorn solves problems several orders of magnitude faster than the state-of-the-art analyzers and CHC transformations play an important role in this.

A new non-termination prover, RevTerm [9] was published recently and has not been part of our tool comparison. Like NtHorn, it does not prove termination. The experimental evaluation [9] suggests that its precision (for non-termination) is on a par with that of VeryMax, but obtained 2–3 times faster. Comparison data from the paper [9] are in agreement with what we have found, for both precision and performance (they use a timeout of 60 s, rather than 300, so the average running times reported are somewhat shorter.)

6 Related Work

There is a rich body of work on proving non-termination, e.g., [2, 7, 10, 11, 24, 31, 32, 39]. Most of these provers either provide a stem (a sequential part from entry to loop) and the loop, or some precondition from which there exists a non-terminating run as a witness to non-termination. But for some applications like web-servers, a sufficient precondition (under which no trace is finite) is more useful. To our knowledge, prior to NtHorn, HipTNT+ [32] was the only tool able to infer sufficient conditions for non-termination. Le et al. [32] propose a specification logic and Hoare-style reasoning to infer sufficient preconditions for both termination and non-termination of programs and, unlike ours, can handle programs manipulating pointers. We infer preconditions for non-termination only, relying on reduction to precondition inference for safety. But our approach is considerably simpler, as we combine existing techniques, refined iteratively.

Many non-termination provers [22, 24, 26, 39] search exhaustively for candidate lassos (simple while loops without branches), and attempt to prove non-termination by deriving a recurrence set using constraint solving [22, 24, 39] or automata based approaches [26]. An orthogonal approach [33] considers lassos with linear arithmetic and represents infinite runs as geometric series.

We exploit the notion of closed recurrence set [10] as it is useful not only for automation using a safety prover, but also for proving non-termination of non-deterministic programs and programs involving aperiodic non-termination. The method of Chen et al. [10] inserts appropriate reachability queries and uses a safety prover to eliminate terminating paths iteratively until it finds a program under-approximation and a closed recurrence set in it. The method is likely to diverge as there can be infinitely many terminating paths. Hence we use abstract interpretation to derive initial conditions that lead to the terminating paths. We negate the conditions to bar those paths. Similar to our approach, the method [31] (implemented in VeryMax [6]) searches for witnesses to non-termination in the form of quasi-invariants (sets of states that do not exit the loop once entered) whose reachability from initial states is checked using a safety prover. Where VeryMax infers such invariants using Max-SMT solving, we do it using abstract interpretation.

Chatterjee et al. [9] rely on syntactic program reversal (applicable only to while programs; corresponding to linear CHCs) to derive backward polynomial conjunctive invariants using off-the-shelf tools and prove NT. Our method is more generally applicable to programs with procedures and can also infer preconditions as disjunction of linear constraints. Unlike our method, theirs provides relative completeness guarantees, that is, it is guaranteed to find the proof of NT under certain conditions. Bakhirkin [2], as we do, uses forward and backward abstract interpretation to find potential recurrence sets whose reachability implies non-termination. The approach can be applied to heap manipulating programs but is limited to simple while program. Ben-Amram et al. [4] derive a recurrence set from a failed attempt to prove termination of multi-phase loops, while our approach is direct and only proves non-termination.

While the above methods target programs with linear arithmetic, Cook et al. [11] prove non-termination of programs with non-linear arithmetic and heap-based operations. The key is the notion of live abstraction, an abstraction heuristic that ensures that any abstract trace corresponding to a terminating concrete trace is also terminating. In other words, it does not introduce any non-termination and is a sound abstraction heuristic for non-termination. This allows over-approximating non-linear assignments and heap-based commands with non-deterministic linear assignments.

7 Concluding Remarks

We have presented a new approach to preconditions for non-termination. The problem is reduced to inference of preconditions for safety, via insertion of “reachability queries” in program loops. The reduction enables us to use existing tools and techniques for safety preconditions. A prototype implementation is competitive with the state-of-the-art tools for automated proof of non-termination.

NtHorn can only infer preconditions for non-termination and is limited to programs manipulating linear integer arithmetic, whose applicability is determined by the underlying tool for inferring preconditions for safety. In future, we plan to complement it with termination analysis as done in other tools and also extend to programs that manipulate structured data, a la Cook et al. [11].