Abstract
A quantum bit commitment scheme is to realize bit (rather than qubit) commitment by exploiting quantum communication and quantum computation. In this work, we study the binding property of the quantum string commitment scheme obtained by composing a generic quantum perfectly(resp. statistically)-hiding computationally-binding bit commitment scheme (which can be realized based on quantum-secure one-way permutations(resp. functions)) in parallel. We show that the resulting scheme satisfies a stronger quantum computational binding property, which we will call predicate-binding, than the trivial honest-binding. Intuitively and very roughly, the predicate-binding property guarantees that given any inconsistent predicate pair over a set of strings (i.e. no strings in this set can satisfy both predicates), if a (claimed) quantum commitment can be opened so that the revealed string satisfies one predicate with certainty, then the same commitment cannot be opened so that the revealed string satisfies the other predicate (except for a negligible probability).
As an application, we plug a generic quantum perfectly(resp. statistically)-hiding computationally-binding bit commitment scheme in Blum’s zero-knowledge protocol for the NP-complete language Hamiltonian Cycle. This will give rise to the first quantum perfect(resp. statistical) zero-knowledge argument system (with soundness error 1/2) for all NP languages based solely on quantum-secure one-way permutations(resp. functions). The quantum computational soundness of this system will follow immediately from the quantum computational predicate-binding property of commitments.
The full version of this paper is referred to [35].
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Cryptographic protocols
- Quantum bit commitment
- Quantum computational binding
- Parallel composition
- Quantum zero-knowledge argument
1 Introduction
Bit commitment is an important cryptographic primitive; it can be viewed as an electronic realization of a locked box [16]. Roughly speaking, a bit commitment scheme is a two-stage (consisting of a commit stage and a reveal stage) interactive protocol between a sender and a receiver, providing two security guarantees: hiding and binding. Intuitively, the hiding property states that the commitment to 0 and that to 1 are indistinguishable (to the receiver) in the commit stage, whereas the binding property states that any (claimed) bit commitment cannot be opened (by the sender) as both 0 and 1 (except for a negligible probability) later in the reveal stage. Unfortunately, hiding and binding properties cannot be satisfied information-theoretically at the same time; one of them has to be conditional, e.g. based on complexity assumptions such as the existence of one-way functions.
Turning to the quantum setting, there are two different meanings of quantum bit commitment in the literature (depending on the context). The first refers to the classical realization of bit commitment that is secure against quantum attacks, or the post-quantum secure (classical) bit commitment [1, 31, 32]. The second refers to a realization of bit commitment by exploiting quantum features [4, 7, 8, 10, 11, 14, 15, 23, 24, 34, 36]; that is, now the honest parties are allowed to be quantum computers and exchange quantum messages. (But it is still a classical bit that is secured.) Clearly, the first meaning of quantum bit commitment can be viewed as a special case of the second one. In this paper, the term “quantum bit commitment" will be reserved for the second, more general meaning, which will also be the focus of this work.
The concept of quantum bit commitment is natural and sounds exciting. Though unconditional quantum bit commitment is still impossible [25, 27], as a compromise we may consider quantum bit commitment based on complexity assumptions like in the classical cryptography. Somewhat counter-intuitive at the first glance, but the binding property of a general quantum bit commitment is inherently weaker than the classical binding property (that is guaranteed by a classical bit commitment secure against classical attacks, which roughly states that any claimed bit commitment is bound to a unique bit that is typically referred to as the committed value). In more detail, this weakness of the general quantum binding property comes from the possible superposition attack of the sender of the quantum bit commitment, who may commit to an arbitrary superposition of bits 0 and 1, and later open the commitment as this superposition (rather than a classical 0 or 1) successfully with certainty [10, 14]. By this kind of quantum superposition attack, a fixed quantum bit commitment is no longer bound to a unique classical bit any more. The quantum binding property that can be guaranteed by a general quantum bit commitment is often referred to as sum-binding (named after [31]).
Difficulties in Basing Security on Quantum Binding. It is natural to ask what happen if we replace classical bit commitment with quantum bit commitment in cryptographic applications. Due to the weakness of the general quantum binding property as aforementioned, the security based on the classical binding property may deteriorate after the replacement.
In greater detail, note that in applications we typically commit to a binary string by committing it in a bitwise fashion; later, a subset of bit commitments may be opened for some verification. For example, it is helpful to keep GMW-type zero-knowledge protocols [5, 17] in one’s mind. When quantum bit commitments are used, we can no longer say that a claimed quantum commitment to an m-bit string is really bound to some m-bit string; instead, the committed value of such a quantum string commitment could be a superposition of a bunch of m-bit strings of the form  , where the integer \(m \ge 1\) and complex coefficients \(\alpha _s\)’s satisfy \(\sum _{s \in \{0,1\}^m} \left| \alpha _s \right| ^2 = 1\). One may tend to argue in security analysis that this superposition behaves similar to its induced probability distribution \((\left| \alpha _s \right| ^2)_{s \in \{0,1\}^m}\): if this is true, then the classical security analysis extend to the quantum setting straightforwardly. Unfortunately, this argument is not necessarily true, because a superposition is generally not equivalent to its induced probability distribution; in fact, this is usually where the quantum advantage comes from in algorithm design. Actually, if one goes into detail of the security analysis, one will find that a malicious quantum sender of commitments may attack by making the opening information (which is entangled with quantum commitments and their decommitments) about which bit commitments will be opened as what value in an arbitrary superposition. By tuning this superposition, the sender may adjust the receiver’s acceptance probabilities in different verifications. This kind of superposition attack will make the security analysis based on the general quantum binding property (if possible) much harder than that based on the classical binding property.
, where the integer \(m \ge 1\) and complex coefficients \(\alpha _s\)’s satisfy \(\sum _{s \in \{0,1\}^m} \left| \alpha _s \right| ^2 = 1\). One may tend to argue in security analysis that this superposition behaves similar to its induced probability distribution \((\left| \alpha _s \right| ^2)_{s \in \{0,1\}^m}\): if this is true, then the classical security analysis extend to the quantum setting straightforwardly. Unfortunately, this argument is not necessarily true, because a superposition is generally not equivalent to its induced probability distribution; in fact, this is usually where the quantum advantage comes from in algorithm design. Actually, if one goes into detail of the security analysis, one will find that a malicious quantum sender of commitments may attack by making the opening information (which is entangled with quantum commitments and their decommitments) about which bit commitments will be opened as what value in an arbitrary superposition. By tuning this superposition, the sender may adjust the receiver’s acceptance probabilities in different verifications. This kind of superposition attack will make the security analysis based on the general quantum binding property (if possible) much harder than that based on the classical binding property.
Why Quantum Bit Commitment Is Interesting? Besides the weakness as well as technical difficulties in security analysis mentioned above, another shortcoming of quantum bit commitment is that by today’s quantum technology, the physical realization of a general quantum bit commitment scheme is still far beyond our reach. In spite of this, quantum bit commitment still interests us for several reasons. First, since as early as 2000 researchers have come to realize that merely based on quantum-secure one-way functions/permutations, one can construct non-interactive quantum bit commitments of both flavors (i.e. statistical binding and statistical hiding), whose commit and reveal stages consist of just a single quantum message from the sender to the receiver [14, 23, 24, 34]. It turns out that these constructions are not coincidences: recently, Yan [34] has shown that any (interactive) quantum bit commitment scheme can be converted into a non-interactive one of a generic formFootnote 1 (whose informal definition is referred to the first graph of “Notations" in Subsect. 1.3, and formal definition to Definition 2). This is in contrast to the constant [26] or even polynomial [20] number of rounds in the commit stage by classical constructions of bit commitment. Thus, using quantum bit commitments instead of the classical ones in applications can potentially reduce the number of rounds of the interactionFootnote 2 while keeping the complexity assumption to the minimum.
More interestingly, Fang, Unruh, Yan and Zhou [15] and Yan [34] also observe that the (either statistical or computational) binding of a generic non-interactive quantum bit commitment scheme is automatically information-theoretically strictFootnote 3. Here, the strictness of the quantum binding extends the one in [30] for a classical construction of bit commitment, which roughly states that not only the revealed value but also the decommitment state used in opening a quantum bit commitment are “unique". We highlight that this strictness of the quantum binding originates from the entanglement between the commitment and its decommitment, as opposed to the classical correlation in the definition of the classical strict-binding [30]. We also stress that even the quantum computational binding can be information-theoretically strict simultaneously (which may sound contradictory as it appears)Footnote 4. This is in contrast to the computational binding of a classical bit commitment, which is impossible to be information-theoretically strict: though it may be computationally hard to find an alternative opening, there actually exist a bunch of them! It turns out that this strictness of the quantum binding can play an important role in applications; in particular, it can help circumvent existing barriers only known for classical constructions, as confirmed in [15] and this paper (Theorem 1).
Overall, if we are optimistic about the development of quantum technology and believe that general quantum computation and communication will be available in future, then the application of quantum bit commitment as a primitive in quantum cryptography is worthy of study.
Progress and Perspective Towards Basing Security on Quantum Binding. In the past two decades, there were only few works studying the security based on the binding property of a general quantum bit commitment [36]. Recently, some generic techniques to cope with the quantum perfect/statistical binding property are developed in [15], by which in many cases the security based on the classical statistical binding property can be lifted to the quantum setting. Unfortunately, when it comes to the question of the security based on the quantum computational binding property, the answer remains elusive. To the best of our knowledge, we are aware of no such results before. In our opinion, the perhaps most important open question towards using quantum bit commitment as a primitive in quantum cryptography is:
Can we base quantum security on the computational binding property of a general quantum bit commitment?
Based on the state-of-the-art knowledge, the answer to the question above is unclear. On one hand, intuitively it will be true if we can view the superposition of strings underlying quantum bit commitments as its induced probability distribution (as aforementioned). Actually, this motivates Unruh [31, 32] to introduce (computationally) collapse-binding commitments. Unfortunately, general quantum commitments cannot be collapse-binding [34]. In spite of this, it turns out that by some tricks this intuitive strategy is enabled to work (in many cases) when perfectly/statistically-binding quantum bit commitments are used [15]. More positive evidences come from the success in various security analysis in the quantum random oracle model, in which adversaries can query a random oracle in an arbitrary superposition [6].
On the other hand, however, after a first attempt towards the security analysis, it turns out that for a naive analysis (r.f. Subsect. 1.3) to work it requires that the binding error be sub-exponentially or even exponentially small, rather than negligiblly small as typical in cryptography. We will refer to this technical difficulty as “exponential curse", which arises from the fact that polynomial number of qubits could be in a superposition of exponentially many basis states. Moreover, the impossibility of the general quantum rewinding [18], as well as other related impossibility results on classical constructions of bit commitment secure against quantum attacks [2], may suggest a negative answer to the open question above.
One motivation of this work is to explore the application of general quantum computationally-binding bit commitmentsFootnote 5 in cryptographic applications, notably in constructing quantum zero-knowledge arguments for NP languages.
1.1 Our Contribution
In spite of the technical difficulty and negative evidences just mentioned, we make some progress towards answering the main open question affirmatively in this work. Interestingly, our security analysis will use a more straightforward strategy that is completely different from that of viewing the superposition of strings underlying quantum bit commitments as its induced probability distribution.
Specifically, our contribution is two-fold.
1. A quantum construction of perfect/statistical zero-knowledge argument system (with soundness error 1/2 ) for all NP languages
We prove the following main theorem of this paper:
Theorem 1
Plugging a generic quantum perfectly(resp. statistically)-hiding computationally-binding bit commitment scheme (Definition 2) in Blum’s protocol [5] gives rise to a three-round public-coin quantum perfect(resp. statistical) zero-knowledge argument system for the NP-complete language Hamiltonian Cycle, with perfect completeness and soundness error 1/2.
Following [14, 23, 24, 34], since a generic quantum perfectly(resp. statistically)-hiding computationally-binding bit commitment scheme can be constructed from quantum-secure one-way permutations(resp. functions), the theorem above gives the first quantum perfect(resp. statistical) zero-knowledge argument for all NP languages based on the same assumption.
Compared with classical GMW-type statistical zero-knowledge arguments secure against classical attacks for NP [21, 28], our quantum construction reduces the rounds of the interaction from polynomial to three, thanks to the non-interactivity of a generic quantum computationally-binding bit commitment scheme. Compared with the classical statistical zero-knowledge argument for NP secure against quantum attacks given in [31, 32], which assumes collapsing hash functions, our quantum construction relies on a weaker (perhaps minimum) complexity assumption without setup.
We highlight that our proof of Theorem 1 relies heavily on (though implicitly) that the (computational) binding of a generic quantum bit commitment scheme is information-theoretically strict (as aforementioned). It is this strict-binding property that enables a simple quantum rewinding [15, 36] to work even in our quantum computational soundness analysis. This circumvents a barrier which is only known for classical constructions [2].
As a final remark, in this work we only study stand-alone Blum’s protocol. But we believe it should be meaningful as a first step toward using non-interactive computationally-binding quantum bit commitments in more general protocols. Some remarks on the sequential and the parallel compositions of Blum’s atomic protocol is referred to the end of Sect. 4.
2. A non-trivial computational binding property of the quantum string commitment scheme obtained by composing a generic quantum bit commitment scheme in parallel
A natural way to construct a string commitment is to compose a bit commitment scheme in parallel, i.e. committing a string in a bitwise fashion. For the purpose of proving Theorem 1, we introduce a new binding property of quantum string commitments which we call “predicate-binding". And we show that the parallel composition of a generic quantum computationally-binding bit commitment scheme gives rise to a quantum computationally predicate-binding string commitment scheme. When we instantiate Blum’s protocol with a generic quantum computationally-binding bit commitment scheme, the quantum computational soundness of the protocol (which is required towards establishing Theorem 1) can be easily based on the predicate-binding property of quantum string commitments.
In more detail, we first formalize a kind of predicates which we will call “pattern-predicates" (Definition 3): informally speaking, for a string to satisfy a pattern-predicate, it should exhibit a certain “pattern" somewhere. The intuition underlying our definition is that in typical applications of bit commitments, the receiver (of commitments) will check whether the value of the opened commitments will cause it to accept. For example, in Blum’s protocol the (honest) verifier’s verification corresponding to each challenge naturally induces a pattern-predicate.
With our definition of pattern-predicate, the predicate-binding property (Definition 4, or fomally Definition 5) guarantees that given an arbitrary pair of inconsistent pattern-predicates on a set of strings of the same length (i.e. no strings in this set can satisfy both predicates), if a (claimed) quantum commitment can be opened such that the revealed stringFootnote 6 satisfies one predicate with certainty, then the same commitment cannot be opened so as to satisfy the other predicate (except for a negligible probability)Footnote 7.
The proof of predicate-binding is the main technical contribution of this work, which is highly non-trivial; in particular, the trivial reduction (via a simple hybrid argument) from string binding to bit binding in the classical setting will fail completely here. Actually, for a technical reason we did not prove the full predicate-binding property (i.e. w.r.t. the most general inconsistent pattern-predicate pairs) in this work; rather, we can only show predicate-binding such that one predicate is allowed to be of the general form, whereas the other is subject to the restriction that it only depends on a fixed portion of the string (Thereom 2, or formally Theorem 3). In spite of this restriction, the predicate-binding property we obtain is more than enough to prove Theorem 1. Any extension of our result is left as an open problem. We believe that quantum predicate-binding string commitments could be of independent interest and will be found useful elsewhere.
A Comparison with Existing Quantum Computational String Binding Properties. The parallel composition of a generic quantum bit commitment scheme trivially gives a quantum honest-binding string commitment scheme [36]. Roughly speaking, the honest-binding states that the honest commitment to a string cannot be opened as any other string (except for a negligible probability). Unfortunately, this binding property seems too weak to be useful in applications. This is because a malicious sender may not commit honestly.
In [10], a so-called computational f-binding property w.r.t. a function \(f: \{0,1\}^m \rightarrow \{0,1\}^l\) for quantum string commitments is proposed, where integers \(l \le m\). Unfortunately, no constructions for quantum f-binding commitments are provided in [10]. Our predicate-binding implies the f-binding w.r.t. to any efficiently computable function f whose image is just the set \(\{0,1\}\) (i.e. \(l=1\)), if we view preimages mapped to 0 as inducing one predicate while preimages mapped to 1 as inducing the other.
Damgård, Fehr and Salvail [12] introduced the so-called Q-binding property for classical commitments secure against quantum attacks, which can be extended to quantum commitments in a straightforward way. Here, the “Q" stands for an arbitrary predicate whose form is close to our pattern-predicateFootnote 8: very roughly, this predicate Q can be viewed as combining various pattern-predicates into one by introducing a “choice" parameter u, and the predicate-binding we establish here can also be viewed as the Q-binding w.r.t. the predicate Q of a special form such that \(\left| U \right| =2\) and \(p_{\textsc {ideal}} = 1\) (in the notation used in [12]). The general framework for constructing Q-binding (classical) commitments in [12] requires a setup and relies on much stronger assumptions than quantum-secure one-way functions; in particular, one crucial assumptionFootnote 9 on which it relies has a similar structure as the security game in defining Q-binding, which makes the security proof for Q-binding there much more straightforward than ours for predicate-binding here.
Unruh [31, 32] introduced computational collapse-binding classical commitments secure against quantum attacks. However, a straightforward extension of collapse-binding to quantum commitments cannot hold generally, as aforementioned; more detail is referred to [34].
1.2 A Comparison with Two Recent Works
In two concurrent and independent recent works, statistically-hiding [3] (resp. computationally-hiding [19]) computationally-binding quantum bit commitments that additionally satisfy two nice properties called extractable and equivocal properties are constructed, also based solely on quantum-secure one-way functions. Compared with our scheme used in this work, i.e. the generic statistically-hiding computationally-binding quantum bit commitment scheme (Definition 2), theirs are more advantageous in the following aspects:
-
1.
Their schemes satisfy both extractable and equivocal properties simultaneously, whereas ours is generally unlikely to satisfy.
-
2.
The committed value of the commitments by running the commit stage of their schemes is a probability distribution over the set \(\{0,1\}\)Footnote 10, rather than a superposition as our scheme. This makes the quantum (computational) binding property of their schemes almost as strong as the classical binding property. As such, their schemes are likely to be more versatile in applications than ours; and the corresponding security analysis with their commitments should be easier, too. In this regard, we believe that plugging their commitments in Blum’s protocol will yield a quantum zero-knowledge argument-of-knowledge (rather than just argument as achieved in this paper) system for NP, whose security analysis can be adapted from the classical one in a straightforward way (avoiding the issue arisen from the general quantum binding as studied in this paper).
-
3.
Both their schemes and ours use quantum communication. But theirs only send (and receive) BB84 states, in contrast to arbitrary quantum states that might be sent by our scheme.
In spite of the above, we stress that commitments in [3, 19] achieve better properties (than ours) at the cost of the extremely high round complexity: they need polynomial (in the security parameter) rounds of the interaction at least in the commit stageFootnote 11, which makes them almost impractical even when quantum computation and communication are realized one day. This is in sharp contrast to the non-interactivity of both the commit and the reveal stages of our scheme.
1.3 Technical Overview
We sketch the soundness analysis of Blum’s protocol instantiated with a generic quantum computationally-binding bit commitment scheme, which is the key step towards establishing Theorem 1. Our goal is to reduce the soundness of the resulting protocol to the predicate-binding property of quantum string commitment (Lemma 3).
We assume that readers are familar with Blum’s protocol [5], which is also sketched in Subsect. 2.3. In its soundness analysis, the (possibly cheating) prover’s first message constitutes a (claimed) quantum string commitment. The (honest) verifier’s acceptance conditions corresponding to challenges 0 and 1 induce two predicates on graphs with the same number of vertices as the input graph. When the input graph is not Hamiltonian, these two predicates will become inconsistent, in that no single graph can satisfy both of them simultaneously. Technically, at the heart of the reduction from the soundness of Blum’s protocol to the predicate-binding property of the quantum string commitment lies a simple quantum rewinding technique (Lemma 1) that extends from ones used in [15, 36] but for the quantum statistical binding setting. We remark that though this extension is technically trivial, conceptually why it is possible relies heavily on that a generic quantum computationally-binding bit commitment scheme is information-theoretical strict-binding.
We are then left with showing that the parallel composition of a generic quantum computationally-binding bit commitment scheme indeed gives rise to a quantum computationally predicate-binding string commitment scheme (a special case in Lemma 2 and a more general case in Theorem 3). This is the main technical part of the paper. In the below, we first explain a technical difficulty towards this goal by a naive try, and then sketch at a high level how to overcome it. But before doing this, we first set up some notations that are necessary for our exposition.
Notations. A generic quantum bit commitment commitment scheme can be represented by a quantum circuit pairFootnote 12 \((Q_0, Q_1)\) performing on quantum registers \((\textsf {C}, \textsf {R})\). To commit a bit \(b \in \{0,1\}\), in the commit stage the sender performs the quantum circuit \(Q_b\) on quantum registers \((\textsf {C}, \textsf {R})\) initialized in the state  , and then sends the commitment register C to the receiver; later in the reveal stage, the sender sends the bit b together with the decommitment register R to the receiver, who then does the reversible computation (i.e. performing the quantum circuit \(Q_b^{\dag }\)) to decide whether to accept or not (i.e. checking whether the registers \((\textsf {C}, \textsf {R})\) return to the all
, and then sends the commitment register C to the receiver; later in the reveal stage, the sender sends the bit b together with the decommitment register R to the receiver, who then does the reversible computation (i.e. performing the quantum circuit \(Q_b^{\dag }\)) to decide whether to accept or not (i.e. checking whether the registers \((\textsf {C}, \textsf {R})\) return to the all  state). Informally, we say that the quantum bit commitment scheme \((Q_0, Q_1)\) is computationally binding if for any polynomial-time realizable unitary transformation U performing on the register R, the inner product
state). Informally, we say that the quantum bit commitment scheme \((Q_0, Q_1)\) is computationally binding if for any polynomial-time realizable unitary transformation U performing on the register R, the inner product  is negligible; that is, unit vectors
is negligible; that is, unit vectors  and
and  are almost orthogonalFootnote 13.
are almost orthogonalFootnote 13.
To commit a string of length m, we commit it in a bitwise fashion using the scheme \((Q_0, Q_1)\). Let \(Q_s\) denote the corresponding quantum circuit used to commit the string s; that is, \(Q_s = \bigotimes _{i=1}^m Q_{s_i} \), which performs on m copies of the quantum registers \((\textsf {C}, \textsf {R})\).
Let \(P_1, P_2\) be two (pattern-)predicatesFootnote 14 on all m-bit strings. We use \(s \in P_1\) (resp. \(P_2\)) to denote that the string \(s \in \{0,1\}^m\) satisfies the predicate \(P_1\) (resp. \(P_2\)). We say that two predicates \(P_1, P_2\) are inconsistent if no string \(s \in \{0,1\}^m\) can satisfy both \(P_1\) and \(P_2\). More details about the formalization of predicates are referred to Subsect. 3.1.
A Technical Difficulty: Exponential Curse. We first consider the simplest scenario, in which an m-bit string is firstly committed and later all (bit) commitments will be opened. Note that a cheating sender can first prepare an arbitrary superposition of the form  (resp.
(resp.  ) in registers \((\textsf {D}, \textsf {C}^{\otimes m}, \textsf {R}^{\otimes m})\), and then send all commitment registers \(\textsf {C}^{\otimes m}\) to the receiver in the commit stageFootnote 15. Later in the reveal stage, the sender sends the register D (which is supposed to contain the classical information about what string is to reveal), together with all decommitment registers \(\textsf {R}^{\otimes m}\), to the receiver. By this strategy, the sender can open all commitments successfully with certainty as a distribution (which is determined by coefficients \(\alpha _s\)’s (resp. \(\beta _s\)’s)) of strings that satisfy the predicate \(P_1\) (resp. \(P_2\)). To show predicate-binding, it is sufficient to show that up to any polynomial-time realizable unitary transformation U that does not touch commitment registers \(\textsf {C}^{\otimes m}\) (which represents the sender’s strategy in opening commitments), any two superpositions
) in registers \((\textsf {D}, \textsf {C}^{\otimes m}, \textsf {R}^{\otimes m})\), and then send all commitment registers \(\textsf {C}^{\otimes m}\) to the receiver in the commit stageFootnote 15. Later in the reveal stage, the sender sends the register D (which is supposed to contain the classical information about what string is to reveal), together with all decommitment registers \(\textsf {R}^{\otimes m}\), to the receiver. By this strategy, the sender can open all commitments successfully with certainty as a distribution (which is determined by coefficients \(\alpha _s\)’s (resp. \(\beta _s\)’s)) of strings that satisfy the predicate \(P_1\) (resp. \(P_2\)). To show predicate-binding, it is sufficient to show that up to any polynomial-time realizable unitary transformation U that does not touch commitment registers \(\textsf {C}^{\otimes m}\) (which represents the sender’s strategy in opening commitments), any two superpositions  and
and  are almost orthogonal, i.e. their inner product is negligible, w.r.t. any inconsistent predicate pair \((P_1, P_2)\). A technical difficulty in showing this lies in that a potential exponential blow-up may occur in bounding this inner product. This difficulty is referred to as the exponential curse in [15, 36], which we believe is universal when one tries to base security on quantum binding; a similar difficulty also appears in [10]. Now let us go into some detail in the below.
are almost orthogonal, i.e. their inner product is negligible, w.r.t. any inconsistent predicate pair \((P_1, P_2)\). A technical difficulty in showing this lies in that a potential exponential blow-up may occur in bounding this inner product. This difficulty is referred to as the exponential curse in [15, 36], which we believe is universal when one tries to base security on quantum binding; a similar difficulty also appears in [10]. Now let us go into some detail in the below.
By the computational binding property of the quantum bit commitment scheme \((Q_0, Q_1)\), the inner product  where \(s \ne s'\) can be bounded by its binding error, which is negligible (as typical in cryptography). Thus, a naive way to bound the inner product
where \(s \ne s'\) can be bounded by its binding error, which is negligible (as typical in cryptography). Thus, a naive way to bound the inner product

is first to expand it and bound each term indexed by \((s, s')\) using the binding error bound (while neglecting its coefficient that can be bounded by 1), and then apply the triangle inequality. However, when there are super-polynomial (typically exponentially many) strings \(s \in P_1\) or \(s' \in P_2\), this naive approach will fail.
Actually, whether the inner product above could really be bounded by some negligible quantity is questionable a prior. This is because generally, two superpositions of the form  and
and  , where
, where  and
and  are two orthonormal bases, are not necessarily almost orthogonal, even when
are two orthonormal bases, are not necessarily almost orthogonal, even when  and
and  are almost orthogonal for each (x, y) pair. To see this, consider the following simple example. The Hilbert space is induced by m qubits, where
are almost orthogonal for each (x, y) pair. To see this, consider the following simple example. The Hilbert space is induced by m qubits, where  is the standard basis and
is the standard basis and  is the Hadamard basis. Then consider an arbitrary vector in this space, which can be written as a superposition of basis vectors either in the standard basis or the Hadamard basis. Clearly, these two superpositions are actually the same vector, so that their inner product is one. But the inner product between
is the Hadamard basis. Then consider an arbitrary vector in this space, which can be written as a superposition of basis vectors either in the standard basis or the Hadamard basis. Clearly, these two superpositions are actually the same vector, so that their inner product is one. But the inner product between  and
and  for arbitrary \(x, y \in \{0,1\}^m\) is exponentially small! This example tells us that to bound the inner product aforementioned, we need to exploit the structures of the two superpositions (which are induced by the structures of predicates \(P_1\) and \(P_2\)).
for arbitrary \(x, y \in \{0,1\}^m\) is exponentially small! This example tells us that to bound the inner product aforementioned, we need to exploit the structures of the two superpositions (which are induced by the structures of predicates \(P_1\) and \(P_2\)).
The similar technical difficulty also appears in the quantum statistical binding setting, where two generic techniques were invented to overcome this exponential curse: perturbation and hypothetical commitment measurement [15, 36]. Unfortunately, neither of them extend to the quantum computational binding setting straightforwardly. Reasons are as below. We note that the fundamental difference between these two settings lies in that in the quantum statistical binding setting, the bit commitment to 0 and that to 1 (stored in the commitment register C) themselves are already almost orthogonal, and which will never be touched by the (possibly cheating) sender after they are sent. Thus, we can assume that commitments will collapse immediately by hypothetical commitment measurements at the moment they are sent; after the collapse, everything will be similar to that in the classical perfect binding setting. However, in case of quantum computational binding, the commitment to 0 and that to 1 could be close or even identical, where we are only guaranteed that in the reveal stage the joint states of the commitment register C and the decommitment register R are almost orthogonal. But the state of the decommitment register R can be affected by the sender’s operation after the commitment stage. As such, the hypothetical-collapse trick to handle quantum statistically-binding commitments [15] fails completely here.
In summary, new techniques are needed to establish the quantum computational predicate-binding property (if possible).
Our Approach. For the ease of the exposition, instead of considering the aforementioned inner product, now let us equivalently consider the projection of an arbitrary superposition of the form  on the subspace
on the subspace  , up to any polynomial-time realizable unitary transformation U that does not touch commitment registers \(\textsf {C}^{\otimes m}\). We overload the notation and denote this projection also by \(P_2\) for simplicity. Our goal then becomes to show that this projection is negligible (in the security parameter which we have dropped to simplify the notation; see footnote 12). Our idea is based on the following key observation: when the predicate \(P_1\) is sparse, i.e. the number of the m-bit strings satisfying it is polynomially bounded, then combining a new perturbation technique (which looks similar but is inherently different from the one developed in the quantum statistical binding setting [15, 36]) and the triangle inequality, we can bound the aforementioned projection by a negligible quantity. However, to remove this sparsity requirement, we still need to overcome the exponential curse. To this end, we need to take into account of the coefficients of the superposition, and make an essential use of the following structure of predicates \(P_1\) and \(P_2\): to check whether a string satisfies \(P_1\) or \(P_2\), all its bits are to examine.
, up to any polynomial-time realizable unitary transformation U that does not touch commitment registers \(\textsf {C}^{\otimes m}\). We overload the notation and denote this projection also by \(P_2\) for simplicity. Our goal then becomes to show that this projection is negligible (in the security parameter which we have dropped to simplify the notation; see footnote 12). Our idea is based on the following key observation: when the predicate \(P_1\) is sparse, i.e. the number of the m-bit strings satisfying it is polynomially bounded, then combining a new perturbation technique (which looks similar but is inherently different from the one developed in the quantum statistical binding setting [15, 36]) and the triangle inequality, we can bound the aforementioned projection by a negligible quantity. However, to remove this sparsity requirement, we still need to overcome the exponential curse. To this end, we need to take into account of the coefficients of the superposition, and make an essential use of the following structure of predicates \(P_1\) and \(P_2\): to check whether a string satisfies \(P_1\) or \(P_2\), all its bits are to examine.
For more technical details, we are to bound the norm

where in the summation there could be exponentially many terms. At a high level, our trick is to order these terms properly in such a way that they can be treated as leaves of a binary tree, whose internal nodes will correspond to the summation of leaves of the subtree it determines; in particular, the root of the tree will correspond to the summation of all leaves, whose norm is just what we want to bound. We will actually bound norms of all internal nodes, including the root, in a bottom-up fashion. The formal proof (of Lemma 2) is by induction on the depth of internal nodes. Within the induction step, we will use the triangle inequality. It turns out that the accumulated error will grow only linearly in the depth of the tree, which is just m.
Extension. However, the (simplest) scenario (i.e. all commitments will be opened) considered above is usually not sufficient for applications. This is because in many cases where bit commitments are used in a larger protocol, not all bit commitments will be opened for a verification. Even worse, positions of which bit commitments will be opened may not even be fixed: they might depend on the party who plays the role of the (cheating) sender. For example, consider an execution of Blum’s protocol in which a Hamiltonian cycle is challenged to open.
Fortunately, we can extend the predicate-binding property established in the simplest case to a more general case in which it holds that for at least one predicate (\(P_1\) or \(P_2\)), the positions of which bit commitments will be opened for its verification are fixed, while the other predicate could be arbitrary (Theorem 3). It turns out that this extension already suffices for our purpose of establishing Theorem 1.
For the formal proof of such an extension, there are more technical issues we need to handle.
Organization. We first give preliminaries in Sect. 2. In Sect. 3, we formally introduce and establish the computational predicate-binding property of the quantum string commitment scheme that is obtained by composing a generic quantum computationally-binding bit commitment scheme in parallel. As an application of predicate-binding, in Sect. 4 we show that Blum’s zero-knowledge protocol for the NP-complete language Hamiltonian Cycle with a generic quantum computationally-binding bit commitment scheme plugged in is sound against any quantum computationally bounded prover. We conclude with Sect. 5.
2 Preliminaries
A quantum system or register induces a Hilbert space. A quantum operation performing on a quantum system induces an operator acting on the Hilbert space associated with the system. In particular, a unitary operation induces a unitary transformation, and a binary projective measurement induces a projector (corresponding to the outcome one). We will interchangeably use quantum system and its induced Hilbert space, quantum operation and its induced operator. For example, we may say that a unitary transformation or a projector perform on or do not touch a quantum register.
Notations. We will explicitly write quantum register(s) as a superscript of an operator to indicate or highlight on which register(s) this operator performs. Similarly, we will also explicitly write quantum register(s) as a superscript of a quantum state to indicate or highlight in which register(s) this quantum state is stored. For example, let A be a quantum register. Then we may write \(U^A\),  (resp. \(\rho ^A\)), to indicate that the operator U performs on the register A, the quantum pure (resp. mixed) state
(resp. \(\rho ^A\)), to indicate that the operator U performs on the register A, the quantum pure (resp. mixed) state  (resp. \(\rho \)) is stored in the register A, respectively. We may also write \(U \otimes \mathbbm {1}^A\) to highlight that the operation U does not touch the register A. But when it is clear from the context, we often drop such superscripts or the tensor product with the identity to simplify the notation; this in particular happens in many of derivations within our proofs, where we often write out registers as superscripts or the tensor product with the identity explicitly in the first step, while dropping them subsequently. When there are m copies of the register A, for a subset \(T \subseteq \left\{ 1, 2, \dots , m\right\} \), we write \(\textsf {A}^{\otimes T}\) to refer to the copies of the register A indexed by the subset T; when the subset T is the whole set, we may just write \(\textsf {A}^{\otimes m}\).
(resp. \(\rho \)) is stored in the register A, respectively. We may also write \(U \otimes \mathbbm {1}^A\) to highlight that the operation U does not touch the register A. But when it is clear from the context, we often drop such superscripts or the tensor product with the identity to simplify the notation; this in particular happens in many of derivations within our proofs, where we often write out registers as superscripts or the tensor product with the identity explicitly in the first step, while dropping them subsequently. When there are m copies of the register A, for a subset \(T \subseteq \left\{ 1, 2, \dots , m\right\} \), we write \(\textsf {A}^{\otimes T}\) to refer to the copies of the register A indexed by the subset T; when the subset T is the whole set, we may just write \(\textsf {A}^{\otimes m}\).
Efficiently Realizable Quantum Computation. In this work, without loss of generality, we restrict to consider the following quantum computational model:
-
1.
Quantum systems or registers are constituted of qubits.
-
2.
There are only two kinds of quantum operations: unitary transformation and projective measurement.
We also need to formalize efficiently realizable quantum operations. By [37], any efficiently realizable quantum algorithm or unitary transformation can be formalized by a family of quantum circuits \(\left\{ Q_n\right\} _{n \ge 1}\) such that:
-
1.
Each gate of the quantum circuit \(Q_n\) comes from a pre-fixed finite, unitary, and universal quantum gate set, e.g. \(\left\{ \mathrm{Hadamard}, \mathrm{phase}, \textsc {cnot}, \pi /8\right\} \) [29].
-
2.
Quantum circuit \(Q_n\) is of polynomial size (w.r.t. the index n).
-
3.
The quantum circuit family \(\left\{ Q_n\right\} _{n \ge 1}\) can be uniformly generated, i.e. there exists a polynomial-time classical algorithm A which on input \(1^n\) outputs the description of the quantum circuit \(Q_n\).
Since any projective measurement can be realized by first performing a unitary transformation, followed by a measurement of all qubits in the standard basis, we say that a projective measurement is efficiently realizable if the corresponding unitary transformation is efficiently realizable.
Any projector \(\varPi \) induces a binary measurement \(\left\{ \varPi , \mathbbm {1}- \varPi \right\} \), which produces the outcome 1 (resp. 0) when the quantum state collapses into the subspace induced the projector \(\varPi \) (resp. \(\mathbbm {1}- \varPi \)). We say that the projector \(\varPi \) is efficient realizable if its induced binary measurement is efficiently realizable.
Quantum Rewinding. A quantum rewinding technique as stated in the lemma below is adapted from the one given in [15] directly, whereas now we restrict to consider projectors and unitary transformations that are efficiently realizable. In spite of this, its proof follows the same line as the one in [15].
Lemma 1 (A quantum rewinding)
Let \(\mathcal {X}\) and \(\mathcal {Y}\) be two Hilbert spaces. Unit vector  . Efficiently realizable projectors \(\varGamma _1, \dots , \varGamma _k\) perform on the space \(\mathcal {X} \otimes \mathcal {Y}\), and efficiently realizable unitary transformations \(U_1, \dots , U_k\) perform on the space \(\mathcal {Y}\). If
. Efficiently realizable projectors \(\varGamma _1, \dots , \varGamma _k\) perform on the space \(\mathcal {X} \otimes \mathcal {Y}\), and efficiently realizable unitary transformations \(U_1, \dots , U_k\) perform on the space \(\mathcal {Y}\). If  , where \(0 \le \eta \le 1\), then
, where \(0 \le \eta \le 1\), then

2.1 A Generic Quantum Bit Commitment Scheme
We first need to define quantum (in)distinguishability based on the efficiently realizable quantum computation we fixed above. Our definition follows [33].
Definition 1 ((In)distinguishability of quantum state ensembles)
Two quantum state ensembles \(\left\{ \rho _n\right\} _{n \ge 1}\) and \(\left\{ \xi _n\right\} _{n \ge 1}\) are quantum statistically (resp. computationally) indistinguishable if for any quantum state ensemble \(\left\{ \sigma _n\right\} _{n \ge 1}\) and any unbounded (resp. efficiently realizable) quantum algorithm D which outputs a single qubit that will be measured in the standard basis, it holds that
for sufficiently large n, where \(negl(\cdot )\) is some negligible function.
Following Yan [34], the definition of a generic quantum computationally-binding bit commitment scheme is given as below.
Definition 2 (A generic computationally-binding quantum bit commitment scheme)
A generic computationally-binding quantum bit commitment scheme is a two-party, two-stage protocol. It can be represented by an ensemble of polynomial-time uniformly generated quantum circuit pair \(\left\{ (Q_0(n), Q_1(n))\right\} _{n \ge 1}\). Specifically,
-
The scheme involves two parties, a sender and a receiver, proceeding in two stages: a commit stage followed by a reveal stage.
-
In the commit stage, to commit bit \(b \in \{0,1\}\), the sender performs the quantum circuit \(Q_b(n)\) on quantum registers \((\textsf {C}, \textsf {R})\) initialized in all
 ’s stateFootnote 16. Then the sender sends the commitment register C, whose state at this moment denoted by \(\rho _b(n)\), to the receiver.
’s stateFootnote 16. Then the sender sends the commitment register C, whose state at this moment denoted by \(\rho _b(n)\), to the receiver. -
In the (canonical) reveal stage, the sender announces b, and sends the decommitment register R to the receiver. The receiver then performs \(Q_b(n)^{\dag }\) on the registers (C, R), accepting if (C, R) return to all
 ’s state. (This can be done by a measurement in the computational basis on each qubit that belongs to the registers (C, R).)
’s state. (This can be done by a measurement in the computational basis on each qubit that belongs to the registers (C, R).)
We are next to define the hiding (or concealing) and the binding properties of the scheme \(\left\{ (Q_0(n), Q_1(n))\right\} _{n \ge 1}\).
-
Statistically hiding. We say that the scheme is statistically hiding if the quantum state ensembles \(\left\{ \rho _0(n)\right\} _{n \ge 1}\) and \(\left\{ \rho _1(n)\right\} _{n \ge 1}\) are quantum statistically indistinguishable.
-
Computationally \(\epsilon (n)\)-binding. We say that the scheme is quantum computationally \(\epsilon (n)\)-binding if for any state
 in auxiliary register Z, and any efficiently realizable unitary transformation U performing on (R, Z),
in auxiliary register Z, and any efficiently realizable unitary transformation U performing on (R, Z),  (2)
(2)By the reversibility of quantum computation, the binding property can also be equivalently defined by swapping the roles of \(Q_0\) and \(Q_1\) in the above. Then the inequality (2) becomes
 (3)
(3)We call \(\epsilon (n)\) the binding error. When \(\epsilon (n)\) is some negligible function, we usually drop it and just say that the scheme is computationally binding.
Remark
-
1.
The (computational) binding property stated in the definition above is actually the honest-binding, which is equivalent to the sum-binding w.r.t. a generic quantum bit commitment scheme [34].
-
2.
On instantiations of non-interactive computationally-bindng quantum bit commitments of the generic form based on quantum-secure one-way functions/permutations, one is referred to [34] for the details. Briefly, it is argued in [34] that any interactive quantum bit commitment schemes (including both classical and quantum constructions) secure against the purification attackFootnote 17, which in particular include schemes proposed in [11, 14, 24, 28], can be converted into a non-interactive one of the generic form with the same flavors of hiding and binding properties.
In the sequel, to simplify the notation we often drop the security parameter n and just write \((Q_0, Q_1)\) to denote a generic quantum computationally-binding bit commitment scheme.
We will use the scheme \((Q_0, Q_1)\) to commit a binary string in a bitwise fashion. Namely, the quantum circuit to commit a string \(s = s_1 s_2 \cdots s_m \in \{0,1\}^m\) is given by
which performs on m copies of the quantum register pair \((\textsf {C}, \textsf {R})\).
2.2 Modeling an Attack of the Sender of Quantum Commitments
Consider a running of a larger two-party protocol in which a generic quantum bit commitment scheme is used and the sender of quantum commitments is malicious. The other party who will be referred to as the receiver is honest. The sender is supposed to commit to a string in \(\{0,1\}^m\) in a bitwise fashion at some moment, and later try to open the commitments in a way as determined by the larger protocol. Then the behavior of the sender can be modeled by  such that:
such that:
-
1.
The sender prepares the system \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\) in the quantum state
 at the end of the commit stage, and sends the commitment registers \(\textsf {C}^{\otimes m}\) to the receiver.
at the end of the commit stage, and sends the commitment registers \(\textsf {C}^{\otimes m}\) to the receiver. -
2.
In the reveal stage, the sender first performs the unitary transformation U on the system \((\textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and then sends registers \((\textsf {R}^{\otimes m}, \textsf {D})\) to the receiver. The register D is supposed to contain the classical information indicating which quantum bit commitments will be opened as what value, and \(\textsf {R}^{\otimes m}\) are decommitment registers.
We have two remarks about the modeling as above:
-
1.
We note that there might be other operations performed by both the sender and the receiver between the end of the commit stage and the beginning of the reveal stage within the larger protocol. But in many cases, this can be simulated by absorbing these operations and auxiliary states introduced into the operation U and the state
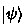 , respectively. Anyway, in this work we just restrict to consider the modeling as above for simplicity.
, respectively. Anyway, in this work we just restrict to consider the modeling as above for simplicity. -
2.
In the second item above, we assume without loss of generality that all decommitment registers \(\textsf {R}^{\otimes m}\) are sent to the receiver in the reveal stage, though sometimes only a proper subset of commitments will be openedFootnote 18. We can do this because the receiver is honest; sending all decommitment registers will not affect the security against the sender.
2.3 Blum’s Zero-Knowledge Protocol for Hamiltonian Cycle
Basically, Blum’s protocol [5] proceeds as follows: on input a graph G (assuming it is represented by its adjacency matrix) with n vertices:
-
1.
The prover first chooses a random permutation \(\varPi \in S_n\), where \(S_n\) consists of all permutations over the set \(\left\{ 1, 2, \dots , n\right\} \). Then it commits to the graph \(\pi (G)\), sending all \(n^2\) (quantum) bit commitments to the verifier.
-
2.
Upon receiving the prover’s commitments, the verifier tosses a random coin to obtain the challenge bit \(b \in \{0,1\}\) and sends it to the prover.
-
3.
If the challenge \(b = 0\), then the prover sends the permutation \(\pi \) together with the decommitment registers for all bit commitments to the verifier. If the challenge \(b = 1\), then the prover sends the location of a Hamiltonian cycle H together with the decommitment registers for the commitments of all edges of the cycle H to the verifier.
-
4.
If the challenge \(b = 0\), then the verifier accepts if all bit commitments are opened as \(\pi (G)\) successfully. If the challenge \(b = 1\), then the verifier accepts if the H is a possible location of a Hamiltonian cycle and all commitments to the edges of H are opened as 1 successfully.
3 The Predicate-Binding Property of Quantum String Commitments
In this section, we first introduce the notion of pattern-predicate and then the predicate-binding property of quantum string commitments. Next, we show that the parallel composition of a generic quantum computationally-binding bit commitment scheme gives rise to a quantum string commitment scheme that is predicate-binding w.r.t. a pair of inconsistent pattern-predicates of a special form. Last, we extend this predicate-binding property to a setting that is sufficient for our application, i.e. quantum zero-knowledge arguments for NP.
3.1 Pattern-Predicate
Informally, the pattern-predicate defined in the below states that for a string to satisfy some predicate, it should exhibit a certain “pattern" somewhere. The intuition underlying our definition is that in typical applications of bit commitments, the receiver will check whether the value of the opened commitments will cause it to accept.
Definition 3 (Pattern-predicate)
A pattern-predicate P on binary strings \(\{0,1\}^m\) (\(m \ge 1\)) can be represented by a triplet of functions \((\mathsf {val}(\cdot ), T(\cdot ), s(\cdot ))\), where given a candidate witness \(w \in \{0,1\}^{\text {poly}(m)}\) as input: \(\mathsf {val}(w)=1\) if w is a valid witness, and 0 otherwiseFootnote 19; T(w) is a subset of \(\left\{ 1, 2, \dots , m\right\} \); s(w) is a string of length \(\left| T(w) \right| \); all three functions \(\mathsf {val}(\cdot )\), \(T(\cdot )\), and \(s(\cdot )\) can be computed in \(\text{ poly }(m)\) time. A string \(str \in \{0,1\}^m\) satisfies the predicate P if there exists a (valid) witness \(w \in \{0,1\}^{\text {poly}(m)}\) satisfying \(\mathsf {val}(w)=1\) and \(str[T(w)] = s(w)\), where str[T(w)] denotes the substring obtained from the string str by projecting it on coordinates in the subset T(w).
Remark. Intuitively, a valid witness w for a string str guides us to find a pattern s(w) locating at positions specified by T(w) efficiently. This pattern will certify that the string str satisies the pattern-predicate P. However, it might be computationally hard to find a valid witness for a given string str.
In this work, for simplicity we often drop the prefix “pattern" and just write “predicate" to refer to a pattern-predicate. For a predicate P, it induces a subset P (by abusing the notation) of strings in \(\{0,1\}^m\) such that a string \(s \in P\) if and only if it satisfies the predicate P; we will identify a predicate as the subset induced by it. We say that two predicates \(P_1, P_2\) on the set \(\{0,1\}^m\) are inconsistent if \(P_1 \cap P_2 = \emptyset \); that is, no strings in \(\{0,1\}^m\) can satisfy both \(P_1\) and \(P_2\) simultaneously.
In a typical application of commitments within a larger protocol, at some stage of this protocol the party who plays the role of the possibly cheating sender of commitments will open commitments, and the party who plays the role of the honest receiver of commitments will do some verification. We note that it is this verification that natually induces a pattern-predicate. See the following example.
Example 1. Consider a running of Blum’s zero-knowledge protocol for the NP-complete language Hamiltonian Cycle, in which the verifier is honest while the prover might be cheating, and the common input graph G has n vertices. Let \(m = n^2\). Each graph with n vertices can be represented by an m-bit string. This running of Blum’s protocol induces two predicates on strings over \(\{0,1\}^m\), corresponding to the verifier’s verifications w.r.t. two possible challenges, respectively. In more detail, when the verifier’s challenge is 0, it will check that all bit commitments are opened as a graph that is isomorphic to the input graph. This induces a predicate \(P_0\) which consists of all graphs that are isomorphic to the input graph. Formally, the predicate \(P_0\) can be represented by a triplet of functions \((\mathsf {val}(\cdot ), T(\cdot ), s(\cdot ))\) such that: given a claimed permutation \(\pi \) over \(\left\{ 1, 2, \dots , n\right\} \), \(\mathsf {val}(\pi ) = 1\) if \(\pi \) indeed represents a valid permutation; \(T(\cdot ) \equiv \left\{ 1, 2, \dots , m\right\} \), and \(s(\pi ) = \pi (G)\). When the verifier’s challenge is 1, it will check that n (out of \(n^2\)) bit commitments are opened as all 1’s; moreover, these n positions (of opened bit commitments) should correspond to a possible location of a Hamiltonian cycle. This induces a predicate \(P_1\) which consists of all n-vertices graphs containing a Hamiltonian cycle. Formally, the predicate \(P_1\) can be represented by a triplet of functions \((\mathsf {val}(\cdot ), T(\cdot ), s(\cdot ))\) such that: given a claimed Hamiltonian cycle H, \(\mathsf {val}(H) = 1\) if H indeed represents a possible location of a Hamiltonian cycle; T(H) is set of coordinates corresponding to edges of H, and \(s(\cdot ) \equiv 1^n\). If the input graph is not Hamiltonian, then the two predicates \(P_0\) and \(P_1\) are obviously inconsistent.
Another example given below consider a simpler scenario, where a special form of pattern-predicates is introduced. In the sequel, we will study these special pattern-predicates first before more general ones.
Example 2. Consider the following scenario. The sender first commits to a string in a bitwise fashion. Later, all (bit) commitments will be opened, and the receiver (of commitments) will check whether the whole revealed string satisfies an efficiently computable predicate P in the common sense (i.e. a predicate which can be evaluated on any input string in polynomial time, rather than pattern-predicate introduced in this work). Let \(\mathsf {A}(\cdot )\) be an algorithm which runs in time \(\text {poly}(m)\) and can decide whether a string \(str \in \{0,1\}^m\) satisies P. We note that the predicate P can also be viewed as a pattern-predicate \((\mathsf {A}(\cdot ), T(\cdot ), s(\cdot ))\) where \(T(\cdot ) \equiv \left\{ 1, 2, \dots , m\right\} \) and \(s(\cdot )\) is the identity function; any string \(str \in P\) itself serves as its witness.
3.2 String Predicate-Binding
We first give an informal definition of the predicate-binding property of a quantum string commitment scheme, and then informally state we have achieved towards predicate-binding by composing a generic computationally-binding quantum bit commitment scheme in parallel. Last, we restate the definition of the predicate-binding w.r.t. the parallization of a generic computationally-binding quantum bit commitment scheme in a formal way for the purpose of proving predicate-binding in the sequel.
Definition 4 (Predicate-binding, informal)
Let \(P_1, P_2\) be two inconsistent pattern-predicates. We say that a quantum string commitment scheme is predicate-binding w.r.t. \((P_1, P_2)\) if any cheating sender, who can succeed in convincing the receiver that the committed value of the (claimed) quantum string commitment satisfies the predicate \(P_1\) with certainty, will fail to convince the receiver that the committed value satisfies the predicate \(P_2\) (except for a negligible probability). We say that a quantum string commitment scheme is predicate-binding if it is predicate-binding w.r.t. any pair of inconsistent predicates.
Remark. Classical commitments secure against classical attacks are trivially predicate-binding, simply because there is at most one string (i.e. the committed value) associated with each (claimed) commitment. However, this no longer holds w.r.t. either classical or quantum commitments secure against quantum attacks.
Restricting to consider the quantum string commitment scheme obtained by composing a generic computationally-binding quantum bit commitment scheme \((Q_0, Q_1)\) in parallel, our goal is to show that it is predicate-binding w.r.t. inconsistent pattern-predicates pairs that are general enough for our application (Sect. 4). Informally, we can prove a theorem as below. We highlight (again) that we do not achieve the full predicate-binding, which is left as an interesting open problem.
Theorem 2
Suppose that the quantum bit commitment scheme \((Q_0, Q_1)\) is computationally binding. Let \(P_1, P_2\) be two inconsistent predicates on the set \(\{0,1\}^m\) such that for (at least) one of them, the verification of whether an m-bit string satisfies it needs to examine the bits at some fixed positions of the string (regardless of the witness provided). Then the parallel composition of the scheme \((Q_0, Q_1)\) gives rise to a quantum string commitment scheme that is computationally predicate-binding w.r.t. \((P_1, P_2)\).
For the purpose of proving Theorem 2, now let us restate Definition 4 w.r.t. the parallization of a generic computationally-binding quantum bit commitment scheme in a more formal way.
Suppose that a cheating sender who is modeled as in Sect. 2.2 tries to convince the (honest) receiver that the committed value of a (claimed) quantum string commitment satisfies a predicate \(P = (\mathsf {val}(\cdot ), T(\cdot ), s(\cdot ))\), i.e. the (claimed) commitment can be opened in such a way that if w is a valid witness, then the bit commitments indexed by the subset T(w) are opened as the string s(w). The predicate P natually induces a projector P (also by abusing the notation) whose expression is given by

Its explanation follows. The summation is over all valid witnessesFootnote 20 for m-bit strings in \(P_1\); the quantum circuit \(Q_{s(w)}\) (whose meaning is referred to the equation (4)) performs on the copies of the quantum register pair \((\textsf {C}, \textsf {R})\) indexed by the subset T(w); in the reveal stage, the receiver will perform the binary measurement \(\left\{ P, \mathbbm {1}- P\right\} \) on its system to decide whether to accept or not. Hence, the sender’s success probability of convincing the receiver to accept is given by  , where recall that
, where recall that  is the quantum state of the whole system at the end of the commit stage and U is the sender’s operation in the reveal stage. We also note that the projector P is efficiently realizable, since all functions \(\mathsf {val}(\cdot )\), \(T(\cdot )\) and \(s(\cdot )\) are efficiently computable.
is the quantum state of the whole system at the end of the commit stage and U is the sender’s operation in the reveal stage. We also note that the projector P is efficiently realizable, since all functions \(\mathsf {val}(\cdot )\), \(T(\cdot )\) and \(s(\cdot )\) are efficiently computable.
Based on the expression (5), we can formalize the predicate-binding property of the parallelization of a generic quantum bit commitment scheme as follows.
Definition 5 (Predicate-binding w.r.t. the parallel composition of QBC)
Let \(P_1, P_2\) be two inconsistent pattern-predicates. We say that the quantum string commitment scheme obtained by composing a generic quantum bit commitment scheme \((Q_0, Q_1)\) in parallel is predicate-binding w.r.t. \((P_1, P_2)\) if  is negligible, where
is negligible, where  is an arbitrary state of registers \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and U could be any efficiently realizable unitary transformations that do not touch the quantum commitment (i.e. the commitment registers \(\textsf {C}^{\otimes m}\)). We say that this quantum string commitment scheme is predicate-binding if it is predicate-binding w.r.t. any pair of inconsistent pattern-predicates.
is an arbitrary state of registers \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and U could be any efficiently realizable unitary transformations that do not touch the quantum commitment (i.e. the commitment registers \(\textsf {C}^{\otimes m}\)). We say that this quantum string commitment scheme is predicate-binding if it is predicate-binding w.r.t. any pair of inconsistent pattern-predicates.
In the subsequent two subsections, we will prove Theorem 2. We will first establish predicate-binding w.r.t. a special form of inconsistent pattern-predicate pair (as formalized in Lemma 2), and then extend it to a general case (as formalized in Theorem 3).
3.3 Towards Predicate-Binding: A Special Case
We first restrict to consider pattern-predicates arising in Example 2 in Subsect. 3.1, and try to establish predicate-binding w.r.t. such a pair of inconsistent predicates.
By instantiating the predicate P in the Eq. (5) with the predicate of the form introduced in Example 2, the expression of the projector P will become

For any inconsistent predicate pair \((P_1, P_2)\) whose corresponding projectors \(P_1\) and \(P_2\) are both of the form (6), we can prove the following main technical lemma of this work.
Lemma 2
Suppose that the scheme \((Q_0, Q_1)\) is computationally \(\epsilon \)-binding for some arbitrary negligible function \(\epsilon (\cdot )\). Both predicates \(P_1 \) and \(P_2 \) are of the form given by the expression (6). Then for any quantum state  of registers \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and any efficiently realizable unitary transformation U that does not touch the commitment registers \(\textsf {C}^{\otimes m}\), we have
of registers \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and any efficiently realizable unitary transformation U that does not touch the commitment registers \(\textsf {C}^{\otimes m}\), we have  .
.
Proof
According to the expression (6), we can write


where for each \(s \not \in P_1\), we let \(\alpha _s = 0\) and  be arbitraryFootnote 21; moreover, the complex coefficients \(\alpha _s\)’s satisfy \(\sum _{s \in \{0,1\}^m} \left| \alpha _s \right| ^2 \le 1\). For convenience, we introduce the shorthand
be arbitraryFootnote 21; moreover, the complex coefficients \(\alpha _s\)’s satisfy \(\sum _{s \in \{0,1\}^m} \left| \alpha _s \right| ^2 \le 1\). For convenience, we introduce the shorthand

for each \(s \in \{0,1\}^m\). With these notations, our goal becomes to show

We will actually prove a strengthening of the inequality (10) by induction. Specifically, we will prove that for each k (\(0 \le k \le m\)) and each string \(x \in \{0,1\}^{m-k}\), it holds that

where \(\{0,1\}^k \circ x\) denotes the set of all m-bit strings with a suffix x of length \(m - k\). For each \(x \in \{0,1\}^{m-k}\) where \(0 \le k \le m\), if we view it as inducing an internal node/leaf of a binarty tree which corresponds to the summation  , then we will bound the (squared) norm of each internal node in a bottom-up way. Thus, the root of the tree will correspond to the case where \(k = m\) (then x becomes an empty string), i.e. l.h.s. of the inequality (10) without the squared norm. If we can prove the inequality (11), then plugging in \(k=m\) and the inequality \(\sum _{s \in \{0,1\}^m} \left| \alpha _s \right| ^2 \le 1\), we will arrive at the inequality (10).
, then we will bound the (squared) norm of each internal node in a bottom-up way. Thus, the root of the tree will correspond to the case where \(k = m\) (then x becomes an empty string), i.e. l.h.s. of the inequality (10) without the squared norm. If we can prove the inequality (11), then plugging in \(k=m\) and the inequality \(\sum _{s \in \{0,1\}^m} \left| \alpha _s \right| ^2 \le 1\), we will arrive at the inequality (10).
Now we are ready to prove the inequality (11) by induction on k, where \(0 \le k \le m\).
Base. We show that the inequality (11) holds when \(k=0\). In this case, x is a string of length m. Since the coefficient \(\alpha _x = 0\) for \(x \not \in P_1\), in which case the inequality (11) holds trivially, it suffices to fix an arbitrary \(x \in P_1\) and show that  . To this end, our technique is the perturbation that is similar to the quantum statistical binding setting [15]. Specifically, we will first show that the unit vector
. To this end, our technique is the perturbation that is similar to the quantum statistical binding setting [15]. Specifically, we will first show that the unit vector  is negligibly close to the (unnormalized) vector
is negligibly close to the (unnormalized) vector

where \(\bar{x}_i = 1 - x_i\), and the projector  performs on the i-the copy of the register pair \((\textsf {C}, \textsf {R})\). Second, we show that from the inconsistency of the predicate pair \((P_1, P_2)\), it follows that the vector \(| \tilde{\psi }_x \rangle \) is orthogonal to the subspace \(P_2\). Combining these two facts, we know that
performs on the i-the copy of the register pair \((\textsf {C}, \textsf {R})\). Second, we show that from the inconsistency of the predicate pair \((P_1, P_2)\), it follows that the vector \(| \tilde{\psi }_x \rangle \) is orthogonal to the subspace \(P_2\). Combining these two facts, we know that  is negligible. Detail follows.
is negligible. Detail follows.
We first show that  via a simple hybrid argument. Specifically, we introduce hybrids for each \(0 \le j \le m\) such that
via a simple hybrid argument. Specifically, we introduce hybrids for each \(0 \le j \le m\) such that  ; then
; then  and \(| \tilde{\psi }_x \rangle = \textsf {H}_m\). It suffices to show that any two adjacent hybrids are negligibly close: if this is true, then applying the triangle inequality of the operator norm m times will yield the desired bound.
and \(| \tilde{\psi }_x \rangle = \textsf {H}_m\). It suffices to show that any two adjacent hybrids are negligibly close: if this is true, then applying the triangle inequality of the operator norm m times will yield the desired bound.
Indeed, for each \(1 \le j \le m\),

where the last “<" follows from the quantum computational binding property by considering the j-th quantum bit commitment.
We then show that the (unnormalized) vector \(| \tilde{\psi }_x \rangle \) is orthogonal to the subspace \(P_2\), i.e. \(\big \Vert P_2 | \tilde{\psi }_x \rangle \big \Vert = 0\). This follows straightforwardly from the assumption that the predicate \(P_2\) is inconsistent with the predicate \(P_1\). In greater detail, for each \(s \in P_2\), we know that it is different from the string \(x \in P_1\); that is, there exists some index j (\(1 \le j \le m\)) such that \(s_j = \bar{x}_j\). Combining this with the Eq. (12), it follows that

Then summing over all \(s \in P_2\), we obtain

Combining  with \(\big \Vert P_2 | \tilde{\psi }_x \rangle \big \Vert = 0\), we arrive at
with \(\big \Vert P_2 | \tilde{\psi }_x \rangle \big \Vert = 0\), we arrive at  .
.
Induction. Now suppose that the inequality (11) holds for \(k-1\) and each binary string x of length \(m - (k-1)\). We are to show that it also holds for k and an arbitrary binary string x of length of \(m - k\).
For an arbitrary \(x \in \{0,1\}^{m-k}\), we first expand the l.h.s. of the inequality (11):

For convenience, we introduce shorthands

Without loss of generality, we can assume that all \(\alpha _{0x}, \alpha _{1x}, \alpha _x \ge 0\). With these notations, our goal (i.e. inequality (11)) becomes to show

and the induction hypothesis implies

The remainder of the analysis splits into two cases.
Case 1: either \(\alpha _{0x} = 0\) or \(\alpha _{1x} = 0\). Without loss of generality, we can assume that \(\alpha _{1x} = 0\). This implies that \(\alpha _{s'} = 0\) for each \(s' \in \{0,1\}^{k-1} \circ 1x\). Thus,

where the first “\(\le \)" uses the induction hypothesis.
Case 2: both \(\alpha _{0x} > 0\) and \(\alpha _{1x} > 0\). Following the inequality (13) and using the induction hypothesis, we have

We claim (refer to Claim 1 in the below) that the absolute value \((*)\) in the above can be bounded by \(2 \epsilon \). Then

The induction step is thus completed in both cases.
We finish the proof the inequality (11), and in turn the whole lemma.
We are left to prove the following claim, whose proof is referred to the full version of this paper [35].
Claim 1
The absolute value \((*)\) is less than \(2 \epsilon \).
3.4 Extension
By slightly adapting its proof, we can extend Lemma 2 so that it holds w.r.t. more general inconsistent predicate pairs (and thus could be useful in cryptographic applications). Specifically, we can prove Theorem 2. Now let us restate Theorem 2 in a more formal way.
Suppose that \((P_1, P_2)\) is an inconsistent pattern-predicate pair such that the predicate \(P_2\) is of the most general form as described by the Eq. (5). The predicate \(P_1\) is restricted to be such that the verification of whether an m-bit string satisfies it only needs to examine the bits at some fixed positions of the string (regardless of the witness provided). Formally, let \(T_1\) be the fixed subset that prescribes which bits are to examine for the verification of \(P_1\), and \(l = \left| T_1 \right| \). Then whether a string \(str \in \{0,1\}^m \) satisfies the predicate \(P_1\) actually only depends on its substring \(str[T_1]\). The predicate \(P_1\) in turn induces a predicate \(P_1[T_1]\) on the set \(\{0,1\}^l\) which consists of strings obtained by projecting strings in \(P_1\) on positions prescribed by the subset \(T_1\). Specifically, \(P_1 = (\mathsf {val}(\cdot ), T(\cdot ), s(\cdot ))\), where \(T(\cdot ) \equiv T_1\) and \(\left| s(\cdot ) \right| \equiv l\). Following the equation (5), the projector \(P_1\) can be written as


Then Theorem 2 can be restated as follows formally.
Theorem 3
Suppose that the scheme \((Q_0, Q_1)\) is computationally \(\epsilon \)-binding. Let \(P_1, P_2\) be two inconsistent predicates on the set \(\{0,1\}^m\), which induce two projectors of the form (15) and (5), respectively. Then for any quantum state  of registers \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and any efficiently realizable unitary transformation U that does not touch the commitment registers \(\textsf {C}^{\otimes m}\), we have
of registers \((\textsf {C}^{\otimes m}, \textsf {R}^{\otimes m}, \textsf {D}, \textsf {Z})\), and any efficiently realizable unitary transformation U that does not touch the commitment registers \(\textsf {C}^{\otimes m}\), we have  .
.
Due to the space limitation, an informal discussion on why such an extension as described in Theorem 2 (or formally Theorem 3) is possible, as well as the proof of Theorem 3 is referred to the full version of this paper [35].
4 Application: Quantum Zero-Knowledge Argument
In this section, we give an application of the quantum computationally predicate-binding string commitment scheme as shown in the proceeding section. Specifically, we show that Blum’s protocol for the NP-complete language Hamiltonian Cycle [5] with a generic quantum computationally-binding bit commitment scheme plugged in gives rise to a quantum zero-knowledge argument system. While its quantum (perfect or statistical) zero-knowledge property can be obtained by a straightforward application of Watrous’s quantum rewinding techniqueFootnote 22 [30, 32, 33, 36], its quantum computational soundness is established by Lemma 3 as stated below. Combing them we arrive at Theorem 1.
Lemma 3
Blum’s protocol for the language Hamiltonian Cycle with a generic quantum computationally-binding bit commitment scheme \((Q_0, Q_1)\) plugged in is sound against any quantum provers who are polynomial-time bounded, with soundness error \(1/2 + negl(\cdot )\).
Proof
This can be proved by instantiating Theorem 3 with proper predicates induced by Blum’s protocol. Detail follows.
Suppose that the binding error of the scheme \((Q_0, Q_1)\) is \(\epsilon (\cdot )\), which is a negligible function. We inherit notations as introduced in Subsect. 2.3. Following Subsect, 2.2, we can model a generic attack of the prover of Blum’s protocol in the following way. The combined (quantum) system of the (cheating) prover and the (honest) verifier is given by \((\textsf {P}, \textsf {D}, \textsf {C}^{\otimes n^2}, \textsf {R}^{\otimes n^2})\), where the \(n^2\) copies of the register pair \((\textsf {C}, \textsf {R})\) are used for (in total \(n^2\)) quantum bit commitments; the register D will hold the classical information of the prover’s response (i.e. the permutation \(\pi \) when the challenge \(b = 0\) or the location of a Hamiltonian cycle H when \(b = 1\)); the register P is the prover’s (private) workspace. Suppose that the whole system is initialized in the state  . The prover sends the quantum register \(\textsf {C}^{\otimes n^2}\) to the verifier as its first message. Then depending on the challenge b, the prover will perform some polynomial-time realizable unitary transformation \(U_b\) on the registers \((\textsf {P}, \textsf {D}, \textsf {R}^{\otimes n^2})\). After receiving the prover’s response, the verifier will perform some binary measurement, which also depends on the challenge b (as prescribed in the below), to decide to whether accept or not.
. The prover sends the quantum register \(\textsf {C}^{\otimes n^2}\) to the verifier as its first message. Then depending on the challenge b, the prover will perform some polynomial-time realizable unitary transformation \(U_b\) on the registers \((\textsf {P}, \textsf {D}, \textsf {R}^{\otimes n^2})\). After receiving the prover’s response, the verifier will perform some binary measurement, which also depends on the challenge b (as prescribed in the below), to decide to whether accept or not.
Formally, depending on the challenge b, the verifier’s accepting conditions induce two pattern-predicates, which in turn induces two efficiently realizable projectors/binary measurements as follows:
-
1.
The projector corresponding to \(b = 0\) is given by

-
2.
The projector corresponding to \(b = 1\) is given by
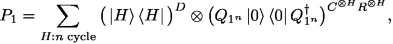
where the projector
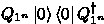 performs on the n copies of the register pair \((\textsf {C}, \textsf {R})\) that are determined by the location of the Hamiltonian cycle H.
performs on the n copies of the register pair \((\textsf {C}, \textsf {R})\) that are determined by the location of the Hamiltonian cycle H.
We highlight that here we implicitly assume that the verifier just performs a big binary measurement (induced by either \(P_0\) or \(P_1\)) to decide whether to accept or not; it in particular does not measure the register D to extract any classical information. It is easy to see that whether measuring the register D or not will not change the verifier’s acceptance probability. But by doing this, we are then allowed to apply the quantum rewinding lemma (Lemma 1).
Now we are ready to argue the quantum computational soundness of Blum’s protocol. Suppose for contradiction that there exists a efficiently realizable cheating prover given by  as aforementioned who can break the quantum computational soundness. Namely,
as aforementioned who can break the quantum computational soundness. Namely,

where c is some constant. Then applying the quantum rewinding lemma (Lemma 1), it follows that

On the other hand, we invoke Theorem 3 by doing the replacements as summarized in the following table:

In case that the input graph G is not Hamiltonian, the two predicates \(P_0\) and \(P_1\) are inconsistent. Applying Theorem 3 will yield an upper bound \(n^4 \epsilon ^2 + 3 n^2 \epsilon \) of the squared norm  , which is negligible. But this contradicts with the inequality (16).
, which is negligible. But this contradicts with the inequality (16).
We finish the proof of the lemma.
On Compositions. In this section, we only consider the stand-alone Blum’s protocol, whose soundness error is not tolerable in practice. It is not hard to see that if we compose it in sequence, it gives rise to a quantum perfect or statistical zero-knowledge arguments for NP with negligible soundness error (but at the cost of a significant increase of the round complexity). We may also consider composing Blum’s atomic protocol in parallel, which we believe can reduce the soundness error to be negligibleFootnote 23, too However, we do not known whether the parallelization preserves the quantum zero-knowledge property. Actually, the same problem is notorious hard w.r.t. classical zero-knowledge secure against quantum attacks [9, 22].
5 Conclusion
In this work, we show that the parallel composition of a generic quantum computationally-binding bit commitment scheme gives rise to a quantum string commitment scheme that is computationally predicate-binding, which is non-trivial and turns out to be useful in constructing quantum zero-knowledge arguments for NP languages. The main technical part of this work lies in establishing this quantum computational predicate-binding property.
Notes
- 1.
Actually, it is shown in [34] a much stronger result that any quantum bit commitment schemes just secure against the purification attack can be converted into a non-interactive one of the generic form. For this reason, in this paper we can focus on this generic form without loss of generality. At a very high level, the basis idea of how such a quantum round-collapse is possible is similar to the old idea of converting any non-interactive quantum bit commitment scheme into the generic form [15, 36].
- 2.
The round complexity of any cryptographic task might be one of the most important parameters.
- 3.
We do not claim that this holds w.r.t. a general quantum bit commitment. But any quantum bit commitment scheme can be converted to the generic form [34], as aforementioned.
- 4.
All mentioned above about the strictness of the quantum binding will become clear once one reads Definition 2, which is quite simple and intuitive.
- 5.
- 6.
Generally, the revealed value of a quantum string commitment could be a probability distribution over this set of strings.
- 7.
We note that the parallel composition of classical bit commitments secure against classical attacks gives a string commitment that is trivially predicate-binding secure against classical attacks. This is simply because the resulting string commitment (by the parallel composition) is bound to a unique classical string.
- 8.
As communicated by the authors of [12] recently [13], the definition of Q-binding in the conference version of [12] has a flaw: it misses an additional information z as another input of the predicate Q to make it efficiently computable, and the sentence “We do not require Q to be efficiently computable" there should be removed.
- 9.
Namely, the third assumption in [12, section “A General Framework"].
- 10.
This can be seen from the extractability of their commitments.
- 11.
It appears that even the reveal stage of the commitment scheme given in [19] also needs polynomial rounds of the interaction.
- 12.
For the moment, we drop the security parameter to simplify the notation.
- 13.
The formal definitions of a generic quantum bit commitment scheme and its computational binding propery are referred to Definition 2. Here for simplification, we neglect the auxiliary input state that the cheating sender may receive.
- 14.
For the moment, we can think of them as efficiently computable predicates in the common sense for simplicity.
- 15.
The tensor product m in superscripts indicates that there are m copies of the corresponding quantum register.
- 16.
The number of qubits in the state
 that are needed depends on the quantum circuit \(Q_0 (n)\) (or \(Q_1 (n)\)).
that are needed depends on the quantum circuit \(Q_0 (n)\) (or \(Q_1 (n)\)). - 17.
Informally speaking, this is a kind of security that turns out to be just slightly stronger than the semi-honest security yet much weaker than the full security.
- 18.
For example, consider a running of Blum’s zero-knowledge protocol for the language Hamiltonian Cycle in which the cheating prover responds to the challenge 1 of the verifier.
- 19.
Sometimes, it will be more covenient to identify the function \(\mathsf {val}(\cdot )\) as an algorithm that decides the validity of a candidate witness.
- 20.
We point out that a string in \(P_1\) may have multiple witnesses.
- 21.
Here, our purpose of introducing \(\alpha _s\) and
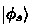 for \(s \not \in P_1\) is mainly for a cleaner way of writing the proof; it will not affect the places in the subsequent proof where the quantum computational binding property is applied.
for \(s \not \in P_1\) is mainly for a cleaner way of writing the proof; it will not affect the places in the subsequent proof where the quantum computational binding property is applied. - 22.
We highlight that in the literature we cite, various quantum zero-knowledge properties are based on different hiding properties of (classical or quantum) commitments (secure against quantum attacks) than the one considered in this work. However, their proofs extend to our setting straightforwardly, especially the proof of quantum zero-knowledge in [36].
- 23.
References
Adcock, M., Cleve, R.: A quantum Goldreich-Levin theorem with cryptographic applications. In: Alt, H., Ferreira, A. (eds.) STACS 2002. LNCS, vol. 2285, pp. 323–334. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45841-7_26
Ambainis, A., Rosmanis, A., Unruh, D.: Quantum attacks on classical proof systems: the hardness of quantum rewinding. In: FOCS, pp. 474–483 (2014)
Bartusek, J., Coladangelo, A., Khurana, D., Ma, F.: One-way functions imply secure computation in a quantum world. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12825, pp. 467–496. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84242-0_17
Bennett, C.H., Brassard, G.: Quantum cryptography: Public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, vol. 175 (1984)
Blum, M.: How to prove a theorem so no one else can claim it. In: Proceedings of the International Congress of Mathematicians, vol. 1, p. 2 (1986)
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Brassard, G., Crépeau, C.: Quantum bit commitment and coin tossing protocols. In: Menezes, A.J., Vanstone, S.A. (eds.) CRYPTO 1990. LNCS, vol. 537, pp. 49–61. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-38424-3_4
Chailloux, A., Kerenidis, I., Rosgen, B.: Quantum commitments from complexity assumptions. In: ICALP, no. 1, pp. 73–85 (2011)
Chia, N., Chung, K., Liu, Q., Yamakawa, T.: On the impossibility of post-quantum black-box zero-knowledge in constant rounds (2021). CoRR abs/2103.11244, https://arxiv.org/abs/2103.11244
Crépeau, C., Dumais, P., Mayers, D., Salvail, L.: Computational collapse of quantum state with application to oblivious transfer. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 374–393. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_21
Crépeau, C., Légaré, F., Salvail, L.: How to convert the flavor of a quantum bit commitment. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 60–77. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_5
Damgård, I., Fehr, S., Salvail, L.: Zero-knowledge proofs and string commitments withstanding quantum attacks. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 254–272. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_16
Damgård, I., Fehr, S., Salvail, L.: Private communication (2021)
Dumais, P., Mayers, D., Salvail, L.: Perfectly concealing quantum bit commitment from any quantum one-way permutation. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 300–315. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_21
Fang, J., Unruh, D., Yan, J., Zhou, D.: How to base security on the perfect/statistical binding property of quantum bit commitment? (2020). https://eprint.iacr.org/2020/621
Goldreich, O.: Foundations of Cryptography, Basic Tools, vol. I. Cambridge University Press, Cambridge (2001)
Goldreich, O., Micali, S., Wigderson, A.: Proofs that yield nothing but their validity or all languages in NP have zero-knowledge proof systems. J. ACM 38(3), 691–729 (1991)
van de Graaf, J.: Towards a formal definition of security for quantum protocols. PhD thesis, Université de Montréal (1997)
Grilo, A.B., Lin, H., Song, F., Vaikuntanathan, V.: Oblivious transfer is in MiniQCrypt. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12697, pp. 531–561. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_18
Haitner, I., Hoch, J.J., Reingold, O., Segev, G.: Finding collisions in interactive protocols - a tight lower bound on the round complexity of statistically-hiding commitments. In: FOCS, pp. 669–679 (2007)
Haitner, I., Nguyen, M.H., Ong, S.J., Reingold, O., Vadhan, S.P.: Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function. SIAM J. Comput. 39(3), 1153–1218 (2009)
Jain, R., Kolla, A., Midrijanis, G., Reichardt, B.W.: On parallel composition of zero-knowledge proofs with black-box quantum simulators. Quant. Inf. Comput. 9(5), 513–532 (2009)
Koshiba, T., Odaira, T.: Statistically-hiding quantum bit commitment from approximable-preimage-size quantum one-way function. In: Childs, A., Mosca, M. (eds.) TQC 2009. LNCS, vol. 5906, pp. 33–46. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10698-9_4
Koshiba, T., Odaira, T.: Non-interactive statistically-hiding quantum bit commitment from any quantum one-way function (2011). arXiv:1102.3441
Lo, H.K., Chau, H.F.: Why quantum bit commitment and ideal quantum coin tossing are impossible. Physica D Nonlinear Phenom. 120(1), 177–187 (1998)
Mahmoody, M., Pass, R.: The curious case of non-interactive commitments – on the power of black-box vs. non-black-box use of primitives. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 701–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_41
Mayers, D.: Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 78(17), 3414–3417 (1997)
Naor, M., Ostrovsky, R., Venkatesan, R., Yung, M.: Perfect zero-knowledge arguments for NP using any one-way permutation. J. Cryptol. 11(2), 87–108 (1998)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Informatioin. Cambridge University Press, Cambridge (2000)
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Unruh, D.: Collapse-binding quantum commitments without random oracles. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 166–195. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_6
Unruh, D.: Computationally binding quantum commitments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 497–527. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_18
Watrous, J.: Zero-knowledge against quantum attacks. SIAM J. Comput. 39(1), 25–58 (2009)
Yan, J.: General properties of quantum bit commitments (2020). https://eprint.iacr.org/2020/1488
Yan, J.: Quantum computationally predicate-binding commitment with application in quantum zero-knowledge argument for np. Cryptology ePrint Archive, Report 2020/1510 (2020). https://eprint.iacr.org/2020/1510
Yan, J., Weng, J., Lin, D., Quan, Y.: Quantum bit commitment with application in quantum zero-knowledge proof (extended abstract). In: Elbassioni, K., Makino, K. (eds.) ISAAC 2015. LNCS, vol. 9472, pp. 555–565. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48971-0_47
Yao, A.C.C.: Quantum circuit complexity. In: FOCS, pp. 352–361 (1993)
Acknowledgements
We thank Dominique Unruh for helpful and inspiring discussions on the strictness of the quantum binding property and the possibility of basing quantum zero-knowledge argument for NP on computationally-binding quantum bit commitments at an early stage of this work. We are also grateful to the anonymous referees of Crypto 2021, QCrypt 2021, and Asiacrypt 2021 for their corrections and useful suggestions for the presentation of this paper.
This work was supported by the National Natural Science Foundation of China (Grant No. 61602208, No. 61932019, No. 61772521, No. 62171202, No. 61771222, and No. 61772522), by the PhD Start-up Fund of Natural Science Foundation of Guangdong Province, China (Grant No. 2014A030310333), by the Key Research Program of Frontier Sciences, CAS (Grant No. QYZDB-SSW-SYS035), and by the Open Project Program of the State Key Laboratory of Information Security, IIE, CAS (Grant No. 2015-MS-08).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Yan, J. (2021). Quantum Computationally Predicate-Binding Commitments with Application in Quantum Zero-Knowledge Arguments for NP. In: Tibouchi, M., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2021. ASIACRYPT 2021. Lecture Notes in Computer Science(), vol 13090. Springer, Cham. https://doi.org/10.1007/978-3-030-92062-3_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-92062-3_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92061-6
Online ISBN: 978-3-030-92062-3
eBook Packages: Computer ScienceComputer Science (R0)





 ’s state
’s state ’s state. (This can be done by a measurement in the computational basis on each qubit that belongs to the registers (
’s state. (This can be done by a measurement in the computational basis on each qubit that belongs to the registers ( in auxiliary register
in auxiliary register 

 at the end of the commit stage, and sends the commitment registers
at the end of the commit stage, and sends the commitment registers 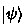 , respectively. Anyway, in this work we just restrict to consider the modeling as above for simplicity.
, respectively. Anyway, in this work we just restrict to consider the modeling as above for simplicity.
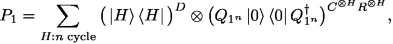
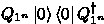 performs on the n copies of the register pair
performs on the n copies of the register pair  that are needed depends on the quantum circuit
that are needed depends on the quantum circuit 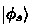 for
for 